Hydrogen-bond-modulated negative linear compressibility in a V-shaped molecular crystal

Abstract

A material with the “hidden” negative linear compressibility (NLC) will expand along a specific crystal direction upon uniformly compression to a critical pressure; such materials are thought to be promising candidates for non-linear actuators, switches and sensors. Herein, we use density functional theory (DFT) calculations to uncover the hidden NLC in a V-shaped molecular crystal, bis(5-amino-1,2,4-triazol-3-yl)methane (BATZM). The calculations indicate that the crystal is normally compressed over the pressure range of 0–3 GPa while it expands along the b-axis when the external hydrostatic pressure exceeds 3 GPa. The compressive behavior of the BATZM crystal is modulated by inter-molecular hydrogen bonds, which act as highly compressible springs at low pressures but robust struts at high pressures. Hence, the crystal prefers to compress the hydrogen bonds coupled with PLC at first and flatten the molecules, coupled with later NLC to resist the increasing external pressure. The compressive behavior of BATZM provides a strategy to design more hidden NLC materials via the rational use of the hydrogen bonds.

---

Introduction

The application of a uniform external force to conventional materials will cause them to shrink in all directions. However, some exceptions have been found in recent years that exhibit abnormal compression behaviors, i.e., so-called negative linear/area compressibility (NLC/NAC)^1,2 or zero linear/area compressibility (ZLC/ZAC);^3–8 these materials expand or remain unchanged along one or two directions under high hydrostatic pressure. Mechanical metamaterials with such fantastic properties are thought to be promising candidates for application in fields including deep-sea acoustic detection and ultra-sensitive optical sensors.^1,9,10

To date, known mechanisms for continuous NLC effects include (1) polyhedral rotation, (2) helices, (3) framework hinging and (4) layer sliding.^1,11 Polyhedral rotation usually occurs in inorganic systems that contain polyhedral atom groups, which rotate under high pressure to give rise to elongation along one crystal direction, such as the NLC effect in YFe(CN)₆, which arises from the rotation of YN₆ units.¹² The helix mechanism has been proposed in NLC effects in Se and Te.^1,13 Metal–organic frameworks or molecular frameworks exhibiting NLC mostly follow the framework hinging mechanism, in which geometrical deformation compensates for the bond shrinkage in their crystal structure under high pressure. Wine-rack and deformed honey-comb motifs are two typical crystal structure models that give rise to NLC properties.^14,15 The layer sliding mechanism is proposed in the case of Co(SCN)₂(pyrazine)₂, in which the pressure-driven sliding of 2D infinite-Co-pyrazine-layers leads to a moderate NLC effect.¹¹

Most reported NLC materials exhibit NLC behavior at the beginning of compression at ambient conditions because they possess rigid struts in their crystal structures. However, a few “normal” materials also exhibit NLC phenomena only when compressed to a critical pressure without a phase transition; this phenomenon is known as “hidden” NLC.^16–21 For example, the crystal of ammonium oxalate monohydrate shrinks along all directions at pressures below 5.1 GPa; thereafter, the c-axis begins to expand, which is explained by the pressure-induced strengthening of hydrogen bonds.²¹ Materials with hidden NLC are thought to be applicable as non-linear actuators, switches and sensors, as the NLC response is “off” at low pressures but can be switched “on” above a certain critical pressure.¹⁶ However, hidden NLC materials are very rare. Therefore, it is a vital issue to seek out more materials with these properties.

Our strategy to acquire hidden NLC materials is to focus on materials with weak interactions (such as van der Waals interactions and hydrogen bonds), which will be easily compressed at low pressure but could potentially be strengthened to a hard-to-compress level by pressure. The V-shaped organic molecule bis(5-amino-1,2,4-triazol-3-yl)methane (BATZM, C₅H₈N₈) aggregates to form a crystal via intermolecular N–H⋯N hydrogen bonds. The V-shaped molecule itself is naturally anisotropic and would exhibit an abnormal compressibility in one direction by reason of the closing/opening of the “V” angle driven by pressure. However, as the connector between two molecules, the original weak hydrogen bond acts as a buffer to help release the stress applied on the crystal, which delays the potential abnormal compressive behavior of the BATZM crystal to exhibit hidden NLC behavior. In this work, we have investigated the elastic constants and compressive behavior of the BATZM crystal under high pressure using density functional theory (DFT) calculations. The results show that BATZM exhibits a hidden NLC effect along the b-axis modulated by the hydrogen bond at pressures higher than 3 GPa. The findings demonstrate the feasibility of our strategy to identify materials with so-called hidden NLC, which should shed light on the discovery of other materials with such a fantastic property.

Computational details

The Vienna Ab initio Simulation Package (VASP)²² based on plane-wave pseudo potential methods was used to conduct the first-principles calculations of pressure-dependent lattice parameters on the basis of density functional theory (DFT). The reported experimental crystallographic data of BATZM was used as the initial structure model for geometrical optimization of the crystal structure. The calculations were performed using the projected augmented wave (PAW) formalism of the Kohn–Sham density functional theory with the generalized gradient approximation (GGA) for exchange correlation as given by Perdew, Burke, and Ernzerhof (PBE).^22–25 A kinetic energy cutoff of 700 eV was adopted for plane-wave pseudo-potential. Monkhorst–Pack k-point meshes with a grid density of 0.2 Å⁻¹ were used for structure optimizations to ensure that the total energy converged to within 1 meV per atom. Taking into account the fact that the hydrogen bonds have a key role in affecting the compressive behavior of this organic material, different van der Waals interaction correction methods were used for lattice relaxion at 0 GPa, after which the DFT dispersion correction with Becke–Johnson damping (DFT-D3(BJ))^26,27 van der Waals scheme was selected for further calculations.

Results and discussion

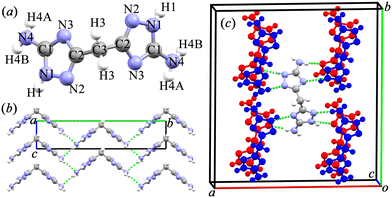
Experimentally, BATZM crystallizes in the orthogonal Fdd2 space group with lattice parameters of 18.632, 19.933 and 4.3095 Å for a-, b- and c-axis, respectively.²⁸ The X-ray structure of the V-shaped BATZM molecule with atom labels is shown in Fig. 1a. The molecule is two-fold axisymmetric with the symmetry axis parallel to the c-axis passing through the central C3 atom. BATZM molecules are stacked along the c-axis with a distance equalling the length of the c-axis, as shown in Fig. 1b. In the bc-plane, one BATZM molecule connects to four molecules via very weak intermolecular N4–H4B⋯N4 hydrogen bonds with an N4⋯N4 distance of 3.204 Å (shown as a dashed line in Fig. 1b). The end atom, N4, of the V-shaped molecule serves as a donor (D) and an acceptor (A) of two N4–H4B⋯N4 hydrogen bonds, respectively, forming one-dimensional zigzag hydrogen bond chains along the c-axis. In the ab-plane, one BATZM molecule connects to eight molecules in two adjacent sets via four N1H1⋯N3 and four N4H4A⋯N2 hydrogen bonds with D⋯A distances of 2.782 and 3.082 Å, respectively. Along the c-axis, i.e., the stacking direction of the BATZM molecules, there are no direct interactions between two parallel molecules, making the c-axis the most compressible direction under ambient conditions.

Fig. 1 (a) X-ray structure of the BATZM molecule with atom labels. (b) Zigzag hydrogen bond chains along the c-axis formed by one BATZM molecule connecting to four other BATZM molecules, viewed along the a-axis. (c) One BATZM molecule connecting with eight other BATZM molecules from neighbor sets through hydrogen bonds, viewed approximately along the c-axis. Only partial molecules are shown and molecules from different layers are distinguished by red/blue colors for clarity.

The experimental crystal structure data were used as the beginning model for full structural relaxation to obtain the ground state for BATZM at 1 atm. To take into account the effect of the hydrogen bonds on the compressive behavior of this organic material, different van der Waals interaction correction methods were used for lattice relaxions at 0 GPa, as shown in Table 1. The DFT dispersion correction with Becke–Johnson damping (DFT-D3(BJ)) van der Waals scheme gives the best description of the lattice parameters (especially the b-axis) and intermolecular N4⋯N4 distance in the N4–H4B⋯N4 hydrogen bond. DFT-D3(BJ) is selected for further high-pressure calculations. The calculated lattice parameters a = 18.3938, b = 19.9132 and c = 4.1998 Å at 0 GPa are in excellent agreement with experimentally reported values, with discrepancies of −1.28%, 0.10% and 2.54%, respectively.

Table 1 Comparison of calculated and experimental lattice parameters of BATZM

	a (Å)	b (Å)	c (Å)	N4⋯N4 distance (Å)
Expt.	18.6320	19.9330	4.3095	3.204
DFT-GGA	18.4504	20.2671	4.4751	3.323
DFT-D2	18.3641	20.5132	4.3157	3.277
DFT-D3	18.3640	20.5264	4.3203	3.280
DFT-D3(BJ)	18.3938	19.9132	4.1998	3.120
DFT-D4	18.3316	20.3767	4.4461	3.310
DFT-TS	18.3659	20.5228	4.3122	3.277
DFT-TS/HI	18.3606	20.5192	4.3184	3.279
DFT-dDsC	18.3534	20.5052	4.3162	3.277
optB86-vdW	18.3722	20.5277	4.3151	3.279
optPBE-vdW	18.3947	20.5415	4.3217	3.282
optB88-vdW	18.3700	20.5292	4.3158	3.279

---

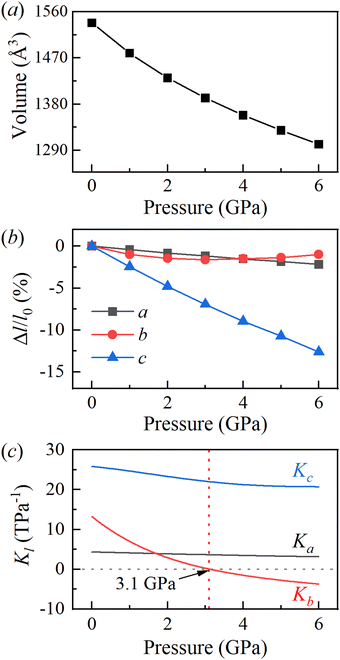
To investigate the mechanical response of BATZM to pressure, we applied hydrostatic pressures from 0 to 6 GPa in full lattice relaxations of BATZM with the DFT-D3(BJ) dispersion correction. No phase transitions occurred over the whole pressure range. The pressure-dependent cell volume data were fitted to a very smooth V(P) curve utilizing the third-order Birch–Murnaghan equation of state, calculated using PASCal,²⁹ as depicted in Fig. 2a. The fitting yields the zero-pressure bulk modulus B₀ with a value of 23.07 GPa, which is comparable to those of other hydrogen-bonded materials such as 3-methyl-4-nitropyridine N-oxide (B₀ = 23 GPa for phase-I).³⁰Fig. 2b shows the evolution of the relative change rates of the lattice parameters as a function of pressure. It is clearly seen that the BATZM crystal exhibits highly anisotropic compression, with the c-axis undergoing a remarkable reduction of about 12% up to 6 GPa, while the a-axis decreased by about 2%. Fantastically, below 3 GPa, the length of the b-axis decreased normally with increasing pressure, exhibiting a greater compressibility than that of the a-axis, but began to increase abnormally when the pressure was raised above 3 GPa, giving rise to an anomalous NLC behavior.

Fig. 2 Evolution of the (a) unit cell volume, (b) relative change rate and (c) linear compressibility of the lattice parameters as a function of pressure. All data were calculated with the DFT-D3(BJ) dispersion correction.

The online tool PASCal calculates linear compressibility based on the l–p curve fitted according to an empirical expression with the form l = l₀ + λ(p − p_c)^ν,²⁹ which is only applicable to those cases in which the length of the lattice parameter l changes monotonically as a function of pressure over the whole fitting pressure range. As the b-axis exhibited an increase after the initial decrease above 3 GPa, PASCal is inapplicable to calculate the linear compressibility of the b-axis, and hence we fitted the l–p curve to the fifth-order polynomial function l = a₀ + a₁p + a₂p² + ⋯ to obtain a highly smooth l–p curve,^31,32 as shown in Fig. S1 (ESI†), for linear compressibility calculations on the basis of −dl/(ldp). As depicted in Fig. 2c, the linear compressibility of the lattice parameters indicates a large mechanical anisotropy in the structure. The a-axis has a nearly constant compressibility with the value varying around 4 TPa⁻¹ over the whole compression process. The small K_a indicates that the a-axis is relatively hard to compress. The compressibility of the c-axis at 0 GPa is initially large with a value of about 26 TPa⁻¹, in accordance with the rapid shortening of inter-molecular distances. It is worth stressing that the compressibility of the b-axis is positive at the beginning of the compression process; however, it becomes negative after compression to a simulated pressure of about 3.1 GPa, as shown in Fig. 2c; hence, the b-axis increases with pressure in the pressure range of 3 to 6 GPa. The mean compressibility along the b-axis calculated using the formula K_l = −Δl/(l₀Δp) over the pressure range of 3–6 GPa is −2.0 TPa⁻¹, which is comparable to that of many known NLC materials, such as methanol monohydrate (K_a = −3.1 TPa⁻¹),³² silver(I) tricyanomethanide (K_a = −3.5 TPa⁻¹, K_c = −4.0 TPa⁻¹),³³ silver(I) 2-methylimidazolate (K_∼c = −4.32 TPa⁻¹),³⁴ ammonium oxalate monohydrate (K_b = −2.3 TPa⁻¹)²¹ and perovskite MOFs [NH₄][Zn(HCOO)₃] (K_c = −1.8 TPa⁻¹)³⁵ and [NH₂NH₃][Co(HCOO)₃] (K_b = −2.3 TPa⁻¹).³⁶ It is worth emphasizing that the PLC-to-NLC axis in other materials has the minimum change rate in length (namely the hardest axis) at low pressure.^{16,18–21,36,37} Taking ammonium oxalate monohydrate as an example, the PLC-to-NLC axis (b-axis) slightly contracted by about 0.1%, which was far less than the a-axis (∼2%) and c-axis (∼7%).¹⁹ In contrast, the b-axis in BATZM is not the hardest and contracts faster than the a-axis, as shown in Fig. 2b.

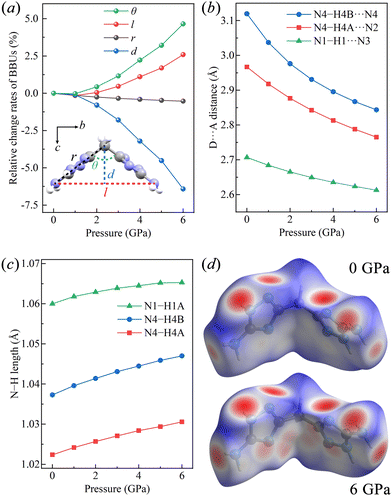
We then turned to the structural basic building unit (BBU)³⁴ parameters to elucidate the origin of the NLC along the b-axis of BATZM from 3 to 6 GPa. As depicted in the inset of Fig. 3a, two fundamental parameters r and θ are assigned to the length of two arms (i.e., C3⋯N4 distance) of the symmetrical V-shaped motif and hinge angle (i.e. C3⋯N4⋯C3) between two edges, respectively. The changes in r and θ cooperatively determine the deformations of two dependent parameters l and d, where l represents the opening distance of V-shape characterized by the intra-molecular N4⋯N4 distance and d (parallel to the c-axis) describes the height of the V-shape. It is clearly seen in Fig. 3a that r and θ remain nearly unchanged in the low-pressure (LP) region, especially from 0 to approximately 1 GPa and begin to change faster after 1 GPa; however, in the high-pressure (HP) region, r remains nearly unchanged while θ undergoes a tremendous rise. Therefore, l and d are invariable in the LP region, while in the HP region, l and d undergo a colossal increase and decrease, respectively, following geometrical relationships l = 2r sin(θ/2) and d = r cos(θ/2). As d is parallel to the c-axis, and l is approximately parallel to the b-axis, with discrepancies of 4.96° and 7.08° at 0 GPa and 6 GPa, respectively, the changes in the lengths of the b- and c-axes can be ascribed to the changes in l and d, respectively. The shortening of d leads to the continuous shrinkage of the c-axis during the entire compression process, while the elongation of l in HP dominates the abnormal expansion of the b-axis.

Fig. 3 (a) Relative change rates of BBUs as a function of pressure from 0 to 6 GPa. Evolution of the (b) D⋯A distance of hydrogen bonds and (c) N–H length as a function of pressure. (d) Hirshfeld surface of BATZM at ambient pressure (top) and 6 GPa (bottom). All data are calculated using the DFT-D3(BJ) dispersion correction.

The intermolecular hydrogen bonds were also monitored to comprehensively understand the variation in the lattice parameters. The hydrogen bonds in BATZM, including the intra- and inter-molecular ones, are all of the N–H⋯N type, as depicted in Fig. 1. Previous reports in the literature indicate that N–H⋯N bond lengths (N⋯N distances) vary from 2.526 to 3.793 Å and are distributed intensively around 2.98 Å.^38–41 The intermolecular N4–H4B⋯N4 interaction within the bc-plane (shown as a green dashed line in Fig. 1b) with an initial large D⋯A distance of 3.1198 Å is quite weak and highly compressible. As shown in Fig. 3b, N4–H4B⋯N4 is compressed dramatically in the LP region and later becomes stronger and harder to compress in the HP region due to the pressure-driven shortening of the D⋯A distance. The persistence of l and θ indicates the absence of geometrical deformation in the BATZM molecule in the LP region; therefore, the shrinkage of the b-axis in the LP region is mainly caused by N4–H4B⋯N4 shortening. In the HP region, N4–H4B⋯N4 is too robust to shrink drastically; hence, the increase in strain to balance the elevated external pressure is mainly generated from the opening effect of the V-shaped molecule. Thus, the BBU parameter θ begins to increase and NLC along the b-axis occurs, as shown in Fig. 3a. N4–H4A⋯N2 and N1–H1⋯N3 (Fig. 1c) are arranged mainly along the a-axis and hence determine the evolution of the length of this axis under pressure. At ambient pressure, the N⋯N distance in N1–H1⋯N3 is 2.7071 Å, which makes the hydrogen bond robust enough to avoid suffering tremendous contractions. The nearly incompressible N1–H1⋯N3 finally gives rise to a modest contraction of the a-axis.

It can be seen from Fig. 3c that all of N–H bonds in the three types of N–H⋯N hydrogen bonds simultaneously elongate under pressure as a result of the increased electrostatic interaction between the acceptor N and H, which demonstrates the enhancement of the hydrogen bonds.⁴² The elongation of D–H segments in enhanced hydrogen bonds is very common in hydrogen-bonded organics such as biurea,⁴³ glycinium oxalate⁴⁴ and sulfamide.⁴⁵ The Hirshfeld surface produced using CrystalExplorer was analysed to visualize intermolecular interactions, especially the hydrogen bonds.⁴⁶ As shown in Fig. 3d, red spots indicate contacts shorter than van der Waals radii, while white and blue regions represent distances equal to and longer than the van der Waals radii, respectively. At high pressure, H⋯N contacts are apparently intensified, as revealed by expanded red spots. The most prominent change occurs in N4–H4B⋯N4 (the two ends of the molecule), which is nearly invisible at ambient pressure (Fig. 3d, top) but becomes a large red spot in the left/right side of the Hirshfeld surface at 6 GPa (Fig. 3d, bottom). The 2D fingerprint of the N–H distance shown in Fig. S2 (ESI†) exhibits a prominent shift toward the origin, which also implies the shortening and consequent strengthening of N⋯H nonbonds.

A schematic of the mechanism of the abnormal mechanical behavior is depicted in Fig. 4. To simplify the V-shaped molecule and while preserving its main characteristics, two solid lines are used to represent rigid planar triazol groups linking end N atoms from amino groups and hinge C atom from the substituted methane group together. The original N4–H4B⋯N4 hydrogen bond is described as a relaxed spring. In the LP region, the initial relaxed spring is relatively weaker than the rigid BATZM molecule; hence, the former is more sensitive to external pressure stimuli. Under compression, the molecule tends to exhibit drastic shrinkage in the length of spring but hold its molecular shape at the same time. The drastic compression of the spring strengthens its stiffness from ambient pressure up to the critical pressure; the stiff spring changes subtly, and the flattening of the V-shaped BATZM molecule starts to be activated by the external pressure stimulus under higher pressures. The flattening of the molecular shape exceeds the sum of decreases in bond length and intermolecular distance in amplitude, resulting in NLC behavior along the b-axis.

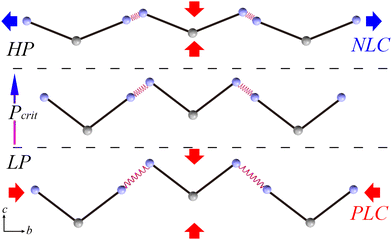Fig. 4 Schematic of the mechanism of the abnormal mechanical behavior along the b-axis of the BATZM crystal.

To investigate whether the hidden NLC is dispersion-correction-independent, we also performed full lattice relaxion without dispersion corrections over the pressure range of 0–10 GPa. The relative changes in the lattice parameters are shown in Fig. S3a (ESI†). The length of the b-axis first decreases and later starts to increase above 6 GPa, confirming the existence of the hidden NLC along the b-axis. However, the critical pressure for the PLC–NLC conversion is somewhat higher than obtained in the dispersion corrected results using DFT-D3(BJ). The change in the BBU parameter θ also exhibits such a delay: it changes very slightly over the pressure range of 0–3 GPa (Fig. S3b, ESI†) compared to the change in the range of 0–1 GPa in the DFT-D3(BJ) result. The uncorrected (by DFT-GGA) initial intermolecular N4⋯N4 distance at 0 GPa (3.323 Å) is longer than the DFT-D3(BJ) corrected one (3.120 Å), which plays as a key role in the conversion of PLC–NLC; the longer initial N4⋯N4 distance requires a higher pressure to compress it to an incompressible trend; hence, the uncorrected result shows a higher critical pressure (6 GPa) than the corrected result (3 GPa, DFT-D3(BJ)). Taking into account the fact that the experimental initial N4⋯N4 distance (3.204 Å at ambient condition) is intermediate between those of DFT-GGA and DFT-D3(BJ), the experimentally observed critical pressure for the conversion of PLC–NLC may presumably fall in between 3 and 6 GPa.

Conclusions

In conclusion, we have investigated the compressive behavior of BATZM from 0 to 6 GPa using DFT calculations with dispersion correction (DFT-D3(BJ)). The linear compressibility of the b-axis of the BATZM crystal is positive at low pressure, but becomes negative when the external pressure surpasses the critical pressure of 3 GPa. This is the first material for which the potential NLC axis is not the hardest axis under ambient conditions. The intermolecular hydrogen bonds arranged parallel mainly to the bc-plane serve as the key to modulate the compressive behavior of the b-axis. They act as easily compressed springs at low pressure but robust struts at high pressure. Hence, the crystal increases the internal stress to resist the applied external pressure by compressing the hydrogen bonds at low pressure and flattens the molecules at high pressure, respectively. Another set of DFT calculations without any dispersion correction confirms the existence of the hidden NLC. The discovery of the hidden NLC (PLC-to-NLC) in BATZM provides a strategy to design and search for more materials with such properties by rationally using the hydrogen bond, which will also of great benefit for the applications of such metamaterials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge funding from the National Natural Science Foundation of China (NSFC) (no. 12004144, 12074154, and 11722433), Science and Technology Project of Xuzhou (no. KC19010), Six Talent Peaks Project and 333 High-Level Talents Project of Jiangsu Province, Natural Science Foundation of Colleges and Universities in Jiangsu Province (no. 20KJB140018), Open Project of State Key Laboratory of Superhard Materials, Jilin University (no. 202009), Scientific Research Program for Doctoral Teachers of JSNU (no. 19XSRX017) and Postgraduate Research & Practice Innovation Program of Jiangsu Normal University (no. 2022XKT1329). All the calculations were performed at the High-Performance Computing Center of the School of Physics and Electronic Engineering of Jiangsu Normal University.

References

1. A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465.
2. Q. Zeng, K. Wang and B. Zou, Langmuir, 2022, 38, 9031–9036.
3. Q. Zeng, W. Qiu, J. Hao, K. Wang and Y. Li, ACS. Mater. Lett., 2022, 4, 541–547.
4. X. Jiang, Y. Yang, M. S. Molokeev, P. Gong, F. Liang, S. Wang, L. Liu, X. Wu, X. Li, Y. Li, S. Wu, W. Li, Y. Wu and Z. Lin, Adv. Mater., 2018, 30, e1801313.
5. Q. Zeng, K. Wang and B. Zou, ACS Appl. Mater. Interfaces, 2018, 10, 23481–23484.
6. D. Jiang, T. Wen, H. Song, Z. Jiang, C. Li, K. Liu, W. Yang, H.-K. Mao and Y. Wang, CCS Chem., 2022, 4, 3246–3253.
7. W. Qiu, Q. Zeng, C. Li, J. Hao and Y. Li, J. Phys. Chem. C, 2023, 127, 9957–9963.
8. X. Zhang, Y. Liu, M. S. Molokeev, B. Xu, X. Jiang and Z. Lin, Angew. Chem., Int. Ed., 2024, 63, e202318401.
9. A. L. Goodwin, D. A. Keen and M. G. Tucker, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 18708–18713.
10. R. H. Baughman, Nature, 2003, 425, 667.
11. Q. Zeng, K. Wang, Y. Qiao, X. Li and B. Zou, J. Phys. Chem. Lett., 2017, 8, 1436–1441.
12. S. G. Duyker, V. K. Peterson, G. J. Kearley, A. J. Studer and C. J. Kepert, Nat. Chem., 2016, 8, 270–275.
13. R. Keller, W. B. Holzapfel and H. Schulz, Phys. Rev. B: Condens. Matter Mater. Phys., 1977, 16, 4404–4412.
14. Q. Zeng, K. Wang and B. Zou, ACS. Mater. Lett., 2020, 2, 291–295.
15. Q. Zeng, K. Wang and B. Zou, J. Am. Chem. Soc., 2017, 139, 15648–15651.
16. H. H. Yeung, R. Kilmurray, C. L. Hobday, S. C. McKellar, A. K. Cheetham, D. R. Allan and S. A. Moggach, Phys. Chem. Chem. Phys., 2017, 19, 3544–3549.
17. Y. Zhao, C. Fan, C. Pei, X. Geng, G. Xing, T. Ben and S. Qiu, J. Am. Chem. Soc., 2020, 142, 3593–3599.
18. M. Szafrański, J. Phys. Chem. C, 2020, 124, 11631–11638.
19. E. L. Harty, A. R. Ha, M. R. Warren, A. L. Thompson, D. R. Allan, A. L. Goodwin and N. P. Funnell, Chem. Commun., 2015, 51, 10608–10611.
20. P. S. Ghosh and I. Ponomareva, J. Phys. Chem. Lett., 2022, 13, 3143–3149.
21. Y. Qiao, K. Wang, H. Yuan, K. Yang and B. Zou, J. Phys. Chem. Lett., 2015, 6, 2755–2760.
22. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
23. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
24. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
26. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
27. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
28. H. Li, B. Yan, H. Ma, Z. Sun, Y. Ma and Z. Zhang, Acta Crystallogr., Sect. C, 2020, 76, 64–68.
29. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
30. W. Cai, J. He, W. Li and A. Katrusiak, J. Mater. Chem. C, 2014, 2, 6471–6476.
31. D. R. McCann, L. Cartz, R. E. Schmunk and Y. D. Harker, J. Appl. Phys., 1972, 43, 1432–1436.
32. A. D. Fortes, E. Suard and K. S. Knight, Science, 2011, 331, 742–764.
33. S. A. Hodgson, J. Adamson, S. J. Hunt, M. J. Cliffe, A. B. Cairns, A. L. Thompson, M. G. Tucker, N. P. Funnell and A. L. Goodwin, Chem. Commun., 2014, 50, 5264–5266.
34. J. M. Ogborn, I. E. Collings, S. A. Moggach, A. L. Thompson and A. L. Goodwin, Chem. Sci., 2012, 3, 3011–3017.
35. W. Li, M. R. Probert, M. Kosa, T. D. Bennett, A. Thirumurugan, R. P. Burwood, M. Parinello, J. A. Howard and A. K. Cheetham, J. Am. Chem. Soc., 2012, 134, 11940–11943.
36. P. S. Ghosh and I. Ponomareva, J. Phys. Chem. Lett., 2021, 12, 7560–7565.
37. C. J. McMonagle, P. Comar, G. S. Nichol, D. R. Allan, J. González, J. A. Barreda-Argüeso, F. Rodríguez, R. Valiente, G. F. Turner, E. K. Brechin and S. A. Moggach, Chem. Sci., 2020, 11, 8793–8799.
38. W. Fuller, J. Phys. Chem., 1959, 63, 1705–1717.
39. L. N. Kuleshova and P. M. Zorkii, Acta Crystallogr., Sect. B, 1981, 37, 1363–1366.
40. Z. Malarski, L. Sobczyk and E. Grech, J. Mol. Struct., 1988, 177, 339–349.
41. O. Knop, K. N. Rankin and R. J. Boyd, J. Phys. Chem. A, 2001, 105, 6552–6566.
42. J. Joseph and E. D. Jemmis, J. Am. Chem. Soc., 2007, 129, 4620–4632.
43. T. Yan, K. Wang, X. Tan, K. Yang, B. Liu and B. Zou, J. Phys. Chem. C, 2014, 118, 15162–15168.
44. H. Bhatt, C. Murli, A. K. Mishra, A. K. Verma, N. Garg, M. N. Deo, R. Chitra and S. M. Sharma, J. Phys. Chem. B, 2016, 120, 851–859.
45. K. Wang, J. Liu, K. Yang, B. Liu and B. Zou, J. Phys. Chem. C, 2014, 118, 18640–18645.
46. M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32.

---

Footnote

† Electronic supplementary information (ESI) available: Lattice parameter–pressure curve fitting, 2D fingerprint of N–H distance. See DOI: https://doi.org/10.1039/d4cp01102c

---