 Open Access Article
Open Access ArticleBenchmark ab initio characterization of the complex potential energy surfaces of the HOO− + CH3Y [Y = F, Cl, Br, I] reactions†
Domonkos A.
Tasi
 * and
Gábor
Czakó
* and
Gábor
Czakó
 *
*
MTA-SZTE Lendület Computational Reaction Dynamics Research Group, Interdisciplinary Excellence Centre and Department of Physical Chemistry and Materials Science, Institute of Chemistry, University of Szeged, Rerrich Béla tér 1, Szeged H-6720, Hungary. E-mail: dtasi@chem.u-szeged.hu; gczako@chem.u-szeged.hu
First published on 7th May 2024
Abstract
The α-effect is a well-known phenomenon in organic chemistry, and is related to the enhanced reactivity of nucleophiles involving one or more lone-pair electrons adjacent to the nucleophilic center. The gas-phase bimolecular nucleophilic substitution (SN2) reactions of α-nucleophile HOO− with methyl halides have been thoroughly investigated experimentally and theoretically; however, these investigations have mainly focused on identifying and characterizing the α-effect of HOO−. Here, we perform the first comprehensive high-level ab initio mapping for the HOO− + CH3Y [Y = F, Cl, Br and I] reactions utilizing the modern explicitly-correlated CCSD(T)-F12b method with the aug-cc-pVnZ [n = 2–4] basis sets. The present ab initio characterization considers five distinct product channels of SN2: (CH3OOH + Y−), proton abstraction (CH2Y− + H2O2), peroxide ion substitution (CH3OO− + HY), SN2-induced elimination (CH2O + HY + HO−) and SN2-induced rearrangement (CH2(OH)O− + HY). Moreover, besides the traditional back-side attack Walden inversion, the pathways of front-side attack, double inversion and halogen-bond complex formation have also been explored for SN2. With regard to the Walden inversion of HOO− + CH3Cl, the previously unaddressed discrepancies concerning the geometry of the corresponding transition state are clarified. For the HOO− + CH3F reaction, the recently identified SN2-induced elimination is found to be more exothermic than the SN2 channel, submerged by ∼36 kcal mol−1. The accuracy of our high-level ab initio calculations performed in the present study is validated by the fact that our new benchmark 0 K reaction enthalpies show excellent agreement with the experimental data in nearly all cases.
I. Introduction
Theoretical and experimental investigations of the gas-phase bimolecular nucleophilic substitution (SN2) reactions have gained increasing prominence since the 1970s.1–10 In step with the progress of computational chemistry and experimental methodology,11–16 the initially conceived simple picture of the elemental SN2 reactions has been found to be incomplete, as it became apparent that along with the traditional Walden inversion and front-side attack, several alternative mechanisms may also occur depending on the reactants and the reaction conditions.17–21Transcending the conventional reactions between halide ions and methyl halides, our understanding of SN2 was also reshaped by the examination of reactions involving HO−.22–38 In 2002, Sun et al. investigated the HO− + CH3F SN2 reaction by performing direct dynamics simulations and revealed that the reaction avoids the region of the deep H-bonded CH3OH⋯F− minimum in the exit channel.22 Since then, other theoretical studies have uncovered a novel oxide ion substitution for the HO− + CH3F reaction utilizing quasi-classical trajectory (QCT), as well as, direct dynamics calculations.39–41 Over the years, the primary focus has been on the dynamical characterization of the HO− + CH3I reaction.42–48 Wester and co-workers examined several SN2 reactions experimentally, including HO− + CH3I, with the crossed-beam ion-imaging technique.10,14,49 Direct dynamics simulations were also performed by Hase and co-workers, paving the way for comprehensive experimental–theoretical studies of the HO− + CH3I reaction.50–52 Furthermore, the present authors developed several global analytical ab initio potential energy surfaces (PESs) for HO− + CH3I at seven different levels of theory using the in-house ROBOSURFER program package.53,54 Afterwards, on the final PES, which was confirmed to be the most suitable for further investigations, more than half a million trajectories were computed, comparing the results with the results of revised crossed-beam experiments in order to analyze the dynamics of the reaction in a more detailed manner.55 Recently, the mode specificity in the dynamics of the reaction was also studied at several collision energies by exciting certain vibrational modes of the reactants.56,57
Besides considering di- or polyatomic ‘normal’ nucleophiles (e.g., HO−, CN−, NH2−, PH2−etc.),10,24,58–63 a significant emphasis has been placed on α-nucleophiles (e.g., HOO−, ClO−, BrO−, CH3OO−, HOHN−, NH2O−, etc.) participating in SN2 reactions.8,9,64–71 In the case of these α-nucleophiles, one or more lone-pair electrons are located on the atom adjacent to the nucleophilic center, inducing enhanced reactivity compared to that expected from the Brønsted-type correlation.72 This phenomenon is known as the α-effect.73 While the existence of the α-effect was beyond doubt in solution, the situation was not as clearly defined in the gas phase.72,74,75 By comparing the branching ratios for the reactions of HO− and HOO− with methyl formate, DePuy and co-workers concluded that HOO− does not show the α-effect in the gas phase.76 In addition, Villiano et al. unveiled that a noticeable α-effect cannot be observed for the HOO−/ClO−/BrO− + CH3R (R = CH3, CH3CH2, etc.) systems, as well.65 In contrast, the opposite of these findings has been confirmed, and several studies have verified that the α-effect stems from the intrinsic properties of α-nucleophiles validating the manifestation of this phenomenon in the gas phase.77–85 However, the identification of these intrinsic properties of α-nucleophiles remained disputed.86–93 Recently, Hamlin et al. reported an extensive theoretical survey on the origin of the α-effect in the gas phase.71 They employed the activation strain model of reactivity in combination with Kohn–Sham molecular orbital theory and arrived at the conclusion that the adjacent atom of α-nucleophiles induces a reduction in Pauli repulsion between the reactants by polarizing orbital density away from the nucleophilic center. As a result, an enhancement of the reactivity can be obtained for α-nucleophiles compared to their ‘normal’ counterparts.
Regarding SN2 reactions involving HOO−, several theoretical investigations have concentrated on the stationary-point and dynamical characterization, as well.74,88,94–97 In the course of the aforementioned α-effect examinations, the stationary points of the corresponding Walden-inversion pathways were determined for several SN2 reactions of HOO− at various levels of theory. The HOO−⋯CH3Y → [HOO⋯CH3⋯Y]− → CH3OOH⋯Y− path was explored by Evanseck et al. for Y = Cl at the level of HF/6-31+G(d).74 Later, in the theoretical surveys of Ren et al., the geometries of the [HOO⋯CH3⋯Y]− transition states were optimized in the case of Y = F and Cl at the MP2/6-31+G(d) level of theory, and the corresponding energies were determined with the G2(+) method.78,79 Associated with the microsolvated variants of the HOO− + CH3Cl SN2 reaction, the unsolvated Walden-inversion pathways were also characterized in the studies of Thomsen et al.88 and Hu et al.97 utilizing the MP2/6-311++G(d,p) level of theory in combination with G3 and CCSD(T)/aug-cc-pVTZ energy calculations, respectively. The most thorough ab initio mapping was achieved by Wu et al. in the case of the HOO−(H2O)n + CH3Y [Y = F, Cl, Br, I; n = 0, 1, 2] SN2 reactions, whereby they identified two H-bonded stationary points in the entrance channel, as well.96 The dynamics of the HOO−(H2O)n + CH3Cl reactions, where n = 0 or 1, was also examined with direct dynamics simulations.94,95 It is noteworthy that, based on the earlier work of Anick et al.,98 the only stable structure for the singly hydrated hydroperoxide ion is HO−(HOOH), which indicates that in the SN2 reaction with CH3Cl, two distinct pathways may be possible, leading to the CH3OOH + Cl− + H2O and CH3OH + Cl− + H2O2 products. Recently, dynamics simulations performed by Zhao et al.95 have substantiated that both reaction routes are viable, indicating the fact that a single solvent water molecule can induce a new nucleophile in SN2 reactions, which opens the door for an alternative pathway. Moreover, for the unsolvated HOO− + CH3Cl reaction, similar to the case of ClO− + CH3Cl,65,69 a novel non-SN2 pathway generating the CH2O + HCl + HO− products was also unveiled. Besides the dynamical description, the PES of the considered product channels of the HOO− + CH3Cl reaction was mapped at the MP2/6-31+G(d,p) level of theory.95
In the present work, based on the prominent attention paid to the SN2 reactions involving hydroperoxide ions, we perform a comprehensive benchmark ab initio characterization of HOO− + CH3Y [Y = F, Cl, Br and I] using the explicitly-correlated CCSD(T)-F12b method with the aug-cc-pVnZ [n = 2 (D), 3 (T) and 4 (Q)] basis sets. Besides the traditional Walden-inversion path, we analyze the halogen-bonded complex mechanism48 and the possible SN2 retention routes of front-side attack and double inversion.19 We identify the stationary points of the proton-abstraction channel, as well; furthermore, relying on the previous study of Xie and co-workers,95 our high-level stationary-point mapping also considers other possible pathways. Detailed insights into the applied ab initio methods can be found in Section II. In the subsequent Section III, a comprehensive description and discussion of the results are presented, followed by a brief summary of the work in Section IV.
II. Computational details
The stationary points of the title reactions are searched and preoptimized using the second-order Møller–Plesset perturbation theory (MP2)99 with the augmented correlation-consistent polarized-valence-double-ζ (aug-cc-pVDZ) basis set.100 The exploration of the stationary points was conducted based on previous studies and chemical intuition;24,38,95 nevertheless, it is important to note that automated methods and approaches for identifying reaction pathways and stationary points in chemical reactions are becoming more and more prevalent.101–103 Thereafter, in order to attain more accurate geometries, energies and harmonic frequencies for the stationary points, the explicitly-correlated coupled-cluster singles, doubles, and perturbative triples (CCSD(T)-F12b) method104–106 is utilized with the aug-cc-pVDZ and aug-cc-pVTZ basis sets.100 To achieve a more in-depth mapping, intrinsic reaction coordinate (IRC) computations are also carried out from the saddle points at the MP2/aug-cc-pVDZ level of theory. In order to avoid any spurious stationary point, it is important to note that for all geometry optimizations, the default (3 × 10−4) required accuracy of the optimized gradient is changed to 10−5 in atomic units. Small-core relativistic effective core potentials (ECPs)107 are employed for Br and I, and the aug-cc-pVnZ-PP [n = 2–4] basis sets are applied to replace the inner-core 1s2 2s2 2p6 (Br) and 1s2 2s2 2p6 3s2 3p6 3d10 (I) electrons. For the stationary points identified in the present work, the computed T1-diagnostic values are below 0.02 in every case, except for FSTS and FSTS2 (see Fig. 1), where the values are between 0.02 and 0.04, validating that the multi-reference character is not a probable issue for the HOO− + CH3Y [Y = F, Cl, Br and I] systems. The benchmark classical (adiabatic) relative energies are computed for the CCSD(T)-F12b/aug-cc-pVTZ structures as follows:| ΔE[CCSD(T)-F12b/aug-cc-pVQZ] (+ΔZPE[CCSD(T)-F12b/aug-cc-pVTZ]), | (1) |
III. Results and discussion
The complex PESs of the HOO− + CH3Y [Y = F, Cl, Br and I] reactions showing the benchmark classical (adiabatic) relative energies of the stationary points along the considered pathways are presented in Fig. 1. The ab initio energies determined at the MP2/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVnZ [n = 2, 3 and 4] levels of theory are summarized in Tables 1 and 2. Taking a cue from previous studies on the HOO−/ClO− + CH3Cl and HO− + CH3F reactions,40,65,69,95 in addition to the typical SN2 (CH3OOH + Y−) and proton-abstraction (CH2Y− + H2O2) routes, alternative channels of peroxide ion substitution (CH3OO− + HY), SN2-induced elimination (CH2O + HY + HO−) and SN2-induced rearrangement (CH2(OH)O− + HY) are also analyzed. It should be noted that in the case of the HOO− + CH3Cl reaction, the dynamical characterization reported by Xie and co-workers did not reveal the existence of the corresponding peroxide ion substitution, SN2-induced rearrangement and proton abstraction, presumably, due to the fact that overall 1154 trajectories were run at one sole collision energy of 0.9 kcal mol−1.95 However, the pathways of peroxide ion substitution and SN2-induced rearrangement were also considered in the course of their stationary-point survey.| HOO− + CH3F | MP2 | CCSD(T)-F12b | ΔZPEe | Adiabaticf | ||
|---|---|---|---|---|---|---|
| DZa | DZb | TZc | QZd | |||
| a MP2/aug-cc-pVDZ. b CCSD(T)-F12b/aug-cc-pVDZ. c CCSD(T)-F12b/aug-cc-pVTZ. d CCSD(T)-F12b/aug-cc-pVQZ at CCSD(T)-F12b/aug-cc-pVTZ geometry. e ΔZPE(CCSD(T)-F12b/aug-cc-pVTZ). f QZ + ΔZPE. g CCSD(T)-F12b/aug-cc-pVDZ geometry and frequencies. h MP2/aug-cc-pVDZ geometry and frequencies. | ||||||
| HMIN1 | −14.41 | −13.95 | −13.69 | −13.47 | 1.09 | −12.38 |
| HTS1 | −14.00 | −13.49 | −13.32 | −13.15 | 0.67 | −12.49 |
| PreMIN | −14.45 | −14.01 | −13.80 | −13.59 | 0.84 | −12.74 |
| WaldenTS | −6.77 | −3.37 | −3.44 | −3.27 | 0.66 | −2.61 |
| FSTS1 | 29.87 | 33.40 | 33.50 | 33.87 | 0.25 | 34.12 |
| FSTS2 | 25.76 | 29.26 | 29.28 | 29.64 | 0.59 | 30.23 |
| DITS | 21.68 | 21.81 | 22.37 | 22.72 | −0.37 | 22.35 |
| PostHMIN | −53.64 | −50.43 | −49.99 | −49.74 | 1.11 | −48.63 |
| WaldenPostHMIN | −32.77 | −28.62 | −28.08 | −27.91 | 1.26 | −26.65 |
| ABSTS | −11.38 | −11.00 | −10.71g | −10.52g | 0.44g | −10.08g |
| ABSMIN2 | 12.34 | 12.43 | 13.00 | 13.37 | 0.28 | 13.65 |
| PostTS | −28.42 | −23.65 | −22.93 | −22.62 | −2.89 | −25.51 |
| PostDHMIN | −127.02 | −121.31 | −120.63 | −120.45 | 4.07 | −116.38 |
| HOO− + CH3Cl | MP2a | DZb | TZc | QZd | ΔZPEe | Adiabaticf |
|---|---|---|---|---|---|---|
| HMIN1 | −17.02 | −16.26 | −16.14 | −15.97 | 0.89 | −15.08 |
| HTS1 | −16.57 | −15.78 | −15.74 | −15.62 | 0.62 | −15.00 |
| HTS2 | −15.45 | −15.04 | −14.98 | −14.82 | 0.59 | −14.23 |
| FSMIN | −1.81 | −3.25 | −2.87 | −2.73 | 0.47 | −2.27 |
| HBTS | 1.54 | 0.80 | 1.06g | 1.14g | 0.26g | 1.40g |
| PreMIN | −16.35 | −15.73 | −15.72 | −15.57 | 0.79 | −14.78 |
| WaldenTS | −14.39 | −13.03 | −13.33 | −13.24 | 0.62 | −12.62 |
| FSTS1 | 18.84 | 19.20 | 19.19 | 19.40 | 0.48 | 19.88 |
| FSTS2 | 18.12 | 17.44 | 17.80 | 18.07 | 0.85 | 18.93 |
| DITS | 9.64 | 9.13 | 9.61 | 9.82 | −0.02 | 9.81 |
| PostHMIN | −68.49 | −65.91 | −65.58 | −65.61 | 3.26 | −62.34 |
| WaldenPostHMIN | −57.10 | −53.75h | −53.44h | −53.55h | 2.48h | −51.07h |
| ABSTS | −14.49 | −13.79 | −13.59 | −13.43 | 0.45 | −12.98 |
| ABSMIN2 | 3.08 | 2.71 | 3.03 | 3.23 | 0.52 | 3.75 |
| PostTS | −38.33 | −27.93 | −27.17 | −27.01 | −3.75 | −30.76 |
| PostDHMIN | −141.29 | −136.29 | −135.89 | −136.00 | 5.14 | −130.86 |
| HOO− + CH3Br | MP2a | DZb | TZc | QZd | ΔZPEe | Adiabaticf |
|---|---|---|---|---|---|---|
| HMIN1 | −17.61 | −17.21 | −16.92 | −16.74 | 0.74 | −15.99 |
| HMIN2 | −17.22 | −16.57h | −16.18h | −15.97h | 0.82h | −15.15h |
| HTS1 | −17.13 | −16.72 | −16.49 | −16.35 | 0.54 | −15.81 |
| HTS2 | −15.90 | −15.92 | −15.71 | −15.53 | 0.42 | −15.11 |
| FSMIN | −10.48 | −11.07 | −10.89 | −10.76 | 0.37 | −10.39 |
| HBTS | −0.36 | −0.67 | −0.70g | −0.62g | 0.39g | −0.23g |
| PreMIN | −16.87 | −16.88 | −16.73 | −16.57 | 0.79 | −15.77 |
| WaldenTS | −16.35 | −16.41 | −16.45 | −16.32 | 0.62 | −15.70 |
| FSTS1 | 14.09 | 12.96 | 12.98 | 13.17 | 0.78 | 13.95 |
| FSTS2 | 14.10 | 13.18h | 13.29h | 13.55h | 0.95h | 14.50h |
| DITS | 7.23 | 6.88 | 7.42 | 7.69 | 0.05 | 7.73 |
| PostHMIN | −72.09 | −71.45 | −70.85 | −70.93 | 3.71 | −67.22 |
| ABSTS | −15.27 | −14.80 | −14.48 | −14.30 | 0.41 | −13.89 |
| ABSMIN1 | −11.03 | −11.55 | −11.18 | −10.89 | 0.00 | −10.90 |
| ABSMIN2 | 0.38 | −0.79 | −0.37 | −0.12 | 0.57 | 0.45 |
| PostTS | −40.96 | −28.82 | −27.82 | −27.63 | −4.16 | −31.80 |
| PostDHMIN | −144.57 | −141.54 | −140.79 | −140.94 | 5.48 | −135.46 |
| HOO− + CH3I | MP2a | DZb | TZc | QZd | ΔZPEe | Adiabaticf |
|---|---|---|---|---|---|---|
| HMIN1 | −18.52 | −18.05 | −17.75 | −17.57 | 0.72 | −16.84 |
| HMIN2 | −18.45 | −17.96 | −17.60 | −17.40 | 0.79 | −16.61 |
| HTS1 | −18.02 | −17.56 | −17.31 | −17.17 | 0.53 | −16.64 |
| HTS2 | −16.44 | −16.51 | −16.27 | −16.10 | 0.54 | −15.56 |
| FSMIN | −22.36 | −22.28 | −22.11 | −22.03 | 0.44 | −21.59 |
| HBTS | −2.65 | −3.19 | −3.37 | −3.30 | 0.40 | −2.90 |
| FSTS1 | 9.16 | 7.85 | 7.91 | 8.04 | 0.87 | 8.91 |
| FSTS2 | 10.01 | 8.46h | 8.67h | 8.93h | 1.08h | 10.01h |
| DITS | 3.40 | 2.68 | 3.11 | 3.36 | 0.19 | 3.55 |
| PostHMIN | −75.63 | −75.15 | −74.52 | −74.74 | 3.94 | −70.80 |
| ABSTS | −16.32 | −15.83 | −15.48 | −15.30 | 0.28 | −15.02 |
| ABSMIN1 | −14.52 | −14.76 | −14.42 | −14.15 | 0.28 | −13.88 |
| ABSMIN2 | −2.98 | −4.37 | −3.97 | −3.75 | 0.66 | −3.09 |
| PostTS | −36.02 | −27.58 | −26.36 | −26.15 | −4.08 | −30.23 |
| PostDHMIN | −147.56 | −144.70 | −143.92 | −144.19 | 5.79 | −138.40 |
| HOO− + CH3F | MP2 | CCSD(T)-F12b | ΔZPEe | Adiabaticf | Experimentg | ||
|---|---|---|---|---|---|---|---|
| DZa | DZb | TZc | QZd | ||||
| a MP2/aug-cc-pVDZ. b CCSD(T)-F12b/aug-cc-pVDZ. c CCSD(T)-F12b/aug-cc-pVTZ. d CCSD(T)-F12b/aug-cc-pVQZ at CCSD(T)-F12b/aug-cc-pVTZ geometry. e ΔZPE(CCSD(T)-F12b/aug-cc-pVTZ). f QZ + ΔZPE. g Data obtained from the latest version (1.130) of the Active Thermochemical Tables (ATcT).113,114 The uncertainties are derived using the Gaussian error-propagation law on the uncertainties of each 0 K enthalpy of formation provided in ATcT. | |||||||
| CH3OOH + F− | −18.24 | −13.38 | −13.06 | −13.13 | 1.46 | −11.67 | −11.82 ± 0.14 |
| CH2F− + H2O2 | 34.54 | 34.87 | 35.22 | 35.32 | −1.84 | 33.48 | — |
| CH3OO− + HF | −11.24 | −10.28 | −10.08 | −10.02 | −1.11 | −11.12 | −11.00 ± 0.15 |
| CH2O + HF + HO− | −51.98 | −43.50 | −42.94 | −43.06 | −4.92 | −47.98 | −47.99 ± 0.10 |
| CH2(OH)O− + HF | −85.40 | −79.85 | −79.22 | −79.15 | −0.70 | −79.85 | — |
| HOO− + CH3Cl | MP2a | DZb | TZc | QZd | ΔZPEe | Adiabaticf | Experimentg |
|---|---|---|---|---|---|---|---|
| CH3OOH + Cl− | −48.79 | −45.72 | −45.61 | −45.83 | 2.44 | −43.39 | −43.07 ± 0.14 |
| CH2Cl− + H2O2 | 22.01 | 21.82 | 21.80 | 21.81 | −1.33 | 20.48 | 21.64 ± 0.49 |
| CH3OO− + HCl | −3.64 | −3.44 | −3.10 | −2.89 | −1.77 | −4.66 | −4.31 ± 0.14 |
| CH2O + HCl + HO− | −44.38 | −36.66 | −35.97 | −35.93 | −5.58 | −41.51 | −41.30 ± 0.09 |
| CH2(OH)O− + HCl | −77.81 | −73.01 | −72.24 | −72.02 | −1.36 | −73.39 | — |
| HOO− + CH3Br | MP2a | DZb | TZc | QZd | ΔZPEe | Adiabaticf | Experimentg |
|---|---|---|---|---|---|---|---|
| CH3OOH + Br− | −54.91 | −54.21 | −53.65 | −53.98 | 2.85 | −51.14 | −50.60 ± 0.14 |
| CH2Br− + H2O2 | 18.32 | 16.94 | 17.14 | 17.15 | −1.17 | 15.98 | — |
| CH3OO− + HBr | −0.72 | −1.04 | −0.51 | −0.37 | −1.86 | −2.23 | −1.85 ± 0.14 |
| CH2O + HBr + HO− | −41.46 | −34.26 | −33.37 | −33.41 | −5.68 | −39.08 | −38.84 ± 0.10 |
| CH2(OH)O− + HBr | −74.89 | −70.61 | −69.65 | −69.50 | −1.46 | −70.96 | — |
| HOO− + CH3I | MP2a | DZb | TZc | QZd | ΔZPEe | Adiabaticf | Experimentg |
|---|---|---|---|---|---|---|---|
| CH3OOH + I− | −61.29 | −60.78 | −60.32 | −60.89 | 3.25 | −57.64 | −56.97 ± 0.14 |
| CH2I− + H2O2 | 13.49 | 11.84 | 11.92 | 11.84 | −0.95 | 10.89 | — |
| CH3OO− + HI | 2.44 | 1.68 | 2.14 | 2.24 | −1.93 | 0.32 | 0.83 ± 0.14 |
| CH2O + HI + HO− | −38.30 | −31.54 | −30.72 | −30.80 | −5.74 | −36.54 | −36.16 ± 0.10 |
| CH2(OH)O− + HI | −71.72 | −67.89 | −67.00 | −66.89 | −1.52 | −68.41 | — |
As seen in Fig. 1, in the entrance channel of the back-side attack Walden inversion, several H-bonded stationary points can be found for HOO− + CH3Y: HMIN1 [Y = F, Cl, Br and I], HTS1 [Y = F, Cl, Br and I], HMIN2 [Y = Br and I] and HTS2 [Y = Cl, Br and I]. The energetics of these minima and transition states are similar, and the differences in the relative energies are within ∼1.5 kcal mol−1. Moreover, the typical PreMIN ion–dipole complex does not demonstrate notable distinctions, as well. On the other hand, for the alternative pre-reaction halogen-bonded complex pathway, a different situation can be found. In line with HO− + CH3Y,24,38 FSMIN is situated above HMIN1 by 13.2 (12.8) and 6.0 (5.6) kcal mol−1 for Y = Cl and Br, in order; while for Y = I, FSMIN is below HMIN1 by 4.5 (4.7) kcal mol−1. Note that the back-side attack Walden-inversion mechanism is submerged except for Y = F, where HBTS is positioned above the reactant asymptote by 1.1 (1.4) kcal mol−1. With the atomic number of Y, the barrier height of HBTS is increasing: 3.9 (3.7), 10.1 (10.2) and 18.7 (18.7) kcal mol−1 relative to the corresponding FSMIN, for Y = F, Cl, Br and I, respectively. The deep well of the FSMIN complex at Y = I points out the common occurrence of the front-side complex formation mechanism in SN2 reactions involving CH3I.48,60,109 The energy profile of the conventional stationary points of the Walden-inversion pathway (PreMIN → WaldenTS → WaldenPostMIN/PostHMIN) is also profoundly comparable with that of the HO− case.24,38 For instance, the classical (adiabatic) barrier heights of WaldenTS are 10.3 (10.1), 2.3 (2.2) and 0.2 (0.1) kcal mol−1 for Y = F, Cl and Br, respectively, while in the case of HO− at the same level of theory, these values are 11.2 (11.4), 2.4 (2.4) and 0.2 (0.1) kcal mol−1, in the same order. The global minimum of SN2 is also located at PostHMIN, although, compared to HO− + CH3Y, higher classical energies of −49.7, −65.6, −70.9 and −74.7 kcal mol−1 can be determined for HOO− in the case of Y = F, Cl, Br and I, respectively. In tandem with this, a notable disparity emerges in the reaction enthalpies of the SN2 channels: HOO− + CH3Y happens to be more endothermic by exactly 6.1 kcal mol−1 in all cases. As a result, in the case of the SN2 reactions of HOO−, larger dissociation energies can be observed for the leaving Y− at PostHMIN, indicating a more significant post-reaction hydrogen-bonded complex formation. Here, one may highlight the relevance of peroxide ion substitution, as well, because the formation of the CH3OO− + HY products is also more exothermic than that of the HO− cases, predicting a substantially increased probability for peroxide ion substitution, especially for HOO− + CH3F.40 WaldenPostHMIN also plays a significant role, as Zhao et al.95 uncovered, and the reaction can proceed through this minimum towards PostTS, leading to the unusual CH2O + HY + HO− products. In the case of Y = Cl, WaldenPostHMIN could not be identified at the CCSD(T)-F12b/aug-cc-pVnZ [n = 2, 3] levels of theory. It is noteworthy that for Y = F, the novel mechanism of SN2-induced elimination is exceedingly more exothermic than SN2, submerged by 29.9 (36.3) kcal mol−1. The global minimum of the PES is situated at the double H-bonded PostDHMIN complex, and the most exothermic process corresponds to the SN2-induced rearrangement channel, but it is supposedly an improbable reaction route considering the multiple bond-breaking and -forming processes involved. Concerning the SN2 pathways that result in the retention of the initial CH3Y configuration, two different transition states (FSTS1 and FSTS2) can be identified for front-side attacks. According to the study of Ma et al.,110 double inversion may not be an IRC path through a DITS-like transition state; despite that, theoretical investigations underscored its crucial character in the mechanism.111,112 Similarly to the HO− case, the transition state of double inversion has lower energy than that of front-side attack; however, no submerged DITS can be obtained.24,38 The most endothermic channel is proton abstraction with reaction enthalpies of 33.5 (F), 20.5 (Cl), 16.0 (Br) and 10.9 (I) kcal mol−1. The entrance channel of proton abstraction is found to be the same as that for SN2 and is supported by IRC calculations, in which three stationary points (two minima and one transition state) are explored along the pathway: ABSTS [Y = F, Cl, Br and I], ABSMIN1 [Y = Br and I], and ABSMIN2 [Y = F, Cl, Br and I].
The structures of the stationary points featuring the selected bond lengths and angles are shown in Fig. 2. The associated stationary points in the reactant channels (HMIN1/HTS1 and HMIN2/HTS2) demonstrate slight differences in their geometries, and the most pronounced disparity is discerned in the orientation of the corresponding HOO− group. Regarding WaldenTS, two distinct structures are characterized depending on Y: the dihedral angle of O–O⋯C–H is ∼180° (trans arrangement) at Y = F, whereas a value of ∼0° (cis arrangement) is obtained at Y = Cl and Br, as seen in Fig. 2. According to earlier investigations on SN2 reactions, similar discrepancies observed at CH3F are not uncommon;24 for instance, in the case of HO− + CH3Y,38 for Y = Cl, Br and I FSTS has Cs symmetry, while for Y = F, the symmetry is broken. It should be noted that previous studies on the HOO− + CH3Cl SN2 reaction reported a trans alignment for the O–O⋯C–H torsion angle of WaldenTS computed at the MP2/6-311++G(d,p) level of theory.96,97 The geometries of PreMIN and WaldenTS defined in the early work of Evanseck et al. are discrepant from our benchmark results due to their implemented symmetry-constrained geometry optimizations.74 Moreover, Ren et al. revealed two different transition states for Walden inversion with a trans alignment of the corresponding O–O⋯C–H torsion angle for both cases.78 Nevertheless, in other investigations, the geometry of the uncovered WaldenTS of HOO− + CH3Cl is in accordance with that presented in this benchmark work.79,88,95 It should also be highlighted that Wu et al. identified PreMIN and WaldenTS for Y = I at the MP2/6-311++G(d,p) level of theory,96 although, in the course of the present study, WaldenTS cannot be found for Y = I at the MP2/aug-cc-pVDZ and CCSD(T)-F12b/aug-cc-pVnZ [n = 2, 3] levels of theory. Hence, the issues regarding these stationary points underline the relevance of employing higher-level ab initio methods for theoretical investigations. Concerning PostHMIN, alternative conformational isomers cannot be determined in contrast to the HO− + CH3F reaction.40 As shown in Fig. 2, the transition states of the front-side attack mechanism differ from each other in the orientation of the HOO− group, and owing to the additional Y⋯HO bond, FSTS2 is below FSTS1 in the case of Y = F and Cl. It is noteworthy that all the stationary-point characterizations can be performed without imposing symmetry restrictions, except for ABSMIN1, which has Cs symmetry. There are cases, where a Cs symmetry would also be expected (e.g., HTS1, ABSTS); however, the corresponding geometry optimizations do not converge. The most accurate, CCSD(T)-F12b/aug-cc-pVTZ Cartesian coordinates of the stationary points, as well as of reactants and products, are provided in the ESI.†
The calculated classical and adiabatic ab initio relative energies of the products and the available “experimental” reaction enthalpies obtained from the active thermochemical tables (ATcT)113,114 are given in Table 2. The benchmark structures of the reactants and products are shown in Fig. 3. The reaction enthalpies of SN2 and proton abstraction decrease with increasing atomic weight of Y, whereas for the other pathways, a reverse tendency is revealed. Alongside the proton-abstraction channels for Y = F, Cl, Br and I, peroxide ion substitution is also an endothermic pathway in the case of Y = I. It is notable that for Y = F, the difference between the reaction enthalpies of SN2 and peroxide ion substitution is only 0.5 kcal mol−1. In most instances, our benchmark results are in satisfactory agreement with the experimental data, except for the CH2Cl− + H2O2 products, where a difference of 1.2 kcal mol−1 emerges. However, it should be noted that the derived uncertainty of the experimental reaction enthalpy is remarkably substantial (±0.5 kcal mol−1). Similarly, for the F− + CH3Cl → CH2Cl− + HF proton-abstraction channel, a large deviation (0.9 kcal mol−1) can also be observed between the experimental and our calculated benchmark reaction enthalpy with a significant uncertainty (0.5 kcal mol−1) of the experimental value.112 Thus, these cases may highlight the inaccuracy of the available 0 K enthalpy of formation for CH2Cl− in the ATcT. In the case of the HOO− + CH3Y [Y = F and Cl] SN2 reactions, the reaction energies of −13.0 (F) and −45.3 (Cl) kcal mol−1, obtained by Wu et al. utilizing CCSD(T)/aug-cc-pVTZ(-PP) energy calculations at the MP2/6-311++G(d,p) geometries,96, in kcal mol−1 are in conformity with our benchmark values of −13.0 (F) and −45.8 (Cl) kcal mol−1. Although, for Y = Br and I, their SN2 reaction energies of −50.9 and −56.4 kcal mol−1 are higher than our results by 3.1 and 4.5 kcal mol−1, respectively. The classical energies of the stationary points of the present work can also be compared with the results of Wu et al.96 They characterized five stationary points (HMIN1, HTS2, PreMIN, WaldenTS and PostHMIN) along the back-side attack Walden inversion, mainly, their computed CCSD(T)/aug-cc-pVTZ(-PP) energies are in good agreement with our benchmark data. In an earlier study on HOO− + CH3Cl by Zhao et al.,95 the reported energies of PreMIN and PostHMIN at the MP2/6-31+G(d,p) level of theory are in good agreement with the present benchmark values. For WaldenTS, a difference of more than 2 kcal mol−1 occurs; moreover, an enormous deviation of 13.2 kcal mol−1 is obtained at WaldenPostHMIN, remarkably. Motivated by this discrepancy, we characterized the corresponding stationary points of HOO− + CH3Cl at the MP2/6-31+G(d,p) level of theory using the MOLPRO program package.108 In the course of computations, spherical harmonic basis functions are used; however, it is noteworthy that by employing Cartesian functions, comparable relative energies can be obtained within ±0.3 kcal mol−1. Our obtained MP2/6-31+G(d,p) classical energies of −14.9 (PreMIN), −10.5 (WaldenTS), −64.6 (PostHMIN), −53.2 (WaldenPostHMIN), −31.5 (PostTS), and −136.5 (PostDHMIN), in kcal mol−1, are in conformity with the benchmark data. While our optimized structures of the stationary points show satisfactory alignment with those determined by Zhao et al.,95 significant inexplicable disparities are unveiled for the classical energies in a few cases. We also determined the classical (adiabatic) energies of the products at the MP2/6-31+G(d,p) level; CH2Cl− + H2O2: 29.4 (27.7), CH3OOH + Cl− −45.7 (−43.5), CH3OO− + HCl: −2.1 (−3.7), CH2O + HCl + HO−: −40.0 (−45.8) and CH2(OH)O− + HCl: −75.2 (−76.8), in kcal mol−1. It can be seen that for certain cases, the provided energies differ from the experiment by more than 4 kcal mol−1; especially for proton abstraction, an enormous difference of 6.1 kcal mol−1 occurs, which casts doubt on the reliability of MP2/6-31+G(d,p). The G2+ adiabatic energies of WaldenTS (−13.5 kcal mol−1) and the SN2 products (−43.2 kcal mol−1), computed by Ren et al. for HOO− + CH3Cl, are also in consonance with the present study.79
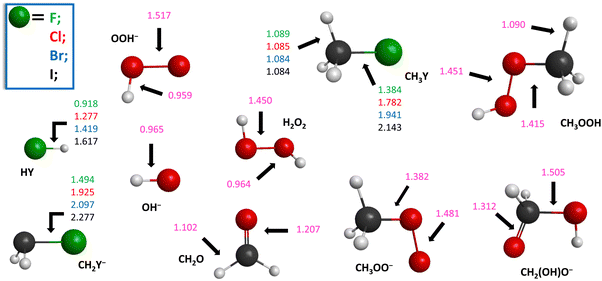 | ||
| Fig. 3 Structures of the reactants and products of the HOO− + CH3Y [Y = F, Cl, Br, I] reactions showing the most important bond lengths (Å) obtained at the CCSD(T)-F12b/aug-cc-pVTZ level of theory. | ||
As shown in Fig. 4 and 5, the basis-set convergence of the CCSD(T)-F12b relative energies is also investigated for the title reactions. In most cases, a fast and smooth basis-set convergence can be recognized, except for WaldenTS [Y = F and Br], HBTS [Y = Br], FSTS1 [Y = Cl] and CH3OOH + Y− [Y = Cl, Br and I], as in these instances the relative energy differences between aug-cc-pVDZ (DZ) and aug-cc-pVQZ (QZ) are smaller than the corresponding values of aug-cc-pVTZ (TZ) and QZ. The largest differences emerge at PostTS [Y = Br and I] and CH2(OH)O− + HBr, where the deviations between the DZ and QZ relative energies are found to be in the range of 1.1–1.4 kcal mol−1. In contrast, the energy differences between TZ and QZ are within ±0.4 kcal mol−1, except at CH3OOH + I− (0.57 kcal mol−1). Regarding the ZPE effects, the most significant contributions appear at the post-reaction stationary points (PostHMIN, WaldenPostHMIN, PostTS and PostDHMIN) and for the products of CH3OOH + Y− and CH2O + HY + HO−. The vast majority of the stationary points have positive ZPE corrections, whereas, in the case of the reaction channels, positive ZPE effects occur only for the CH3OOH + Y− products.
IV. Summary and conclusions
In this study, we have characterized the complex potential energy surfaces of the HOO− + CH3Y [Y = F, Cl, Br and I] reactions using the modern explicitly-correlated CCSD(T)-F12b method with the aug-cc-pVnZ [n = 2–4] basis sets. For SN2, we have considered the pathways of back-side attack Walden inversion, front-side attack, double inversion19 and halogen-bonded complex formation.48 In most cases, the entrance channel of HOO− + CH3Y comprises seven stationary points: two H-bonded, a front-side halogen-bonded and a traditional ion–dipole minima, as well as two H-bonded and front-side halogen-bonded transition states. Similar to the HO− + CH3Y SN2 reactions,24,38 no typical transition state has been identified for the Walden inversion in the case of Y = I, and in light of the discrepancy of the earlier findings, we have clarified the accurate structure of the Walden-inversion transition state for Y = Cl. In the exit channel of SN2, two H-bonded minima are situated: Y−⋯HOOCH3 and Y−⋯HCH2OOH. Based on the findings of Xie and co-workers,95 the HOO− + CH3Cl reaction can proceed through Cl−⋯HCH2OOH towards the [Cl⋯H⋯CH2O⋯OH]− transition state generating the unusual products of CH2O + HCl + HO−. It should be highlighted that for HOO− + CH3F, the reaction enthalpy of this novel SN2-induced elimination is more negative by 36.3 kcal mol−1 than the corresponding SN2 process. Concerning the retention paths of SN2, two distinct transition states have been recognized for front-side attacks, and as observed for HO− + CH3Y, double inversion is a lower-energy process than front-side attack.24,38 Building upon the earlier work of Xie and co-workers,95 besides SN2-induced elimination, we have also investigated other channels such as proton abstraction (CH2Y− + H2O2), peroxide ion substitution (CH3OO− + HY) and SN2-induced rearrangement (CH2(OH)O− + HY). In the case of Y = F, Cl and Br, the peroxide ion substitution has been found to be exothermic with reaction enthalpies of −11.1 (F), −4.7 (Cl) and −2.2 (Br) kcal mol−1. The most exothermic path is SN2-induced rearrangement; however, it is presumed to be an improbable reaction channel due to the complex bond-breaking and -forming processes involved. The benchmark reaction enthalpies presented in this work are usually in excellent agreement with those obtained from ATcT.113,114 We have also assessed the basis-set convergence of the CCSD(T)-F12b method and the ZPE contributions of the stationary points.We are confident that the present benchmark characterization of HOO− + CH3Y supports further theoretical and experimental investigations regarding reaction dynamics as well as the influence of the α-effect related to HOO−.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
We acknowledge the financial support of the National Research, Development and Innovation Office-NKFIH, K-125317 and K-146759; project no. TKP2021-NVA-19 provided by the Ministry of Innovation and Technology of Hungary from the National Research, Development and Innovation Fund, financed under the TKP2021-NVA funding scheme; the National Young Talent Scholarship (Grant no. NTP-NFTÖ-22-B-0050 for D. A. T.); and the Momentum (Lendület) Program of the Hungarian Academy of Sciences.References
- A. Dedieu and A. Veillard, J. Am. Chem. Soc., 1972, 94, 6730 CrossRef CAS.
- W. N. Olmstead and J. I. Brauman, J. Am. Chem. Soc., 1977, 99, 4219 CrossRef CAS.
- A. Merkel, R. Zahradník and Z. Havlas, J. Am. Chem. Soc., 1988, 110, 8355 CrossRef CAS.
- S. S. Shaik, H. B. Schlegel and S. Wolfe, Theoretical Aspects of Physical Organic Chemistry: The SN2 Mechanism, Wiley, New York, 1992 Search PubMed.
- W. L. Hase, Science, 1994, 266, 998 CrossRef CAS PubMed.
- M. L. Chabinyc, S. L. Craig, C. K. Regan and J. I. Brauman, Science, 1998, 279, 1882 CrossRef CAS PubMed.
- J. K. Laerdahl and E. Uggerud, Int. J. Mass Spectrom., 2002, 214, 277 CrossRef CAS.
- E. Uggerud, Adv. Phys. Org. Chem., 2017, 51, 1 CrossRef CAS.
- T. A. Hamlin, M. Swart and F. M. Bickelhaupt, ChemPhysChem, 2018, 19, 1315 CrossRef CAS PubMed.
- R. Wester, Mass Spectrom. Rev., 2022, 41, 627 CrossRef PubMed.
- A. J. R. Heck and D. W. Chandler, Annu. Rev. Phys. Chem., 1995, 46, 335 CrossRef CAS PubMed.
- M. N. R. Ashfold, N. H. Nahler, A. J. Orr-Ewing, O. P. J. Vieuxmaire, R. L. Toomes, T. N. Kitsopoulos, I. A. Garcia, D. A. Chestakov, S. M. Wu and D. H. Parker, Phys. Chem. Chem. Phys., 2006, 8, 26 RSC.
- D. C. Clary, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 12649 CrossRef CAS PubMed.
- J. Mikosch, S. Trippel, C. Eichhorn, R. Otto, U. Lourderaj, J. X. Zhang, W. L. Hase, M. Weidemüller and R. Wester, Science, 2008, 319, 183 CrossRef CAS PubMed.
- J. Meyer and R. Wester, Annu. Rev. Phys. Chem., 2017, 68, 333 CrossRef CAS PubMed.
- J. Li, B. Zhao, D. Xie and H. Guo, J. Phys. Chem. Lett., 2020, 11, 8844 CrossRef CAS PubMed.
- J. I. Brauman, Science, 2008, 319, 168 CrossRef CAS PubMed.
- P. Manikandan, J. Zhang and W. L. Hase, J. Phys. Chem. A, 2012, 116, 3061 CrossRef CAS PubMed.
- I. Szabó and G. Czakó, Nat. Commun., 2015, 6, 5972 CrossRef PubMed.
- M. Stei, E. Carrascosa, M. A. Kainz, A. H. Kelkar, J. Meyer, I. Szabó, G. Czakó and R. Wester, Nat. Chem., 2016, 8, 151 CrossRef CAS PubMed.
- J. Xie and W. L. Hase, Science, 2016, 352, 32 CrossRef CAS PubMed.
- L. Sun, K. Song and W. L. Hase, Science, 2002, 296, 875 CrossRef CAS PubMed.
- L. Sun, K. Song, W. L. Hase, M. Sena and J. M. Riveros, Int. J. Mass Spectrom., 2003, 227, 315 CrossRef CAS.
- D. A. Tasi, Z. Fábián and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 7924 RSC.
- S. R. Hare, L. A. Bratholm, D. R. Glowacki and B. K. Carpenter, Chem. Sci., 2019, 10, 9954 RSC.
- T. Tsutsumi, Y. Ono, Z. Arai and T. Taketsugu, J. Chem. Theory Comput., 2020, 16, 4029 CrossRef CAS PubMed.
- D. A. Tasi, C. Tokaji and G. Czakó, Phys. Chem. Chem. Phys., 2021, 23, 13526 RSC.
- T. Tsutsumi, Y. Ono and T. Taketsugu, Chem. Commun., 2021, 57, 11734 RSC.
- T. Tsutsumi, Y. Ono and T. Taketsugu, Top. Curr. Chem., 2022, 380, 19 CrossRef CAS PubMed.
- S. Zhao, G. Fu, W. Zhen, L. Yang, J. Sun and J. Zhang, Phys. Chem. Chem. Phys., 2022, 24, 24146 RSC.
- H. Tachikawa, M. Igarashi and T. Ishibashi, J. Phys. Chem. A, 2002, 106, 10977 CrossRef CAS.
- H. Tachikawa and M. Igarashi, Chem. Phys., 2006, 324, 639 CrossRef CAS.
- H. Yin, D. Wang and M. Valiev, J. Phys. Chem. A, 2011, 115, 12047 CrossRef CAS PubMed.
- Y. Xu, T. Wang and D. Wang, J. Chem. Phys., 2012, 137, 184501 CrossRef PubMed.
- S. Giri, E. Echegaray, P. W. Ayers, A. S. Nuñez, F. Lund and A. Toro-Labbé, J. Phys. Chem. A, 2012, 116, 10015 CrossRef CAS PubMed.
- J. Chen, Y. Xu and D. Wang, J. Comput. Chem., 2014, 35, 445 CrossRef CAS PubMed.
- T. Tsutsumi, Y. Ono, Z. Arai and T. Taketsugu, J. Chem. Theory Comput., 2018, 14, 4263 CrossRef CAS PubMed.
- D. A. Tasi, Z. Fábián and G. Czakó, J. Phys. Chem. A, 2018, 122, 5773 CrossRef CAS PubMed.
- Y. G. Proenza, M. A. F. de Souza and R. L. Longo, Chem. – Eur. J., 2016, 22, 16220 CrossRef CAS PubMed.
- D. A. Tasi and G. Czakó, Chem. Sci., 2021, 12, 14369 RSC.
- J. Qin, Y. Liu and J. Li, J. Chem. Phys., 2022, 157, 124301 CrossRef CAS PubMed.
- R. Otto, J. Brox, S. Trippel, M. Stei, T. Best and R. Wester, Nat. Chem., 2012, 4, 534 CrossRef CAS PubMed.
- J. Xie, R. Otto, J. Mikosch, J. Zhang, R. Wester and W. L. Hase, Acc. Chem. Res., 2014, 47, 2960 CrossRef CAS PubMed.
- J. Xie, J. Zhang and W. L. Hase, Int. J. Mass Spectrom., 2015, 378, 14 CrossRef CAS.
- J. Xie, R. Otto, R. Wester and W. L. Hase, J. Chem. Phys., 2015, 142, 244308 CrossRef PubMed.
- E. Carrascosa, J. Meyer and R. Wester, Chem. Soc. Rev., 2017, 46, 7498 RSC.
- J. Xie, X. Ma, J. Zhang, P. M. Hierl, A. A. Viggiano and W. L. Hase, Int. J. Mass Spectrom., 2017, 418, 122 CrossRef CAS.
- X. Ji, C. Zhao and J. Xie, Phys. Chem. Chem. Phys., 2021, 23, 6349 RSC.
- R. Otto, J. Xie, J. Brox, S. Trippel, M. Stei, T. Best, M. R. Siebert, W. L. Hase and R. Wester, Faraday Discuss., 2012, 157, 41 RSC.
- J. Xie, R. Sun, M. R. Siebert, R. Otto, R. Wester and W. L. Hase, J. Phys. Chem. A, 2013, 117, 7162 CrossRef CAS PubMed.
- J. Xie, S. C. Kohale, W. L. Hase, S. G. Ard, J. J. Melko, N. S. Shuman and A. A. Viggiano, J. Phys. Chem. A, 2013, 117, 14019 CrossRef CAS PubMed.
- J. Xie, J. Zhang, R. Sun, R. Wester and W. L. Hase, Int. J. Mass Spectrom., 2019, 438, 115 CrossRef CAS.
- D. A. Tasi, T. Győri and G. Czakó, Phys. Chem. Chem. Phys., 2020, 22, 3775 RSC.
- T. Győri and G. Czakó, J. Chem. Theory Comput., 2020, 16, 51 CrossRef PubMed.
- D. A. Tasi, T. Michaelsen, R. Wester and G. Czakó, Phys. Chem. Chem. Phys., 2023, 25, 4005 RSC.
- S. Rao and D. Wang, Chin. J. Chem. Phys., 2023, 36, 169 CrossRef CAS.
- D. A. Tasi and G. Czakó, J. Chem. Phys., 2024, 160, 044305 CrossRef CAS PubMed.
- E. Carrascosa, M. Bawart, M. Stei, F. Linden, F. Carelli, J. Meyer, W. D. Geppert, F. A. Gianturco and R. Wester, J. Chem. Phys., 2015, 143, 184309 CrossRef CAS PubMed.
- Z. Kerekes, D. A. Tasi and G. Czakó, J. Phys. Chem. A, 2022, 126, 889 CrossRef CAS PubMed.
- D. A. Tasi and G. Czakó, J. Chem. Phys., 2022, 156, 184306 CrossRef CAS PubMed.
- X. Liu, S. Tian, B. Pang, H. Li and Y. Wu, Phys. Chem. Chem. Phys., 2023, 25, 14812 RSC.
- X. Liu, W. Guo, H. Feng, B. Pang and Y. Wu, J. Phys. Chem. A, 2023, 127, 7373 CrossRef CAS PubMed.
- A. Gutal and M. Paranjothy, Phys. Chem. Chem. Phys., 2023, 25, 15015 RSC.
- W. P. Hu and D. G. Truhlar, J. Am. Chem. Soc., 1996, 118, 860 CrossRef CAS.
- S. M. Villano, N. Eyet, W. C. Lineberger and V. M. Bierbaum, J. Am. Chem. Soc., 2009, 131, 8227 CrossRef CAS PubMed.
- L. Junxi, W. Yanbin, Z. Qiang, L. Yu, G. Zhiyuan and W. Xiuhong, J. Mol. Model., 2013, 19, 1739 CrossRef PubMed.
- L. Junxi, S. Qiong, L. Yu, Z. Qiang and G. Zhiyuan, Can. J. Chem., 2014, 92, 868 CrossRef CAS.
- L. Junxi, S. Qiong, W. Yanbin and G. Zhiyuan, Bull. Chem. Soc. Jpn., 2015, 88, 110 CrossRef.
- F. Yu, J. Phys. Chem. A, 2016, 120, 1813 CrossRef CAS PubMed.
- L. Yun-Yun, Q. Fang-Zhou, Z. Jun, R. Yi and L. Kai-Chung, J. Mol. Model., 2017, 23, 192 CrossRef PubMed.
- T. Hansen, P. Vermeeren, F. M. Bickelhaupt and T. A. Hamlin, Angew. Chem., Int. Ed., 2021, 60, 20840 CrossRef CAS PubMed.
- S. Hoz and E. Buncel, Isr. J. Chem., 1985, 26, 313 CrossRef CAS.
- J. O. Edwards and R. G. Pearson, J. Am. Chem. Soc., 1962, 84, 16 CrossRef CAS.
- J. D. Evanseck, J. F. Blake and W. L. Jorgensen, J. Am. Chem. Soc., 1987, 109, 2349 CrossRef CAS.
- E. Buncel and I. H. Um, Tetrahedron, 2004, 60, 7801 CrossRef CAS.
- C. H. DePuy, E. W. Della, J. Filley, J. J. Grabowski and V. M. Bierbaum, J. Am. Chem. Soc., 1983, 105, 2481 CrossRef CAS.
- E. V. Patterson and K. R. Fountain, J. Org. Chem., 2006, 71, 8121 CrossRef CAS PubMed.
- Y. Ren and H. Yamataka, Org. Lett., 2006, 8, 119 CrossRef CAS PubMed.
- Y. Ren and H. Yamataka, Chem. – Eur. J., 2007, 13, 677 CrossRef CAS PubMed.
- Y. Ren and H. Yamataka, J. Org. Chem., 2007, 72, 5660 CrossRef CAS PubMed.
- A. M. McAnoy, M. R. L. Paine and S. J. Blanksby, Org. Biomol. Chem., 2008, 6, 2316 RSC.
- Y. I. Ren and H. Yamataka, J. Comput. Chem., 2009, 30, 358 CrossRef CAS PubMed.
- J. M. Garver, S. Gronert and V. M. Bierbaum, J. Am. Chem. Soc., 2011, 133, 13894 CrossRef CAS PubMed.
- J. M. Garver, Z. Yang, N. Wehres, C. M. Nichols, B. B. Worker and V. M. Bierbaum, Int. J. Mass Spectrom., 2012, 330–332, 182 CrossRef CAS.
- Y. Ren, X. G. Wei, S. J. Ren, K. C. Lau, N. B. Wong and W. K. Li, J. Comput. Chem., 2013, 34, 1997 CrossRef CAS PubMed.
- I. H. Um, L. R. Im and E. Buncel, J. Org. Chem., 2010, 75, 8571 CrossRef CAS PubMed.
- X. G. Wei, X. M. Sun, X. P. Wu, Y. Ren, N. B. Wong and W. K. Li, J. Org. Chem., 2010, 75, 4212 CrossRef CAS PubMed.
- D. L. Thomsen, J. N. Reece, C. M. Nichols, S. Hammerum and V. M. Bierbaum, J. Am. Chem. Soc., 2013, 135, 15508 CrossRef CAS PubMed.
- D. L. Thomsen, J. N. Reece, C. M. Nichols, S. Hammerum and V. M. Bierbaum, J. Phys. Chem. A, 2014, 118, 8060 CrossRef CAS PubMed.
- D. L. Thomsen, C. M. Nichols, J. N. Reece, S. Hammerum and V. M. Bierbaum, J. Am. Soc. Mass Spectrom., 2014, 25, 159 CrossRef CAS PubMed.
- W. Y. Zhao, J. Yu, S. J. Ren, X. G. Wei, F. Z. Qiu, P. H. Li, H. Li, Y. P. Zhou, C. Z. Yin, A. P. Chen, H. Li, L. Zhang, J. Zhu, Y. Ren and K. C. Lau, J. Comput. Chem., 2015, 36, 844 CrossRef CAS PubMed.
- N. Singh, Y. Karpichev, R. Sharma, B. Gupta, A. K. Sahu, M. L. Satnami and K. K. Ghosh, Org. Biomol. Chem., 2015, 13, 2827 RSC.
- E. Juaristi, G. Dos Passos Gomes, A. O. Terent’ev, R. Notario and I. V. Alabugin, J. Am. Chem. Soc., 2017, 139, 10799 CrossRef CAS PubMed.
- F. Yu, J. Chem. Phys., 2018, 148, 014302 CrossRef PubMed.
- C. Zhao, X. Ma, X. Wu, D. L. Thomsen, V. M. Bierbaum and J. Xie, J. Phys. Chem. Lett., 2021, 12, 7134 CrossRef CAS PubMed.
- X. Wu, C. Zhao and J. Xie, ChemPhysChem, 2022, 23, e202200285 CrossRef CAS PubMed.
- Y. Hu, X. Wu and J. Xie, Phys. Chem. Chem. Phys., 2023, 25, 1947 RSC.
- D. J. Anick, J. Phys. Chem. A, 2011, 115, 6327 CrossRef CAS PubMed.
- C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618 CrossRef.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007 CrossRef CAS.
- R. Van de Vijver and J. Zádor, Comput. Phys. Commun., 2020, 248, 106947 CrossRef CAS.
- M. Kuwahara, Y. Harabuchi, S. Maeda, J. Fujima and K. Takahashi, Digit. Discovery, 2023, 2, 1104 RSC.
- E. Kraka, J. J. Antonio and M. Freindorf, Chem. Commun., 2023, 59, 7151 RSC.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479 CrossRef CAS.
- T. B. Adler, G. Knizia and H. J. Werner, J. Chem. Phys., 2007, 127, 221106 CrossRef PubMed.
- G. Knizia, T. B. Adler and H. J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113 CrossRef CAS.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., Molpro, version 2015.1, a package of ab initio programs, see https://www.molpro.net Search PubMed.
- I. Szabó, B. Olasz and G. Czakó, J. Phys. Chem. Lett., 2017, 8, 2917 CrossRef PubMed.
- Y.-T. Ma, X. Ma, A. Li, H. Guo, L. Yang, J. Zhang and W. L. Hase, Phys. Chem. Chem. Phys., 2017, 19, 20127 RSC.
- B. Olasz and G. Czakó, Phys. Chem. Chem. Phys., 2019, 21, 1578 RSC.
- G. Czakó, T. Győri, B. Olasz, D. Papp, I. Szabó, V. Tajti and D. A. Tasi, Phys. Chem. Chem. Phys., 2020, 22, 4298 RSC.
- B. Ruscic, R. E. Pinzon, M. L. Morton, G. Von Laszevski, S. J. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff and A. F. Wagner, J. Phys. Chem. A, 2004, 108, 9979 CrossRef CAS.
- D. H. Ruscic and B. Bross, Active Thermochemical Tables (ATcT) values based on ver. 1.130 of the Thermochemical Network, 2023, available at ATcT.anl.gov Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Benchmark Cartesian coordinates (Å) and energies (Eh) of the stationary points. See DOI: https://doi.org/10.1039/d4cp01071j |
| This journal is © the Owner Societies 2024 |




