A new compositional microscopic degree of freedom at grain boundaries in complex compounds: a case study in spinel

Abstract

The accurate computational treatment of polycrystalline materials requires the rigorous generation of grain boundary (GB) structures as many quantities of interest depend strongly on the specifics of the macroscopic and microscopic degrees of freedom (DoFs) used in their creation. In complex materials, containing multiple sublattices and where atomic composition can vary spatially through the system, we introduce a new microscopic DoF based on this compositional variation which we find governs observable properties. In spinel – a wide class of complex oxides where this compositional variation manifests as cation inversion – we exploit this DoF to generate and analyze low-energy microstates of two GBs with three spinel chemistries (FeCr₂O₄, NiCr₂O₄ and MgAl₂O₄). This treatment is found to allow for the co-redistribution of cations at the GBs which acts to modify the spatial charge distribution, defect segregation energy and defect transport through these regions. Additionally, we generate low-energy metastable microstates of the GB system with an induced cation disorder, simulating those which may develop as a result of damage events. These are then analyzed to discover their composition and defect transport properties which depend strongly on the amount of induced damage. We conclude that considering this new DoF is important in describing the properties of GBs in complex materials.

---

I. Introduction

The study of A²⁺B₂³⁺O₄, spinel structured materials is of increasing interest in applications of nuclear reactors^1–5 due to their ability to accommodate defects without amorphizing, resulting in significant radiation tolerance for some chemistries.^6,7 This radiation tolerance is primarily a result of the accommodation of point defects through the creation of cation antisites, called spinel inversion.^6–8 At the same time, nanostructured spinels have also been shown to exhibit remarkable properties. For instance, the radiation tolerance of MgGa₂O₄ was shown to increase substantially as the grain size was reduced from microns to nanometers.⁹ On the other hand, nanostructured MgAl₂O₄ is being studied for its high mechanical strength as an armor material.^10–14 Thus, there is increasing need to understand how these two aspects of the spinel structure – antisite disorder and grain boundaries – interact to govern the properties of these materials.

The ground state structure of bulk spinels is either ‘normal’ or ‘inverse’, depending on the exact chemistry.¹ The spinel structure consists of two crystallographic sites for cations, an octahedral site and a tetrahedral site. In a normal spinel, the octahedral site is filled with the B cation while the tetrahedral site contains the A cation – the process of inversion causes cations to swap sites. In a fully inverse spinel, the tetrahedral site is filled with B cations while the octahedral sites are split between A and B cations. A spinel's inversion parameter, commonly i, is a measure of the number of A cations on octahedral sites thereby quantifying the disorder of the cations compared to the ‘normal’ reference. Therefore, for a normal spinel, the inversion parameter can be loosely thought of as a measure of disorder that might be introduced by irradiation (or temperature), with the limit of full disorder corresponding to a random mixture of the cations or i = 2/3. Furthermore, the evolution of damage in spinel can significantly modify defect transport through regions of inversion and exhibit non-intuitive mechanisms.^5,15,16 In particular, defects in complex oxides can act to reduce cation disorder by mechanisms of migration and antisite repair.^5,17 These mechanisms act to provide spinel with its remarkable radiation tolerance.⁷

In many materials, grain boundaries (GBs) play a significant role in the strengthening of a material due to their ability to absorb defects.^18,19 As discussed, spinel has an intrinsic mechanism – cation inversion – for accommodating these induced defects and it is not well known what the synergistic effects of these two mechanisms will be. Previous work has suggested that GBs naturally exhibit a higher degree of inversion than the bulk matrix.^20,21 This can result in a negative correlation between inversion and grain size due to increasing grain boundary area as the grain size is reduced.^16,22–24 This inversion modifies properties such as defect segregation to GBs²² which is thought to impact defect transport in these regions.

It is well-known that the identification of thermodynamically relevant GB structures is of paramount importance to generating accurate defect transport dynamics throughout a material, since GBs can act as sinks for defects and pathways for their migration, both impacting material properties and evolution.^18,19 Historically, GB structure generation is done through controlling the 5 macroscopic degrees of freedom (DoFs) which define the inter-grain orientation and the GB habit plane; these macroscopic DoFs are readily determined via diffraction experiments. These macroscopic DoFs are accompanied by microscopic DoFs that correlate with details of the atomic arrangements at the GB. The gamma surface, mapped by translating the two grains across each other thus identifying the ground-state for that particular orientation relationship, is the most widely considered microscopic DoF.

More recently, there has been increasing interest in a second microscopic DoF which can be thought of, in some sense, as the atomic density of the GB. In single-specie compounds, previous authors have used grand-canonical type schemes in conjunction with the gamma-surface mapping to discover low-energy structures. For example, von Althan et al. used this idea of varying GB density to find low energy, ordered twist GBs in Si;²⁵ without this method only amorphous GBs were found.^26,27 Additionally, Frolov et al.²⁸ formalized this idea using an evolutionary grand-canonical scheme (EGCS) to canvas many low-angle W GBs, finding their ground-state structure and density. However, in complex, multi-component compounds this process becomes highly non-trivial as compound stoichiometry, charge neutrality, and the presence of electrostatic contributions^29–31 must be considered in these contexts. Regardless of these complexities, some studies have been successful in finding that allowing for stoichiometric changes at interfaces in complex compounds may result in low energy structures being discovered.^20,21,32 Similarly, Wang et al.²⁰ has found that GBs in SiC can exhibit non-stoichiometry. These examples emphasize the requirement to both consider the macroscopic and microscopic DoFs to generate low-energy GBs and interfaces.

Recently, Uberuaga et al.²² suggested that, at GBs in complex oxides, the ground state is only attained through allowing for a redistribution in the cations in the GB region even while keeping the density of the GB the same. Given this idea, we postulate in this work that in complex multi-component compounds there is a third microscopic DoF which can be thought of as the chemical composition or distribution.

This work aims to elucidate how this proposed DoF manifests through the mechanisms of spinel inversion and what the observable effects are when generating low-energy microstates with this DoF. We will do this by studying two GBs commonly studied computationally and expected to be present in polycrystalline spinel. These GBs are a Σ3(111) tilt GB and a Σ5(013)[100] tilt GB, discussed in Sections IIIA and IIIB, respectively. Within each of these sections the ground-state atomic composition local to the GB is discovered and analyzed. We then study the compositional changes at the GB as a result of induced inversion and predict how the transport of O vacancy defects will be affected by this inversion. Then in Section IIIC, we discuss the dependence of our observed trends on GB type and spinel chemistry.

II. Methodology

To understand the dependence of spinel chemistry on low-energy GB compositions, we consider three different spinel chemistries; FeCr₂O₄, NiCr₂O₄ and MgAl₂O₄, which for the sake of brevity are referred to as FCO, NCO and MAO, respectively, in the figures. The atomistic simulation package LAMMPS^33,34 has been used with atomic interactions for FeCr₂O₄/NiCr₂O₄ modeled with a Buckingham–Coulomb potential plus a Morse potential form by Chartier et al.³⁵ and MgAl₂O₄ with a Buckingham–Coulomb potential form by Smith et al.³⁶ Each of these models is fixed charge, meaning they do not allow for charge transfer and, in particular, FeCr₂O₄ and NiCr₂O₄ use partial charges, i.e., (Fe/Ni)^1.2+, Cr^1.8+ and O^1.2− while MgAl₂O₄ uses full formal charges: Mg²⁺, Al³⁺ and O²⁻ which reflects the differing ionic behavior in the materials.

These chemistries are chosen as we do not anticipate that charge transfer will play a significant role in the properties discussed here, unlike in some other spinel chemistries such as Fe₃O₄ where charge transfer between Fe²⁺ and Fe³⁺ will be prevalent.³⁷ Moreover, while these models have fixed charges they have succeeded in capturing cation disordering effects in other studies^38–41 and since the cation disorder is fundamentally connected to the electrostatics of the material⁴² this implies that there are relatively weak charge transfer effects on cation disorder. Finally, we do not anticipate the effects of magnetism to play a role, something the potential forms would not capture, since the Néel temperature is <100 K in these materials,^43,44 well below the temperatures we are interested in for real application in radiation damage or armor scenarios.

Two spinel GB structures are used in this work. A Σ3(111) tilt GB taken directly from Hasan et al.⁴⁵ and a Σ5(013)[100] in which the initial structure was generated using the ACME code⁴⁶ and the gamma-surface mapped using LAMMPS^33,34 with the lowest energy structure selected; both structures were initially created for the MgAl₂O₄ chemistry. Each atomic system contains two oppositely polarized GBs to ensure periodicity and the simulation box, as well as the atomic positions, were relaxed with each chemistry. Therefore, the size of the supercells varied by a small amount in each direction; the values quoted here are for FeCr₂O₄. The Σ3 GB has a size of approximately 51.7 × 19.9 × 22.9 ų and contains 2464 atoms. The Σ5 GB had a size of approximately 98.1 × 48.8 × 8.4 ų and contains 3808 atoms. In this simulation setup, x is the direction normal to the GB plane, y is the direction normal to the tilt axis and z is the direction parallel to the tilt axis. Both of these initial GB structures are available in the ESI† while their structures are provided in Fig. 1.

Fig. 1 Structure of (left) the Σ3 and (right) the Σ5 grain boundaries considered in this work. These structures represent the initial state for the subsequent MC simulations, as described in the text. As noted in the legend, A cations are represented by red spheres, B by yellow spheres, and oxygen by blue spheres.

Initially, these spinels and, in particular, their grain boundary compositions are ‘normal’ that is, all A²⁺ cations occupy tetrahedral sites and all B³⁺ cations occupy octahedral sites; the ground state for all three of these spinels in a bulk environment.^1,6 In this work, we first aim to relax the GBs to lower energy GB compositions to discover their ground state composition and then drive them to higher energy compositions to understand the non-equilibrium distribution of inversion through the GB system as might be induced by irradiation. This is done through a Metropolis-based Monte Carlo (MC)^47,48 algorithm with a simulation procedure identical to Hatton et al.⁴¹ where the MC temperature is used as a rough proxy for irradiation. The analysis of the spatial location of inversion uses the Wigner–Seitz defect identification tool, as implemented by Ovito,⁴⁹ and requires a definition of the ‘GB region.’ Here, this is defined as a window around the GB center with width of ≃9.4 Å and ≃11.2 Å in the Σ3 and Σ5 GB structures, respectively. These widths were chosen by inspecting the atomic energies of different species in the ‘normal’ GBs and noting the distance from the GB place where the atom energies diverged from the bulk value. The structure outside the GB regions is considered the bulk.

To assess how the transport of defects is affected by compositional changes at the GB, we use oxygen vacancies as a representative defect; this defect is chosen as it avoids the complexity of cation mixing which would occur with a migrating cation vacancy resulting in changing inversion over time,^5,41 complicating analysis. To quantify the transport of an O vacancy we calculate the mean first passage time (MFPT) from some initial vacancy position to a given final vacancy position. This method requires generating an absorbing Markov Chain which describes the hopping rate between all connected defect positions with an absorbing state at the desired final vacancy position. The algorithm outlined by Novotny⁵⁰ is then used to produce the MFPT – the average time that the defect would take to move from the initial state to the final state. This method is analogous to the limit of generating infinitely many kinetic Monte Carlo (KMC) realizations, measuring the time for the vacancy to go from the initial to final state, and taking the average time over those KMC realizations. However, it has the advantage of being significantly less computationally expensive and has been used successfully in previous studies to measure defect transport times.^51–56

This method does, however, require knowledge of the rate between connected defect positions (states) which could be generated through an extensive nudged elastic band (NEB)⁵⁷ campaign seeking individual energy barriers and thus generating the required transition matrix. This is very computationally expensive, to the point that it is prohibitive for systems of the sizes considered here. However, a reasonable approximation of this method can be created by assuming a ‘typical’ energy barrier between two states and modifying this barrier by the ΔE between the states. This method has been previously shown to be successful when generating KMC models and so will be employed here.^58–60 In particular, we define the hopping rate between two connected states, ij, to be given by,

where A is the Arrhenius pre-factor which we fix to a typical value of 10¹⁴ s⁻¹, ΔE_ij is the energy change between the vacancy in state i versus j, and E^typical_a is the typical energy barrier for an O vacancy to migrate in the bulk environment for each of the spinel chemistries. k_b is Boltzmann's constant and T is the temperature. The temperature is purely analytical and no dynamics are directly simulated at this temperature. An unphysically high temperature of 4000 K is chosen in eqn (1) as it provides numerical stability when inverting the transition matrix required by the algorithm in Novotny.⁵⁰ The consequence of choosing this temperature will be the diluting of any trend in the MFPT as, in the limit of infinite temperature, all rates are equal and the effects of any compositional or structural heterogeneity would be lost; so any trends in the MFPT described here would be more pronounced if a more realistic temperature could be chosen.

More specifically, the calculation of ΔE_ij, for any two O sites i and j, requires computing the energy of the system with a vacancy present at each O site. This is done by sequentially deleting an O atom from one site, minimizing the atomic configuration, and repeating the same procedure for the other site. The ΔE between any two vacancy sites is then known.

E ^typical_a is the result of a NEB calculation to find the energy barrier for an O vacancy to migrate between two stable sites in each of the spinel chemistries in a ‘normal’ bulk environment. It is meant to be representative of a typical migration barrier for an O vacancy in the material.

Finally, we note that the goal of this kinetic treatment is to provide a qualitative estimate of how large of an impact this new microscopic degree of freedom would have on functional properties such as transport. We are not trying to provide a quantitative prediction of transport, which would require determining every migration barrier in the system with higher fidelity models. Rather, our goal is to assess the importance of this inherent GB disorder on the properties of the GB.

III. Results

A. Inversion at the Σ3 GB

We first seek the ground state cation composition of the Σ3 GB by conducting the previously described MC procedure at a low MC temperature of 10 K. At this temperature, only atomic swaps which decrease the energy of the system are accepted. The energy per atom at each MC step for each of the three chemistries is shown in Fig. 2. The significant energy decrease in all spinel chemistries indicate that the ‘normal’ chemical distribution of the as-constructed Σ3 GB is high energy and therefore thermodynamically irrelevant in any real application since these compositions are never likely to form. Instead, it is clear that the ground state GB and/or near-GB regions contain some amount of ‘inversion’ giving rise to these energy decreases. This fact is accentuated in NiCr₂O₄ which required >1.5 million trialed MC steps to equilibrate, implying a high degree of ‘inversion’ in this case.

Fig. 2 Energy per atom of the Σ3 grain boundary structure as a function of Monte Carlo step for the three chemistries – FCO, MAO and NCO – conducted at 10 K.

Fig. 3(a) quantifies the variation and spatial location of the compositional changes induced by the MC procedure and thus the associated inversion by measuring the number of A cations in a given region compared to the ‘normal’ reference composition. In this formulation a positive (negative) value indicates an abundance of A_B (B_A) antisites in that region. We find that ground-state inversion is concentrated at the center of the GBs and their peripheries, as highlighted by the grey shaded regions. In particular, we see there is a preference for the A_B cation antisite to form at the center of the GB and an A cation depletion at the GB periphery, indicating the B_A cation antisite is preferred there. Both FeCr₂O₄ and MgAl₂O₄ exhibit similar levels of GB inversion which is consistent with our MC results showing a similar energy decrease for both compounds when allowed to relax. Conversely, NiCr₂O₄ relaxes further, which correlates with the greater degree of inversion.

Fig. 3 (a) Composition, measured as the number of excess A cations at each distance and (b) the relative charge through the structure where grey regions indicate the approximate GB regions. Both quantities are measured for an ‘inverted’ structure relative to the as-constructed ‘normal’ structure. Dashed lines at 0.0 indicate a ‘normal’ composition. Solid lines indicate the mean values of each quantity with data collected over the last 25 000 MC steps taken at intervals of 1000 steps; the widths of the shaded regions are then 2 standard deviations of the data.

In the bulk regions away from the GB we see a relatively flat compositional variation for FeCr₂O₄ and MgAl₂O₄ indicating no bulk inversion; consistent with the fact that in bulk systems the ‘normal’ composition is the ground-state for these spinel chemistries. Conversely, in NiCr₂O₄ there are indications of inversion further from the GB, into the bulk region, at ≃0.35–0.50. This alongside the large Ni signal at the GB centers imply that GBs in NiCr₂O₄ exhibit a strong preference for high levels of inversion and this influences the nearby bulk regions. Overall, these results indicate that at Σ3 GBs, spinels energetically prefer to exhibit a large degree of inversion in the GB, allowing for the co-redistribution of A cations to the GB center and B cations to the GB periphery with Ni concentrating most preferentially at the GB center.

This inversion will induce changes in the charge distribution through the GB system. In our case, these changes are due to the redistribution of ions at and near the GB plane – each ion carries a specific but static charge. As the ions redistribute, this naturally leads to changes in the charge distribution within the system. In areas where we see enrichment in A cations, we anticipate to see a negative charge compared to the ‘normal’ GB structures since A_B antisites have a negative effective charge. Similarly, areas rich in B_A antisites would induce a positive effective charge. The precise charge distribution through the system is shown in Fig. 3(b). The oxygen ions are not considered in this analysis to reduce noise in the charge distribution and because they do not redistribute during the MC procedure. The values of the charge are presented relative to the bulk region. It should be noted here that, while there is a larger number of Ni atoms at the GB center of NiCr₂O₄ compared to Mg in MgAl₂O₄, MgAl₂O₄ is described using full formal charges while the potential for NiCr₂O₄ uses partial charges. This gives rise to a similar charge concentration at the GB in NiCr₂O₄ and MgAl₂O₄.

In harsh radiation environments, spinels have been observed to undergo non-equilibrium disordering processes characterized by a large concentration of antisites.^6,7 We again use the MC algorithm to understand the partitioning of a given total amount of inversion at the GB versus in the bulk regions. In the MC algorithm, the generation of damage is simulated by increasing the temperature parameter, thereby allowing the algorithm to accept cation swaps which increase the system energy. This process is conducted at temperatures of 1000–5000 K and is an identical process to that conducted in bulk spinel environments in Hatton et al.⁴¹ While some of these temperatures may seem unphysical, the authors remind the reader that no dynamics are being run here, rather the temperature is simply a computational tool to drive inversion in our system which, in reality, will be driven by some radiation damage events. We also note that this thermally-driven inversion process is not equivalent to that induced by irradiation, but the point of the high-temperature MC is to drive the system to higher levels of inversion similar to what would happen under irradiation. To be clear, we are not claiming that this MC procedure describes the radiation damage process. Rather, both high temperature MC and radiation damage will tend to drive the cations towards a random distribution.⁶ Thus, the MC is used here to generate cation distributions that are sensitive to the local microstructure (the grain boundaries) and drive the system in a way similar to what irradiation might do.

The resulting partitioning of the inversion at the GB and bulk for temperatures 10 K and 1000–5000 K in 1000 K increments are shown in Fig. 4. Note that the initial ‘normal’ structured GBs would be located at [0.0, 0.0] on this figure. Colored circles are the average inversion in both the GB and bulk environment over the last 25 000 trialed MC steps; the length of the error bars is two standard deviations of the data. As previously defined in the methodology, the GB region is based on a fixed window width around its center. However, it is known that the GB width increases with inversion⁸ and so the data presented here could be considered a lower bound on GB inversion and, indeed, an upper bound on bulk inversion.

Fig. 4 Bulk inversion and grain boundary inversion for the Σ3 GB structure at temperatures of 10 K and 1000–5000 K in increments of 1000 K with increasing opacity indicating increasing temperature for each chemistry. MC temperatures are labeled for NCO but follow the same pattern for FeCr₂O₄ and MgAl₂O₄. The vertical dashed line at 2/3 indicates the maximum inversion which can be reached by disordering processes, corresponding to a fully random spinel. The solid black line is a dividing line between the inversion being energetically preferred at the GB versus the Bulk.

From Fig. 4 we see that all spinel chemistries prefer to accommodate low levels of inversion primarily in the GB, until a critical value of GB inversion is reached – i_GB ≃ 0.2–0.4 – at which point the bulk region begins to disorder. Inversion in MgAl₂O₄ appears to increase linearly after i_GB ≃ 0.3 and FeCr₂O₄ exhibits a similar trend in i_GBvs. i_bulk except that it takes higher temperatures to drive inversion in both the GB and the bulk as compared to MgAl₂O₄.

NiCr₂O₄ shows the most striking trend in that it inverts at lower temperatures than the other chemistries and the Σ3 GB can reach an inversion value of i_GB ≃ 0.4 before the bulk is significantly impacted by inversion, implying that antisites feel a strong thermodynamic attraction to the GB. NiCr₂O₄ also shows an interesting turn-over in GB inversion at the highest MC temperatures, seemingly then to prefer having antisites in the bulk region rather than the GB region. However, we find that at these high levels of disorder the point-defect identifying WS algorithm breaks down and the presence of this turnover becomes very sensitive to WS parameter selections. Therefore, we do not analyze this data point further other than to say that due to the high concentration of antisites at the GB and the many resulting atomic relaxations in these regions, the antisites can seemingly no longer be thought of as point defects as they have significantly disordered the nature of the GB.

The trend in total inversion as a function of MC temperature between the spinel chemistries is that, at a given MC temperature, i^driven_NCO > i^driven_MAO >i^driven_FCO which agrees with the trend in single-crystal spinel.⁴¹ This agreement implies that, in this case, spinel chemistries in which the bulk regions disorder at lower temperatures will also prefer to exhibit a higher degree of disorder in this GB.

To provide a metric of how ionic transport, crucial for understanding radiation damage, corrosion, and sintering processes, is impacted by GB inversion, we calculate the MFPT of O vacancies as a function of the compositional changes at the GB and throughout the system due to antisite-inducing damage. Results can be seen in Fig. 5(a)–(c). Fig. 5(d)–(f) give a schematic explanation of what is being measured in each of the metrics in (a)–(c). In essence, we start the O vacancy at the lowest energy site in the structure and measure, as described in the Methodology, the average time it would take the vacancy to reach an equivalent site in the simulation box's periodic image. This is done in three independent directions: normal to the GB plane (Fig. 5(d)) where the vacancy would traverse both GB structures (shaded regions) present in our simulation cell, parallel to the tilt axis (Fig. 5(e)), and normal to the tilt axis (Fig. 5(f)). The MFPT is measured in both the ‘normal’ (as-constructed) GB and the inverted structures as found from the MC simulations. Finally, Fig. 5(g) gives the segregation energy of the O vacancy to the lowest energy site at either of the GB structures present in our simulation cell compared to the bulk value, which will be used to help interpret trends in the MFPT. Further, the MFPT data presented here are used to indicate the trend in the transport as a function of cation inversion rather than exact values that can be compared to experiment or included in a higher length scale model. The authors also caution the reader against comparing the MFPT of different directions against each other. This is because the distances that are traversed by the vacancy are different in each direction which will impact the time to traverse the simulation cell. What we want to emphasize here is the impact of inversion on the transport in any given direction.

Fig. 5 (a)–(c) Mean First Passage Time (MFPT) of an O vacancy in (a) FCO, (b) MAO and (c) NCO in directions normal to the tilt axis, parallel to the tilt axis, and normal to GB plane versus total cation inversion. (d)–(f) Schematic diagrams of the geometries of the MFPT calculations shown in (a)–(c). The lighter/dashed regions indicate periodic images of the primary simulation cell. (g) O vacancy segregation energy to the Σ3 GB in each spinel chemistry against cation inversion.

First, consider the case of FeCr₂O₄ (Fig. 5(a)). Comparing the MFPT in the thermodynamically irrelevant ‘normal’ composition (i = 0) to the ground-state inversion (10 K MC, i ≃ 0.04) we clearly see a ≃4–5 orders of magnitude decrease in the MFPT. The reason for this difference can be seen in Fig. 5(g) which shows the O vacancy segregation energy. We find that in the ‘normal’ structure there are deep traps which, if a vacancy were to land there, would take a long time to escape, giving rise to a longer MFPT. In contrast, the ground-state structure does not contain these deep traps which can be seen from the ≃5 eV decrease in segregation energy. As we move to higher overall levels of inversion we see complex but significant variations in the MFPT of ≃1 order of magnitude, these variations are also consistent with the trend in the segregation energy in the higher inversion cases (Fig. 5(g)). This analysis in FeCr₂O₄ underlines the need to generate thermodynamically relevant GB compositions in order to extract experimentally comparable transport properties.

In the case of MgAl₂O₄ we see a ≃1 order of magnitude spread in the MFPT as we drive to different inversion levels, again correlating with the change in segregation energy. At this GB there is not a significant change in the segregation energy due to the compositional changes which manifests as a smaller variation in the MFPT. Thus, while MgAl₂O₄ tends to exhibit a greater propensity for inversion than FeCr₂O₄, that inversion has a smaller impact on defect energetics.

This behavior is even more exaggerated in NiCr₂O₄. In this case, we surprisingly see that, even though NiCr₂O₄ showed the most dramatic compositional changes in the GB region of all of the chemistries considered (Fig. 3), this does not seem to impact the transport time of O vacancies through these regions. These findings are again consistent with the smaller variation in the segregation energy in NiCr₂O₄ caused by the inversion (Fig. 5(g)). Further, there is a small turnover in the value of the MFPT for each direction of travel at the highest levels of inversion in NiCr₂O₄. This turnover does indeed correlate with the turnover in inversion profile observed in Fig. 4 underlining the complex dependence of compositional variation to the defect transport metrics outlined here.

With the current methodology, these results imply that, to first order, GB inversion acts to modify the defect segregation energy at the GBs and that effect is dominant in determining the relative defect transport rates through these regions. That is, the actual local compositional changes at the GB have only a limited effect on the defect transport if they are not primarily acting to modify the defect segregation energy; as evidenced in the case of NiCr₂O₄. However, this effect may also be a result of the fact that the barriers used in our transition matrix are based on ‘typical’ barriers sourced from the bulk modified by the ΔE between the states, as described in the methodology. It could be that the actual barriers for O vacancy motion between states at the GB are significantly altered by the composition, something that is not captured by our methodology.

B. Inversion at the Σ5 GB

In an effort to understand the dependence of the trends outlined in Section IIIA on GB structure, we completed a similar study of the Σ5(013)[100] GB. There are well-known computational complications when simulating this type of GB in ionic systems. In particular, the GB structure induces an electrostatic dipole which acts in the direction normal to the GB plane. This dipole causes a spatial bias in the atomic energies through the simulation cell and in the case of the spinel structure (FeCr₂O₄) it manifests as illustrated in Fig. 6. This effect has been documented in many atomistic studies of defects in and around the Σ5 GB (and other more complex GBs and interfaces) in ionic systems.^29–31,61 Recent work in UO₂ suggests that the true ground state of the Σ5 GB does not exhibit these dipoles.³¹ However, in multi-component systems such as the spinels studied here, it is highly non-trivial to generate low energy GB structures with the constraints of charge neutrality and maintaining stoichiometry; indeed, the main conclusion of the current work is that there is an additional microscopic DoF – the chemical distribution – that must be accounted for in these systems. Additionally, there are methods for ‘manually’ removing the electrostatic dipoles at other material's interfaces and with other computational methodologies,^30,62,63 these have not been employed here. Conversely, the ubiquitous nature of the finding of the electrostatic dipole at GBs in many different atomic systems has led some authors to argue that this is a real effect of the material which could be exploited in materials design.²⁹ This current work will stay impartial to the discussion of whether the dipole is a real effect or an artifact of the simulation and present the results as they have been found. Instead, we will make comments where we believe the presented results may be impacted by the presence of the electrostatic dipole.

Fig. 6 Energy per atom (eV) of Fe/O/Cr in the direction normal to the Σ5 FCO GB plane showing the effect of the electrostatic dipole on the energetics of each atomic species. Shaded grey regions are approximate GB position.

As before we use MC to find the ground-state chemical distribution of the three spinels at this GB structure. Results of the MC procedure can be seen in Fig. 7. While the results for NiCr₂O₄ and MgAl₂O₄ are reminiscent of those for the Σ3 GB, FeCr₂O₄ interestingly exhibits only a single accepted MC swap for the full run of 100 000 attempted swaps. This indicates that the ‘normal’ GB structure in FeCr₂O₄ is essentially it's ground-state, in drastic contrast to the case of the Σ3 GB. Further, we see that the NiCr₂O₄ chemistry no longer exhibits a dramatic energy decrease and, in fact, MgAl₂O₄ exhibits the greater decrease in energy as a result of the MC. This indicates the strong dependence between GB type and local composition in addition to the clear dependence on chemistry.

Fig. 7 Energy per atom of the Σ5 Grain Boundary structure as a function of Monte Carlo step for the three chemistries; FCO, MAO and NCO conducted at 10 K.

While we cannot be confident that this structure is the ground-state, due to the previously discussed computational challenges with these types of GBs, we do have confidence that these are at least the ground-state compositions for this atomic structure. It should also be noted that the MC procedure in this case does not remove the electrostatic dipole but that the MC is likely impacted by the presence of the dipole since there will be a bias on MC swaps which move atoms to a lower energy position.

The composition of the MC-determined inverse structure compared to ‘normal’ is shown in Fig. 8(a). Note that, in FeCr₂O₄, there is no difference in composition or charge since the GB essentially remains ‘normal.’ Both NiCr₂O₄ and MgAl₂O₄ show a large positive signal at the center of the GB and a large negative signal at its peripheries indicating the large redistribution of the A cations to the GB center and a corresponding co-redistribution of B cations to the peripheries of the GB. In both cases, the inversion is confined to the GB region which induces the variation in charge distribution presented in Fig. 8(b).

Fig. 8 (a) Composition, measured as the number of excess A cations at each point relative to the normal starting point, of the supercell containing two Σ5 GBs and (b) the relative charge through the structure. The grey regions indicate the approximate GB regions. Dashed lines at 0.0 indicate a ‘normal’ composition. Solid lines indicate the mean values of each quantity with data collected over the last 25 000 MC steps taken at intervals of 1000 steps; the widths of the shaded regions are then 2 standard deviations of the data.

Fig. 9 presents the complex partitioning of overall inversion, induced by different MC temperatures, on the level of disorder at the GB versus in the bulk. The general trend in MgAl₂O₄ and NiCr₂O₄ is that the inversion is concentrated at the GB until an inversion value of i_GB ≃ 0.35, at which point we see the inversion in the bulk increase until i_bulk ≃ 0.4 is reached. There is seemingly a convergence of the GB vs. bulk inversion to the dividing line indicating that at high levels of disorder there is no preference for inversion to be located in either region, possibly a result of the large amount of disorder which would be present at these higher temperatures. Additionally, there is also a large jump in the NiCr₂O₄ bulk inversion value between MC temperatures of 2000 K and 3000 K indicating there is a threshold of total inversion after which point inversion becomes driven to disorder the bulk-like region away from the GB.

Fig. 9 Bulk inversion and grain boundary inversion for the Σ5 GB structure at temperatures of 10 K and 1000–5000 K in increments of 1000 K with increasing opacity of the points indicating increasing temperature for each chemistry. MC temperatures are labeled for NCO but follow the same pattern for FeCr₂O₄ and MAO. The dashed line at 2/3 indicates the maximum inversion which can be reached by disordering process. The solid black line is a dividing line between the inversion being energetically preferred at the GB versus bulk.

In FeCr₂O₄, an MC temperature of >3000 K is required to induce any significant amount of inversion. In this case, the GB accommodated an inversion value of i_GB ≃ 0.2 before bulk inversion is induced, at which point both increase linearly. However, the overall inversion that was reached was not high enough to make direct comparison with the trends seen in NiCr₂O₄ and MgAl₂O₄.

Fig. 10 shows the MFPT of an O vacancy as a function of total inversion for each of our spinel chemistries. Although FeCr₂O₄ exhibited only small amounts of inversion compared to the other chemistries it exhibits a dramatic change in transport with increasing inversion. In particular, the MFPT has a 6 orders of magnitude variation between the lowest and highest cation inversion value. Also, there is a divergence in the MFPT data between the different directions of travel as the overall inversion increases. MgAl₂O₄ exhibits a similar profile in the MFPT, also exhibiting a 6 orders of magnitude increase in MFPT normal to the GB plane, though this shift is a bit more abrupt with a sudden increase at the highest levels of inversion. The transport of O vacancies in NiCr₂O₄ is the least affected by cation inversion, giving the smallest spread in MFPT, though it still varies by ≃2 orders of magnitude. Interestingly, it is non-monotonic with inversion, first increasing and then decreasing as inversion is increased for two of the directions.

Fig. 10 Mean first passage time (MFPT) of an O vacancy in (a) FCO, (b) MAO and (c) NCO in directions normal to the tilt axis, parallel to the tilt axis, and normal to the GB plane versus cation inversion. See Fig. 5(d)–(f) for schematic descriptions of these MFPT metrics.

Overall the effect of cation inversion on defect transport appears enhanced at this GB compared to the previously discussed Σ3 GB. At the same time, the transport properties are a very complex function of the inversion, challenging our ability to develop predictive models of this relationship. Defect segregation is not presented here due to the presence of the electrostatic dipole which will corrupt these calculations. That said, we can speculate that the greater variation in MFPT compared to Σ3 is likely a consequence of a stronger dependence on trapping with inversion at this structure.

C. Discussion

The computational search for the ground-state GB structures in multicomponent ionic systems is a highly non-trivial exercise. It is well-known that one must consider both macroscopic DoFs, which define inter-grain orientations and angles, as well as microscopic DoFs, which define atomic density/stoichiometry and the relative translation of the two grains. In compounds characterized by multiple atomic sublattices, such as the spinel structure analyzed here, we have provided strong evidence of the existence of an additional microscopic DoF – the chemical distribution. This must be considered to generate low-energy microstates; independent of any previously discussed macroscopic or microscopic DoF.

As discussed extensively in this work, this new compositional DoF directly leads to spatially varying inversion near GBs in spinel. We find that, in the majority of cases, the ground-state GB exhibited a high degree of inversion consistent with previous findings²² (the counter example to this is the Σ5 GB in FeCr₂O₄ which has a ground-state composition that is fully ‘normal’). Additionally, we find this GB inversion drives the redistribution of A cations to the first atomic layer of the GB and a redistribution of B cations to the periphery of the GB. We suspect that this co-redistribution behavior occurs to maintain local charge neutrality – that the redistribution of the A cations induces a space charge layer that is then neutralized by the co-redistributing B cations. Further work will be needed to evaluate this conjecture though it is consistent with other previous work of defects and interfaces in complex ionic materials.^64–67

Additionally, we find two interesting observations from our results. Firstly, the high level of inversion seen for GBs in NiCr₂O₄ is surprising and we postulate that, since Ni experiences a strong thermodynamic tendency to redistribute to the GB center, this driving force pushes NiCr₂O₄ to high inversion even at low temperatures. Secondly, there does appear to be a consistent trend in the amount of disorder observed in the GB ground-state as a function of spinel chemistry. Namely, in terms of inversion, i^ground_NCO > i^ground_MAO > i^ground_FCO, though more GBs will need to be characterized to investigate the robustness of this trend.

Experimental observations of GB compositions in spinel are sparse but some studies do exist for GBs in MgAl₂O₄.^68–70 These studies are not able to achieve the atomic fidelity possible computationally but generally find that GB centers are more Al (B cation) rich than bulk regions, seemingly in contrast to our results (Fig. 3(a) and 8(a)). However, our data uses the ‘normal’ GB structure as the reference rather than the bulk composition as in experimental analysis. If we reformulate our composition metric to match the experimental metric of Al (B)/Mg (A) ratio then we produce Fig. 11 which presents data for a Σ3 GB in MgAl₂O₄. This metric also reveals higher B cation concentration at the GB center – compared to the bulk – in qualitative agreement with experimental data.^68,69 While our atomistic work is essentially completed in a stoichiometric sample, experimental observations of GB composition depend strongly on spinel stoichiometry⁷⁰ which further underlines the complex dependencies on compositional variations in spinel.

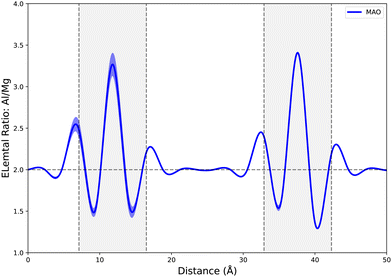Fig. 11 Elemental ratio (Al (B)/Mg (A)) for MAO through the Σ3 GB structure where grey regions indicate the approximate GB regions. The source data here is the same as in Fig. 3, it is simply presented as a local stoichiometry rather than an elemental excess. The dashed line at 2.0 indicates the bulk Al : Mg ratio and the width of the shaded regions are 2 standard deviations.

The use of this chemical distribution-based DoF has also allowed us to find low-energy metastable microstates of the GB system at a given level of overall inversion. This has been done as an approximation of the level of damage which spinel may exhibit in reactor environments – an important possible application for these materials. We find that as we drive the spinels to higher degrees of overall inversion, both GB types and all spinel chemistries exhibit a complicated relationship between the variation of GB vs. bulk inversion. It is clear though that in all cases the inversion is preferentially accommodated at the GB first and then there is a competition between bulk and GB inversion at higher overall inversion levels. We do not see a sudden transition from GB to bulk inversion, indicating that the GBs are not saturating in inversion before the bulk begins to invert. Rather, we see a critical level of GB inversion at which the bulk also begins to invert, suggesting that the GBs are simply easier to invert than bulk-like regions. Similarly to both bulk spinel and the behavior of the ground state GBs, we find the same trend in the driven response in these systems, i^driven_NCO > i^driven_MAO > i^driven_FCO.

The highly non-trivial profiles of inversion lead to a complex picture of the defect transport properties through the GB regions and we find in some cases there is large variation in the O vacancy transport depending on GB inversion. These transport metrics correlate well with GB segregation energies which are modified by the presence of GB inversion. In particular, we find that in many cases using the ‘normal’ GB to calculate defect transport metrics would result in a significant over/under estimation of transport by many orders of magnitude, again depending on the GB type, chemistry, and direction of defect transport with respect to the GB. Additionally, it appears that the trend in variation of the transport is different between the GBs. That is, in Σ3 we generally see a decrease in MFPT with increasing inversion, whereas in Σ5 we see an increase in MFPT.

Further, there is seemingly not a direct correlation between the change in defect transport and compositional variation as a result of inversion, evidenced by NiCr₂O₄ which experienced the highest inversion at low temperatures but in which the defect transport was least affected. There is, however, a correlation between defect segregation energy and defect transport through the GB regions. So, if the compositional variations induced by inversion act to significantly modify the defect segregation energy then, in turn, the defect transport will be significantly modified.

To better understand some of the factors that drive the chemical redistribution of cations at these grain boundaries, we have examined the coordination and bonding environment of both A and B cations at the Σ3 GB. We find that, generally, greater inversion is accompanied by an increase in the coordination of A cations and a corresponding decrease in the B cation coordination. This is counter-intuitive as, in the bulk, the B cations favor the octahedral site which has greater coordination. At the same time, we find that there is an increase in A–A coordination – A cations prefer to have other A cations as nearest neighbors (neglecting the intermediate oxygen), with again a corresponding drop in B–B coordination. Thus, the chemical redistribution seems to be driven, in part, by a preference for A cations to have greater coordination and more A neighbors at the GB than they do in the bulk.

Thus, we have shown that the investigated quantities of interest strongly depend on the microstate of the system generated by this chemical redistribution-driven DoF, independent of any other GB DoF. That is, we have not remapped the gamma surface nor altered the density of the GBs; we have only allowed for chemical redistribution through the mechanism of spinel inversion which has allowed us to discover new low-energy GBs. However, it is shown in previous work^25,28,71,72 that considering GB DoFs independently is not sufficient. Therefore, we postulate that only by considering all 3 microscopic DoFs simultaneously – gamma-surface mapping, atomic fraction mapping and finally the newly proposed atomic redistribution-driven DoF – can we truly canvas the ground-state structures and compositions of complex multi-component compounds. Furthermore, we believe that this will also be the case in other complex materials (wherever chemical redistribution is possible) and, indeed, at other interfaces and extended defects such as dislocations.

Of course, there are several limitations to our study. First and foremost is that we are using a classical model for interatomic interactions that does not account for charge transfer between ions. While we have specifically chosen spinel chemistries in which the ionic charges are fairly rigid, there is always the possibility for charge transfer to modify the behavior observed here. In principle, density functional theory (DFT) calculations could aid in addressing this point, but the system sizes and the Monte Carlo treatment considered here render that computationally prohibitive. We do expect that charge transfer would modify the details as new mechanisms to accommodate defects at the grain boundaries would arise, but we also see no reason to think that the basic result – that the grain boundaries exhibit a higher degree of disorder than the bulk – would change. Our past experience comparing results from these types of empirical potentials and DFT for grain boundary properties such as segregation⁷³ and even subtle effects like structurally-induced electrostatic dipoles,²⁹ as well as complex defects,^74–77 in these ionic oxides demonstrates that these types of models do well in describing the general physical behavior of these materials and structures. Finally, our treatment of charge as fixed to the ion cores is of course an approximation, but one that has been used to study, for example, the formation of space charges at dislocation cores in ionic oxides.^66,78 Thus, while it does not allow for charge transfer as DFT calculations might, it still provides a first-order treatment of the charges associated with charge redistribution in real materials.

Further, temperature is at best an imperfect proxy for irradiation. However, the goal here is to drive the disorder to highly non-equilibrium configurations and high temperature serves that purpose. In addition, in our Monte Carlo procedure, the anions are not included in the sampling process. While, for any new cation configuration, their positions are minimized, their location within the structure is not searched which could further modify the overall grain boundary structure.

This last point deserves to be expanded upon. To truly find the ground state structure of a grain boundary, one would need to perform an optimization that considers all microscopic degrees of freedom simultaneously: finding the minimum on the gamma surface, adjusting the atomic number in a grand canonical simulation,^25,28 and, in a compound, swapping atoms. There is currently no algorithm that would perform such a combined search in this high dimensional space. Thus, what we have shown here is that, in addition to the recognized microscopic degrees of freedom, chemical disorder must be added.

Finally, the general observation that grain boundaries, even in their ground state, accommodate more disorder than the bulk crystal and that this is an aspect that must be considered when describing grain boundaries, should apply broadly beyond the specific case of spinels considered here. Indeed, we think that any compound in which antisites are possible, including other complex oxides, semiconducting compounds such as GaAs, and even ordered intermetallic alloys, would exhibit the same behavior. Based upon our results, the degree would depend on both the grain boundary structure and the chemical nature of the compound, but the salient result is that the structural motifs at grain boundaries, which are inherently different than in the bulk crystal, can stabilize and promote antisite disorder even within the ground state and we see no reason that other compounds would not behave similarly.

IV. Conclusion

This work has used atomistic simulations with molecular statics techniques to analyze GBs in different spinel chemistries as a case study for a proposed chemical redistribution-driven DoF for GBs and interfaces in complex compounds. We have presented strong evidence that independently varying the atomic distribution at the GB results in the discovery of ground-state microstates of the spinel GB unattainable through the control of other previously known macroscopic or microscopic DoFs. The features of these GB microstates are highly dependant on both the spinel chemistry and the GB type. Common themes do arise from further analysis which indicate that at their ground-state, GBs energetically prefer to have an A cation rich center with a B cation rich periphery when compared to the ‘normal’ chemical distribution – the ground state bulk distribution for these chemistries. Further to this, we find that at high levels of cation disorder, as may result from radiation damage processes, we continue to see that antisites are thermodynamically very easy to form at spinel GBs leading to further compositional variations in these regions.

We also find that observable properties such as defect transport and segregation energy depend strongly on the composition of the GB. Indeed, we find that defect transport can be modified by many orders of magnitude, either up or down depending on the GB structure and chemistry. Therefore, we conclude that GB microstates must be generated through this DoF in order to accurately treat GBs in complex materials. Finally, we postulate that spinel GBs are not an isolated edge case for these ideas. In fact, we expect this to be a necessary consideration in any complex compound which can exhibit atomic distribution variations which also contains any extended defect structure.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Paul Fossati for assistance in using his ACME structure generation code. They also acknowledge the fruitful discussions with Danny Perez concerning the evaluation of the mean first passage time metric and the support of Enrique Martinez when using his Monte Carlo simulation code. This research used resources provided by the Los Alamos National Laboratory Institutional Computing Program, which is supported by the U.S. Department of Energy National Nuclear Security Administration under contract no. 89233218CNA000001. This work was supported as part of FUTURE (Fundamental Understanding of Transport Under Reactor Extremes), an Energy Frontier Research Center funded by the U.S. Department of Energy (DOE), Office of Science, Basic Energy Sciences. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (contract no. 89233218CNA000001).

References

1. K. E. Sickafus, J. M. Wills and N. W. Grimes, Structure of spinel, J. Am. Ceram. Soc., 1999, 82(12), 3279–3292.
2. M. Satalkar, S. Kane, P. Kulriya and D. Avasthi, Swift heavy ion irradiated spinel ferrite: a cheap radiation resistant material, Nucl. Instrum. Methods Phys. Res., Sect. B, 2016, 379, 235–241.
3. C. Kinoshita, K. Fukumoto, K. Fukuda, F. Garner and G. Hollenberg, Why is magnesia spinel a radiation-resistant material?, J. Nucl. Mater., 1995, 219, 143–151.
4. J. Robertson, The mechanism of high temperature aqueous corrosion of stainless steels, Corros. Sci., 1991, 32(4), 443–465.
5. C. R. Kreller and B. P. Uberuaga, The role of cation ordering and disordering on mass transport in complex oxides, Curr. Opin. Solid State Mater. Sci., 2021, 25(2), 100899.
6. K. Sickafus, A. Larson, N. Yu, M. Nastasi, G. Hollenberg and F. Garner, et al., Cation disorder in high dose, neutron-irradiated spinel, J. Nucl. Mater., 1995, 219, 128–134.
7. K. Sickafus, L. Minervini, R. Grimes, J. Valdez, M. Ishimaru and F. Li, et al., Radiation tolerance of complex oxides, Science, 2000, 289(5480), 748–751.
8. B. P. Uberuaga, M. Tang, C. Jiang, J. A. Valdez, R. Smith and Y. Wang, et al., Opposite correlations between cation disordering and amorphization resistance in spinels versus pyrochlores, Nat. Commun., 2015, 6(1), 1–8.
9. T. D. Shen, S. Feng, M. Tang, J. A. Valdez, Y. Wang and K. E. Sickafus, Enhanced radiation tolerance in nanocrystalline MgGa₂O₄, Appl. Phys. Lett., 2007, 90(26), 263115.
10. M. C. Patterson, A. Digiovanni, G. Gilde and D. W. Roy Spinel armor—clearly the way to go. In: 27th Annual Cocoa Beach Conference on Advanced Ceramics and Composites: A: Ceramic Engineering and Science Proceedings. Wiley Online Library; 2003. p. 441-446.
11. J. J. Swab, J. C. Lasalvia, G. A. Gilde, P. J. Patel and M. J. Motyka Transparent armor ceramics: AlON and spinel. In: 23rd Annual Conference on Composites, Advanced Ceramics, Materials, and Structures: B: Ceramic Engineering and Science Proceedings. Wiley Online Library; 1999. p. 79-84.
12. E. Strassburger, M. Hunzinger, P. Patel and J. W. McCauley, Analysis of the fragmentation of AlON and spinel under ballistic impact, J. Appl. Mech., 2013, 80(3), 031807.
13. T. Benitez, S. Y. Gómez, A. P. N. de Oliveira, N. Travitzky and D. Hotza, Transparent ceramic and glass-ceramic materials for armor applications, Ceram. Int., 2017, 43(16), 13031–13046.
14. D. N. Muche, M. A. Marple, I. Hung, Z. Gan, R. H. Castro and S. Sen, Size-induced structural disorder enables ultrahard oxides, J. Phys. Chem. C, 2017, 121(25), 13898–13905.
15. B. P. Uberuaga and G. Pilania, Inversion, chemical complexity, and interstitial transport in spinels, J. Am. Ceram. Soc., 2021, 104(5), 2313–2324.
16. B. Uberuaga, D. Bacorisen, R. Smith, J. Ball, R. Grimes and A. Voter, et al., Defect kinetics in spinels: Long-time simulations of MgAl₂O₄, MgGa₂O₄, and MgIn₂O₄, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(10), 104116.
17. R. Perriot, B. P. Uberuaga, R. J. Zamora, D. Perez and A. F. Voter, Evidence for percolation diffusion of cations and reordering in disordered pyrochlore from accelerated molecular dynamics, Nat. Commun., 2017, 8(1), 1–8.
18. I. J. Beyerlein, M. J. Demkowicz, A. Misra and B. Uberuaga, Defect-interface interactions, Prog. Mater. Sci., 2015, 74, 125–210.
19. E. Martínez, B. P. Uberuaga and I. J. Beyerlein, Atomic-scale studies of defect interactions with homo-and heterophase interfaces, JOM, 2016, 68(6), 1616–1624.
20. X. Wang, H. Zhang, T. Baba, H. Jiang, C. Liu and Y. Guan, et al., Radiation-induced segregation in a ceramic, Nat. Mater., 2020, 19(9), 992–998.
21. N. Swaminathan, M. Wojdyr, D. D. Morgan and I. Szlufarska, Radiation interaction with tilt grain boundaries in β-SiC, J. Appl. Phys., 2012, 111(5), 054918.
22. B. P. Uberuaga and R. Perriot, Spatially-varying inversion near grain boundaries in MgAl₂O₄, RSC Adv., 2020, 10(20), 11737–11742.
23. S. Wu, J. Xue, R. Wang and J. Li, Synthesis, characterization and microwave dielectric properties of spinel MgGa₂O₄ ceramic materials, J. Alloys Compd., 2014, 585, 542–548.
24. A. Kan, T. Moriyama, S. Takahashi and H. Ogawa, Cation distributions and microwave dielectric properties of spinelstructured MgGa₂O₄ ceramics, Jpn. J. Appl. Phys., 2013, 52(9S1), 09KH01.
25. S. von Alfthan, K. Kaski and A. Sutton, Order and structural units in simulations of twist grain boundaries in silicon at absolute zero, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74(13), 134101.
26. P. Keblinski, S. Phillpot, D. Wolf and H. Gleiter, Thermodynamic criterion for the stability of amorphous intergranular films in covalent materials, Phys. Rev. Lett., 1996, 77(14), 2965.
27. P. Keblinski, S. R. Phillpot, D. Wolf and H. Gleiter, On the thermodynamic stability of amorphous intergranular films in covalent materials, J. Am. Ceram. Soc., 1997, 80(3), 717–732.
28. T. Frolov, Q. Zhu, T. Oppelstrup, J. Marian and R. E. Rudd, Structures and transitions in bcc tungsten grain boundaries and their role in the absorption of point defects, Acta Mater., 2018, 159, 123–134 . Available from: https://www.sciencedirect.com/science/article/pii/S1359645418305871.
29. P. Nerikar, C. Stanek, S. Phillpot, S. Sinnott and B. Uberuaga, Intrinsic electrostatic effects in nanostructured ceramics, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(6), 064111.
30. C. Tao, D. Mutter, D. F. Urban and C. Elsässer, Atomistic calculations of charged point defects at grain boundaries in SrTiO₃, Phys. Rev. B, 2021, 104(5), 054114.
31. L. Yang and B. Wirth, Tilt grain boundary stability in uranium dioxide and effect on xenon segregation, J. Nucl. Mater., 2023, 577, 154302.
32. A. L. S. Chua, N. A. Benedek, L. Chen, M. W. Finnis and A. P. Sutton, A genetic algorithm for predicting the structures of interfaces in multicomponent systems, Nat. Mater., 2010, 9(5), 418–422.
33. S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19 , Available from: https://www.sciencedirect.com/science/article/pii/S002199918571039X.
34. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown and P. S. Crozier, et al., LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171.
35. A. Chartier, B. Golovchuk, S. Gossé and L. Van Brutzel, Disordering and grain boundaries of (Ni, FeCr₂O₄) spinels from atomistic calculations, J. Chem. Phys., 2013, 139(13), 134702.
36. R. Smith, D. Bacorisen, B. Uberuaga, K. Sickafus, J. Ball and R. Grimes, Dynamical simulations of radiation damage in magnesium aluminate spinel, MgAl₂O₄, J. Phys.: Condens. Matter, 2005, 17(6), 875.
37. S. Srivastava, B. P. Uberuaga and M. Asta, Density functional theory study of local environment effects on oxygen vacancy properties in magnetite, J. Phys. Chem. C, 2023, 127(35), 17460–17472.
38. T. Yamamoto, A. Chartier, K. Yasuda, C. Meis, K. Shiiyama and S. Matsumura, Molecular dynamics simulation of point defect accumulation in MgAl₂O₄, Nucl. Instrum. Methods Phys. Res., Sect. B, 2008, 266(12–13), 2676–2682.
39. A. Chartier, T. Yamamoto, K. Yasuda, C. Meis and S. Matsumura, Frenkel pair accumulation induced crystallization of amorphous MgAl₂O₄, J. Nucl. Mater., 2008, 378(2), 188–192.
40. L. Van Brutzel, A. Chartier, B. Sicaud and M. Sauzay, Mechanical behavior of (Ni, Fe)Cr₂O₄ spinel grain boundaries studied by molecular dynamics simulations, J. Chem. Phys., 2019, 151(1), 014701.
41. P. Hatton and B. P. Uberuaga, Short Range Order in Disordered Spinel and the Impact on Cation Vacancy Transport, J. Mater. Chem. A, 2023, 11, 3471.
42. V. Stevanović, M. d’Avezac and A. Zunger, Simple pointion electrostatic model explains the cation distribution in spinel oxides, Phys. Rev. Lett., 2010, 105(7), 075501.
43. G. Shirane, D. Cox and S. Pickart, Magnetic structures in FeCr₂S₄ and FeCr₂O₄, J. Appl. Phys., 1964, 35(3), 954–955.
44. R. Batulin, M. Cherosov, A. Kiiamov, A. Zinnatullin, F. Vagizov and D. Tayurskii, et al., Synthesis and single crystal growth by floating zone technique of FeCr₂O₄ multiferroic spinel: Its structure, composition, and magnetic Properties, Magnetochemistry, 2022, 8(8), 86.
45. M. M. Hasan, P. P. Dholabhai, S. Dey, B. P. Uberuaga and R. H. Castro, Reduced grain boundary energies in rare-earth doped MgAl₂O₄ spinel and consequent grain growth inhibition, J. Eur. Ceram. Soc., 2017, 37(13), 4043–4050.
46. C. O. Galvin, M. W. D. Cooper, P. C. Fossati, C. R. Stanek, R. W. Grimes and D. A. Andersson, Pipe and grain boundary diffusion of He in UO₂, J. Phys.: Condens. Matter, 2016, 28(40), 405002.
47. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, Equation of state calculations by fast computing machines, J. Chem. Phys., 1953, 21(6), 1087–1092.
48. E. Martínez and A. Caro, Atomistic modeling of long-term evolution of twist boundaries under vacancy supersaturation, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(21), 214109.
49. A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18(1), 015012.
50. M. Novotny, Monte Carlo algorithms with absorbing Markov chains: Fast local algorithms for slow dynamics, Phys. Rev. Lett., 1995, 74(1), 1.
51. C. Y. Lu, D. Perez, D. D. Hickmott and A. F. Voter, Insights into microscopic diffusion processes at a solid/fluid interface under supercritical conditions: a study of the aqueous calcite (1014) surface, J. Phys. Chem. C, 2012, 116(49), 25934–25942.
52. T. D. Swinburne and D. Perez, Automated calculation and convergence of defect transport tensors. NPJ Computational, Materials, 2020, 6(1), 190.
53. R. B. Garza, J. Lee, M. H. Nguyen, A. Garmon, D. Perez and M. Li, et al., Atomistic mechanisms of binary alloy surface segregation from nanoseconds to seconds using accelerated dynamics, J. Chem. Theory Comput., 2022, 18(7), 4447–4455.
54. T. D. Swinburne and D. Perez, Self-optimized construction of transition rate matrices from accelerated atomistic simulations with Bayesian uncertainty quantification, Phys. Rev. Mater., 2018, 2(5), 053802.
55. M. Athenes, S. Kaur, G. Adjanor, T. Vanacker and T. Jourdan, Elastodiffusion and cluster mobilities using kinetic Monte Carlo simulations: Fast first-passage algorithms for reversible diffusion processes, Phys. Rev. Mater., 2019, 3(10), 103802.
56. G. Nandipati, Y. Shim and J. G. Amar, First-passage time approach to kinetic Monte Carlo simulations of metal (100) growth, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(23), 235415.
57. G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113(22), 9901–9904,  DOI:10.1063/1.1329672 . Available from:.
58. P. P. Dholabhai, E. Martínez, N. T. Brown and B. P. Uberuaga, On the mobility of carriers at semi-coherent oxide heterointerfaces, Phys. Chem. Chem. Phys., 2017, 19(34), 23122–23130.
59. A. Van der Ven, G. Ceder, M. Asta and P. Tepesch, Firstprinciples theory of ionic diffusion with nondilute carriers, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64(18), 184307.
60. A. Van der Ven and G. Ceder, First principles calculation of the interdiffusion coefficient in binary alloys, Phys. Rev. Lett., 2005, 94(4), 045901.
61. D. Duffy, Grain boundaries in ionic crystals, J. Phys. C-Solid State Phys., 1986, 19(23), 4393.
62. B. Meyer and D. Vanderbilt, Ab initio study of BaTiO₃ and PbTiO₃ surfaces in external electric fields, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63(20), 205426.
63. C. Freysoldt and J. Neugebauer, First-principles calculations for charged defects at surfaces, interfaces, and twodimensional materials in the presence of electric fields, Phys. Rev. B, 2018, 97(20), 205425.
64. R. A. De Souza, The formation of equilibrium space-charge zones at grain boundaries in the perovskite oxide SrTiO₃, Phys. Chem. Chem. Phys., 2009, 11(43), 9939–9969.
65. D. S. Mebane and R. A. De Souza, A generalised space-charge theory for extended defects in oxygen-ion conducting electrolytes: from dilute to concentrated solid solutions, Energy Environ. Sci., 2015, 8(10), 2935–2940.
66. J. M. Börgers, J. Kler, K. Ran, E. Larenz, T. E. Weirich and R. Dittmann, et al., Faster diffusion of oxygen along dislocations in (La, Sr)MnO₃ + d is a spacecharge phenomenon, Adv. Funct. Mater., 2021, 31(51), 2105647.
67. F. Gunkel, R. Waser, A. H. Ramadan, R. A. De Souza, S. Hoffmann-Eifert and R. Dittmann, Space charges and defect concentration profiles at complex oxide interfaces, Phys. Rev. B, 2016, 93(24), 245431.
68. N. Nuns, F. Beclin and J. Crampon, Space charge characterisation by EDS microanalysis in spinel MgAl₂O₄, J. Eur. Ceram. Soc., 2005, 25(12), 2809–2811.
69. N. Nuns, F. Béclin and J. Crampon, Grain-boundary characterization in a nonstoichiometric fine-grained magnesium aluminate spinel: effects of defect segregation at the space-charge layers, J. Am. Ceram. Soc., 2009, 92(4), 870–875.
70. M. Halabi, V. Ezersky, A. Kohn and S. Hayun, Charge distribution in nano-scale grains of magnesium aluminate spinel, J. Am. Ceram. Soc., 2017, 100(2), 800–811.
71. T. Frolov, M. Asta and Y. Mishin, Phase transformations at interfaces: observations from atomistic modeling, Curr. Opin. Solid State Mater. Sci., 2016, 20(5), 308–315.
72. T. Frolov, W. Setyawan, R. Kurtz, J. Marian, A. R. Oganov and R. E. Rudd, et al., Grain boundary phases in bcc metals, Nanoscale, 2018, 10(17), 8253–8268.
73. M. Hong, B. P. Uberuaga, S. R. Phillpot, D. A. Andersson, C. R. Stanek and S. B. Sinnott, The role of charge and ionic radius on fission product segregation to a model UO₂ grain boundary, J. Appl. Phys., 2013, 113(13), 134902.
74. B. P. Uberuaga, R. Smith, A. Cleave, F. Montalenti, G. Henkelman and R. Grimes, et al., Structure and mobility of defects formed from collision cascades in MgO, Phys. Rev. Lett., 2004, 92(11), 115505.
75. B. P. Uberuaga and R. Perriot, Insights into dynamic processes of cations in pyrochlores and other complex oxides, Phys. Chem. Chem. Phys., 2015, 17(37), 24215–24223.
76. X. Y. Liu, B. P. Uberuaga, D. Andersson, C. R. Stanek and K. Sickafus, Mechanism for transient migration of xenon in UO₂, Appl. Phys. Lett., 2011, 98(15), 151902.
77. A. Banerjee, A. A. Kohnert, E. F. Holby and B. P. Uberuaga, Interplay between defect transport and cation spin frustration in corundum-structured oxides, Phys. Rev. Mater., 2021, 5(3), 034410.
78. V. Metlenko, A. H. Ramadan, F. Gunkel, H. Du, H. Schraknepper and S. Hoffmann-Eifert, et al., Do dislocations act as atomic autobahns for oxygen in the perovskite oxide Sr–TiO₃?, Nanoscale, 2014, 6(21), 12864–12876.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp01070a

---