 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Changing aromatic properties through stacking: the face-to-face dimer of Ni(II) bis(pentafluorophenyl)norcorrole†
Qian
Wang
 a,
Dage
Sundholm
a,
Dage
Sundholm
 *a,
Jürgen
Gauss
*a,
Jürgen
Gauss
 b,
Tommaso
Nottoli
b,
Tommaso
Nottoli
 c,
Filippo
Lipparini
c,
Filippo
Lipparini
 c,
Shota
Kino
d,
Shusaku
Ukai
d,
Norihito
Fukui
c,
Shota
Kino
d,
Shusaku
Ukai
d,
Norihito
Fukui
 de and
Hiroshi
Shinokubo
de and
Hiroshi
Shinokubo
 d
d
aDepartment of Chemistry, Faculty of Science, University of Helsinki, P.O. Box 55 (A.I. Virtanens plats 1), FIN-00014, Finland. E-mail: Dage.Sundholm@helsinki.fi
bDepartment Chemie, Johannes Gutenberg-Universität Mainz, Duesbergweg 10-14, D-55128 Mainz, Germany
cDipartimento di Chimica e Chimica Industriale, Università di Pisa, Via G. Moruzzi 13, I-56124 Pisa, Italy
dDepartment of Molecular and Macromolecular Chemistry, Graduate School of Engineering and Integrated Research Consortium on Chemical Sciences (IRCCS), Nagoya University, Furo-cho, Chikusa-ku, Nagoya, Aichi 464-8603, Japan
eGraduate School of Engineering, Nagoya University, 2JST PRESTO, Japan
First published on 1st May 2024
Abstract
Nuclear magnetic resonance (NMR) shielding constants have been calculated for Ni(II) bis(pentafluorophenyl)norcorrole and its face-to-face stacked dimer at the Hartree–Fock (HF), second-order Møller–Plesset perturbation theory (MP2), complete-active-space self-consistent-field (CASSCF) levels as well as at density functional theory (DFT) levels using several functionals. The calculated 1H NMR shielding constants agree rather well with the experimental ones. The shielding constants of N and Ni calculated at DFT, HF, and MP2 levels differ from those obtained in the CASSCF calculations due to near-degeneracy effects at the Ni atom. The calculated magnetically induced current densities show that the monomer is antiaromatic, sustaining a strong global paratropic ring current, and the dimer is aromatic, sustaining a strong diatropic ring current. Qualitatively the same current density is obtained at the employed levels of theory. The most accurate ring-current strengths are probably obtained at the MP2 level. The aromatic dimer has a short intermolecular distance of less than 3 Å. The intermolecular interaction changes the nature of the frontier orbitals leading to a formal double bond between the norcorrole macrocycles.
1 Introduction
Molecular rings with an even number of orbitals in the cyclic conjugation are antiaromatic, whereas aromatic molecules have odd number of conjugated orbitals in the ring.1 The generalized aromaticity rule holds for singlet, triplet and high-spin states.1 For closed-shell planar molecular rings, it leads to the well-known aromaticity rule stating that ring-shaped molecules with 4n π electrons are antiaromatic. Antiaromatic rings stacked in a parallel fashion can form aromatic cyclophanes, i.e., cyclic aromatic face-to-face-oriented dimers, when the interaction between the monomers is strong enough to alter the occupation of the frontier orbitals.2–13 It was recently reported that the bonding between antiaromatic Ni(II) bis(pentafluorophenyl)norcorrole macrocycles is a multi-centered double bond that leads to a short intermolecular distance of less than 3.0 Å, where the chemical bond between the two stacked antiaromatic molecules is formed by two binding molecular orbitals involving both molecules.14 Energy decomposition calculations yielded a stacking energy of 79.5 kJ mol−1 of which 28.5 kJ mol−1 is between the Ni atoms, whereas the rest consists of small interaction energies distributed among 14 C–C and N–N pairs of the stacked norcorroles.14 Weak Ni–Ni interaction has previously been observed for a dibenzotetraaza[14]annulene Ni(II) complex that leads to a molecular splitting of the atomic fine-structure levels of the Ni atoms. Ni(II) dibenzotetraaza[14]annulene is paramagnetic in the solid state at temperatures above 13 K.15Norcorrole with its 12 conjugated orbitals in the macrocycle is the smallest antiaromatic porphyrinoid.16,17 Nozawa et al. have synthesized an antiaromatic Ni(II) norcorrole with phenyl substituents in the meso positions that forms a triple-decker π–π stacked structure in the solid state.4 They have also synthesized and characterized a cyclophane that consists of two antiaromatic Ni(II) norcorrole moieties connected with two bithiophene linkers, which leads to a distance between the face-to-face stacked norcorrole macrocycles that is shorter than the sum of their van der Waals distances.6 Calculations of the magnetically induced current-density susceptibility (MICD) and the measured 1H NMR chemical shifts showed that the bithiophene-linked Ni(II) norcorrole dimer is a three-dimensional aromatic molecule with MICD pathways between the two norcorrole moieties.6 A Ni(II) norcorrole cyclophane has also been synthesized as micellar capsules in water.18
In this work, we calculate the MICD and NMR chemical shifts of Ni(II) bis(pentafluorophenyl)norcorrole (1) and its stacked dimer (12) at the density functional theory (DFT), Hartree–Fock (HF) and ab initio correlated levels. The calculated chemical shifts are compared to available experimental data.14 The stacked Ni(II) bis(pentafluorophenyl)norcorrole dimer has no linkers that force the norcorrole macrocycles close to each other. The short Ni–Ni distance of 2.97 Å in the solid state is most likely due to the aromatic stabilization of the antiaromatic norcorrole rings and the formation of a multicenter chemical bond between the norcorrole macrocycles.
The bonding of 12 is further strengthened by the pentafluorphenyl substituents in the meso positions. The fluorine atoms attract electrons and thereby increase the van der Waals attraction between the Ni(II) norcorrole macrocycles and between the phenyl rings. Ni(II) norcorrole with phenyl substituents (2) does not form an aligned face-to-face stacked dimer with the phenyl ring pointing in the same direction but the Ni(II) norcorrole rings are rotated relatively to each other,19 whereas in 12 they have an almost perfect face-to-face stacked structure.14
Calculations show that the order and character of the frontier orbitals change when two Ni(II) norcorrole molecules approach each other forming a chemical bond between the two molecules of the dimer.14,19 The binding combination of the lowest unoccupied molecular orbital (LUMO) of the monomers becomes the highest occupied molecular orbital (HOMO) of the dimer in the face-to-face stacked structure and the binding combination of the HOMO of the monomers becomes the HOMO−1 of the dimer, whereas in the twisted phenyl-substituted Ni(II) norcorrole dimer the character of the frontier orbitals does not change when the two monomers approach each other.14,19
The article is organised as follows: The employed computational methods are presented in Section 2. The experimental 1H NMR spectra of the studied molecules are discussed in Section 3.1 and the corresponding computational studies in Section 3.2. The calculated magnetically induced current densities are reported in Section 3.3. The origin of the aromatic character of the dimer based on the nature of the frontier orbitals is discussed in Section 3.4. The main conclusions are summarized in Section 4.
2 Computational methods
The molecular structures of 1 and 12 were optimized with Turbomole20 at the DFT level using the B3LYP functional21,22 and triple-ζ polarization quality basis sets (def2-TZVP).23 Dispersion interactions were considered by using the D3(BJ) semi-empirical term in the Hamiltonian.24 The optimized structure of 1 in Fig. 1 belongs to the Cs point group, which was verified by calculating the vibrational frequencies with the aoforce module of Turbomole.25 The molecular structure of 12 was assumed to belong to the C2h point group. The dimer consists of two stacked monomers in a face-to-face orientation with a Ni–Ni distance of 2.75 Å, which is slightly shorter than in the X-ray structure. The stacked pentafluorophenyl substituents of the dimer are parallel but they do not completely overlap as shown in the ESI.†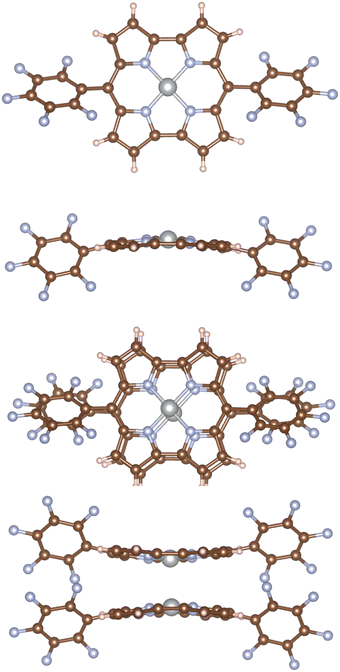 | ||
| Fig. 1 The molecular structure of 1 (upper half) and 12. In the upper picture of 12, the Ni–Ni bond at the center of the molecule pointing towards the readers is parallel to the applied external magnetic field. The pictures have been made with VESTA26 and PowerPoint. | ||
Model structures of 1′ and  were constructed by replacing the pentafluorophenyl substituents with hydrogen atoms. The position of all atoms except the new hydrogen atoms were kept frozen in the subsequent structure optimization. The Cartesian coordinates of the optimized molecular structure are given in the ESI.†
were constructed by replacing the pentafluorophenyl substituents with hydrogen atoms. The position of all atoms except the new hydrogen atoms were kept frozen in the subsequent structure optimization. The Cartesian coordinates of the optimized molecular structure are given in the ESI.†
Nuclear magnetic resonance (NMR) shielding constants were calculated for 1 and 12 as well as for the simplified models 1′ and 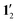 at the DFT level with the mpshift module of Turbomole20,27–29 using the B3LYP,21,22 ωB97X-D,30 CAM-B3LYP31 and BHLYP32 functionals and the def2-TZVP basis sets.23 The NMR shielding constants were also calculated with mpshift and CFOUR33,34 at the HF and second-order Møller–Plesset perturbation theory (MP2) levels.35–38 Gauge-including atomic orbitals (GIAO) were used in the NMR shielding calculations.39–41 Since the studied molecules contain Ni(II) with a partially filled d shell, static electron correlation effects might be significant. The NMR shielding constants were therefore also calculated at the complete-active-space self-consistent-field (CASSCF) level42 using CFOUR.33,34 The coupled-perturbed CASSCF (CP-CASSCF) equations for the computation of the NMR shielding constants were solved with a direct algorithm using GIAOs and Cholesky decomposed two-electron integrals43–47 rendering CASSCF calculations of NMR shielding constants for large molecules with more than 1000 basis functions feasible.46
at the DFT level with the mpshift module of Turbomole20,27–29 using the B3LYP,21,22 ωB97X-D,30 CAM-B3LYP31 and BHLYP32 functionals and the def2-TZVP basis sets.23 The NMR shielding constants were also calculated with mpshift and CFOUR33,34 at the HF and second-order Møller–Plesset perturbation theory (MP2) levels.35–38 Gauge-including atomic orbitals (GIAO) were used in the NMR shielding calculations.39–41 Since the studied molecules contain Ni(II) with a partially filled d shell, static electron correlation effects might be significant. The NMR shielding constants were therefore also calculated at the complete-active-space self-consistent-field (CASSCF) level42 using CFOUR.33,34 The coupled-perturbed CASSCF (CP-CASSCF) equations for the computation of the NMR shielding constants were solved with a direct algorithm using GIAOs and Cholesky decomposed two-electron integrals43–47 rendering CASSCF calculations of NMR shielding constants for large molecules with more than 1000 basis functions feasible.46
The one-electron density matrix and the magnetically perturbed density matrices in the atomic orbital basis obtained in NMR shielding calculations, the Cartesian coordinates of the molecular structure and basis-set information were used as input data in the calculations of the magnetically induced current-density susceptibility (MICD) using the GIMIC program.48–52 Since GIAOs were used in the calculations of the NMR shielding constants and the MICDs, the calculated MICDs have no dependence to any gauge origin.40,41
Molecules sustaining a net diatropic ring current are aromatic, whereas in antiaromatic molecules the ring current flows in the paratropic (opposite) direction.29–32 The MICD was analyzed by calculating ring-current strengths, which are obtained by integrating the MICD passing through a plane intersecting chemical bonds or cutting through the molecule.48–50,52 The MICD was also separated into-gauge-independent diatropic and paratropic contributions that were visualized.53
The magnetic field was applied perpendicularly to the norcorrole macrocycle. The unit for the ring-current (susceptibility) strengths is nA T−1. The MICD was visualized using the Paraview program.54
3 Results and discussion
3.1 Experimental 1H NMR shielding constants
The measured 1H NMR chemical shifts for the hydrogen atoms (Hβ) connected to the β-carbon atoms (Cβ) are −0.147 ppm for 1 and 6.14 ppm for 12. The 1H NMR signal in solution at low temperature is 6.5 ppm. The corresponding chemical shifts for 2 and 22 are 1.69 ppm and 4.70 ppm, respectively. The difference between the 1H NMR chemical shift of the monomer and the dimer increases from 3.0 ppm to 6.3 ppm when perfluorinating the phenyl substituents. Perfluorination of aromatic rings weakens their aromaticity because the fluorine atoms withdraw electrons from the aromatic ring.55 The electron depletion of aromatic rings also strengthen the van der Waals interaction between them.562 forms a triple-decker stacking structure in the solid state, whereas the solid-state material of 1 consists of dimers. The short distance between the pentafluorophenyl substituted Ni(II) norcorrole molecules leads to a down-field shift of the 1H NMR chemical shifts of the Hβ nuclei suggesting that the dimer is aromatic. 1 is antiaromatic with an up-field shift of the 1H NMR signal of the Hβ nuclei. The measured 1H NMR chemical shifts suggest that the coupling between the Ni(II) norcorrole rings is stronger in 12 than for 22 and that 1 sustains a stronger paratropic ring current than 2.To compare with the calculated values, measured 1H NMR chemical shifts (δexp) can be converted to experimental nuclear magnetic shielding constants (σexp) by accounting for the nuclear magnetic shielding constant of the reference (σref).
 | (1) |
The experimental 1H NMR shielding constant of an isolated tetramethylsilane (TMS) molecule is 30.783(5) ppm and 32.873 ppm for neat TMS at 300 K.57,58 Using the experimental shielding constant for TMS of 32.87 ppm yields an experimental 1H NMR shielding constant of 33.02 ppm for the Hβ nuclei of 1 and for 12 it is 26.73 ppm. By using the TMS reference value of 31.89 ppm calculated using the CAM-B3LYP functional, the experimental 1H NMR shielding constants are about 1 ppm smaller and in better agreement with the calculated values. The remaining discrepancy can be assigned mainly to vibrational and solvent effects. The corresponding 1H NMR shielding constants of 2 are 30.20 ppm (31.18 ppm) and 27.19 ppm (28.17 ppm) for 22. The values in parentheses are obtained with the reference value of neat TMS. The calculated isotropic 1H NMR shielding constant of TMS is rather independent of the employed level of theory. It is 31.93 ppm at the B3LYP/def2-TZVP level and 31.81 ppm at the MP2/def2-TZVP and MP2/def2-SVP levels.
3.2 Shielding constants calculated at different levels
The average isotropic nuclear magnetic shielding constants of the Hβ atoms calculated at different levels of theory are compared to experimental values in Table 1. The experimental 1H NMR shielding constants for 1 and 12 are 32.04 ppm and 25.75 ppm, respectively, while they are 30.20 ppm for 2 and 27.19 ppm 22. A TMS reference value of 31.89 ppm is used. The 1H NMR shielding constants of 1 decreases with increasing amount of HF exchange in the functional, whereas for 12 they are less dependent on the amount of HF exchange. The difference in the 1H NMR shielding constants of 12 and 22 is due to different relative orientation of the monomers and their distance in the dimer.| Level | 1 | 1 2 | 1′ | |
|---|---|---|---|---|
| a The pentafluorophenyl groups are replaced by hydrogen atoms. b The core orbitals were not correlated in the calculations with CFOUR. c All electrons were correlated in the mpshift calculations with Turbomole.37,38 d (electrons, active orbitals). e The measured 1H NMR chemical shifts for the Hβ atoms of 2 and 22 are 1.69 ppm and 4.70 ppm, respectively.4 A TMS reference value of 31.89 ppm is used. f The measured 1H NMR chemical shifts for the Hβ atoms of 1 and 12 are −0.147 ppm and 6.14 ppm, respectively.14 A TMS reference value of 31.89 ppm is used. | ||||
| B3LYP/TZVP | 30.97 | 24.20 | 30.55 | 24.16 |
| BHLYP/TZVP | 29.84 | 23.94 | 29.38 | 23.91 |
| CAM-B3LYP/TZVP | 29.35 | 23.93 | 28.98 | 23.90 |
| ωB97X-D/TZVP | 29.00 | 23.97 | 28.67 | 23.93 |
| HF/TZVP | 28.27 | 24.01 | 27.94 | 24.16 |
| HF/SVP | 28.34 | 24.22 | 27.92 | 24.26 |
| MP2/SVPb | 31.05 | |||
| MP2/SVPc | 31.11 | 30.18 | 24.12 | |
| CASSCF(16,15)/SVPd | 28.12 | 24.21 | ||
| CASSCF(12,12)/SVPd | 27.09 | 24.19 | ||
| Experimente | 30.20 | 27.19 | ||
| Experimentf | 32.04 | 25.75 | ||
The substituents do not significantly influence the 1H NMR shielding constants since the calculated values for 1 and 12 are similar to those obtained for 1′ and  , i.e., when the pentafluorophenyl groups are replaced with hydrogen atoms without changing the position of the rest of the atoms.
, i.e., when the pentafluorophenyl groups are replaced with hydrogen atoms without changing the position of the rest of the atoms.
The magnetic shielding constants for 1 and 1′ calculated at the DFT levels agree well with experimental data. The paratropic ring current is weaker when using functionals containing a large amount of HF exchange.
1H NMR shielding constants of 24.2 ppm, 23.9 ppm, 23.9 ppm and 24.0 ppm were obtained for 12 in calculations at the B3LYP, BHLYP, CAM-B3LYP, and ωB97X-D levels, respectively, which suggests that 12 is aromatic. The experimental value is 25.75 ppm. The 1H NMR shielding constant of 24.12 ppm calculated at the MP2 level also agrees well with the experimental value. The calculated values are systematically about 1.5 ppm smaller than the experimental one. At the MP2 level, the pentafluorophenyl substituents increase the 1H NMR shielding constant of 1 by about 1 ppm, whereas at the DFT levels the pentafluorophenyl substituents have a smaller effect of less than 0.5 ppm on the Hβ shielding constants of 1. The pentafluorophenyl substituents have almost no effect on the Hβ shielding constants of 12. Similar trends were obtained in the CASSCF calculations.
We performed CASSCF calculations of NMR shielding constants with very large active spaces (AS). The active spaces were determined using the UNO approach.59 The largest AS had 16 electrons in 16 orbitals (16,16) yielding about 165 million Slater determinants. The AS consisting of 14 electrons in 14 orbitals is the largest common AS when using the def2-TZVP basis sets. The difference between the 1H NMR shielding constants of the monomer and the dimer in Tables 2 and 3 is 2–3 ppm smaller at the CASSCF level than at the other levels of theory and than the ones obtained experimentally, suggesting that the paratropic ring current of 1 is predicted to be slightly too weak at the CASSCF level. The 1H NMR shielding constants of the antiaromatic monomer depend on the size of the AS. The CASSCF calculation with an AS of (16,16) yielded an average 1H NMR shielding constant of 27.29 ppm for the monomer, whereas the one obtained with an AS of (16,15) is 28.12 ppm. Thus, converged values for the 1H NMR shielding constants of the monomer are not obtained even with the largest AS.
| Level | AS | H | Ni | C | N |
|---|---|---|---|---|---|
| a The def2-SVP basis set was used. b The def2-TZVP basis set was used. c For 1′, i.e., the pentafluorophenyl groups are replace by hydrogen atoms. | |||||
| CASSCFa | (16,16) | 27.29 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 130 130 |
75.2 | 65.6 |
| CASSCFa | (16,15) | 28.12 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 324 324 |
74.4 | 57.6 |
| CASSCFa | (8,11) | 27.59 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 131 131 |
74.6 | 66.8 |
| CASSCFa | (8,7) | 28.12 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 287 287 |
74.3 | 57.7 |
| CASSCFa,c | (14,15) | 26.98 | −8056 | 76.6 | 61.3 |
| CASSCFa,c | (14,14) | 26.92 | −7284 | 76.8 | 58.5 |
| CASSCFa,c | (14,11) | 27.69 | −8920 | 75.8 | 50.4 |
| CASSCFa,c | (12,14) | 27.19 | −8304 | 76.2 | 58.7 |
| CASSCFa,c | (12,12) | 27.09 | −7349 | 76.5 | 55.5 |
| CASSCFa,c | (8,12) | 27.10 | −11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 935 935 |
75.9 | 67.8 |
| CASSCFa,c | (8,8) | 27.04 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 079 079 |
75.9 | 66.5 |
| CASSCFb,c | (14,14) | 26.89 | −7684 | 64.9 | 37.2 |
| CASSCFb,c | (12,15) | 27.19 | −9119 | 64.3 | 37.3 |
| CASSCFb,c | (12,12) | 27.07 | −7756 | 64.6 | 33.4 |
| CASSCFb,c | (8,8) | 27.05 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 146 146 |
63.8 | 47.2 |
| B3LYPb | 30.97 | −4353 | 66.0 | −15.7 | |
| BHLYPb | 29.84 | −7242 | 69.3 | 2.52 | |
| CAM-B3LYPb | 29.35 | −4650 | 67.2 | −6.57 | |
| ωB97X-Db | 29.00 | −4772 | 69.6 | −2.35 | |
| HFb | 28.27 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 608 608 |
78.0 | 32.3 | |
| HFb,c | 27.94 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 556 556 |
79.4 | 32.7 | |
| HFa | 28.34 | −14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055 055 |
88.7 | 55.8 | |
| MP2a | 31.11 | 2797 | 93.8 | 37.2 | |
| MP2a,c | 30.18 | 2742 | 95.2 | 41.4 | |
 calculated at the CASSCF level using different active spaces (AS) are compared to values obtained in DFT, and MP2 calculations. The shielding constants of Hmeso are omitted. The average 13C NMR shielding constants are calculated for the Cβ atoms that are closer to the direct pyrrole–pyrrole link. The experimental 13C NMR chemical shifts of the Cβ atoms are 118.188 (83.3) ppm and 129.228 (72.3) ppm.14 The estimated chemical shifts are given in parentheses. NMR shielding constants are given in the ESI
calculated at the CASSCF level using different active spaces (AS) are compared to values obtained in DFT, and MP2 calculations. The shielding constants of Hmeso are omitted. The average 13C NMR shielding constants are calculated for the Cβ atoms that are closer to the direct pyrrole–pyrrole link. The experimental 13C NMR chemical shifts of the Cβ atoms are 118.188 (83.3) ppm and 129.228 (72.3) ppm.14 The estimated chemical shifts are given in parentheses. NMR shielding constants are given in the ESI
| Level | AS | H | Ni | C | N |
|---|---|---|---|---|---|
a The def2-SVP basis set was used.
b The def2-TZVP basis set was used.
c For  . .
|
|||||
| CASSCFa,c | (16,15) | 24.21 | −8400 | 72.1 | 93.3 |
| CASSCFa,c | (16,14) | 24.23 | −8642 | 72.1 | 93.8 |
| CASSCFa,c | (14,14) | 24.19 | −9919 | 71.8 | 98.2 |
| CASSCFa,c | (12,12) | 24.19 | −11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 403 403 |
71.7 | 102.3 |
| B3LYPb | 24.20 | −4189 | 54.8 | 34.3 | |
| BHLYPb | 23.94 | −6784 | 56.6 | 52.5 | |
| CAM-B3LYPb | 23.93 | −4455 | 54.6 | 40.3 | |
| ωB97X-Db | 23.97 | −4597 | 57.2 | 42.8 | |
| HFb | 24.01 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 498 |
61.9 | 84.6 | |
| HFb,c | 24.16 | −13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 496 496 |
56.1 | 34.3 | |
| HFa,c | 24.26 | −12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 919 919 |
75.1 | 105.0 | |
| MP2a,c | 24.12 | 2886 | 88.9 | 79.2 | |
A much smoother convergence with increasing size of the basis set is obtained for the 1H NMR shielding constants of the aromatic dimer. The CASSCF calculations show that near-degeneracy effects do not play an important role for the 1H NMR shielding constants, most likely because the hydrogen atoms are relatively far from the Ni atom, whereas the NMR shielding constant of Ni and its adjacent nitrogen atoms are more accurate at the CASSCF level than at the DFT levels of theory. The shielding constant of Ni has the opposite sign at the CASSCF and MP2 levels of theory. The shielding constant of Ni calculated at the DFT and HF levels of theory has the same sign as the one obtained in the CASSCF calculations. The values calculated at the DFT levels are generally smaller than the CASSCF reference value and HF calculations yield larger shielding constants for Ni. The BHLYP functional yielded the best agreement with the CASSCF reference value. Even though the 1H NMR and 13C NMR shielding constants calculated at the MP2 level agree well with the experimental ones, the shielding constant of Ni calculated at the MP2 level are inaccurate. The 1H NMR shielding constants calculated with def2-SVP and def2-TZVP basis sets largely agree, whereas there are significant basis-set effects for the shielding constants of the other atoms.
The 1H NMR shielding constants calculated at the DFT levels show that Ni(II) norcorrole is more antiaromatic than free-base norcorrole, which is also supported by the calculated ring-current strength that is 70% weaker for free-base norcorrole than for Ni(II) norcorrole. However, the CASSCF calculations yield more or less the same 1H NMR shielding constants for free-base norcorrole and Ni(II) norcorrole showing that CASSCF calculations with limited description of the dynamic correlation have difficulties to describe the antiaromatic character of norcorroles. The weaker antiaromaticity of free-base norcorrole suggests that the Ni atoms are necessary for formation of a bound dimer. The NMR shielding constants for free-base norcorrole are reported in Table 4.
The calculated 61Ni NMR shielding constants are large and negative due to the strong paratropic atomic current of the partially filled d shell of the Ni atom. The atomic current is stronger in the antiaromatic monomer than in the dimer leading to a more negative shielding constant of the monomer. The 61Ni NMR shielding constants obtained in the largest CASSCF calculations are the most reliable ones. However, since dynamic correlation effects are missing, the 61Ni NMR shielding constants calculated using the largest active space are still only qualitative. The CASSCF calculations show that the 61Ni NMR shielding constants calculated at the DFT and MP2 levels are not very accurate. 61Ni NMR chemical shifts can be estimated by using a reference value of −4048 ppm that was calculated for Ni(CO)4 at the CASSCF(6,6)/def2-SVP level using a molecular structure optimized at the B3LYP/def2-SVP/D3(BJ) level. Using different active spaces, we obtained 61Ni NMR chemical shifts of 3236–4872 ppm for the monomer without the C6F5 substituents. For the monomer with the C6F5 substituents, the corresponding range is 8082–8276 ppm. The 61Ni NMR chemical shifts of the molecules with the C6F5 substituents are less accurate because some C6F5 orbitals belong to the active space implying that there are fewer correlation orbitals near the Ni atoms.
3.3 Current-density calculations
The separated diatropic and paratropic contributions to the current density of the monomer in the left half of Fig. 2 show that there is a weak diatropic ring current of 2.0 nA T−1 around the edge of monomer and a very strong paratropic ring current of −46.2 nA T−1 in the inner part of 1. The net ring-current strength calculated at the CAM-B3LYP level is −44.2 nA T−1 indicating that 1 is strongly antiaromatic. The atomic current density around the Ni atom is not included in the reported ring-current strengths. | ||
| Fig. 2 The separated current density of 1 (left) and 12 (right) calculated at the CAM-B3LYP/def2-TZVP level. The spaghetti plots of the diatropic contribution are shown in the upper pictures and the paratropic contribution is shown in the lower ones. The strongest current density is shown in white, then yellow and red. The weakest ones are black. The current-density pictures have been made with Paraview.54 | ||
The diatropic and paratropic contributions to the current density of 12 are shown in the right half of Fig. 2. The integrated ring current strength calculated at the CAM-B3LYP level is 39.6 nA T−1, which consists of a global diatropic contribution of 46.9 nA T−1 around the norcorrole macroring and a local paratropic ring current of −7.3 nA T−1 inside the direct link between two of the pyrrole rings. The ring-current profiles calculated through different planes are given in the ESI.†
Comparing the ring-current strengths calculated with and without the pentafluorophenyl substituents shows that the ring currents are 2 nA T−1 stronger for the molecules lacking substituents in the meso positions, i.e., the antiaromatic 1′ is slightly more antiaromatic than 1 and 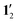 is slightly more aromatic than 12. However, the substituent effect is only about 5%.
is slightly more aromatic than 12. However, the substituent effect is only about 5%.
The current-density calculations at the CASSCF level yielded the second strongest diatropic ring current of 47.7 nA T−1 for the dimer and the weakest paratropic ring current of −16.9 nA T−1 for the monomer. Comparison of calculated and measured 1H NMR chemical shifts suggests that the paratropic ring current of the monomer calculated at the CASSCF level is too weak, whereas the strength of the diatropic ring current of the dimer is only slightly stronger than the ones obtained at the other levels of theory that consider electron correlation effects. The strongest diatropic ring current of the dimer of 51.9 nA T−1 was obtained at the HF level. The HF calculation on the monomer yielded a ring-current strength of −27.5 nA T−1, which is about halfway between the strengths obtained at the CASSCF and DFT levels of theory. At the DFT levels, the ring-current strength of the dimer decreases somewhat with increasing amount of HF exchange in the functional. However, the employed functionals yielded ring-current strengths of the dimer in the range of [39.3, 45.5] nA T−1 (Table 5) which agree well with the ring-current strength of 47.7 nA T−1 calculated at the CASSCF level. The ring-current strength of 42.3 nA T−1 calculated for the dimer at the MP2 level agrees well with the ones obtained in the DFT calculations. The weakest diatropic ring current of the dimer was obtained with the B3LYP functional.
 ,-and free-base (FB) norcorrole (in nA T−1) calculated at different levels of theory. The pentafluorophenyl substituents are replaced with hydrogen atoms. Ring-current profiles are given in the ESI
,-and free-base (FB) norcorrole (in nA T−1) calculated at different levels of theory. The pentafluorophenyl substituents are replaced with hydrogen atoms. Ring-current profiles are given in the ESI
| Method | Monomer | Dimer | FB-norcorrole |
|---|---|---|---|
| CASSCF(14,14) | −16.9 | 47.7 | — |
| B3LYP | −55.4 | 39.3 | −40.5 |
| BHLYP | −44.4 | 45.5 | −32.0 |
| CAM-B3LYP | −42.0 | 41.6 | −29.1 |
| ωB97X-D | −38.9 | 40.9 | −26.9 |
| HF | −27.5 | 51.9 | −19.5 |
| MP2 | −52.2 | 42.3 | — |
Comparison of calculated and measured 1H NMR chemical shifts suggests that the ring-current strength calculated at the MP2 level is accurate even though the current density around the Ni atoms is not described very well. The ring-current profile shows that the atomic current density at Ni is diatropic at the MP2 level, whereas at the other employed levels of theory it is paratropic there. The similar ring-current profiles (shown in the ESI†) were obtained for the dimer at the CASSCF, DFT, and HF levels of theory. The only exception is MP2.
The employed DFT functionals yielded ring-current strengths of the monomer in the range of [−55.4, −38.9] nA T−1 (Table 5). The paratropic ring-current strength of the monomer calculated at the MP2 level is −52.2 nA T−1. Thus, the same antiaromatic character is obtained at these levels of theory. The 1H NMR shielding constants calculated at the MP2 level are in the closest agreement with experimental data,14 suggesting that the MP2 calculations yield the most accurate ring-current strength. The ring-current strength of the monomer of −16.9 nA T−1 calculated at the CASSCF level is too weak judged from the ring-current strengths calculated at the other levels of theory and from the comparison to experimental 1H NMR shielding constants. When the magnetic field is oriented along the Ni–Ni axis, the current density passing from one molecule of the dimer to the other one is very weak as shown in the ESI.†
3.4 Discussion
The aromatic nature of 12 can be rationalized by employing the porphyrin-perimeter model, which is based on an approximation of the MOs.60,61 In the perimeter model, the angular expansion of the MOs of 1 gives rise to σ, π, δ, … type orbitals with angular quantum numbers of m = 0, 1, 2,… The Aufbau principle of the perimeter model yields for aromatic rings the well-known magic numbers of 4n+2. Ni(II) norcorrole has 24 electrons in the conjugated MOs, suggesting that its HOMO shell, according to the perimeter model, is formally half filled leading to antiaromaticity. The perimeter model can be extended by considering the reflection plane between the norcorrole macrorings of the dimer. The angular and parity expansion of the MOs of 12 is then σg, σu, πu, πg, δg, δu … with angular quantum numbers of m = 0, 1, 2,… having even and odd parity. According to the Aufbau principle of the extended perimeter model, all shells are closed when the number of electrons is 4n.In a stacked dimer of weakly interacting antiaromatic macrocycles with a large intermolecular separation, the nature of the two outermost MOs remain unaltered and formally half filled. Consequently, the dimer is then still antiaromatic. In contrast, when the interaction between the two antiaromatic macrocycles is strong, the occupation of the frontier orbitals is reorganized to a closed-shell configuration and the dimer becomes aromatic. Since 12 consists of two strongly interacting norcorrole molecules in a face-to-face orientation, the Aufbau principle of the perimeter model leads to closed shells for the dimer with magic numbers of 4n.62 Thus, the dimer has cylindrical aromaticity like B20.62–64 The 48 electrons in the conjugated MOs of 12 close the outermost HOMO shell with an angular quantum number of m = 6 and even parity. The HOMO shell of 12 with even parity containing four electrons according to the perimeter model confirms that a double bond is formed between the norcorrole macrocycles.
Due to the strong interaction between the norcorrole macrorings the frontier orbitals are reordered. The nature of the occupied frontier orbitals of 12 differs from the ones of weakly interacting monomers. The HOMO orbital of 12 is the binding combination of the LUMOs of 1, whereas the LUMO of 12 is the antibonding combination of the HOMOs of 1. The binding combination of the HOMO of 1 forms the HOMO−1 of 12 and the antibonding combination of the LUMO of 1 becomes LUMO+1 of 12. The orbital diagram is shown in Fig. 3.
The frontier orbitals of 12 can be formally written as
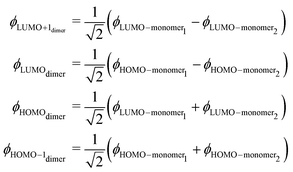 | (2) |
The aromatic nature of the monomer and dimer can also be understood from the symmetry of the frontier orbitals. The HOMO of the dimer belongs to the Ag irreducible representation of the C2h point group and the LUMO belongs to Au. The dipole operators belong to Au and Bu, whereas the operators of the magnetic transition belong to Ag and Bg. Molecules dominated by magnetically allowed transitions between HOMO and LUMO are antiaromatic, whereas when the HOMO–LUMO transition is dipole allowed the molecule may be aromatic sustaining a diatropic ring current.65 At long distances between the stacked Ni(II) norcorrole molecules the HOMO belongs to Au thus leading to antiaromaticity. The HOMO–LUMO transition of 12 is dipole allowed because the product Ag ⊗ (Au or Bu) ⊗ Au = Ag or Bg contains the total symmetric irreducible representation, whereas it is magnetically forbidden because the product Ag ⊗ (Ag or Bg) ⊗ Au = Au or Bu does not contain Ag.
Since HOMO and HOMO−1 of 12 are almost degenerate binding orbitals, there is a double bond between the stacked Ni(II) norcorrole rings. HOMO and HOMO−1 are degenerate in the perimeter model. The binding energy is 79.5 kJ mol−1.14 The change in the aromatic nature from antiaromaticity for 1 to aromaticity for 12 also affects bond lengths and stabilizes the dimer. A picture of the electron density of 12 and the frontier orbitals are shown in the ESI.†
4 Conclusions
We calculated NMR shielding constants for 1 and 12 at the Hartree–Fock (HF), second-order Møller–Plesset perturbation theory (MP2), complete-active-space self-consistent-field (CASSCF) levels as well as at density functional theory (DFT) levels using several functionals. Comparison of calculated and experimental 1H NMR shielding constants suggests that the wave function and magnetic response of 1 is not well described at the CASSCF level, whereas the shielding constants calculated at the CASSCF level for 12 are in close agreement with the experimental ones. DFT calculations with the employed functionals and MP2 calculations yield 1H NMR shielding constants in rather good agreement with the experimental ones for both 1 and 12. The 1H NMR shielding constants calculated at the MP2 level are in closest agreement with the experimental ones. Calculations with the B3LYP (20% HF exchange) and BHLYP (50% HF exchange) hybrid functionals yield 1H NMR shielding constants for the antiaromatic monomer that are in better agreement with experimental data than the ones obtained with the range-separated CAM-B3LYP and ωB97X-D functional, which have 65% and 100% HF exchange at long interelectronic distances, respectively. Due to near-degeneracy effects the shielding constants of Ni calculated at DFT, HF and MP2 levels differ significantly from the more accurate ones obtained in the CASSCF calculations. The shielding constants of N calculated at the DFT level are less accurate than those obtained in the MP2 and CASSCF calculations. Basis-set truncation errors are also significant for the shielding constants of C, N and Ni when using the def2-SVP basis sets.Calculations at the CASSCF level are crucial for obtaining reliable shielding constants of N and Ni, whereas MP2 calculations yield accurate shielding constants for C and H. Even though the Ni atoms introduce near-degeneracy effects into the wave function, the shielding constants of the C and H nuclei are accurate because they are spatially separated from the Ni atoms. NMR shielding constants are a local property that mainly depends on the quality of the wave function and the current density near the studied nucleus.
DFT functionals with a small amount of HF exchange often overestimate the antiaromatic character of strongly antiaromatic molecules, whereas a large amount of HF exchange may lead to an underestimation of the antiaromaticity. The BHLYP and CAM-B3LYP functionals are often a good compromise. For aromatic molecules all functionals yield qualitatively the same degree of aromaticity. For larger molecules it may be necessary to use a functional with a larger amount of HF exchange to avoid spurious charge-transfer effects.
Calculations of 1H NMR shielding constants for 1, 12, 1′, and  showed that the pentafluorophenyl substituents have a small direct effect on the shielding constants. The ring-current strengths of 1′ and
showed that the pentafluorophenyl substituents have a small direct effect on the shielding constants. The ring-current strengths of 1′ and  are 2 nA T−1 stronger than for 1 and 12, which have pentafluorophenyl substituents in the meso position.
are 2 nA T−1 stronger than for 1 and 12, which have pentafluorophenyl substituents in the meso position.
Calculations of the current density show that 1 is antiaromatic sustaining a strong paratropic ring current around the norcorrole macroring and a weak diatropic ring current along the outer edge of the molecule. 12 is aromatic sustaining a strong diatropic ring current. Local paratropic current-density vortices appear only in the inner rings and around the Ni atom. Qualitatively the same current density is obtained at all employed levels of theory. However, the ring current strength of 1 calculated at the CASSCF is significantly weaker than the strengths obtained at the other levels of theory, whereas largely the same ring-current strength was obtained for 12 at all employed levels of theory. The most accurate ring-current strengths are most likely obtained at the MP2 level.
Calculations of the 1H NMR shielding constants and the magnetically induced current density show that the antiaromatic 1 forms an aromatic dimer 12 with a short intermolecular distance of less than 3 Å, where the interaction between the norcorrole macrocyles changes the nature of the frontier orbitals leading to a formal double bond between them.
Author contributions
Q. W., D. S. and T. N. performed electronic structure calculations and calculations of NMR shielding constants. Q. W. calculated the current densities and visualized them. J. G., T. N. and F. L. developed the employed methods for calculating NMR shielding constants at the CASSCF level. S. K., S. U., N. F. and H. S. performed the experimental studies. D. S. and H. S. developed the theoretical model describing the change of the aromatic nature upon dimerization. All authors contributed to writing the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the Academy of Finland (340583). Q. W. thanks the China Scholarship Council for a pre-doctoral fellowship. Computational resources from the CSC-IT Center for Science (Finland) are acknowledged. It was also supported by JSPS KAKENHI grants JP20H05862, JP20H05863, JP20H05867, JP22H04974, and JP22K19025. S. U. is grateful to a JSPS Research Fellowship for Young Scientists (JP20J11883).References
- R. R. Valiev, T. Kurtén, L. I. Valiulina, S. Y. Ketkov, V. N. Cherepanov, M. Dimitrova and D. Sundholm, Magnetically induced ring currents in metallocenothiaporphyrins, Phys. Chem. Chem. Phys., 2022, 24, 1666–1674 RSC.
- C. Corminboeuf, P. von Ragué Schleyer and P. Warner, Are antiaromatic rings stacked face-to-face aromatic, Org. Lett., 2007, 9, 3263–3266 CrossRef CAS PubMed.
- D. E. Bean and P. W. Fowler, Stacked-Ring Aromaticity: An Orbital Model, Org. Lett., 2008, 10, 5573–5576 CrossRef CAS PubMed.
- R. Nozawa, H. Tanaka, W.-Y. Cha, Y. Hong, I. Hisaki, S. Shimizu, J.-Y. Shin, T. Kowalczyk, S. Irle, D. Kim and H. Shinokubo, Stacked antiaromatic porphyrins, Nat. Commun., 2016, 7, 13620 CrossRef CAS PubMed.
- D. Sundholm, M. Rauhalahti, N. Özcan, R. Mera-Adasme, J. Kussmann, A. Luenser and C. Ochsenfeld, Nuclear Magnetic Shieldings of Stacked Aromatic and Antiaromatic Molecules, J. Chem. Theory Comput., 2017, 13, 1952–1962 CrossRef CAS PubMed.
- R. Nozawa, J. Kim, J. Oh, A. Lamping, Y. Wang, S. Shimizu, I. Hisaki, T. Kowalczyk, H. Fliegl, D. Kim and H. Shinokubo, Three-dimensional aromaticity in an antiaromatic cyclophane, Nat. Commun., 2019, 10, 3576 CrossRef PubMed.
- M. Orozco-Ic, A. Restrepo, A. Muñoz-Castro and G. Merino, Molecular Helmholtz coils, J. Chem. Phys., 2019, 151, 014102 CrossRef PubMed.
- V. Vijay, M. Madhu, R. Ramakrishnan, A. Benny and M. Hariharan, Through-space aromatic character in excimers, Chem. Commun., 2020, 56, 225–228 RSC.
- M. Orozco-Ic and D. Sundholm, On the antiaromatic-aromatic-antiaromatic transition of the stacked cyclobutadiene dimer, Phys. Chem. Chem. Phys., 2023, 25, 12777–12782 RSC.
- K. Okazawa, Y. Tsuji and K. Yoshizawa, Frontier Orbital Views of Stacked Aromaticity, J. Phys. Chem. A, 2023, 127, 4780–4786 CrossRef CAS PubMed.
- Y. Tsuji, K. Okazawa and K. Yoshizawa, Hückel Molecular Orbital Analysis for Stability and Instability of Stacked Aromatic and Stacked Antiaromatic Systems, J. Org. Chem., 2023, 88, 14887–14898 CrossRef CAS PubMed.
- T. Nishiuchi, Y. Makihara, R. Kishi, H. Sato and T. Kubo, Stacked antiaromaticity in the π -congested space between the aromatic rings in the anthracene dimer, J. Phys. Org. Chem., 2023, 36, e4451 CrossRef CAS.
- R. Sugimori, K. Okada, R. Kishi and K. Y, Stacked-ring aromaticity from the viewpoint of the effective number of π-electrons, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-rrpw2-v2x.
- S. Kino, S. Ukai, N. Fukui, R. Haruki, R. Kumai, Q. Wang, S. Horike, Q. M. Phung, D. Sundholm and H. Shinokubo, Close Stacking of Antiaromatic Ni(II) Norcorrole Originating from a Four-Electron Multicentered Bonding Interaction, J. Am. Chem. Soc., 2024, 146, 9311–9317 CrossRef CAS PubMed.
- H. Rabaâ, H. Khaledi, M. M. Olmstead and D. Sundholm, Computational Studies of a Paramagnetic Planar Dibenzotetraaza[14]annulene Ni(II) Complex, J. Phys. Chem. A, 2015, 119, 5189–5196 CrossRef.
- T. Ito, Y. Hayashi, S. Shimizu, J.-Y. Shin, N. Kobayashi and H. Shinokubo, Gram-Scale Synthesis of Nickel(II) Norcorrole: The Smallest Antiaromatic Porphyrinoid, Angew. Chem., Int. Ed., 2012, 51, 8542–8545 CrossRef CAS PubMed.
- J. Conradie, C. Foroutan-Nejad and A. Ghosh, Norcorrole as a Delocalized, Antiaromatic System, Sci. Rep., 2019, 9, 4852 CrossRef PubMed.
- S.-Y. Liu, N. Kishida, J. Kim, N. Fukui, R. Haruki, Y. Niwa, R. Kumai, D. Kim, M. Yoshizawa and H. Shinokubo, Realization of stacked-ring aromaticity in a water-soluble micellar capsule, J. Am. Chem. Soc., 2022, 145, 2135–2141 CrossRef PubMed.
- H. Kawashima, S. Ukai, R. Nozawa, N. Fukui, G. Fitzsimmons, T. Kowalczyk, H. Fliegl and H. Shinokubo, Determinant Factors of Three-Dimensional Aromaticity in Antiaromatic Cyclophanes, J. Am. Chem. Soc., 2021, 143, 10676–10685 CrossRef CAS PubMed.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, TURBOMOLE: Modular program suite for ab initio quantum-chemical and condensed-matter simulations, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- P. Deglmann, K. May, F. Furche and R. Ahlrichs, Nuclear second analytical derivative calculations using auxiliary basis set expansion, Chem. Phys. Lett., 2004, 384, 103–107 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. Ahlrichs, M. Bär, M. Häser, H. Horn and C. Kölmel, Electronic Structure Calculations on Workstation Computers: The Program System Turbomole, Chem. Phys. Lett., 1989, 162, 165–169 CrossRef CAS.
- K. Reiter, F. Mack and F. Weigend, Calculation of Magnetic Shielding Constants with meta-GGA Functionals Employing the Multipole-Accelerated Resolution of the Identity: Implementation and Assessment of Accuracy and Efficiency, J. Chem. Theory Comput., 2018, 14, 191–197 CrossRef CAS PubMed.
- S. Gillhuber, Y. J. Franzke and F. Weigend, Paramagnetic NMR Shielding Tensors and Ring Currents: Efficient Implementation and Application to Heavy Element Compounds, J. Phys. Chem. A, 2021, 125, 9707–9723 CrossRef CAS PubMed.
- J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- A. D. Becke, A new mixing of Hartree-Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- Stanton, J. F.; Gauss, J.; Cheng, L.; Harding, M. E.; Matthews, D.; Szalay, P. cfour, a quantum chemical program package with contributions also from A. Asthana, A. A. Auer, R. J. Bartlett, U. Benedikt, C. Berger, D. E. Bernholdt, S. Blaschke, Y. J. Bomble, S. Burger, O. Christiansen, D. Datta, F. Engel, R. Faber, J. Greiner, M. Heckert, O. Heun, M. Hilgenberg, C. Huber, T. C. Jagau, D. Jonsson, J. Jusélius, T. Kirsch, M. P. Kitsaras, K. Klein, G. M. Kopper, W. J. Lauderdale, F. Lipparini, J. Liu, T. Metzroth, L. A. Mück, T. Nottoli, D. P. O'Neill, J. Ostwald, D.R. Price, E. Prochnow, C. Puzzarini, K. Ruud, F. Schiffmann, W. Schwalbach, C. Simmons, S. Stopkowicz, A. Tajti, T. Uhlirova, J. Vázquez, F. Wang, J. D. Watts, P. Yergün, C. Zhang, X. Zheng and the integral packages MOLECULE (J. Almlöf and P. R. Taylor), PROPS (P. R. Taylor), ABACUS (T. Helgaker, H. J. Aa. Jensen, P. Jørgensen, and J. Olsen), and ECP routines by A. V. Mitin and C. van Wüllen. For the current version, see https://www.cfour.de (accessed 23.8.2023).
- D. A. Matthews, L. Cheng, M. E. Harding, F. Lipparini, S. Stopkowicz, T.-C. Jagau, P. G. Szalay, J. Gauss and J. F. Stanton, Coupled-cluster techniques for computational chemistry: The CFOUR program package, J. Chem. Phys., 2020, 152, 214108 CrossRef CAS PubMed.
- J. Gauss, Calculation of NMR chemical shifts at second-order many-body perturbation theory using gauge-including atomic orbitals, Chem. Phys. Lett., 1992, 191, 614–620 CrossRef CAS.
- J. Gauss, Effects of electron correlation in the calculation of nuclear magnetic resonance chemical shifts, J. Chem. Phys., 1993, 99, 3629–3643 CrossRef CAS.
- M. Kollwitz and J. Gauss, A direct implementation of the GIAO-MBPT(2) method for calculating NMR chemical shifts. Application to the naphthalenium and anthracenium ions, Chem. Phys. Lett., 1996, 260, 639–646 CrossRef CAS.
- M. Kollwitz, M. Häser and J. Gauss, Non-Abelian point group symmetry in direct second-order many-body perturbation theory calculations of NMR chemical shifts, J. Chem. Phys., 1998, 108, 8295–8301 CrossRef CAS.
- F. London, Théorie quantique des courants interatomiques dans les combinaisons aromatiques, J. Phys. Radium, 1937, 8, 397–409 CrossRef CAS.
- R. Ditchfield, Self-consistent perturbation theory of diamagnetism I. A gauge-invariant LCAO method for N.M.R. chemical shifts, Mol. Phys., 1974, 27, 789–807 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157 CrossRef CAS.
- N. H. F. Beebe and J. Linderberg, Simplifications in the generation and transformation of two-electron integrals in molecular calculations, Int. J. Quantum Chem., 1977, 12, 683–705 CrossRef CAS.
- H. Koch, A. S. de Merás and T. B. Pedersen, Reduced scaling in electronic structure calculations using Cholesky decompositions, J. Chem. Phys., 2003, 118, 9481–9484 CrossRef CAS.
- S. Burger, F. Lipparini, J. Gauss and S. Stopkowicz, NMR chemical shift computations at second-order Møller-Plesset perturbation theory using gauge-including atomic orbitals and Cholesky-decomposed two-electron integrals, J. Chem. Phys., 2021, 155, 074105 CrossRef CAS PubMed.
- T. Nottoli, S. Burger, S. Stopkowicz, J. Gauss and F. Lipparini, Computation of NMR shieldings at the CASSCF level using gauge-including atomic orbitals and Cholesky decomposition, J. Chem. Phys., 2022, 157, 084122 CrossRef CAS PubMed.
- J. Gauss, S. Blaschke, S. Burger, T. Nottoli, F. Lipparini and S. Stopkowicz, Cholesky decomposition of two-electron integrals in quantum-chemical calculations with perturbative or finite magnetic fields using gauge-including atomic orbitals, Mol. Phys., 2023, 121, e2101562 CrossRef.
- J. Jusélius, D. Sundholm and J. Gauss, Calculation of Current Densities Using Gauge-Including Atomic Orbitals, J. Chem. Phys., 2004, 121, 3952–3963 CrossRef PubMed.
- H. Fliegl, S. Taubert, O. Lehtonen and D. Sundholm, The Gauge Including Magnetically Induced Current Method, Phys. Chem. Chem. Phys., 2011, 13, 20500–20518 RSC.
- D. Sundholm, H. Fliegl and R. J. F. Berger, Calculations of Magnetically Induced Current Densities: Theory and Applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 378–639 Search PubMed.
- D. Sundholm, M. Dimitrova and R. J. F. Berger, Current Density and Molecular Magnetic Properties, Chem. Commun., 2021, 57, 12362–12378 RSC.
- Jusélius, J.; Sundholm, D. Co-workers, GIMIC, Gauge-Including Magnetically Induced Currents, a stand-alone program for the calculation of magnetically induced current density. https://github.com/qmcurrents/gimic and https://zenodo.org/record/8180435.
- Q. Wang, J. Pyykkö, M. Dimitrova, S. Taubert and D. Sundholm, Current-density pathways in figure-eight-shaped octaphyrins, Phys. Chem. Chem. Phys., 2023, 25, 12469–12478 RSC.
- J. Ahrens, B. Geveci and C. Law in Visualization Handbook, Hansen, C. D., Johnson, C. R., ed., 2005, pp. 717–731 Search PubMed.
- M. Kaipio, M. Patzschke, H. Fliegl, F. Pichierri and D. Sundholm, The effect of fluorine substitution on the aromaticity of polycyclic hydrocarbons, J. Phys. Chem. A, 2012, 116, 10257–10268 CrossRef CAS PubMed.
- U. Ahmed, M. P. Johansson and D. Sundholm, Effects of hydrogen bonding on the π depleation and π−π stacking interactions, Phys. Chem. Chem. Phys., 2024 Search PubMed (manuscript).
- W. Makulski and K. Jackowski, 1H, 13C and 29Si magnetic shielding in gaseous and liquid tetramethylsilane, J. Magn. Reson., 2020, 313, 106716 CrossRef CAS PubMed.
- K. Jackowski, M. Jaszuński and M. Wilczek, Alternative Approach to the Standardization of NMR Spectra. Direct Measurement of Nuclear Magnetic Shielding in Molecules, J. Phys. Chem. A, 2010, 114, 2471–2475 CrossRef CAS PubMed.
- J. M. Bofill and P. Pulay, The unrestricted natural orbital-complete active space (UNO-CAS) method: An inexpensive alternative to the complete active space-self-consistent-field (CAS-SCF) method, J. Chem. Phys., 1989, 90, 3637–3646 CrossRef CAS.
- J. Waluk and J. Michl, Perimeter model and magnetic circular dichroism of porphyrin analogs, J. Org. Chem., 1991, 56, 2729–2735 CrossRef CAS.
- J. R. Platt, Classification of Spectra of Cata-Condensed Hydrocarbons, J. Phys. Chem., 1929, 17, 484–495 CrossRef.
- D. Sundholm, H. Fliegl and R. J. Berger, Calculations of magnetically induced current densities: theory and applications, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 639–678 CAS.
- M. P. Johansson, On the Strong Ring Currents in B20 and Neighboring Boron Toroids, J. Phys. Chem. C, 2009, 113, 524–530 CrossRef CAS.
- D. E. Bean and P. W. Fowler, Double Aromaticity in Boron Toroids, J. Phys. Chem. C, 2009, 113, 15569–15575 CrossRef CAS.
- E. Steiner and P. W. Fowler, Patterns of Ring Currents in Conjugated Molecules: A Few-Electron Model Based on Orbital Contributions, J. Phys. Chem. A, 2001, 105, 9553–9562 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Cartesian coordinates of the optimized molecular structure, picture of the molecular structure of 12, analysis of the magnetically induced current density, isotropic magnetic shielding constants, pictures and energies of the frontier orbitals, and the electron density of the dimer are reported. See DOI: https://doi.org/10.1039/d4cp00968a |
| This journal is © the Owner Societies 2024 |


