A fully dynamical description of time-resolved resonant inelastic X-ray scattering of pyrazine†
Received
1st March 2024
, Accepted 24th July 2024
First published on 30th July 2024
Abstract
Recent advancements in ultrashort and intense X-ray sources have enabled the utilisation of resonant inelastic X-ray scattering (RIXS) as a probing technique for monitoring photoinduced dynamics in molecular systems. To account for dynamic phenomena like non-adiabatic transitions across the relevant electronic state manifold, a time-dependent framework is crucial. Here, we introduce a fully time-dependent approach for calculating transient RIXS spectra using wavepacket dynamics simulations, alongside an explicit treatment of the X-ray probe pulse that surpasses Kramers–Heisenberg–Dirac constraints. Our analysis of pyrazine at the nitrogen K-edge underscores the importance of considering nuclear motion effects in all electronic states involved in the transient RIXS process. As a result, we propose a numerically exact approach to computationally support and predict cutting-edge time-resolved RIXS experiments.
1 Introduction
Resonant inelastic X-ray scattering (RIXS)1,2 is a Raman spectroscopy technique that exploits X-ray resonances to create an intermediate core-excited state, followed by a spontaneous photon emission that propels the quantum system to a lower excited state. The energy difference between incident and emitted X-ray photon provides an excitation spectrum that is not only element-specific but also specific to the particular chemical environment of an atom. Moreover, RIXS can populate final excited states that cannot be directly probed by conventional one-photon absorption spectroscopy due to restrictions imposed by dipole selection rules.3–6 A complicating factor in this process is the role of vibronic coupling between core-excited states, which can facilitate transitions that are otherwise forbidden due to symmetry restrictions. This is particularly relevant for molecules with equivalent atoms, as they possess delocalised core orbitals and, consequently, energetically degenerate core-excited states. Vibronic coupling may induce dynamical distortions and a loss of symmetry, resulting in a localisation of the core excitations.1,3,7 While environmental factors such as solvent interactions or temperature may also cause structural heterogeneity, already resulting in a localised configuration in the ground state, the motional effects arising from non-adiabatic core-excited state dynamics can be distinctly determined by adjusting the excitation energy in RIXS measurements, thereby controlling the scattering time and the evolution of nuclear dynamics.8–10
In the condensed phase, where solids and solvents prohibit measurement of UV absorption spectra beyond ≲9 eV, RIXS allows accessing spectra up to energies in the extreme ultraviolet, i.e. inner-valence excitations.11 As the spectral resolution is not constrained by the core-hole lifetime broadening of the initial core-excitation, transition bands in RIXS spectra can exhibit vibrational substructure, providing information on the underlying nuclear dynamics and corresponding potential energy surfaces.10,12–15 RIXS with hard X-rays usually targets core-excited final states because of the very low yield of valence-excited final states (resulting from so-called valence-to-core transitions of electrons that fill the core-hole). RIXS studies with soft X-rays generally target final states that are valence- or vibrationally excited (or of other nature such as magnons). The versatility of RIXS to valence-excited final states is demonstrated by its application in various studies, encompassing molecules,16–18 liquids,19–22 and solids.23–25
Initially enabled by synchrotron radiation X-ray sources with increased spectral brightness,26 RIXS experienced a further advancement with the emergence of X-ray free-electron lasers (XFELs).27–30 This development facilitated the extension of RIXS to time-resolved studies,31–33 exploiting nonlinear processes in optical pump/RIXS probe spectroscopy with applications in fields ranging from condensed matter physics34 to molecular chemistry.18 Within the present work, we focus on chemical applications where recent successful inquiries into photodissociation dynamics,35–37 charge-transfer excitations,38–40 and excited-state proton transfer41 underscore the potential of time-resolved RIXS as a spectroscopic tool that provides element-specific Raman spectra of transient species on ultrafast timescales from vibrational frequencies to the vacuum ultraviolet in the condensed phase.
The complex nature of the underlying processes necessitates the utilisation of advanced computational techniques to decode mechanistic information from experimental data, aid in their analysis, and even forecast complicated spectral features. Consequently, a range of methods,42 both time-independent and time-dependent, have emerged to describe (steady-state) RIXS spectra for molecules where conventional time-independent approaches typically rely on the established Kramers–Heisenberg–Dirac formula employing an eigenstate representation of the system in the frequency domain.43,44 Conversely, time-dependent methods based on wavepacket propagation compute the scattering amplitude by the time-dependent overlap between initial and final vibronic states providing an equivalent time domain approach under steady-state conditions.45,46
Previous in silico time-resolved RIXS studies of molecules considered pump-induced states as isolated quasi-static snapshots, for which steady-state RIXS spectra were simulated.36,37,40,47 This approach enabled identification of contributions from the considered chemical species to the overall RIXS spectrum in a simplified manner, neglecting real-time motion effects. However, when a molecule is impulsively excited, the created wavepacket will evolve in time depending on the shape of the corresponding potential energy surfaces. These dynamics and interplay between the resulting population transfers can significantly impact the nuclear motion and therefore the overall experimental signal measured. Hence, for a description that incorporates nuclear motion effects arising from both the pump-induced valence and intermediate core-excited state dynamics, as well as from dynamics of the final ground and valence-excited states, a time-dependent framework is required that is able to describe non-adiabatic phenomena.
In this work, we present a full quantum dynamical treatment of femtosecond (fs-) RIXS spectroscopy employing the multiconfiguration time-dependent Hartree (MCTDH) method which extends our previous work on steady-state RIXS simulations.48 For this purpose, we utilise a vibronic coupling Hamiltonian encompassing all electronic states involved in the fs-RIXS process as well as an explicit description of the coherent X-ray probe pulse. We conduct calculations of transient RIXS spectra at the nitrogen K-edge of pyrazine. Pyrazine is chosen as an interesting likewise complex benchmark system due to its pronounced non-adiabatic behavior in both the valence and core excited state manifolds. Through explicit assignment of specific spectral features to nuclear motion, we highlight the significance of adopting a comprehensive time-domain approach to achieve an accurate description of time-resolved RIXS signals including all dynamical dimensions.
2 Methodology
2.1 Quantum dynamics
The time-dependent Schrödinger equation for the nuclear dynamics is solved employing the multi-layer (ML-) MCTDH49–51 wavepacket propagation method. The total MCTDH52,53 wavefunction ansatz reads| |  | (1) |
where Aj1…jf are expansion coefficients of the low-dimensional single particle functions (SPFs) φji. Using a linear combinations of time-independent primitive basis functions χri, the time-dependent SPFs are themselves represented by| | 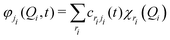 | (2) |
providing a discrete variable representation (DVR) grid. The equations of motion are finally derived by applying the Dirac–Frenkel variational principle.54,55
Within ML-MCTDH, the SPFs are recursively expanded in the form of eqn (1) until the last layer of time-dependent SPFs is represented by the discrete time-independent grid. This variant of MCTDH provides an efficient tool to treat larger systems fully quantum mechanically.
2.2 Vibronic coupling Hamiltonian
Justified by the large energy gap, we completely decouple the valence- and core-excited states concerning non-adiabatic transitions. Moreover, the group approximation is employed separating both, the valence- and core-excited state manifold of pyrazine, into individual subsets of states, resulting in the subsequent matrix representation of the molecular Hamiltonian| | 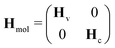 | (3) |
where Hv = diag(Hv1, Hv2) and Hc = diag(Hc1, Hc2) denote the sub-Hamiltonians acting on the valence- and core-excited state manifolds, respectively. In this model, Hv1 contains all valence-excited states relevant for the pump-induced dynamics while Hv2 augments the valence-excited state manifold with higher lying excited states only reached by the RIXS process. There are dipole allowed transitions from Hv1 to both sub-Hamiltonians Hc1 and Hc2 where each consists of two nearly degenerate, vibronically coupled core-excited states. Other core-excited states have been neglected due to the short core–hole lifetime that suppresses internal conversion processes beyond the immediate Franck–Condon region.
In order to avoid singularities in the non-adiabatic coupling terms,56,57 we represent the molecular Hamiltonian Hmol in a diabatic electronic basis such that each sub-Hamiltonian can be written as
| | Hx = ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 + Wx, x ∈ {v1, v2, c1, c2} 1 + Wx, x ∈ {v1, v2, c1, c2} | (4) |
with the kinetic energy operator
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif)
and the diabatic potential matrix
Wx. We further invoke a vibronic coupling model
7,56,58 where the diabatic potentials are expanded as Taylor series around the Franck–Condon point
| | | Hx = H(0) + W(0)x + W(1)x + W(2)x + … | (5) |
where the zero-order Hamiltonian is the harmonic ground-state Hamiltonian
| |  | (6) |
with
ωi representing the frequency of mode
Qi. The diabatic potential matrix up to first order is defined by
| | 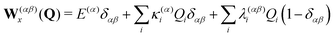 | (7) |
with the vertical excitation energies
E(α) to the
α-th electronic state and the linear intra- and interstate coupling parameters
| | 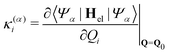 | (8) |
| |  | (9) |
between state |
α〉 and |
β〉. In order to include changes in the frequencies, we also include on-diagonal quadratic intrastate coupling constants
γ(α) for
Hv1 and
Hc representing the most relevant excited states in this investigation.
For strongly anharmonic modes the harmonic expression of the diabatic potentials are replaced by state-specific quartic or Morse potentials with on-diagonal matrix elements
| |  | (10) |
| |  | (11) |
respectively, where
ε(α)i denotes the quartic expansion coefficient,
D(α)0 is the state-specific dissociation energy,
a(α)i defines the curvature of the potential, and
Q0 is the equilibrium position.
2.3 Pump–probe spectra
We use a semiclassical approach, where the full laser-driven Hamiltonian H reads| | | H(t) = Hmol + Hint(t) | (12) |
with the classical light–matter interaction operator Hint acting as a perturbation to the molecular quantum Hamiltonian Hmol. Within the dipole and Condon approximation and assuming a single polarisation direction, the coupling to the external field is given by| | 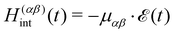 | (13) |
where μαβ is the transition dipole moment. The total electric field| |  | (14) |
is composed of an ultrashort δ-like pump pulse  at time t0 = 0 fs triggering the valence-excited state dynamics and a second pulse
at time t0 = 0 fs triggering the valence-excited state dynamics and a second pulse  probing the induced dynamics after a specific time delay Δτ. In particular, the initial wavepacket in the valence-excited states is generated by a vertical projection of the ground state wavefunction at 0 K onto the excited state manifold while the probe pulse is explicitly described using a time-dependent operator.
probing the induced dynamics after a specific time delay Δτ. In particular, the initial wavepacket in the valence-excited states is generated by a vertical projection of the ground state wavefunction at 0 K onto the excited state manifold while the probe pulse is explicitly described using a time-dependent operator.
When calculating transient X-ray absorption spectra, we also assume a δ-like probe pulse striking the system at time τ > 0. This induces transitions from the valence- to the core-excited state manifold with Hamiltonians Ĥv and Ĥc, respectively. The absorption cross section can then be obtained by the Fourier transform
| |  | (15) |
of the dipole–dipole correlation function
| |  | (16) |
| |  | (17) |
where
Ψv and
Ψc denote wavepackets in the valence- and core-state manifolds, respectively, and
![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) cv
cv is the transition dipole moment operator.
59
In absorption spectroscopy, δ-pulses are conceptualised as idealisations, allowing for simultaneous interrogation of the entire spectral range. On the contrary, the RIXS process depends on narrow-band excitations to precisely define the incoming photon energy. Employing RIXS as a probe for non-stationary systems thus requires an excitation pulse that strikes a balance: it must be long enough to mitigate uncertainties in the excitation process yet short enough to achieve adequate time resolution for probing the underlying dynamics. In this work, we use Gaussian-shaped X-ray probe pulses
| | 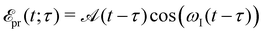 | (18) |
| |  | (19) |
centered at time
τ with carrier frequency
ωI and temporal full width at half maximum (fwhm) duration

of the intensity profile invoking the RIXS process. Assuming no temporal overlap of the pump and probe pulse, the transient RIXS signal can be calculated using the following expression for the RIXS spectrum induced by a coherent light source
48| |  | (20) |
where
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) S
S =
ωS −
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) I
I is the energy loss of the system with
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) I
I =
ωI +
Ei and scattering frequency
ωS. Further, * denotes the convolution and

is the Fourier transform
| |  | (21) |
of the Gaussian-envelope function

of the probe pulse defined in
eqn (19). Furthermore, the evolving wavepacket

is defined by the core-to-valence state projection

of the Raman wavefunction
| | 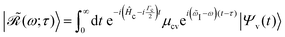 | (22) |
collecting all dynamical information prior to the scattering event. In particular, the Raman wavefunction is a time-independent intermediate state that only parametrically depends on
τ.
3 Computational details
The molecular Hamiltonian is divided into four energetically separated subsets of states. All parameters for the valence excited states, contained in Hv1 and Hv2, and two lowest N-1s core-excited states in Hc1 were adapted from previous studies.48,60 The values to parameterise Hc2 were obtained by fitting the diabatic potential terms from ab initio quantum chemistry calculation using the fc-CVS-EOM-CCSD method61 with the Dunning correlation consistent basis set aug-cc-pVDZ62 matching the level of theory applied in ref. 48. All electronic structure calculations were carried out using the quantum chemistry software package Q-Chem.63 The fitting procedure were performed using the VCHam tools, as part of the Heidelberg MCTDH package.64
Quantum dynamics propagations were run using the ML-MCTDH method as implemented in the Heidelberg MCTDH package. The layer structure, DVR, number of grid points and SPF basis size were adapted from ref. 48 with an increased number of 24 electronic states. The output was written such that a sufficient time resolution and frequency span for subsequent Fourier transforms is guaranteed.
The most relevant parameters and computational details are listed in tabular form in the ESI.†
3.1 Model Hamiltonian
The vibronic coupling model Hamiltonian was obtained using all 24 mass- and frequency scaled normal modes of the ground state D2h structure of pyrazine. While we utilise the (fc-CVS-) EOM-CCSD/aug-cc-pVDZ based linear vibronic coupling model for Hv2 and Hc1 from our recent study on steady-state RIXS of pyrazine,48 we favour the vibronic model from Sala et al.60 obtained from XMCQDPT2/aug-cc-pVDZ calculations to describe Hv1 containing the ground and lowest four valence excited states where non-adiabatic transitions to the ground state are excluded within the model due to the large energy gap. This model was constructed to simulate the UV absorption spectrum of pyrazine and yielded an excellent agreement with experimental data demonstrating its suitability to accurately describe the valence-excited state behaviour after excitation to the B2u(ππ*) state. In order to maintain the energy gap between Hv1 and Hv2 as given in ref. 48 the vertical excitation energies in Hv2 are consistently shifted by −0.6 eV. Moreover, we assume an intrinsic core-excited state lifetime of 8 fs65 covered by an imaginary energy term in the core Hamiltonian Hc. Fig. 1 shows cuts of potential energy surfaces along one of the totally symmetric normal modes and along one of the core-excited state coupling modes.
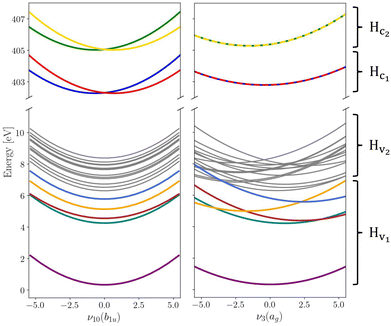 |
| | Fig. 1 Cuts through the diabatic potential energy surfaces along the asymmetrical ν10(b1u) and totally symmetrical ν3(ag) vibrational normal modes. Electronic states that are coupled by the X-ray probe pulse are highlighted in colour while the other states that are thus playing a less significant role are held in grey for the sake of overview. Label and symmetry for each state can be found in the ESI.† | |
Populations in the ground and the three lowest valence-excited states give rise to strongly dipole-allowed transitions to three N-1s core-excited states66 where the lower two, X1 and X2, build Hc1. The third core excited state, X3, is furthermore vibronically coupled to a nearly degenerate fourth state, X4, necessitating its inclusion in the Hamiltonian Hc2. The energies and linear coupling parameters obtained in this work for Hc2 are listed in Table 1. Transition dipole moments to valence- and core-excited states were computed at the Franck–Condon point employing the EOM-CCSD and fc-CVS-EOMCCSD method, respectively. The norm of the corresponding transition dipole moments are given in Table 2. A complete list of parameters of the full molecular Hamiltonian can be found in ref. 60 and 48 or in the form of an operator file in the ESI,† to this study.
Table 1 Vertical excitation energies E(α) as well as linear intra- and interstate coupling constants κ(α)i and λ(αβ)i, respectively, for the core-excited states contained in Hc2. All values are in eV
|
|
Symmetry |
E
|
| X3 |
B1g |
405.05 |
| X4 |
Au |
405.06 |
|
|
κ
3
|
κ
11
|
κ
15
|
κ
20
|
| X3 |
0.1231 |
−0.0787 |
−0.1236 |
−0.2731 |
| X4 |
0.1230 |
−0.0787 |
−0.1240 |
−0.2754 |
|
|
λ
10
|
λ
14
|
λ
18
|
λ
22
|
| (X3, X4) |
0.0998 |
0.1087 |
0.0213 |
0.0224 |
Table 2 Norm of transition dipole moments μαβ between two states |α〉 and |β〉. The transition dipole moments to valence- and core-excited states are obtained from EOM-CCSD and fc-CVS-EOM-CCSD calculations, respectively
| State transition |
μ
αβ
|
| S3 ← S0 |
0.25 |
| S1 ← S0 |
0.82 |
| X2 ← S0 |
0.10 |
| X1 ← S1 |
0.06 |
| X3 ← S2 |
0.06 |
| X3 ← S3 |
0.03 |
| X2 ← S4 |
0.04 |
| X1 ← S6 |
0.02 |
| X4 ← S7 |
0.04 |
| X3 ← S12 |
0.05 |
| X1 ← S16 |
0.04 |
| X1 ← S18 |
0.04 |
4 Results
4.1 Time-resolved X-ray absorption spectra
To ascertain appropriate excitation energies for investigating the UV-induced dynamics of pyrazine with RIXS at the nitrogen K-edge, we compute time-resolved spectra in the X-ray absorption near-edge structure (XANES) region. For this purpose, we assume δ-pulses for both the pump and probe steps and calculate the spectra according to eqn (15). The diabatic valence-excited state population dynamics subsequent to the pump pulse along with a three-dimensional collection of differential absorption spectra are shown in Fig. 2. At time t = 0 fs, the system is primarily excited to S3 with minor contributions to S1 according to their transition dipole moments given in Table 2. S3 rapidly depopulates to both the bright S1 and the dark S2 state followed by oscillatory population dynamics between S1 and S2. This diabatic population behaviour can be traced back to low-lying conical intersections between all state pairs, S1/S2, S1/S3 and S2/S3.60
 |
| | Fig. 2 Valence-excited state population after instantaneous, vertical excitation to the bright S3 and S1 states at the Franck–Condon point (left) and a three-dimensional map showing all computed differential X-ray absorption spectra for time delays between 0 and 200 fs (right). A figure showing fs-XANES spectra for all individual transitions can be found in the ESI.† | |
The population dynamics are well reflected in the transient absorption spectra, where the strong negative bleach signal located around 402.5 eV corresponds to X2 ← S0 transitions while the positive excitation bands at approximately 399.0 eV and 401.8 eV stem from excited state absorption. Within the first few femtoseconds, S3 is mainly populated leading to an absorption band around 400.5 eV. Due to vibrational relaxation in S3 as well as X-ray excitation to potentially higher vibronic states in X3, the X3 ← S3 transitions are then shifted to higher frequencies by about 1.3 eV where they energetically overlap with the X3 ← S2 transition band. The absorption band at 399.0 eV only stems from X1 ← S1 transitions. The non-adiabatic oscillatory population dynamics between S1 and S2 are accurately mapped in the intensity variations of the two main excited state absorption bands in good agreement with previous simulations.66 However, it is worth noting that we formerly used a reduced pyrazine model that comprised only the 9 most dominant vibrational normal modes. In this study, a full 24-dimensional model is used leading to more delocalised wavepackets on the valence excited state manifold that manifest in broader and somewhat asymmetrical line shapes of the excitation bands. This behaviour is particularly pronounced in the strongly fluctuating absorption band around 401.8 eV which also overlaps with the bleach signal at some time delays. In contrast, our previous calculations showed this absorption band to be well separated from the bleach signal for the entire propagation time.
Based on the time-dependent differential absorption map in Fig. 2, we choose excitation energies of 399.0 eV and 401.5 eV for the following fs-RIXS simulations, probing the dynamics on S1 and S3/S2, respectively. The latter X-ray excitation energy was chosen slightly below the center of the fluctuating absorption band to exclude contributions from ground-state bleaching. Moreover, the ESI,† also contains fs-RIXS calculations for an excitation energy of 402.5 eV to show the behaviour in the overlap region of the bleach signal and the close-lying excited state absorption.
4.2 Femtosecond resonant inelastic X-ray scattering
The dynamics triggered by the optical pump pulse primarily involve three valence excited states and are mainly driven by the interstate coupling parameters between the state pairs S1/S3 and S1/S2 with oscillation periods of 19 fs and 21 fs, respectively.60 We therefore choose a Gaussian X-ray probe pulse with a temporal FWHM duration of Ft ≈ 8 fs enabling to follow this ultrafast dynamics without loosing relevant information due to spectral broadening caused by a broadband excitation pulses.48
The transient RIXS spectra are computed using eqn (20) with carrier frequencies of 399.0 eV and 401.5 eV and at time-delays Δτ ranging from 5 to 200 fs. A three-dimensional collection of all spectra along with a single fs-RIXS spectrum for Δτ = 100 fs is shown in Fig. 3. Moreover, a two dimensional representation of the time evolution of the fs-RIXS spectrum in 10 fs steps for both excitation energies can be found in the ESI.†
 |
| | Fig. 3 Top: Three-dimensional collection of calculated fs-RIXS spectra for time delays Δτ between 5 fs and 200 fs with a step size of 5 fs using excitation energies of 399.0 eV (left) and 401.5 eV (right). Bottom: fs-RIXS spectrum at time delay Δτ = 100 fs. Transitions stemming from X1, X2, X3 and X4 are highlighted in blue, red, green and yellow, respectively. The final electronic state of each transition is annotated in the plot. | |
As discussed in the previous section, RIXS probing at 399.0 eV only promotes X1 ← S1 transitions entailing four dipole allowed scattering transitions back to valence excited states S1, S6, S16 and S18 (see Table 2) with transition bands located at approximately 0.0 eV, 3.0 eV, 4.0 eV and 4.5 eV, respectively. These values correspond to the vertical energy gap of the electronics states to S1. Moreover, the RIXS spectrum exhibits a strong anti-Stokes signal at −3.8 eV and a weaker transition band at 2.0 eV belonging to transitions to S0 and S4, respectively, which are dipole forbidden from the initially excited X1 state. However, due to the delocalised nature of the N-1s core orbitals over the equivalent nitrogen atoms, pyrazine naturally posses nearly degenerate core-excited states, X1 and X2, that are vibronically coupled through asymmetrical normal modes of symmetry b1u.48 This coupling leads to ultrafast symmetry breaking of the system within the core–hole lifetime accompanied by a localisation of the core orbitals that finally permits the dipole allowed S0 ← X2 and S4 ← X2 transitions. Furthermore, besides the rather weak and spectrally overlapping signals at higher energy loss, the clearly distinguishable S0 ← X2 and S1 ← X1 transition bands can be seen over the entire time range as demonstrated in the upper left panel of Fig. 3. Consequently, after photo-excitation to S3 the system leaves the immediate Franck–Condon region but remains in a configurations where the two nitrogen atoms are equivalent holding the system close to the conical intersection seam formed along the four normal modes with symmetry b1u. These modes are responsible for disturbing the equivalence of the nitrogen atoms. This result particularly confirms the assumption that none of these vibrational normal modes plays a prominent role in the UV induced dynamics of pyrazine. They can thus be neglected in linear UV absorption simulations.60 Lastly, we note that the overall signal strengths vary in accordance with the population dynamics of S1 shown in Fig. 2.
X-ray excitations at 401.5 eV addresses X3 ← S2 as well as X3 ← S3 transitions where the latter only significantly contribute within the first 20–30 fs due to the rapid depopulation of S3. The related fs-RIXS spectra show two dominant spectral bands where the lower band actually originates from three energetically overlapping transitions. As before, there are two nearly degenerate core-excited states, X3 and X4, that are vibronically coupled along the b1u normal modes with coupling strengths listed in Table 1. Due to their large overlap, ultrafast nuclear motion cannot be separately attributed to individual transitions within this spectral region. Contrary to probe excitations at 399.0 eV, the transient RIXS spectra at 401.5 eV do not contain anti-Stokes signals. Thus, the absence of transitions to the ground state indicate the symmetry of the core-excited state at 401.5 eV. Moreover, an increase of the overall signal strength can be observed for time delays Δτ beyond 100 fs. On the one hand, this trend can be explained by the considerable lower transition dipole moment μX3←S3 compared to μX3←S2 yielding less likely transitions at very early times, and, on the other hand by the strong modulation of the absorption band (see Fig. 2) resulting in a large detuning effect for time delays between 20 fs and 80 fs.
Fig. 4 presents differential XANES spectra and RIXS maps as a function of excitation energy ωI of the X-ray probe pulse and energy loss ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) S to the molecule at specific time delays. Both the transient absorption and the RIXS spectra exhibits positive features stemming from valence-excited state transitions and negative bleach signals related to ground-state transitions of the non-excited system. The bleach signal remains the same for all time delays as there is no radiationless relaxation mechanism from excited states back to the ground state on the femtosecond timescale. Moreover, X-ray transitions involving the ground state S0 are considerably more likely compared to valence-excited state transitions (see Table 2) resulting in a very dominant bleach signal at approximately 402.5 eV. Overall the shape of the excited-state transition bands is rather broad and asymmetrical for both probing techniques which must be therefore traced back to the evolution of the nuclear wavepacket of the pumped system. Additionally, the fs-RIXS maps also contain dynamical features from the intermediate core-excited states as well as from the final ground and valence-excited states.
S to the molecule at specific time delays. Both the transient absorption and the RIXS spectra exhibits positive features stemming from valence-excited state transitions and negative bleach signals related to ground-state transitions of the non-excited system. The bleach signal remains the same for all time delays as there is no radiationless relaxation mechanism from excited states back to the ground state on the femtosecond timescale. Moreover, X-ray transitions involving the ground state S0 are considerably more likely compared to valence-excited state transitions (see Table 2) resulting in a very dominant bleach signal at approximately 402.5 eV. Overall the shape of the excited-state transition bands is rather broad and asymmetrical for both probing techniques which must be therefore traced back to the evolution of the nuclear wavepacket of the pumped system. Additionally, the fs-RIXS maps also contain dynamical features from the intermediate core-excited states as well as from the final ground and valence-excited states.
 |
| | Fig. 4 fs-XANES (left) and corresponding fs-RIXS spectra (right) for time delays Δτ = 20 fs (top) and Δτ = 55 fs (bottom). fs-RIXS spectra are computed for excitation energies ωI ranging from 397.0 eV to 404.9 eV with 0.1 eV stepsize. | |
For both time delays shown in Fig. 4 the RIXS bleach signal consists of five transition bands (stemming from six core-to-valence state transitions). The higher four bands are energetically separated from the lowest transition band by about 3.9 eV, 5.3 eV, 6.5 eV and 7.5 eV. As the lowest transition band of the bleach signal is located just above 0 eV it can be uniquely assigned to the electronic ground state. Moreover, for 20 fs time delay the energy-level separation pattern of the bleach signal repeats in the excited-state signals at 399.0 eV shifted by −3.9 eV. This suggests that the corresponding initial ground and valence-excited states address the same core-excited state pair leading in turn to similar emission bands. However, the progressive valence-excited state dynamics after 55 fs smear out the recurrences, thereby making a direct assignment without additional analysis support difficult.
The spectral proximity of the RIXS band around 401.5 eV masks parts of the time-dependent signal. Particularly at 55 fs the dominant time-independent bleach signal overlaps with the stronger part of the excited-state signal. Within the first 20 fs after valence excitation the two signals do not overlap appreciably before population transfer to S2 sweeps the resonance – and hence, the RIXS signal – to higher energy. As already discussed above, the missing energy-gain features at 401.5 eV clearly indicate X-ray transitions to another pair of core-excited states.
In essence, time-resolved RIXS emerges as a dependable tool to unravel the ultrafast photophysical actions of pyrazine, augmenting the capabilities of other ultrafast X-ray spectroscopic methodos such as fs-XANES spectroscopy. Although fs-XANES adeptly probes the dynamics induced by UV radiation, time-resolved RIXS delves deeper into dynamic facets, unveiling symmetry distortions resulting from non-adiabatic transitions within core-excited states. Furthermore, it furnishes insights into higher-lying valence excited states, which remain inaccessible in transient absorption spectroscopy due symmetry constraints or weak transition dipole moments.
5 Conclusion
While steady-state soft X-ray RIXS has already proven appropriate in probing the chemical and physical properties of molecular systems, time-resolved RIXS experiments have been less common due to the even more demanding spectral brightness requirements. However, advances in XFEL technology, accompanied by new instrumentation such as the hRIXS instrument at European XFEL and the ChemRIXS instrument at LCLS-II,67 hold promise of making time-resolved RIXS a routinely employed technique in the coming years. Moreover, our approach can be expanded to describe stimulated processes which will benefit from advances in seeding technology with a further leap in spectral brightness of XFEL sources. To effectively extract the rich information contained within the experimental data, theoretical progress in truly describing dynamics are imperative to support these expanded experimental capabilities.
In this study, we presented a fully time-dependent quantum mechanical approach to simulating time-resolved RIXS experiments. Leveraging the capabilities of the MCTDH method, we establish a robust framework to accurately describe the intricate photophysics of pyrazine, encompassing all relevant dynamical dimensions. The interplay between population transfers within the valence-excited state manifold and the symmetry-breaking nuclear motions after X-ray interrogation can only be faithfully captured through nuclear quantum dynamics simulations that incorporate non-adiabatic phenomena. Our study further discloses challenges in building reduced-dimensionality models in larger molecules and elucidates the necessity of incorporating symmetry-breaking degrees of freedom. In particular, our time-dependent approach enables simulations beyond steady-state conditions contributing to the growing field of nonlinear spectroscopy at pulsed X-ray sources of high spectral brightness.
Data availability
The data supporting this article have been included as part of the ESI.†
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
A. F. acknowledges financial support from the International Max Planck Graduate School for Ultrafast imaging & Structural Dynamics (IMPRS-UFAST) and from the Christiane-Nüsslein-Vollhard-Foundation. O. V. acknowledges financial support from the German Science Foundation (DFG) through the project number 493826649. This work is supported by the Cluster of Excellence ‘CUI: Advanced Imaging of Matter’ of the Deutsche Forschungsgemeinschaft (DFG) – EXC 2056 – project ID 390715994 (A. F. & N. H.).
References
- F. Gel'mukhanov and H. Ågren, Phys. Rep., 1999, 312, 87–330 CrossRef.
- L. J. P. Ament, M. van Veenendaal, T. P. Devereaux, J. P. Hill and J. van den Brink, Rev. Mod. Phys., 2011, 83, 705–767 CrossRef CAS.
- F. Gel'mukhanov and H. Ågren, Phys. Rev. A: At., Mol., Opt. Phys., 1994, 49, 4378–4389 CrossRef PubMed.
- P. Skytt, J. Guo, N. Wassdahl, J. Nordgren, Y. Luo and H. Ågren, Phys. Rev. A: At., Mol., Opt. Phys., 1995, 52, 3572–3576 CrossRef CAS PubMed.
- Y. Luo, H. Ågren, F. Gel'mukhanov, J. Guo, P. Skytt, N. Wassdahl and J. Nordgren, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14479–14496 CrossRef CAS PubMed.
- Y.-P. Sun, A. Pietzsch, F. Hennies, Z. Rinkevicius, H. O. Karlsson, T. Schmitt, V. N. Strocov, J. Andersson, B. Kennedy, J. Schlappa, A. Föhlisch, F. Gel'mukhanov and J.-E. Rubensson, J. Phys. B: At., Mol. Opt. Phys., 2011, 44, 161002 CrossRef.
- W. Domcke and L. Cederbaum, Chem. Phys., 1977, 25, 189–196 CrossRef CAS.
- P. Skytt, P. Glans, J.-H. Guo, K. Gunnelin, C. Såthe, J. Nordgren, F. K. Gel'mukhanov, A. Cesar and H. Ågren, Phys. Rev. Lett., 1996, 77, 5035–5038 CrossRef CAS PubMed.
- D. Maganas, P. Kristiansen, L.-C. Duda, A. Knop-Gericke, S. DeBeer, R. Schlögl and F. Neese, J. Phys. Chem. C, 2014, 118, 20163–20175 CrossRef CAS.
- S. Eckert, V. Vaz da Cruz, M. Ochmann, I. von Ahnen, A. Föhlisch and N. Huse, J. Phys. Chem. Lett., 2021, 12, 8637–8643 CrossRef CAS PubMed.
- M. Ochmann, V. Vaz da Cruz, S. Eckert, N. Huse and A. Föhlisch, Chem. Commun., 2022, 58, 8834–8837 RSC.
- F. Hennies, A. Pietzsch, M. Berglund, A. Föhlisch, T. Schmitt, V. Strocov, H. O. Karlsson, J. Andersson and J.-E. Rubensson, Phys. Rev. Lett., 2010, 104, 193002 CrossRef PubMed.
- A. Pietzsch, Y.-P. Sun, F. Hennies, Z. Rinkevicius, H. O. Karlsson, T. Schmitt, V. N. Strocov, J. Andersson, B. Kennedy, J. Schlappa, A. Föhlisch, J.-E. Rubensson and F. Gel'mukhanov, Phys. Rev. Lett., 2011, 106, 153004 CrossRef CAS PubMed.
- V. Vaz da Cruz, E. Ertan, R. C. Couto, S. Eckert, M. Fondell, M. Dantz, B. Kennedy, T. Schmitt, A. Pietzsch, F. F. Guimarães, H. Ågren, F. Gel'mukhanov, M. Odelius, A. Föhlisch and V. Kimberg, Phys. Chem. Chem. Phys., 2017, 19, 19573–19589 RSC.
- J. Söderström, R. Stefanuik, F. Hennies, T. Schmitt, V. N. Strocov, J. Andersson, B. Kennedy, J. Schlappa, A. Föhlisch, A. Pietzsch and J.-E. Rubensson, Phys. Rev. A, 2020, 101, 062501 CrossRef.
- T. Marchenko, S. Carniato, L. Journel, R. Guillemin, E. Kawerk, M. Žitnik, M. Kavčič, K. Bučar, R. Bohinc, M. Petric, V. V. da Cruz, F. Gel'mukhanov and M. Simon, J. Phys.: Conf. Seri., 2015, 635, 112012 Search PubMed.
- M. Žitnik, M. Kavčič, R. Bohinc, K. Bučar, A. Mihelič, W. Cao, R. Guillemin, L. Journel, T. Marchenko, S. Carniato, E. Kawerk, M. Piancastelli and M. Simon, J. Electron Spectrosc. Relat. Phenom., 2015, 204, 356–364 CrossRef.
-
M. Lundberg and P. Wernet, in Resonant Inelastic X-ray Scattering (RIXS) Studies in Chemistry: Present and Future, ed. E. J. Jaeschke, S. Khan, J. R. Schneider and J. B. Hastings, Springer International Publishing, Cham, 2020, pp. 2315–2366 Search PubMed.
- M. Blum, M. Odelius, L. Weinhardt, S. Pookpanratana, M. Bär, Y. Zhang, O. Fuchs, W. Yang, E. Umbach and C. Heske, J. Phys. Chem. B, 2012, 116, 13757–13764 CrossRef CAS PubMed.
- L. Weinhardt, M. Blum, O. Fuchs, A. Benkert, F. Meyer, M. Bär, J. Denlinger, W. Yang, F. Reinert and C. Heske, J. Electron Spectrosc. Relat. Phenom., 2013, 188, 111–120 CrossRef CAS.
- L. Kjellsson, K. D. Nanda, J.-E. Rubensson, G. Doumy, S. H. Southworth, P. J. Ho, A. M. March, A. Al Haddad, Y. Kumagai, M.-F. Tu, R. D. Schaller, T. Debnath, M. S. Bin Mohd Yusof, C. Arnold, W. F. Schlotter, S. Moeller, G. Coslovich, J. D. Koralek, M. P. Minitti, M. L. Vidal, M. Simon, R. Santra, Z.-H. Loh, S. Coriani, A. I. Krylov and L. Young, Phys. Rev. Lett., 2020, 124, 236001 CrossRef CAS PubMed.
- L. Young, E. T. Nienhuis, D. Koulentianos, G. Doumy, A. M. March, S. H. Southworth, S. B. Clark, T. M. Orlando, J. A. LaVerne and C. I. Pearce, Appl. Sci., 2021, 11, 701 CrossRef CAS.
- A. Kotani and S. Shin, Rev. Mod. Phys., 2001, 73, 203–246 CrossRef CAS.
- A. Revelli, M. M. Sala, G. Monaco, P. Becker, L. Bohatý, M. Hermanns, T. C. Koethe, T. Fröhlich, P. Warzanowski, T. Lorenz, S. V. Streltsov, P. H. M. van Loosdrecht, D. I. Khomskii, J. van den Brink and M. Grüninger, Sci. Adv., 2019, 5, eaav4020 CrossRef CAS PubMed.
- M. Magnaterra, M. Moretti Sala, G. Monaco, P. Becker, M. Hermanns, P. Warzanowski, T. Lorenz, D. I. Khomskii, P. H. M. van Loosdrecht, J. van den Brink and M. Grüninger, Phys. Rev. Res., 2023, 5, 013167 CrossRef CAS.
-
P. Willmott, An Introduction to Synchrotron Radiation: Techniques and Applications, Wiley, Hoboken, 2019 Search PubMed.
- B. W. J. McNeil and N. R. Thompson, Nat. Photonics, 2010, 4, 814–821 CrossRef CAS.
- C. Pellegrini, A. Marinelli and S. Reiche, Rev. Mod. Phys., 2016, 88, 015006 CrossRef.
- Z. Zhao, D. Wang, Q. Gu, L. Yin, M. Gu, Y. Leng and B. Liu, Appl. Sci., 2017, 7, 607 CrossRef.
- E. A. Seddon, J. A. Clarke, D. J. Dunning, C. Masciovecchio, C. J. Milne, F. Parmigiani, D. Rugg, J. C. H. Spence, N. R. Thompson, K. Ueda, S. M. Vinko, J. S. Wark and W. Wurth, Rep. Prog. Phys., 2017, 80, 115901 CrossRef CAS PubMed.
- M. Beye, P. Wernet, C. Schüßler-Langeheine and A. Föhlisch, J. Electron Spectrosc. Relat. Phenom., 2013, 188, 172–182 CrossRef CAS.
- H. Lu, A. Gauthier, M. Hepting, A. S. Tremsin, A. H. Reid, P. S. Kirchmann, Z. X. Shen, T. P. Devereaux, Y. C. Shao, X. Feng, G. Coslovich, Z. Hussain, G. L. Dakovski, Y. D. Chuang and W. S. Lee, Sci. Rep., 2020, 10, 22226 CrossRef CAS PubMed.
- F. Gel'mukhanov, M. Odelius, S. P. Polyutov, A. Föhlisch and V. Kimberg, Rev. Mod. Phys., 2021, 93, 035001 CrossRef.
- M. Mitrano and Y. Wang, Commun. Phys., 2020, 3, 184 CrossRef.
- P. Wernet, K. Kunnus, I. Josefsson, I. Rajkovic, W. Quevedo, M. Beye, S. Schreck, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M. F. de Groot, K. J. Gaffney, S. Techert, M. Odelius and A. Föhlisch, Nature, 2015, 520, 78–81 CrossRef CAS PubMed.
- K. Kunnus, I. Josefsson, I. Rajkovic, S. Schreck, W. Quevedo, M. Beye, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, K. J. Gaffney, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, S. Techert, P. Wernet, M. Odelius and A. Föhlisch, New J. Phys., 2016, 18, 103011 CrossRef.
- K. Kunnus, I. Josefsson, I. Rajkovic, S. Schreck, W. Quevedo, M. Beye, C. Weniger, S. Grübel, M. Scholz, D. Nordlund, W. Zhang, R. W. Hartsock, K. J. Gaffney, W. F. Schlotter, J. J. Turner, B. Kennedy, F. Hennies, F. M. F. de Groot, S. Techert, M. Odelius, P. Wernet and A. Föhlisch, Struct. Dyn., 2016, 3, 043204 CrossRef CAS PubMed.
- R. M. Jay, J. Norell, S. Eckert, M. Hantschmann, M. Beye, B. Kennedy, W. Quevedo, W. F. Schlotter, G. L. Dakovski, M. P. Minitti, M. C. Hoffmann, A. Mitra, S. P. Moeller, D. Nordlund, W. Zhang, H. W. Liang, K. Kunnus, K. Kubiček, S. A. Techert, M. Lundberg, P. Wernet, K. Gaffney, M. Odelius and A. Föhlisch, J. Phys. Chem. Lett., 2018, 9, 3538–3543 CrossRef CAS PubMed.
- J. Norell, R. M. Jay, M. Hantschmann, S. Eckert, M. Guo, K. J. Gaffney, P. Wernet, M. Lundberg, A. Föhlisch and M. Odelius, Phys. Chem. Chem. Phys., 2018, 20, 7243–7253 RSC.
- R. M. Jay, S. Eckert, B. E. Van Kuiken, M. Ochmann, M. Hantschmann, A. A. Cordones, H. Cho, K. Hong, R. Ma, J. H. Lee, G. L. Dakovski, J. J. Turner, M. P. Minitti, W. Quevedo, A. Pietzsch, M. Beye, T. K. Kim, R. W. Schoenlein, P. Wernet, A. Föhlisch and N. Huse, J. Phys. Chem. Lett., 2021, 12, 6676–6683 CrossRef CAS PubMed.
- S. Eckert, J. Norell, P. S. Miedema, M. Beye, M. Fondell, W. Quevedo, B. Kennedy, M. Hantschmann, A. Pietzsch, B. E. Van Kuiken, M. Ross, M. P. Minitti, S. P. Moeller, W. F. Schlotter, M. Khalil, M. Odelius and A. Föhlisch, Angew. Chem., Int. Ed., 2017, 56, 6088–6092 CrossRef CAS PubMed.
- P. Norman and A. Dreuw, Chem. Rev., 2018, 118, 7208–7248 CrossRef CAS PubMed.
- H. A. Kramers and W. Heisenberg, Z. Phys., 1925, 31, 681–708 CrossRef CAS.
- P. Dirac and R. Fowler, Proc. R. Soc. London, Ser. A, 1927, 114, 710–728 Search PubMed.
- S. Lee and E. J. Heller, J. Chem. Phys., 1979, 71, 4777–4788 CrossRef CAS.
- D. J. Tannor and E. J. Heller, J. Chem. Phys., 1982, 77, 202–218 CrossRef CAS.
- A. Banerjee, R. M. Jay, T. Leitner, R.-P. Wang, J. Harich, R. Stefanuik, M. R. Coates, E. V. Beale, V. Kabanova, A. Kahraman, A. Wach, D. Ozerov, C. Arrell, C. Milne, P. J. M. Johnson, C. Cirelli, C. Bacellar, N. Huse, M. Odelius and P. Wernet, Chem. Sci., 2024, 15, 2398–2409 RSC.
- A. Freibert, D. Mendive-Tapia, N. Huse and O. Vendrell, J. Chem. Theory Comput., 2024, 20, 2167–2180 CrossRef PubMed.
- H. Wang and M. Thoss, J. Chem. Phys., 2003, 119, 1289–1299 CrossRef CAS.
- U. Manthe, J. Chem. Phys., 2008, 128, 164116 CrossRef PubMed.
- O. Vendrell and H.-D. Meyer, J. Chem. Phys., 2011, 134, 044135 CrossRef PubMed.
- M. Beck, A. Jäckle, G. Worth and H.-D. Meyer, Phys. Rep., 2000, 324, 1–105 CrossRef CAS.
- in Multidimensional Quantum Dynamics: MCTDH Theory and Applications, ed. G. A. W. Hans-Dieter Meyer and F. Gatti, WILEY-VCH Verlag GmbH & Co. KGaA, 2009 Search PubMed.
- P. A. M. Dirac, Math. Proc. Cambridge Philos. Soc., 1930, 26, 376–385 CrossRef CAS.
-
J. Frenkel, Wave mechanics; advanced general theory, The Clarendon press, Oxford, 1934 Search PubMed.
-
H. Köppel, W. Domcke and L. S. Cederbaum, Multimode Molecular Dynamics Beyond the Born-Oppenheimer Approximation, John Wiley & Sons, Ltd, 1984, pp. 59–246 Search PubMed.
- G. A. Worth and L. S. Cederbaum, Annu. Rev. Phys. Chem., 2004, 55, 127–158 CrossRef CAS PubMed.
- L. Cederbaum, W. Domcke, H. Köppel and W. Von Niessen, Chem. Phys., 1977, 26, 169–177 CrossRef CAS.
- S.-Y. Lee, W. Pollard and R. A. Mathies, Chem. Phys. Lett., 1989, 160, 531–537 CrossRef CAS.
- M. Sala, B. Lasorne, F. Gatti and S. Guérin, Phys. Chem. Chem. Phys., 2014, 16, 15957–15967 RSC.
- M. Vidal, X. Feng, E. Epifanovsky, A. I. Krylov and S. Coriani, J. Chem. Theory Comput., 2019, 15, 3117–3133 CrossRef CAS PubMed.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- E. Epifanovsky,
et al.
, J. Chem. Phys., 2021, 155(8), 084801 CrossRef CAS PubMed.
-
G. A. Worth, M. H. Beck, A. Jäckle, H. Meyer, F. Otto, M. Brill and O. Vendrell, The MCTDH package, version 8.6, 2020, https://mctdh.uni-hd.de Search PubMed.
- K. Prince, M. Vondráček, J. Karvonen, M. Coreno, R. Camilloni, L. Avaldi and M. de Simone, J. Electron Spectrosc. Relat. Phenom., 1999, 101–103, 141–147 CrossRef CAS.
- A. Freibert, D. Mendive-Tapia, N. Huse and O. Vendrell, J. Phys. B: At., Mol. Opt. Phys., 2021, 54, 244003 CrossRef CAS.
-
P. Abbamonte, F. Abild-Pedersen, P. Adams, M. Ahmed, F. Albert, R. A. Mori, P. Anfinrud, A. Aquila, M. Armstrong, J. Arthur, J. Bargar, A. Barty, U. Bergmann, N. Berrah, G. Blaj, H. Bluhm, C. Bolme, C. Bostedt, S. Boutet, G. Brown, P. Bucksbaum, M. Cargnello, G. Carini, A. Cavalleri, V. Cherezov, W. Chiu, Y. Chuang, D. Cocco, R. Coffee, G. Collins, A. Cordones-Hahn, J. Cryan, G. Dakovski, M. Dantus, H. Demirci, P. Denes, T. Devereaux, Y. Ding, S. Doniach, R. Dorner, M. Dunne, H. Durr, T. Egami, D. Eisenberg, P. Emma, C. Fadley, R. Falcone, Y. Feng, P. Fischer, F. Fiuza, L. Fletcher, L. Foucar, M. Frank, J. Fraser, H. Frei, D. Fritz, P. Fromme, A. Fry, M. Fuchs, P. Fuoss, K. Gaffney, E. Gamboa, O. Gessner, S. Ghimire, A. Gleason, S. Glenzer, T. Gorkhover, A. Gray, M. Guehr, J. Guo, J. Hajdu, S. Hansen, P. Hart, M. Hashimoto, J. Hastings, D. Haxton, P. Heimann, T. Heinz, A. Hexemer, J. Hill, F. Himpsel, P. Ho, B. Hogue, Z. Huang, M. Hunter, G. Hura, N. Huse, Z. Hussain, M. Ilchen, C. Jacobsen, C. Kenney, J. Kern, S. Kevan, J. Kim, H. Kim, P. Kirchmann, R. Kirian, S. Kivelson, C. Kliewer, J. Koralek, G. Kovacsova, A. Lanzara, J. LaRue, H. Lee, J. Lee, W. Lee, Y. Lee, I. Lindau, A. Lindenberg, Z. Liu, D. Lu, U. Lundstrom, A. MacDowell, W. Mao, J. Marangos, G. Marcus, T. Martinez, W. McCurdy, G. McDermott, C. McGuffey, M. Minitti, S. Miyabe, S. Moeller, R. Moore, S. Mukamel, K. Nass, A. Natan, K. Nelson, S. Nemsak, D. Neumark, R. Neutze, A. Nilsson, D. Nordlund, J. Norskov, S. Nozawa, H. Ogasawara, H. Ohldag, A. Orville, D. Osborn, T. Osipov, A. Ourmazd, D. Parkinson, C. Pellegrini, G. Phillips, T. Rasing, T. Raubenheimer, T. Recigno, A. Reid, D. Reis, A. Robert, J. Robinson, D. Rolles, J. Rost, S. Roy, A. Rudenko, T. Russell, R. Sandberg, A. Sandhu, N. Sauter, I. Schlichting, R. Schlogl, W. Schlotter, M. Schmidt, J. Schneider, R. Schoenlein, M. Schoeffler, A. Scholl, Z. Shen, O. Shpyrko, T. Silva, S. Sinha, D. Slaughter, J. Sobota, D. Sokaras, K. Sokolowski-Tinten, S. Southworth, J. Spence, C. Stan, J. Stohr, R. Stroud, V. Sundstrom, C. Taatjes, A. Thomas, M. Trigo, Y. Tsui, J. Turner, A. van Buuren, S. Vinko, S. Wakatsuki, J. Wark, P. Weber, T. Weber, M. Wei, T. Weiss, P. Wernet, W. White, P. Willmott, K. Wilson, W. Wurth, V. Yachandra, J. Yano, D. Yarotski, L. Young, Y. Zhu, D. Zhu and P. Zwart, New Science Opportunities Enabled by LCLS-II X-Ray Lasers, United States, 2015 DOI:10.2172/1630267.
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab,
David
Mendive-Tapia
*ab,
David
Mendive-Tapia
 b,
Oriol
Vendrell
b,
Oriol
Vendrell
 *b and
Nils
Huse
*b and
Nils
Huse
 a
a

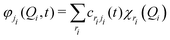
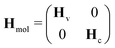
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) 1 + Wx, x ∈ {v1, v2, c1, c2}
1 + Wx, x ∈ {v1, v2, c1, c2}![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) and the diabatic potential matrix Wx. We further invoke a vibronic coupling model7,56,58 where the diabatic potentials are expanded as Taylor series around the Franck–Condon point
and the diabatic potential matrix Wx. We further invoke a vibronic coupling model7,56,58 where the diabatic potentials are expanded as Taylor series around the Franck–Condon point
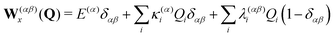
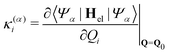



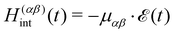

 at time t0 = 0 fs triggering the valence-excited state dynamics and a second pulse
at time t0 = 0 fs triggering the valence-excited state dynamics and a second pulse  probing the induced dynamics after a specific time delay Δτ. In particular, the initial wavepacket in the valence-excited states is generated by a vertical projection of the ground state wavefunction at 0 K onto the excited state manifold while the probe pulse is explicitly described using a time-dependent operator.
probing the induced dynamics after a specific time delay Δτ. In particular, the initial wavepacket in the valence-excited states is generated by a vertical projection of the ground state wavefunction at 0 K onto the excited state manifold while the probe pulse is explicitly described using a time-dependent operator.



![[small mu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b3.gif) cv is the transition dipole moment operator.59
cv is the transition dipole moment operator.59
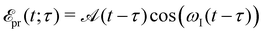

 of the intensity profile invoking the RIXS process. Assuming no temporal overlap of the pump and probe pulse, the transient RIXS signal can be calculated using the following expression for the RIXS spectrum induced by a coherent light source48
of the intensity profile invoking the RIXS process. Assuming no temporal overlap of the pump and probe pulse, the transient RIXS signal can be calculated using the following expression for the RIXS spectrum induced by a coherent light source48
![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) S = ωS −
S = ωS − ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) I is the energy loss of the system with
I is the energy loss of the system with ![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) I = ωI + Ei and scattering frequency ωS. Further, * denotes the convolution and
I = ωI + Ei and scattering frequency ωS. Further, * denotes the convolution and  is the Fourier transform
is the Fourier transform
 of the probe pulse defined in eqn (19). Furthermore, the evolving wavepacket
of the probe pulse defined in eqn (19). Furthermore, the evolving wavepacket  is defined by the core-to-valence state projection
is defined by the core-to-valence state projection  of the Raman wavefunction
of the Raman wavefunction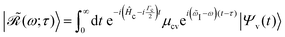


![[small omega, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10f.gif) S to the molecule at specific time delays. Both the transient absorption and the RIXS spectra exhibits positive features stemming from valence-excited state transitions and negative bleach signals related to ground-state transitions of the non-excited system. The bleach signal remains the same for all time delays as there is no radiationless relaxation mechanism from excited states back to the ground state on the femtosecond timescale. Moreover, X-ray transitions involving the ground state S0 are considerably more likely compared to valence-excited state transitions (see Table 2) resulting in a very dominant bleach signal at approximately 402.5 eV. Overall the shape of the excited-state transition bands is rather broad and asymmetrical for both probing techniques which must be therefore traced back to the evolution of the nuclear wavepacket of the pumped system. Additionally, the fs-RIXS maps also contain dynamical features from the intermediate core-excited states as well as from the final ground and valence-excited states.
S to the molecule at specific time delays. Both the transient absorption and the RIXS spectra exhibits positive features stemming from valence-excited state transitions and negative bleach signals related to ground-state transitions of the non-excited system. The bleach signal remains the same for all time delays as there is no radiationless relaxation mechanism from excited states back to the ground state on the femtosecond timescale. Moreover, X-ray transitions involving the ground state S0 are considerably more likely compared to valence-excited state transitions (see Table 2) resulting in a very dominant bleach signal at approximately 402.5 eV. Overall the shape of the excited-state transition bands is rather broad and asymmetrical for both probing techniques which must be therefore traced back to the evolution of the nuclear wavepacket of the pumped system. Additionally, the fs-RIXS maps also contain dynamical features from the intermediate core-excited states as well as from the final ground and valence-excited states.

