Beryllium carbonyl Be(CO)_n (n = 1–4) complex: a p-orbital analogy of Dewar–Chatt–Duncanson model

Abstract

Transition metal–carbonyl bonds are rationalized by M ← CO σ donation and M → CO π back donation where the d orbital of the transition metal is involved. This bonding model provided by Dewar, Chatt and Duncanson (DCD) has rationalized many transition metal–ligand bonds. The involvement of p orbital in such a DCD model can be intriguing. Alkaline earth metals with ns²np⁰ configuration may appear suitable as ns⁰np² excitation has been recognized in many complexes. Herein, a theoretical study is presented for the Be(CO)_n (n = 1–4) complex to verify this assumption. Detailed electronic structure analyses confirmed the involvement of the p orbital of beryllium in M → CO π back donation, thereby supporting the hypothesis. EDA-NOCV results reveal that the π-back donation from the central Be atom to CO ligands significantly predominates over the σ donation from the ligands for both Be(CO)₃ and Be(CO)₄. Our calculations reveal that Be(CO)₄ is the highest carbonyl that may be experimentally detected.

---

Introduction

Bonding in metal carbonyls is generally rationalized by the Dewar–Chatt–Duncanson model,^1,2 where M ← CO σ donation and M → CO π back donation take place simultaneously. This synergistic bonding situation (Scheme 1a) results in the weakening of the CO bond, which can be traced using IR spectroscopy. This bonding situation was first introduced by Dewar¹ in 1951 to explain the peculiar structure of Zeise's salt PtCl₃(C₂H₄)⁻. The Dewar–Chatt–Duncanson (DCD) model has become the standard bonding model of transition metal complexes.³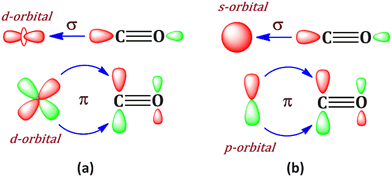

Scheme 1 Bonding situation in (a) transition metal carbonyls where d orbitals are involved and (b) bonding situation in metal carbonyls where s and p orbital of metal are involved.

Generally, transition metal having d orbital is best suited for this type of bonding, which favours backdonation from the filled d orbital to π* orbital of the CO ligand. However, an alternative situation may also be envisioned where the metal uses its filled p_z-orbital for the M → CO (π*) back donation (Scheme 1b) and vacant s, p_x and p_y orbitals of metal for M ← CO σ donation. To realize this, the choice of the metal is very crucial. One such obvious choice is alkaline earth metal, among which beryllium is very lucrative. Braunschweig and co-workers have reported the first example of neutral zero valent beryllium complex L–Be–L (L = cyclic (alkyl)(amino)carbene).⁴ The bonding situation was described as a donor–acceptor interaction between the ground state of L ligands and Be(0), which is in 1s²2s⁰2p² electronic configuration.⁴ Similarly, the OCBe(CO)₃ complex has also been reported by Chen et al.⁵ This indicates that beryllium can show a bonding feature involving its excited 1s²2s⁰2p² electronic configuration where the valence 2s orbital is empty and 2p orbital is filled, a perfect match to fulfill the hypothetical bonding situation in Scheme 1b. It should be noted that Be(0) compounds have been predicted theoretically.^6,7 However, to the best of our knowledge, such a connection between the p-orbital analogy of the DCD model has never been highlighted in those Be(0) compounds; however, in this study, the beryllium carbonyl complex, Be(CO)_n (n = 1–4), has been theoretically studied, and it shows such a bonding situation. Involvement of beryllium 2s, 2p_x and 2p_y orbitals in M ← CO σ donation and 2p_z orbital in M → CO (π*) back donation is clearly established.

Computational details

Geometry optimization and vibrational frequency calculations were performed using TPSSh/def2-TZVP⁸ and M06-2X/def2-TZVP⁹ levels in both singlet and triplet spin states. Zero-point corrections were included in bond dissociation energy calculations. All these calculations were performed using the Gaussian 16 suite program.¹⁰ Single point CCSD(T)/cc-pVTZ calculations on TPSSh/def2-TZVP optimized geometries were performed using the ORCA 4.2.1 program.^11,12 We checked the multireference character using the T₁ diagnostic value of the converged CCSD wavefunction. They are smaller than the prescribed threshold (0.02), indicating a single reference character of the studied systems. Electron localization function (ELF)^13,14 calculation was performed using the Multiwfn program code.¹⁵

Energy decomposition analysis¹⁶ in conjunction with the natural orbital for chemical valence¹⁷ (EDA-NOCV) was performed at the BP86/TZ2P level¹⁸ using the ADF2020.102 program package¹⁹ on TPSSh optimized geometries. The interaction energy between fragments A and B in the molecule A–B can be considered as an indicator of bond strength between the two fragments under consideration. EDA mainly focuses on the intrinsic interaction energy (ΔE_int). This interaction energy is related to another physical observable, the bond dissociation energy (D_e), as can be seen in the following equation:

ΔE_int = −D_e + ΔE_prep

where ΔE_prep = (E_A^GS + E_B^GS) − (E_A + E_B)

The fragments A and B in their respective ground states are excited to the frozen electronic and geometric states in the molecule A–B by providing them the required excitation energy (ΔE_prep). E_A^GS and E_B^GS refer to the electronic energy of the fragments A and B in their respective ground states, while E_A and E_B refer to the electronic energy of the corresponding fragments in their frozen geometries of the molecule.

The instantaneous interaction energy (ΔE_int) of a bond A–B is partitioned into chemically meaningful components as follows:

ΔE_int = ΔE_elect + ΔE_Pauli + ΔE_orb + ΔE_disp.

The term ΔE_elect refers to the quasi-classical electrostatic interactions. The frozen electron density distribution of the fragments in the geometry of the molecules is calculated by quantum mechanics, and the interaction between the nuclei and electrons is calculated by classical laws. It is usually an attractive component and gives an estimate of electrostatic interactions that are excluded from the orbital-based analysis. ΔE_Pauli corresponds to the repulsive interactions between fragments of like spin as they approach each other. However, note that this term is not indicative of ionic bonding and is calculated by the anti-symmetrization and renormalization of the Kohn–Sham determinant of the orbitals. ΔE_orb is associated with the stabilization of orbitals during bond formation and is an attractive component. It includes the effects of charge transfer, relaxation, and polarization by deformation of the charge distribution of the fragments during bond formation.

Developed by Mitoraj and Michalak, the EDA-NOCV scheme further decomposes ΔE_orb term into contributions from each irreducible representation in the point group of the interacting system. The natural orbitals for chemical valence (NOCV) provide insight into each specific orbital interaction between the fragments and the contribution of each pair of the interacting orbitals (Ψ_−n/Ψ_n) to the total bond energy. Within this scheme, ΔE_orb is expressed in terms of NOCVs as

where −F^TS_−n,−n and F^TS_n,n are the Kohn–Sham matrix elements defined over NOCV pairs with eigenvalues −v_n and v_n, respectively, with respect to the transition-state density. This transition-state density is the intermediate density between that of the molecule and the superimposed fragments. The orbitals with a negative value exhibit antibonding nature and those with a positive value exhibit bonding nature. The strength of the pairwise orbital interactions can be quantitatively estimated and the associated change in charge density can be visualized via deformation densities.

Results and discussion

Let us start with the BeCO molecule (Fig. 1). Both TPSSh and M06-2X show similar geometrical features; hence, the discussion throughout the text will be based on TPSSh results. Although the optimized geometry of BeCO shows a strongly bonded complex in a triplet ground state, it is unstable with respect to separated Be and CO. This is in tune with previous experimental observations.²⁰ Moreover, the triplet ground state of BeCO provides a hint that the excitation from the 2s² configuration of beryllium to 2s¹2p¹ takes place in the presence of a single CO ligand. Therefore, it is expected that the addition of another CO ligand will create more excitation of beryllium electron configuration and may reach the desired 2s⁰2p² configuration. Indeed, the linear triplet Be(CO)₂ complex is stable with respect to dissociation to Be (¹S) and two CO molecules (bond dissociation energy is 40.2 kcal mol⁻¹ for the loss of two CO molecules). Previous theoretical calculations by Sunil et al. confirmed this fact, further predicting that a stable dimer of Be(CO)₂ having a Be=Be double bonded complex may be realized in D_2h (CO)₂BeBe(CO)₂ species in the ¹A_g, ground state.²¹ However, there is a difference in the geometry of the Be(CO)₂ complex. The present study predicts it to have a linear D_∞h geometry while the calculation of Sunil et al. at the HF level predicted a C_2v geometry.²¹ In fact, no local minimum in the C_2v geometry of Be(CO)₂ is found at the TPSSh/def2-TZVP level. This might be due to the non-inclusion of the electron correlation in predicting the geometry.²¹ To confirm this, we have optimized the geometry of Be(CO)₂ at CCSD(T)/cc-pVTZ, which could not locate any C_2v geometry, rather it locates a linear D_∞h geometry. We therefore prefer to discuss the linear D_∞h geometry of Be(CO)₂. The Be–C bond length in Be(CO)₂ is 1.608 Å and the CO bond is extremely elongated, resulting in a dramatic lowering of the IR active CO stretching frequency in the complex. This indicates a significant Be (2p) → CO (π*) back donation. The next addition of another CO to triplet Be(CO)₂ results in trigonal planar Be(CO)₃ complex. Remarkably, the singlet state is 18.6 kcal mol⁻¹ more stable than the triplet. Both the structure and stability of Be(CO)₃ have been previously explored using BP86/def2-TZVPP and M06-2X/def2-TZVPP levels.⁷ Significant reduction in CO stretching frequency is observed and the molecular orbital analysis confirmed the Be(2p) → CO (π*) back donation. It should be noted that both Be(CO)₂ and Be(CO)₃ were experimentally identified.²⁰

Fig. 1 Optimized geometries of (a) free CO (b) triplet Be(CO)₂ and (c) singlet Be(CO)₃ complex. Bond lengths are in Å, Mayer's bond orders are in parenthesis and IR active CO stretching frequencies (cm⁻¹) in red font. Shapes of the molecular orbitals responsible for Be (2p_z) → CO (π*) back donation and M ← CO σ donation are also shown.

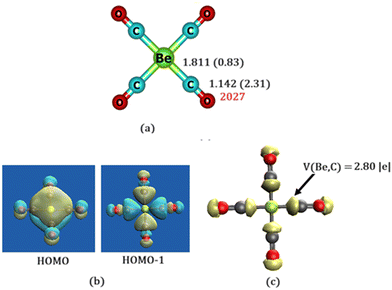
Let us turn our attention now to Be(CO)₄. It adopts a perfectly square planar geometry in its singlet electronic ground state (Fig. 2a). The triplet state is 10.7 kcal mol⁻¹ higher in energy at TPSSh/def2-TZVP and 14.2 kcal mol⁻¹ at the CCSD(T)/cc-pVTZ//TPSSh/def2-TZVP level. The tetrahedral geometry is also a saddle point on the potential energy surface. All other manually constructed isomers are also saddle points on the potential energy surface. It implies that the square planar geometry of Be(CO)₄ is the lowest energy structure. While BeCO has a triplet ground state,²⁰ the ground state of Be(CO)₄ is a closed-shell singlet. Moreover, while the triplet electronic states of BeCO and Be(CO)₂ are more stable, singlet electronic states become more stable for Be(CO)₃ and Be(CO)₄ complexes. All Be–C bond lengths in Be(CO)₄ are equal (1.811 Å) at the TPSSh level. Moreover, M06-2X level produces similar Be–C distances (1.816 Å). Mayer's bond order for the Be–C bond is 0.83, indicating significant covalency and a stronger Be–CO bond. The computed Hirshfeld charge at the Be atom is near zero (−0.05 e) and slightly positive (0.1 e) at the carbon atom indicating that the bonding situation should not be described as Be⁺(CO)₄⁻ or Be²⁺(CO)₄²⁻, rather as common DCD model, which recovers covalency in the metal–ligand bond.^1,2 The CO bond is elongated by 0.013 Å compared to its length in the free form (1.129 Å). This reflects Be → CO back donation, which is also evident from the lowering of the IR active stretching frequency (unscaled) of the CO group (2027 cm⁻¹) compared to its free value (2184 cm⁻¹). The calculated bond dissociation energy for the loss of four molecules of CO from Be(CO)₄ is 65.6 kcal mol⁻¹ (46.2 kcal mol⁻¹ at CCSD(T)/cc-pVTZ level), indicating that the Be–CO bonds are stronger. This indicates that the possibility of its experimental observation may be in the low-temperature neon matrix where the isolation of M(CO)₈ (M = Ca, Sr or Ba) has been reported.²²

Fig. 2 (a) Optimized geometry of Be(CO)₄ complex. Bond lengths are in Å, Mayer's bond orders are in parenthesis and IR active CO stretching frequencies (cm⁻¹) in red font, (b) shapes of HOMO and HOMO−1 and (c) ELF disynaptic V(Be,C) basin with population in |e| of the Be(CO)₄ complex.

Fig. 2b shows the shapes of the highest occupied molecular orbital (HOMO) and HOMO−1 of Be(CO)₄ complex. HOMO represents the Be → CO π* back donation and is delocalized among all four carbon centres. This delocalization stabilizes the square planar geometry over the tetrahedral one. HOMO−1 represents the CO → Be σ donation, thereby establishing the synergism observed in the common DCD model. Interestingly, the Be → CO π* back donation involves Be 2p_z orbital. Thus, the present bonding situation can be considered as a p-orbital analog of the DCD model. Electron localization function (ELF)^12,13 analysis also reveals the presence of disynaptic V(Be,C) basins with a population greater than 2.00 |e| (Fig. 2c), indicating a partial double Be–C bonding character. The bonding situation is exactly similar to that observed for the experimentally observed neutral zero valent beryllium complex L–Be–L (L = cyclic (alkyl)(amino)carbene)⁴ and OCBe(CO)₃ complex⁵ and theoretically proposed Be(0) compounds.^6,7

Are higher carbonyl complexes possible? We tried to optimize Be(CO)_n with n = 5–8 in both singlet and triplet electronic states. However, geometry optimisation leads to dissociation of CO ligand(s). This indicates that the beryllium atom can accommodate a maximum of four CO groups.

To gain an insight into the quantitative nature of the bonding description in Be(CO)₃ and Be(CO)₄, we carried out energy decomposition analysis coupled with natural orbital for chemical valence (EDA-NOCV). In both the systems, the central beryllium atom in 1s²2s⁰2p_z² electronic state is considered as one fragment and the ground state singlet carbonyl ligands, namely, three CO ligands in Be(CO)₃ and four CO ligands in Be(CO)₄, as another fragment. The bonding scheme considered here features purely dative interactions, with σ-donations from the CO ligands and π-back donations from the central beryllium atom (Table 1).

Table 1 EDA-NOCV results (in kcal mol⁻¹) of Be(CO)₃ and Be(CO)₄ at the BP86/TZ2P level of theory

		Be(CO)3		Be(CO)4
a The values in parentheses give the percentage contribution to the total attractive interactions ΔEelstat + ΔEorb. b The values in parentheses give the percentage contribution to the total orbital interactions ΔEorb. c ΔErest = ΔEorb − (ΔEσ + ΔEπ). d Dissociation energy (De).
Fragment 1		Be(1s^22s^02pz^2)		Be(1s^22s^02pz^2)
Fragment 2		3CO		4CO
ΔEint		−256.3		−266.8
ΔEPauli		69.2		37.9
ΔEelstat^a		−87.0 (26.9%)		−78.7 (26%)
ΔEdisp		−1.8		−1.9
ΔEorb^a		−236.7 (73.1%)		−224.1 (74%)
ΔEσ^b	ΔEσ(+ + +)^b	−17.1 (7.2%)	ΔEσ(+ + + +)^b	−18.2 (8.1%)
	ΔEσ(+ − +)^b	−40.3 (17.0%)	ΔEσ(· + · −)^b	−32.8 (14.6%)
	ΔEσ(+ · −)^b	−40.3 (17.0%)	ΔEσ(+ · − ·)^b	−32.8 (14.6%)
			ΔEσ(+ − + −)^b	−8.1 (3.6%)
ΔEπ^b		−128.3 (54.2%)		−123.7 (55.3%)
ΔErest^c		−10.7 (4.6%)		−8.5 (3.8%)
ΔEprep		179.2		196.6
−De^d		−77.1		−70.2

---

The interaction energy ΔE_int, which can be considered as a measure of the Be–C bond strength, is found to be only slightly higher for Be(CO)₄ (−266.8 kcal mol⁻¹) as compared to Be(CO)₃ (−256.3 kcal mol⁻¹). Note that the total attractive component of interaction energy is higher for Be(CO)₃. The slightly higher value of ΔE_int for Be(CO)₄ mainly arises from the significantly lower value of Pauli repulsion (37.9 kcal mol⁻¹). The orbital stabilization energy, ΔE_orb in Be(CO)₃ and Be(CO)₄ are found to be −236.7 and −224.1 kcal mol⁻¹, respectively, which contributes significantly to the attractive component of the interaction energy (73.1% in Be(CO)₃ and 74.0% in Be(CO)₄).

The beryllium in the excited state with 1s²2s⁰2p_z² electronic configuration has three vacant in-plane orbitals, which can form σ bonds with three CO ligands. Hence, the Be–C bonds in Be(CO)₃ can be considered formal 2c–2e bonds. However, the multicentre bonding concept needs to be invoked to explain four Be–C σ-bonds in Be(CO)₄. This is corroborated by the geometrical pattern where the Be–C bonds in Be(CO)₃ (1.655 Å) are shorter than those in Be(CO)₄ (1.811 Å).

To understand the variation in σ and π interaction among Be(CO)₃ and Be(CO)₄, we decomposed the ΔE_orb into the contribution from atomic orbitals of beryllium. Since Be(CO)₃ and Be(CO)₄ are perfectly trigonal planar (D_3h) and square planar (D_4h) molecules, the ligand group orbitals of (CO)₃ and (CO)₄ are similar to those shown in Scheme 1. The all (+) combination of the ligand group orbital (a′₁ for Be(CO)₃ and a_1g for Be(CO)₄) are right symmetry to interact with the 2s orbital of the Be atom. Note that the energy stabilization due to this interaction is only slightly higher for Be(CO)₄. The second σ(+ − +) and third set σ(+ · −) of the ligand group orbitals of (CO)₃ are right symmetry to interact with 2p_y and 2p_x, respectively (Scheme 2).

Scheme 2 Atomic orbitals of Be atom in the excited state (1s²2s⁰2p_z²) interacting with ligands group orbitals of (CO)₃ and (CO)₄ fragments in Be(CO)₃ and Be(CO)₄.

The energy stabilization due to this interaction is more than two times that of the former interaction in Be(CO)₃ (Table 1). Hence, we wish to propose that 2p orbitals of beryllium atoms are better σ acceptors as compared to the 2s orbital. Similarly, the second σ(+ · − ·) and third σ(· + · −) set of ligand group orbitals of (CO)₄ also have the right symmetry to interact with 2p_y and 2p_x orbitals of the Be atom. The corresponding energy stabilization is lower than those in Be(CO)₃. Nevertheless, the energetics indicate that 2p orbitals are better σ acceptors as compared to 2s orbitals. The deformation densities corresponding to σ and π interactions in both the systems are shown in Fig. 3. Δρ₂ – Δρ₄ shows the accumulation of red region around ligand group orbitals along with an accumulation of blue region in the direction of 2s/2p orbitals of central Be atom. Thus, the flow of charge density from red → blue reaffirms σ donation from CO ligands to the Be centre.

Fig. 3 (a) Plot of NOCV deformation densities (Δρ₁ – Δρ₄) and orbital interaction energies (kcal mol⁻¹) from each NOCV pair of Be(CO)₃. (b) A plot of NOCV deformation densities (Δρ₁ – Δρ₅) and orbital interaction energies (kcal mol⁻¹) from each NOCV pair of Be(CO)₄. The direction of the charge flow in the deformation density plot is from red → blue. The isosurface value for NOCV deformation densities is 0.003.

The fourth combination of ligand group orbital of (CO)₄ does not have a right symmetrical orbital to interact with beryllium. The energy stabilization for this interaction arises from the polarization of ligand orbitals towards a more electropositive beryllium centre. The total orbital stabilization energy due to σ-donation from the CO group in Be(CO)₃ is −97.7 kcal mol⁻¹, whereas the corresponding value for Be(CO)₄ is −91.9 kcal mol⁻¹. The π-back donation from central Be atom to CO ligands (ΔE_π = −128.3 kcal mol⁻¹ and −123.7 kcal mol⁻¹ in Be(CO)₃ and Be(CO)₄ respectively) considerably predominates over the σ donation for both Be(CO)₃ and Be(CO)₄. The deformation density Δρ₁ in Fig. 3 represents a π-back donation from the 2p_z orbital of Be to the π-symmetric ligand group orbitals. Important NOCV pairs of orbitals Ψ_−n/Ψ_n associated with respective deformation densities are plotted in Fig. S1 and S2 of ESI.†

Conclusion

In summary, density functional calculations were carried out in the Be(CO)_n (n = 1–4) complex. The present study predicts a stable beryllium carbonyl complex Be(CO)₄, which adopts perfect square planar geometry in its lowest energy singlet ground state. Detailed bonding analysis reveals that Be ← CO σ donation takes place at the vacant 2s, 2p_x and 2p_y orbitals of beryllium and Be → CO (π*) back donation takes place from the occupied 2p_z orbital of beryllium, thus exactly mimicking the DCD model for transition metal carbonyl complexes. The beryllium atom forms donor–acceptor bonds with four CO groups in its 1s²2s⁰2p_z² electronic configuration. EDA analysis further elucidates the extent of σ and π interaction in Be(CO)_3–4. It is found that the stabilization energy associated with π-backdonation is considerably higher than that of σ-donation. The proposed Be(CO)₄ complex is stable and expected to be detected experimentally, which may be a low-temperature noble gas matrix. The present bonding situation may rationalize the formation of Be(0) compounds stabilized by σ donor/π acceptor ligands such as CO and cyclic(alkyl)(amino)carbene. We feel that the present bonding model may be considered as a p-orbital analog of the famous DCD model and will inspire the design of many alkaline earth metal organometallic complexes in their low oxidation states.^4–6

Author contributions

S. K. P and A. K. G. performed all the calculations and A. K. G. wrote the draft. S. K. dedicates this article to his mother Mrs Kalpana Purkayastha. Shahnaz S. Rohman: methodology, data curation, writing and editing of EDA-NOCV results. Pattiyil Parameswaran: EDA data curation and analysis, writing – review, editing and interpretation of EDA results.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

Computational facility of Cotton University is acknowledged. P.P. thanks DST-SERB for research funding. S. S. R. is grateful to Science and Engineering Research Board (SERB) for the fellowship and funding under National Post-Doctoral Fellowship Scheme with reference no. PDF/2022/003034. P. P and S. S. R. also thank the Centre for Computational Modelling and Simulation (CCMS) at NITC.

References

1. M. J. S. Dewar, Bull. Soc. Chim. Fr., 1951, 18, C79.
2. Modern Coordination Chemistry: The Legacy of Joseph Chatt, ed. G. J. Leigh and N. Winterton, Royal Society, London, 2002.
3. G. Frenking and N. Fröhlich, Chem. Rev., 2000, 100, 717–774.
4. M. Arrowsmith, H. Braunschweig, M. A. Celik, T. Dellermann, R. D. Dewhurst, W. C. Ewing, K. Hammond, T. Kramer, I. Krummenacher, J. Mies and K. Radacki, Nat. Chem., 2016, 8, 890–894.
5. M. Chen, Q. Zhang, M. Zhou, D. M. Andrada and G. Frenking, Angew. Chem., Int. Ed., 2015, 54, 124.
6. S. A. Couchman, N. Holzmann, G. Frenking, D. J. Wilson and J. L. Dutton, Dalton Trans., 2013, 42, 11375–11384.
7. S. De and P. Parameswaran, Dalton Trans., 2013, 42, 4650–4656.
8. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
9. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
10. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
11. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327.
12. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
13. B. Silvi and A. Savin, Nature, 1994, 371, 683–686.
14. A. D. Becke and K. E. A. Edgecombe, J. Chem. Phys., 1990, 92, 5397–5403.
15. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.
16. (a) K. Morokuma, J. Chem. Phys., 1971, 55, 1236–1244; (b) L. Zhao, M. Hermann, W. H. E. Schwarz and G. Frenking, Nat. Rev. Chem., 2019, 3, 48–63.
17. A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939.
18. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098.
19. (a) ADF2020.102, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, https://www.scm.com; (b) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. F. Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
20. L. Andrews, T. J. Tague, G. P. Kushto and R. D. Davy, Inorg. Chem., 1995, 34, 2952–2961.
21. K. K. Sunil, J. Am. Chem. Soc., 1992, 114, 3985.
22. X. Wu, L. Zhao, J. Jin, S. Pan, W. Li, X. Jin, G. Wang, M. Zhou and G. Frenking, Science, 2018, 361, 912–916.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1 and S2 and cartesian coordinates of all the optimized geometries. See DOI: https://doi.org/10.1039/d4cp00908h

---