Resilience of Hund's rule in the chemical space of small organic molecules

Abstract

We embark on a quest to identify small molecules in the chemical space that can potentially violate Hund's rule. Utilizing twelve TDDFT approximations and the ADC(2) many-body method, we report the energies of S₁ and T₁ excited states of 12 880 closed-shell organic molecules within the bigQM7ω dataset with up to 7 CONF atoms. In this comprehensive dataset, none of the molecules, in their minimum energy geometry, exhibit a negative S₁–T₁ energy gap at the ADC(2) level while several molecules display values <0.1 eV. The spin-component-scaled double-hybrid method, SCS-PBE-QIDH, demonstrates the best agreement with ADC(2). Yet, at this level, a few molecules with a strained sp³-N center turn out as false-positives with the S₁ state lower in energy than T₁. We investigate a prototypical cage molecule with an energy gap <−0.2 eV, which a closer examination revealed as another false positive. We conclude that in the chemical space of small closed-shell organic molecules, it is possible to identify geometric and electronic structural features giving rise to S₁–T₁ degeneracy; still, there is no evidence of a negative gap. We share the dataset generated for this study as a module, to facilitate seamless molecular discovery through data mining.

---

1 Introduction

Studies from the 1970s onward, some even titled “violation of Hund's (multiplicity) rule…” have explored the possibility of an electronic state of lower spin-multiplicity being more stable than its higher multiplicity counterpart.^1–7 Although no experimentally known cases of Hund's rule violation exist among molecules in their ground state, ab initio wavefunction models have suggested that dynamic spin polarization effects may favor open-shell singlets over triplets.¹ In 1980, Leupin et al. suggested the likelihood of a more stable lowest excited singlet state, S₁, compared to the triplet state, T₁, based on fluorescence measurements of cycl[3.3.3]azines.⁸ Likewise, in 1985, certain non-alternant polycyclic hydrocarbons were considered to exhibit negative S₁–T₁ gaps (STGs).² Typically, S₁ and T₁ are represented primarily by singly excited configurations, ¹χ_a→r and ³χ_a→r, where a and r are the occupied and virtual molecular orbitals (MOs) determined using the self-consistent-field (SCF) method for the ground state configuration, ¹χ₀. Hence, the expressions for the excitation energies are E(¹χ_a→r) − E(¹χ₀) = ε_r − ε_a − J_ar + 2K_ar and E(³χ_a→r) − E(¹χ₀) = ε_r − ε_a − J_ar, where ε is the MO energy, while J and K are Coulomb and exchange integrals, respectively. This indicates STG = E(¹χ_a→r) − E(³χ_a→r) = 2K_ar (twice the exchange integral). As the overlap between the densities of the a and r MOs diminishes, a reduction in K_ar leads to degenerate S₁ and T₁.⁸ Along with vanishing K_ar, a decrease in the percentage contribution of the ¹χ_a→r configuration and an increased contribution from the doubly-excited configuration, ¹χ_aa→rr, was hypothesized to be a factor to selectively stabilize the S₁ state over T₁ resulting in a negative STG.⁹

In 2019, two independent studies confirmed STGs < 0 in the prototypical cycl[3.3.3]azines—cyclazine¹⁰ and heptazine¹¹—using time-dependent density functional theory (TDDFT) approximations, as well as a few correlated wavefunction methods. Since then, there has been a renewed interest in exploring the historically significant inverse-STG candidates: N-containing triangular molecules^12–20 and non-alternant hydrocarbons.^21–23 Besides these classes of molecules, Bedogni et al.¹⁸ showed the possibility of STG < 0 in C_nH_nN_n aza-rings.

Despite mounting computational evidence supporting the likelihood of Hund's rule violation, the credibility of negative STGs still attracts criticisms.²⁴ This skepticism arises from the failure to account for the experimental conditions in computational modeling and the challenges posed by the large molecules for accurate ab initio calculations. More recently, Loos et al.²⁵ confirmed negative STGs in triangulene systems through composite excited states modeling and provided theoretical best estimates (TBEs).

The present study aims to report STGs calculated using a many-body method and double-hybrid density functional theory (dh-DFT) models for 12 880 small organic molecules with systematically varying compositions and structures. Using this data, we verify the possibility of Hund's rule violation in the chemical space. Our workflow for data generation and the design of the module pymoldis for querying the reported data is illustrated in Fig. 1. The rest of this article discusses the qualitative aspects of the data, their analysis, and the technical details of the calculations.

Fig. 1 Workflow outlining the design of the pymoldis module²⁶ for data mining S₁ and T₁ energies across 12 880 molecules with up to 7 CONF atoms in the bigQM7ω dataset.²⁷ ADC(2) and TDDFT calculations were performed as a part of the present work. See (ESI†) for screenshots of example queries.

2 Results and discussions

Fig. 2 shows the range spanned by the STGs of all the molecules in the bigQM7ω dataset determined using various ab initio methods in the form of cumulative distributions. In both subplots, (a) and (b), of this figure, ADC(2) is used as the reference theory for evaluating the accuracy of other methods. In the (ESI†), we have discussed the accuracy of ADC(2) in combination with the def2-TZVP basis set for modeling STG of 10 triangle-shaped molecules using TBEs reported in a previous study.²⁵ Additionally, we have benchmarked the performance of the TDDFT version of SCS-PBE-QIDH within the Tamm–Dancoff approximation (TDA), see Tables S1–S4 (ESI†).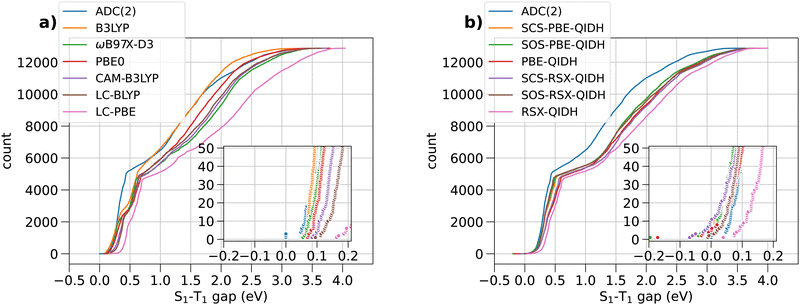

Fig. 2 Cumulative distribution of S₁–T₁ energy gaps of 12 880 bigQM7ω molecules calculated with various ab initio methods. The inset shows the distribution in the range of −0.2 to 0.2 eV.

Fig. 2(a) shows the cumulative count of STGs of 12 880 molecules predicted with ADC(2) and selected hybrid-DFT, long-range-corrected-DFT, and long-range-corrected-hybrid-DFT approximations. All the theoretical models featured in this plot predict positive STGs. Past studies^17,28,29 have shown that explicit incorporation of electron correlation, for example, at the MP2-level (second-order many-body perturbation theory) as in dh-DFT, is a requirement to predict STG < 0. However, it has come as a surprise that at the ADC(2) level, which is the excited-state equivalent to MP2, none of the 12 880 molecules show a negative STG. Similar results from dh-DFT methods, along with their spin-component-scaled (SCS) and opposite-spin-component-scaled (SOS), are shown in Fig. 2(b). The zoomed-in inset shows the distribution of values from RSX-QIDH to shift towards the positive domain compared to ADC(2) values. Upon SCS/SOS corrections,³⁰ the distribution is shifted slightly to the negative domain. At the dh-DFT level, SCS-PBE-QIDH, an accurate method for modeling STGs of triangulenes, a few molecules exhibit STG < 0 eV; we give a detailed discussion of individual values later.

Fig. 3 illustrates the effect of SCS corrections to PBE-QIDH predicted values of STG in the form of probability densities of the shift in S₁ and T₁ energies with the inclusion of SCS. Overall, the SCS corrections lower the S₁ energies while raising the T₁ values, illustrating why SCS-PBE-QIDH favors smaller STGs than the unscaled method, PBE-QIDH. Fig. S1 of the ESI† displays similar plots for SOS-PBE-QIDH, SCS-RSX-QIDH, and SOS-RSX-QIDH. While the SCS/SOS variants of RSX-QIDH shift the S₁ and T₁ energies further apart compared to the PBE-QIDH variants, previous benchmark studies^25,31 have shown SCS-PBE-QIDH to be more accurate for modeling molecules with negative STGs. Hence, one can conclude scaled-RSX-QIDH to result in more false-positive predictions (i.e. spurious predictions of STG < 0 eV) than scaled-PBE-QIDH. Notably, the SCS/SOS corrections applied to the PBE-QIDH and RSX-QIDH dh-DFT methods are specifically tailored for the TD-DFT framework.³⁰ Hence, STGs predicted using the ΔSCF approach will be similar in unscaled and scaled DFT methods.

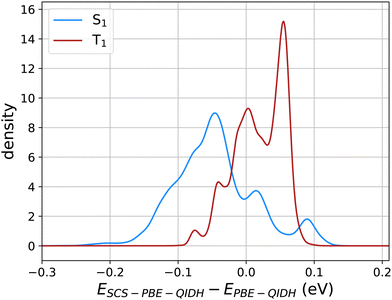Fig. 3 Probability density of the shift in S₁ and T₁ energies (in eV) for 12 880 molecules upon the inclusion of spin-component-scaling (SCS) in PBE-QIDH.

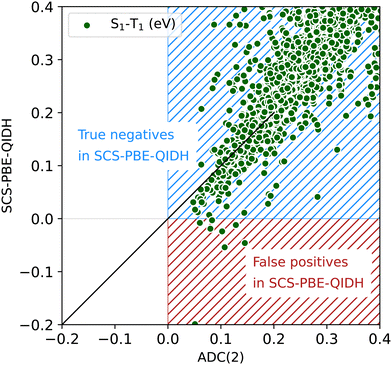
The scatterplot in Fig. 4 offers a detailed view of the distribution of STGs around 0 eV. We find that the predominant entries shown in this plot are in the blue region denoted “true negatives in SCS-PBE-QIDH”, implying that the TDDFT method agrees with ADC(2), both predicting these molecules as Hund's rule obeying systems with positive STGs. Molecules shown in the red region of Fig. 4 are “false positives in SCS-PBE-QIDH” as these systems show STG > 0.04 eV according to ADC(2), while in the TDDFT formalism they show STG < 0 eV. As already highlighted in Fig. 2, there are no “true positives” or “false negatives” as none of the 12 880 molecules in the bigQM7ω dataset exhibit a negative STG at the ADC(2) level.

Fig. 4 Scatterplot of S₁–T₁ energy gap ≤0.4 eV from SCS-PBE-QIDH and ADC(2) for the bigQM7ω molecules.

The boundary separating positives and negatives in Fig. 4 is not sharp as both ADC(2) and SCS-PBE-QIDH have uncertainties >0.1 eV in their predictions (see benchmarks in the ESI†). Fig. S2 (ESI†) shows scatterplots of the joint distributions of STG with the S₁ and T₁ energies at both the SCS-PBE-QIDH and ADC(2) methods. At both levels of theories, one finds the small STG systems to have S₁ and T₁ energies in the range of 6–8 eV. Additionally, we find a molecule with S₁ and T₁ energies in the 3–4 eV range to have a small STG at the SCS-PBE-QIDH level (see Fig. S2c and d, ESI†). By querying the dataset using the pymoldis module (see Fig. S3–S12, ESI†), we found the corresponding molecule to be 2,6-dihydro-1H-pyridin-3-one (SMILES: O=C1CNCC=C1), which is cyclohexenone with an N atom at the δ-position.

To identify geometrical aspects common to the small STG molecules, we have queried the pymoldis database for ten molecules with the smallest STG according to TDA/SCS-PBE-QIDH. Fig. 5 shows a screenshot of the query. A geometric moiety common to all N-containing systems is a substantial deviation of the bonding environment of the sp³-N center from the ideal geometry. For the ten benchmark triangular systems, the S₁ and T₁ excitation energies are <3 eV due to the possibility of a low-energy n → π* transition. However, in the systems shown in Fig. 5, the S₁/T₁ excitations are of the n → σ* type with excitation energies >6 eV. Nine of the ten molecules shown in Fig. 5 contain a 3-membered heterocyclic ring, while one is a fluorinated cyclopropane derivative; the S₁ and T₁ excitation energies of the latter are >8 eV, at both TDDFT and ADC(2) levels while the corresponding STG = −0.01 eV and 0.13 eV at TDDFT and ADC(2) levels, respectively. The molecule corresponding to SMILES, CC1C2CCN1C2, in Fig. 5 contains a propellane-type cage with STG = −0.01 eV at the TDDFT level and an STG of 0.06 eV at the ADC(2) level. The bigQM7ω dataset comprises several such cage systems with small STGs.

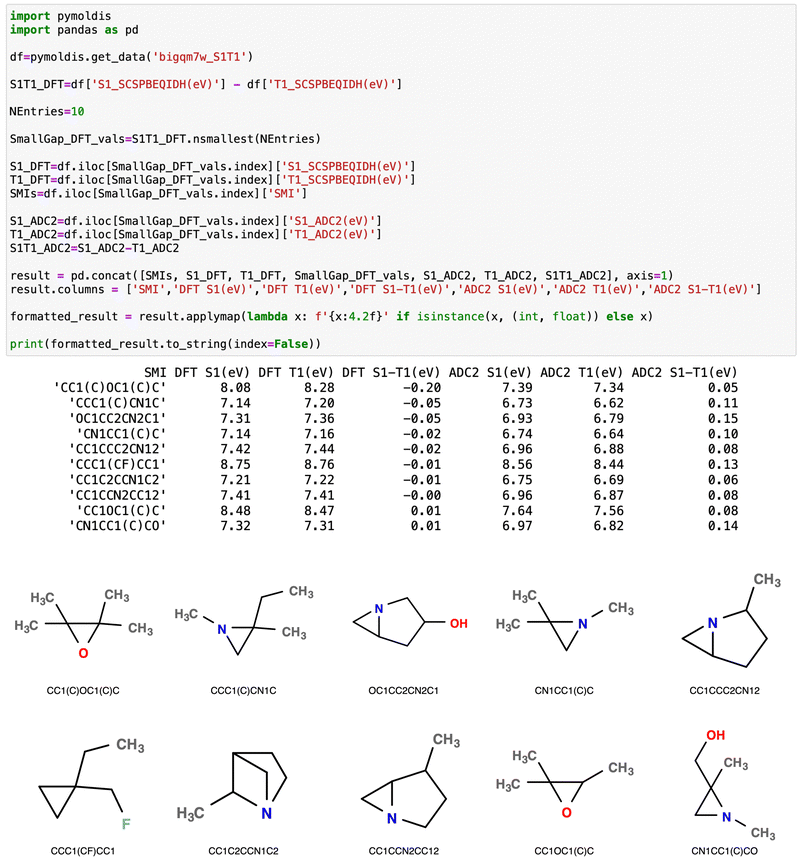Fig. 5 Data-mining the bigQM7ω dataset in pymoldis²⁶ to identify molecules with small S₁–T₁ gaps. For the ten molecules with the lowest gaps according to TDA-SCS-PBE-QIDH, SMILES strings and S₁/T₁ energies are displayed. The corresponding ADC(2) values are also given alongside. Molecular structures are displayed in cartoon format below. See the ESI† for more examples of data-mining exercises.

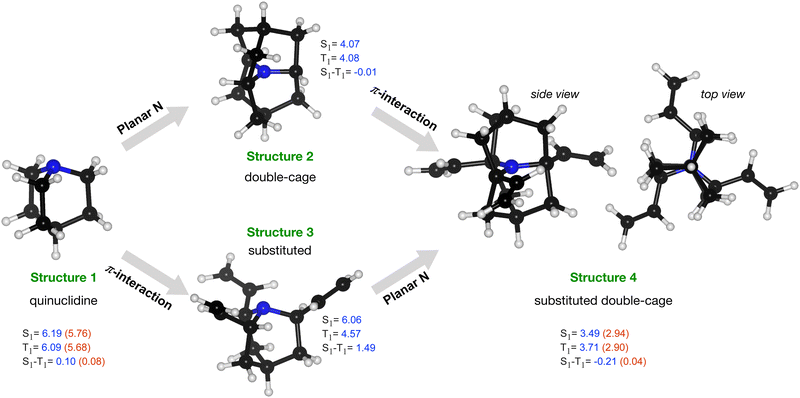
Starting with a cage-type molecule with a strained N, we have explored the possibility to design a molecule with the character of the lowest excitation as n → π*. We started with a symmetric cage system, quinuclidine, a [2.2.2]propellane with an axial CH group replaced by an N atom, structure 1 in Fig. 6. This molecule has an STG of 0.1 eV at the TDA-SCS-PBE-QIDH/def2-TZVP level. This small gap is because the excitation is primarily from non-bonding MO of N (highest occupied MO, HOMO) to C–H σ* of the cage (lowest unoccupied MO, LUMO); their corresponding densities show poor overlap leading to a small value of exchange integral, K_ar. Further, to arrive at a local-geometric environment of the N atom as in cycl[3.3.3]azines, we have introduced an additional cage to constrain the N-center to a plane (structure 2 in Fig. 6). This structure comprises perfectly co-planar C–N bonds resulting in degenerate S₁–T₁ levels. We have also modified quinuclidine by attaching three ethylene groups (structure 3). In this structure, the S₀ → S₁ excitation has the character n → π* (MO indices, n: 52, which is the HOMO, and π*: 53–55) while the S₀ → T₁ excitation has the character π → π* (MO indices, π: 49–51) with a large STG of 1.5 eV. Finally, we combined structural modifications introduced in structure 2 and structure 3 to arrive at structure 4 with a planar N interacting with π moieties through space. Interestingly, this system resulted in an STG of −0.21 eV at the DFT level. To verify this prediction of a negative STG, we have also performed ADC(2)/def2-TZVP calculations. For both structure 1 and structure 4, we find the magnitudes of the ADC(2) excitation energies to be lower than the DFT values. While both energies drop by a similar magnitude in the former, in structure 4, the energy of T₁ drops more than the S₁ energy, giving rise to a nearly zero STG at the ADC(2) level. This case study indicates that for molecules such as structure 4, even some of the best double-hybrid DFT methods can spuriously predict a negative STG; hence, one may consider many-body methods such as ADC(2) as a baseline theory.

Fig. 6 TDA/SCS-PBE-QIDH predictions of S₁, T₁ and S₁–T₁ energies (in eV) of 1-azabicyclo[2.2.2]octane (aka quinuclidine) and its derivatives. For selected structures, additionally, ADC(2) values are in parentheses. White, black, and blue atoms correspond to H, C, and N atoms, respectively.

While structure 4 is a minimum on the potential energy surface as verified through vibrational frequency analysis, we do not expect the system to be relevant to the thermally activated delayed fluorescence (TADF) applications.^{10,13,32–34} On the other hand, it is a compelling computational chemistry exercise to modulate a molecule's STG by chemical modifications. Hence, even though structure 4 seems to be yet another false positive in the search for a Hund's rule-violating molecule, we have examined it further. We inspected the shape of the MOs involved in the S₁ and T₁ excitations and found the excitations to be primarily HOMO→LUMO type. These MOs are on display in Fig. 7, from which we visually conclude that the densities of HOMOs and LUMOs do not overlap. For a more quantitative analysis, we calculated the Λ-index³⁵ defined as 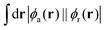using Multiwfn,³⁶ and obtained the values: 0.37 and 0.40 for the S₁ and the T₁ states, respectively. The Λ-index quantifies the degree of overlap between hole and electron in S₀ → S₁ and S₀ → T₁ excitations. In comparison, for both cyclazine and heptazine, the values of Λ for the S₁ and T₁ states are nearly 0.50.

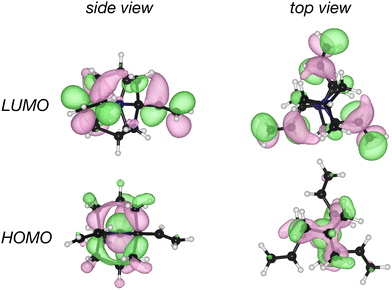Fig. 7 Plots of HOMO and LUMO of the ethylene substituted double cage derivative of quinuclidine, structure 4, shown in Fig. 6.

3 Computational details

The bigQM7ω dataset^27,37 features 12 880 molecules with up to 7 CONF atoms with equilibrium geometries determined with the ωB97X-D DFT method and the def2-TZVP basis set. Molecular graphs of bigQM7ω molecules, encoded as SMILES, were sourced from the GDB11³⁸ chemical space, which contains several common molecules, such as acetic acid and benzoic acid, which the subsequent databases GDB13³⁹ and GDB17⁴⁰ filtered out. Consequently, bigQM7ω offers over thrice the number of molecules with up to 7 CONF atoms than the QM9 dataset⁴¹ derived from GDB17. The geometries of the bigQM7ω molecules were optimized²⁷ using the connectivity preserving geometry optimization (ConnGO) workflow to prevent covalent bond rearrangements during geometry optimization.⁴² Further, vibrational frequency analysis at the ωB97X-D/def2-TZVP level verified each structure in bigQM7ω to be an energy minimum. Along with the minimum energy geometries, bigQM7ω offers several ground-state properties ranging from partial charges to thermochemistry energies along with excited state properties.³⁷

For all 12 880 molecules in bigQM7ω, we performed single-point vertical excited state calculations of the S₁ and T₁ energies using 12 DFT methods: PBE0,⁴³ B3LYP,⁴⁴ CAM-B3LYP,⁴⁵ ωB97X-D3,⁴⁶ LC-BLYP,⁴⁷ LC-PBE,⁴⁸ PBE-QIDH,⁴⁹ SCS-PBE-QIDH, SOS-PBE-QIDH,³⁰ RSX-QIDH,⁵⁰ SCS-RSX-QIDH³⁰ and SOS-RSX-QIDH.³⁰ We also calculated S₁ and T₁ energies using the correlated excited state method: second-order algebraic diagrammatic construction, ADC(2). The accuracy of ADC(2) and SCS-PBE-QIDH in combination with other settings is evaluated in the ESI† using previously reported²⁵ TBEs of 10 triangular systems as references. For these systems and the cage-type molecules, we performed geometry optimization – using the ωB97X-D3 DFT method with tightscf and tightopt keywords in combination with the def2-TZVP basis set. Minimum energy structures and S₁/T₁ energies of the bigQM7ω molecules can be queried using the pymoldis module presented in this study (see Fig. S8 and S12 in the ESI†).

We performed ADC(2) calculations using QChem 6.0.2 and DFT calculations using ORCA 5.0.4.^51,52 With in TDDFT, we calculated twelve energy eigenvalues—six singlets and six triplets—which we sorted separately to extract S₁ and T₁ excitation energies. In all calculations, we used the resolution-of-identity (RI) approximation.^53,54 In DFT calculations, we used the ‘chain-of-spheres’ (COS) algorithm for exchange integrals (RIJCOSX). In dh-DFT calculations, we used the universal fitting auxiliary basis sets by Weigend⁵⁵ (denoted def2/J) along with the def2-TZVP/C and aug-cc-pVTZ/C basis sets for the orbital basis sets def2-TZVP, and aug-cc-pVTZ, respectively.

4 Conclusions

We have probed the violation of Hund's rule in the chemical space of about 13 000 small organic molecules with up to 7 atoms of C/O/N/F. We performed high-throughput calculations of excited states with various DFT methods and a more accurate theory, ADC(2). We selected these methods based on their accuracies when compared with the previously reported theoretical best estimates for the STGs of ten triangular molecules. ADC(2) with a triple-zeta basis set provides an effective cost-accuracy trade-off for generating large-scale data. Further, this method has been shown²⁵ to agree with composite excited state methods for predicting STG < 0 with an average error of <0.05 eV. The critical result of the present study is that Hund's rule⁵⁶ prevails across thousands of organic molecules with systematically varying structures covering almost all prototypical small organic molecules.

The data presented in this study is importable in Python code for data mining endeavors. Using this infrastructure, we identified molecules with vanishing STGs, some of which have negative values at the SCS-PBE-QIDH level while not violating Hund's rule as per ADC(2) predictions. A common geometric feature of these molecules was a substantial deviation of an N-atom from the typical sp³ environment with both singlet and triplet excitations showing the n → σ* character and potentially vanishing exchange interaction integral between the MOs involved in excitation.

We have selected a cage structure and attached ethylene groups to mimic the environment of the N atom as in the well-known cases of cycl[3.3.3]azines. The corresponding MOs involved in S₁/T₁ excitations exhibit characteristics seen in previously studied triangular negative-STG systems. Upon further scrutiny, we showed this molecule to obey Hund's rule. Yet, introducing a polarizable environment in this system through donor–acceptor groups may selectively stabilize S₁ over T₁.^10,23 In this study, we did not investigate the practical utility of the small molecules studied here in the context of TADF. Such exploration necessitates meticulous consideration of adiabatic effects on a case-by-case basis, a task that exceeds the scope of our present investigation. The present study demonstrates that a data-driven approach allows for gaining insight into the molecular structural factors that can quench the singlet–triplet energy gap. We offered evidence that the chemical space of small closed-shell organic molecules lacks geometric and electronic structural factors that may be necessary for a negative S₁–T₁ energy gap.

Theoretical studies have identified only a few molecular fingerprints to favor negative STGs. Dynamic spin polarization, attributed to double excitation effects involving frontier orbitals, has emerged as a potential mechanism to induce a negative STG.^1,57,58 While a quantitative relationship exists between molecular structural features and zero STG, a corresponding structure–property relation for negative STG remains elusive. Introducing functional groups is one promising avenue for designing large synthetically tractable molecules with negative STGs. For theoretical explorations, our research highlights the limitations of using DFT methods, which can result in false positives. Consequently, there is a pressing need for efficient strategies to accelerate predictions using correlated wavefunction methods. For large-scale investigations, data-driven approaches such as machine learning can complement first-principles modeling, especially when combined with inverse-design strategies, such as genetic algorithms.^59,60

Data availability

The data supporting the findings of this study are available within the article and its ESI.†

Author contributions

AM: conceptualization (equal); analysis (equal); data collection (equal); writing (equal); revision (equal). RR: conceptualization (equal); analysis (equal); data collection (equal); funding acquisition; project administration and supervision; resources; writing (equal); revision (equal).

Conflicts of interest

The author has no conflicts of interest to disclose.

Acknowledgements

We acknowledge the support of the Department of Atomic Energy, Government of India, under Project Identification No. RTI 4007. All calculations have been performed using the Helios computer cluster, which is an integral part of the MolDis Big Data facility, TIFR Hyderabad (https://moldis.tifrh.res.in).

Notes and references

1. H. Kollmar and V. Staemmler, Violation of Hund's rule by spin polarization in molecules, Theor. Chim. Acta, 1978, 48, 223–239,  DOI:10.1007/BF00938691.
2. S. Koseki, T. Nakajima and A. Toyota, Violation of Hund’s multiplicity rule in the electronically excited states of conjugated hydrocarbons, Can. J. Chem., 1985, 63(7), 1572–1579,  DOI:10.1139/v85-267.
3. W. T. Borden, H. Iwamura and J. A. Berson, Violations of Hund’s rule in non-kekule hydrocarbons: theoretical prediction and experimental verification, Acc. Chem. Res., 1994, 27(4), 109–116,  DOI:10.1021/ar00040a004.
4. A. Toyota and T. Nakajima, Violation of Hund's multiplicity rule in the lowest excited singlet-triplet pairs of cyclic bicalicene and its higher homologues, J. Chem. Soc., Perkin Trans. 2, 1986,(11), 1731–1734,  10.1039/P29860001731.
5. A. Toyota, Violation of Hund's rule in the lowest excited singlet-triplet pairs of dicyclohepta [cd,gh] pentalene and dicyclopenta [ef,kl] heptalene, Theor. Chim. Acta, 1988, 74, 209–217,  DOI:10.1007/BF00527144.
6. D. A. Hrovat and W. T. Borden, Violations of Hund's rule in molecules—where to look for them and how to identify them, J. Mol. Struct.: THEOCHEM, 1997, 398, 211–220,  DOI:10.1016/S0166-1280(96)04930-5.
7. J. C. Sancho-Garcia, E. Bremond, G. Ricci, A. J. Pérez-Jiménez, Y. Olivier and C. Adamo, Violation of Hund’s rule in molecules: Predicting the excited-state energy inversion by TD-DFT with double-hybrid methods, J. Chem. Phys., 2022, 156(3), 034105,  DOI:10.1063/5.0076545.
8. W. Leupin and J. Wirz, Low-lying electronically excited states of cycl [3.3.3] azine, a bridged 12. pi.-perimeter, J. Am. Chem. Soc., 1980, 102(19), 6068–6075,  DOI:10.1021/ja00539a016.
9. V. Bonacic-Koutecky and J. Michl, Charge-transfer-biradical excited states: relation to anomalous fluorescence. “Negative” S1-T1 splitting in twisted aminoborane, J. Am. Chem. Soc., 1985, 107(6), 1765–1766,  DOI:10.1021/ja00292a055.
10. P. de Silva, Inverted singlet-triplet gaps and their relevance to thermally activated delayed fluorescence, J. Phys. Chem. Lett., 2019, 10(18), 5674–5679,  DOI:10.1021/acs.jpclett.9b02333.
11. J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, Singlet-triplet inversion in heptazine and in polymeric carbon nitrides, J. Phys. Chem. A, 2019, 123(38), 8099–8108,  DOI:10.1021/acs.jpca.9b06215.
12. J. Sanz-Rodrigo, G. Ricci, Y. Olivier and J.-C. Sancho-Garcia, Negative singlet-triplet excitation energy gap in triangle-shaped molecular emitters for efficient triplet harvesting, J. Phys. Chem. A, 2021, 125(2), 513–522,  DOI:10.1021/acs.jpca.0c08029.
13. R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Organic molecules with inverted gaps between first excited singlet and triplet states and appreciable fluorescence rates, Matter, 2021, 4(5), 1654–1682,  DOI:10.1016/j.matt.2021.02.017.
14. G. Ricci, E. San-Fabián, Y. Olivier and J.-C. Sancho-Garca, Singlet-triplet excited-state inversion in heptazine and related molecules: assessment of TD-DFT and ab initio methods, ChemPhysChem, 2021, 22(6), 553–560,  DOI:10.1002/cphc.202000926.
15. A. L. Sobolewski and W. Domcke, Are heptazine-based organic light-emitting diode chromophores thermally activated delayed fluorescence or inverted singlet-triplet systems?, J. Phys. Chem. Lett., 2021, 12(29), 6852–6860,  DOI:10.1021/acs.jpclett.1c01926.
16. N. Aizawa, Y.-J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama, K.-I. Nakayama and S. Maeda, et al., Delayed fluorescence from inverted singlet and triplet excited states, Nat. Commun., 2022, 609(7927), 502–506,  DOI:10.1038/s41586-022-05132-y.
17. L. Tučková, M. Straka, R. R. Valiev and D. Sundholm, On the origin of the inverted singlet-triplet gap of the 5th generation light-emitting molecules, Phys. Chem. Chem. Phys., 2022, 24(31), 18713–18721,  DOI:10.3389/fchem.2023.1239604.
18. M. Bedogni, D. Giavazzi, F. Di Maiolo and A. Painelli, Shining light on inverted singlet-triplet emitters, J. Chem. Theory Comput., 2023, 20(2), 902–913,  DOI:10.1021/acs.jctc.3c01112.
19. H. Kim, G. Scholes and S. K. Min, Extension of molecules with inverted singlet-triplet gap with conjugated branches to alter the oscillator strength, Phys. Chem. Chem. Phys., 2024, 26(6), 5508–5516,  10.1039/D3CP05580A.
20. D. Blasco, R. Nasibullin, R. R. Valiev, M. Monge, J. M. López-de Luzuriaga and D. Sundholm, Experimental and computational studies of the optical properties of 2,5,8-tris (phenylthiolato) heptazine with an inverted singlet-triplet gap, Phys. Chem. Chem. Phys., 2024, 26(7), 5922–5931,  10.1039/D3CP05242G.
21. J. Terence Blaskovits, M. H. Garner and C. Corminboeuf, Symmetry-induced singlet-triplet inversions in non-alternant hydrocarbons, Angew. Chem., Int. Ed., 2023, 62(15), e202218156,  DOI:10.1002/anie.202218156.
22. M. E. Sandoval-Salinas, G. Ricci, A. J. Pérez-Jiménez, D. Casanova, Y. Olivier and J.-C. Sancho-Garcia, Correlation vs. exchange competition drives the singlet-triplet excited-state inversion in non-alternant hydrocarbons, Phys. Chem. Chem. Phys., 2023, 25(39), 26417–26428,  10.1039/D3CP02465B.
23. M. H. Garner, J. T. Blaskovits and C. Corminboeuf, Enhanced inverted singlet-triplet gaps in azaphenalenes and non-alternant hydrocarbons, Chem. Commun., 2024, 60(15), 2070–2073,  10.1039/D3CC05747J.
24. A. Dreuw and M. Hoffmann, The inverted singlet-triplet gap: a vanishing myth?, Front. Chem., 2023, 11, 1239604,  DOI:10.3389/fchem.2023.1239604.
25. P.-F. Loos, F. Lipparini and D. Jacquemin, Heptazine, cyclazine, and related compounds: Chemically-accurate estimates of the inverted singlet-triplet gap, J. Phys. Chem. Lett., 2023, 14, 11069–11075,  DOI:10.1021/acs.jpclett.3c03042.
26. R. Ramakrishnan, Pymoldis: A python suite for molecular discovery using quantum chemistry big data, 2021. https://github.com/moldis-group/pymoldis.
27. P. Kayastha, S. Chakraborty and R. Ramakrishnan, The resolution-vs.-accuracy dilemma in machine learning modeling of electronic excitation spectra, Digital Discovery, 2022, 1(5), 689–702,  10.1039/D1DD00031D.
28. S. Ghosh and K. Bhattacharyya, Origin of the failure of density functional theories in predicting inverted singlet-triplet gaps, J. Phys. Chem. A, 2022, 126(8), 1378–1385,  DOI:10.1021/acs.jpca.1c10492.
29. M. Kondo, Singlet-triplet energy gap of multiresonant molecular systems: A double hybrid time-dependent density functional theory study, Chem. Phys. Lett., 2022, 804, 139895,  DOI:10.1016/j.cplett.2022.139895.
30. M. C. Paez and L. Goerigk, Time-dependent long-range-corrected double-hybrid density functionals with spin-component and spin-opposite scaling: A comprehensive analysis of singlet–singlet and singlet–triplet excitation energies, J. Chem. Theory Comput., 2021, 17(8), 5165–5186,  DOI:10.1021/acs.jctc.1c00535.
31. M. Alipour and T. Izadkhast, Do any types of double-hybrid models render the correct order of excited state energies in inverted singlet-triplet emitters?, J. Chem. Phys., 2022, 156(6), 064302,  DOI:10.1063/5.0077722.
32. J. Li, Z. Li, H. Liu, H. Gong, J. Zhang, Y. Yao and Q. Guo, Organic molecules with inverted singlet-triplet gaps, Front. Chem., 2022, 10, 999856,  DOI:10.3389/fchem.2022.999856.
33. X. Wang, A. Wang, M. Zhao and N. Marom, Inverted lowest singlet and triplet excitation energy ordering of graphitic carbon nitride flakes, J. Phys. Chem. Lett., 2023, 14(49), 10910–10919,  DOI:10.1021/acs.jpclett.3c02835.
34. T. Won, K.-I. Nakayama and N. Aizawa, Inverted singlet-triplet emitters for organic light-emitting diodes, Chem. Phys. Rev., 2023, 4(2), 021310,  DOI:10.1063/5.0152834.
35. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation energies in density functional theory: An evaluation and a diagnostic test, J. Chem. Phys., 2008, 128(4), 044118,  DOI:10.1063/1.2831900.
36. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592,  DOI:10.1002/jcc.22885.
37. P. Kayastha and R. Ramakrishnan, bigQM7ω: A high-quality dataset of ground-state properties and excited state spectra of 12880 molecules containing up to 7 atoms of CONF, 2021. https://moldis-group.github.io/bigQM7w.
38. T. Fink, H. Bruggesser and J.-L. Reymond, Virtual exploration of the small-molecule chemical universe below 160 daltons, Angew. Chem., Int. Ed., 2005, 44(10), 1504–1508,  DOI:10.1002/anie.200462457.
39. L. C. Blum and J.-L. Reymond, 970 million druglike small molecules for virtual screening in the chemical universe database GDB-13, J. Am. Chem. Soc., 2009, 131(25), 8732–8733,  DOI:10.1021/ja902302h.
40. L. Ruddigkeit, R. Van Deursen, L. C. Blum and J.-L. Reymond, Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17, J. Chem. Inf. Model., 2012, 52(11), 2864–2875,  DOI:10.1021/ci300415d.
41. R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. Von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules, Sci. Data, 2014, 1(1), 1–7,  DOI:10.1038/sdata.2014.22.
42. S. Senthil, S. Chakraborty and R. Ramakrishnan, Troubleshooting unstable molecules in chemical space, Chem. Sci., 2021, 12(15), 5566–5573,  10.1039/D0SC05591C.
43. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110(13), 6158–6170,  DOI:10.1063/1.478522.
44. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Chem. Phys., 1994, 98(45), 11623–11627,  DOI:10.1021/j100096a001.
45. T. Yanai, D. P. Tew and N. C. Handy, A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP), J. Phys. Chem. Lett., 2004, 393(1–3), 51–57,  DOI:10.1016/j.cplett.2004.06.011.
46. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10(44), 6615–6620,  10.1039/B810189B.
47. Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, A long-range-corrected time-dependent density functional theory, J. Chem. Phys., 2004, 120(18), 8425–8433,  DOI:10.1063/1.1688752.
48. H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, A long-range correction scheme for generalized-gradient-approximation exchange functionals, J. Chem. Phys., 2001, 115(8), 3540–3544,  DOI:10.1063/1.1383587.
49. É. Brémond, J. C. Sancho-Garca, Á. J. Pérez-Jiménez and C. Adamo, Communication: Double-hybrid functionals from adiabatic-connection: The QIDH model, J. Chem. Phys., 2014, 141(3), 031101,  DOI:10.1063/1.4890314.
50. E. Bremond, M. Savarese, Á. J. Pérez-Jiménez, J. C. Sancho-Garca and C. Adamo, Range-separated double-hybrid functional from nonempirical constraints, J. Chem. Theory Comput., 2018, 14(8), 4052–4062,  DOI:10.1021/acs.jctc.8b00261.
51. F. Neese, The orca program system, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78,  DOI:10.1002/wcms.81.
52. F. Neese, Software update: The Orca program system, version 4.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8(1), 1–6,  DOI:10.1002/wcms.1327.
53. O. Vahtras, J. Almlöf and M. W. Feyereisen, Integral approximations for LCAO-SCF calculations, Chem. Phys. Lett., 1993, 213(5–6), 514–518,  DOI:10.1016/0009-2614(93)89151-7.
54. R. A. Kendall and H. A. Früchtl, The impact of the resolution of the identity approximate integral method on modern ab initio algorithm development, Theor. Chim. Acta, 1997, 97(1), 158–163.
55. F. Weigend, Accurate Coulomb-fitting basis sets for H to Rn, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065,  10.1039/B515623H.
56. W. Kutzelnigg and J. D. Morgan, Hund's rules, Z. Phys. D: At., Mol. Clusters, 1996, 36, 197–214,  DOI:10.1007/BF01426405.
57. R. Pollice, B. Ding and A. Aspuru-Guzik, Rational design of organic molecules with inverted gaps between the first excited singlet and triplet, Matter, 2024, 7(3), 1161–1186,  DOI:10.1016/j.matt.2024.01.002.
58. D. Drwal, M. Matousek, P. Golub, A. Tucholska, M. Hapka, J. Brabec, L. Veis and K. Pernal, Role of spin polarization and dynamic correlation in singlet-triplet gap inversion of heptazine derivatives, J. Chem. Theory Comput., 2023, 19(21), 7606–7616,  DOI:10.1021/acs.jctc.3c00781.
59. A. K. Nigam, R. Pollice, P. Friederich and A. Aspuru-Guzik, Artificial design of organic emitters via a genetic algorithm enhanced by a deep neural network, Chem. Sci., 2024, 15(7), 2618–2639,  10.1039/D3SC05306G.
60. A. Gupta, S. Chakraborty, D. Ghosh and R. Ramakrishnan, Data-driven modeling of S0 → S1 excitation energy in the bodipy chemical space: High-throughput computation, quantum machine learning, and inverse design, J. Chem. Phys., 2021, 155(24), 244102,  DOI:10.1063/5.0076787.

---

Footnote

† Electronic supplementary information (ESI) available: Contains the following: assessment of S₁–T₁ gaps from ADC(2) and SCS-PBE-QIDH for 10 triangular molecules. Table S1 compares S₁/T₁ energetics calculated using the ADC(2) method with theoretical best estimates. Table S2 compares the S₁/T₁ energetics predicted by TDDFT and TDA. Table S3 contains ADC(2) and TDA energies calculated using DFT-level geometries. Table S4 provides various error metrics for ADC(2) and SCS-PBE-QIDH predicted S₁/T₁ energetics. Fig. S1 illustrates the shifts in S₁ and T₁ due to SCS/SOS corrections to PBE-QIDH and RSX-QIDH methods. Fig. S2 shows a scatterplot of S₁ and T₁ energies with S₁–T₁ gaps. Fig. S3–S12 offer screenshots of data mining exercises. Minimum energy geometries of structures 1–4 in Fig. 6 are also listed. Sample Python notebooks and further details are available at https://github.com/moldis-group/pymoldis.²⁶ See DOI: https://doi.org/10.1039/d4cp00886c

---