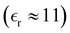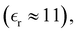An efficient method to establish electrostatic screening lengths of restricted primitive model electrolytes†
Received
6th February 2024
, Accepted 2nd July 2024
First published on 3rd July 2024
Abstract
We present a novel, and computationally cheap, way to estimate electrostatic screening lengths from simulations of restricted primitive model (RPM) electrolytes. We demonstrate that the method is accurate by comparisons with simulated long-ranged parts of the charge density, at various Bjerrum lengths, salt concentrations and ion diameters. We find substantial underscreening in low dielectric solvent, but with an “aqueous” solvent, there is instead overscreening, the degree of which increases with ion size. Our method also offers a possible path to (future) more accurate classical density functional treatments of ionic fluids.
1 Introduction
Interactions between charged surfaces are crucially important in many systems of biological and industrial importance, and they have been extensively studied for many decades. A simple and common strategy is to adopt a dielectric continuum description of the solvent – the primitive model – and use the mean-field Poisson–Boltzmann (PB) theory to predict ion distributions and surface interactions. This approach was utilised to construct the famous DLVO theory1,2 of colloidal interactions. Including ion correlations takes us beyond the mean-field approach and is of vital importance in systems with strong electrostatic coupling.3–15 Phenomena resulting from ion correlations, such as overcharging and like-charge attractions are now relatively well-understood.
The characteristic fluctuation length-scale that emerges from mean-field treatments of primitive models is the so-called Debye length, λD, which provides a useful measure for the effective range of electrostatic potentials of mean force in dilute salt solutions at low coupling. The Debye length decreases with concentration for an electrolyte, which is indicative of the increased ionic screening expected from a mean-field treatment. However, some recent surface force apparatus (SFA) and surface force balance (SFB) measurements suggest a remarkable deviation from this (generally accepted) behaviour.16–19 These measurements appear to indicate that the decay length for charged surface interactions in simple aqueous electrolytes, as well as in ionic liquids, not only significantly exceeds λD, but also increases with salt concentration, above some threshold value. This phenomenon can be denoted as anomalous under-screening.20 While qualitatively similar results have been reproduced by several different groups, its physical explanation has been subject to considerable debate.
This notwithstanding, it should be noted that there have been other experimental reports which are seemingly in conflict with purported anomalous under-screening. For instance, recent atomic force microscopy (AFM) measurements by Kumar et al.21 were consistent with mean-field predictions, without any indications of anomalies. In earlier AFM measurements on a pure ionic liquid, by Hjalmarsson et al.,22 there was a peculiar temperature effect, with short-ranged interactions at 353 K turning very long-ranged at 393 K. Nayeri and Bergenholtz23 investigated interactions between charged colloidal spheres using Total Internal Reflection Microscopy. Their data was also in good agreement with mean-field predictions. Colloidal stability measurements by Yuan et al.24 indicated a re-dispersion trend, in aqueous solutions, but for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts the re-entrant trend was quite weak and mainly significant at exceptionally high concentrations.
1 salts the re-entrant trend was quite weak and mainly significant at exceptionally high concentrations.
Theoretical work to date does not seem to indicate any clear mechanism for the observed anomalous under-screening. One oft-used argument is that ionic clustering, which is presumably more prevalent at higher concentration (and at large coupling), plays an important role. That is, the measured screening length is a renormalised Debye length dominated by the smaller number of “free” ions, given that clusters will be few in number and are likely to have a zero or at least near-neutral charge. Recent molecular dynamics (MD) simulations by Härtel et al.,20 using the restricted primitive model (RPM) did predict screening lengths that exceeded the Debye length, but only when the dielectric constant used to mimic the solvent was sufficiently low, and much lower than that indicated by experiments. Those authors noted a significant degree of ion clustering accompanied the under-screening and were able to semi-quantitatively explain their results by identifying cluster populations and calculating a renormalised Debye length of the type described above. All-atom simulations by Coles et al.,25 as well as Zeman et al.,26 have established screening lengths for simple salts in an explicit aqueous solvent. The simulated screening lengths remained roughly constant for concentrations exceeding a threshold value of about 1 M, which is not consistent with the dramatic increase seen in the SFA/SFB measurements at concentrations even below this value. The story is similar for analytical and semi-analytical approaches27–29 where, despite concerted effort, there are to date no calculations (using realistic parameters) that are able to reproduce the SFA/SFB results, even qualitatively. In summary then it is fair to say that more theoretical and experimental studies are required to establish the physical mechanisms that underpin purported anomalous under-screening. The work presented here will unfortunately not provide a definitive answer to that mechanistic question. Instead, we demonstrate a new method to extract electrostatic electrostatic screening lengths from computer simulations, which is numerically inexpensive and also provides some new insights as to why they may deviate from the Debye length. This provides an addition to the theoretical tool-box that will hopefully help to uncover the physics behind anomalous underscreening.
In computer simulations, the electrostatic decay length is invariably obtained by simply fitting to the long-ranged part of correlation functions. In this regime the values of the correlation functions are both small and generally subject to substantial uncertainty. For this reason, one generally needs long simulations of large numbers of particles so as to probe these asymptotic regimes accurately. There is also an unfortunate ambiguity regarding the range across which the fit is made. Below, we will introduce an alternative and computationally cheaper way to obtain these screening lengths. Briefly put, our method is based on an exact density expansion of the excess free energy functional. This expansion will relate the screening length (at least to first-order) to changes in the individual ion excess chemical potentials upon varying the number density of only one ion type while maintaining overall neutrality by using a uniform background density of counterions. As it turns out, the first-order approximation we use here is very accurate for a wide range of system parameters for the RPM electrolyte model studied here. This was ascertained by comparing our results with direct fits to the correlation functions.
Previous theoretical treatments of the RPM model have shown that at low density one predicts monotonic decay of the charge–charge correlations (of a Yukawa form) at long range. This translates to a long-range exponential decay of the potential of mean force between flat charged surfaces. A purely exponential decay is seemingly observed in those experiments where anomalous under-screening occurs. At low density, and when the coupling is low, the RPM has been shown to display correlation functions with an asymptotic Yukawa form, having a screening length that is equal to, or below, the Debye length. This monotonic decay transitions to damped oscillatory (sinusoidal) behaviour beyond a threshold concentration; the so-called Kirkwood transition. Here, the sinusoidal variation of the charge correlations oscillates between positive and negative values with amplitudes that also decay according to a Yukawa form. This decay length does increase with concentration, but at a rate too low compared to anomalous under-screening. Furthermore, the oscillatory form is not consistent with the purely exponential surface forces seen in experiments. Indeed, the increase in decay length of the charge oscillations is more consistent with the onset of long-range structure as the density of the electrolyte increases, rather than direct electrostatic screening. Our work here will only focus on systems which display exponential decay, without oscillations. From the work of Härtel et al.,20 it seems that in highly-coupled RPM models, one is able to establish a regime wherein charge correlations are non-oscillatory, while the screening length increases with electrolyte concentration, consistent with observed anomalous under-screening.
2 Theory and simulation details
2.1 Density functional theory
In the RPM description, the Coulomb interaction (free) energy between ions i and j, separated a distance r, is:| |  | (1) |
where β is the inverse thermal energy and the valency of ion i is denoted by zi. Apart from this, ions interact via a hard sphere potential, where both ions have a radius of d. We define the Bjerrum length as  where e is the elementary charge,
where e is the elementary charge,  is the relative dielectric constant of the implicit solvent, and
is the relative dielectric constant of the implicit solvent, and  is the permittivity of vacuum. We will here restrict the treatment to symmetric RPM electrolytes, i.e., (z:z) salts whose valencies are equal in magnitude but opposite in sign (z+ = −z− = z).
is the permittivity of vacuum. We will here restrict the treatment to symmetric RPM electrolytes, i.e., (z:z) salts whose valencies are equal in magnitude but opposite in sign (z+ = −z− = z).
Using classical density functional theory (DFT), the grand potential for an RPM electrolyte solution in the presence of an external point charge, q0 at r0, can be written as a functional of the ionic densities, {ni(r); i = ±},
| |  | (2) |
where
Fex is a functional of {
ni(
r);
i = ±} and contains all excluded volume and ionic correlation terms and
μi is the chemical potential of
i type ions in the bulk where
ni(
r) →
nb. Upon minimisation, wrt to
ni(
r), we obtain,
| |  | (3) |
where
ψ(
r) is the average electrostatic potential at
r:
| |  | (4) |
and
βμexi (=
βμi − ln(
nb)) is the excess (beyond its ideal value) chemical potential of species
i in the bulk,
| |  | (5) |
We now expand the excess free energy:
| |  | (6) |
where Δ
ni(
r) ≡
ni(
r) −
nb. This is a valid approximation in the asymptotic regime at a large distance for the perturbing charge. In this regime one can also linearize
eqn (3). We begin by writing,
| | 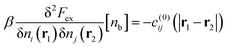 | (7) |
If
cij(|
r1 −
r2|) is the direct correlation function, then
c(0)ij(|
r1 −
r2|) =
cij(|
r1 −
r2|) −
βϕijCoul(
r) is the residual part after subtraction of the (long-ranged) pair interaction contribution. The net charge density is directly related to the ion densities:
| |  | (8) |
where we recall that the ion densities themselves were given by
eqn (3). Assuming a relatively weak average potential, we can linearise the exponential in
eqn (3), and by using the expansion of the excess free energy,
eqn (6), we arrive at the following expression for the net charge density:
| |  | (9) |
where we have used,
| | 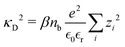 | (10) |
where the Debye screening length is defined as
λD = 1/
κD. The second term in
eqn (9) can be further expanded to get,
| | 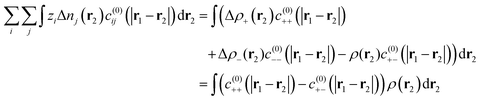 | (11) |
where Δ
ρi(
r) =
ziΔ
ni(
r). Due to the symmetry of the RPM electrolyte we have
c(0)++(
r) =
c(0)−−(
r) and from analyticity we also have
c(0)+−(
r) =
c(0)−+(
r). This allows us to write,
| |  | (12) |
where Δ
c(0)(
r) =
c(0)++(
r) −
c(0)+−(
r), and
ψ(
r) is the mean electrostatic potential. In Fourier space we obtain,
| |  | (13) |
which can be rewritten as,
| |  | (14) |
where the Fourier transform is defined here as
| |  | (15) |
Gauss's Law gives,
| |  | (16) |
which in Fourier space is,
| |  | (17) |
Substitution into
eqn (13) gives,
| |  | (18) |
where
![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif)
(
k) = 1/(1 −
nbΔ
ĉ(0)(
k)). Finally we obtain,
| | 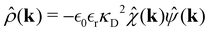 | (19) |
The asymptotic decay of ρ(r) is given by the pole of the expression on the RHS eqn (18) with the smallest imaginary part. If that pole is purely imaginary, i.e., k = iκ, one obtains a Yukawa decay (∼exp(−κr)/r). On the other hand, if the pole has instead non-zero real part then the decay will have a Yukawa form with an oscillatory amplitude. The thermodynamic point at which Yukawa decay turns to oscillatory Yukawa decay is denoted as the so-called Kirkwood transition.
2.2 Connection to dressed ion theory
It is instructive to define the charge correlation function Δĥ(0)(k) = ĥ(0)++(k) − ĥ(0)+−(k). We can relate Δĥ(0)(k) to Δĉ(0)(k) via the following Orstein–Zernike equation| |  | (20) |
which gives ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (k) = 1 + nbΔĥ(0)(k). The quantity zi
(k) = 1 + nbΔĥ(0)(k). The quantity zi![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (r) corresponds to a supposedly short-ranged charge density profile centred at an ion of species i, which includes the charge zi plus an associated atmosphere of additional ions. This corresponds to an ion charge and its “dress”, the latter being due to short-ranged correlations, as described in the dressed ion theory of Kjellander and Mitchell.30,31 For small k, we write,
(r) corresponds to a supposedly short-ranged charge density profile centred at an ion of species i, which includes the charge zi plus an associated atmosphere of additional ions. This corresponds to an ion charge and its “dress”, the latter being due to short-ranged correlations, as described in the dressed ion theory of Kjellander and Mitchell.30,31 For small k, we write,| | 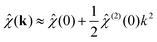 | (21) |
As we will discuss in more detail below, the quantity  can be thought of as the total average charge of ion clusters that contain the species i. This will be equal in magnitude and opposite in sign for anions and cations in this symmetric model. The characteristic average length-scale of these clusters, denoted by Rc, can be estimated from the second term on the RHS of eqn (21), which gives the second moment of the so-called ion dress, i.e.,
can be thought of as the total average charge of ion clusters that contain the species i. This will be equal in magnitude and opposite in sign for anions and cations in this symmetric model. The characteristic average length-scale of these clusters, denoted by Rc, can be estimated from the second term on the RHS of eqn (21), which gives the second moment of the so-called ion dress, i.e.,  .
.
If ionic correlations are neglected, then we have ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (k) = 1. Under these conditions we obtain,
(k) = 1. Under these conditions we obtain,
| |  | (22) |
This corresponds to the classic Debye–Hückel (D–H) theory for the point-like RPM electrolyte. In this case, the potential (and charge density decays with a Yukawa form), as the pole on the RHS of
eqn (22) is purely imaginary (
k =
iκD). Including ion correlations, we consider the asymptotic region of the charge density profile. In particular, if we assume that in this region the profile is sufficiently small in magnitude and slowly varying we can use the second order expansion of
eqn (21) in
eqn (18). After a little algebra one obtains the following expression,
| |  | (23) |
Thus we obtain a D–H like theory with a new effective screening length, given by
λeff = 1/
κeff, where,
| |  | (24) |
where as stated above

is the average cluster charge centred about an ion of type
i. We also have,
| |  | (25) |
which is a renormalised dielectric constant. Similar expressions was first obtained by Kjellander and Mitchell.
30,31 We shall make the approximation that
κD2![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif)
(0)
Rc2 is small compared to unity (allowing us to write

) which is equivalent to saying the screening length,
λeff, is large compared to
Rc, the size of the dressed ion. This approximation will be verified below in specific simulated systems.
2.3 Qualitative cluster analysis
The cluster nature of the approach above is not immediately obvious from eqn (24), but can be elucidated from the following argument. Consider a given typical configuration of the electrolyte consisting of a total of N anions and the same number of cations in a volume V. This could be obtained as say a snapshot from a simulation after equilibration. This configuration could in principle be divided into “clusters” of ions according to a set of criteria consistent with the definition of Δh(0)(r). These criteria are not obvious a priori but would correspond to collections of ions of average size Rc such that when the ion distributions within these clusters are averaged over the ensemble they reproduce Δh(0)(r). We note that appropriately defined clusters may not always be easily identifiable for some systems in the thermodynamic parameter space of the RPM, especially at low density and for weakly coupled systems. For this reason, this analysis is most appropriate to cases where clusters are easily identifiable and where a subsequent mean-field treatment of the clusters is accurate. This would be when Rc is small compared to the electrostatic screening length (as assumed above).
Given this caveat, we can imagine labelling clusters according to the number of anions and cations they contain. That is, clusters of type c say are characterized by having n(c)− anions and n(c)+ cations. We then obtain,  as
as
| |  | (26) |
where
Nc is the number of clusters of type c with charge

and 〈…〉 denotes the ensemble average. Thus we can rewrite
eqn (24) as,
| |  | (27) |
which is the expected expression for a D–H treatment of a mixture of charges, averaged over the ensemble. This analysis makes more concrete the connection between dressed ion theory (and the work in this paper) and “cluster” expressions for the Debye length, as used in simulation studies.
20
2.4 Alternative expression for ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/h3_i_char_e10c.gif) (0)
(0)
We earlier obtained the following expression for the individual ion excess chemical potential (beyond the ideal value) of the bulk electrolyte,| | 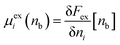 | (28) |
We now consider increasing the bulk density of just the j species by an increment δnj, while leaving the i species at density nb. This gives the following| | 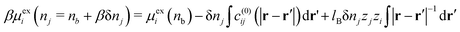 | (29) |
where we have used| |  | (30) |
In eqn (29), we have accounted for the fact that we need to use the full direct correlation function to calculate the change in the excess chemical potential, as the system is no longer electro-neutral: hence the presence of the last term on the RHS of eqn (29). In fact, this term becomes infinite in the thermodynamic limit. We can think of this term as being equivalent to the interaction the i type ions with a uniform background of density, δnj, consisting of ions of type j. Subtracting this contribution from both sides of eqn (29), rearranging terms and letting δnj → 0, we can define the following finite partial derivative,| |  | (31) |
The function μexi(nb; nj) which appears in eqn (31) can be generally defined as the excess chemical potential of species i in a bulk electrolyte where the average density nj may be different to that of species i, given by ni (=nb). To avoid divergence, the system has an implicit neutralizing uniform background of type i ions with density nj − nb. From eqn (29) we then obtain,| |  | (32) |
which finally gives,| | 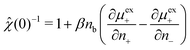 | (33) |
Under-screening thus corresponds to ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) < 1, while the opposite is true for over-screening. This provides us with a thermodynamic criterion which is intimately related to the structure within the fluid.
(0) < 1, while the opposite is true for over-screening. This provides us with a thermodynamic criterion which is intimately related to the structure within the fluid.
2.5 Simulation details
In the systems we investigate below, we assume that the long-ranged part of the charge density profile, described above as the response to a small test charge, q0, can be investigated by considering the appropriate combination of correlation functions in a bulk electrolyte. That is, a given ion in the bulk electrolyte effectively acts as a perturbing “external” charge to the rest of the electrolyte. In order to apply our analysis we required charge–charge correlations in the bulk solution to decay monotonically according to a Yukawa form. This was indeed confirmed by direct observation. The characteristic decay length of these correlations can then be related to the value of ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) (from eqn (33)) for that bulk electrolyte.
(0) (from eqn (33)) for that bulk electrolyte.
We chose to use canonical ensemble simulations and a modified version of a simulation method to calculate individual ion chemical potentials. The latter was suggested by Sloth and Sörensen,32 as an alternative to an earlier proposition by Svensson and Woodward.33 Sloth and Sörensen described an ensemble in which uniform neutralising background charge densities were employed to treat bulk simulations of electrolytes in a grand canonical ensemble that allowed non-electroneutral fluctuations of explicit ions. Thus it is directly applicable to the system described above for obtaining the excess chemical potential derivatives that appear in eqn (33). A neutralising background charge can also be applied to calculate excess chemical potentials when a virtual ion is either inserted in the system (Widom method34) or a virtual attempt is made to remove an ion (the inverse Widom method35). In principle either of these methods allows us to evaluate individual ion chemical potentials μex+ at a given electrolyte concentration. However, it is well-known that the inverse Widom method is unable to directly account for excluded volume contributions to the chemical potential36 which, for our system, corresponds to the free energy associated with inserting a hard sphere into the electrolyte. Fortunately, our expressions require us to calculate differences in excess chemical potential upon changes in anion or cation densities and this will lead to cancellation of the excluded volume contributions in the RPM. It turns out that the inverse Widom method is computationally much more efficient than the Widom approach. This is illustrated in the ESI.† More specifically, we are required to calculate μex+ upon varying the anion or cation densities, n− and n+, respectively, by increasing the number of specific ions to change their concentration from their bulk value while adding a uniform background charge to maintain electroneutrality. The excess chemical potentials determined for these systems will be denoted as μex+(c;n+) and μex+(c;n−), where c is the simulated bulk electrolyte concentration. The values for ni in the simulations ranged from slightly above to slightly below c. This will allow us to numerically obtain the chemical potential derivatives in the expression for ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) in eqn (33).
(0) in eqn (33).
To summarise our strategy to obtain ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) is:
(0) is:
• perform separate canonical simulations and use inverse (important from a statistical perspective) Widom to estimate μex+, at the target density but also at a small excess of cations, as well as a small excess of anions, in each case a uniform background charge is added to maintain electroneutrality.
• plot μex+(c;n+) and μex+(c;n−), and perform a linear regression to the data. A higher order polynomial is an option but a linear fit was sufficient for our investigated cases.
• use the slopes of the linear fits to estimate ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0), and thus the electrostatic screening length, λeff =
(0), and thus the electrostatic screening length, λeff = ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0)λD.
(0)λD.
Eqn (33) indicates that the screening length is ultimately determined by the short-ranged functions, c(0)ij(r). This suggests that modest sized simulations may only be required in order to obtain accurate estimates for the screening length, using the (inverse) Widom approach. This contrasts with conventional approaches which attempt to fit the long-ranged tail of correlation functions. These generally involve large simulated systems in order to obtain reasonably accurate representations of the tail contributions, especially at high electrolyte concentrations where short-ranged oscillations can be significant. This notwithstanding, in order to verify the accuracy of the (inverse) Widom approach it was necessary for us to simulate large systems in order to faithfully obtain the decay of correlation functions at long range. That is, the decay length, λeff, determined via the (inverse) Widom method were compared to those obtained by directly fitting to the long-ranged tail of Δg(r) ≡ g+−(r) − (g++(r) + g−−(r))/2,‡ which measures the charge–charge correlations in the bulk electrolyte. Here gij(r) is the radial distribution function between ion species i and j. In the systems we studied Δg(r) seemed to decay asymptotically according to a Yukawa potential, which allowed us to establish an independent measure of the decay length by numerical fitting. Note that we perform our fits to Δg(r), and not |Δg(r)|. We present some arguments favouring our choice in the ESI.† In order to verify that much smaller simulations could have been used for the (inverse) Widom approach, we also performed simulations with fewer ion pairs for both high and low electrolyte concentrations and compared the results of the with those of the larger systems.
All simulations were performed using the Metropolis Monte Carlo method, in a cubic simulation box with a side length L. Standard cubic periodic boundary conditions were applied along each Cartesian coordinate axis. In all cases investigated, we have set the temperature to 298 K. With a low-dielectric solvent, we have combined standard single ion attempted moves with attempted cluster moves, in order to improve statistics and convergence. We managed the long-ranged Coulomb interactions using four different methods: (a) minimum image (MI) truncation; (b) Ewald sums with cubic truncation in real (MI) as well as reciprocal space; (c) Ewald sums with spherical truncation in real (with truncation radius equal to L/2) as well as reciprocal space, and (d) the so-called “SP3” method, suggested by Fanourgakis et al.37 The Ewald splitting parameter was set to 6.3/L, and with cubic truncation of reciprocal space, 1800 reciprocal vectors were used. As we shall demonstrate, all methods produce identical results, within statistical errors. With the Widom approach (from now on we will drop the term inverse, for convenience), we always utilised MI truncation.
We have focused on two different RPM electrolyte systems. One with a low-dielectric solvent,  and the other using a high-dielectric constant,
and the other using a high-dielectric constant,  mimicking an aqueous solvent. In the former case, we considered parameters similar to some of those recently investigated by Härtel et al.20 Only a single ion diameter, d = 3 Å, was used. For the high-dielectric case, we explored two different choices for the ion diameter: d = 3 Å, 4 Å. We investigated a range of concentrations for each system. For the low-dielectric RPM we used c = 50 mM, 100 mM, 200 mM and 400 mM, and for the other c = 100 mM, 400 mM, 1 M, 1.5 M and 2 M. Radial distribution functions were sampled using a fine-grained histogram (with bin widths δr = 0.05 Å or 0.1 Å) in order to better resolve short-ranged structure. However, since this work focuses on the long-ranged tails, we have reduced the noise in the asymptotic regime by performing running averages over 3 Å (i.e. approximately one ionic diameter). While the radial distribution functions, presented here have been averaged in this manner, the raw data (without averaging) is available upon request.
mimicking an aqueous solvent. In the former case, we considered parameters similar to some of those recently investigated by Härtel et al.20 Only a single ion diameter, d = 3 Å, was used. For the high-dielectric case, we explored two different choices for the ion diameter: d = 3 Å, 4 Å. We investigated a range of concentrations for each system. For the low-dielectric RPM we used c = 50 mM, 100 mM, 200 mM and 400 mM, and for the other c = 100 mM, 400 mM, 1 M, 1.5 M and 2 M. Radial distribution functions were sampled using a fine-grained histogram (with bin widths δr = 0.05 Å or 0.1 Å) in order to better resolve short-ranged structure. However, since this work focuses on the long-ranged tails, we have reduced the noise in the asymptotic regime by performing running averages over 3 Å (i.e. approximately one ionic diameter). While the radial distribution functions, presented here have been averaged in this manner, the raw data (without averaging) is available upon request.
We have also made a comparison of our MC results with calculations using integral equation theory. Here, we utilised a renormalised Ornstein–Zernike (OZ) approach using the hyper-netted chain (HNC) closure, which is suitable for ionic fluids.38 A brief introduction is available in the ESI.† A direct iteration method via Picard mixing was used, with real space discretisation of 218 points at a spacing interval of 0.005 Å, complying with the requirement of vanishing zeroth and second order moments.39,40 Convergence was achieved when the root-mean-squared difference between consecutive iterations fell below 10−6. The effective screening lengths were here extracted by fitting to the calculated ln[rΔg(r)] functions.
3 Results and discussion
We begin by highlighting a qualitative difference between the structure of the long-ranged tails of g++(r) (equivalent to g−−(r)) and g+−(r), for the high- and low-dielectric RPM systems. In Fig. 1a we show the correlation functions in the high-dielectric model at a concentration of 400 mM. For g++(r), the tail approaches its limiting value (unity) from below, while for g+−(r) the approach is from above. This is consistent with simple mean-field treatments wherein the correlation functions are monotonic. Compare this with results for the low-dielectric model at a significantly lower concentration of 100 mM. In this case, both like–like and unlike correlation functions approach unity from above and, furthermore, are surprisingly similar, see Fig. 1b. This is obviously a consequence of ion correlations and will thus not be captured by mean-field treatments. Indeed, this phenomenon does suggest the formation of ion clusters. Clusters will contain both positive and negative ions, and will likely be close to electro-neutral. This means that, as far as spatial correlations are concerned, anions and cations will behave similarly at long range. Thus, both like–like and unlike correlation functions will have similar tails. Some slight differences may occur due to contributions to the correlations between unclustered ions, which is why (as we will see later) we can discern a long-range tail of Δg(r), defined above. As the density in the electrolyte increases, it is possible that the long-ranged behaviour of Δg(r) will actually have a shorter decay than that of density–density correlations (g++(r) + g+−(r)). In this regime we expect that the asymptotic tails of g++(r) and g+−(r) will actually coalesce. That is, the solution is essentially dominated by neutral clusters. This does not seem to be the case in the examples studied below.
 |
| | Fig. 1 Long-range trends of g++(r) and g+−(r), in a solvent with a high (a) and low (b) dielectric constant. In both cases, d = 3 Å. | |
3.1 Low dielectric model
We will now focus on the results for the RPM with a low-dielectric solvent. Here we anticipate significant influence of ion correlations and a noticeable degree of ion clustering. It is worth noting that, for simulation volumes which are large enough to capture the tail regions of Δg(r), all four methods we used to manage long-ranged electrostatics produced the same results. This is illustrated in Fig. 2 for the case, c = 100 mM. We refrain from comparing the noise, since the data were obtained from simulations of different lengths. While we cannot address computational efficiency from this graph alone, the SP3 method certainly offers advantages due to its simplicity. In any case, this comparison clearly demonstrates that, for system sizes we typically used, there is considerable freedom regarding the choice of method for dealing with finite-size effects.
 |
| | Fig. 2 Structural comparisons, using various approaches for the Coulomb interactions. | |
In Fig. 3, we present excess individual chemical potentials using two different system sizes: N = 5000, and N = 2800, with a salt concentration of 100 mM. Here N represents the number of cations, or anions. We note almost perfect linear dependence of μex+(c;n+) as well as μex+(c;n−), with ni and (importantly) there are no significant size effects. We also tested standard (insertion) Widom, the results of which are not shown. However, those results were subject to considerably more noise, so the inverse method is definitively preferable. Extracting the slopes via linear regression fits to μex+(c;n+) and μex+(c;n−), we calculated the electrostatic screening length λeff to be 21.9 Å, using eqn (33) and (24). This is about six times larger than the Debye length indicating pronounced under-screening. We compared this result with a fit to the tail of Δg(r). It should be noted that the simulation lengths required for obtaining accurate asymptotic behaviour of Δg(r) proved much more tedious, even if we account for the extra simulations required to obtain μex+(c;ni) for ni on either side of c. In Fig. 4, we have tested two different methods to obtain the decay length from the long-ranged fitting. In Fig. 4a, we have performed linear regression to fit ln(rΔg), which gave a slope of λeff ≈ 22.0 Å. If we instead import the Widom screening length (21.9 Å), and fit the amplitude A of Ae−κeffr/r to the tail part of Δg, we obtain the blue curve in Fig. 4b. Both methods indicate an excellent agreement. Curiously, the screening length measured by Härtel et al. for an identical model was, as far as we can tell, shorter; around 15 Å. We have no explanation for this discrepancy.
 |
| | Fig. 3 Inverse Widom results, at c = 100 mM, in a low-dielectric solvent 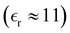 . . | |
 |
| | Fig. 4 Two different ways to fit the tail of Δg to a Yukawa function, at 100 mM salt in a low-dielectric solvent. (a) Linear regression fit to ln(r*Δg). (b) Amplitude (A) fit of Ae−κeffr/r to Δg. | |
The agreement between the Widom method and the fitted values suggest that the theoretical approximations inherent in eqn (33) are vindicated. From our theoretical discussions it is then justifiable to attribute the substantial under-screening seen here to ion clustering. That is, it is likely that most clusters will not be highly charged, which would cause the electrostatic screening as calculated in eqn (28) to be significantly diminished. Indeed, the presence of clusters is confirmed by the simulation snapshot shown in Fig. 5. Consistent with this, from Fig. 3, we note that μex+(c;n+) increases with n+ while μex+(c;n−) decreases with n−. This can be explained as follows. Increasing the number of cations in a system that tends to cluster will mean some of those cations will join the clusters, pushing the average cluster charge toward more positive values. Due to the relatively close proximity of positive ions in a cluster (stabilised by the presence of anions) the additional electrostatic repulsion within clusters cannot be countered effectively by a uniform background of neutralizing negative charge. Thus, μex+(c;n+) will generally increase with n+. The opposite is true when anions are introduced. These excess anions will likely join clusters and lower the energy of cations there and this effect will only be partially countered by the neutralizing positive background density. We would not necessarily expect this to be the case for the high-dielectric case. Here, the depletion hole manifest in g++(r) (shown in Fig. 1a) suggests that it may be quite plausible that μex+(c;n+) will decrease with increasing n+. That is, the small number of additional cations won't affect the depletion hole, while the ubiquitous background will dominate the energy change, due to its ability to penetrate the depletion hole. On the other hand, whether μex+(c;n−) increases or decreases with n−, depends upon the degree of association between unlike charged ions (ion pairing). As we shall see below, all the high-dielectric systems investigated actually display a small degree of over-screening. At an even lower concentration of 50 mM, see Fig. 6a and b, we found an even greater degree of under-screening. The estimated screening length was about 6.6 times larger than the Debye length. Again there is excellent agreement between the Widom method and the direct fitting to Δg(r), see Fig. 6b. This indicates similar clustering is at play even at this reduced concentration. Similar agreement is found at c = 400 mM, as shown in Fig. 7, though the degree of under-screening is more modest, with λeff ≈ 4.5λD.
 |
| | Fig. 5 Simulation snapshot, at c = 100 mM, in a low-dielectric solvent, 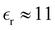 . Cations and anions are indicated by blue and red spheres. This is a “zoomed-in” view at a central part of the simulation box, illustrating some typical equilibrium cluster structures, under these conditions. The image was constructed using the VMD software (developed with NIH support by the Theoretical and Computational Biophysics group at the Beckman Institute, University at Illinois at Urbana-Champaign).41 . Cations and anions are indicated by blue and red spheres. This is a “zoomed-in” view at a central part of the simulation box, illustrating some typical equilibrium cluster structures, under these conditions. The image was constructed using the VMD software (developed with NIH support by the Theoretical and Computational Biophysics group at the Beckman Institute, University at Illinois at Urbana-Champaign).41 | |
 |
| | Fig. 6 Estimating the electrostatic screening length in a low-dielectric solvent  at a concentration c = 50 mM. (a) Widom results. (b) Amplitude (A) fit of Ae−κeffr/r to the tail part of Δg, using the κeff established by Widom. at a concentration c = 50 mM. (a) Widom results. (b) Amplitude (A) fit of Ae−κeffr/r to the tail part of Δg, using the κeff established by Widom. | |
 |
| | Fig. 7 Estimating the electrostatic screening length in a low-dielectric solvent  at a concentration c = 400 mM. (a) Widom results. (b) Amplitude (A) fit of Ae−κeffr/r to the tail part of Δg, using the κeff established by Widom. at a concentration c = 400 mM. (a) Widom results. (b) Amplitude (A) fit of Ae−κeffr/r to the tail part of Δg, using the κeff established by Widom. | |
Fig. 8 summarises the screening lengths obtained by us for the low-dielectric system. Note that this graph contains data at c = 200 mM, but given the results for concentrations on either side of this value, we did not proceed with the computationally expensive fit to Δg(r). While under-screening is demonstrated here, the change in the screening length with salt concentration is not consistent with the anomalous under-screening seen in SFA/SFB measurements. Those experiments indicate the screening length increases directly with salt concentration, whereas in the systems investigated here the screening length decreases with concentration (just not as quickly as the Debye length does). In fact, the approximately linear relation shown in Fig. 8, suggest the following dependence λeff ∼ γκD−1 − δ, where γ∼ 6.5 and δ∼ 1.
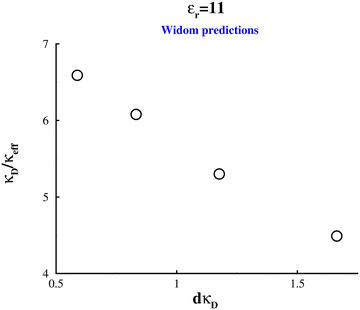 |
| | Fig. 8 The variation of the electrostatic screening length, 1/κeff, with the Debye length, 1/κD, in a low-dielectric solvent  . Estimates of κeff were obtained by the Widom method. . Estimates of κeff were obtained by the Widom method. | |
3.2 High-dielectric model
With a larger dielectric constant, the simulations become computationally cheaper and cluster moves are no longer required. In Fig. 9 we plot the individual excess chemical potentials obtained via the Widom method for c = 400 mM and d = 3 Å. As anticipated above, for this low-coupled system μex+(c;n+) decreases with n+, while the variation of μex+(c;n−) with n− is weak. The end result is overscreening, as ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) > 1.
(0) > 1.
 |
| | Fig. 9 Widom results, at 400 mM and “aqueous” conditions  , and d = 3 Å. , and d = 3 Å. | |
In Fig. 10 we see that the Widom method and the fits to Δg(r), at c = 400 mM, agree very well for two different ion diameters d = 3 Å (a), and d = 4 Å. Both systems display a modest overscreening which increases with the ion diameter. The larger the ion diameter, the greater is the decrease of μex+(c;n+) with n+ due to the neutralizing background penetrating a larger core. On the other hand, the decrease of μex+(c;n−) with n− is diminished. Both these effects serve to increase ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) further. From a physical point of view, the larger core helps to keep like ions apart and diminish ion pairing. This acts to lower the free energy cost of local charge fluctuations and decreases the characteristic length-scale over which they occur. In Fig. 11a, we see that the degree of overscreening also increases with salt concentration and as expected this increase is more pronounced with larger ions. Predictably, the results converge to the Debye screening length at low salt concentrations. Here we also show the results from our OZ-HNC which are essentially in quantitative agreement with the simulation results.
(0) further. From a physical point of view, the larger core helps to keep like ions apart and diminish ion pairing. This acts to lower the free energy cost of local charge fluctuations and decreases the characteristic length-scale over which they occur. In Fig. 11a, we see that the degree of overscreening also increases with salt concentration and as expected this increase is more pronounced with larger ions. Predictably, the results converge to the Debye screening length at low salt concentrations. Here we also show the results from our OZ-HNC which are essentially in quantitative agreement with the simulation results.
 |
| | Fig. 10 Comparing linear regression fits to ln(r*Δg), with Widom predictions of κeff, in “aqueous” RPM:s at c = 400 mM, for two different ion diameters: d = 3 Å (a), and d = 4 Å (b). | |
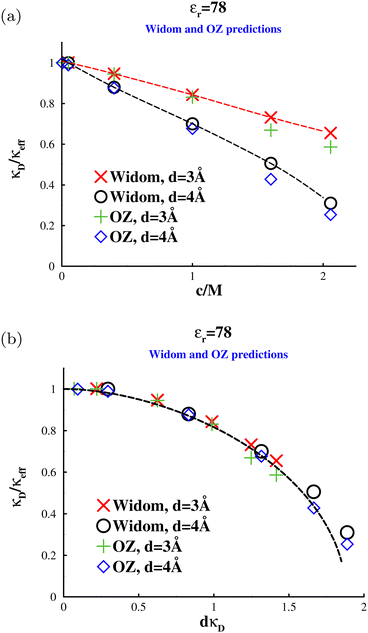 |
| | Fig. 11 Electrostatic screening lengths, in an “aqueous” solvent, at various salt concentrations, and for two different ion sizes. Comparisons between data from the Widom method and OZ calculations. (a) The variation of κeff/κD with salt concentration. The dashed lines are splined fits. The OZ data, which are based on tail fits, are subject to significant uncertainty at high concentrations. (b) The variation of κeff/κD with dκD. The dashed line shows predictions by eqn (34). | |
It is possible to use D–H theory to estimate the excess chemical potentials, μex+(c;n+) and μex+(c;n−) as follows. As already described, we require the change in chemical potential upon incrementing the density of “real” ions, of a particular type with an accompanying neutralising background. The effect of this on, say, a chosen cation will be as follows. The added real ions will be excluded by the hard core of the cation, though they will still respond to the cationic charge. On the other hand, the neutralising background will able to penetrate the excluded volume core of the cation but remain otherwise non-responsive. If we were to assume that the real ions together with the part of the neutralising background outside the core cancel their charge exactly, then the only change in the cation chemical potential comes from the part of the background that penetrates the core. This will mean that μex+(c;n+) will be a decreasing function of n+ and μex+(c;n−) will decrease with n−. This explains over-screening and the role of the ionic radius, but the effect will be over-estimated. The neglected contribution due to the ions outside the core can be reintroduced (analytically) using D–H theory. We simply need to calculate the potential contribution due to the charge profile outside the core which is the linear response to the background charge inside the core. This allows us to eventually arrive at an analytical expression for the over-screening effect,
| |  | (34) |
This expression suggests that
κD/
κeff will be a universal function of
κDd. In
Fig. 11b we see that this provides a reasonable scaling of the computer simulation (as well as the OZ-HNC) results and that our simple D–H expression from
eqn (34) also provides a reasonable estimate of the overall behaviour.
It is interesting to reflect that the agreement between the Widom method and fitted correlation function tails suggests that the cluster model is a reasonable one also for the high-dielectric systems. If this is indeed the case, then over-screening can be interpreted as the formation of like-charged clusters, which will enhance electrostatic screening. This can be interpreted as meaning that like-charged species will tend to have a greater association (due to ion–ion correlations) than is predicted by mean-field theory. While the simulations do not indicate the presence of compact like-charged clusters, even loose clustering in a system which is dilute enough to be treated via mean-field theory will display over-screening. While this picture is reasonable at low concentrations, it likely breaks down at higher concentrations, as will the accuracy of the Widom method we employ here. In fact, it is known that the high dielectric RPM system will undergo a Kirkwood transition at high enough concentration, which is outside of the thermodynamic regime to which the method we describe here is applicable.20 We noted that with increasing concentration, our plots of ln[rΔg(r)] functions begin to demonstrate extensive curvature, indicative of systems approaching the Kirkwood transition, thus increasing the difficulty of fitting a linear function to extract the effective screening lengths. This is exemplified in the ESI.† For concentrations above 1 M, OZ-HNC underestimates the Widom method results.
3.3 Accuracy of the Widom approach for small simulated systems
As stated earlier, the Widom approach is based on an expression for the screening length in terms of short-ranged correlation functions. Thus, while κeff determines long-ranged correlations, it is itself, largely independent of them. In order to test this, we repeated our screening length calculations for the low dielectric system at 100 mM using 5000, 625 and 100 ion pairs. Fig. 12(a) shows the result of fitting the tails of Δg(r). We see that the measured decay lengths increases significantly at smaller system sizes (though not monotonically). On the other hand, the Widom calculations, Fig. 12(b), display essentially no variation with system size. It is worth noting that, while the absolute values of the chemical potentials, μex+(c;ni), did vary with system size, their derivatives did not. That is, the variation of these functions with respect to density is determined primarily by short-ranged correlations. We note that similar results were obtained for even higher concentrations, even at system sizes that were too small to discern a monotonic tail in the correlation functions. That is the Widom approach gave an accurate estimate of κeff, for simulations which were too small to properly fit the tail of Δg(r).
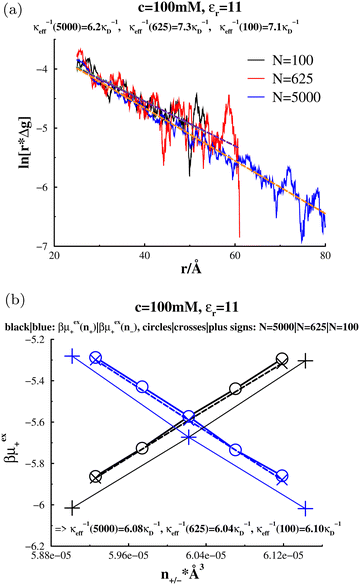 |
| | Fig. 12 Comparing linear regression fits to ln(r*Δg), with Widom predictions of κeff, in “aqueous” RPM:s at c = 100 mM, d = 3 Å, and a low-dielectric solvent 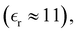 for various system sizes: 100, 625 and 5000 ion pairs (N). The Widom approach (graph (b)) is compared with results from fits to the tail of Δg(r) (graph (a)). As indicated, the fitted effective screening lengths, obtained via regression (graph (a)), are 1/κeff(N = 100) = 7.1/κD, 1/κeff(N = 625) = 7.3/κD, and 1/κeff(N = 5000) = 6.2/κD. The calculated effective screening lengths, obtained with the Widom method (graph (b)), are 1/κeff(N = 100) = 6.10/κD, 1/κeff(N = 625) = 6.04/κD, and 1/κeff(N = 5000) = 6.08/κD, where the last digit is subject to statistical noise. (a) Tail regression approach. (b) Widom approach. for various system sizes: 100, 625 and 5000 ion pairs (N). The Widom approach (graph (b)) is compared with results from fits to the tail of Δg(r) (graph (a)). As indicated, the fitted effective screening lengths, obtained via regression (graph (a)), are 1/κeff(N = 100) = 7.1/κD, 1/κeff(N = 625) = 7.3/κD, and 1/κeff(N = 5000) = 6.2/κD. The calculated effective screening lengths, obtained with the Widom method (graph (b)), are 1/κeff(N = 100) = 6.10/κD, 1/κeff(N = 625) = 6.04/κD, and 1/κeff(N = 5000) = 6.08/κD, where the last digit is subject to statistical noise. (a) Tail regression approach. (b) Widom approach. | |
4 Conclusions
We have described a new Widom method for calculating electrostatic screening in systems which display Yukawa (monotonic) decay of the charge–charge correlation functions. We have established the connection between our approach and the dressed ion theory of Kjellander and co-workers and also elucidated the connection to a cluster model within a mean-field setting. This latter interpretation is most obviously suitable when the characteristic cluster size is small compared to the electrostatic decay length, which can been established by the agreement between the Widom method and direct fits to the correlation function decay. Thus, our method strengthens the argument that clusters in highly-coupled systems are responsible for anomalous under-screening. It also appears that even for less-coupled systems, such as in the high-dielectric RPM, loose clustering (between like charges) is also a useful explanatory model, at least for low to moderate electrolyte concentrations.
Alternatively, our method provides us with a direct thermodynamic criterion for under- and over-screening, viaeqn (33). Specifically, the relative values of  and
and  determines whether the observed decay length is greater or less than the Debye length. These individual chemical potential derivatives are determined by the opposing effects of adding real charged particles together with a neutralizing uniform background of counter-charge. Ion correlations are important to explain these contributions, both core exclusion (real particles exclude one another, whereas the uniform background can penetrate into particle cores) as well as short-ranged electrostatic correlations (oppositely charged particles tend to cluster and like charges repel). In the case of the high-dielectric RPM system the dominance of core exclusion allowed us explain the effect of concentration and ion size on the observed over-screening.
determines whether the observed decay length is greater or less than the Debye length. These individual chemical potential derivatives are determined by the opposing effects of adding real charged particles together with a neutralizing uniform background of counter-charge. Ion correlations are important to explain these contributions, both core exclusion (real particles exclude one another, whereas the uniform background can penetrate into particle cores) as well as short-ranged electrostatic correlations (oppositely charged particles tend to cluster and like charges repel). In the case of the high-dielectric RPM system the dominance of core exclusion allowed us explain the effect of concentration and ion size on the observed over-screening.
Finally, we need to point out that the systems we have investigated here unfortunately do not corroborate the anomalous under-screening seen in experiments. Further theoretical investigations will be required in order to confirm the veracity of those measurements.
Data availability
All generated data, as well as all codes used to generate these data, are freely available upon reasonable request.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
J. F. acknowledges financial support by the Swedish Research Council. The Centre for Scientific and Technical Computing at Lund University, LUNARC, is acknowledged for providing computational resources.
References
- B. V. Derjaguin and L. Landau, Acta Physicochim. URSS, 1941, 14, 633–662 Search PubMed.
-
E. J. W. Verwey and J. T. G. Overbeek, Theory of the Stability of Lyophobic Colloids, Elsevier Publishing Company Inc., Amsterdam, 1948 Search PubMed.
- L. Guldbrand, B. Jönsson, H. Wennerström and P. Linse, J. Chem. Phys., 1984, 80, 2221 CrossRef CAS.
- R. Kjellander and S. Marcelja, Chem. Phys. Lett., 1986, 127, 402–407 CrossRef CAS.
- J. Valleau, R. Ivkov and G. M. Torrie, J. Phys. Chem., 1991, 95, 520–532 CrossRef CAS.
- M. A. G. Dahlgren, Å. Waltermo, E. Blomberg, P. M. Claesson, L. Sjöström, T. Åkesson and B. Jönsson, J. Phys. Chem., 1993, 97, 11769 CrossRef CAS.
- Z. Tang, L. E. Scriven and H. T. Davis, J. Chem. Phys., 1994, 100, 4527–4530 CrossRef CAS.
- M. A. G. Dahlgren, H. C. M. Hollenberg and P. M. Claesson, Langmuir, 1995, 11, 4480–4485 CrossRef CAS.
- R. R. Netz, Eur. Phys. J. E: Soft Matter Biol. Phys., 2001, 5, 557 CrossRef CAS.
- J. Forsman, J. Phys. Chem. B, 2004, 108, 9236–9245 CrossRef CAS.
- W. Lin, P. Galletto and M. Borkovec, Langmuir, 2004, 20, 7465–7473 CrossRef CAS PubMed.
- K. Bestemann, M. A. G. Zevenbergen, H. A. Heering and S. G. Lemay, Phys. Rev. Lett., 2005, 93, 170802 CrossRef PubMed.
- M. Trulsson, B. Jönsson, J. Forsman and C. Labbez, Phys. Rev. Lett., 2006, 97, 068302 CrossRef PubMed.
- G. Gillies, W. Lin and M. Borkovec, J. Phys. Chem. B, 2007, 111, 8626–8633 CrossRef CAS PubMed.
- I. Popa, G. Gillies, G. Papastavrou and M. Borkovec, J. Phys. Chem. B, 2010, 113, 8458–8461 CrossRef PubMed.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- M. A. Gebbie, H. A. Dobbs, M. Valtiner and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7432–7437 CrossRef CAS PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157–2163 CrossRef CAS PubMed.
- Y. K. C. Fung and S. Perkin, Faraday Discuss., 2023, 370–386 RSC.
- A. Härtel, M. Bültmann and F. Coupette, Phys. Rev. Lett., 2023, 130, 108202 CrossRef PubMed.
- S. Kumar, P. Cats, M. B. Alotaibi, S. C. Ayirala, A. A. Yousef, R. van Roij, I. Siretanu and F. Mugele, J. Colloid Interface Sci., 2022, 622, 819–827 CrossRef CAS PubMed.
- N. Hjalmarsson, R. Atkin and M. W. Rutland, Chem. Commun., 2017, 53, 647–650 RSC.
- M. Nayeri, Z. Abbas and J. Bergenholtz, Colloids Surf., A, 2013, 429, 74–81 CrossRef CAS.
- H. Yuan, W. Deng, X. Zhu, G. Liu and V. S. J. Craig, Langmuir, 2022, 38, 6164–6173 CrossRef CAS PubMed.
- S. W. Coles, C. Park, R. Nikam, M. Kanduc, J. Dzubiella and B. Rotenberg, J. Phys. Chem. B, 2020, 124, 1778–1786 CAS.
- J. Zeman, S. Kondrat and C. Holm, Chem. Commun., 2020, 56, 15635–15638 RSC.
- B. Rotenberg, O. Bernard and J.-P. Hansen, J. Phys.: Condens. Matter, 2018, 30, 054005 CrossRef PubMed.
- R. Kjellander, Phys. Chem. Chem. Phys., 2020, 22, 23952–23985 RSC.
- P. Cats, R. Evans, A. Härtel and R. van Roij, J. Chem. Phys., 2021, 154, 124504 CrossRef CAS PubMed.
- R. Kjellander and D. J. Mitchell, Chem. Phys. Lett., 1992, 200, 76–82 CrossRef CAS.
- R. Kjellander and D. J. Mitchell, J. Chem. Phys., 1994, 101, 603–626 CrossRef CAS.
- P. Sloth and T. S. Sörensen, Chem. Phys. Lett., 1990, 173, 51–56 CrossRef CAS.
- B. R. Svensson and C. E. Woodward, Mol. Phys., 1988, 64, 247–259 CrossRef CAS.
- B. Widom, J. Chem. Phys., 1963, 39, 2808–2812 CrossRef CAS.
- K. Shing and K. Gubbins, Mol. Phys., 1982, 46, 1109–1128 CrossRef CAS.
- N. G. Parsonage, J. Chem. Soc., Faraday Trans., 1995, 91, 2971–2973 RSC.
- G. S. Fanourgakis, J. Phys. Chem. B, 2015, 119, 1974–1985 CrossRef CAS PubMed.
- T. Ichiye and A. D. J. Haymet, J. Chem. Phys., 1988, 89, 4315–4324 CrossRef CAS.
- A. McBride, M. Kohonen and P. Attard, J. Chem. Phys., 1998, 109, 2423–2428 CrossRef CAS.
- P. Attard, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1993, 48, 3604–3621 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00546e |
| ‡ with gαβ(r) denoting the α − β radial distribution function, α,β ∈ {+,-}. |
|
| This journal is © the Owner Societies 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
David
Ribar
*a,
David
Ribar
 a and
Clifford E.
Woodward
a and
Clifford E.
Woodward
 b
b
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 salts the re-entrant trend was quite weak and mainly significant at exceptionally high concentrations.
1 salts the re-entrant trend was quite weak and mainly significant at exceptionally high concentrations.
 where e is the elementary charge,
where e is the elementary charge,  is the relative dielectric constant of the implicit solvent, and
is the relative dielectric constant of the implicit solvent, and  is the permittivity of vacuum. We will here restrict the treatment to symmetric RPM electrolytes, i.e., (z:z) salts whose valencies are equal in magnitude but opposite in sign (z+ = −z− = z).
is the permittivity of vacuum. We will here restrict the treatment to symmetric RPM electrolytes, i.e., (z:z) salts whose valencies are equal in magnitude but opposite in sign (z+ = −z− = z).





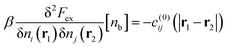


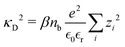
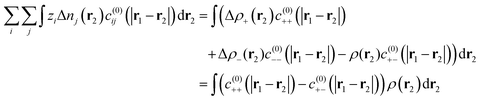







![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (k) = 1/(1 − nbΔĉ(0)(k)). Finally we obtain,
(k) = 1/(1 − nbΔĉ(0)(k)). Finally we obtain,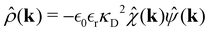

![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (k) = 1 + nbΔĥ(0)(k). The quantity zi
(k) = 1 + nbΔĥ(0)(k). The quantity zi![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (r) corresponds to a supposedly short-ranged charge density profile centred at an ion of species i, which includes the charge zi plus an associated atmosphere of additional ions. This corresponds to an ion charge and its “dress”, the latter being due to short-ranged correlations, as described in the dressed ion theory of Kjellander and Mitchell.30,31 For small k, we write,
(r) corresponds to a supposedly short-ranged charge density profile centred at an ion of species i, which includes the charge zi plus an associated atmosphere of additional ions. This corresponds to an ion charge and its “dress”, the latter being due to short-ranged correlations, as described in the dressed ion theory of Kjellander and Mitchell.30,31 For small k, we write,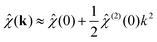
 can be thought of as the total average charge of ion clusters that contain the species i. This will be equal in magnitude and opposite in sign for anions and cations in this symmetric model. The characteristic average length-scale of these clusters, denoted by Rc, can be estimated from the second term on the RHS of eqn (21), which gives the second moment of the so-called ion dress, i.e.,
can be thought of as the total average charge of ion clusters that contain the species i. This will be equal in magnitude and opposite in sign for anions and cations in this symmetric model. The characteristic average length-scale of these clusters, denoted by Rc, can be estimated from the second term on the RHS of eqn (21), which gives the second moment of the so-called ion dress, i.e.,  .
.
![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (k) = 1. Under these conditions we obtain,
(k) = 1. Under these conditions we obtain,


 is the average cluster charge centred about an ion of type i. We also have,
is the average cluster charge centred about an ion of type i. We also have,
![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0)Rc2 is small compared to unity (allowing us to write
(0)Rc2 is small compared to unity (allowing us to write  ) which is equivalent to saying the screening length, λeff, is large compared to Rc, the size of the dressed ion. This approximation will be verified below in specific simulated systems.
) which is equivalent to saying the screening length, λeff, is large compared to Rc, the size of the dressed ion. This approximation will be verified below in specific simulated systems.
 as
as
 and 〈…〉 denotes the ensemble average. Thus we can rewrite eqn (24) as,
and 〈…〉 denotes the ensemble average. Thus we can rewrite eqn (24) as,
![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/h3_i_char_e10c.gif) (0)
(0)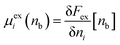
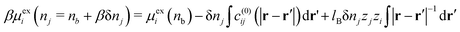



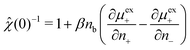
![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) < 1, while the opposite is true for over-screening. This provides us with a thermodynamic criterion which is intimately related to the structure within the fluid.
(0) < 1, while the opposite is true for over-screening. This provides us with a thermodynamic criterion which is intimately related to the structure within the fluid.
![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) (from eqn (33)) for that bulk electrolyte.
(0) (from eqn (33)) for that bulk electrolyte.
![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) in eqn (33).
(0) in eqn (33).![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) is:
(0) is:![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0), and thus the electrostatic screening length, λeff =
(0), and thus the electrostatic screening length, λeff = ![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0)λD.
(0)λD. and the other using a high-dielectric constant,
and the other using a high-dielectric constant,  mimicking an aqueous solvent. In the former case, we considered parameters similar to some of those recently investigated by Härtel et al.20 Only a single ion diameter, d = 3 Å, was used. For the high-dielectric case, we explored two different choices for the ion diameter: d = 3 Å, 4 Å. We investigated a range of concentrations for each system. For the low-dielectric RPM we used c = 50 mM, 100 mM, 200 mM and 400 mM, and for the other c = 100 mM, 400 mM, 1 M, 1.5 M and 2 M. Radial distribution functions were sampled using a fine-grained histogram (with bin widths δr = 0.05 Å or 0.1 Å) in order to better resolve short-ranged structure. However, since this work focuses on the long-ranged tails, we have reduced the noise in the asymptotic regime by performing running averages over 3 Å (i.e. approximately one ionic diameter). While the radial distribution functions, presented here have been averaged in this manner, the raw data (without averaging) is available upon request.
mimicking an aqueous solvent. In the former case, we considered parameters similar to some of those recently investigated by Härtel et al.20 Only a single ion diameter, d = 3 Å, was used. For the high-dielectric case, we explored two different choices for the ion diameter: d = 3 Å, 4 Å. We investigated a range of concentrations for each system. For the low-dielectric RPM we used c = 50 mM, 100 mM, 200 mM and 400 mM, and for the other c = 100 mM, 400 mM, 1 M, 1.5 M and 2 M. Radial distribution functions were sampled using a fine-grained histogram (with bin widths δr = 0.05 Å or 0.1 Å) in order to better resolve short-ranged structure. However, since this work focuses on the long-ranged tails, we have reduced the noise in the asymptotic regime by performing running averages over 3 Å (i.e. approximately one ionic diameter). While the radial distribution functions, presented here have been averaged in this manner, the raw data (without averaging) is available upon request.


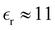 . Cations and anions are indicated by blue and red spheres. This is a “zoomed-in” view at a central part of the simulation box, illustrating some typical equilibrium cluster structures, under these conditions. The image was constructed using the VMD software (developed with NIH support by the Theoretical and Computational Biophysics group at the Beckman Institute, University at Illinois at Urbana-Champaign).41
. Cations and anions are indicated by blue and red spheres. This is a “zoomed-in” view at a central part of the simulation box, illustrating some typical equilibrium cluster structures, under these conditions. The image was constructed using the VMD software (developed with NIH support by the Theoretical and Computational Biophysics group at the Beckman Institute, University at Illinois at Urbana-Champaign).41
 . Estimates of κeff were obtained by the Widom method.
. Estimates of κeff were obtained by the Widom method.![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) > 1.
(0) > 1.
![[small chi, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e10c.gif) (0) further. From a physical point of view, the larger core helps to keep like ions apart and diminish ion pairing. This acts to lower the free energy cost of local charge fluctuations and decreases the characteristic length-scale over which they occur. In Fig. 11a, we see that the degree of overscreening also increases with salt concentration and as expected this increase is more pronounced with larger ions. Predictably, the results converge to the Debye screening length at low salt concentrations. Here we also show the results from our OZ-HNC which are essentially in quantitative agreement with the simulation results.
(0) further. From a physical point of view, the larger core helps to keep like ions apart and diminish ion pairing. This acts to lower the free energy cost of local charge fluctuations and decreases the characteristic length-scale over which they occur. In Fig. 11a, we see that the degree of overscreening also increases with salt concentration and as expected this increase is more pronounced with larger ions. Predictably, the results converge to the Debye screening length at low salt concentrations. Here we also show the results from our OZ-HNC which are essentially in quantitative agreement with the simulation results.


 and
and  determines whether the observed decay length is greater or less than the Debye length. These individual chemical potential derivatives are determined by the opposing effects of adding real charged particles together with a neutralizing uniform background of counter-charge. Ion correlations are important to explain these contributions, both core exclusion (real particles exclude one another, whereas the uniform background can penetrate into particle cores) as well as short-ranged electrostatic correlations (oppositely charged particles tend to cluster and like charges repel). In the case of the high-dielectric RPM system the dominance of core exclusion allowed us explain the effect of concentration and ion size on the observed over-screening.
determines whether the observed decay length is greater or less than the Debye length. These individual chemical potential derivatives are determined by the opposing effects of adding real charged particles together with a neutralizing uniform background of counter-charge. Ion correlations are important to explain these contributions, both core exclusion (real particles exclude one another, whereas the uniform background can penetrate into particle cores) as well as short-ranged electrostatic correlations (oppositely charged particles tend to cluster and like charges repel). In the case of the high-dielectric RPM system the dominance of core exclusion allowed us explain the effect of concentration and ion size on the observed over-screening.