Binary conformers of a flexible, long-chain fluoroalcohol: dispersion controlled selectivity and relative abundances in a jet

Abstract

The complex conformational panorama of binary 4,4,4-trifluoro-1-butanol (TFB) aggregates was investigated using chirped-pulse Fourier transform microwave spectroscopy, aided by conformational searches using CREST (Conformer-Rotamer Ensemble Sampling Tool) and quantum chemistry calculations. From nearly 1500 initial dimer geometries, 16 most stable binary candidates were obtained within a relative energy window of ∼4 kJ mol⁻¹. Rotational spectra of five binary conformers were experimentally observed in supersonic expansion and assigned. Interestingly, three out of the five observed binary conformers are composed solely of monomer conformers, which were not observed in their isolated gas phase forms in jet expansion. In addition, an observed dimer that is made exclusively of the most stable TFB monomer subunits does not correspond to the global minimum. The intricate kinetically and thermodynamically controlled dimer formation mechanisms are discussed, and a modified kinetic-thermodynamic model was developed, providing conformational abundances that are in good agreement with the experiment. Subsequent non-covalent interaction analyses reveal that the observed conformers are held together by one primary O–H⋯O hydrogen bond and secondary intermolecular C–H⋯O, C–H⋯F, and/or O–H⋯F interactions, as well as C–H⋯H–C London dispersion interactions between the methylene groups. Further symmetry-adapted perturbation theory analyses of the TFB dimer conformers and related alcohol dimers reveal a considerable rise in dispersion contributions with increasing n-alkyl carbon chain length and highlight the role of dispersion interactions in preferentially stabilizing the global minimum of the TFB dimer.

---

Introduction

The non-covalent interactions (NCIs) in aggregates of alcohol molecules have attracted significant spectroscopic and theoretical interest in recent years.^1,2 One fascinating aspect is that these flexible alcohol molecules can exist in gauche− and gauche+, a pair of (transiently) chiral conformations, and an achiral trans conformation, associated with the alcoholic OH group. While hydrogen-bonding interactions usually provide the dominant attractive interactions in these clusters, researchers have been exploring the role of dispersion interactions in preferentially stabilizing specific subunit conformations and in fine-tuning the outcome of chirality recognition. For example, trans-trifluoroethanol (tTFE), which is unstable as an isolated monomer, becomes a significant contributor (∼30%) in its trimer,³ and reaches ∼40% abundance in liquid TFE.⁴ On the other hand, while the 1,1,1,3,3,3-hexafluoroisopropanol (HFIP) monomer has an intrinsic preference for its achiral trans-conformation, the observed trimer is made exclusively of the least stable gauche-HFIP subunit.⁵ The latter result provides deep insights into how flexible molecules with an intrinsic preference for an achiral conformation can evolve into chiral assemblies made of chiral constituents under the influence of NCIs.⁵ Interestingly, while dimers of mono-fluoroethanol (FE), TFE and HFIP exhibit a diverse preference for heterochiral,^6,7 strong homochiral,^8,9 or achiral subunit compositions,⁵ respectively, the associated trimers all demonstrate a heterochiral preference.^3,5,10 More recently, chirality recognition in the cyclohexanol dimer² and aggregates of benzyl alcohol¹¹ was investigated using jet-cooled rotational and Rovibronic spectroscopies, along with theoretical modelling. These studies reveal that the existence of multiple stereoisomers with similar stability is a common occurrence in these alcohol aggregates and also discuss the challenges in using the experimental conformational abundances to benchmark theoretical relative energy ordering of these clusters.

In recent years, chirped-pulse (CP)–Fourier transform (FT) microwave (MW) spectroscopy, has emerged as a powerful spectroscopic technique to provide very detailed, often decisive information about structures, energetics and internal dynamics of small, non-covalently bonded clusters.^12,13 In this work, we focus on using CP-FTMW spectroscopy of binary aggregates of 4,4,4-trifluoro-1-butanol (TFB). TFB serves widely as an important intermediate in liquid crystal, organic semiconductor and pharmaceutical productions.¹⁴ As the n-alkyl carbon chain length increases, alcohol molecules become much more flexible, resulting in more intricate conformational landscapes. For instance, while TFE has only two rotational spectroscopically distinguishable monomer conformers, TFB has fourteen including thirteen enantiomeric pairs.¹⁵ Therefore one can anticipate a considerably more complicated conformational landscape of the TFB dimer, compared to the aforementioned alcohol dimers. By using a combination of experimental CP-FTMW data and theoretical calculations, we aim to explore the conformational diversity in the TFB dimer and evaluate the influence of dispersion interactions associated with the n-alkyl carbon chain on the energy ordering of binary conformers. In addition, we aim to develop a modified kinetic–thermodynamic model to explain the observation and non-observation of certain low energy conformers of alcohol dimers in jet expansion, offering a comprehensive connection between experimental abundances and theoretical relative energies. Furthermore, we compare the relative electrostatic, induction, dispersion and exchange-repulsion contributions to the intermolecular interactions among a range of n-alkyl alcohol dimers to appreciate the importance of dispersion interactions in the current system.

Methods

Experimental details

The rotational spectrum of the TFB dimer in the frequency region of 2–6 GHz was collected using a broadband CP-FTMW spectrometer, similar to that described by Pate and co-workers.¹⁶ The details of spectrometer have been provided elsewhere.^17,18 The accuracy of the frequency measurements is estimated to be ca. 5 kHz, and the full line width at half height is about 120 kHz. A small amount of liquid commercial sample of TFB (98% purity, Sigma-Aldrich) was placed directly into a home-made nozzle cap¹⁹ fitted to a pulsed nozzle (Parker, General Valve Series 9) and kept at room temperature for further experiments, while helium carrier gas at a constant backing pressure of 3 bar was utilized. 1 μs long chirped MW pulses (2–6 GHz) were produced using a 12 Gs s⁻¹ arbitrary waveform generator (AWG) and subsequently amplified using a traveling wave tube (TWT) amplifier (2.5–7.5 GHz) with a maximum output power of 400 W. The MW radiation was broadcasted using a horn antenna and perpendicularly intercepted a pulsed supersonic jet expansion. The resulting free induction decays (FIDs) were collected using a second identical detection horn antenna for 20 μs and digitized using a 25 Gs s⁻¹ digital oscilloscope. For each molecular pulse, 12 FIDs were collected and the nozzle repetition rate was 2 Hz. Finally, 1.4 million FIDs were co-added, weighted with a Kaiser–Bessel window function, and Fourier transformed to produce the frequency spectrum.

Computational details

To strive for an as complete as possible conformational search, we utilized CREST (Conformer-Rotamer Ensemble Sampling Tool), a powerful searching approach which combines semiempirical GFN-xTB²⁰ quantum chemistry methods with a meta-dynamics driven search algorithm,^21,22 in addition to manual potential energy surface (PES) scans along several important dihedral angles. The CREST approach has been successfully utilized by rotational spectroscopists for exploring conformational landscapes of a wide range of (in)organic compounds,^23,24 hydrogen-bonded clusters^25,26 and even very weakly bound van der Waals clusters.²⁷ About 1500 CREST binary TFB candidates were generated and a multi-tier approach²⁸ was used to identify low energy candidates. Subsequently, the candidates were optimized at the B3LYP-D3BJ/def2-TZVP level of theory, and harmonic vibrational frequency analyses were carried out to verify that all optimized structures were true energy minima and to obtain their relative zero-point corrected energies. All the geometry optimizations and frequency calculations were performed using the Gaussian16 program package.²⁹

The quantum theory of atoms in molecules (QTAIM)³⁰ and the NCI approaches³¹ were employed to characterize and visualize the intra- and intermolecular interactions occurring in the binary TFB conformers by means of the Multiwfn³² and VMD³³ programs. Symmetry-adapted perturbation theory (SAPT) analyses³⁴ at the SAPT2+(3)/aug-cc-pVDZ level of theory were conducted to decompose the total interaction energies of the TFB dimer and other related alcohol dimers into electrostatic, induction, dispersion and exchange-repulsion components using the PSI4 program.³⁵

Results and discussion

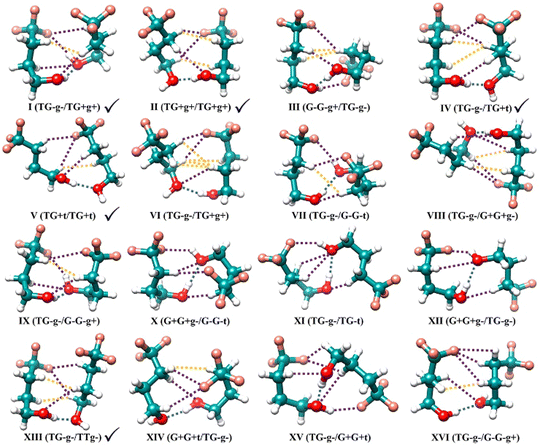
The TFB monomer conformations are mainly characterized by three dihedral angles: τ(C–C–C–C), τ(C–C–C–O), and τ(C–C–O–H).¹⁵ They can adopt the gauche forms, corresponding approximately to a dihedral angle value of +60° (G+ or g+) and −60° (G− or g−), or trans form of 180° (T or t). Consequently, the TFB monomer has 27 possible conformations which include 13 enantiomeric pairs with transient chirality and an achiral conformation: TG+t/TG−t, TG+g+/TG−g−, G+G+t/G−G−t, G+G+g−/G−G−g+, TG+g−/TG−g+, TTt, TTg+/TTg−, G+G+g+/G−G−g−, G+Tt/G−Tt, G+Tg+/G−Tg−, G+G−g+/G−G+g−, G+Tg−/G−Tg+, G+G−t/G−G+t, and G+G−g−/G−G+g+ (see Fig. 2 of ref. 15), in the order of increasing relative energy. The two uppercase letters refer to τ(C–C–C–C) and τ(C–C–C–O) dihedral angles, and the lowercase letters correspond to the τ(C–C–O–H) dihedral angle.

Without considering more subtle differences in the secondary non-covalent interactions and assuming that binary TFB conformers are connected through an intermolecular O–H⋯O hydrogen bond, one can expect 677 dimer conformers, i.e., 2 × (switch the role of proton donor and acceptor) × (13 (with TTt) + 13 × 24 (with the remaining enantiomeric pairs)) + 1 (TTt dimer) + 13 × 2 (with themselves). Here one counts a pair of mirror-imaged binary conformations as one conformer as their rotational spectra are the same. If one further considers that the proton donor can either bind to the left- or right-hand lone pair of the O atom of the proton acceptor or how the extended n-alkyl carbon chains of the two subunits interact with each other, the number of potential binary conformations increases greatly. It is therefore essential to enlist the assistance of CREST in identifying all low-energy dimer candidates. The subsequent DFT calculations resulted in 102 stable TFB dimer conformers within a relative energy span of 10 kJ mol⁻¹ at the B3LYP-D3BJ/def2-TZVP level. Each conformer is named with a Roman numeral, which indicates its ΔE₀ ranking with I being the most stable, and with the monomer identification of its proton donor and acceptor, for example, I(TG−g−/TG+g+). Geometries of the 16 most stable conformers within a narrow, relative energy window of ∼4 kJ mol⁻¹ are shown in Fig. 1, while their energetic and spectroscopic properties are given in Table 1, and the energetic and spectroscopic parameters of the 102 conformers are collated in Table S1, (ESI†).

Fig. 1 Optimized geometries of the 16 lowest energy conformers of the TFB dimer obtained at the B3LYP-D3BJ/def2-TZVP level of theory. The experimentally observed conformers are marked with blue checkmarks. The O–H⋯O hydrogen bonds are labelled with blue dotted lines, while the purple dashed lines denote the C–H⋯O, C–H⋯F and O–H⋯F weak hydrogen bonds, and the orange dashed lines represent the C–H⋯H–C London dispersion interactions, identified by the NCI analyses discussed later in the main text.

Table 1 Theoretical spectroscopic parameters of the 16 conformers of the TFB dimer at the B3LYP-D3BJ/def2-TZVP level of theory^a

Conformers	Family^b	ΔE	ΔE0	A	B	C	|μa|	|μb|	|μc|
a ΔE andΔE0 denote the raw and ZPE corrected relative energies (in kJ mol^−1), respectively, and A, B, and C are the rotational constants (in MHz). |μg| (g = a, b, c) are the magnitudes of the electric dipole moment components (in Debye). b Each family label consists of the names of the two monomer subunits. Please see the discussions presented in the section titled “Rationale for the (non)-observation of the low energy TFB dimer conformers”.
I(TG−g−/TG+g+)	(TG,TG)	0.0	0.0	0.565	0.299	0.272	1.1	1.8	1.3
II(TG+g+/TG+g+)	(TG,TG)	2.2	1.2	0.539	0.281	0.234	0.5	3.4	2.0
III(G−G−g+/TG−g−)	(TG,GG)	1.6	1.6	0.608	0.280	0.269	0.5	1.2	1.1
IV(TG−g−/TG+t)	(TG,TG)	3.2	1.8	0.512	0.320	0.257	0.9	5.0	2.1
V(TG+t/TG+t)	(TG,TG)	4.2	2.4	0.636	0.247	0.196	6.7	3.3	0.2
VI(TG−g−/TG+g+)	(TG,TG)	3.8	2.6	0.555	0.249	0.202	0.1	2.9	0.5
VII(TG−g−/G−G−t)	(TG,GG)	3.1	2.8	0.614	0.302	0.265	0.1	2.2	0.9
VIII(TG−g−/G+G+g−)	(TG,GG)	2.7	2.8	0.823	0.199	0.180	0.0	0.9	0.0
IX(TG−g−/G−G−g+)	(TG,GG)	2.8	3.0	0.604	0.323	0.263	0.4	2.5	0.1
X(G+G+g−/G−G−t)	(GG,GG)	2.8	3.0	0.679	0.268	0.264	0.3	0.6	1.3
XI(TG−g−/TG−t)	(TG,TG)	4.8	3.4	0.763	0.195	0.186	2.4	1.1	1.4
XII(G+G+g−/TG−g−)	(TG,GG)	3.5	3.5	0.788	0.206	0.195	1.4	1.7	1.0
XIII(TG−g−/TTg−)	(TG,TT)	4.5	3.6	0.515	0.312	0.233	0.7	3.0	2.0
XIV(G+G+t/TG−g−)	(TG,GG)	4.7	3.6	0.567	0.290	0.243	0.0	3.1	0.9
XV(TG−g−/G−G−t)	(TG,GG)	2.9	3.6	0.818	0.230	0.216	0.7	1.2	0.2
XVI(TG−g−/G−G−g+)	(TG,GG)	4.9	3.8	0.604	0.252	0.204	0.4	0.7	0.3

---

For comparison, additional calculations for these 16 conformers were also carried out at the B3LYP-D3BJ/6-311++G(2d,p), B2PLYP-D3BJ/def2-TZVP, B2PLYP-D3BJ/6-311++G(2d,p), and MP2/6-311++G(2d,p) levels of theory, and the results are collated in Tables S2–S5 in the ESI.† Although some minor switches in the energy ordering were observed, similar to that reported in the case of cyclohexanol dimer,² the general relative energy trend remains.

Spectroscopic analyses and conformational assignments

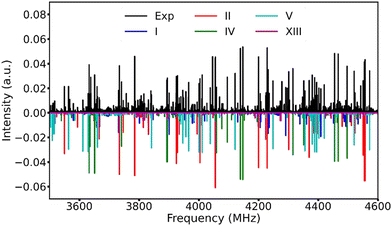
After removing the known transition lines corresponding to the TFB monomer and its rarer isotopologues,¹⁵ as well as the TFB⋯H₂O adduct,³⁶ the resulting broadband spectrum still appears very dense (Fig. 2), reflecting the rich conformational panorama of the TFB dimer and the coexistence of many low energy conformers. Based on the theoretical predictions, we first searched for the a-type transitions of conformer V because its large μ_a electric dipole moment component. A series of a-type ΔJ = 1 rotational transitions were soon identified and assigned. Subsequently, some weak b-type rotational transitions were assigned. No c-type rotational transitions were detected because of the very small μ_c magnitude. After removing the transitions of conformer V from the experimental spectrum, three new separate sets of rotational transitions with a-, b-, and c-type transitions belonging to three different species were identified and assigned. Based on the comparison between the experimental and theoretical rotational constants as well as the relative intensity of the a-, b-, and c-type transitions, the carriers of these three sets of rotational transitions can be unambiguously assigned as conformers I, II and IV, respectively. Once the rotational transitions belonging to all the above-identified conformers were excluded from the broadband spectrum, a further new set of weak rotational transitions corresponding to conformer XIII was also successfully assigned. The rotational transitions of the five TFB dimer conformers observed were fitted with Watson's S-reduction semi-rigid rotor Hamiltonian in its I^r representation³⁷ using the Pgopher program.³⁸ The resulting experimental spectroscopic parameters are summarized in Table 2, and all the measured rotational transitions are provided in Tables S6–S10, ESI.†

Fig. 2 A section of the experimental broadband rotational spectrum recorded with 1.4 million FIDs with known transitions of the TFB monomer and its rarer isotopologues as well as the TFB⋯H₂O adduct removed. The simulated spectra were produced with the experimental rotational constants, the theoretical permanent electric dipole moment components and an estimated rotational temperature of 1 K, as well as their estimated experimental relative abundances.

Table 2 Experimental spectroscopic parameters of the five observed conformers of the TFB dimer

Parameter	I(TG−g−/TG+g+)	II(TG+g+/TG+g+)	IV(TG−g−/TG+t)	V(TG+t/TG+t)	XIII(TG−g−/TTg−)
a Errors in parentheses are expressed in units of the least significant digit. b Relative magnitudes of the three experimental dipole moment components. c σ is the standard deviation of the fit. d N is the number of rotational transitions included in the fit.
A (MHz)	564.70358(5)^a	543.64824(7)	515.73096(3)	634.88225(7)	517.9661(2)
B (MHz)	293.04485(5)	271.46605(4)	313.29220(3)	242.50349(2)	305.1570(1)
C (MHz)	266.28527(5)	227.56674(4)	250.91942(3)	192.84574(2)	229.22660(8)
D K (kHz)	0.2956(8)	0.2825(7)	0.2293(2)	0.294(2)	0.334(3)
D JK (kHz)	−0.3025(8)	−0.1962(7)	−0.2289(2)	0.0171(2)	−0.356(4)
D J (kHz)	0.1325(2)	0.0849(1)	0.1260(1)	0.05079(5)	0.1848(9)
d 1 (kHz)	0.060(5)	0.058(2)	0.1127(3)	0.0645(5)	0.018(3)
d 2 (Hz)	22.9(1)	20.87(8)	43.63(3)	11.22(2)	49.7(4)
μ a/μb/μc^b (D)	μ b ≫ μa ≈ μa	μ b > μ c ≫ μa	μ b ≫ μc > μa	μ a >μ b, no μc	μ b > μ c ≫ μa
σ (kHz)	3.2	3.8	2.8	2.3	3.7
N	373	355	510	381	145

---

Utilizing a Python routine, the best agreement between the simulated and experimental intensities was achieved at a rotational temperature of ∼1 K where the simulated Pgopher line intensities were calculated using the theoretical dipole moment components and the experimental spectroscopic constants with a rotational temperature step size of 0.1 K. Note that the intensities of all the experimental transition lines with signal-to-noise better than 5 in the 3.4–4.6 GHz range were used. The experimental relative abundances of the five observed conformers, I : II : IV : V : XIII, were estimated to be about 9 : 3 : 3 : 1 : 1 in the supersonic jet expansion. An overview of the experimental broadband rotational spectrum and the simulated spectra of the five observed TFB dimer conformers is displayed in Fig. 2.

Comparisons of the experimental rotational constants with those calculated at five different levels of theory are summarized in Table S11, ESI† and graphically presented in Fig. S1, ESI,† where the B2PLYP-D3BJ/def2-TZVP level of theory offers the best agreement with a maximum deviation of <1.6%.

Rationale for the (non)-observation of the low energy TFB dimer conformers

At first glance, the observed dimer conformers do not seem to follow their relative energy ordering. For example, conformers III and VI–XII were not detected whereas IV, V and XIII were observed. A similar observation was puzzled over in the jet-cooled rotational study of the cyclohexanol dimer.² Previously, the detection of much less stable dimers of tetrahydro-2-furoic acid were quantitatively justified using a kinetically controlled dimer formation process where the abundances of its monomer conformations played a crucial role.^19,39 One initial challenge in applying a similar kinetically controlled process to the abundances of alcohol aggregates in a jet is that some particular monomer conformations, for example t-TFE, do not exist in its isolated form.

In the case of TFB, the three experimentally observed TFB monomer conformers in a jet expansion are TG+t/TG−t, G+G+t/G−G−t, and TTt. On the other hand, three out of five observed TFB dimer conformers are exclusively made of non-observed TFB monomer subunits and only one of them is made of two observed TFB monomer subunits. Detailed examinations of the conformational abundances of several previously reported fluoroalcohol aggregates including trifluoropropanol (TFP)^40,41 and 2,2,3,3,3-pentafluoro-1-propanol⁴² suggested that the intermolecular hydrogen bonding interactions can easily modify the OH orientation (i.e. g−, g+ and t-form of OH) of the associated alcohol subunits. Therefore, a modified kinetically controlled model was proposed. Acknowledging that the g−, g+ and t forms of OH can interconvert easily in a jet expansion, we grouped the TFB monomer conformers into five families, TG (90.3%), GG (6.2%), TT (2.9%), GT (0.5%) and G+G− (0.1%), where the abundances in the brackets are calculated assuming a Boltzmann distribution using the relative monomer energies and a previously reported conformational temperature of 120 K.¹⁵ Based on the kinetically controlled dimer formation process, it became immediately obvious that only three dimer families: (TG,TG) (81.7%), (TG,GG) (11.2%), and (TG,TT) (5.2%), have abundances >1% (see Fig. S2, ESI† for details). The respective binary families for each of the 16 predicted TFB binary conformers are also listed in Table 1.

The observed I, II, IV and V are the four most stable conformers in the (TG,TG) family, while the observed XIII is the most stable conformer in the (TG,TT) family. Within each family, conformer conversions are easily possible as these are associated with different OH orientation directions. In the current modified kinetic-thermodynamic model, we assumed that the abundances of conformers within each family are largely governed by their relative energies which can be predicted based on a Boltzmann distribution at a specified conformational temperature, for example 120 K. For conciseness, we considered only the 16 conformers listed in Table 1 and predicted their abundances (Fig. S2, ESI†) based on the above described modified kinetic–thermodynamic model and the ZPE corrected relative energies listed in Table 1. It is important to recognize that the relative energy ordering shows only slight variation among the four different DFT levels of theory, whereas that predicted at the MP2 level differs a bit more.

Despite the minor uncertainties in the predicted energy ordering, it is easy to appreciate, based on the above model, why X was not observed and XIII was detected. X belongs to the family (GG,GG) which has a total shared abundance of only ∼0.4%, below the current experimental detection limit. The next obvious question is why was III not observed? III is the most stable conformer in the family (TG,GG) with a shared abundance of 11.2%. With eight (TG,GG) conformers listed in Table 1, the abundance of III was predicted to be ∼5%, similar to that of V. V, however, has an extremely large μ_a of 6.7 D, whereas the largest dipole component of III is only ∼1.2 D, about five to six times smaller. Since the observed line intensity is proportional to the square of μ_a,b,c, the strongest lines of III are expected to be about 30 times weaker than those of V, rendering it undetectable. The current modified kinetic–thermodynamic model predicts the theoretical abundances ratio of I : II : IV : V : XIII to be 10 : 3 : 2 : 1 : 1, based on ΔE₀ at the B3LYP-D3BJ/def2-TZP level, in good agreement with the experimental ratio of 9 : 3 : 3 : 1 : 1.

Non-covalent interactions

As mentioned before, four out of five of the observed TFB dimer conformers are exclusively/partially made up of non-detected TFB monomer subunits. To understand how these specific TFB subunits help in stabilizing the observed TFB dimer conformers, we conducted QTAIM, NCI and SAPT analyses to qualitatively and quantitatively appreciate the nature of the intermolecular interactions.

The NCI analyses of the five observed TFB dimer conformers are shown in Fig. 3, together with the same analyses of the most stable TFE⁸ and TFP⁴¹ dimer conformers, for comparison. As can be seen from Fig. 3, all the observed TFB dimer conformers exhibit a blue(-green) isosurface corresponding to an attractive O–H⋯O hydrogen bond whose bond length ranges from 1.870 to 1.947 Å at the B2PLYP-D3BJ/def2-TZVP level. In addition, there exist one C–H⋯F and two C–H⋯O hydrogen bonds for conformer I, and two C–H⋯F and one C–H⋯O hydrogen bonds for conformers II, IV, V and XIII. In addition, conformer I also features a weakly attractive O–H⋯F linkage as indicated by the green iso-surface. Interestingly, the NCI plots also reveal the presence of attractive C–H⋯H–C dispersion interactions between the H atoms of the methylene groups of the two subunits in all the observed TFB dimer conformers, whereas attractive C–H⋯H–C interactions are not found in the most stable conformers of the TFE and TFP homodimers. The result suggests that the longer n-alkyl carbon chain in TFB compared to TFE and TFP moves the distance of C–H⋯H–C into the van der Waals interaction region, facilitating the weak attractive interaction.

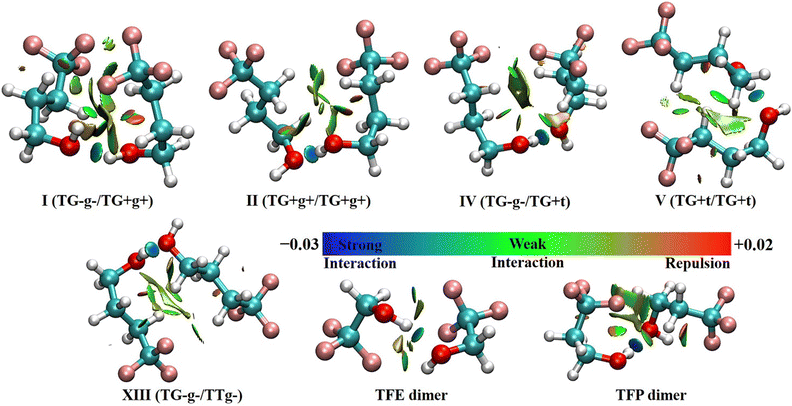Fig. 3 NCI plots (s = 0.55) of the five observed TFB dimer conformers, as well as the most stable TFE and TFP conformers based on the optimized geometries at the B2PLYP-D3BJ/def2-TZVP level. Blue regions represent strong attractive interactions, green regions represent weak attractive interactions, and red regions represent repulsive interactions. Please also refer to Fig. S3 (ESI†) for identification of specific NCI interactions in the five observed TFB dimer conformers by the QTAIM analyses.

The results from the QTAIM analyses (see Fig. S3, ESI†) reveal that there exist five, six, five, five, and six bond critical points (BCPs) in conformers I, II, IV, V, and XIII, respectively. For conformer I, a BCP associated with C–H⋯H–C was not identified. It should be noted that all the BCPs identified by the QTAIM analyses exhibit corresponding green or blue isosurfaces in the NCI plots. The energy associated with each BCP was estimated using a simplified approach,⁴³i.e., E = 0.5V(r), where V(r) indicates the electronic potential density at the corresponding BCP. In all the observed conformers, the energies of the O–H⋯O hydrogen bonds range from −26.5 to −33.6 kJ mol⁻¹, and the C–H⋯O hydrogen bonds have energies of −4.1 to −8.7 kJ mol⁻¹. The energies of the C–H⋯F hydrogen bonds vary between −2.6 kJ mol⁻¹ and −4.6 kJ mol⁻¹, and the energy of the O–H⋯F hydrogen bond in conformer I was computed to be −9.9 kJ mol⁻¹. The attractive C–H⋯H–C dispersion interactions in all the conformers II, IV, V, and XIII exhibit an energy between −1.8 and −3.3 kJ mol⁻¹, which indicates that the existence of such dispersion interactions plays a crucial role in stabilizing and establishing the relative energy ordering of the studied binary conformers.

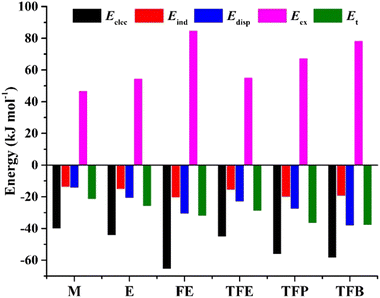
To quantitatively appreciate the physical nature of the intermolecular interactions in the five observed TFB dimer conformers, an energy decomposition analysis based on the SAPT method was conducted and the results are summarized in Table S12, ESI.† Similar SAPT analyses (Table S12, ESI†) of the most stable conformers of the dimers of water, methanol, ethanol, FE, TFE, and TFP were also performed. A comparison of the energy decomposition results of the five observed TFB conformers and the most stable binary conformers of five shorter chain alcohols is graphically displayed in Fig. S4, ESI† while a concise comparison with only the most stable conformers of the six alcohol dimers is given in Fig. 4. Among the five observed TFB dimer conformers, conformer V, which is made of two most stable monomer subunits TG+t (or TG−t), is least efficient in binding with a total interaction energy of 29.5 kJ mol⁻¹, while II, IV, and XIII have quite similar interaction energies ranging from 32.1 to 34.0 kJ mol⁻¹, and finally, I is most efficient at 38.0 kJ mol⁻¹. The relative importance of the electrostatic, induction, and dispersion contributions remains about 50%, 17% and 33%, respectively, in all these five conformers, with I leading in all these categories in terms of their absolute magnitudes. Among the three trifluoro-alcohols, the total interaction energy increases from 29.0 to 38.0 kJ mol⁻¹ as the alkyl carbon chain gets longer, and so do the electrostatic and dispersion contributions. While the electrostatic contribution maximizes at FE, the dispersion contribution peaks at TFB. Among the six related aliphatic alcohol dimers, the electrostatic and dispersion interactions are the major contributors to their stabilization. Overall, both fluorination and the alkyl chain length have important effects on the nature of NCIs and the total interaction energies.

Fig. 4 Comparison of the SAPT decompositions of the total interaction energy of the most stable conformers of the following dimers: methanol (M), ethanol (E), 2-fluoroethanol (FE), 2,2,2-trifluoroethanol (TFE), 3,3,3-trifluoro-1-propanol (TFP), and 4,4,4-trifluoro-1-butanol (TFB), at their respective B3LYP-D3BJ/def2-TZVP geometries.

Conclusions

The highly intricate conformational landscape of the TFB homodimer was investigated using CP-FTMW spectroscopy in conjunction with high-level theoretical computations. Extensive CREST conformational searches and subsequent DFT geometry optimizations revealed over 100 dimer conformers within a 10 kJ mol⁻¹ window and 16 of them within 4 kJ mol⁻¹. Rotational spectra of five TFB dimer conformers were unambiguously assigned and their respective molecular carriers were identified based on the comparison of experimental and theoretical rotational constants and dipole moment components. Of the six different levels of theory used, B2PLYP-D3BJ/def2-TZVP offers the best agreement with experimental rotational constants with a maximum deviation of less than 1.6%.

Interestingly, the experimental abundances do not follow a simple theoretical Boltzmann distribution, an issue previously reported for other alcohol dimers such as the cyclohexanol dimer.² By developing a modified kinetic-thermodynamic model, the (non-)observation of certain low energy TFB conformers was satisfactorily rationalized and the predicted conformational abundances show good agreement with the experimental ones. This analysis is important in terms of current efforts to benchmark theoretical conformational energy ordering using high quality data such as jet-cooled rotational spectra.

The QTAIM, NCI and SAPT analyses offer deep insights into the nature of the intermolecular interactions involved in stabilizing the observed TFB dimer conformers. While the electrostatic interactions provide the dominant attractive stabilization effects for the alcohol dimers discussed, the dispersion contributions noticeably increase with increasing alkyl chain length and peaks with TFB, the one with the longest chain considered here. The study demonstrates the synergistic interplay between London dispersion interactions and several different hydrogen bonds, and also the noticeable impact of dispersion interactions on the energy ordering of the TFB dimer conformers.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the University of Alberta, the Natural Sciences and Engineering Research Council (NSERC) of Canada and the National Natural Science Foundation of China (Grant No. 22263003). The authors gratefully acknowledge access to the computing facilities of the Shared Hierarchical Academic Research Computing Network (SHARCNET: https://www.sharcnet.ca), the Western Canada Research Grid (Westgrid) and Compute/Calcul Canada. TL is grateful for financial support from the China Scholarships Council (CSC) in terms of a research fellowship. FX acknowledges the support of a H. E. Gunning Research Fellowship. YX is a Tier I Canada Research Chair in Chirality and Chirality Recognition.

References

1. X.-D. An and J. Xiao, Chem. Rec., 2020, 20, 142–161.
2. M. Juanes, I. Usabiaga, I. León, L. Evangelisti, J. A. Fernández and A. Lesarri, Angew. Chem., Int. Ed., 2020, 59, 14081–14085 ( Angew. Chem. , 2020 , 132 , 14185–14189 ).
3. J. Thomas, N. A. Seifert, W. Jäger and Y. Xu, Angew. Chem., Int. Ed., 2017, 56, 6289–6293 ( Angew. Chem. , 2017 , 129 , 6386–6390 ).
4. I. Bako, T. Radnai, M. Claire and B. Funel, J. Chem. Phys., 2004, 121, 12472–12480.
5. S. Oswald, N. A. Seifert, F. Bohle, M. Gawrilow, S. Grimme, W. Jäger, Y. Xu and M. A. Suhm, Angew. Chem., Int. Ed., 2019, 58, 5080–5084 ( Angew. Chem. , 2019 , 131 , 5134–5138 ).
6. X. Liu, N. Borho and Y. Xu, Chem. – Eur. J., 2009, 15, 270–277.
7. T. Scharge, T. N. Wassermann and M. A. Suhm, Z. Phys. Chem., 2008, 222, 1407–1452.
8. J. Thomas and Y. Xu, J. Phys. Chem. Lett., 2014, 5, 1850–1855.
9. T. Scharge, C. Cezard, P. Zielke, A. Schutz, C. Emmeluth and M. A. Suhm, Phys. Chem. Chem. Phys., 2007, 9, 4472–4490.
10. J. Thomas, O. Sukhorukov, W. Jäger and Y. Xu, Angew. Chem., Int. Ed., 2014, 53, 1156–1159 ( Angew. Chem. , 2014 , 126 , 1175–1178 ).
11. R. Medel, A. Camiruaga, R. T. Saragi, P. Pinacho, C. Pérez, M. Schnell, A. Lesarri, M. A. Suhm and J. A. Fernández, Phys. Chem. Chem. Phys., 2021, 23, 23610–23624.
12. C. B. Park and R. W. Field, J. Chem. Phys., 2016, 144, 200901.
13. M. Becucci and S. Melandri, Chem. Rev., 2016, 116, 5014–5037.
14. T. Hasui, N. Ohyabu, T. Ohra, K. Fuji, T. Sugimoto, J. Fujimoto, K. Asano, M. Oosawa, S. Shiotani, N. Nishigaki and K. Kusumoto, Bioorg. Med. Chem., 2014, 22, 5428–5445.
15. T. Lu, F. Xie, N. A. Seifert, W. Jäger and Y. Xu, J. Mol. Struct., 2020, 1217, 128359.
16. C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1–15.
17. F. Xie, N. A. Seifert, M. Heger, J. Thomas, W. Jager and Y. Xu, Phys. Chem. Chem. Phys., 2019, 21, 15408–15416.
18. C. D. Carlson, N. A. Seifert, M. Heger, F. Xie, J. Thomas and Y. Xu, J. Mol. Spectrosc., 2018, 351, 62–67.
19. F. Xie, N. A. Seifert, W. Jäger and Y. Xu, Angew. Chem., Int. Ed., 2020, 59, 15703–15710 ( Angew. Chem. , 2020 , 132 , 15833–15840 ).
20. S. Grimme, J. Chem. Theory Comput., 2019, 15, 2847–2862.
21. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
22. C. Plett and S. Grimme, Angew. Chem., Int. Ed., 2023, e202214477 ( Angew. Chem. , 2023 , e202214477 ).
23. M. Melosso, S. Alessandrini, L. Spada, A. Melli, X. Wang, Y. Zheng, C. Duan, J. Li, W. Du, Q. Gou, L. Bizzocchi, L. Dore, V. Barone and C. Puzzarini, Phys. Chem. Chem. Phys., 2023, 25, 31281–31291.
24. V. W. Y. Tsoi, E. Burevschi, S. Saxena and M. E. Sanz, J. Phys. Chem. A, 2022, 126, 6185–6193.
25. A. S. Hazrah, A. Insausti, J. Ma, M. H. Al-Jabiri, W. Jäger and Y. Xu, Angew. Chem., Int. Ed., 2023, 62, e202310610 ( Angew. Chem. , 2023 , 135 , e202310610 ) DOI:10.1002/anie.202310610.
26. F. Xie, M. Fusè, A. S. Hazrah, W. Jäger, V. Barone and Y. Xu, Angew. Chem., Int. Ed., 2020, 59, 22427–22430 ( Angew. Chem. , 2020 , 132 , 22613–22616 ).
27. B. Wu, N. A. Seifert, S. Oswald, W. Jäger and Y. Xu, J. Phys. Chem. A, 2021, 125, 5355–5364.
28. H. Wang, M. Heger, M. H. Al-Jabiri and Y. Xu, Molecules, 2022, 27, 38,  DOI:10.3390/molecules27010038.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016.
30. R. F. W. Bader, Chem. Rev., 1991, 91, 893–928.
31. E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
32. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
33. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
34. T. M. Parker, L. A. Burns, R. M. Parrish, A. G. Ryno and C. D. Sherrill, J. Chem. Phys., 2014, 140, 094106.
35. R. M. Parrish, L. A. Burns, D. G. A. Smith, A. C. Simmonett, A. E. DePrince III, E. G. Hohenstein, U. Bozkaya, A. Yu. Sokolov, R. Di Remigio, R. M. Richard, J. F. Gonthier, A. M. James, H. R. McAlexander, A. Kumar, M. Saitow, X. Wang, B. P. Pritchard, P. Verma, H. F. Schaefer III, K. Patkowski, R. A. King, E. F. Valeev, F. A. Evangelista, J. M. Turney, T. D. Crawford and C. D. Sherrill, J. Chem. Theory Comput., 2017, 13, 3185–3197.
36. T. Lu, F. Xie, N. A. Seifert, W. Jäger and Y. Xu (under preparation).
37. J. K. G. Watson, in Vibrational Spectra and Structure, ed. J. R. Durig, Elsevier, Amsterdam, 1977, vol. 6, pp. 1–89.
38. C. M. Western, J. Quant. Spectrosc. Radiat. Transfer, 2017, 186, 221–242.
39. F. Xie, X. Ng, N. A. Seifert, J. Thomas, W. Jäger and Y. Xu, J. Chem. Phys., 2018, 149, 224306.
40. A. N. Mort and Y. Xu, J. Mol. Spectrosc., 2023, 392, 111745.
41. A. N. Mort, F. Xie, A. S. Hazrah and Y. Xu, Phys. Chem. Chem. Phys., 2023, 25, 16264–16272.
42. B. Wu, N. A. Seifert, A. Insausti, J. Ma, S. Oswald, W. Jäger and Y. Xu, Phys. Chem. Chem. Phys., 2022, 24, 14975–14984.
43. I. Mata, I. Alkorta, E. Espinosa and E. Molins, Chem. Phys. Lett., 2011, 507, 185–189.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00401a

‡ Present address: Deutsches Elektronen-Synchrotron (DESY), Notkestraße 85, 22607 Hamburg, Germany.

---