Electrocatalytic OER behavior of the Bi–Fe–O system: an understanding from the perspective of the presence of oxygen vacancies

Abstract

This study aims to understand and correlate the role of the nature and relative concentration of oxygen vacancies with the trend observed in the OER with the Bi–Fe–O system. To understand this, we first investigated the system of oxides using X-ray photoelectron spectroscopy (XPS) and electron paramagnetic resonance (EPR), which revealed the presence of oxygen vacancies in the system. Density functional theory (DFT) was employed to investigate the relative concentration of these vacancies by calculating their formation energies. Positron annihilation lifetime spectroscopy (PALS) was carried out to understand the nature of these oxygen vacancies. We observed that the presence of a higher concentration of monovacancies created due to the absence of oxygen from the structure of Bi₂Fe₄O₉ was mainly responsible for the high performance of the oxide towards the OER compared to that of the other oxides viz—BiFeO₃ and Bi₂₅FeO₄₀ of the Bi–Fe–O system.

---

Introduction

Transition metals and rare earth metal oxides are in high demand for electrocatalytic and photocatalytic studies due to variable oxidation states of the metal center, vacancies, and surface defects. Defects in crystal structures are irregularities or imperfections in the orderly arrangement of atoms, ions, or molecules within a crystalline material. These defects can occur naturally during crystal growth or be intentionally introduced for various purposes in materials engineering. Crystal defects can significantly influence the physical, chemical, and mechanical properties of materials. A good knowledge of the defect types, sites, concentrations, and availability can be useful for understanding their role in the area of catalysis, biomedicine, designing semiconductors, perovskite solar cells, or multiferroics. The presence of defects in the structure mostly helps in enhancing the practical aspects of a material. For instance, defect sites like line defects, atomic-sized defects, or vacancies in graphene, an inert and ultrastrong material, can trigger different properties in the material, enabling a range of applications.¹ The introduction of appropriate dopants has led to the creation of defect clusters in di- and trivalently doped ceria, which influenced the ionic conductivities, enabling their use as ionic conductors in electrochemical devices.² Moreover, with the advent of defect engineering, defects were tailored in ceramics like A-site vacancies in bismuth sodium titanate–perovskite ceramics for advanced pulsed power system (APPS) applications,³ in lead-based ceramics to achieve high piezoelectric behaviors,⁴ and in 2D materials⁵ for energy storage devices, optoelectronics, electrocatalysis, and other applications. These examples showcase the need for extensive study of the type, location, surrounding environment, and concentration of defects. Defects can influence the geometric, electronic, and chemical properties, charge distribution, and band structure of the system. Hence, fine tuning of the crystal structures and defects can effectively improve the catalytic performance of the materials.^6,7

Among the various kinds of defects present in metal oxides, oxygen vacancies are known to influence the catalytic (both photocatalytic and electrocatalytic) performance of a catalyst. For instance, Sun's group⁸ reported the comparative study of oxygen vacancy-rich and perfect Co₃O₄ towards OER performance, which revealed higher performance for oxygen vacancy-rich Co₃O₄. The oxygen vacancies in the system were confirmed by XPS, XANES, and EXAFS studies. Another defect present in metal oxides is cation vacancies, which can also influence the catalytic performance. For example, Zhang and co-workers⁹ reported a facile wet synthesis of ferroxyhyte (δ-FeOOH) nanosheets rich in iron vacancies on Ni foam. They showed that the nanosheets required a lower overpotential to reach a current density of 10 mA cm⁻² than that of bulk δ –FeOOH towards HER electrocatalysis. The introduction of multi-vacancy defects had also proved helpful in increasing the efficiency of the catalyst, as reported by Peng et al.¹⁰ They synthesized CoFe layered double hydroxides with multiple vacancies (Co, Fe, and O) to increase the efficiency towards OER performance, as revealed from the current density and Nyquist plots. EXAFS and XPS showcased the presence of multiple vacancies in the system. Therefore, from the above examples, we can comprehend that vacancies and defects influence the energy state of the system, which facilitates electron transfer during the catalytic processes. So, proper recognition of this aspect of the material is required.

In our previous study,¹¹ we explored the effect of the crystal structure in the Bi–Fe–O system on OER performance. The system contained the same elements but differed in composition and crystal structure. Three different phases of the Bi–Fe–O system were considered for the study: BiFeO₃ has a perovskite structure with a R3c space group, Bi₂Fe₄O₉ has a mullite structure crystallizing in a Pbam space group, and Bi₂₅FeO₄₀ crystallizes in the I23 space group and has a sillenite structure. In this study, we focused on analyzing the observed trend in the OER performance of the Bi–Fe–O system from the perspective of the presence of defects. As discussed above, the presence of defects, especially oxygen vacancies, has an influencing role in the electrocatalytic performance of the oxide. Thus, we have investigated the nature and relative amount of oxygen vacancies using XPS, EPR, and PALS studies on BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀. To the best of our knowledge, a comparative study on understanding the OER performances of the oxides from the perspective of the presence of oxygen vacancies in the Bi–Fe–O system has not been carried out so far. We believe that this study is of significance to the scientific community and will provide an insight into how the variation in the nature and relative concentration of oxygen vacancies with the crystal structure among different sets of oxides in a ternary system affects the OER performance of the oxides.

Experimental

Materials required

Bismuth nitrate pentahydrate (Bi(NO₃)₃·5H₂O (99%)), iron nitrate nonahydrate (Fe(NO₃)₃·9H₂O (99%)), and Nafion resin solution were purchased from Sigma Aldrich. Sodium hydroxide pellets (NaOH), potassium hydroxide pellets (KOH), and nitric acid were purchased from Merck.

Synthesis

The synthesis of Bi–Fe–O-based oxides was carried out based on our previous study.¹¹ Briefly, bismuth nitrate was dissolved in a mixture of 1 mL of concentrated nitric acid and 6.5 mL of water. To this mixture, iron nitrate was added. The synthesis of BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀ was performed by varying the Bi to Fe ratio and using a combination of NaOH and KOH.

To obtain BiFeO₃, a Bi to Fe ratio of 1 : 1 was used, while for Bi₂Fe₄O₉ and Bi₂₅FeO₄₀, the ratios were 1 : 2 and 25 : 1, respectively. To the solution containing Bi³⁺ and Fe³⁺, 2 M KOH solution (for BiFeO₃ and Bi₂Fe₄O₉) or 2 M NaOH solution (for Bi₂₅FeO₄₀) was added to maintain a pH of 13 under constant stirring. The resulting precipitates were washed with DI (deionized) water to eliminate the ions. The precipitates of BiFeO₃ were mixed with 12 M KOH (40 mL), while those of Bi₂Fe₄O₉ and Bi₂₅FeO₄₀ were mixed with 14 M NaOH (40 mL) under continuous stirring. The resultant suspension was then transferred to a Teflon-lined hydrothermal vessel and heated at 180 °C for 12 hours. The resulting products were centrifuged, washed with DI water and ethanol, and dried at 70 °C.

The obtained products for BiFeO₃ and Bi₂Fe₄O₉ were washed and dried at room temperature, while for Bi₂₅FeO₄₀, the product was calcined at 700 °C for 12 hours to obtain pure Bi₂₅FeO₄₀.

Characterization

Powder X-ray diffraction (PXRD) was carried out using a Bruker D8 Advance Eco diffractometer with a Cu–Kα X-ray source. The instrument was operated at 25 mA and 40 kV. The scan speed was 3 s per step with a step size of 0.0183°. A JEOL JSM-1T300 scanning electron microscope (SEM) was used to investigate the morphology of the samples. All electrochemical assessments were conducted using a Metrohm Multi Autolab three-electrode electrochemical workstation. The details of the experimental technique and conditions are reported in our previous study.¹¹ The values of various parameters, i.e., average current density, overpotential, and charge transfer resistance, have been used from our previous study.¹¹ X-ray photoelectron spectroscopy was performed on a PHI 5000 Versa Prob II, FEI Inc with the following settings: a pass setting of 23.5 eV, 0.025 eV/0.05 eV step, 50 ms time per step and 10 cycles, source Al k-alpha-1486 eV, dual-beam Neut. Deconvolution of the XPS peak was carried out using XPSpeak 41. Electron paramagnetic resonance spectroscopy (EPR) was carried out on a Bruker spectrometer (EMX Series) operated in X band frequency (9.45 GHz) with field modulation at 100 KHz and an amplitude of 1 Gauss. The resonance signals were calibrated using DPPH (2,2-diphenylpicrylhydrazyl) as the standard. Positron annihilation lifetime spectra were acquired on the powder sample. The sample covered the Na-22 radioactive source. The positron lifetime spectrometer was constructed from two identical BaF₂ scintillation detectors with fast-timing electronics. The time resolution of the spectrometer was 250 ps. One million counts were acquired for each spectrum, and the spectrum was analyzed using PALSFit software¹² to extract positron lifetimes.

Computational methods

Density functional theory calculations

The initial coordinates for the three systems were taken from ref. 11. A 2 × 2 × 1 supercell was used for BiFeO₃, with the Fe³⁺ ions in the most stable G-type antiferromagnetism.¹³ A 2 × 1 × 2 supercell was used for Bi₂Fe₄O₉, with the Fe³⁺ ions antiferromagnetically aligned along the b axis (this configuration was lower in energy than a ferromagnetic configuration). Finally, a 1 × 1 × 1 supercell was used for Bi₂₅FeO₄₀, which we built from an ideal sillenite structure by placing one Bi and one Fe atom at the two tetrahedral sites. All density functional theory calculations were performed with the QUICKSTEP program of CP2K¹⁴ using the GTH pseudopotentials proposed by Goedecker, Teter, and Hutter.¹⁵ Calculations were performed at the Γ-point with a plane wave cut-off of 800 Ry, which ensured a convergence of 0.01 eV per formula unit in all supercells. The structures were first optimized at the PBE level¹⁶ with the DZVP-MOLOPT basis set.¹⁷ We adopted a limited memory algorithm (LBFGS)¹⁸ with a force convergence criterion of 0.01 eV Å⁻¹. Single point energies were then taken at the PBE0 level,¹⁹ and the cFIT3 basis set for the auxiliary density matrix method.²⁰

Formation energy and concentration of oxygen vacancies

The formalism adopted for the thermodynamics of the oxygen vacancies follows that of ref. 21. The formation energies E_f of the oxygen vacancies were calculated using the following formula:

E_f = E(def) – E(clean) + μ_O (1)

where E(def) and E(clean) are the energy of the supercell with and without the vacancies, respectively, and μ_O is the oxygen chemical potential. We have used the Arrhenius formula to calculate the concentration c of oxygen vacancies with temperature:

c = c₀ exp(−E_f/k_BT) (2)

where c₀ is the number of available vacancy sites per unit volume, k_B is the Boltzmann constant, and T is the temperature.

The chemical potential of a species α can be written as μ_α = μ_α^el + Δμ_α, where μ_α^el is the chemical potential of the elemental species (with O₂ in a triplet state as a reference for oxygen), which can be calculated using density functional theory (DFT), and Δμ_α is subject to constraints imposed by the competing phases. Since μ_α must be lower than μ_α^el to avoid the formation of the elemental species, the following three conditions must hold Δμ_Bi < 0, Δμ_Fe < 0, Δμ_O < 0. All chemical potentials are related to those of the bulk phase considered, i.e., for BiFeO₃, μ_Bi + μ_Fe + 3μ_O = μ_BiFeO3 or Δμ_Bi + Δμ_Fe + 3Δμ_O = ΔH(BiFeO₃), where ΔH(BiFeO₃) is the formation enthalpy of BiFeO₃. In addition, for the formation of BiFeO₃, the chemical potentials must ensure that no other bismuth ferrite or oxide phase is formed, i.e. 2Δμ_Bi + 4Δμ_Fe + 9Δμ_O < ΔH(Bi₂Fe₄O₉), 25Δμ_Bi + Δμ_Fe + 40Δμ_O < ΔH(Bi₂₅FeO₄₀), 2Δμ_Bi + 3Δμ_O < ΔH(Bi₂O₃), and 2Δμ_Fe + 3Δμ_O < ΔH(Fe₂O₃). We have used the equations above, together with the formation enthalpies of the solids,^22,23 to plot in Fig. S1 (ESI†) the stability diagram of the three phases, from which we have obtained the allowed ranges for Δμ_O listed in Table S1 (ESI†).

Results and discussion

PXRD studies on Bi–Fe–O samples are shown in Fig. 1. No impurity phase was observed in BiFeO₃. All the peaks could be indexed to rhombohedral BiFeO₃ having a space group R3c. 1.5% of BiFeO₃ was present as an impurity phase in Bi₂Fe₄O₉. All other peaks could be indexed to the orthorhombic crystal structure with a space group Pbam. An impurity phase of Bi₂O₃ (2.6%) was observed with Bi₂₅FeO₄₀. Other peaks were indexed to the cubic crystal structure (I23).

Fig. 1 PXRD patterns of (a) BiFeO₃, (b) Bi₂Fe₄O₉ and (c) Bi₂₅FeO₄₀. * and # represents BiFeO₃ and Bi₂O₃, respectively.

The SEM images of BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀, respectively, are shown in Fig. 2a–c. For BiFeO₃, we observed flower-like clusters formed from the assembly of cuboids (∼5–10 μm) (Fig. 2a). For Bi₂Fe₄O₉ and Bi₂₅FeO₄₀, we observed square-shaped plates with a size of 2 μm (Fig. 2b) and cubes of ∼800 nm (Fig. 2c), respectively.

Fig. 2 SEM images of (a) BiFeO₃, (b) Bi₂Fe₄O₉, and (c) Bi₂₅FeO₄₀.

From our previous study,¹¹ it was observed that the electrochemical water oxidation activity, i.e., the performance of the Bi–Fe–O system towards the OER was highest for Bi₂Fe₄O₉ followed by BiFeO₃ and Bi₂₅FeO₄₀. This was indicated from the observed average current densities, which was found to follow the following trend:¹¹ Bi₂Fe₄O₉ > BiFeO₃ > Bi₂₅FeO₄₀ while the overpotential (calculated at a current density of 1 mA cm⁻²; details of calculations are given in the ESI†) and charge transfer resistance were shown to follow the opposite trend: Bi₂₅FeO₄₀ > BiFeO₃ > Bi₂Fe₄O₉ (Fig. 3). The high performance of Bi₂Fe₄O₉ towards the OER was then attributed to the plate-like morphology and the presence of Fe_(oct)–O–Fe_(td) linkages, probably resulting in covalency completion and creation of either Fe_(oct)–O and Fe_(td)– or Fe_(td)–O and Fe_(oct)-units facilitating adsorption of OH⁻ ions.

Fig. 3 Plot showing the observed average current densities, overpotential, and charge transfer resistance of BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀. The values of the average current densities, overpotential, and charge transfer resistance were used from ref. 11.

The water splitting reaction is dependent on the concentration of oxygen vacancies. The presence of oxygen vacancies can dictate the thermodynamic behavior of the material. The presence of these vacancies also leads to changes in the electronic behavior of the material. Both the electronic behavior and thermodynamic changes in the material affect the rate and efficiency of the catalysts for the water splitting reaction. Many reports in the literature support this fact. In one of our studies,²⁴ we have also shown that oxygen vacancies present in oriented assemblies of SrTiO₃ had a significant role in the HER. The presence of defect structures is a result of various factors. The key role in the formation of oxygen vacancies is based on the strength of the O–M bond, which in turn depends on the crystal structure of the material. Thus, to achieve a correlation between the structure and the properties, it is important to analyze the nature and relative concentration of the defects. To understand if defects have any major role in the OER behavior of Bi–Fe–O-based oxides, we carried out XPS, EPR, and PALS studies. Theoretical studies were carried out to understand the reason for different concentrations of defects, if any, in the three kinds of oxides.

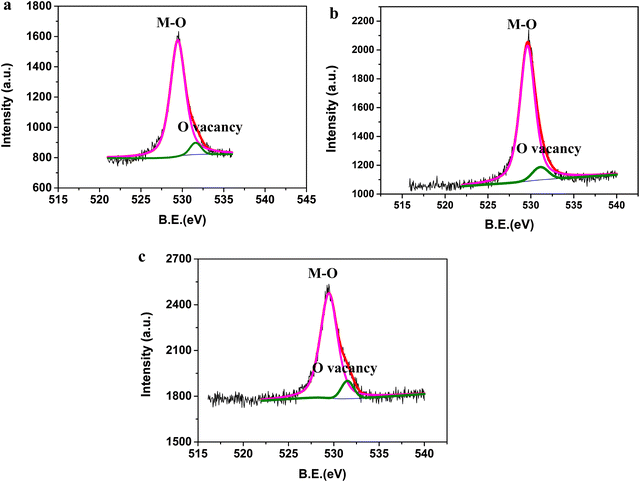
The presence of oxygen vacancies in the three oxides was first analyzed using XPS studies (Fig. 4a–c). The peak corresponding to the metal–oxygen bond was observed in the high-resolution spectra of O 1s at 529.45, 529.6, and 529.45 eV for BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀, respectively. In addition to the metal–oxygen bond, peaks at 531.6, 531.1, and 531.5 eV were observed in the high-resolution spectra of O 1s for BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀. The peak centered at ∼531 eV corresponds to the presence of defects that are created due to oxygen vacancies in the oxide.^24–28 Thus, analysis of the oxides using XPS confirmed the presence of defects arising due to oxygen vacancies. This observation led us to analyze further the oxides for the nature of the vacancies and their concentration.

Fig. 4 High resolution O 1s spectra of (a) BiFeO₃, (b) Bi₂Fe₄O₉, and (c) Bi₂₅FeO₄₀.

In this regard, the first study we carried out was electron paramagnetic resonance (EPR), which is used for studying paramagnetic species, i.e., atoms, molecules, or ions that possess one or more unpaired electrons. Most defect sites show paramagnetic characteristics and thus can be identified by EPR spectra. Oxygen vacancies leave behind unpaired electrons that exhibit paramagnetic behavior. Typically, a peak at 2.001∼2.004 is attributed to natural surface oxygen vacancies, as reported in the literature.²⁹ For the Bi–Fe–O system, EPR spectra (Fig. 5) were recorded for the three systems, BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀. In BiFeO₃, bismuth and iron both exist in the +3 oxidation state, with the possible presence of oxygen vacancies. For BiFeO₃, the g value was slightly higher than 2 (2.049), which may be due to the existence of the (Fe³⁺–OV) defect complex (OV, oxygen vacancy). In Bi₂Fe₄O₉ and Bi₂₅FeO₄₀, the g value was observed at 2.029 and 2.061, respectively, also attributed to the oxygen vacancies. A peak at g = 1.69 is also observed in Bi₂₅FeO₄₀, possibly due to small iron oxide clusters, which were untraceable in XRD. The intensity of the EPR signal could be proportional to the concentration of oxygen vacancies in the material. Thus, the increased intensity in Bi₂Fe₄O₉ followed by that in BiFeO₃ and Bi₂₅FeO₄₀ can be interpreted by the presence of a higher concentration of oxygen vacancies in Bi₂Fe₄O₉ and least in Bi₂₅FeO₄₀ (Fig. 5). This can possibly be from the fact that oxygen vacancies are likely to be formed at the surface with much ease in Bi₂Fe₄O₉ due to its inherent crystal structure and bonding of the constituent atoms, i.e., the presence of Fe_(Oct)–O–Fe_(Td) linkages in Bi₂Fe₄O₉. The trend in the intensity of the EPR signal, an indicator of the concentration of the oxygen vacancies present in the oxide, and the trend observed for the performance of the oxide as an electrocatalyst towards the OER correlate with each other. This suggests that the crystal structure and stoichiometry of the elements in the Bi–Fe–O system plays a significant role in the formation of oxygen vacancies, which govern the performance of the oxides towards the OER.

Fig. 5 EPR plot of BiFeO₃, Bi₂Fe₄O₉ and Bi₂₅FeO₄₀.

To further understand the influence of the crystal structure on the formation of oxygen vacancies, theoretical studies using DFT calculations were performed. Table 1 reports the vacancy formation energies at the inequivalent sites of the three phases depicted in Fig. 6, both under O-poor and O-rich conditions, i.e., at the two experimental μ_O boundaries. The values of BiFeO₃ are in line with those of previous investigations,^30–35 confirming the validity of our computational setup. Formation energies of Bi₂Fe₄O₉ vary across the oxygen sites. The energy required to form a vacancy is lowest at O4, requiring 0.92 and 3.77 eV under O-poor and O-rich conditions, respectively. We find that vacancies at O1 and O3 sites of Bi₂₅FeO₄₀ migrate towards O5, exhibiting negative formation energies, namely −0.89 and −0.45 eV under O-poor and O-rich conditions, respectively. The stoichiometry of the sillenite bismuth ferrite has been a matter of controversy. Some studies have reported the presence of one tetrahedral Bi⁵⁺ ion in the unit cell (in addition to 24 Bi³⁺ ions and one tetrahedral Fe³⁺ ion), resulting in a Bi₂₅FeO₄₀ formula.^36,37 Other studies have instead suggested the presence of a tetrahedral Bi³⁺ ion with an oxygen vacancy at one of its vertices, i.e. a Bi₂₅FeO₃₉ composition.^38,39 While our Bi₂₅FeO₄₀ model with cations not randomly distributed at the tetrahedral sites suggests a cautious interpretation of the results, the negative formation energy at O5 lends strong support to a Bi₂₅FeO₃₉ formula with an oxygen vacancy in each tetrahedron. Unfortunately, however, a reliable model of Bi₂₅FeO₃₉ would require randomising also the oxygen vacancies, in addition to the tetrahedral Bi³⁺ and Fe³⁺ ions, in a prohibitively large supercell.⁴⁰ For this reason, we have not pursued the computational investigation of Bi₂₅FeO₃₉ further.

Table 1 Formation energies to form oxygen vacancies of the three bismuth ferrite phases under O-poor and O-rich conditions. Labels correspond to those of Fig. 6

Sample	Site	Formation energy (eV)
		O-poor	O-rich
BiFeO3	O1	1.94	3.96
Bi2Fe4O9	O1	1.51	4.36
	O2	1.38	4.23
	O3	1.71	4.56
	O4	0.92	3.77
Bi25FeO40	O1	Unstable	Unstable
	O2	0.82	1.26
	O3	Unstable	Unstable
	O4	0.49	0.93
	O5	−0.89	−0.45
	O6	0.48	0.92

---

Fig. 6 The three bismuth ferrite phases investigated were (a) BiFeO₃, (b) Bi₂Fe₄O₉, and (c) Bi₂₅FeO₄₀. Inequivalent oxygen sites are labelled.

To better interpret the difference in vacancy formation energies between BiFeO₃ and Bi₂Fe₄O₉, the concentration of oxygen vacancies under the two extreme oxygen conditions is shown in Fig. 7. Our results show that the amount of oxygen vacancies present in Bi₂Fe₄O₉ is much larger than that in BiFeO₃, with a difference that can be up to a few orders of magnitude under O-poor conditions. Thus, the formation of a large number of oxygen vacancies owing to lower formation energy for Bi₂Fe₄O₉ explains the trend observed for the intensity of the EPR signal arising due to the presence of oxygen vacancies, as discussed in the previous section.

Fig. 7 Concentration of oxygen vacancies in BiFeO₃ and Bi₂Fe₄O₉ as a function of temperature under both O-poor (solid lines) and O-rich (dashed lines) conditions.

To further understand the type of oxygen vacancies present in the three kinds of oxides in the Bi–Fe–O system, PALS studies were carried out. Positrons on striking the sample can get trapped in it. It may then be localized at neutral and negative vacancies due to the missing positive ion core. These results showing observable changes in the positron lifetime can be used to probe defects/voids/free volume at the sub-nm scale in a material. The annihilation data are used to obtain the concentration of the vacancies. They can also be used to obtain information about the type of vacancies and their chemical environment. The positron lifetimes are fitted using the following equation (eqn (3)):

where λ_i is the annihilation rate, which can be correlated to the lifetime using eqn (4).

λ_i = τ⁻¹_i (4)

where I_i is the intensity of the i^th component, and n is the number of different states from which the positrons are annihilated. The lifetime (dwelling time) of the injected positrons against the sample void size after fitting the data is obtained. Binding of the positron with the electron having opposite spin results in the formation of para-positronium (p-Ps) while an ortho-positronium (o-Ps) is formed when the electron has the same spin as the positron. The annihilation lifetime of p-Ps is 0.125 ns in a vacuum, while that of o-Ps is 140 ns in a vacuum. o-Ps in matter (ex vacuo) annihilate faster due to the pick-off process, resulting from the annihilation of o-Ps with an electron in surrounding media, rather than its partner electron, emitting two photons with a characteristic lifetime greater than 1 ns. The positron lifetime spectra of the samples are shown in Fig. 8. The spectra could be fitted as the sum of the three exponentials (n = 3) convoluted with the time resolution of the spectrometer after correcting for positron annihilations in the source. The longest-lived component, 1.5 ns, is less than 0.5% and is expected to be due to positronium formation on the surface of the particles in the powder samples. This is not discussed further. The other two positron lifetimes and their relative intensities are given in Table 2, along with the weighted average lifetime of the two components. It is to be noted that, in general, the first positron lifetime (τ₁) is from delocalized bulk, and the second lifetime (τ₂) originates due to the positron trapped in the defects. However, in our case, the first positron lifetime was observed to be more than 200 ps, suggesting that the signal may not be from pure delocalized bulk but also has a contribution from the defect states, such as oxygen vacancies, which are poor positron traps. From Table 2, we observe that the lifetime τ₁ follows the trend Bi₂Fe₄O₉ > Bi₂₅FeO₄₀ > BiFeO₃. In PALS, the characteristic lifetime increases with the size of the open volume created due to the presence of defects.⁴¹ Based on this, it is presumed that the open volume created by the formation of monovacancies as a result of the loss of the oxygen atom is largest in Bi₂Fe₄O₉ and least in BiFeO₃. The increased lifetime, τ₁, i.e., the large presence of the open volume of the defects, could be attributed to the mullite structure of Bi₂Fe₄O₉. It has also been reported that in mullite, when oxygen atoms that bridge the tetrahedra are removed, oxygen vacancies are formed. These oxygen vacancies are then coordinated with the neighbouring cations in a 3-fold symmetry, forming tetrahedral tri-clusters.⁴² The second positron lifetime, τ₂, was observed to be above 300 ps in the Bi–Fe–O system. The second positron lifetime depends on the open volume. The lifetime of more than 300 ps suggests that the signal is not observed from isolated vacancies, but there exist vacancy clusters in the material. This component contributes to surface defects. Such a value of τ₂ was also observed in BiFeO₃ by Dai et al.⁴³ and Mukherjee et al.,⁴⁴ which was attributed to defect clusters by the authors. Other significant information obtained from PALS studies is the relative intensity, which provides information on the distribution of the defects. The intensity gives us an idea about the concentration of defects present in the material. The relative intensity of the first-lifetime component (I₁) is higher than the second (I₂) in BiFeO₃ and Bi₂Fe₄O₉, which suggests that monovacancies are in higher concentration here. Comparing the intensity of the first-lifetime component of BiFeO₃ with Bi₂Fe₄O₉, it was observed that I₁ is higher in Bi₂Fe₄O₉ than that in BiFeO₃, suggesting the presence of a higher concentration of oxygen vacancies in Bi₂Fe₄O₉. It is likely that the presence of Fe_(Oct)–O–Fe_(Td) linkages in Bi₂Fe₄O₉ has a significant role in the formation of higher concentrations of oxygen vacancies. For Bi₂₅FeO₄₀, the relative intensity pattern shows the opposite trend, suggesting that the intensity of the defect cluster is higher here. We identify these clusters with the short-range ordered chains of oxygen vacancies of sillenite-type bismuth ferrite crystals modeled by Scurti et al. in their diffraction experiments.⁴⁰ Formation of Bi₂₅FeO₄₀ at high temperature (700 °C) could have possibly contributed to the formation of these clusters.

Fig. 8 Positron annihilation lifetime spectra for the Bi–Fe–O system.

Table 2 Positron annihilation lifetime data of BiFeO₃, Bi₂Fe₄O₉ and Bi₂₅FeO₄₀

Sample	τ 1 (ps)	I 1 (%)	τ 2 (ps)	I 2 (%)	τ ave (ps)
BiFeO3	212 ± 5	74 ± 1	323 ± 16	26 ± 1	241 ± 7
Bi2Fe4O9	258 ± 2	89 ± 2	470 ± 20	11 ± 2	282 ± 10
Bi25FeO40	223 ± 4	19 ± 1	390 ± 2	81 ± 1	358 ± 4

---

Correlating the information from PALS studies and the trend observed during the OER with the Bi–Fe–O system as an electrocatalyst, it can be concluded that the presence of monovacancies enhances the catalytic behavior of the oxides. The electrocatalytic activity of a material is affected by the presence of active sites and their accessibility. It has been known⁴⁵ that when vacancies are present in the system, they introduce local modifications in the binding energies of the atoms, thus affecting the activity. For the oxygen evolution reaction in an alkaline medium, the mechanism of the OER is very well established in the literature,⁴⁶ wherein the adsorption of OH⁻ on the surface of the material occurs to form M–OOH intermediates, which further evolves O₂. The adsorption of OH⁻ is increased when vacancy sites are present, which leads to higher activity in the OER. In this study, the concentration of the monovacancies, as observed from the I₁ of the PALS study, was found to follow the trend: Bi₂Fe₄O₉ > BiFeO₃ > Bi₂₅FeO₄₀, which correlated with the trend of the three oxides observed towards the electrochemical OER. We presume that the increased concentration of the monovacancies with the order Bi₂Fe₄O₉ > BiFeO₃ > Bi₂₅FeO₄₀ is likely to affect the cumulative adsorption of OH⁻ ions, which affected the OER activity. However, the atomic-level mechanism behind the increased performance remains unknown. Future computational investigations comparing the OER energy diagrams of Bi₂Fe₄O₉ and other oxides with and without monovacancies can provide important insights. Monovacancies and defect clusters present in a system are influenced by the crystal structure of the system. The oxygen vacancies created in a structure are dependent on the surrounding atoms, bond strengths, and stability of the system.

Monovacancies formed in the system are easily accessible sites as they are generally surface defects, whereas the defect clusters formed are deeply trapped.^47,48 For this reason, there is the possibility that the efficiency of these clusters towards participating in the OER is lower than that of the systems with monovacancies. A schematic representation of the OER in the presence of monovacancies and defect clusters is showcased in Fig. 9 for better clarity. The open-circuit voltage (OCV) measured for our system is BiFeO₃: 1.207 V, Bi₂Fe₄O₉: 1.208 V and Bi₂₅FeO₄₀: 1.349 V. The stability studies of BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀ were carried out at 1.7 V vs. RHE for BiFeO₃ and Bi₂₅FeO₄₀, while at 1.8 V vs. RHE for Bi₂Fe₄O₉. Under alkaline conditions, the catalysts were found to be stable for 10 hours under continuous measurements (Fig. S2a–c, ESI†). Thus, overall, it was reflected from the study that the nature and relative concentration of oxygen vacancies were greatly influenced by the crystal structure and the stoichiometry of the elements in the Bi–Fe–O system, which influenced the OER carried out with these systems. PALS studies reflected that monovacancies within the system have a greater influence on the OER than the defect clusters.

Fig. 9 Schematic diagram showcasing the OER in the presence of (a) only monovacancies (using Bi₂Fe₄O₉ as the represented structure; color representation: red: Fe; green: Bi; blue: O; yellow: H; white: O vacancies) and (b) defect clusters (one defect cluster encircled) along with monovacancies (using Bi₂₅FeO₄₀ as the represented structure consisting of 1 unit cell along ‘a’, 3 unit cell along ‘b’, 2 unit cell along ‘c’; color representation: green: Bi, corner and body center of each unit cell has a partial occupancy of Fe along with Bi, blue: O, yellow: H, and white: O vacancies).

Conclusions

The electrocatalytic behavior of three distinct Bi–Fe–O systems—namely, BiFeO₃, Bi₂Fe₄O₉, and Bi₂₅FeO₄₀—exhibited notable variations attributed to different crystal structures within each system. Thus, defect studies via XPS, EPR, and PALS were carried out to understand the underlying mechanism of their behaviors for the electrochemical OER based on the crystal structures. The XPS and EPR studies confirmed the presence of oxygen vacancies in all three systems, from the characteristic peak at ∼531 eV in XPS and the g value for oxygen vacancies of around 2.029 in EPR. The intensities in EPR indicated a concentration of oxygen vacancies, which was the highest for Bi₂Fe₄O₉, followed by BiFeO₃ and Bi₂₅FeO₄₀, which correlated well with the observed trend of the OER with these oxides. Theoretical studies also supported the conclusion from the XPS and EPR by showcasing the low energy of formation energy and high concentration of oxygen vacancies in Bi₂Fe₄O₉. Furthermore, PALS studies indicated the presence of the majority of oxygen monovacancies in BiFeO₃ and Bi₂Fe₄O₉ and defect clusters in Bi₂₅FeO₄₀. The study carried out showcased that the nature and relative concentration of oxygen vacancies were greatly influenced by the crystal structure and the stoichiometry of the elements in the Bi–Fe–O system. This had a major influence on the OER carried out with these systems. Thus, the study carried out was an effort to understand the electrochemical behaviour of the three oxides in the Bi–Fe–O system from the perspective of the presence of oxygen vacancies. However, more advanced in situ experimental techniques in conjunction with EPR, XPS, etc., could help in understanding the effect of vacancies on electrochemical behaviour under real conditions of electrocatalysis.

Conflicts of interest

There are no conflicts of interest.

Acknowledgements

SJ and AV thank INST for the fellowship. SV thanks CSIR (01(2943)/18-EMR-II), Govt. of India, for funding. Via UT's membership of the UK's HEC Materials Chemistry Consortium funded by EPSRC (EP/R029431, EP/X035859/1), this work used the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk).

References

1. A. Eckmann, A. Felten, A. Mishchenko, L. Britnell, R. Krupke, K. S. Novoselov and C. Casiraghi, Nano Lett., 2012, 12, 3925.
2. L. Vicarelli, S. J. Heerema, C. Dekker and H. W. Zandbergen, ACS Nano, 2015, 9, 3428.
3. F. Yan, K. Huang, T. Jiang, X. Zhou, Y. Shi, G. Ge, B. Shen and J. Zhai, Energy Storage Mater., 2020, 30, 392.
4. Y. Yan, Z. Li, L. Jin, H. Du, M. Zhang, D. Zhang and Y. Hao, ACS Appl. Mater. Interfaces, 2021, 13, 38517.
5. H. Liu, W. Lei, Z. Tong, X. Li, Z. Wu, Q. Jia, S. Zhang and H. Zhang, Adv. Mater. Interfaces, 2020, 7, 2000494.
6. M. V. Ganduglia-Pirovano, A. Hofmann and J. Sauer, Surf. Sci. Rep., 2007, 62, 219.
7. C.-Z. Yuan, S. Huang, H. Zhao, J. Li, L. Zhang, Y. Weng, T.-Y. Cheang, H. Yin, X. Zhang and S. Ye, Energy Adv., 2023, 2, 73.
8. Z. Cai, Y. Bi, E. Hu, W. Liu, N. Dwarica, Y. Tian, X. Li, Y. Kuang, Y. Li, X.-Q. Yang, H. Wang and X. Sun, Adv. Energy Mater., 2018, 8, 1701694.
9. B. Liu, Y. Wang, H.-Q. Peng, R. Yang, Z. Jiang, X. Zhou, C.-S. Lee, H. Zhao and W. Zhang, Adv. Mater., 2018, 30, 1803144.
10. P. Zhou, Y. Wang, C. Xie, C. Chen, H. Liu, R. Chen, J. Huo and S. Wang, Chem. Commun., 2017, 53, 11778.
11. A. Vijay, K. V. Ramanujachary, S. E. Lofland and S. Vaidya, Electrochim. Acta, 2022, 407, 139887.
12. J. V. Olsen, P. Kirkegaard, N. J. Pedersen and M. Eldrup, Phys. Status Solidi C, 2007, 4, 4004.
13. E. Heifets, E. A. Kotomin, A. A. Bagaturyants and J. Maier, J. Phys. Chem. Lett., 2015, 6, 2847.
14. T. D. Kühne, M. Iannuzzi, M. D. Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103.
15. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703.
16. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
17. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
18. R. H. Byrd, P. Lu, J. Nocedal and C. Zhu, SIAM J. Sci. Comput., 1995, 16, 1190.
19. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158.
20. M. Guidon, J. Hutter and J. VandeVondele, J. Chem. Theory Comput., 2010, 6, 2348.
21. P. Erhart and K. Albe, J. Appl. Phys., 2008, 104, 044315.
22. P. Hermet, M. Goffinet, J. Kreisel and P. Ghosez, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 220102.
23. S. Phapale, R. Mishra and D. Das, J. Nucl. Mater., 2008, 373, 137.
24. A. Vijay, S. Priya S, U. Terranova, M. Maity and S. Vaidya, ChemNanoMat, 2022, 8, e202200283.
25. S. Kumar and C. Rath, Phys. Status Solidi A, 2020, 217, 1900756.
26. W. Cao, O. K. Tan, J. S. Pan, W. Zhu and C. V. Gopal Reddy, Mater. Chem. Phys., 2002, 75, 67.
27. J. Bao, X. Zhang, B. Fan, J. Zhang, M. Zhou, W. Yang, X. Hu, H. Wang, B. Pan and Y. Xie, Angew. Chem., Int. Ed., 2015, 54, 7399.
28. Y. Tian and F. Xue, J. Mater. Sci.: Mater. Electron., 2019, 30, 15452.
29. Y. Zhang, Z. Chen and Z. Lu, Nanomater, 2018, 8, 261.
30. S. J. Clark and J. Robertson, Appl. Phys. Lett., 2009, 94, 022902.
31. G. Geneste, C. Paillard and B. Dkhil, Phys. Rev. B, 2019, 99, 024104.
32. T. R. Paudel, S. S. Jaswal and E. Y. Tsymbal, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 104409.
33. T. Shimada, T. Matsui, T. Xu, K. Arisue, Y. Zhang, J. Wang and T. Kitamura, Phys. Rev. B, 2016, 93, 174107.
34. Q. Xu, M. Sobhan, Q. Yang, F. Anariba, K. Phuong Ong and P. Wu, Dalton Trans., 2014, 43, 10787.
35. Z. Zhang, P. Wu, L. Chen and J. Wang, Appl. Phys. Lett., 2010, 96, 012905.
36. D. C. Craig and N. C. Stephenson, J. Solid State Chem., 1975, 15, 1.
37. A. Ramanan and J. Gopalakrishnan, Indian J. Chem., 1985, 24A, 594.
38. S. F. Radaev, L. A. Muradyan and V. I. Simonov, Acta Crystallogr., Sect. B: Struct. Sci., 1991, 47, 1.
39. M. Valant and D. Suvorov, Chem. Mater., 2002, 14, 3471.
40. C. A. Scurti, N. Auvray, M. W. Lufaso, S. Takeda, H. Kohno and D. J. Arenas, AIP Adv., 2014, 4, 087125.
41. D. Lozano-Castello, D. Cazorla-Amorós, A. Linares-Solano, P. Hall and J. Fernández, Stud. Surf. Sci. Catal., 2000, 128, 523.
42. H. Schneider, J. Schreuer and B. Hildmann, J. Eur. Ceram. Soc., 2008, 28, 329.
43. H. Dai, F. Ye, Z. Chen, T. Li and D. Liu, J. Alloys Compd., 2018, 734, 60.
44. A. Mukherjee, M. Banerjee, S. Basu, P. M. G. Nambissan and M. Pal, J. Phys. D: Appl. Phys., 2013, 46, 495309.
45. L. Fu, S. Zhou, M. Xiang, J. Yang, W. Fan, Z. Yang and J. Ou, J. Electroanal. Chem., 2022, 921, 116650.
46. K. Zhang and R. Zou, Small, 2021, 17, 2100129.
47. Z.-P. Li, T. Mori, J. Zou and J. Drennan, Mater. Res. Bull., 2013, 48, 807.
48. J. A. Kilner, Chem. Lett., 2008, 37, 1012.

---

Footnote

† Electronic supplementary information (ESI) available: Calculation of overpotential; measurement of open circuit voltage (OCV); stability phase diagram of bismuth ferrite; stability studies of the three oxides during the electrocatalytic OER; oxygen chemical potentials in the three bismuth ferrite phases. See DOI: https://doi.org/10.1039/d4cp00348a

---