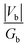Geometry and electronic structure of Yb(III)[CH(SiMe₃)₂]₃ from EPR and solid-state NMR augmented by computations

Abstract

Characterization of paramagnetic compounds, in particular regarding the detailed conformation and electronic structure, remains a challenge, and – still today it often relies solely on the use of X-ray crystallography, thus limiting the access to electronic structure information. This is particularly true for lanthanide elements that are often associated with peculiar structural and electronic features in relation to their partially filled f-shell. Here, we develop a methodology based on the combined use of state-of-the-art magnetic resonance spectroscopies (EPR and solid-state NMR) and computational approaches as well as magnetic susceptibility measurements to determine the electronic structure and geometry of a paramagnetic Yb(III) alkyl complex, Yb(III)[CH(SiMe₃)₂]₃, a prototypical example, which contains notable structural features according to X-ray crystallography. Each of these techniques revealed specific information about the geometry and electronic structure of the complex. Taken together, both EPR and NMR, augmented by quantum chemical calculations, provide a detailed and complementary understanding of such paramagnetic compounds. In particular, the EPR and NMR signatures point to the presence of three-centre–two-electron Yb-γ-Me-β-Si secondary metal–ligand interactions in this otherwise tri-coordinate metal complex, similarly to its diamagnetic Lu analogues. The electronic structure of Yb(III) can be described as a single 4f¹³ configuration, while an unusually large crystal-field splitting results in a thermally isolated ground Kramers doublet. Furthermore, the computational data indicate that the Yb–carbon bond contains some π-character, reminiscent of the so-called α-H agostic interaction.

---

Introduction

Organometallic compounds, perhydrocarbyls in particular (MR_n with M = metal; R = hydrocarbyl), often adopt unusual geometries or bonding patterns due to their low coordination numbers and the associated electronic consequences in metal–carbon bondings.^1,2 These patterns continue to engage the broader community in understanding how preferences in geometric structure relate to the often complex electronic structure and reactivity in these compounds. As an example, among diamagnetic compounds, carbons with single bonds that exhibit significant π character to metals show specific deshielded nuclear magnetic resonance (NMR) chemical shifts and associated reactivity, indicating that alkyl groups are often better described as both σ- and π-donors to the metal (Fig. 1a).^3,4 Reduced J_C–H coupling constants for these carbons, and associated specific structural distortions, provide evidence for agostic interactions.^5,6 Similar bonding peculiarities are also found in compounds with metal–carbon multiple bonds. The prototypical example is Ta(=CH^tBu)(CH₂^tBu)₃, which contains a highly deshielded ¹³C signal and a very low J_C–H coupling constant for the formally sp² hybridized Ta=C carbon. These signatures are consistent with an α-CH interaction, better described as an additional π-donation from the α-carbon to the electron deficient d⁰ metal centre.^3,4,7

Fig. 1 (a) Typically occurred peculiarities in structure of organometallic compounds, in particular, Ln[CH(SiMe₃)₂]₃. (b) Characterization approach, applied to paramagnetic organometallic lanthanide complexes.

Peculiarities in geometric structure from X-ray diffraction analysis are also observed in monomeric lanthanide perhydrocarbyl complexes, Ln[CH(SiMe₃)₂]₃ (Ln = Y,⁸ La,⁹ Ce,⁸ Sm,⁹ Lu¹⁰) that contain three short Ln⋯C_γ contacts between one Si–CH₃ group of each of the three proximal –SiMe₃ groups (Fig. 1a). The Ln⋯C_γ contacts result in lengthening of the Si–CH₃ bonds close to the lanthanide by ∼0.04 Å with respect to the other Si–CH₃ groups, indicating that these proximal Si–CH₃ groups interact with the lanthanide. This interaction helps to satisfy the high coordination numbers required to isolate these f-block homoleptic complexes; a strategy that also facilitates isolation of Yb[C(SiMe₃)₃]₂,¹¹ Ln(AlMe₄)₃,¹² and Ln[C(SiHMe₂)₃]₂.^13,14 Recent studies of Lu[CH(SiMe₃)₂]₃¹⁰ indicated that the Lu⋯C_γ interactions are not a result of γ-C–H agostic interactions (2-electron donation from a C–H bond to an electron deficient metal centre),⁶ but are rather due to a three-centre–two-electron (3c–2e) interaction between the Si–Me bond and Lu. In other words, the Lu⋯C_γ interaction is best described as a pseudo bridging Lu–Me–Si group (Fig. 1a), analogous to Al–Me–Al observed in dimeric AlMe₃^15,16 or Ln(AlMe₄)₃.¹⁷ The critical data in that study¹⁰ were a combination of high quality X-ray diffraction results, variable temperature ¹H and ¹³C NMR spectra in solution, as well as J-resolved ¹H–¹³C and ²⁹Si magic-angle spinning (MAS) solid-state NMR spectra. The experimental results were reliably reproduced using both wave-function based and density functional theory (DFT) models of Lu[CH(SiMe₃)₂]₃, and natural bond orbital (NBO) analysis showed that the charges on C_α and C_γ are negative, while the charges on Si_β and H_γ are positive. This analysis was consistent with the proposed bridging Lu–Me–Si group to describe the Lu⋯C_γ interaction.

Extending this analysis using similar NMR methods to other Ln[CH(SiMe₃)₂]₃ is however challenging, because most lanthanides contain a partially filled f-shell in their +3 oxidation state. The resulting paramagnetism perturbs the magnetic properties of the nearby nuclei, making data acquisition and interpretation complicated at best, and typically impractical in most instances. Similarly, while electron paramagnetic resonance (EPR) could offer a potential alternative for this class of compounds, the signals are typically not detectable at room temperature using routine continuous wave (CW) methods due to the short electronic spin relaxation times and large hyperfine couplings. However, both fields have seen impressive recent progress. In solid-state NMR, fast MAS and broadband adiabatic irradiation sequences allow for measurements on such samples¹⁸ and in EPR, new EPR pulsed techniques¹⁹ were developed for f-block metal complexes.^20,21 In parallel, the recent advances in quantum chemical/DFT methods and dedicated formalisms^22–30 now allow us to interpret NMR and EPR data in terms of the spatial and electronic structure.^31–37

In this study, we showcase a methodology to assess the detailed electronic structure of a prototypical compound, namely Yb[CH(SiMe₃)₂]₃, by combining state-of-the-art EPR, NMR and computation (Fig. 1b). We first synthesized and isolated a series of Yb[CH(SiMe₃)₂]_x[O-2,6-tBu₂-C₆H₃]_3−x (x = 0, 1, 2, 3), and determined their structures by single-crystal X-ray diffraction at 100 K along with their basic magnetic properties by variable-temperature measurements of their magnetic susceptibilities. We next investigate the full geometric and electronic structure of Yb[CH(SiMe₃)₂]₃ based on the most advanced EPR and solid-state NMR, supported by quantum chemical calculations. This approach enables a full characterization of the direct metal–carbon bonding as well as the nature of the secondary Yb⋯C_γ interaction at low and room temperature. We discuss how this interaction influences the structure and ligand dynamics in solution and in the solid state, and how the CH(SiMe₃)₂ ligand leads to an unusual behavior in the crystal field interactions of the Yb(III) ion.

Results and discussion

Synthesis and X-ray diffraction studies of Yb[CH(SiMe₃)₂]₃

The syntheses of Yb[CH(SiMe₃)₂]₃, Yb[CH(SiMe₃)₂]₂[O-2,6-tBu₂-C₆H₃], and Yb[CH(SiMe₃)₂][O-2,6-tBu₂-C₆H₃]₂ are shown in Fig. 2a (see ESI,† Section 1 for detailed synthetic procedures). Similar to the lutetium complexes isolated previously,¹⁰ the alkylation depends on the stoichiometry of the organolithium reagent. Key to successful isolation of these compounds is the use of sufficient volumes of pentane to dissolve the sparingly soluble polymeric Li[CH(SiMe₃)₂].³⁸ Addition of Li[CH(SiMe₃)₂] as a slurry in smaller volumes of pentane results in poor yields and formation of mixtures of these compounds. All organoytterbium compounds shown in Fig. 2a are isolated as crystalline solids from concentrated pentane solutions. Yb[CH(SiMe₃)₂]₃ is blue, Yb[CH(SiMe₃)₂]₂[O-2,6-tBu₂-C₆H₃] is brown, and Yb[CH(SiMe₃)₂][O-2,6-tBu₂-C₆H₃]₂ is red. The study below focuses on the structure and spectroscopic features of Yb[CH(SiMe₃)₂]₃. X-ray structures of Yb[CH(SiMe₃)₂]₂[O-2,6-tBu₂-C₆H₃] and Yb[CH(SiMe₃)₂][O-2,6-tBu₂-C₆H₃]₂ are provided in ESI,† Section 2.2 (see Fig. S3–S6), and their NMR spectra are provided in ESI,† Section 7 (see Fig. S15–S20).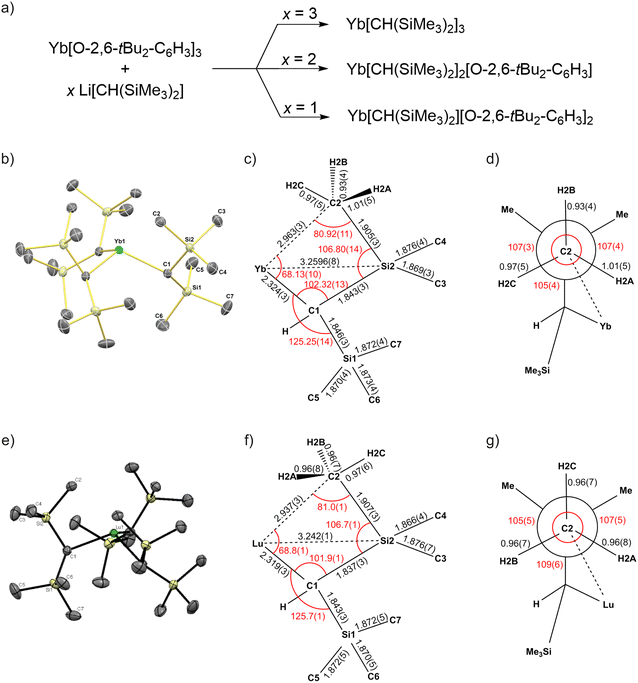

Fig. 2 (a) Synthesis scheme of Yb[CH(SiMe₃)₂]_x[O-2,6-tBu₂-C₆H₃]_3−x (x = 1, 2, 3). (b) Structure of the Yb[CH(SiMe₃)₂]₃ complex with displacement ellipsoids at 50% probability level. For clarity the hydrogen atoms and the solvent molecules CH₂(SiMe₃)₂ are omitted. (c) Sketch of relevant bond lengths and angles of Yb[CH(SiMe₃)₂]₃. The bond lengths are reported in Å, and the bond angles (in red) are reported in degrees (see also Table S2, ESI†). (d) Newman projection down the C(2)–Si(2) bond with bond lengths and angles (in red) obtained from the crystal structure of Yb[CH(SiMe₃)₂]₃. (e) Structure of the Lu[CH(SiMe₃)₂]₃ complex with displacement ellipsoids at 50% probability level. For clarity the hydrogen atoms and the solvent molecules CH₂(SiMe₃)₂ are omitted. (f) Sketch of relevant bond lengths and angles of Lu[CH(SiMe₃)₂]₃. The bond lengths are reported in Å, and the bond angles (in red) are reported in degrees (see also Table S2, ESI†) (f) Newman projection down the C(2)–Si(2) bond with bond lengths and angles (in red) obtained from the crystal structure of Lu[CH(SiMe₃)₂]₃. For comparison panels (e)–(g) are reproduced from ref. 10 with permission from the American Chemical Society, copyright 2016 Conley et al.¹⁰

A view of the Yb[CH(SiMe₃)₂]₃ complex is shown in Fig. 2b and Fig. S2 (ESI†). The relevant bond distances obtained from this structure are shown in Fig. 2c and d (see also Table S2, ESI†). For comparison the previously reported bond distances for Lu[CH(SiMe₃)₂]₃¹⁰ (Fig. 2e) are also shown in Fig. 2f and g (see also Table S2, ESI†). Yb[CH(SiMe₃)₂]₃ crystallizes in the P31c space group and is isostructural with other isolated Ln[CH(SiMe₃)₂]₃. Yb[CH(SiMe₃)₂]₃ adopts a C₃ symmetric structure with the ytterbium displaced from the plane defined by the three Yb–C bonds by 0.783(3) Å. The Yb–C_α (Yb–C₁) distance is 2.324(3) Å, which is nearly the same as the Lu–C_α distance in Lu[CH(SiMe₃)₂]₃ (2.319(3) Å) and the Sm–C_α distance in Sm[CH(SiMe₃)₂]₃ (2.33(2) Å).

Yb[CH(SiMe₃)₂]₃ contains short Yb⋯C_γ contacts at 2.963(3) Å, which is slightly longer than Lu⋯C_γ (2.936(2) Å) and Sm⋯C_γ (2.85(3) Å) distances in Lu[CH(SiMe₃)₂]₃ and Sm[CH(SiMe₃)₂]₃, respectively. The Neumann projection shown in Fig. 2d contains distances and angles for the proximal Si–CH₃ group interacting with Yb. The C–H bond distances and angles are close to those expected for a tetrahedral sp³ hybridized carbon, again similar to results obtained for Lu[CH(SiMe₃)₂]₃. These structural data infer that a similar 3c–2e Yb–Me–Si interaction is present in Yb[CH(SiMe₃)₂]₃ under the conditions of low-temperature X-ray diffraction studies (i.e. 100 K).

Magnetic susceptibility studies

We performed magnetic susceptibility studies for Yb[CH(SiMe₃)₂]₃, Yb[CH(SiMe₃)₂]₂[O-2,6-tBu₂-C₆H₃], Yb[CH(SiMe₃)₂][O-2,6-tBu₂-C₆H₃]₂, and Yb[O-2,6-tBu₂-C₆H₃]₃ (see ESI,† Section 6, Fig. S11–S14 and Table S11 for more details). The determined experimental values of the effective magnetic moment of all four complexes at 300 K are in the range between μ_eff (300 K) = 4.30 (χT = 2.31 cm³ K mol⁻¹) − 4.53μ_B (χT = 2.57 cm³ K mol⁻¹) and show only slight variations with the different substituents. Furthermore, these values are also in a good agreement with the (Hund-Landé) expectation value for the free Yb(III) ion, which is described by a single ²F_7/2 term (4f¹³) with μ_eff (300 K) = 4.54μ_B (χT = 2.58 cm³ K mol⁻¹), suggesting that all Yb complexes within the investigated series can be described by a single 4f¹³ configuration, similar to those of the free Yb(III) ion.

EPR characterization of Yb[CH(SiMe₃)₂]₃

We characterized the Yb(III) alkyl complex Yb[CH(SiMe₃)₂]₃ using pulse EPR spectroscopy¹⁹ that, in combination with computational studies, enables the successful characterization of the spatial and electronic structure of paramagnetic complexes.^20,37 The continuous-wave (CW) EPR spectrum of Yb[CH(SiMe₃)₂]₃ (Fig. 3a, blue) was reasonably reproduced by simulation (Fig. 3a, red) by modeling the Yb ion as an electronic spin S = 1/2, with g tensor principal values of g_⊥ = 0.7316 and g_‖ = 7.5698. The spectrum also exhibits a well-resolved satellite structure, due to hyperfine coupling to the two spin-active isotopes ¹⁷¹Yb (spin I = 1/2 and natural abundance of 14.31%) and ¹⁷³Yb (spin I = 5/2 and natural abundance of 16.13%) of the lanthanide. From spectral simulation (Fig. 3a, red), the ^171,173Yb hyperfine tensors were determined to be A_⊥(¹⁷³Yb) = 221 MHz, A_‖(¹⁷³Yb) = 1650 MHz, and accordingly A_⊥(¹⁷¹Yb) = 842 MHz, A_‖(¹⁷¹Yb) = 6285 MHz.

Fig. 3 (a) CW EPR spectrum of a solid powder of Yb[CH(SiMe₃)₂]₃, 10 K (blue) and simulation (red), together with an expansion of the low-field region. The black arrow marks the field position of the HYSCORE measurement. (b) Echo-detected EPR spectrum of Yb[CH(SiMe₃)₂]₃. The field position for HYSCORE and EDNMR are marked with a black and red arrow, respectively. (c) HYSCORE spectrum of Yb[CH(SiMe₃)₂]₃ (blue to yellow, see also Fig. S8, ESI†) and simulation (red) based on a single ¹H hyperfine coupling A_iso(¹H) = 3.8 ± 0.3 MHz. Anti-diagonal lines indicate the ¹H and ²⁹Si nuclear Zeeman frequencies. Spurious peaks at 21.5/2.0 MHz and 23.5/23.5 MHz are electronic artefacts. (d) ¹H region of EDNMR spectrum of Yb[CH(SiMe₃)₂]₃ (blue), together with simulation (red) of a single effective ¹H coupling with A_eff(¹H) = 13 ± 1 MHz (gray) and a ¹H matrix peak (gray dashed) at a ¹H nuclear Zeeman frequency of 39.4 MHz.

A higher-resolution picture can be provided by pulsed EPR spectroscopy, which has evolved into a robust tool for the determination of geometry and electronic configuration of organometallic complexes of paramagnetic d- and f-block metals. In particular, 2D hyperfine sub-level correlation spectroscopy (HYSCORE)³⁹ allows us to detect magnetically active nuclei (e.g.¹H, ¹³C, ²⁹Si etc.) that are coupled to paramagnetic centres by hyperfine interaction, due to close spatial proximity to these centres. The technique can separate the isotropic (primarily Fermi-contact) and anisotropic (primarily spin-dipolar) parts of the hyperfine interaction tensors that are linked to the electronic properties of the systems (e.g. metal–ligand spin density transfer), and bonding between the nuclei and the paramagnetic centre. The HYSCORE spectrum of Yb[CH(SiMe₃)₂]₃ (Fig. 3c and Fig. S8, ESI†) reveals the presence of hyperfine coupling to protons in the CH(SiMe₃)₂ alkyl ligands. From the simulation of the HYSCORE spectrum a single ¹H hyperfine tensor was determined to have A_iso(¹H) = 3.8 ± 0.3 MHz, T_dip(¹H) = 4.0 ± 0.5 MHz (A_dip = [−4.0 ± 0.5; −4.0 ± 0.5; 8.0 ± 1.0] MHz), with the tensors principal axes frame (PAF) rotated by 45° ± 15° with respect to the z axis of the PAF of the g tensor. This interpretation of the HYSCORE data is consistent with the ELDOR-detected NMR (EDNMR)⁴⁰ spectrum shown in Fig. 3d, from which we can extract a single splitting due to an effective hyperfine coupling to ¹H with A_eff(¹H) = 13 ± 1 MHz. Based on previous observations of similar isotropic and dipolar parts of hyperfine coupling tensors for the S = 1/2 Ti(III) alkyl complexes,^37,41 the observed ¹H hyperfine couplings could be assigned to the hydrogen atoms that are close in space to the Yb(III) centre, such as α-H atoms of CH(SiMe₃)₂ ligands. The positions of the α-H atoms within the structure of Yb[CH(SiMe₃)₂]₃ were further refined using quantum chemical computations (vide infra). This finding indicates that the transferred spin density is significant only for the closest to the Yb(III) atoms, such as C₁ and H₁, while it is substantially lower for the rest of the ligands. The observed isotropic ¹H hyperfine couplings that are even smaller than those observed for d¹ metal alkyls^37,41 suggest that, in contrast to the case of Cp₃ Yb,²⁰ there is no significant charge and spin density transfer to the ligands in Yb[CH(SiMe₃)₂]₃. This is also consistent with the preferential presence of the unpaired electron in the 4f orbital rather than in the valence 5d orbital, which would result in more significant distribution of the spin density into the ligands of Yb(III). A difficulty of promoting 4f electrons of Yb(III) to the 5d orbital, which effectively prevents the formation of double Yb=C bonds, was previously discussed based on CASSCF calculations.⁴² Taking into account the results of magnetic susceptibility measurements (vide supra), we propose that the ground state of the Yb[CH(SiMe₃)₂]₃ complex has a single electronic configuration of 4f¹³ (S = 1/2), close to the one of Yb(III) free ion.

NMR characterization of Yb[CH(SiMe₃)₂]₃

Over the last twenty years, the development of instrumentation and spectroscopic methods in NMR allows us to target paramagnetic lanthanide complexes such as Yb[CH(SiMe₃)₂]₃. Specifically, solid-state NMR with fast MAS and broadband adiabatic irradiation sequences¹⁸ can now be used to obtain data on microcrystalline powders, where the complex dynamics are simplified and only the relevant internal ligand motions are retained. Nonetheless, obtaining high-quality magnetic resonance data on these systems represents only part of the challenge, since the resulting spectra are often very difficult to interpret using standard assignment methods. In this respect, recent progress in wave-function based/DFT methods for the computation of NMR parameters of paramagnetic complexes has also been impressive. For NMR, there have been significant advances both in the development of the formalism of the paramagnetic shifts^22–30 and the computational implementation.^31–36 However, applying the developed methods to lanthanides has been a much more difficult matter.

For the Yb[CH(SiMe₃)₂]₃ complex, we are able to draw the conclusions regarding its electronic structure and on the positions of ¹H nuclei closest to the metal centre (α-H atoms of [CH(SiMe₃)₂] ligands, H₁) based on the EPR data and quantum chemistry calculations. However, the weak hyperfine interactions between the unpaired electron and the more distant nuclei prevented us from obtaining any high-resolution information about the rest of the molecule by EPR. This gap could, however, be filled by paramagnetic NMR.¹⁸ Note that the signals of H1 nuclei, most likely, cannot be observed by NMR, in particular, due to a severe reduction of sensitivity because the large paramagnetic relaxation enhancement expected for these nuclei in close proximity to Yb, or due to the fact that potentially large shifts push them out of the excitation window. Therefore, EPR and NMR spectroscopies could be seen as complementary techniques for the characterization of paramagnetic lanthanide organometallic compounds like Yb[CH(SiMe₃)₂]₃, allowing to obtain the information from both internal and external coordination environment of the metal center.

The ligands of the complex are expected to exhibit substantial dynamics, which has the effect of averaging the signals. This was observed in the case of the Lu analogue, where variable temperature ¹H solution NMR data were required to partially freeze out these motions and the individual ¹H resonances were obtained by cooling the sample. However, this approach was not successful for the present Yb complex, where no such resolution was obtained over a temperature range between 285 and 182 K, and no detection was possible beyond that because of increased line-broadening (see ESI,† Section 3 and Fig. S7).

We therefore proceeded to examine the Yb[CH(SiMe₃)₂]₃ complex via solid-state MAS NMR, which has the advantage of eliminating molecular rotational diffusion, so that only the internal ligand dynamics remain. Such spectra relate to the room-temperature crystal structure, thereby providing a direct bridge to the low-temperature XRD data.

One-dimensional solid-state MAS NMR spectra of ¹H, ¹³C and ²⁹Si are shown in Fig. 4a–c. Each of these spectra exhibits poorly resolved patterns, due to hyperfine interactions with the unpaired electron, which induce large shifts and shift anisotropies and extremely large inhomogeneous line-broadenings. We see shift anisotropies that are very large for all three nuclei, of the order of hundreds of ppm, in contrast to the Lu analogue, where the ¹H and ¹³C diamagnetic chemical shift anisotropies (CSAs) were too small to be measured and for ²⁹Si were of the order of tens of ppm. In particular, for the Lu analogue, ²⁹Si CSAs were used to characterize the metal–ligand interaction. That approach is not at first sight obviously applicable to the paramagnetic Yb complex, since the interpretation of the shift anisotropy is more complex.

Fig. 4 NMR spectra of a solid powder of Yb[CH(SiMe₃)₂]₃, 300 K: (a) ¹H MAS spectra at 30 kHz MAS, (b) ¹³C MAS spectra of at 14.286 kHz MAS and (c) ²⁹Si MAS spectra at 30 kHz MAS, showing two distinct ²⁹Si signals. The spinning sidebands are marked with asterisks (*). 2D aMAT spectrum: (d) ¹H at 30 kHz, (e) ¹³C at 20 kHz and (f) ²⁹Si at 20 kHz. The indirect dimension projections were deconvolved using asymmetric Gaussian functions to extract the isotropic shifts and quantify shift dispersion. (g)–(i) Extracted slices with isotropic shift corresponding to the maxima of the deconvolved projections and labelled with Roman numerals. Each slice was subsequently fitted considering a simple CSA model using the Haeberlen convention⁴³ ( Δδ = [small delta, Greek, tilde]_zz − δ_iso and η = ([small delta, Greek, tilde]_yy − [small delta, Greek, tilde]_xx)/Δδ, where δ_xx, δ_xx and are the components of the CSA tensor in the principal axes frame). See ESI,† Section 1.6 for more details.

The first problem to be addressed is the lack of resolution of the individual signals in each of the three spectra, due to the overlapping spinning sideband manifolds of neighboring resonances. To solve this problem, we employed the 2D adiabatic magic-angle turning (aMAT) experiment,⁴⁴ which correlates each spinning side-band manifold to its isotropic shift, thus removing the overlap, as seen in Fig. 4d–f for ¹H, ¹³C and ²⁹Si, respectively. In all three cases, the aMAT spectra are able to resolve two resonances with distinct isotropic shifts. For ²⁹Si, the interpretation is relatively straightforward, with the two signals V and VI being due to the two inequivalent Si nuclei (specifically, one due to Si₁ and the other to Si₂). By extension, it is reasonable to tentatively interpret each ¹³C signal (III and IV) as being from the three methyl groups attached to each of the Si (C_2/3/4 and C_5/6/7), and each ¹H signal (I and II) to the corresponding group of protons (H_2/3/4 and H_5/6/7).

For each of the signals I–VI, a slice extracted from the aMAT spectra was fitted to determine the parameters of the shift tensor (isotropic shift δ, shift anisotropy Δδ and asymmetry parameter η) (Fig. 4g–i). For each of the three nuclei, within each pair one signal (II, IV and V) possesses a larger isotropic shift and shift anisotropy compared to the second (I, III and VI). We can tentatively assign the former set of three signals to the same SiMe₃ group, and the latter set of signals to the other SiMe₃ group. This interpretation is supported by a transferred-echo double resonance (TEDOR) experiment⁴⁵ (Fig. 5a), which displays a first unambiguous correlation between I and III, a second unambiguous correlation between II and IV, and no other correlations. These solid-state NMR spectra and our tentative interpretation indicate that each group of ¹H, ¹³C and ²⁹Si resonances represents a single SiMe₃ group in which there are rotations about the C₁–Si bond and about the Si–C bonds of each of the three methyls. The rate constants describing each rotation are larger than the spread of the individual chemical shifts of the exchanging sites. Note that the predicted shifts of H₁ nuclei (see ESI,† Section 5.3 for the details) lie within a range between 230 and 200 ppm (Fig. 5b), and are not observed in any of the ¹H NMR spectra (1D, aMAT, TEDOR), as expected.

Fig. 5 (a) ¹H–¹³C correlation spectrum achieved by using the TEDOR experiment⁴⁵ at 30 kHz MAS, yielding two distinct correlations of the resonances (III/I) and (IV/II), shown in Fig. 4, which were subsequently used to model the paramagnetic shifts in the following section. The spinning sidebands are marked with asterisks (*). (b) ¹H NMR shift distributions considering solely the contributions arising from the presence of the unpaired electron and neglecting long-range PCS effects stemming from parametric centres in neighboring unit cells (δ_p). The shifts were calculated considering the Moon and Patchkovski,²³ Vaara et al.^24,25,28 and van den Heuvel and Soncini^26,27 formalism using the g tensor obtained using multi-reference perturbation theory (SO-CASPT2) on the DFT optimized geometry (see Sections 1.8 and 5.3 of the ESI,† for details) and the experimental ¹H hyperfine tensor. A distribution of relative orientations of the g and A tensors were considered using Zaremba, Conroy, Wolfsberg orientational averaging scheme with 1154 orientations.^46–48 The relative orientation of the z axes of the g and A tensors was kept fixed at 45°, in order to match with the EPR results.

Therefore, we suggest that the observed signals are consistent with the presence of the two distinct types of SiMe₃ groups, associated with Si₁ and Si₂ nuclei. Note that the span (Ω = δ₁₁ − δ₃₃) of Si₁ is Ω(Si₁) = 676 ppm, and the span of Si₂ is Ω(Si₂) = 479 ppm. These values are significantly larger than those previously obtained for Lu[CH(SiMe₃)₂]₃ (Ω(Si₁) = 46.8 ppm), Ω(Si₂ = 30.2 ppm),¹⁰ which is expected because that compound is diamagnetic. The pattern, observed for Lu[CH(SiMe₃)₂]₃, was the strongest experimental evidence that, combined with the DFT interpretations, showed that Si₁ was interacting with Lu through a Lu–Me–Si 3c–2e interaction.¹⁰ Although the Ω values for Yb[CH(SiMe₃)₂]₃ are significantly larger, a similar pattern emerges; Si₁ has a larger Ω(Si) than Si₂, suggesting that Si₁ is also interacting with Yb to form a 2c–2e Yb–Me–Si.

Computational studies of Yb[CH(SiMe₃)₂]₃

Ab initio electronic structure. The molecular geometry obtained by XRD was optimized using DFT using the ORCA package⁴⁹ (see Fig. S9, and Tables S7 and S8 for the details of DFT-optimized structure of Yb[CH(SiMe₃)₂]₃, ESI†). Both the starting and optimized geometries were then used to calculate the electronic energy levels using complete active space (CAS) methods using the MOLCAS package.^50,51 The results, reported in Table 1, are similar, and in the following we confined our discussion on the results obtained on the DFT-optimized structure.

Table 1 Ab initio energy levels (in cm⁻¹) of the ²F (at spin-free level) and ²F_7/2–5/2 (at spin–orbit coupling level) manifolds in Yb^III (CH(SiMe₃)₂)₃. The spin–orbit energy levels are doubly degenerate

	E 1	E 2	E 3	E 4	E 5	E 6	E 7
a In ORCA.
XRD
SF-CASSCF	0	144	682	687	1031	1123	1203
SF-CASPT2	0	205	823	928	1181	1392	1769
SO-CASSCF	0	525	889	1088	10 387	11 007	11 341
SO-CASPT2	0	659	1043	1452	10 420	11 166	11 660
Optimized
SF-CASSCF	0	168	694	694	1074	1083	1203
SF-CASPT2	0	383	949	1002	1331	1393	1729
SF-CASSCF^a	0	172	746	748	1161	1172	1297
SO-CASSCF	0	526	888	1070	10 387	11 006	11 327
SO-CASPT2	0	689	1068	1386	10 428	11 189	11 613
SO-CASSCF^a	0	565	959	1154	9214	9891	10 241

---

The seven inner-core active 4f orbitals are shown in Fig. 6 along with the three energetically higher bonding type orbitals of the Yb–C_a bonds. Out of the seven active orbitals, the lowest one is non-bonding, followed by two sets of doubly-degenerate orbitals: one undergoes a slight π anti-bonding interaction with the C_α p_z orbitals and the other one is non-bonding. The final two orbitals characterize a σ bonding interaction with the C_α hybrid orbitals. The seven 4f orbitals are very little admixed with the ligand orbitals, yet the ligand field splitting at the orbital level, or at the many-electron level, is relatively large compared to the case of O and N donor ligands (usually 200–300 cm⁻¹). This is similar to the case of YbCp₃, which has also been shown to exhibit a large ligand field splitting.²⁰ The active 4f orbitals are mostly perturbed by electrostatic interactions, while the Yb valence 6s, 6p and 5d orbitals mostly participate in the bonding interactions with the C_α hybrid orbitals. As a result, population analysis of the ground spin-free CASSCF state (see Table 2) leads to significant electron occupations in the Yb(III) atomic valence and Rydberg orbitals.

Fig. 6 Surface plots of the three Yb–C_α bonding orbitals and the seven 4f active orbitals of the Yb^III(CH(SiMe₃)₂)₃ complex (separated by the vertical line) from the SF-CASSCF states. The canonical energies (in cm⁻¹) are given in parentheses. The isosurface value is at ±0.02 a.u. The dominant compositions of the orbitals are also shown.

Table 2 The Mulliken (M) and Löwdin (L) charge populations of the Yb atomic orbitals in Yb^III(CH(SiMe₃)₂)₃ from different calculation methods

	s Populations	p Populations	d Populations	f excess^d
a Basis set: ANO-RCC-TZVP(Yb, Si and Ca) + ANO-RCC-DZP (C,H) in MOLCAS. b Basis set: SARC-DKH-TZVP(Yb) and IGLO-III (rest) in ORCA. c Basis set: SARC-ZORA-TZVP(Yb) and TZVP (rest) in ORCA. d Excess of combined 4f + 5f orbital occupations than the formal 4f electron number.
SF-CASSCF (M)^a	0.50(6s + 7s)	1.52(6p + 7p)	1.22(5d + 6d)	0.02
SF-CASSCF (M)^b	0.48(6s + 7s)	0.76(6p + 7p)	1.13(5d + 6d)	0.14
SF-CASSCF (L)^b	0.19(6s + 7s)	0.60(6p + 7p)	1.87(5d + 6d)	0.52
ZORA-DFT(PBE0) (M)^c	0.72(6s + 7s)	1.06(6p + 7p)	1.84(5d + 6d)	0.18
ZORA-DFT(PBE0) (L)^c	0.32(6s + 7s)	0.77(6p + 7p)	2.28(5d + 6d)	0.60

---

At the spin-free (SF) CASSCF level, the ²F manifold of the central Yb(III) ion splits into three singlets, of relative energies of 0, 168 and 1203 cm⁻¹, and two orbital doublets at 694 and ∼1074 cm⁻¹, following the energy stabilization of the unpaired electron or hole in the trigonal ligand field. Dynamic correlation energy correction at the MS-CASPT2 method further increases the energy splitting by further stabilizing and destabilizing the bonding and anti-bonding type orbitals. At the spin–orbit (SO) level, the four Kramers doublets (KDs) of the ground J = 7/2 manifold are split by the axial ligand field in the order m_J = ±7/2 < ±5/2 < ±3/2 < ±1/2. The ligand field splitting is around 1400 cm⁻¹, seven times larger than the room temperature thermal energy (200 cm⁻¹). In fact, the first excited KD characterized by m_J = ±5/2 is around 690 cm⁻¹ and is not meaningfully populated at room temperature. The irreducible spherical tensor ligand-field parameters extracted from the model spaces of the ground L (at SF) and J (at SO) manifolds are given in Table 3. The dominant ligand-field parameter is the second-rank axial component B₀², but the components of orders three and six are also significant, as expected from the three-fold symmetry axis. The B₀² component is related to the quadrupole moment of the ligand field and its negative value corresponds to an oblate coordinating sphere. The excited J = 5/2 manifold is energetically well separated by more than 10 000 cm⁻¹ in accordance with the SO coupling strength (ζ_4f ≈ 2900 cm⁻¹) of the Yb 4f electrons.⁵²

Table 3 The irreducible spherical tensor ligand-field components of rank k and order m (B^k_m) and strength parameters (S) (in cm⁻¹) of Yb^III(CH(SiMe₃)₂)₃ determined from the ab initio ground L (SF) and J (SO) manifolds

	B 0 ^2	B 2 ^2	B 0 ^4	B 2 ^4	B 3 ^4	B 4 ^4	B 0 ^6	B 2 ^6	B 3 ^6	B 4 ^6	B 6 ^6	S
SF-CASSCF	−1839	11	−24	3	317	3	43	2	185	3	216	487
SF-CASPT2	−2302	74	−97	173	374	161	−465	58	331	62	550	630
SO-CASSCF	−1854	11	−33	3	316	3	36	2	167	3	221	490
SO-CASPT2	−2319	75	−104	168	368	164	−454	51	296	55	580	634

---

Computational interpretation of the EPR data. Based on the DFT-computed structure of Yb(CH(SiMe₃)₂)₃ (Fig. S9, ESI†), we first performed a calculation of hyperfine couplings for the α-H atoms of [CH(SiMe₃)₂] ligands (H₁) with PBE0 functional (see ESI,† Section 1.8 for the details). While the precise prediction of isotropic hyperfine couplings for H₁ nuclei is unlikely due to the close proximity of H₁ to Yb, which requires high-level relativistic electronic structure methods for accurate determination of spin density delocalization, the dipolar (anisotropic) part of the hyperfine coupling tensor could still be a reliable descriptor for comparison between experimental and computed hyperfine couplings. The computed hyperfine coupling tensors for all three H₁ nuclei of the [CH(SiMe₃)₂] ligands, similarly to the experimental ones, appeared to be nearly axial: A_iso(1) = −0.26 MHz, A_dip(1) = [−4.00 −4.50 8.51] MHz; A_iso(2) = −0.15 MHz, A_dip(2) = [−3.80 −3.84 7.64] MHz; A_iso(3) = −0.21 MHz, A_dip(3) = [−4.47 −4.32 8.79] MHz. Furthermore, the calculated dipolar hyperfine tensor values A_dip are in a very good agreement with the experimental values (A_dip = [−4.0 ± 0.5; −4.0 ± 0.5; 8.0 ± 1.0] MHz). This indicates that the position of the α-H (H₁) atoms of the [CH(SiMe₃)₂] ligands of Yb(CH(SiMe₃)₂)₃, including the related Yb–H distances and the unusually short Yb–C–H angles of ca. 93° (see Tables S7 and S8, ESI†), are nicely reproduced within the DFT-optimized structure (Fig. S9, ESI†).

Next, the SO-CASPT2 g factors, g_⊥ = 0.72 and g_‖ = 7.77 (see Table 4) are also in very good agreement with the experimental values and show a substantial improvement as compared to the SO-CASSCF values (g_⊥ = 0.40, g_‖ = 7.91, respectively) due to the better inclusion of the electron dynamical correlation. The anisotropic orbital and spin contributions to the magnetic moments as a result of the figand field and spin–orbit coupling admixing of the 4f orbitals are also shown. The magnetic moment of the ground KD is significantly anisotropic, as characterized by the prolate m_J = ±7/2 state stabilizing the unpaired electron in the bonding active 4f_{y(3x²−y²)} and 4f_{x(x²−3y²)} orbitals, as shown in Fig. 6. In addition, the EPR hyperfine coupling parameters to the central ¹⁷¹Yb (I = 1/2) nucleus were calculated from first principle methods using a finite nuclear model. The SO-CASSCF calculations are in good agreement with experiments as shown in Table 4. Quantitative evaluation of the hyperfine coupling value in the strong relativistic limit requires a forefront level of computational methods and is still in the developing phase. The Fermi contact (A_FC), spin-dipolar (A_SD) and orbital (A_orb) contributions to the hyperfine tensor in Table 4 indicate a dominant anisotropic nuclear spin – electron orbit coupling which leads to the large Yb(III) hyperfine A_⊥ and A_‖ components. The good agreement between calculated and experimental g tensor values and ¹⁷¹Yb hyperfine couplings indicates that our computational approach, based on DFT-optimized geometry and CAS methods, describes well the electronic structure of Yb(CH(SiMe₃)₂)₃.

Table 4 The ab initio g-factors and hyperfine coupling parameters (in MHz) of the central ¹⁷¹Yb (I = 1/2) in Yb^III(CH(SiMe₃)₂)₃. L and S are the orbital and spin contributions, respectively, to the magnetic moments. The spin-dipolar (SD), orbital (orb) and Fermi contact (FC) contributions to the calculated hyperfine values are shown

	g ^L x	g ^L y	g ^L z	g ^S x	g ^S y	g ^S z	g x	g y	g z	g iso	Δgax
a SO-CASSCF in ORCA, experimental gx,y = 0.73, gz = 7.57 and A⊥ = 842 MHz, A‖ = 6285 MHz.
SO-CASSCF	0.27	0.27	5.92	0.13	0.13	1.99	0.40	0.40	7.91	2.90	7.51
SO-CASPT2	0.50	0.45	5.81	0.25	0.24	1.96	0.75	0.69	7.77	3.10	7.05
SO-CASSCF^a	0.27	0.27	5.92	0.13	0.13	1.99	0.38	0.38	7.90	2.89	7.52

---

	A ⊥,SD	A ‖,SD	A ⊥,orb	A ‖,orb	A ⊥,FC	A ‖,FC	A ⊥	A ‖
SO-CASSCF^a	−24	−748	287	6728	105	108	368	6088

---

Computational interpretation of the magnetic susceptibility data. For comparison the first principal calculated molar magnetic susceptibilities of Yb^III(CH(SiMe₃)₂)₃ are provided in Table 5. The main magnetic axis (χ_z) coincides with the axis. The calculated isotropic part of the magnetic susceptibility χT at 300 K is 2.30 cm³ K mol⁻¹ and is comparable to the experimental result of 2.57 cm³ K mol⁻¹. The axial anisotropy of the molar magnetic susceptibility Δχ_ax = χ_z − (χ_x + χ_y)/2 is very large in this complex and dominated by the anisotropic contribution from the ground KD (calculated to be Δχ^KD1_ax = 23.44 × 10⁻⁸ m³ mol⁻¹), and is due to the large ligand field splitting and consequent non-homogeneous population in the 4f orbitals.

Table 5 The molar magnetic susceptibilities of Yb^III(CH(SiMe₃)₂)₃ (in 10⁻⁸ m³ mol⁻¹) at 300 K from ab initio calculations

	χ ^L x	χ ^L y	χ ^L z	χ ^S x	χ ^S y	χ ^S z	χ x	χ y	χ z	χ iso	χ iso T	Δχax
a SQUID value = 2.57 in CGS unit.
SO-CASSCF	2.23	2.26	17.56	0.82	0.83	5.87	3.05	3.09	23.43	9.85	2.37	20.36
SO-CASPT2	1.63	1.91	17.69	0.63	0.73	5.94	2.26	2.63	23.63	9.50	2.29^a	21.19

---

NBO and QTAIM analyses. The DFT optimized structure (Fig. S9, ESI†) is in particular notable for the unusually short (ca. 93°) Yb–C–H₁ angles for all the [CH(SiMe₃)₂]₃ ligands (see Table S7, ESI†). The shortened Yb–C–H angles for the α-H atoms of the [CH(SiMe₃)₂]₃ ligands might be explained by a simultaneous electrostatic repulsion from the Yb centre and the two Si atoms of the CH(SiMe₃)₂ ligand. A similar effect was previously observed for the [CH(SiMe₃)₂]₃ ligands of the Lu(III)¹⁰ or Ti(III) analogues.⁴¹ This interaction is essentially described as the donation of electrons from the filled molecular orbital corresponding to the C–H bond to a metal d-orbital of appropriate symmetry, and has been related to a metal–carbon bond acquiring a π (or alkylidene) character, often called α-H agostic interaction in metal alkyls.^3,4,7 In order to investigate the possible presence of the π character within the Yb–C bonds, we conducted a natural bond orbital (NBO) analysis,⁵³ using the program NBO 7.0⁵⁴ (see ESI,† Section 5.2 for more details). The molecular orbital set for the NBO analysis was generated with DFT, using the PBE0 functional.

Indeed, the NBO analysis revealed a high degree of deviation of the natural hybrid orbitals (NHO) on α-C atoms from the Yb–C axis (θ_NHO–C–Yb = 17.8° for one [CH(SiMe₃)₂]₃ ligand and 17.9° for the other two alkyl ligands). The value of such deviation can be used as a quantitative descriptor of the degree of the π character within the metal–carbon bonds (for a pure σ bond, no deviation would be expected).⁴ In fact, the degree of the π character within the Yb–C bonds is higher than the one observed for Ti(III), Ti(IV) and Zr(IV) neutral alkyl complexes, while being somewhat smaller than for the related cationic complexes.^4,37

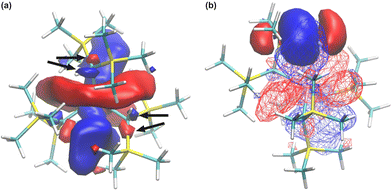
Furthermore, the NBO analysis revealed three low-lying natural orbitals, which have been attributed to the low-lying 5d orbitals, with their occupancies being slightly higher than 5% (see Table S11, ESI†). The spatial distribution of these orbitals (Fig. 7a) includes, in particular, three lobes of p-type on each of the α-C atoms of the[CH(SiMe₃)₂]₃ ligands, all being in antiphase with the central d-type lobes (Fig. 7a, marked with arrows). These parts of the orbital can be viewed as π* orbitals of the Yb–C bonds,³⁷ thus confirming the partial alkylidenic character of these bonds.^3,4

Fig. 7 (a) Natural spin-α orbital, representing one 5d orbital of Yb[CH(SiMe₃)₂]₃ (red for positive and blue for negative signs of the wavefunction, the same in all panels). The p-type parts of the orbital (two out of three) are marked with arrows. (b) Overlap of the same 5d orbital (wireframe contour) with natural spin-α orbital, corresponding to the bonding orbital of one of Si-C_γ bonds (solid contour).

The obtained significant stabilization energies for these 5d orbitals (see Table S9, ESI†) imply that there are other secondary interactions within the structure of Yb[CH(SiMe₃)₂]₃ that involve these 5d orbitals. One example of such an interaction is the three-centre–two-electron Yb–Me–Si interaction, previously observed for the Lu[CH(SiMe₃)₂]₃ analogue.¹⁰ Indeed, the NBO analysis reveals the constructive overlap between these 5d orbitals and the bonding orbitals of the Si–C_γ bonds (Fig. 7b), thus showing that such interactions are also predicted for the Yb[CH(SiMe₃)₂]₃ complex.

Next, to further probe the chemical bonding interactions, the DFT computed electron density was analysed by the quantum theory of atoms in molecules (QTAIM) method. The QTAIM approach is based on the topological analysis of the physically observable electron density, and is thus theoretically independent of the computational method. The bonding descriptors, namely the electron density (ρ_b), its Laplacian (∇²ρ_b), the potential energy density (V_b) and the kinetic energy density (G_b) at the so-called line critical point (LCP, i.e. the inflection point at the gradient path between two neighboring atoms) are of interest in this kind of analysis. Generally at the LCP, ρ_b > 0.20 a.u. with a negative Laplacian indicates a shared electron interaction between two atoms. Accompanied by |V_b|/G_b > 1 and H_b = V_b + G_b < 0, this typically indicates bound electrons at the LCP, often interpreted as a covalent interaction. For Yb[CH(SiMe₃)₂]₃, the C–H bonds yield typical values of closed shell interactions with ρ_b > 0.25 and negative Laplacian, while the Si–C bonds give ρ_b ≈ 0.11 with a positive Laplacian, which is characteristic of an ionic interaction. By contrast, the values for both the Yb–C_α and Yb–C_γ (ρ_b = 0.078 a.u. and 0.016 a.u. respectively, with positive Laplacians, see Table 6) indicate donor–acceptor type bonding interactions.

Table 6 Bonding descriptors at the Yb–C_α and Yb–C^(ag)_γ line critical points. The NBO and QTAIM charges are indicated for the atoms concerned by the agostic interactions

Bonds	ρ b	∇^2ρb		H b
a On Lu^III(CH(SiMe3)2)3 complex.
Yb–Cα	0.078	0.149	1.434	−0.0286
Yb–C^(ag)γ	0.016	0.058	0.865	0.0018

---

Charges	q Yb	q Ca	q Sib
NBO^a	1.32	−1.38	1.81	−1.11
QTAIM	3.21	−2.03	2.82	−0.82

---

The NBO and QTAIM charges vary due to their different ways of partitioning the total electron density onto the individual atoms, but both indicate that a Yb–C_γ interaction is caused by the Coulomb attraction between the positively charged Yb and negatively charged C_γ atoms.

Computational interpretation of the NMR data. In order to confirm our tentative interpretation and provide a site-specific assignment, we calculated the NMR shift tensors of all the spin-active nuclei in the complex. The total NMR shift can be expressed as:

δ = δ_orb + δ_FC + δ_PSO + δ_SD + δ_LR, (1)

where δ_orb corresponds to the orbital chemical shift, i.e. the contribution from the orbital motion of the electrons, δ_FC is the Fermi contact shift due to the through-bond hyperfine interaction, δ_PSO is the paramagnetic spin–orbital shift due to the interaction between the nuclear spin and the electron orbital angular momentum, δ_SD and δ_LR are the short-range intra-molecular and long-range inter-molecular pseudo-contact shifts (PCS) due to the through-space hyperfine interactions, respectively. To account for long-range contributions, we calculated through-space magnetic dipolar contributions using the semi-classical point-dipolar equation (eqn (S10), ESI†) and a spherical bath of surrounding paramagnetic ions up to 50 Å distant in the crystal structure. The intramolecular contributions to the NMR shielding tensor of each nucleus were calculated according to the following equation,where σ^orb is the diamagnetic orbital contribution calculated using a scalar relativistic ZORA-DFT method employing the PBE0 functional, χ^s is the spin-only magnetic susceptibility tensor calculated from the SO-CASPT2 method and the hyperfine tensors are computed either from SO-CASSCF or unrestricted DFT methods. μ_B is the Bohr magneton and g_e is the free electron g-factor. In accordance with the tentative assignment of the experimental spectra, a three-site fast exchange model was employed to average the shift tensors both within the methyl groups (along the Si–C_i bonds) and the Me₃Si groups (along the C₁–Si bonds). The total computed shift tensors are presented both before (in Table 7) and after (in Table S10, ESI†) taking into account these rotations.

Table 7 Calculated and experimental shift parameters for the proximal (denoted by p) and distal (denoted by d) –SiMe₃ group of Yb^III(CH(SiMe₃)₂)₃ in the Haeberlen convention after a three-site fast exchange averaging of the shielding tensors. The shielding tensor is computed according to 2 where the magnetic susceptibility tensor has been computed with the SO-CASPT2 method and the hyperfine tensors are either from the SO-CASSCF or DFT(PBE0) methods. Long-range contributions has been accounted using the semi-classical point dipolar equation according to eqn (S10)

Method		^29Si		^13C		^1H
		p	d	p	d	p	d
	δ ^orb	−10.7	−9.2	2.8	4.6	0.2	0.4
	δ ^LR	16.9	16.5	28.5	9.5	15.6	27.6
SO-CASPT2/CASSCF	δ ^SD	−67.4	−9.6	−4.4	0.5	7.4	2.1
	δ ^PSO	−201.0	−29.2	−15.9	1.7	21.4	6.6
	δ ^FC	3.0	7.6	2.4	0.5	0.2	0.0
	δ ^total	−259.2	−23.9	13.4	16.8	44.8	36.7
	Δδ	−493.2	−19.3	−41.4	−28.4	10.2	21.8
SO-CASPT2/PBE0	δ ^SD	−61.2	−10.2	−1.1	−0.4	6.3	1.9
	δ ^PSO	−78.4	−10.3	−8.6	1.0	7.4	2.4
	δ ^FC	−24.4	−77.4	67.7	14.7	3.0	0.4
	δ ^total	−157.8	−90.6	89.3	29.4	32.5	32.7
	Δδ	−321.8	−122.0	−256.6	−51.0	25.1	18.3
Exp	δ	−220 ± 20	−30 ± 30	40 ± 20	−20 ± 20	30 ± 20	−20 ± 20
	Δδ	−542 ± 3	409 ± 3	−183 ± 4	140[+30, −270]	153 ± 1	−56 ± 1

---

On examining the computed shift tensors, we see that each nuclear species gives two distinct signals, with the shift and shift anisotropy of one species being consistently larger than those of the other species. There are clear quantitative discrepancies with the experimental values, but the general trends are reproduced. We can therefore assign the signals from the Me₃Si₍₂₎ group, with the larger shifts and shift anisotropies, to the proximal (p) ligand, and the signals from Me₃Si₍₁₎, with the smaller shifts and shift anisotropies, to the distal (d) ligand.

It is instructive to examine the breakdown of the shifts into the contributions given in eqn (1). The FC contribution is negligible in all cases, due to the very limited transfer of the unpaired spin density to these atoms over two, three or four bonds. The intra-molecular PCS is more significant, and is consistently larger for the proximal ligand than for the distal ligand, for all three nuclear species, which is a straightforward consequence of the former being in closer proximity to Yb than the latter. This conclusion is also true in the presence of rotational dynamics, where upon rotation about the C₁–Si bond, the three methyls on Si₂ are on average closer to the Yb ion than those on Si₁. The same trend is seen for the more dominant PSO contribution, which for the same reasons is consistently larger by up to one order of magnitude for the proximal ligand. Finally, the long-range PCS is also dominant, due to the large magnetic anisotropy of Yb(III) in this complex. A comparison between the proximal and distal ligands reveals more comple trends than for the intra-molecular PCS, due to the packing of molecules in the crystal lattice.

Overall, the interpretation of the NMR data provides evidence that the same structural distortions, observed in the low-temperature XRD structure and associated with the presence of 3c–2e Yb–Me–Si interactions, persist at the higher temperature of the solid-state NMR measurements (ca. 300 K). Therefore, the Yb[CH(SiMe₃)₂]₃ complex possesses the Yb⋯C_γ interaction, described as a pseudo bridging Yb–Me–Si group and previously observed¹⁰ for Lu[CH(SiMe₃)₂]₃ (see Fig. 1), at both low- and room-temperature and irrespective of the presence of the incomplete electronic f-shell.

Conclusions

This study establishes that pulsed EPR and paramagnetic solid-state NMR spectroscopies are highly complementary and able, when coupled with the advanced computational methods, to provide detailed information about the geometry and electronic structure of paramagnetic compounds such as Yb[CH(SiMe₃)₂]₃. Besides the specific geometry typically accessible by X-ray diffraction, this study provides direct spectroscopic evidences for the 3c–2e Yb–Me–Si interaction and for the presence of π-character in the Yb–C bond in this paramagnetic compound, paralleling what is observed for the diamagnetic Lu analog10 and so commonly among the corresponding d⁰ organometallics,^3,4,7 often referred to as an α-H agostic interaction. In fact, the magnetic data for Yb[CH(SiMe₃)₂]₃ indicates a f¹³ ground state configuration with no evidence for a multiconfigurational ground state that is often observed in lanthanide compounds,^20,55–58 probably further explaining the observed similarities with the Lu isostructural compound. Yet, while magnetic susceptibility measurements indicate that the magnetic moment is consistent with that of a free Yb(III) ion, CAS-based calculations instead reveal an unusually large crystal-field splitting resulting in a ground KD that is almost completely thermally isolated even at room temperature and which results in a large magnetic anisotropy.

Author contributions

A. A. and D. K. performed EPR measurements. F. A. and M. P. C. developed the synthetic procedures. J. P. C. and K. J. S. conducted NMR measurements. M. A. I., J. P. C. and A. A. performed quantum chemical calculations. M. W. and F. A. performed XRD studies. D. B. and M. D. W. conducted magnetic susceptibility measurements. M. D. W., A. J. P., C. C., G. J., G. P. and R. A. A. supervised the project. All authors participated in writing the manuscript. A. A., F. A., M. A. I., J. P. C., K. J. S. and M. P. C. declare equal contribution.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. A. was supported by a SNF – ANR grant (Mr CAT 2-77275-15). J. P. C. was supported by the Swedish Research Council (2016-03441), M. A. I. by the Agence Nationale de la Recherche (ANR-21-CE29-0010-01) and by an installation grant of the ENS Lyon, and K. J. S. by the European Research Council (ERC-2015-CoG P-MEM-NMR). Calculations were performed thanks to an access grant to the Pôle Scientifique de Modélisation Numérique (PSMN) at the ENS Lyon. We acknowledge Laurent Maron (Université Paul Sabatier, Toulouse) for discussions at the early stage of this project. We acknowledge Maciej Korzynski (ETHZ) for a help with preparation of the manuscript. We acknowledge Elizaveta A. Suturina (University of Bath) and Aleksander Jaworski (Stockholm University) for the advices concerning quantum chemistry calculations in lanthanide complexes. We thank Martin Bröring (Institut für Anorganische und Analytische Chemie) at TU Braunschweig for providing access to the SQUID magnetometer.

References

1. J. Hartwig, Organotransition Metal Chemistry: From Bonding to Catalysis, University Science Books, Mill Valley, California, 2010.
2. G. Wilkinson, G. A. Stone and E. W. Abel, Comprehensive organometallic chemistry: The synthesis, reactions, and structures of organometallic compounds, Pergamon Press, 1982.
3. W. W. Lukens, M. R. Smith and R. A. Andersen, A π-donor spectrochemical series for X in (Me₅C₅)₂TiX, and β-agostic interactions in X = Et and N (Me) Ph, J. Am. Chem. Soc., 1996, 118, 1719–1728.
4. C. P. Gordon, S. Shirase, K. Yamamoto, R. A. Andersen, O. Eisenstein and C. Copéret, NMR chemical shift analysis decodes olefin oligo- and polymerization activity of d⁰ group 4 metal complexes, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5867–5876.
5. M. Brookhart and M. L. H. Green, Carbon-hydrogen-transition metal bonds, J. Organomet. Chem., 1983, 250, 395–408.
6. M. Brookhart, M. L. Green and G. Parkin, Agostic interactions in transition metal compounds, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908.
7. C. P. Gordon, D. B. Culver, M. P. Conley, O. Eisenstein, R. A. Andersen and C. Copéret, π-Bond Character in Metal-Alkyl Compounds for C–H Activation: How, When, and Why?, J. Am. Chem. Soc., 2019, 141, 648–656.
8. A. G. Avent, C. F. Caro, P. B. Hitchcock, M. F. Lappert, Z. Li and X.-H. Wei, Synthetic and structural experiments on yttrium, cerium and magnesium trimethylsilylmethyls and their reaction products with nitriles; with a note on two cerium β-diketiminates, Dalton Trans., 2004, 1567–1577.
9. P. B. Hitchcock, M. F. Lappert, R. G. Smith, R. A. Bartlett and P. P. Power, Synthesis and structural characterisation of the first neutral homoleptic lanthanide metal(III) alkyls: [LnR₃][Ln = La or Sm, R = CH (SiMe₃)₂], J. Chem. Soc., Chem. Commun., 1988, 1007–1009.
10. M. P. Conley, G. Lapadula, K. Sanders, D. Gajan, A. Lesage, I. Del Rosal, L. Maron, W. W. Lukens, C. Coperet and R. A. Andersen, The nature of secondary interactions at electrophilic metal sites of molecular and silica-supported organolutetium complexes from solid-state NMR spectroscopy, J. Am. Chem. Soc., 2016, 138, 3831–3843.
11. C. Eaborn, P. B. Hitchcock, K. Izod and J. D. Smith, A Monomeric Solvent-Free Bent Lanthanide Dialkyl and a Lanthanide Analog of a Grignard Reagent. Crystal Structures of Yb{C(SiMe₃)₃}₂ and [Yb{C(SiMe₃)₃}I·OEt₂]₂, J. Am. Chem. Soc., 1994, 26, 12071–12072.
12. W. J. Evans, R. Anwander and J. W. Ziller, Inclusion of Al₂Me₆ in the Crystalline Lattice of the Organometallic Complexes LnAl₃Me₁₂, Organometallics, 1995, 14, 1107–1109.
13. K. Yan, B. M. Upton, A. Ellern and A. D. Sadow, Lewis Acid-Mediated β-Hydride Abstraction Reactions of Divalent M(C(SiHMe₂)₃)₂THF₂ (M = Ca, Yb), J. Am. Chem. Soc., 2009, 131, 15110–15111.
14. K. Yan, A. V. Pawlikowski, C. Ebert and A. D. Sadow, A tris(alkyl)yttrium compound containing six β-agostic Si–H interactions, Chem. Commun., 2009, 656–658.
15. H. C. Longuet-Higgins, The structure of some electron-deficient molecules, J. Chem. Soc., 1946, 139–143.
16. M. Brookhart, M. L. H. Green and G. Parkin, Molecular structure and bonding in hexamethyldialuminum, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 6908–6914.
17. W. T. Klooster, R. S. Lu, R. Anwander, W. J. Evans, T. F. Koetzle and R. Bau, Neutron Diffraction Study of [Nd(AlMe₄)₃]_0.5Al₂Me₆ at 100 K: The First Detailed Look at a Bridging Methyl Group with a Trigonal-Bipyramidal Carbon Atom, Angew. Chem., Int. Ed., 1998, 37, 1268–1270.
18. A. J. Pell, G. Pintacuda and C. P. Grey, Paramagnetic NMR in solution and the solid state, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 111, 1–271.
19. M. M. Roessler and E. Salvadori, Principles and applications of EPR spectroscopy in the chemical sciences, Chem. Soc. Rev., 2018, 47, 2534–2553.
20. R. G. Denning, J. Harmer, J. C. Green and M. Irwin, Covalency in the 4f Shell of tris-Cyclopentadienyl Ytterbium (YbCp₃) - A Spectroscopic Evaluation, J. Am. Chem. Soc., 2011, 133, 20644–20660.
21. A. Formanuik, A.-M. Ariciu, F. Ortu, R. Beekmeyer, A. Kerridge, F. Tuna, E. J. L. McInnes and D. P. Mills, Actinide covalency measured by pulsed electron paramagnetic resonance spectroscopy, Nat. Chem., 2016, 9, 578–583.
22. R. J. Kurland and B. R. McGarvey, Isotropic NMR shifts in transition metal complexes: the calculation of the Fermi contact and pseudocontact terms, J. Magn. Reson., 1970, 2, 286–301.
23. S. Moon and S. Patchkovskii, Calculation of NMR and EPR Parameters, John Wiley & Sons, Ltd, 2004, ch. 20, pp. 325–338.
24. T. O. Pennanen and J. Vaara, Density-functional calculations of relativistic spin–orbit effects on nuclear magnetic shielding in paramagnetic molecules, J. Chem. Phys., 2005, 123, 174102.
25. T. O. Pennanen and J. Vaara, Nuclear magnetic resonance chemical shift in an arbitrary electronic spin state, Phys. Rev. Lett., 2008, 100, 133002.
26. W. Van den Heuvel and A. Soncini, NMR chemical shift in an electronic state with arbitrary degeneracy, Phys. Rev. Lett., 2012, 109, 073001.
27. W. Van den Heuvel and A. Soncini, NMR chemical shift as analytical derivative of the Helmholtz free energy, J. Chem. Phys., 2013, 138, 054113.
28. J. Vaara, S. A. Rouf and J. Mares, Magnetic couplings in the chemical shift of paramagnetic NMR, J. Chem. Theory Comput., 2015, 11, 4840–4849.
29. G. Parigi, L. Benda, E. Ravera, M. Romanelli and C. Luchinat, Pseudocontact shifts and paramagnetic susceptibility in semiempirical and quantum chemistry theories, J. Chem. Phys., 2019, 150, 144101.
30. L. Lang, E. Ravera, G. Parigi, C. Luchinat and F. Neese, Solution of a puzzle: high-level quantum-chemical treatment of pseudocontact chemical shifts confirms classic semiempirical theory, J. Phys. Chem. Lett., 2020, 11, 8735–8744.
31. S. A. Rouf, J. Mares and J. Vaara, ¹H chemical shifts in paramagnetic Co(II) pyrazolylborate complexes: a first-principles study, J. Chem. Theory Comput., 2015, 11, 1683–1691.
32. R. Pigliapochi, A. J. Pell, I. D. Seymour, C. P. Grey, D. Ceresoli and M. Kaupp, DFT investigation of the effect of spin–orbit coupling on the NMR shifts in paramagnetic solids, Phys. Rev. B, 2017, 95, 054412.
33. A. Mondal, M. W. Gaultois, A. J. Pell, M. Iannuzzi, C. P. Grey, J. Hutter and M. Kaupp, Large-scale computation of nuclear magnetic resonance shifts for paramagnetic solids using CP2K, J. Chem. Theory Comput., 2018, 14, 377–394.
34. A. Mondal and M. Kaupp, Computation of NMR shifts for paramagnetic solids including zero-field-splitting and beyond-DFT approaches. Application to LiMPO₄ (M = Mn, Fe, Co, Ni) and MPO₄ (M = Fe, Co), J. Phys. Chem. C, 2019, 123, 8387–8405.
35. A. Pyykkönen, R. Feher, F. H. Köhler and J. Vaara, Paramagnetic Pyrazolylborate Complexes Tp2M and Tp* 2M: ¹H, ¹³C, ¹¹B, and ¹⁴N NMR Spectra and First-Principles Studies of Chemical Shifts, Inorg. Chem., 2020, 59, 9294–9307.
36. A. B. Andersen, A. Pyykkönen, H. J. A. Jensen, V. McKee, J. Vaara and U. G. Nielsen, Remarkable reversal of ¹³C-NMR assignment in d¹, d² compared to d⁸, d⁹ acetylacetonate complexes: analysis and explanation based on solid-state MAS NMR and computations, Phys. Chem. Chem. Phys., 2020, 22, 8048–8059.
37. A. Ashuiev, F. Allouche, N. Wili, K. Searles, D. Klose, C. Copéret and G. Jeschke, Molecular and supported Ti(III)-alkyls: efficient ethylene polymerization driven by the π-character of metal-carbon bonds and back donation from a singly occupied molecular orbital, Chem. Sci., 2021, 12, 780–792.
38. B. Tecle, A. F. M. Maqsudur Rahman and J. P. Oliver, X-ray crystal structure of trimethylsilylmethyllithium, J. Organomet. Chem., 1986, 317, 267–275.
39. P. Höfer, A. Grupp, H. Nebenführ and M. Mehring, Hyperfine sublevel correlation (HYSCORE) spectroscopy: a 2D ESR investigation of the squaric acid radical, Chem. Phys. Lett., 1986, 132, 279–282.
40. P. Schosseler, T. Wacker and A. Schweiger, Pulsed ELDOR Detected NMR, Chem. Phys. Lett., 1994, 224, 319–324.
41. F. Allouche, D. Klose, C. P. Gordon, A. Ashuiev, M. Wörle, V. Kalendra, V. Mougel, C. Copéret and G. Jeschke, Low-Coordinated Titanium (III) Alkyl—Molecular and Surface—Complexes: Detailed Structure from Advanced EPR Spectroscopy, Angew. Chem., Int. Ed. Engl., 2018, 130, 14741–14745.
42. B. O. Roos and P. Pyykkö, Bonding Trends in Molecular Compounds of Lanthanides: The Double-Bonded Carbene Cations LnCH₂⁺ (Ln = Sc, Y, La–Lu), Chem. – Eur. J., 2010, 16, 270–275.
43. U. Haeberlen, Advances in magnetic resonance, Academic Press, 1976, vol. 1.
44. R. J. Clément, A. J. Pell, D. S. Middlemiss, F. C. Strobridge, J. K. Miller, M. S. Whittingham, L. Emsley, C. P. Grey and G. Pintacuda, Spin-transfer pathways in paramagnetic lithium transition-metal phosphates from combined broadband isotropic solid-state MAS NMR spectroscopy and DFT calculations, J. Am. Chem. Soc., 2012, 134, 17178–17185.
45. G. Kervern, G. Pintacuda, Y. Zhang, E. Oldfield, C. Roukoss, E. Kuntz, E. Herdtweck, J.-M. Basset, S. Cadars and A. Lesage, Solid-state NMR of a paramagnetic DIAD-FeII catalyst: sensitivity, resolution enhancement, and structure-based assignments, J. Am. Chem. Soc., 2006, 128, 13545–13552.
46. S. K. Zaremba, Good lattice points, discrepancy, and numerical integration, Ann. Mat. Pura Appl., 1966, 73, 293–317.
47. H. Conroy, Molecular Schrödinger equation. VIII. A new method for the evaluation of multidimensional integrals, J. Chem. Phys., 1967, 47, 5307–5318.
48. V. B. Cheng, H. H. Suzukawa Jr and M. Wolfsberg, Investigations of a nonrandom numerical method for multidimensional integration, J. Chem. Phys., 1973, 59, 3992–3999.
49. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, The ORCA quantum chemistry program package, J. Chem. Phys., 2020, 152, 224108.
50. I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov and R. K. Carlson, et al., OpenMolcas: from source code to insight, J. Chem. Theory Comput., 2019, 15, 5925–5964.
51. F. Aquilante, J. Autschbach, A. Baiardi, S. Battaglia, V. A. Borin, L. F. Chibotaru, I. Conti, L. De Vico, M. Delcey and I. Fdez. Galván, et al., Modern quantum chemistry with [Open] Molcas, J. Chem. Phys., 2020, 152, 214117.
52. X. Zhou, M. F. Reid, M. D. Faucher and P. A. Tanner, Electronic spectra of Cs2NaYbF6 and crystal field analyses of YbX63-(X = F, Cl, Br), J. Phys. Chem. B, 2006, 110, 14939–14942.
53. F. Weinhold, C. R. Landis and E. D. Glendening, What is NBO analysis and how is it useful?, Int. Rev. Phys. Chem., 2016, 35, 399–440.
54. E. D. Glendening, C. R. Landis and F. Weinhold, NBO 7.0: new vistas in localized and delocalized chemical bonding theory, J. Comput. Chem., 2019, 40, 2234–2241.
55. R. L. Halbach, G. Nocton, J. I. Amaro-Estrada, L. Maron, C. H. Booth and R. A. Andersen, Understanding the Multiconfigurational Ground and Excited States in Lanthanide Tetrakis Bipyridine Complexes from Experimental and CASSCF Computational Studies, Inorg. Chem., 2019, 58, 12083–12098.
56. C. H. Booth, M. D. Walter, D. Kazhdan, Y.-J. Hu, W. W. Lukens, E. D. Bauer, L. Maron, O. Eisenstein and R. A. Andersen, Decamethylytterbocene complexes of bipyridines and diazabutadienes: multiconfigurational ground states and open-shell singlet formation, J. Am. Chem. Soc., 2009, 131, 6480–6491.
57. C. H. Booth, D. Kazhdan, E. L. Werkema, M. D. Walter, W. W. Lukens, E. D. Bauer, Y.-J. Hu, L. Maron, O. Eisenstein and M. Head-Gordon, Intermediate-valence tautomerism in decamethylytterbocene complexes of methyl-substituted bipyridines, J. Am. Chem. Soc., 2010, 132, 17537–17549.
58. M. D. Walter, P. T. Matsunaga, C. J. Burns, L. Maron and R. A. Andersen, Synthesis and Reactions of [Cp₂*Yb]₂(μ-Me) and [Cp₂*Yb]₂(μ-Me)(Me) and Related Yb₂(II,III) and Yb₂(III,III) Compounds, Organometallics, 2017, 36, 4564–4578.

---

Footnotes

† Electronic supplementary information (ESI) available. CCDC 2237830–2237832. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4cp00281d

‡ Richard A. Andersen passed away on June 16, 2019 while the early draft of this manuscript was being written; this manuscript is dedicated to his memory.

---