 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Gaining insight into molecular tunnel junctions with a pocket calculator without I–V data fitting. Five-thirds protocol†
Ioan
Bâldea

Theoretical Chemistry, Heidelberg University, Im Neuenheimer Feld 229, D-69120 Heidelberg, Germany. E-mail: ioan.baldea@pci.uni-heidelberg.de; Fax: +49 6221 545221; Tel: +49 6221 545219
First published on 23rd February 2024
Abstract
The protocol put forward in the present paper is an attempt to meet the experimentalists’ legitimate desire of reliably and easily extracting microscopic parameters from current–voltage measurements on molecular junctions. It applies to junctions wherein charge transport dominated by a single level (molecular orbital, MO) occurs via off-resonant tunneling. The recipe is simple. The measured current–voltage curve I = I(V) should be recast as a curve of V5/3/I versus V. This curve exhibits two maxima: one at positive bias (V = Vp+), another at negative bias (V = Vp−). The values Vp+ > 0 and Vp− < 0 at the two peaks of the curve for V5/3/I at positive and negative bias and the corresponding values Ip+ = I(Vp+) > 0 and Ip− = I(Vp−) < 0 of the current is all information needed as input. The arithmetic average of Vp+ and |Vp−| in volt provides the value in electronvolt of the MO energy offset ε0 = EMO − EF relative to the electrode Fermi level (|ε0| = e(Vp+ + |Vp−|)/2). The value of the (Stark) strength of the bias-driven MO shift is obtained as γ = (4/5)(Vp+ − |Vp−|)/(Vp+ + |Vp−|) sign (ε0). Even the low-bias conductance estimate, G = (3/8)(Ip+/Vp+ + Ip−/Vp−), can be a preferable alternative to that deduced from fitting the I–V slope in situations of noisy curves at low bias. To demonstrate the reliability and the generality of this “five-thirds” protocol, I illustrate its wide applicability for molecular tunnel junctions fabricated using metallic and nonmetallic electrodes, molecular species possessing localized σ and delocalized π electrons, and various techniques (mechanically controlled break junctions, STM break junctions, conducting probe AFM junctions, and large area junctions).
1 Introduction
Conventional semiconductor microelectronics has at its disposal a series of simplified equations to easily gain insight into underlying physics.1,2 This is the case, e.g., of the familiar Shockley equation (“ideal diode law”),3–6 expressing analytically the exponential dependence of the current I on bias V stemming from the microscopically built-in potential barrier at a p–n junction.In an attempt to establish the molecular structure–tunneling transport relationship, starting from ideas put forward by Newns and Schmickler in conjunction with electro/chemisorption,7–9 I have deduced, as a counterpart for molecular electronics, an appealingly simple formula for molecular junctions wherein thermal effects are ignored10,11 and the off-resonant tunneling current is dominated by a single level (molecular orbital MO).12
This off-resonant single level model (orSLM) expresses the current as a function of bias in terms of three key electronic structure parameters: the MO energy offset relative to electrodes’ Fermi energy ε0 = EMO − EF, the average MO coupling  to the two (generic substrate s and tip t) electrodes, and the bias-driven MO shift γ
to the two (generic substrate s and tip t) electrodes, and the bias-driven MO shift γ
 | (1) |
Above, G0 = 2e2/h = 77.48 µS is the conductance quantum and N is the number of molecules per junction. Within eqn (1), asymmetric I–V curves (current rectification) correspond to junctions where the MO energy is shifted by an applied bias (γ ≠ 0). I–V curves are symmetric (no current rectification) in the absence of a bias-driven MO shift (γ = 0, εV = ε0). To be sure, aiming at describing charge transport by tunneling in situations where thermal effects are negligible, eqn (1) has limits of validity precisely formulated.10,11 They should strictly be observed in specific applications to real molecular junctions.
Methodological advantages of the orSLM approach have been highlighted recently.13 One particular aspect worth mentioning is the excellent agreement between the MO offset extracted from transport data and the MO offset obtained from a completely different method, namely independent ultraviolet photoelectron spectroscopy (UPS) data. This finding is all the more important, since it has been reported for completely different homologous molecular series.14–16 This agreement represents perhaps the strongest support that validates the analysis based on the orSLM.
Fitting measured I–V data to eqn (1) and extracting best fitting parameters ε0, Γ (or the low bias conductance G, to which I will loosely refer as a “microscopic” parameter in order to obviate lengthy discussions for junctions with N > 1), and γ should pose no special problem. This is confirmed by numerous applications of the orSLM approach by many independent groups,17–41 which succeeded in correctly reproducing I–V curves measured for molecular junctions fabricated using various techniques.
Notwithstanding the aforementioned, publications also exist wherein, unfortunately, model parameter values have been incorrectly determined data fitting to eqn (1). Because emphasis in this paper is on how to easily and correctly estimate microscopic parameters by means of the orSLM, I intentionally refrain from citing misapplications of this approach. Still, I want to mention a frequent error that can be immediately identified. Those publications report MO offsets |ε0|(<eV/2) incompatible with the bias range (−V, +V) used for data fitting. This can be easily seen by inspecting eqn (1), wherein the denominator becomes negative at too higher biases, beyond the scope of this model. This corresponds to a completely nonphysical situation wherein the current and bias have opposite signs. In fact, as reiterated again and again,10,11 a necessary (“off-resonance”) condition for eqn (1) to apply is that of sufficiently lower biases (usually e|V| ≲ 1.4|ε0|).
Below, I will show that and how the microscopic parameters ε0, γ and G can be directly estimated from appropriately recasting the measured I–V curves obviating the usage of eqn (1) with adjustable model parameters which could lead to the unpleasant situations referred to in the preceding paragraph.
Before proceeding, let me emphasize what is already expressed by the title of this paper. My present aim is to demonstrated that, provided that conditions of validity clearly stated are fulfilled (see ref. 10 and 42 and Fig. 1 below), the orSLM allows to estimate microscopic parameters characterizing real molecular tunnel junctions obviating I–V data fitting. For this reason, a comparison with other data fitting approaches from the literature43–49 would be misplaced and will not be attempted.
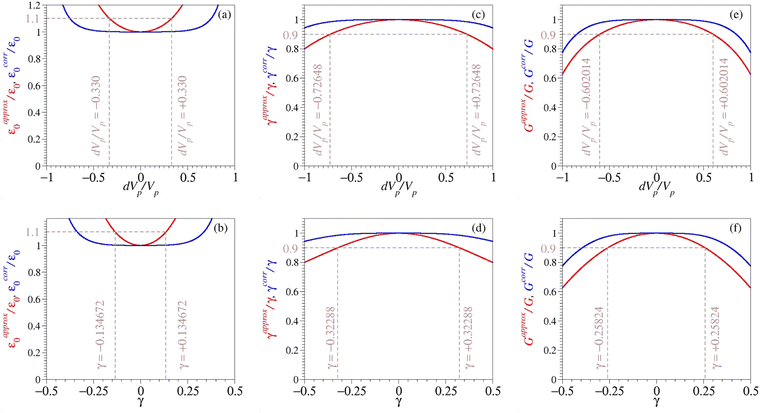 | ||
| Fig. 1 Relative deviations from the exact values of the model parameters ε0, γ, and G computed by eqn (9) and (10) (red and blue lines, respectively) plotted versus the relative peak asymmetry location δVp/Vp (left panels a, c, e) and versus the bias-driven MO shift γ (right panels b, d, f). The vertical brown lines visualize the ranges within which the parameters estimated viaeqn (9) are accuŕate within 10%, a typical value for experimental inaccuracies in real molecular junctions. | ||
2 Basic working equations
Aiming at providing a theoretical basis and generalizing the transition voltage spectroscopy (TVS) approach proposed by Frisbie et al.,50 I showed that the parameters ε0 and γ can be estimated from the so-called transition voltages Vt±12 | (2a) |
 | (2b) |
 | (3) |
Eqn (3) is a particular case (κ = 2) of a more general condition
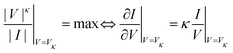 | (4) |
 | (5a) |
 | (5b) |
Above, Vκ+ and Vκ− are the positive and negative biases at the peaks of the plot of |V|κ/|I| versus V. Eqn (5) can also be easily deduced:12 one should plug the expression for the current (eqn (1) into eqn (4)) and solve the quadratic equation thus obtained.
As will be seen shortly below, the formulas for κ = 5/3 are particularly interesting
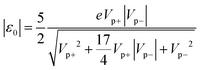 | (6a) |
 | (6b) |
In view of the special role played by the value κ = 5/3 anticipated above, I will write Vp± instead of V5/3± to specify the location of the peaks of |V|5/3/|I|
 | (6c) |
In principle, the parameters ε0 and γ can be computed from Vp±viaeqn (6) just as these parameters can be calculated from the transition voltages Vt±viaeqn (2) (or, in general, from Vκ±viaeqn (5)).
The reason why κ = 5/3 is a special value becomes clear by considering the case of symmetric I–V curves (γ = 0, cf.eqn (1)). In such cases the peaks of V5/3/I are located symmetrically around origin (V5/3+ = |V5/3−| ≡ Vp) and eqn (6a) reduces to
| γ = 0 → |ε0| = eVp | (7) |
That is, eqn (7) allows the most straightforward determination of the MO energy offset from the current–voltage measurements. What one has to do in order to estimate the MO offset ε0 of a junction with symmetric I–V characteristic is merely to draw a plot of V5/3/I versus V. Expressed in electronvolt, the value of the MO energy offset (ε0) is equal to the magnitude in volt of the bias (Vp = Vp+ = |Vp−|) at which the two symmetric peaks of the curve for V5/3/I are located.
To be sure, eqn (7) applies to molecular junctions having symmetric I–V characteristics (I(−V) = −I(V)) while real junctions often possess asymmetric characteristics (I(−V) ≠ −I(V)). Within the orSLM this asymmetry (current rectification) stems from a nonvanishing value γ ≠ 0 (cf.eqn (1)).
Because a nonvanishing γ is directly related (cf.eqn (6b)) to an asymmetric location of the peaks of V5/3/I around origin (Vp+ ≠ −Vp−), it makes sense to define an average peak voltage Vp and to consider Taylor series expansions of eqn (6) in terms of the departure δVp of Vp± from the average Vp
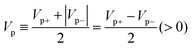 | (8a) |
 | (8b) |
The lowest order expansion of eqn (6) (i.e., neglecting all powers of δVp in the Taylor series) yields the following approximate expressions
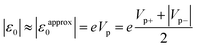 | (9a) |
 | (9b) |
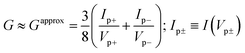 | (9c) |
Notice that in addition to ε0, γ, eqn (9c) presents an approximate estimate for the low bias conductance G. It has been deduced by series expansion of G expressed using eqn (1). Although G is routinely determined by linear fitting of low V data, the estimate viaeqn (9c) may be preferable in cases of noisy data at low bias. This may be a relevant aspect for reliably determining the tunneling attenuation β from conductances Gn ∝ exp(−βn) of menbers of variable size n of a homologous series.
3 Accuracy of the lowest order approximation
The smaller the asymmetry δVp (or, alternatively, the smaller the value or γ), the better the lowest order approximation underlying eqn (9), but the question relevant for practice is how good this approximation actually is.To illustrate the accuracy of the lowest order approximation, in Fig. 1 I depicted by red lines departures from the exact values of the parameters ε0, γ, and G estimated eqn (9) both as a function of the fractional peak voltage asymmetry δVp/Vp (panels a, c, and e) and as a function of the bias driven MO shift (panels b, d, and f). For the reader's convenience, in Fig. 1 I drew vertical lines to delimit the range where the model parameters estimated from eqn (9) are accurate to within 10%, a value typical for accuracy in molecular electronics.
Inspection of Fig. 1 reveals that all three parameters achieve this accuracy for |γ| ≲ 0.134. On this basis one can conclude that eqn (9) is indeed a good approximation. In saying this, I have in mind that for most real molecular tunnel junctions typical values of γ are relatively small (say |γ| ≲ 0.114,15,54–56). This is the case even for molecular junctions exhibiting substantial current rectification.57
To better understand why the lowest order approximations of eqn (9) are adequate for most practical purposes I present below the next-to-leading corrections (i.e., retaining the terms proportional to (δVp/Vp2) in the Taylor series)
 | (10a) |
 | (10b) |
 | (10c) |
They are depicted by blue lines in Fig. 1. As visible above, terms linear in δVp/Vp vanish; only quadratic terms (δVp/Vp)2 contribute.
To avoid misuses, I want to explicitly emphasize what Fig. 1 clearly visualizes. While the general orSLM model can be used to quantitatively analyze molecular junctions exhibiting strong current rectification,58,59 the five-thirds protocol cannot; it is designed to deal expeditiously with cases wherein current rectification is not very pronounced.
4 Practical recipe for the application of the five-thirds protocol
Fig. 2 illustrates how to apply the presently proposed five-thirds protocol to estimate the parameters for molecular junctions possessing symmetric and asymmetric I–V characteristics (additional details in the ESI†):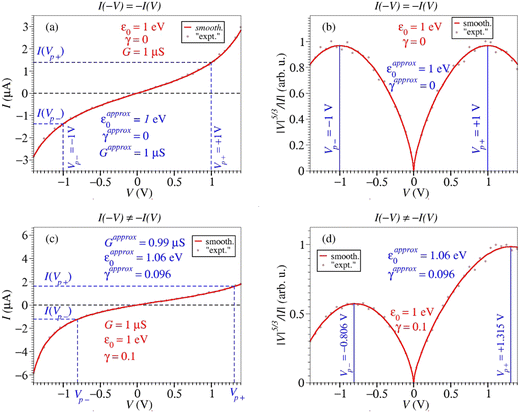 | ||
| Fig. 2 Schematic illustration of the five-thirds protocol at work for junctions with symmetric I–V characteristics (panels a and b) and asymmetric I–V characteristics (panels c and d). The red curves computed by using eqn (1) and parameter values depicted in red which mimic real I–V curves of panel a and c are recast as plots of |V|5/3/|I| versus bias (V) in panel b and d. The maximum locations at Vp± extracted from the right panels along with the corresponding current values Ip± obtained from the left panels are used to estimate the model parameters ε0, γ, and G viaeqn (9). The weak disorder (brown points) overimposed on the red I–V curves is intended to give a flavor of how applications to real junctions look like. | ||
(i) Recast the measured I–V data (panels a and c) as a plot of |V|5/3/|I| versus V (panels b and d).
(ii) Extract the values of the peak voltages Vp+ and Vp− from the maxima of |V|5/3/|I| at positive and negative bias. These values allow the straightforward determination of the MO energy offset ε0 and the MO bias-driven shift γ viaeqn (9a) and (9b), respectively. In cases of symmetric I–V curves Vp+ = −Vp− = Vp (γ = 0) and |ε0| = eVp. To accurately extract the peak positions (Vp±), noisy curves should be smoothed beforehand. This is a straightforward task for common software utilized by experimentalists (e.g., ORIGIN).
(iii) With the values of Vp+ and Vp− in hand, return to the I–V curves and extract the values of the current Ip+ and Ip− at the biases Vp+ and Vp− (Fig. 2a and c). Use these four values (Vp± and Ip±) to estimate the low bias conductance from eqn (9c). In cases of symmetric I–V curves, γ = 0, Ip+ = −Ip− = Ip, Vp+ = −Vp− = Vp = |ε0|, and eqn (9c) reduces to
 | (11) |
(iv) Inspection of Fig. 1a, c, and e allows one to assess the accuracy/reliability of the parameters ε0, γ, and G estimated viaeqn (9) at the value of δVp/Vp computed from the values Vp+ and Vp− directly extracted from the experimental I–V data in question without any assumption.
5 Applications to real junctions
To emphasize the generality of the presently proposed five-thirds protocol, I will consider junctions fabricated with the most frequently utilized fabrication platforms: single-molecule mechanically-controlled break junctions, single-molecule STM break junctions (N = 1), CP-AFM molecular junctions (N ∼ 100), and large area molecular junctions (N ≫ 1).As noted on several occasions (e.g., ref. 11) I–V data alone do not suffice to specify whether conduction is of p-type (ε0 < 0) or n-type (ε0 > 0) (i.e., mediated by an occupied or an unoccupied MO, respectively). However, in order to simplify the analysis of the real junctions considered below, I will (arbitrarily) “postulate” throughout p-type conduction. If the contrary holds true, the magnitudes of the parameters (|ε0| and |γ|) are correct but the values themselves have reversed sings (ε0 → −ε0, γ → −γ).
5.1 Mechanically controlled break junctions
To start with, I will consider two single-molecule mechanically controlled break junctions fabricated with tolane anchored on gold electrodes using thiol and cyano groups (4,4′-bisthiotolane (BTT)) and 4,4′-biscyanotolane (BCT), respectively.60 Digitized I–V curves for these junctions from ref. 60 are depicted by brown points in Fig. 3b and d. | ||
| Fig. 3 Application of the five-thirds protocol to mechanically controlled break junctions fabricated with (4,4′-bisthiotolane (BTT)) (panels a and b) and 4,4′-biscyanotolane (BCT) (panels c and d). The experimental I–V data (brown points) were obtained by digitizing experimental I–V curves reported in ref. 60. Smoothing of the experimental data (brown points) yielded the (red) curves in panels a and c, which allow the reliable extraction of the biases Vp+ and Vp− at the peaks of the |V|5/3/|I| curves. The values Vp+ and Vp− and the corresponding currents Ip+ ≡ I(Vp+) and Ip− ≡ I(Vp−) deduced from the I–V curves (panel b and d) serve as input in eqn (9). The results thus obtained (I–V curves and parameter values depicted in blue in panels b and d) have a quality comparable to those (depicted in red) deduced via data fitting to eqn (1) with adjustable parameters. The values of R2 depicted in blue were computed viaeqn (12). | ||
Due to the substantial noise of the experimental (digitized) curves (brown points in Fig. 3a and c), data smoothing (red curves in Fig. 3a and c) represents the first step needed in reliably extracting the bias values Vp+ and Vp− at the peaks of the curve for |V|5/3/|I|.
Given the fact that the I–V curve for the symmetric BTT molecule is practically symmetric, the maxima are located symmetric around origin Vp+ ≈ −Vp− ≈ 0.38 V. With the value Ip = |I(Vp±| ≈ 0.68 nA) estimated from the experimental I–V curve (Fig. 3a) the conductance at low bias G ≈ 1.8 nS can be deduced using eqn (11).
The I–V curve (brown points in Fig. 3d) for the asymmetric BCT molecule is slightly asymmetric. Accordingly, the peaks of the curve for |V|5/3/|I| are located slightly asymmetric around origin (Vp+ ≈ 0.48 V and Vp− ≈ −0.47 V, cf.Fig. 3c). With these vales, the parameters ε0, γ, and G of the BCT junction shown in the inset of Fig. 3c were estimated using eqn (9).
To illustrate the reliability of the five-thirds protocol for the BTT and BCT junctions considered, along the experimental I–V curve (brown points), I present both the fitting curve (line and parameter values pertaining to it in Fig. 3b and d are depicted in red) obtained using eqn (1) with adjustable model parameters and the I–V curve (line and parameter values pertaining to it in Fig. 3b and d are depicted in blue) computed viaeqn (1) with the model parameters ε0, γ, and G provided by the five-thirds protocol. As visible, the (blue) curves based on the five-thirds protocol and the fitting (red) curves cannot be distinguished from each other within the drawing accuracy. To put this excellent agreement in more quantitative terms, along with the coefficient of determination R2 obtained by data fitting to eqn (1) (values written in red in Fig. 3b and d), I also present the counterparts of R2 for the five-thirds protocol (values written in blue in Fig. 3b and d). The latter was obtained in the standard manner
| R2 = 1 − SSres/SStot | (12a) |
 | (12b) |
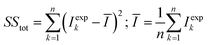 | (12c) |
5.2 STM break junctions
Next I will examine two single-molecule STM-BJ junctions with gold electrodes fabricated using 4,4′-diaminostilbene61 (Fig. 4a–c) and phenyldithiol62 (Fig. 4d and e). | ||
| Fig. 4 Application of the five-thirds protocol to STM break junctions fabricated with 4,4′-diaminostilbene61 (panels a, b, and c) and phenyldithiol (panel d and e).62 The values Vp+ and Vp− at the peaks of the |V|5/3/|I| curves and the corresponding currents Ip+ ≡ I(Vp+) and Ip− ≡ I(Vp−) deduced from the I–V curves (panel b and e) serve as input in eqn (9). The results thus obtained (I–V curves and parameter values depicted in blue in panels b and e) have a quality comparable to those (depicted in red) deduced via data fitting to eqn (1) with adjustable parameters. The values of R2 depicted in blue were computed viaeqn (12). Panel c illustrates that the present five-thirds protocol can be also be applied in situations where the bias range sampled in experiment is too narrow for applying TVS.14,15,50 | ||
In both cases no data smoothing was required to reliably extract Vp+ and Vp− from the peaks of Fig. 4a and d. With these values and the pertaining currents Ip+ and Ip− deduced from the experimental I–V curves of Fig. 4b and e (brown points), I arrived viaeqn (9) at the blue I–V curves. Again, these curves excellently agree with the red I–V curves obtained by data fitting to eqn (1) with model parameters adequately adjusted.
The junction of 4,4′-diaminostilbene allows one to reveal the potential advantage of the present five-thirds protocol over the standard TVS-orSLM approach12,14,15 based on the transition voltage Vt. As visible in Fig. 4c, the range of negative biases sampled in experiment61 was not sufficiently broad. This prevents the determination of the model parameters using eqn (2). That is, the five-thirds protocol can also be applied in cases where the use of eqn (2) is impractical.
5.3 CP-AFM molecular junctions
Smoothing the experimental transport data is also superfluous in analyzing the CP-AFM junctions of 1,1′-,4′,1″-terphenyl-4-thiol and gold electrodes63 (Fig. 5a and b) and of triphenyldithiol and silver electrodes (Fig. 5c and d).64 Data smoothing is necessary to process the experimental I–V curve measured for the recently investigated CP-AFM junctions fabricated with 1-dodecyne (C12A) and silver electrodes anchored via alkynyl groups depicted in Fig. 5e and f.65 | ||
| Fig. 5 Application of the five-thirds protocol to CP-AFM junctions fabricated with 1-,1′-,4′-,1″-terphenyl-4-thiol and gold electrodes (panels a and b),63 with triphenyldithiol and silver electrodes (panels c and d),64 and with 1-dodecyne and silver electrodes (panel e and f).65 The values Vp+ and Vp− at the peaks of the |V|5/3/|I| curves and the corresponding currents Ip+ ≡ I(Vp+) and Ip− ≡ I(Vp−) deduced from the I–V curves (panel b and e) serve as input in eqn (9). The results thus obtained (I–V curves and parameter values depicted in blue in panels b and e) have a quality comparable to those (depicted in red) deduced via data fitting to eqn (1) with adjustable parameters. The values of R2 depicted in blue were computed viaeqn (12). The experimental data of panels d (junctions based on triphenyldithiols) and f (junctions based on 1-dodecyne (C12A)) were measured in conjunction with work reported in ref. 64 and 65 (courtesy of Zuoti Xie). | ||
Inspection of the parameter values in the legends reveals that the five-thirds protocol works for all these cases.
5.4 Large-area molecular junctions
Last but not least, I will focus on three large area molecular junctions completely different from each other (Fig. 6).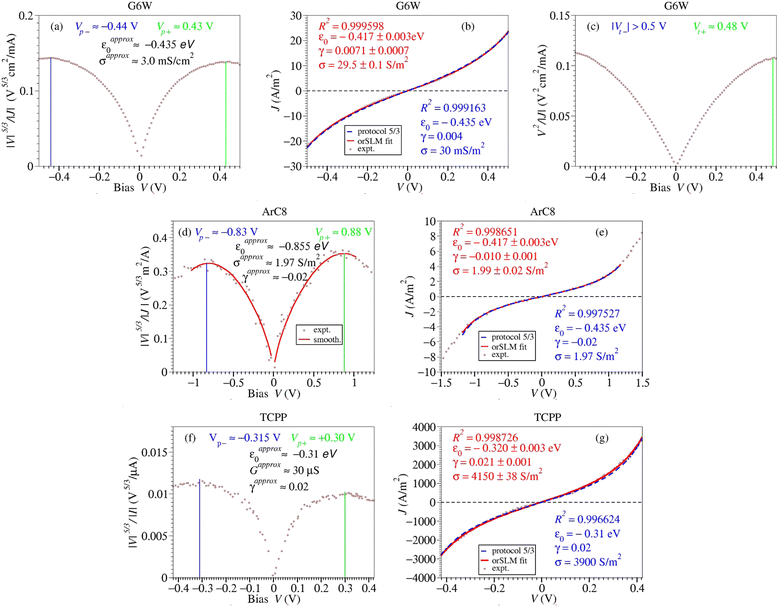 | ||
| Fig. 6 Application of the five-thirds protocol to large area molecular junctions fabricated with a peptide (G6W)66 (panels a, b, and c; experimental data: courtesy of Cunlan Guo), aryl octane (ArC8)49 (panel d and e; experimental data from digitized Fig. 4a of ref. 49), and metal free ITO-based TCPP (panels f and g; experimental from digitized Fig. 4c of ref. 67). The values Vp+ and Vp− at the peaks of the |V|5/3/|I| curves and the corresponding currents Ip+ ≡ I(Vp+) and Ip− ≡ I(Vp−) deduced from the I–V curves (panel b, e and g) serve as input in eqn (9). The results thus obtained (I–V curves and parameter values depicted in blue in panels b, e and g) have a quality comparable to those (depicted in red) deduced via data fitting to eqn (1) with adjustable parameters. The values of R2 depicted in blue were computed from eqn (12). Panel c illustrates that the present five-thirds protocol can be also be applied in situations where the bias range sampled in experiment is too narrow for applying TVS.14,15,50 Because the transport measurements for large area junctions report current densities (J) rather than current intensities (I), values of the conductivity σ rather that conductance G are presented in this figure. In analyzing the ArC849 and TCPP67 data, the bias range considered has been restricted to the bias range for which the orSLM applies.10–12 | ||
The results depicted in Fig. 6a–c refer to a peptide-based junction fabricated with gold substrate and EGaIn top electrodes.66 The specific peptide considered (G6W = GGGGGGW) consists of six glycines (G) with one aromatic amino acid at the C-terminus (tryptophan, W). Fig. 6d and e pertain to a junction consisting of a self-assembled monolayer of aryl octane (ArC8) with graphene contacts as protecting interlayer. The results depicted in Fig. 6f and g are for metal-free ITO-TCPP/PEDOT:PSS molecular junctions.67 They were fabricated using carboxylic acid-modified porphyrin (meso-tetra(4-carboxyphenyl)porphyrin, TCPP) adsorbed to a bottom electrode of indium tin oxide (ITO) and having the conductive PEDOT:PSS (poly(3,4-ethylenedioxythiophene):poly(styrenesulfonate)) polymer as top electrode.67 Recall that ITO is a degenerate n-type semiconductor possessing a wide band gap which makes it a transparent conductive electrode routinely employed in optoelectronic devices.
The message conveyed by the numerical values of the parameters inserted in Fig. 6 should be obvious. As in the preceding cases, they validate the five-thirds protocol also for the large-area junctions considered. To avoid some misunderstandings persisting in the literature, validation of the five-thirds protocol implicitly validates the orSLM for large area molecular tunnel junctions, the model on which this protocol relies. In addition, Fig. 6c reveals the same advantage of the five-thirds protocol over the conventional TVS approach based on eqn (2) already noted in the discussion related to Fig. 4c: to be applicable, the five-thirds protocol requires a narrower bias range than needed for TVS.
6 Additional remarks
For completeness, let me finally mention that, similar to eqn (9), lowest expansions in the location asymmetry (δVκ) of the peaks Vκ+ = Vκ + δVκ and Vκ− = −Vκ + δVκ of the general quantity |V|κ/|I| can also be deduced | (13a) |
 | (13b) |
 | (13c) |
In the particular case κ = 2 (“transition voltage spectroscopy”, TVS), they read
 | (14a) |
 | (14b) |
 | (14c) |
7 Conclusion
By deducing eqn (9), in this paper I aimed at providing experimentalists with an extremely simple recipe (“five-thirds protocol”) that allows straightforward extraction of the microscopic parameters of molecular tunnel junctions obviating I–V data fitting. As anticipated by the title, a pocket calculator is all what one needs for the few arithmetic operations to be performed in applying eqn (9).By validating the “five-thirds protocol” for the platforms most commonly used to fabricate molecular tunnel junctions, I aimed at convincing the molecular electronics community on the generality of this approach enabling to gain important insight into the molecular structure–tunneling transport relationship. As seen, it can be applied even in situations beyond the reach of the (by now) standard TVS-based approach12 whose broad usefulness has already be recognized.13
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research did not receive any specific financial support but benefited from computational support by the state of Baden-Württemberg through bwHPC and the German Research Foundation through Grant No. INST 40/575-1 FUGG (bwUniCluster 2, bwForCluster/HELIX, and JUSTUS 2 cluster).References
-
S. Sze and K. K. Ng, p–n Junctions, John Wiley & Sons, Ltd, 2006, pp. 77–133 Search PubMed
.
-
M. T. Thompson, in Intuitive Analog Circuit Design (Second Edition), ed. M. T. Thompson, Newnes, Boston, 2nd edn, 2014, pp. 53–86 Search PubMed
.
- W. Shockley, Bell Syst. Tech. J., 1949, 28, 435–489 CrossRef
.
-
W. Shockley, Electrons and holes in semiconductors: with applications to transistor electronics, Van Nostrand New York, New York, 1950 Search PubMed
.
- C.-T. Sah, R. N. Noyce and W. Shockley, Proc. IRE, 1957, 45, 1228–1243 Search PubMed
.
- J. Moll, Proc. IRE, 1958, 46, 1076–1082 Search PubMed
.
- D. M. Newns, Phys. Rev., 1969, 178, 1123–1135 CrossRef CAS
.
- P. W. Anderson, Phys. Rev., 1961, 124, 41–53 CrossRef CAS
.
- W. Schmickler, J. Electroanal. Chem., 1986, 204, 31–43 CrossRef CAS
.
- I. Bâldea, Phys. Chem. Chem. Phys., 2023, 25, 19750–19763 RSC
.
- I. Bâldea, Phys. Chem. Chem. Phys., 2024, 26, 6540–6556, 10.1039/D3CP05046G
.
- I. Bâldea, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035442 CrossRef
.
- D. Taherinia and C. D. Frisbie, Phys. Chem. Chem. Phys., 2023, 25, 32305–32316 RSC
.
- Z. Xie, I. Bâldea and C. D. Frisbie, J. Am. Chem. Soc., 2019, 141, 3670–3681 CrossRef CAS PubMed
.
- Z. Xie, I. Bâldea and C. D. Frisbie, J. Am. Chem. Soc., 2019, 141, 18182–18192 CrossRef CAS PubMed
.
- Q. V. Nguyen, Z. Xie and C. D. Frisbie, J. Phys. Chem. C, 2021, 125, 4292–4298 CrossRef CAS
.
- K. Smaali, N. Clément, G. Patriarche and D. Vuillaume, ACS Nano, 2012, 6, 4639–4647 CrossRef CAS PubMed
.
- T. K. Tran, K. Smaali, M. Hardouin, Q. Bricaud, M. Oçafrain, P. Blanchard, S. Lenfant, S. Godey, J. Roncali and D. Vuillaume, Adv. Mater., 2013, 25, 427–431 CrossRef CAS PubMed
.
- D. Fracasso, M. I. Muglali, M. Rohwerder, A. Terfort and R. C. Chiechi, J. Phys. Chem. C, 2013, 117, 11367–11376 CrossRef CAS
.
- S. Guo, G. Zhou and N. Tao, Nano Lett., 2013, 13, 4326–4332 CrossRef CAS PubMed
.
- K. Wu, M. Bai, S. Sanvito and S. Hou, J. Chem. Phys., 2013, 139, 194703 CrossRef PubMed
.
- W.-Y. Lo, W. Bi, L. Li, I. H. Jung and L. Yu, Nano Lett., 2015, 15, 958–962 CrossRef CAS PubMed
.
- A. Xiang, M. Wang, H. Wang, H. Sun, S. Hou and J. Liao, Chem. Phys., 2016, 465–466, 40–45 CrossRef CAS
.
- D. Nose, K. Dote, T. Sato, M. Yamamoto, H. Ishii and Y. Noguchi, J. Phys. Chem. C, 2015, 119, 12765–12771 CrossRef CAS
.
- A. Kovalchuk, T. Abu-Husein, D. Fracasso, D. Egger, E. Zojer, M. Zharnikov, A. Terfort and R. Chiechi, Chem. Sci., 2015, 7, 781–787 RSC
.
- C. Jia, A. Migliore, N. Xin, S. Huang, J. Wang, Q. Yang, S. Wang, H. Chen, D. Wang, B. Feng, Z. Liu, G. Zhang, D.-H. Qu, H. Tian, M. A. Ratner, H. Q. Xu, A. Nitzan and X. Guo, Science, 2016, 352, 1443–1445 CrossRef CAS PubMed
.
- D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440 CrossRef CAS PubMed
.
- Q. Wang, R. Liu, D. Xiang, M. Sun, Z. Zhao, L. Sun, T. Mei, P. Wu, H. Liu, X. Guo, Z.-L. Li and T. Lee, ACS Nano, 2016, 10, 9695–9702 CrossRef CAS PubMed
.
- H. Jeong, Y. Jang, D. Kim, W.-T. Hwang, J.-W. Kim and T. Lee, J. Phys. Chem. C, 2016, 120, 3564–3572 CrossRef CAS
.
- L. Li, W.-Y. Lo, Z. Cai, N. Zhang and L. Yu, Chem. Sci., 2016, 7, 3137–3141 RSC
.
- Z. Cai, W.-Y. Lo, T. Zheng, L. Li, N. Zhang, Y. Hu and L. Yu, J. Am. Chem. Soc., 2016, 10630–10635 CrossRef CAS PubMed
.
- W.-Y. Lo, N. Zhang, Z. Cai, L. Li and L. Yu, Acc. Chem. Res., 2016, 49, 1852–1863 CrossRef CAS PubMed
.
- X. Yi, N. V. Izarova, M. Stuckart, D. Guérin, L. Thomas, S. Lenfant, D. Vuillaume, J. van Leusen, T. Duchoň, S. Nemšák, S. D. M. Bourone, S. Schmitz and P. Kögerler, J. Am. Chem. Soc., 2017, 139, 14501–14510 CrossRef CAS PubMed
.
- Z. Cai, N. Zhang, M. A. Awais, A. S. Filatov and L. Yu, Angew. Chem., Int. Ed., 2018, 57, 6442–6448 CrossRef CAS PubMed
.
- I. Jeong and H. Song, Appl. Spectrosc. Rev., 2018, 53, 246–263 CrossRef
.
- S. Valianti, J.-C. Cuevas and S. S. Skourtis, J. Phys. Chem. C, 2019, 123, 5907–5922 CrossRef CAS
.
- M.-W. Gu, H. H. Peng, I.-W. P. Chen and C.-H. Chen, Nat. Mater., 2021, 20, 658–664 CrossRef CAS PubMed
.
- Y. Liu, X. Qiu, S. Soni and R. C. Chiechi, Chem. Phys. Rev., 2021, 2, 021303 CrossRef
.
- Y. Kim, K. Im and H. Song, Materials, 2022, 15, 774 CrossRef CAS PubMed
.
- M. Carlotti, S. Soni, A. Kovalchuk, S. Kumar, S. Hofmann and R. C. Chiechi, ACS Phys. Chem. Au, 2022, 2, 179–190 CrossRef CAS PubMed
.
- J. Jang, P. He and H. J. Yoon, Acc. Chem. Res., 2023, 56, 1613–1622 CrossRef CAS PubMed
.
- I. Bâldea, Phys. Chem. Chem. Phys., 2024, 26, 7230–7235, 10.1039/D2CP05110A
.
- W. Schmickler and N. Tao, Electrochim. Acta, 1997, 42, 2809–2815 CrossRef CAS
.
- W. Han, E. N. Durantini, T. A. Moore, A. L. Moore, D. Gust, P. Rez, G. Leatherman, G. R. Seely, N. Tao and S. M. Lindsay, J. Phys. Chem. B, 1997, 101, 10719–10725 CrossRef CAS
.
- W. Wang, T. Lee and M. A. Reed, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 035416 CrossRef
.
- I. V. Pobelov, Z. Li and T. Wandlowski, J. Am. Chem. Soc., 2008, 130, 16045–16054 CrossRef CAS PubMed
.
- A. R. Garrigues, L. Yuan, L. Wang, E. R. Mucciolo, D. Thompon, E. del Barco and C. A. Nijhuis, Sci. Rep., 2016, 6, 26517 CrossRef CAS PubMed
.
- V. Delmas, V. Diez-Cabanes, C. van Dyck, E. Scheer, K. Costuas and J. Cornil, Phys. Chem. Chem. Phys., 2020, 22, 26702–26706 RSC
.
- K. Im, D.-H. Seo and H. Song, Crystals, 2022, 12, 767 CrossRef CAS
.
- J. M. Beebe, B. Kim, J. W. Gadzuk, C. D. Frisbie and J. G. Kushmerick, Phys. Rev. Lett., 2006, 97, 026801 CrossRef PubMed
.
- I. Bâldea, Phys. Chem. Chem. Phys., 2015, 17, 15756–15763 RSC
.
- I. Bâldea, Z. Xie and C. D. Frisbie, Nanoscale, 2015, 7, 10465–10471 RSC
.
- I. Bâldea, Europhys. Lett., 2012, 98, 17010 CrossRef
.
- R. M. Metzger, Chem. Rev., 2015, 115, 5056–5115 CrossRef CAS PubMed
.
- M. S. Johnson, L. D. Wickramasinghe, C. N. Verani and R. M. Metzger, J. Phys. Chem. C, 2016, 120, 10578–10583 CrossRef CAS
.
- Z. Xie, I. Bâldea, Q. Nguyen and C. D. Frisbie, Nanoscale, 2021, 13, 16755–16768 RSC
.
- R. P. Sullivan, J. T. Morningstar, E. Castellanos-Trejo, M. E. Welker and O. D. Jurchescu, Nano Lett., 2023, 23, 10864–10870 CrossRef CAS PubMed
.
- R. Metzger, Nanoscale, 2018, 10, 10316–10332 RSC
.
- R. Gupta, J. A. Fereiro, A. Bayat, A. Pritam, M. Zharnikov and P. C. Mondal, Nat. Rev. Chem., 2023, 7, 106–122 CrossRef CAS PubMed
.
- L. A. Zotti, T. Kirchner, J.-C. Cuevas, F. Pauly, T. Huhn, E. Scheer and A. Erbe, Small, 2010, 6, 1529–1535 CrossRef CAS PubMed
.
- J. R. Widawsky, M. Kamenetska, J. Klare, C. Nuckolls, M. L. Steigerwald, M. S. Hybertsen and L. Venkataraman, Nanotechnology, 2009, 20, 434009 CrossRef CAS PubMed
.
- W. Lee and P. Reddy, Nanotechnology, 2011, 22, 485703 CrossRef PubMed
.
- A. Tan, S. Sadat and P. Reddy, Appl. Phys. Lett., 2010, 96, 013110 CrossRef
.
- Z. Xie, I. Bâldea, C. Smith, Y. Wu and C. D. Frisbie, ACS Nano, 2015, 9, 8022–8036 CrossRef CAS PubMed
.
- Y. Chen, I. Bâldea, Y. Yu, Z. Liang, M.-D. Li, E. Koren and Z. Xie, Langmuir, 2024 DOI:10.1021/acs.langmuir.3c03759
.
- L. Su, Y. Zhang, Q. Pan, H. Liang, H. Wang and C. Guo, New J. Chem., 2023, 47, 17277–17283 RSC
.
- S. Sergani, Y. Furmansky and I. Visoly-Fisher, Nanotechnology, 2013, 24, 455204 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Additional details and figures. See DOI: https://doi.org/10.1039/d4cp00217b |
| This journal is © the Owner Societies 2024 |
