Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Manifestation of site energy landscapes for ion transport in borate glasses†
Victor H.
Gunawan
,
Martin
Schäfer
and
Karl-Michael
Weitzel
 *
*
Philipps-Universität Marburg, Chemistry Department, Hans-Meerwein Str. 4, 35043 Marburg, Germany. E-mail: weitzel@chemie.uni-marburg.de
First published on 30th April 2024
Abstract
The potential energy landscape of lithium borate glass of composition Li3B7O12 has been investigated by the charge attachment induced transport (CAIT) technique. Here, native lithium ions have been replaced by foreign alkali ions, M+ = K+, Rb+, Cs+. All experiments exhibit a pronounced decrease of native ion diffusion coefficients over more than 4 orders of magnitude with decreasing local population of Li+. The energy landscape is modelled by a site energy distribution (SED) with a concentration dependent Fermi energy of the native Li+ ions. The width of the populated part of the SED is found to be 250 meV (FWHM). The conclusion is made possible by a combination of a macroscopic ion replacement experiment with a Nernst–Planck–Poisson modelling of concentration depth profiles measured by secondary ion mass spectrometry (SIMS). Possible generalizations of macroscopic transport theory to match an Onsager ansatz are discussed.
1. Introduction
The potential energy landscape of mobile ions in solid-state materials and the atomic scale structure are intimately interrelated.1–4 This interrelation and the resultant properties, e.g. the mobility of the ions,5–11 is of paramount interest in contemporary material science with direct applications in energy storage and conversion. Understanding the interplay of structure, energy landscape and ionic transport of ionic solids is of crucial importance for a knowledge-based development of improved and new functionalities of these materials.Here, we demonstrate combined experimental and theoretical efforts in quantifying such landscapes and its resulting transport function. As a model system we have chosen lithium borate, for which the structure – transport relation has already attracted a considerable amount of attention.12–18 We describe the results of unique transport experiments, where native mobile lithium ions in a lithium borate glass are depleted and replaced uni-directionally by foreign alkali ions M+ = K+, Rb+ and Cs+ in a charge attachment induced transport (CAIT) experiment. The resulting depletion/replacement profiles extend down to several hundred nm into the material as measured by time-of-flight secondary ion mass spectrometry (ToF-SIMS) resembling time-dependent macroscopic transport with characteristic transport coefficients. The experimental data reveal that most of the native lithium ions are indeed mobile but a fraction of several percent of the ions appears to be immobile. In order to understand and rationalize these experimental findings, a macroscopic transport theory is employed. The macroscopic approach is based on the framework of the Nernst–Planck–Poisson theory, focusing on the time dependent macroscopic flux of ion density on a spatial grid with effective diffusion coefficients.
The analysis reveals that the diffusion coefficient of the native mobile lithium ions decreases by approximately 4 orders of magnitude as the molar fraction of the lithium is decreased from 1 to 0.2 (the molar fraction of the foreign ion increases concomitantly). It is observed that a finite fraction of the native lithium ions is effectively immobile because the diffusion coefficient of some native lithium ions becomes significantly smaller than that of the foreign alkali ions, in which case the concentration profiles exhibit a time-independent plateau. The variation of native diffusion coefficients can be translated into a site energy distribution. Employing the concept of a concentration dependent ionic Fermi energy, the width of the populated part of the SED is found to be 250 meV (FWHM).
2. Methodology
2.1 Charge-attachment induced transport
In the first step, concentration depth profiles are generated by means of the charge-attachment induced transport (CAIT) technique.19–21 In this experiment, three samples of Li3B7O12 glass from the same glass batch were shined on each with a different alkali ion beam, i.e. potassium (K+), rubidium (Rb+) and cesium (Cs+), respectively. The charge carriers are attached to the sample surface and induce the transport of charge carriers towards a grounded backside electrode due to a gradient of the electrochemical potential. The result is the evolution of concentration depth profiles in the sample where a part of the native Li+ ions is replaced by foreign ions (i.e., K+, Rb+ or Cs+ ions). The profiles are measured by time-of-flight secondary ion mass spectrometry (ToF-SIMS) and the raw data (Fig. S1, ESI†) subsequently normalized to obtain quantitative information on the concentration of both ion species as function of depth below the front surface (Fig. S2, ESI†). The three concentration profiles obtained are shown in Fig. S3 (ESI†).2.2 Macroscopic transport coefficients
To gain information on the diffusion coefficients operative during the experiment, simulations based on the mathematical framework of the Nernst–Planck–Poisson (NPP) (some literature uses the abbreviation PNP) equations19,21–31 were performed. The coupled set of NPP equations describe the ion transport over macroscopic distances due to gradients of the electrical potential and of the relevant concentrations.The implementation of the NPP equations follows the standard form employed by many groups and demonstrated to be very successful despite the obvious simplifications implied. Essentially, there is one Nernst–Planck equation as given in eqn (1) per chemical species, i, considered.
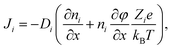 | (1) |
The first term in the brackets is often referred to as the diffusion part and the second as the migration part. In this work Nernst–Planck equations are combined with the Poisson equation and solved numerically on a large grid as function of time. The implementation is outlined in some more detail in the ESI† including the boundary conditions as well as the underlying assumptions being made. The pivotal point to be stressed is, that the diffusion coefficients, Di, involved in the NPP formalism are effective diffusion coefficients, the interpretation of which must not be confused with any of the liquid state assumptions of classical Nernst–Planck (NP) theory. As will be elaborated at a later point, the effective diffusion coefficients measured by the CAIT approach are identical to the diffusion coefficients Dσ, obtained from the low frequency limit of impedance spectroscopy.32,33
3. Results and discussion
3.1 Concentration depth profiles
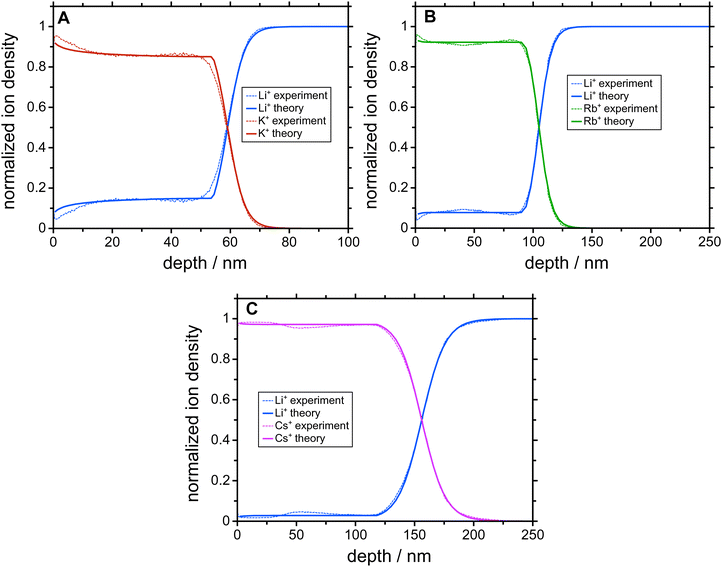
The results of the NPP simulations are concentration depth profiles of the mobile ion species that are compared with the experimentally measured profiles. The only free parameters entering the simulations are the diffusion coefficients of the two mobile ion species. All other parameters are determined by the geometry of the sample and the experimental conditions of the CAIT experiment (Table S1, ESI†). Fig. 1 shows a comparison between experimental and simulated profiles. Evidently, native Li+ ions were replaced by K+, Rb+, and Cs+ ions, respectively, down to approximately 100 nm. The data exhibit a sharp diffusion front and a plateau of nearly constant Li+ concentration in the region left to the diffusion front. This plateau is observed at about 15% of the bulk ion density for the K+-CAIT, at 7% for the Rb+-CAIT and 3% for the Cs+-CAIT. This implies that a corresponding fraction of native Li+ ions is effectively immobile on the time scale of the experiment. In principle, one could consider the possibility that different types of Li+ ions may be present as for example reported by Yamada et al. for a Li3PS4 glass.34 Here, some energetically low-lying part of the population could evade the ion exchange. This possibility cannot be ruled out categorically. However, the fact that the plateau observed is different for different foreign ions suggest that this is rather an effect of the foreign ion.The advancement in the understanding is contained in the diffusion coefficients employed for the simulation. The pivotal finding is that the diffusion coefficient of the native Li+ ions is markedly concentration dependent, but the diffusion coefficient of the foreign ion, i.e., K+, Rb+, and Cs+, is apparently constant, independent of the mobile ion concentration.
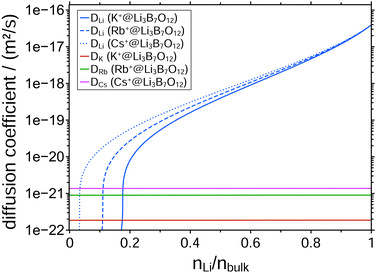
To date, a number of CAIT experiments have been published, for which depletion/replacement profiles have been analyzed in the framework of the NPP transport theory.21,32,35–37 In all but one case, the native diffusion coefficient, Dnative, varied over 3 to 4 orders of magnitude, while the foreign diffusion coefficient, Dforeign, was constant. Since the set of NPP equations cannot universally be inverted analytically to solve for the D functions directly, we performed a large number of NPP calculations with all possibly meaningful combinations of Dnative and Dforeign. But no better agreement between experiment and simulation was found. The diffusion coefficients yielding the best match of the simulated to the observed concentration profiles for the three different CAIT experiments are presented in Fig. 2. For Li+ fractions nLi/nbulk ≥ 0.4, the three Dnative functions are hardly discernible. This lends support to the conclusion that specifically this part of the Dnative functions reflects properties of the original native material. For nLi/nbulk ≤ 0.4 the three native D functions start to differ, reflecting different plateau levels for the foreign ions, K+, Rb+, and Cs+. The nearly constant Li+ concentration in these plateau regions is caused by an orders of magnitude lower Li+ diffusion coefficient compared to that of the foreign ions. The remaining Li+ ions in that region are immobile on the time scale of the experiment. The position of the plateau is encoded in the Li+ fraction nLi/nbulk at which the native diffusion coefficient becomes approximately one order of magnitude smaller than that of the foreign one.
3.2 Rationalization of the dependence of Dnative and Dforeign on ionic concentrations
The main result of this work is that the native diffusion coefficient varies by at least 4 orders of magnitude relative to the bulk value, while the external diffusion coefficient needs to be kept constant for obtaining good agreement between experimental and calculated concentration profiles in the NPP modelling. The variation of the native diffusion coefficient, ultimately, is a result of the energy landscape of the glass.There seems to be consensus that in a perfect crystal, all atoms of the same chemical type at equivalent crystal sites have identical site energy and feel identical barriers, corresponding to delta-distributions of energy minima and maxima.4,38 In an amorphous structure of a glass, broad distributions of site energies (potential minima) and barriers (saddle point energies) characterize the energy landscape for the mobile ions.39,40 As of now, there doesn’t seem to exist a consensual protocol for construction of site energy landscapes, i.e. the site energy distribution (SEDs), which is free from physical assumptions. As a consequence, it is at this point impossible to proof a unique SED, but only to demonstrate that SEDs presented here are compatible with experimental diffusion coefficients, the derivation of which is also based on model assumptions.
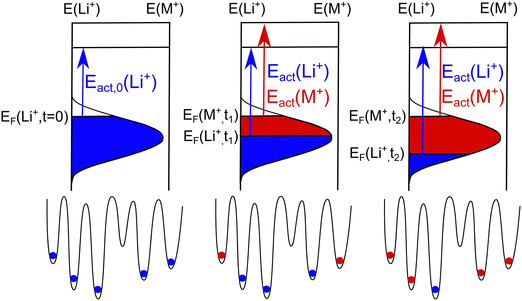
A visualization of a possible SED is given in the left part of Fig. 3. In the glass prior to the CAIT experiment, the sites are filled up with native Li+ ions from the bottom to top of the distribution. The highest occupied energy is indicated as initial ionic Fermi energy, EF(Li+, t = 0). The blue shaded area indicates all populated sites and is referred to as populated site energy distribution (PSED). Energetically, the sites above the Fermi level are shown to be unoccupied (vacancies). Lammert et al. calculated the total number of available sites as a function of the alkali ion density in Li–silicate glasses.41 The authors found about 20% more sites than alkali ions present for very dilute Li concentration and about 3% vacant sites for high Li concentrations. In the current work, we assume 10% vacancies in the SED calculations of this work. In general, the diffusion coefficients derived are hardly affected by the exact number of vacancies assumed to be present. At this point, we do not rule out the possibility that also some of the sites remain vacant energetically below the Fermi level. Note, that the vacancies are not treated explicitly in the NPP formalism.
At bulk density, the measured activation energy can be interpreted to be the result of an energy difference between the highest occupied site energy EF(nbulk) = EF(Li, t = 0) and an energy threshold for long range transport EDC. When the ion transport starts the native PSED is depopulated top down since ions with low effective barrier tend to move before ions with higher activation barrier (compare center and right part of Fig. 3 where the top edge of the blue shaded area is lowered). This leads to the concept of a concentration dependent Fermi energy EF(n). As a result, we may define a concentration dependent activation energy (Eact(n) = EDC − EF(n)).21,31
The concentration dependent activation energy implies that also the effective diffusion coefficient is concentration dependent. Here, the simplest physical model for a variation of diffusion coefficients over several orders of magnitude employing the energy domain is the one reflected in eqn (2).
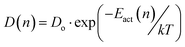 | (2) |
This model is predicting a variation of Dnative over approximately 4 orders of magnitude, if one assumes that the effective activation energy varies by about 0.3 eV as the concentration of the native lithium ions decreases from the bulk value to, e.g., 1/10 of the bulk value which determines the width of the PSED. In the calculations, the concentration dependent diffusion coefficient function, Dnative, (eqn (2)) enters the Nernst–Planck eqn (1). Conceptually one may consider Dnative to be one of the primary observables in the CAIT experiment and subsequently discuss the inversion of eqn (2) leading from a variation of Dnative to a variation of Eact(n), which is then translated into an effective populated site energy distribution. Practically the analysis is implemented in the opposite direction. The calculations start with the construction of the SED, from there the variation of Eact(n) and the variation of Dnative(n) is calculated, which enters the NPP equations. The details of the construction of the SED and the derivation of D(n) is given in the ESI† (part 2.5). Ultimately the SED/PSED are varied until agreement between experimental and modelled concentration depth profiles is obtained, cf.Fig. 1.
While the model presented above offers a simple rationalization of a concentration dependent native ion diffusion coefficient, the observation of an apparently concentration-independent diffusion coefficient for the foreign ion in the CAIT experiment is still puzzling. Within the PSED picture illustrated in Fig. 3 the energetically top level of the foreign ion PSED, i.e. the foreign ion Fermi level, stays effectively constant during the replacement process. This would automatically lead to a constant activation energy and also a constant diffusion coefficient. The question may be asked whether there is additional evidence of a constant Dforeign, which is independent of the SED model proposed. Such an argument is elaborated below.
In our solution of the NPP equations, electroneutrality is maintained in the sample, except in the spatial region of the diffusion front, where a small negative excess charge of less than 1‰ is present. The electroneutrality is correlated with the situation that a site being vacated by a native Li+ ion in the transport direction is filled in by a neighboring foreign ion coming “from behind” in the direction of transport. In the energy domain that neighboring foreign ion will likely originate from anywhere in the SED of those foreign ions. Eventually, another foreign ion enters the sample from the front surface. The important assumption made in the implementation of the energy landscape underlying the modeling by the NPP equations is, that replacement processes dominate at the diffusion front in the spatial domain and at the current Fermi level, EF(n), of the native Li+ ions in the energy domain. Two different PSED‘s evolve - one for the native ion and one for the foreign ion, where that for the foreign ion (red area in Fig. 3) grows at the cost of that for the native ions (blue area in Fig. 3). If these two SEDs do not effectively intermix on the time scale of the experiment, then the Fermi level of the native Li+ ions could monotonically decrease with decreasing lithium ion content in the region of the diffusion front, while the Fermi level of the foreign ion would stay constant. With ongoing CAIT experiment, only sites energetically below the Fermi level of the foreign ions would be occupied. This would explain why the diffusion coefficient of the native ion is markedly concentration-dependent, but the diffusion coefficient of the foreign ion is apparently constant. It is interesting to note that this model would not only apply to the CAIT experiment employed in this work but also to any unidirectional transport experiment involving replacement, e.g. electric field assisted ion exchange42,43 and alkali proton substitution.44,45
Ultimately, the observation of an apparently constant Dforeign could be interpreted as an indication that intermixing of the two SEDs is not operative on the time scale of the experiment. This immediately raises the question, whether the hypothesis could be verified in a future experiment. Eventually, one would expect that the two SEDs should intermix. The question is, how long does this take and what are the essential ingredients? We will come back to this question below and suggest an experiment to test the hypothesis.
At this point, the alternative hypothesis that the blue and the red population in Fig. 3 intermix instantaneously seems incompatible with the model of a concentration dependent Fermi energy for the native ion and a de facto concentration independent Fermi energy for the foreign ion.
From yet another point of view, basically the entire concentration variation is encoded in the diffusion front. For the foreign ion this implies the possibility that the observation of constant Dforeign is a property of the diffusion front correlated with an effective energetic bottleneck and/or strain effects at that front. In fact, the concentration variation of the native ion is also encoded in the diffusion front. On the other hand, there is a known, experimentally measured bulk conductivity and consequently a bulk diffusion coefficient, which is expected to continuously vary from the bulk value to the diffusion front value.
The de facto 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 replacement of native lithium ions by foreign alkali ions can be regarded as the native ions pulling the foreign ions behind or from the foreign ions pushing the native ions ahead. Ultimately, all available information suggests that the picture of native ions pulling the foreign ions behind is operative. To this end, in the ESI† we derive an analytical relation between the diffusion coefficient of the foreign alkali ion, Dforeign, and the native lithium ion, DLi, (part 2.10).
1 replacement of native lithium ions by foreign alkali ions can be regarded as the native ions pulling the foreign ions behind or from the foreign ions pushing the native ions ahead. Ultimately, all available information suggests that the picture of native ions pulling the foreign ions behind is operative. To this end, in the ESI† we derive an analytical relation between the diffusion coefficient of the foreign alkali ion, Dforeign, and the native lithium ion, DLi, (part 2.10).
 | (3) |
3.3 Site energy distribution of Li3B7O12
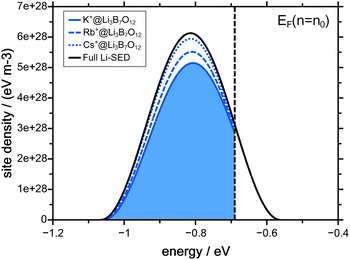
As pointed out in the previous paragraph, the concentration dependent native diffusion coefficient can be interpreted as a result of a PSED which is depopulated top down. The PSED that is connected to the concentration dependent lithium diffusion coefficients shown in Fig. 2 is given in Fig. 4.The black curve in Fig. 4 indicates the full Li-SED. However, some of the native ions remain immobile during the course of the CAIT experiments. The profiles shown in Fig. 1 show that about 3% of the Li+ ions in the Cs-CAIT experiment remain immobile – in the Rb- and the K-CAIT experiment 7% and 15% of the Li+ ions are immobile. Correspondingly, 97% (Cs-CAIT), 93% (Rb-CAIT) and 85% (K-CAIT) of the Li+-ions are mobile and hence only their fraction can be depopulated from the PSED. These mobile parts of the PSED are shown as blue dotted (Cs-CAIT) and blue dashed line (Rb-CAIT) and as blue shaded area (K-CAIT). The difference between the black curve and the blue curves refers to the immobile ions.
The pivotal point is that all three CAIT experiments can be described employing one and the same Li-SED, independent of the foreign ion. It is just the ratio of diffusion coefficients between immobile ions and mobile ions, which differs between the three foreign ions. This lends support to the conclusion that in particular the width of the mobile part of the native PSED indeed reflects a property of the material. For the Li3B7O12 glass, we arrive at a FWHM of the SED of 250 meV.
3.4 Relation between the effective diffusion coefficient and Onsager transport coefficients
This brings us to the point of interpreting the diffusion coefficients derived in this work. It has been emphasized above that the diffusion coefficients derived are effective diffusion coefficients. This triggers the question, to what other diffusion coefficients these numbers may be compared. Here it is important to emphasize that there is a large variety of different diffusion coefficients being discussed in the literature.11,46–51 In order to shed additional light on the relation of different diffusion coefficients, we have elaborated a description of the particle density flux, Ji, in the framework of the Onsager theory of irreversible thermodynamics in the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 52–56 We state the pivotal findings in the main text of this paper and point the reader's attention to the ESI† for details.
52–56 We state the pivotal findings in the main text of this paper and point the reader's attention to the ESI† for details.
The CAIT experiment as developed in the authors group is intrinsically subject to boundary conditions relating the change in particle density and in the chemical potential of the relevant species involved. The requirement of local electroneutrality demands that a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 substitution of native ions by foreign ions and implies for each finite grid element
1 substitution of native ions by foreign ions and implies for each finite grid element
| ∂n1 = −∂n2 | (4) |
| dj1 = −dj2 | (5) |
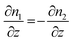 | (6) |
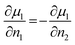 | (7) |
This leads to the conclusion that the chemical part of the flux density, i.e., the part driven by the concentration gradient contains a contribution which scales as twice the diffusion coefficient observable in a chemical tracer diffusion experiment. This difference between a CAIT experiment and a tracer diffusion experiment is rationalized by the fact that the CAIT replacement experiment contains an up-hill diffusion of native lithium ions in the concentration domain and a down-hill diffusion of foreign ions. This is clearly not operative in a tracer diffusion experiment. Note, that the up-hill diffusion of native Li+ ions in the concentration domain is still down-hill in the electrochemical potential domain, similar to analogous discussion in the literature.57–59 For more details, see the ESI.†
The elaboration of the boundary conditions stated above leads to the conclusion that Onsager formalism and NPP formalism are equivalent in the sense that the respective transport coefficients can be transformed from one basis into the other. E.g., in the case that non-diagonal Onsager coefficients can be neglected, the effective transport coefficients in an Onsager formalism and effective diffusion coefficients in the NPP formalism are related by
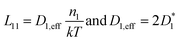 | (8) |
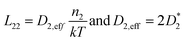 | (9) |
Ultimately, the effective diffusion coefficients determined by a CAIT experiment, Deff = DCAIT, are experimentally identical to the diffusion coefficients, Dσ, obtained in the DC limit of two electrode experiments, e.g. impedance spectroscopy.32,33 As a side note, DCAIT = Dσ equals two times the standard tracer diffusion coefficient, D* (cf. the ESI†).
As briefly pointed out above (and in more detail in the ESI†), in the case that the bulk diffusion coefficient, here D1,eff, of the native ion is much larger than that of the foreign ion, here D2,eff, the latter will numerically appear constant in the NPP analysis. The same holds true for the Onsager coefficients. If the foreign ion has a larger diffusion coefficient than the native bulk value, the native diffusion coefficient will appear constant while the diffusion coefficient of the foreign ion appears concentration dependent.36 In the case that non-diagonal Onsager coefficients cannot be neglected the transformation mentioned above is still possible and given in the ESI.†
Another subtle detail of the analysis pertains to the question whether the glass network is changed during the experiment. Here, the fact that basically the same SED is obtained for three different foreign ions employed in the CAIT experiment indicates that the native glass network is not severely modified by replacing one alkali ion by another. On the other hand, the data presented demonstrate the existence of plateaus of apparently immobile native ions. This apparent immobility of native ions could either arise from increased potential maxima (closed gateway states), or from deep potential minima (trapping sites). The concept of gateway states responsible for blocking of ion transport has also been put forward by Swenson et al. in the context of mismatch in both the energy and the structure domain.60
For alkali silicate glasses Heuer and coworkers demonstrated the absence of relaxation on the time scale of ion transport lending support to a static description of the energy landscape.61
4. Conclusions and outlook
Three lithium borate glass samples from the same batch have been subjected to CAIT experiments employing three different foreign ions, K+, Rb+, Cs+. As the primary observable concentration depth profiles originating from a replacement of native Li+ ions by the respective foreign ion have been obtained. The transport model employed based on a Nernst–Planck–Poisson formalism is capable of rationalizing all observables. This primarily concerns the concentration dependence of native diffusion coefficients but ultimately also the result that the width of the populated part of the site energy distribution of the glasses is 250 meV (FWHM). In previous work we had derived widths of 280 meV for a sodium calcium phosphate glass,31 320 meV for a sodium rubidium borate glass,21 and 113 meV for lithium aluminum germanium phosphate glass.62 Thus, the width of the SED is characteristic for a given glass system. With this result the goal of this work has been achieved.The success of the modelling presented does not preclude the possibility that other models might rationalize the observables as well or even better. Some of these alternative models may just not be known yet. Some other alternatives have not been pursued in this work. It seems appropriate to state, that the model presented here is the one with the least parameters. Clearly, there will be other models with more parameters, e.g., the phenomenological Onsager approach. As shown in the ESI† the effective diffusion coefficients employed in this work can be analytically transformed to the corresponding Onsager coefficients, Lij. Once those Onsager coefficients become available the transformation can be executed. But as long as those parameters – e.g., non-diagonal elements of a transport coefficient matrix – are not known it is not effective to increase the parameter space beyond what is needed. At this point it may help to emphasize, that the CAIT experiment, although it certainly leads to a non-equilibrium state (which can be frozen, however), fulfills the concept of micro-reversibility at each point of the process. Both, the Nernst–Planck as well as the Onsager63 approach appear equally suited to reflect this micro-reversibility of the transport process.
As a subtle detail of the NPP formalism we note, that the migration term in eqn (1) originates from a Nernst–Einstein concept,64–69 implying an ideal electrochemical potential of the type 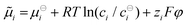 , where the index i indicates the species.30,70–72 The approximations implied could e.g. be overcome by introducing activities and activity coefficients deviating from unity. On the other hand, the approach pursued in this work has the advantage of staying in a particle focused framework. Here, the concentration dependence of native diffusion coefficients introduced is considered equivalent to leaving the approximation of an ideal electrochemical potential as well, while allowing for a simple transformation of a variation of diffusion coefficients to the energy domain.
, where the index i indicates the species.30,70–72 The approximations implied could e.g. be overcome by introducing activities and activity coefficients deviating from unity. On the other hand, the approach pursued in this work has the advantage of staying in a particle focused framework. Here, the concentration dependence of native diffusion coefficients introduced is considered equivalent to leaving the approximation of an ideal electrochemical potential as well, while allowing for a simple transformation of a variation of diffusion coefficients to the energy domain.
Above we speculated that two distinct PSEDs are operative for the native and the foreign ions. If such PSEDs exist for long enough time, this should be possible to proof by a follow-up experiment. This could, e.g., be a sequential double CAIT experiment, where the first M1+-CAIT generates a replacement profile of the type M1+@LBO and a second sequential CAIT experiment of the type M2+@M1+@LBO probes the PSED generated by the first CAIT experiment. Here M1+ is, e.g., a Rb+ ion and M2+ could be a Cs+ ion; LBO is the lithium borate. Such experiments are demanding. They are currently under way in our laboratory. At this point we raise the hypothesis, that the PSED depicted in Fig. 3 represent metastable states. The thermal equilibrium would be represented by intermixed PSEDs. It's likely, that the meta stable state persists for a long time compared to that of the experiment.
Where does the quantification of ion transport in solid state electrochemistry stand right now? From the point of view of the authors, all the formalism for describing long range (DC) transport of ions has been laid down. This includes the relation between the different diffusion coefficients reported in the literature. The effective diffusion coefficients measured by the CAIT technique are equivalent to the diffusion coefficients, Dσ, measured in the DC limit of impedance spectroscopy.32,33 On the other hand pulsed field gradient NMR techniques rather measure a self-diffusion coefficient which is best comparable to a tracer diffusion coefficient D*.73 Readers interested in the Haven ratio relating the tracer diffusion coefficient to DCAIT and Dσ, are referred to the ESI.†
The old challenge of bridging the understanding from the hopping in the local structural landscape – as observed in solid state NMR and impedance spectroscopy74–76 – all the way to long range DC transport as relevant for technical applications remains.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support of this work by the DFG through project P1 of the DFG Research Unit Energy Landscapes and Structure of Ion Conducting Solids (We 1330/23 and 24) is gratefully acknowledged. The authors are grateful for stimulating discussions within the ELSICS consortium.References
- J. Habasaki and Y. Hiwatari, Molecular dynamics study of the mechanism of ion transport in lithium silicate glasses: Characteristics of the potential energy surface and structures, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 144207, DOI:10.1103/PhysRevB.69.144207.
- J. Du, Molecular Dynamics Simulations of the Structure and Properties of Low Silica Yttrium Aluminosilicate Glasses, J. Am. Ceram. Soc., 2009, 92, 87–95, DOI:10.1111/j.1551-2916.2008.02853.x.
- M. Schuch, C. Trott and P. Maass, Network forming units in alkali borate and borophosphate glasses and the mixed glass former effect, RSC Adv., 2011, 1, 1370–1382, 10.1039/C1RA00583A.
- N. L. Allan, S. Conejeros, J. N. Hart and C. E. Mohn, Energy landscapes of perfect and defective solids: from structure prediction to ion conduction, Theor. Chem. Acc., 2021, 140, 151, DOI:10.1007/s00214-021-02834-w.
- H. Tuller, D. Button and D. Uhlmann, Fast ion transport in oxide glasses, J. Non-Cryst. Solids, 1980, 40, 93–118, DOI:10.1016/0022-3093(80)90096-4.
- I. Rubinstein, Electro-diffusion of ions, Society for Industrial and Applied Mathematics (SIAM 3600 Market Street Floor 6 Philadelphia PA 19104), 1990, vol. 11 Search PubMed.
- W. C. Chueh and S. M. Haile, Electrochemistry of mixed oxygen ion and electron conducting electrodes in solid electrolyte cells, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 313–341, DOI:10.1146/annurev-chembioeng-073009-101000.
- K. Kontturi, L. Murtomäki and J. A. Mazanares, Ionic transport processes. In electrochemistry and membrane science, Oxford Univ. Press, 2014 Search PubMed.
- S. W. Martin, R. Christensen, G. Olson, J. Kieffer and W. Wang, New Interpretation of Na + -Ion Conduction in and the Structures and Properties of Sodium Borosilicate Mixed Glass Former Glasses, J. Phys. Chem. C, 2019, 123, 5853–5870, DOI:10.1021/acs.jpcc.8b11735.
- P. Albertus, V. Anandan, C. Ban, N. Balsara, I. Belharouak, J. Buettner-Garrett, Z. Chen, C. Daniel, M. Doeff, N. J. Dudney, B. Dunn, S. J. Harris, S. Herle, E. Herbert, S. Kalnaus, J. A. Libera, D. Lu, S. Martin, B. D. McCloskey, M. T. McDowell, Y. S. Meng, J. Nanda, J. Sakamoto, E. C. Self, S. Tepavcevic, E. Wachsman, C. Wang, A. S. Westover, J. Xiao and T. Yersak, Challenges for and Pathways toward Li-Metal-Based All-Solid-State Batteries, ACS Energy Lett., 2021, 1399–1404, DOI:10.1021/acsenergylett.1c00445.
- J. Maier, Physical chemistry of ionic materials. Ions and electrons in solids, Wiley, 2023 Search PubMed.
- D. Button, L. Mason, H. Tuller and D. Uhlmann, Structural disorder and enhanced ion transport in amorphous conductors, Solid State Ionics, 1983, 9–10, 585–592, DOI:10.1016/0167-2738(83)90299-0.
- C.-P. E. Varsamis, A. Vegiri and E. I. Kamitsos, Cation dynamics in lithium borate glasses, J. Non-Cryst. Solids, 2002, 307–310, 956–962, DOI:10.1016/S0022-3093(02)01560-0.
- G.-H. Greiwe, Z. Balogh and G. Schmitz, Atom probe tomography of lithium-doped network glasses, Ultramicroscopy, 2014, 141, 51–55, DOI:10.1016/j.ultramic.2014.03.007.
- A.-M. Welsch, H. Behrens, D. Murawski and I. Horn, Lithium Mobility in Borate and Phosphate Glass Networks, Z. Phys. Chem., 2017, 231, 1303–1321, DOI:10.1515/zpch-2016-0927.
- M. Storek, J. F. Tilly, K. R. Jeffrey and R. Böhmer, Four-time 7Li stimulated-echo spectroscopy for the study of dynamic heterogeneities: Application to lithium borate glass, J. Magn. Reson., 2017, 282, 1–9, DOI:10.1016/j.jmr.2017.06.010.
- V. K. Michaelis, K. Levin, Y. Germanov, G. Lelong and S. Kroeker, Ultrahigh-Resolution 7 Li Magic-Angle Spinning Nuclear Magnetic Resonance Spectroscopy by Isotopic Dilution, Chem. Mat., 2018, 30, 5521–5526, DOI:10.1021/acs.chemmater.8b01626.
- V. Montouillout, H. Fan, L. Del Campo, S. Ory, A. Rakhmatullin, F. Fayon and M. Malki, Ionic conductivity of lithium borate glasses and local structure probed by high resolution solid-sate NMR, J. Non-Cryst. Solids, 2018, 484, 57–64, DOI:10.1016/j.jnoncrysol.2018.01.020.
- P. V. Menezes, J. Martin, M. Schäfer, H. Staesche, B. Roling and K.-M. Weitzel, Bombardment induced ion transport--part II. Experimental potassium ion conductivities in borosilicate glass, Phys. Chem. Chem. Phys., 2011, 13, 20123–20128, 10.1039/c1cp21216h.
- J. Martin, S. Mehrwald, M. Schäfer, T. Kramer, C. Jooss and K.-M. Weitzel, Transport of ions in a mixed Na +/K+ ion conducting glass - electrodiffusion profiles and electrochemical interphase formation, Electrochim. Acta, 2016, 191, 616–623, DOI:10.1016/j.electacta.2016.01.061.
- M. Schäfer, D. Budina and K.-M. Weitzel, Site energy distribution of sodium ions in a sodium rubidium borate glass, Phys. Chem. Chem. Phys., 2019, 21, 26251–26261, 10.1039/c9cp05194e.
- T. Teorell, Transport Processes and Electrical Phenomena in Ionic Membranes, Prog. Biophys. Biophys. Chem., 1953, 3, 305–369, DOI:10.1016/s0096-4174(18)30049-0.
- M. Kato, Numerical analysis of the Nernst-Planck-Poisson system, J. Theor. Biol., 1995, 177, 299–304, DOI:10.1006/jtbi.1995.0247.
- P. Schaetzel and B. Auclair, The generalized multicomponent Nernst–Planck diffusion equation—diffusion and self diffusion coefficients, Electrochim. Acta, 1998, 43, 3375–3377, DOI:10.1016/S0013-4686(98)00067-X.
- Z. Schuss, B. Nadler and R. S. Eisenberg, Derivation of Poisson and Nernst-Planck equations in a bath and channel from a molecular model, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 36116, DOI:10.1103/PhysRevE.64.036116.
- T. Sokalski, P. Lingenfelter and A. Lewenstam, Numerical Solution of the Coupled Nernst−Planck and Poisson Equations for Liquid Junction and Ion Selective Membrane Potentials, J. Phys. Chem. B, 2003, 107, 2443–2452, DOI:10.1021/jp026406a.
- M. Schäfer and K.-M. Weitzel, Bombardment induced ion transport. Part I, Phys. Chem. Chem. Phys., 2011, 13, 20112–20122, 10.1039/c1cp21215j.
- E. Vøllestad, H. Zhu and R. J. Kee, Interpretation of Defect and Gas-Phase Fluxes through Mixed-Conducting Ceramics Using Nernst–Planck–Poisson and Integral Formulations, J. Electrochem. Soc., 2014, 161, F114–F124, DOI:10.1149/2.067401jes.
- H. Zhu and R. J. Kee, Computational modeling of sodium-iodine secondary batteries, Electrochim. Acta, 2016, 219, 70–81, DOI:10.1016/j.electacta.2016.09.104.
- X. Jin, R. E. White and K. Huang, Simulating Charge Transport in Solid Oxide Mixed Ionic and Electronic Conductors: Nernst-Planck Theory vs Modified Fick's Law, J. Electrochem. Soc., 2016, 163, A2702–A2719, DOI:10.1149/2.0941613jes.
- M. Schäfer and K.-M. Weitzel, Site energy distribution of ions in the potential energy landscape of amorphous solids, Mater. Today Phys., 2018, 5, 12–19, DOI:10.1016/j.mtphys.2018.05.002.
- L. Rossrucker, P. V. Menezes, J. Zakel, M. Schäfer, B. Roling and K.-M. Weitzel, Bombardment Induced Potassium Ion Transport Through a Sodium Ion Conductor: Conductivities and Diffusion Profiles, Z. Phys. Chem., 2012, 226, 11083, DOI:10.1524/zpch.2012.0215.
- J. L. Wiemer, K. Rein and K.-M. Weitzel, The ionic conductivity of alkali aluminum germanium phosphate glasses - comparison of Plasma CAIT with two electrode DC measurements, Z. Phys. Chem., 2022, 236(6–8), 1001–1012, DOI:10.1515/zpch-2021-3091.
- H. Yamada, K. Ohara, S. Hiroi, A. Sakuda, K. Ikeda, T. Ohkubo, K. Nakada, H. Tsukasaki, H. Nakajima, L. Temleitner, L. Pusztai, S. Ariga, A. Matsuo, J. Ding, T. Nakano, T. Kimura, R. Kobayashi, T. Usuki, S. Tahara, K. Amezawa, Y. Tateyama, S. Mori and A. Hayashi, Lithium Ion Transport Environment by Molecular Vibrations in Ion-Conducting Glasses, Energy Environ. Mater., 2023, e12612, DOI:10.1002/eem2.12612.
- J. Zakel, P. V. Menezes, M. Schaefer and K.-M. Weitzel, Low energy bombardment induced cesium ion transport through a sodium ion conductor: Concentration profiles and diffusion coefficients, Solid State Ionics, 2013, 242, 20–25, DOI:10.1016/j.ssi.2013.04.007.
- D. Budina, J. Zakel, J. Martin, P. Menezes, M. Schaefer and K.-M. Weitzel, Bombardment Induced Transport of Rb+ through a K+ Conducting Glass vs. K+ Transport through a Rb+ Conducting Glass, Z. Phys. Chem., 2014, 228, 609–627, DOI:10.1515/zpch-2014-0459.
- A. Hein, J. Martin, M. Schäfer and K.-M. Weitzel, Electrodiffusion versus Chemical Diffusion in Alkali Calcium Phosphate Glasses: Implication of Structural Changes, J. Phys. Chem. C, 2017, 121, 3203–3211, DOI:10.1021/acs.jpcc.6b11113.
- R. Kirchheim, in Solid State Physics, ed. H. Ehrenreich and F. Spaepen, Elsevier, Amsterdam, 2004, vol. 59, pp. 203–291 Search PubMed.
- O. L. Anderson and D. A. Stuart, Calculation of activation energy of ionic conductivity in silica glasses by classical methods, J. Am. Ceram. Soc., 1954, 37, 573–580, DOI:10.1111/j.1151-2916.1954.tb13991.x.
- J. C. Dyre, The random free-energy barrier model for ac conduction in disordered solids, J. Appl. Phys., 1988, 64, 2456–2468, DOI:10.1063/1.341681.
- H. Lammert, M. Kunow and A. Heuer, Complete Identification of Alkali Sites in Ion Conducting Lithium Silicate Glasses: A Computer Study of Ion Dynamics, Phys. Rev. Lett., 2003, 90, 215901, DOI:10.1103/PhysRevLett.90.215901.
- M. Abou-el-leil and A. R. Cooper, Analysis of Field-Assisted Binary Ion Exchange, J. Am. Ceram. Soc., 1979, 62, 390–395, DOI:10.1111/j.1151-2916.1979.tb19086.x.
- J. Fleig, Voltage-assisted (18)O tracer incorporation into oxides for obtaining shallow diffusion profiles and for measuring ionic transference numbers: basic considerations, Phys. Chem. Chem. Phys., 2009, 11, 3144–3151, 10.1039/b822415c.
- T. Ishiyama, J. Nishii, T. Yamashita, H. Kawazoe and T. Omata, Electrochemical substitution of sodium ions with protons in phosphate glass to fabricate pure proton conducting glass at intermediate temperatures, J. Mater. Chem. A, 2014, 2, 3940, 10.1039/c3ta14561a.
- K. Rein and K.-M. Weitzel, Energy Landscapes in Alkali Aluminum Germanium Phosphate Glasses as probed by alkali proton substitution, in preparation Search PubMed.
- C. Wagner, Equations for transport in solid oxides and sulfides of transition metals, Prog. Solid State Chem., 1975, 10, 3–16, DOI:10.1016/0079-6786(75)90002-3.
- H. Schmalzried, Chemical Kinetics of Solids, Wiley-VCH, 1st edn, 2008 Search PubMed.
- Diffusion in condensed matter, ed., P. Heitjans and J. Kärger, Methods, materials, models, Springer, 2005 Search PubMed.
- H. Weingärtner, in Diffusion in condensed matter. ed. P. Heitjans and J. Kärger, Methods, materials, models, Springer, Berlin, Heidelberg, 2005, pp. 555–578 Search PubMed.
- H. Mehrer, Diffusion in Solids – Fundamentals, Methods, Materials, Diffusion-Controlled Processes, Springer-Verlag, 2007 Search PubMed.
- S. Chakraborty and J. Ganguly, Cation diffusion in aluminosilicate garnets: experimental determination in spessartine-almandine diffusion couples, evaluation of effective binary diffusion coefficients, and applications, Contrib. Mineral. Petrol., 1992, 111, 74–86, DOI:10.1007/BF00296579.
- L. Onsager, Reciprocal relations in irreversible processes. I, Phys. Rev., 1931, 37, 405–426, DOI:10.1103/PhysRev.37.405.
- C. Chatzichristodoulou, W.-S. Park, H.-S. Kim, P. V. Hendriksen and H.-I. Yoo, Experimental determination of the Onsager coefficients of transport for Ce(0.8)Pr(0.2)O(2-delta), Phys. Chem. Chem. Phys., 2010, 12, 9637–9649, 10.1039/c000865f.
- M. Martin, in Diffusion in condensed matter. Methods, materials, models, ed. P. Heitjans and J. Kärger, Springer, Berlin, Heidelberg, 2005, p. 226 Search PubMed.
- M. Landstorfer and T. Jacob, Mathematical modeling of intercalation batteries at the cell level and beyond, Chem. Soc. Rev., 2013, 42, 3234–3252, 10.1039/c2cs35050e.
- K. D. Fong, H. K. Bergstrom, B. D. McCloskey and K. K. Mandadapu, Transport phenomena in electrolyte solutions: Nonequilibrium thermodynamics and statistical mechanics, AIChE J., 2020, 66, e17091, DOI:10.1002/aic.17091.
- L. S. Darken, Diffusion of carbon in austenite with a discontinuity in composition, Trans. AIME., 1949, 180, 430–438 Search PubMed.
- M. Colangeli, A. de Masi and E. Presutti, Microscopic models for uphill diffusion, J. Phys. A: Math. Theor., 2017, 50, 435002, DOI:10.1088/1751-8121/aa8c68.
- R. Krishna, Uphill diffusion in multicomponent mixtures, Chem. Soc. Rev., 2015, 44, 2812–2836, 10.1039/c4cs00440j.
- J. Swenson and S. Adams, Mixed Alkali Effect in Glasses, Phys. Rev. Lett., 2003, 90, 155507, DOI:10.1103/PhysRevLett.90.155507.
- H. Lammert, R. D. Banhatti and A. Heuer, The cationic energy landscape in alkali silicate glasses: Properties and relevance, J. Chem. Phys., 2009, 131, 224708, DOI:10.1063/1.3272273.
- J. L. Wiemer, M. Schäfer and K.-M. Weitzel, Li + Ion Site Energy Distribution in Lithium Aluminum Germanium Phosphate, J. Phys. Chem. C, 2021, 125, 4977–4985, DOI:10.1021/acs.jpcc.0c11164.
- J. L. Lebowitz and P. G. Bergmann, Irreversible gibbsian ensembles, Ann. Phys., 1957, 1, 1–23, DOI:10.1016/0003-4916(57)90002-7.
- C. M. A. Brett and A. M. Oliveira Brett, Electrochemistry. Principles, methods, and applications, Oxford Univ. Press, 1st edn, 2005 Search PubMed.
- G. E. Murch, in Phase transformations in materials, ed. G. Kostorz and G. Kostorz, Wiley-VCH, Weinheim, New York, Chichester, 2001, pp. 171–238 Search PubMed.
- R. A. McKee, A generalization of the Nernst-Einstein equation for self-diffusion in high defect concentration solids, Solid State Ionics, 1981, 5, 133–136, DOI:10.1016/0167-2738(81)90210-1.
- G. Peskir, On the Diffusion Coefficient: The Einstein Relation and Beyond, Stochastic Models, 2003, 19, 383–405, DOI:10.1081/STM-120023566.
- M.-C. Pang, M. Marinescu, H. Wang and G. Offer, Mechanical behaviour of inorganic solid-state batteries: can we model the ionic mobility in the electrolyte with Nernst-Einstein's relation?, Phys. Chem. Chem. Phys., 2021, 23, 27159–27170, 10.1039/D1CP00909E.
- Z. Li, R. P. Misra, Y. Li, Y.-C. Yao, S. Zhao, Y. Zhang, Y. Chen, D. Blankschtein and A. Noy, Breakdown of the Nernst-Einstein relation in carbon nanotube porins, Nat. Nanotechnol., 2023, 18, 177–183, DOI:10.1038/s41565-022-01276-0.
- J. Newman and K. E. Thomas-Alyea, Electrochemical systems, Wiley-Interscience, 3rd edn, 2004 Search PubMed.
- S. B. Adler, J. A. Lane and B. C. H. Steele, Electrode Kinetics of Porous Mixed-Conducting Oxygen Electrodes, J. Electrochem. Soc., 1996, 143, 3554–3564, DOI:10.1149/1.1837252.
- W. Lai and S. M. Haile, Impedance Spectroscopy as a Tool for Chemical and Electrochemical Analysis of Mixed Conductors: A Case Study of Ceria, J. Am. Ceram. Soc., 2005, 88, 2979–2997, DOI:10.1111/j.1551-2916.2005.00740.x.
- J. Kärger, P. Heitjans and R. Haberlandt, Diffusion in condensed matter, Vieweg, 1998 Search PubMed.
- S. Faske, H. Eckert and M. Vogel, Li6 and Li7 NMR line-shape and stimulated-echo studies of lithium ionic hopping in LiPO3 glass, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 104301, DOI:10.1103/PhysRevB.77.104301.
- M. Haaks, S. W. Martin and M. Vogel, Relation of short-range and long-range lithium ion dynamics in glass-ceramics: Insights from Li7 NMR field-cycling and field-gradient studies, Phys. Rev. B, 2017, 96, 104301, DOI:10.1103/PhysRevB.96.104301.
- K. Funke, B. Roling and M. Lange, Dynamics of mobile ions in crystals, glasses and melts, Solid State Ionics, 1998, 105, 195–208, DOI:10.1016/S0167-2738(97)00465-7.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting information covering aspects of the data analysis as well as a detailed derivation regarding the relation of Nernst–Planck–Poisson and Onsager approaches is available online. See DOI: https://doi.org/10.1039/d4cp00262h |
| This journal is © the Owner Societies 2024 |