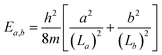A reinvestigation of the boron cluster B₁₅^+/0/−: a benchmark of density functionals and consideration of aromaticity models

Abstract

This study presents a thorough reinvestigation of the B₁₅^+/0/− isomers, first employing coupled-cluster theory CCSD(T) calculations to validate the performance of different DFT functionals. The B₁₅⁺ cation has two planar lowest-lying isomers, while the first 3D isomer is less stable than the global minimum by ∼10 kcal mol⁻¹. The PBE functional, within this benchmark survey, has proved to be reliable in predicting relative energies for boron isomers. Other functionals such as the TPSSh, PBE0 and HSE06 result in good energy ordering of isomers but warrant reconsideration when distinguishing between 2D and 3D forms. Caution is needed for structures having high spin contamination, as it may lead to significant errors. The anomalously lower stability of the B₁₅⁻ anion with respect to its neighbours, in terms of electron detachment energy, was explained through a competition between both rectangle and disk models for its geometry. This elucidates its stability with 12 electrons in rectangle model and instability with 10 electrons in disk-shaped structure, emphasizing the value of employing such geometric models. The proximity of the σ* LUMO to the π HOMO also contributes to the weakening of the B₁₅⁻ stability.

---

1. Introduction

Boron clusters form an intriguing class of chemical compounds in part due to the intrinsic characteristics of the element. Boron has a small covalent radius, electron deficiency, and can form multiple bonds with itself and other atoms; this leads to unpredictability in the shapes and physico-chemical properties of the resulting clusters.¹ While the aromaticity of polycyclic hydrocarbons seemingly relies solely on their π electrons,^2–4 boron clusters could exhibit both π and σ aromatic characters.^5–8 The classical Hückel (4n + 2) electron count rule is commonly employed to rationalize structural motifs and predict stability trends in planar hydrocarbons and organic molecules. For example, while benzene is highly stable with 6 delocalized π electrons, naphthalene achieves its stability with 10 π electrons. The cyclic C₃H₃ represents the smallest ring structure, and the simplest approach for it to satisfy the Hückel rule is a removal of one electron leaving behind 2 π electrons in the cyclic aromatic C₃H₃⁺ cation.⁹ Boron clusters often exhibit multi-center 2-electron bonds in both sets of π and σ electrons, and the number of π electrons in a certain boron cluster could become unpredictable. For example, the simplest cyclic B₃⁻ anion features a double aromaticity with 2 π and 2 σ electrons.¹⁰ Both the B₈²⁻ dianion¹¹ and B₁₂ neutral^5,12 have each 6 π and 6 σ electrons. Another case in point concerns the B₁₅ size. The planar structure of the B₁₅⁺ cation^13,14 has been recognized to be at the same time σ aromatic and π antiaromatic due to its possession of 6 delocalized σ electrons and 8 delocalized π electrons,¹⁴ respectively. The B₁₅⁻ anion which formally results from addition of two π electrons to the B₁₅⁺ cation, has been shown to have a double aromaticity.¹⁵ This implies that the B₁₅⁻ anion is expected to have a high thermodynamic stability. The first vertical detachment energy (VDE1), as reviewed by Wang and coworkers,¹⁶ indicates that B₁₅⁻ has a lower VDE1 (3.43 eV) as compared to its two closed-shell neighbors, namely B₁₃⁻ (3.78 eV) and B₁₇⁻ (4.48 eV), when considering clusters with an odd number of boron atoms in the anion state. This suggests that the thermodynamic stability of B₁₅⁻ is actually diminished rather than enhanced by the anticipated doubly aromatic character. In this context, we aim in the present study to reveal that, in reality, the anion B₁₅⁻ is not a double aromaticity species as previously reported, and this explains the observed decrease in its stability.

When conducting research based on density functional theory (DFT) calculations for a given system it requires a careful initial selection of a functional that has been validated through appropriate benchmarks, aligned with the research objectives. Typically, these benchmarks are carried out on smaller-scale molecular systems due to the computational expense involved in established standards. In addition, an open-shell isomer with high spin contamination in its unrestricted HF reference is a special case that requires calculation by complicated multi-reference methods. Even in some closed-shell structures, a multi-reference character causes a slow convergence of single-reference wavefunctions leading to erroneous total energies. Within a noticeably short period, two consecutive publications have recently reported benchmarks for the study of relative energies based on reference molecules with exceedingly high spin contamination in their unrestricted solutions. The first publication by Khatun et al.¹⁷ was conducted on the series of small triatomic clusters B₃, Al₃ and Ga₃. Subsequently, the paper by Liu et al.¹⁸ focused on the pure boron clusters B_n with n = 1–4. Despite the high spin contamination in the unrestricted solutions of the studied systems, the functionals such as M06, BPBE, VSXC, B1B95 and B2PLYPD3 have been proposed for geometry optimizations of boron clusters. In this context, through an analysis of the geometries of B₁₅^+/0/− clusters, in three charge states, we once again conduct some benchmark calculations to emphasize the necessary caution when treating systems having a high degree spin contamination whose electronic energies are not quite correct due to the multiple solutions of UHF references. The present investigation also underscores the performance of density functionals on structures exhibiting a strong competition between 2D and 3D configurations, a factor often overlooked when benchmarking small-sized structures.

Typically, once a structure is characterized by an aromatic character, leading to a high thermodynamic stability, its properties are readily manifested and easily elucidated. However, in cases where aromaticity diminishes, identification of the underlying reasons for such a reduction becomes significantly more challenging. For this reason, the present study is conducted to figure out the observed decrease in the stability of B₁₅⁻ with respect to its immediate neighbours.

2. Computational methods

Although the geometries of the B₁₅ cluster in the cationic, neutral and anionic states have extensively been determined in previous studies,^{12–16,19–22} we would take this opportunity to explore them again using different quantum chemical methods. The lower-lying isomers are separately searched in each charge state. The PBE functional in conjunction with the 6-31G(d) basis set is used to optimize all initial isomers that are generated by our search algorithm²³ that combines a stochastic algorithm²⁴ and a genetic algorithm.²⁵ Geometries and harmonic vibrational frequencies of lower-lying isomers of B₁₅^+/0/− with relative energies smaller than 3.0 eV with respect to the corresponding lowest-lying isomer are re-optimized using the TPSSh,²⁶ PBE²⁷ and BPBE^28,29 functionals in conjunction with the 6-311+G(d)³⁰ basis set. Finally, single-point electronic energies are carried out using the coupled-cluster theory (U)CCSD(T) with the aug-cc-pVTZ basis set using DFT/6-311+G(d) optimized geometries to verify the suitability of the DFT functionals considered. Relative energies are corrected with zero-point energy (ZPE) corrections determined by DFT/aug-cc-pVTZ harmonic vibrational frequencies without scaling. The unrestricted formalism (UHF, UCC…) is used for open-shell species.

The magnetically induced current density is calculated and visualized by using the SYSMONIC program³¹ which implements the CTOCD-DZ2 method.^32,33 The ring current maps are plotted using the convention that clockwise magnetic current vectors indicate the diatropic character while the counterclockwise magnetic current vectors displayed indicate the paratropic character. Analysis of bonding is also carried out employing the adaptive natural density partitioning (AdNDP) method³⁴ with the Multiwfn 3.8 software.³⁵ The Gaussian 16 program³⁶ is utilized for all calculations.

SEAGrid (https://seagrid.org)^37,38 is acknowledged for computational resources and services for the results presented in this publication.

3. Results and discussion

3.1. Benchmarking of methods

Fig. 1 presents some of the most stable isomers of the B₁₅^−/0/+ system based on calculations using the TPSSh, PBE and BPBE functionals in conjunction with 6-311+G(d) basis set, along with a calibration from single-point (U)CCSD(T)/aug-cc-pVTZ electronic energies making use of the corresponding optimized geometries. As for a convention, each structure considered hereafter is labeled by Xq in which X = 1, 2, 3, … indicates the ordering of isomers in terms of decreasing stability and q = a, n or c stands for an anionic, neutral or cationic form, respectively. While the closed-shell 1a has a T1 diagnostic value of 0.04 for the coupled-cluster CCSD expansion, all remaining structures are characterized by T1 values close to 0.02 for closed-shell systems and 0.04 for open-shell systems (cf. Table S1 of the (ESI†) file), affirming the reliability of CCSD(T) results.³⁹ Although the T1 value of 0.04 for 1a remains significantly lower as compared to the T1 values of the B₂, B₃ or B₄ species (>0.08),¹⁸ the energy of 1a is not included in our benchmarking survey. Incidentally, we also notice some inconsistency in the previous T1 value for the triplet dimer B₂; while Khatun¹⁷ reported a value of 0.042, Liu¹⁸ gave that of 0.072. We recheck this discrepancy and find the Liu's report to be highly questionable. In fact, we find the T1 value for the tetramer B₄ to be equal to 0.024, much smaller than the value of 0.109 reported by Liu.¹⁸ The reason for such a discrepancy is not clear to us.

Fig. 1 Optimized geometries of B₁₅^+/0/− using TPSSh, PBE and BPBE functionals with the 6-311+G(d) basis set with symmetry point group and electronic state. Relative energies (kcal mol⁻¹) are obtained with ZPE corrections without scaling at the respective functional, TPSSh (upper values), PBE (middle) and BPBE (lower). Relative energies obtained by single-point (U)CCSD(T)/aug-cc-pVTZ energies at corresponding DFT geometries and ZPE corrections are given in parentheses.

From calculated results at the TPSS/def2-TZVPP level, Oger et al.²⁰ found four most stable isomers of B₁₅⁺ including three quasi-planar or planar isomers and one 3D isomer. The three 2D isomers were subsequently revisited by Wang et al.¹⁴ through geometry optimizations using the coupled-cluster theory CCSD with the 6-311G(d) basis set that showed that they rather consist of two isomers with both C_2v and C_s symmetry point groups (correspond to the 1c and 2c isomer in Fig. 1). Present single-point CCSD(T) calculations from optimized geometries using the above three different functionals confirm the two lowest-energy isomers 1c and 2c, with an energy difference not exceeding 2 kcal mol⁻¹. Although 1c consistently exhibits a more stable structural conformation, within the expected error margin of ±3 kcal mol⁻¹ of the methods employed we would conclude that both isomers 1c and 2c represent the global competitive energy minima (GM), in contrast to the previous Wang's conclusion which only considered 1c as such. In addition, Oger et al.²⁰ found that a 3D form (being the 4c isomer) is ∼0.12 eV (∼2.8 kcal mol⁻¹) less stable than the GM and its experimental existence has not been confirmed by their experiment. Our results demonstrate that the 4c isomer is much less stable than the GM by ∼10 kcal mol⁻¹, thus lending a greater plausibility for its non-detection. Fig. 1 illustrates the existence of a slightly more stable elongated 3c isomer as compared to the 3D counterpart, albeit less stable than the GM by approximately 9 kcal mol⁻¹. Therefore, it is reasonable that Oger et al.²⁰ were not able to discern it in their experiment.

The shape of 1c is not fully maintained following electron addition. In fact, as discrete electrons are sequentially added to the cation 1c generating the neutral 1n and subsequently the anionic 1a, the corresponding global minima retain the shape but with some important distortions. In fact, while the symmetry of 1n is thus lowered to C_s, 1a no longer has a symmetry (C₁). The underlying cause for such a symmetrical reduction presents an enigmatic phenomenon, which will be comprehensively expounded upon in the following section.

The neutral 2n can also be considered to be a quasi-degenerate GM because it is only slightly less stable than 1n by ∼2 kcal mol⁻¹. The elongated structure tends to move away from the GM when it becomes now less stable than the GM by ∼4 kcal mol⁻¹ in the neutral state and ∼3 kcal mol⁻¹ in the anionic state. The anion 2a, with two B atoms attached to one side of an elongated B₁₆, exhibits a marginal relative energy of less than 1 kcal mol⁻¹ with respect to 1a. Together with six close in energy isomers shown in Fig. 1, it is evident that the B₁₅⁻ anion represents a more flexible configuration having many isomers competing for the GM.

We have recently validated the TPSSh functional for its suitability in exploring the structural characteristics of complex boron clusters involving silicon or lithium,^40,41 while the PBE functional has demonstrated its theoretical adequacy in cases involving a competition between 2D and 3D geometrical configurations.⁴²

One intriguing observation is that despite the substantial differences in relative energies obtained from DFT calculations, particularly between the 3D and 2D forms, 4n compared to 1n, and 4c compared to 1c, the relative energies derived from single-point CCSD(T) energy calculations using DFT optimized geometries show negligible deviation. Consequently, we select the relative energies obtained from CCSD(T) calculations with PBE/6-311+G(d) geometries as reference for subsequent benchmark computations. The benchmarking study incorporates several additional functionals, including the TPSSh, PBE0 and HSE06 that have extensively been demonstrated to be suitable for boron; the M06 and BPBE as proposed by Khatun et al.;¹⁷ the popular B3LYP functional which has repeatedly been shown to be unsuitable for energy exploration in the context of boron clusters, and the VSXC, B1B95 and B2PLYPD3 that were suggested by Liu et al.¹⁸ We would emphasize that double-hybrid functionals such as the B2PLYPD3 are computationally expensive; a substantial computational resource of 500 GB of disk space needs to be allocated for a single calculation on B₁₅ using the latter functional.

To ensure that the benchmark only accounts for isomers without heavy spin contamination. The four most stable isomers for the open-shell neutral state including 1n, 2n, 3n and 4n and the cations 1c, 2c, 3c and 4c all satisfy this condition. Both series are related to 1n and 1c for reference energies, respectively. The selection of isomers in the anionic state is more intricated. As mentioned above, the closed-shell 1a is found to have a relatively larger T1 value (∼0.04) and therefore excluded, and the isomer 2a becomes the reference isomer. The next selected isomers are 3a and 4a, whereas 7a (Fig. 1) is the last isomer considered for additional investigation of singlet–triplet energy differences.

The relative energy ΔE^CCSD(T)_i–r between isomer “i” and the reference isomer “r” is determined using the reference calculation at the CCSD(T)/aug-cc-pVTZ//PBE/6-311+G(d) level. The error in the relative energy, denoted by ΔΔE_i–r, is then computed as the difference between the DFT-calculated relative energy ΔE^DFT_i–r and the reference relative energy ΔE^CCSD(T)_i–r, where “DFT” stands for the density functional used.

The ΔΔE_i–r values obtained for B₁₅^+/0/− in this survey are shown in Fig. 2 and Tables S2–S4 (ESI† file). The mean absolute error (MAE) for three relative energy errors of each DFT level, denoted as:

is computed and illustrated in Fig. 2 and Tables S2–S4 (ESI† file). Minor variations in MAE energy signify precise relative energies alignment.

Fig. 2 ΔΔE_i–r values of different DFT functionals of B₁₅^+/0/− and the average MAE of these three charge states.

In a general context, the difference in errors caused by the basis set employed is negligible as compared to the more significant variation observed when changing the functional. Therefore, the use of the 6-311+G(d) basis set is appropriate for achieving accuracy at a low cost in exploring the relative energies of boron clusters. This can be expected for doped boron clusters that do not include transition metal atoms as dopants. It also can be readily observed that the ΔΔE_i–r values in the anionic state are lower with respect to those found in the neutral and cationic states, where there is a competition between 2D and 3D isomers.

In the anionic state, ΔΔE_3a-2a turns out to be smaller than the ΔΔE_4a-2a and ΔΔE_7a-2a. This is believed to be due to the fact that 7a has a triplet state ground state, and 4a exhibits a mixed 2D and 3D form. While 2a and 3a share more similarities with each other, both are in a 2D shape and a singlet ground state. The relative energy discrepancy between the triplet 7a and the singlet 2a from B1B95 calculations, as compared to CCSD(T), has the smallest absolute values with 0.2 kcal mol⁻¹ for the def2TZVPP basis set and 0.5 kcal mol⁻¹ for the 6-311+G(d).

Subsequently, the M06 and B2PLYPD3 functionals follow with small differences, whereas other functionals exhibit larger |ΔΔE_3a-2a| > 3 kcal mol⁻¹. Particularly noteworthy is the observation that the quantity ΔΔE_3a-2a < 0 for every DFT functional, indicating that the DFT functionals considered tend to overestimate the stability of triplet states as compared to (U)CCSD(T) results, that yield higher energy for triplet states. This implies that in some cases, DFT calculations may suggest a more stable triplet structure, but such a result could be reversed to a more stable singlet structure when further validated by CCSD(T) computations. Further investigation is warranted through a comprehensive examination involving various singlet–triplet structure pairs to draw more accurate conclusions.

The 4a is not entirely a 3D structure since it only involves two B atoms located at an angle in B₁₃, making it classified as a mixed 2D–3D structure. However, the |ΔΔE_4a-2a| divergence becomes noticeable when compared to the quasi-planar structure 2a. TPSSh exhibits the smallest deviation, followed by PBE0, B1B95 and HSE06, while B3LYP remains the functional having the largest discrepancy. Both M06 and VSXC also display substantial errors (>5 kcal mol⁻¹). In general, the B1B95 and B2PLYPD3 functionals have lower MAE values due to their small |ΔΔE_7a-2a| errors.

The ΔΔE_i–r in the neutral and cationic states is significantly higher than that in the anionic state, particularly in terms of ΔΔE_4n-1n and ΔΔE_4c-1c, where all their values fall outside the MAE threshold (cf.Fig. 2). Two prominent hybrid functionals, namely the B3LYP and B2PLYPD3, are worth mentioning. The B3LYP functional has gained great popularity in the study of organic and inorganic compounds, and has extensively been chosen in the studies of boron clusters over the past few decades. However, it has been observed that this functional induces a significant discrepancy between energies of 2D and 3D structures of boron clusters.⁴³ Our present results tend to concur again with this assessment. Both the hybrid B3LYP and double-hybrid B2PLYPD3 underestimate the stability of 3D structures, and as a result, previous studies on boron clusters relying on the B3LYP functional are likely to have overlooked certain 3D isomers. Conversely, the B1B95 and M06 apparently overestimate the stability of 3D structures as compared to planar counterparts. As a matter of fact, on the basis of M06/def2SVP calculations, Khatun et al.¹⁷ drew a significantly erroneous conclusion that the global minimum of the B₁₂ cluster is a 3D structure, even though the C_3v quasi-planar structure has long been established to be its lowest-energy isomer.^5,44,45

In a recent study of Liu et al.,¹⁸ some small errors in the relative energies of small B₃ and B₄ clusters were found for the VSXC functional, but a substantial error in the case of the diatomic B₂. This indicates an inconsistency when using single-reference methods for highly spin-contaminated systems. Fig. 2 reveals that VSXC provides contrasting evaluations with respect to those derived from the TPSSh, PBE0 and HSE06, even though their mean absolute errors (MAE) are similar to each other. The latter functionals push a preference for 3D structures, whereas the former tends to favor 2D configurations. Fig. 2, however, unveils that the VSXC presents divergent assessments in contrast to the TPSSh, PBE0 and HSE06, despite sharing similar MAEs. Again, the latter functionals have a propensity for 3D structures, while the former leans towards favoring 2D configurations. It is rather hard to understand such trends of these current functionals as most, if not all, of them have semi-empirically been constructed with different sets of parameters.

Finally, both BPBE and PBE emerge as the two most suitable functionals for exploring stable structures of boron clusters. While the BPBE is characterized by smaller errors in the cationic state, the PBE shows smaller errors for both neutral and anionic states. Therefore, the average values suggest a slightly better performance for the PBE functional.

3.2. Aromatic character

After benchmarking the performance of the current density functionals for treatment of boron clusters in the specific size of B₁₅, we now focus on their electronic characteristics, in particular their aromatic character, as a mean to understand their thermodynamic stability.

The quasi-planar anion 1a which possesses 10 π electrons, thus according to the classical (4n + 2) electron count, anticipates a π aromaticity, and consequently a high thermodynamic stability. As mentioned above, this B₁₅⁻ isomer has a first vertical detachment energy of VDE1 = ∼3.4 eV, which is smaller than VDE1 values of B₁₃⁻ (∼3.8 eV) and B₁₇⁻ (∼4.5 eV). This observation suggests that the anion 1a exhibits a lower stability with respect to its closed-shell neighbours. To elucidate this phenomenon, let us commence with an examination of two cationic structures 1c and 3c (cf.Fig. 1).

The elongated conformation of 3c whose planar shape is maintained upon successive addition of electrons to form the neutral 3n and anion 3a is of interest. Relative energy of 3q isomer with respect to the corresponding most stable structure gradually decreases throughout electron addition process. In this analysis, we utilize an unrelaxed structure of 1a, referred hereafter to as 1a-C_2v, to have a clearer view of the orbitals and to gain a deeper understanding on its 10 π electrons. The anion 1a is in fact the outcome following a geometry relaxation eliminating two imaginary frequencies (−817i and −121i cm⁻¹) associated with 1a-C_2v (cf.Fig. 7).

The magnetic current density maps from π-electron contribution to a perpendicular external magnetic field B over a plane placed at 1 a.u. above the 1c, 1a-C_2v, 3c and 3a structures are displayed in Fig. 3. It is not surprising that both 1c and 3c possess a π antiaromatic character when each isomer has 8 π electrons. However, upon addition of two electrons, 1a-C_2v does not completely manifest an aromaticity, whereas 3a retains a fully π-aromatic character (cf.Fig. 3).

Fig. 3 The magnetic current density maps from π electron contribution to a perpendicular external magnetic field B over a plane place at 1 a.u. above the (a) 1c, (b) 1a-C_2v, (c) 3c and (d) 3a. Local diatropic and local paramagnetic ring currents are highlighted for the (b) 1a-C_2v by blue and red rings, respectively.

The π bonds, according to an adaptive natural density partitioning (AdNDP) analysis for these isomers, are illustrated in Fig. 4 with the aim to identify some key points for explaining the reduced aromaticity of 1a-C_2v. The most noticeable change is that the three localized π bonds (10, 11 and 12) of 3c are transformed into globally delocalized π bonds (namely 14, 15 and 16) in 3a (cf.Fig. 4), corresponding to a shift from a π antiaromaticity to a π aromaticity. Having 10 π electrons, 1a-C_2v is expected to enjoy an aromaticity according to the (4n + 2) counting rule. However, the 5th bond of 1a-C_2v (cf.Fig. 4) is not a part of a (15c-2e) global delocalized orbital, but rather a (10c-2e) orbital, indicating its partial aromaticity. However, as demonstrated by in-depth analyses on the correlation between magnetization and energetic stability,^46,47 it appears that both the magnetic ring current maps and AdNDP approach only reveal the chemical phenomenon without providing us with a clear explanation. Therefore, we now attempt to delve deeper into the interplay between these structures and aromatic models.

Fig. 4 Chemical π orbitals pattern of (a) 1c, (b) 1a-C_2v, (c) 3c, and (d) 3a isomers on the basis of adaptive natural density partitioning (AdNDP) analysis. Occupation numbers (ONs) are indicated.

To explore the reason for why its 10 π electrons do not confer a higher thermodynamic stability to the 1a-C_2v structure, we now investigate their relationship with those of hydrocarbon molecules possessing 10 π electrons. Of the latter, naphthalene is the most renowned, and its structure is often compared to other 10 π electron boron clusters such as B₁₆²⁻,^48,49 B₁₇⁻,⁵⁰… The π electron spectrum and magnetic ring current properties of C₁₀H₈ are easily discernible⁵¹ through the resolution of polynomial equations employing the method of secular determinants within the framework of linear variational theory,⁵² specifically applying the Hückel molecular orbital theory.^2,53,54 However, it is not feasible to construct secular determinants for boron clusters such as the elongated B₁₆²⁻, or the present 3c, 3a… isomers. In this case, solution of the Schrödinger equation for the particle motion in a specific box becomes an alternative method, leading to the electron level spectrum and, consequently, an accurate solution for the ring current,⁴⁹ despite the absence of bond order prediction as in the Hückel model. In the present case of the B₁₅⁻ anion 1a, its geometry can be modeled either by a rectangle or a circular disk. Let us now analyze in some detail the electronic picture of the anion within these two geometric models.

The rectangle model (RM)^49,55 represents a particle moving within a rectangle potential well characterized by the length L_a and the width L_b, whose eigenstates ψ_a,b and eigenvalues E_a,b are defined by:

that are dependent on two quantum numbers of a = 1, 2, 3, … and b = 1, 2, 3… The ordering of eigenfunctions according to RM varies with the ratio L_a/L_b.

A small and straightforward Python code snippet is presented in the SI file for the computation of the dimensions L_a × L_b of a rectangle box and the root mean square error (RMSE) index for the accuracy of the model:

with m being the number of occupied molecular orbitals; E^DFT_i and E^RM_i represent the energy of the MOs calculated from a DFT method and from the RM, respectively.

The dimensions of the RM depicted in Fig. 5 illustrate that these RMs are broader than the real structure, indicating the enhanced outward mobility of π electrons.⁴⁹ The RMSE for the three referenced rectangular structures is very small, indicating a good fit of the model. However, the RMSE for C₁₀H₈ is larger than that of elongated B₁₅^+/−, suggesting a certain difference between them. This observation can be attributed to the fact that elongated B₁₅^+/− are homogeneous species, while C₁₀H₈ is a heterogeneous molecule composed of both carbon and hydrogen atoms; this leads to energy level shifts caused by the difference in electron affinity between two elements. The RM also reveals that 3a and C₁₀H₈ share the same π electron level spectrum, indicating a similarity in their π aromatic character.

Fig. 5 Correlation between DFT (PBE/6-311+G(d)) orbital energies of (a) 3c, (b) 3a and (c) C₁₀H₈ and eigenvalues of solutions of a particle in a rectangle box. Dimensions of the rectangle for each isomer are drawn in proportion to the size of the isomer. The red circles indicate the occupied levels while the blue squares indicate the unoccupied levels. The solid and dashed arrows correspondingly indicate translational and rotational transition.

In the ipsocentric model,^56,57 a virtual excitation of an electron from an occupied MO to an unoccupied can give rise to a ring current contribution exhibiting diatropic, paratropic, and null characteristics. The diatropic ring current, arising from an allowed translational transition, is manifested when the product of symmetries of the occupied and unoccupied orbitals contains the ΔΛ = 1 condition, indicating a difference in rotational quantum numbers of one between the initial occupied and final unoccupied orbitals. Conversely, the current is deemed to be paratropic if the ΔΛ = 0 condition holds, implying no difference in rotational quantum numbers. On the basis of the allowed translational transition depicted in Fig. 5, we observe a common characteristic: an allowed translational transition increases either of the quantum numbers a or b by one unit while leaving the other quantum number(s) unchanged. The observed translational transitions (Δa = 1, Δb = 0) are identified as ψ_2,2 → ψ_3,2 in 3a and C₁₀H₈ and ψ_1,2 → ψ_2,2 in 3c; and the ψ_3,1 → ψ_3,2 in 3a and C₁₀H₈ transition is example for (Δa = 0, Δb = 1). The ψ_3,1 → ψ_2,2 transition is an allowed rotational transition and thereby contributes significantly to the paratropic current in 3c whereas ψ_1,2 → ψ_4,1 transition has a minor contribution.

In this manner, the RM does not only aid us to elucidate the electronic configuration, delineating the operational range of electrons, but also expounds upon the aromatic character of the structure. Resolution of secular determinants or the Schrödinger equation uniformly concludes that the 10 electrons engaged in aromaticity and 8 electrons participated in anti-aromaticity for structures closely resembling a rectangle shape. It appears that this is consistent with the classical Hückel (4n + 2) counting rule, indicating that the number of electrons 2, 6, 10, 14,… corresponds to structures exhibiting an aromatic character. The Baird's rule,^58,59 conversely, proposes that a structure with a (4n) electron count exhibits aromaticity under the condition of being in a triplet state. This phenomenon arises due to the cyclic shape where the Hückel rule consistently indicates the existence of non-degenerate ground energy levels (requiring 2 electrons), while higher levels always possess a two-fold degeneracy (requiring 4 electrons to fully occupy each level). Consequently, when 2 electrons in the upper level are lost, the structure becomes aromatic in a triplet state. The solution to the Schrödinger equation for a particle moving in a circle⁶⁰ also supports a similar conclusion. Therefore, both the Hückel or Baird rules can readily be observed for organic molecules in the form of a ring annulenes C_nH_n or macrocyclic molecules,⁶¹ but the Baird rule is not found in a rectangle-shaped structure yet.

A legitimate question is as to whether there exists any circular disk-like structure exhibiting an aromaticity with 10 π electrons. We are notably surprised by our inability to identify any disk-like aromatic structure with 10 π electrons, while numerous aromatic structures have been established with 12 π electrons, such as C₁₃H₉⁺,⁶² B₁₉⁻, B₂₀²⁻,⁶³…

The disk model (DM)^11,64,65 representing a particle moving within a circular disk potential has been described in much detail in previous studies. Briefly, the eigenstates ψ_nl and eigenvalues E_nl are dependent on two quantum numbers, namely the principal number of radial n and the rotational number l. The principal quantum number n has value of 0, 1, 2, 3, … whereas the rotational number l has value 0, ±1, ±2, ±3, ±4, ±5 … While the eigenstates where l = 0 are non-degenerate wavefunctions, the rest of l values are two-fold degenerate (±) wavefunctions, and the corresponding eigenstates are denoted as σ (l = 0), π (l = ± 1), δ (l = ± 2), ϕ (l = ± 3), γ (l = ± 4), η (l = ± 5), … The lowest eigenstates in an ascending ordering are ψ_1σ, ψ_1π, ψ_1δ, ψ_2σ, and so on and are shown in Fig. 6a. Fig. 6a illustrates that the large gaps ΔE_1π-1σ and ΔE_1δ-1π are substantial, explaining why 2 and 6 are considered magic numbers. Conversely, the gap ΔE_2σ–1δ is notably smaller compared to the gap ΔE_1π–1σ, and the gap ΔE_1ϕ–2σ is larger than ΔE_2σ–1δ but approximately equal to ∼0.6 the gap ΔE_1π–1σ. Therefore, in these cases 12 electrons may not necessarily be a magic number, but 10 electrons are consistently associated with a relatively lower thermodynamic stability.

Fig. 6 (a) The lowest eigenstates in the disk model. π frontier of (b) C₁₀H₆²⁻, (c) C₁₀H₆ and (d) 1a-C_2v and their π ring current maps.

Fig. 6b displays the ψ_2σ (HOMO) and ψ_1δ (HOMO−1 and HOMO−1′) shapes of the 12 π dianion acepentalene (C₁₀H₆²⁻) and its π ring current maps. The latter shows that it a π aromatic species.⁶⁶ When removing 2 electrons from C₁₀H₆²⁻, the electron loss occurs not in the ψ_2σ orbital but in one of the two-fold degenerate MO of ψ_1δ, leading to a Jahn–Teller effect, as depicted in Fig. 6c, corresponding to C₁₀H₆. It is challenging to identify the MO shape of the LUMO of C₁₀H₆ (assigned as ψ_1δ+) because it belongs to ψ_1δ without considering its transformation during the removal of 2 electrons as described above. In the case of 1a-C_2v, the inherently lower symmetry of the structure causes ψ_1δ to automatically be split into ψ_1δ+ (HOMO−1) and ψ_1δ− (HOMO). Remarkably, the symmetry of ψ_1δ+ and ψ_2σ is quite similar to each other after spitting, akin to a 90° rotation.

The Jahn–Teller effect causes structures with 10 π electrons to become more ellipsoidal than circular, leading to a change in the MO shape of ψ_2σ, which closely resembles ψ_1δ+ after a 90° rotation. This structural deformation results in a more ellipsoidal shape rather than a circular disk. However, for the sake of simplicity, we can view these MOs of 1a-C_2v under a rectangle model. Indeed, the MOs ψ_2σ and ψ_1δ+ under the RM correspond to ψ_1,3 and ψ_3,1, respectively, reflecting their symmetry. Under the C_2v point group, both belong to the b₁ representations, and the ψ_1δ− turn to the ψ_2,2, with the a₂ representations.

The Γ(T_y, R_x) = b₂ = a₂ × b₁ is both translationally and rotationally allowed transition, which results in both the paramagnetic current in π ring current maps of C₁₀H₆ and 1a-C_2v (cf.Fig. 6). Thus, according to the RM, the proximity of the ψ_1δ and ψ_2σ levels, along with their low symmetry, causes a splitting of the ψ_1δ level into both ψ_1δ+ and ψ_1δ−, with ψ_1δ+ exhibiting a symmetry similar to that of ψ_2σ. This results in the antiaromatic nature of both ψ_1δ− → ψ_2σ and ψ_1δ− → ψ_1δ+ transitions. This is a possible reason for why a high symmetry disk-like structure having 10 π electrons has not yet to be identified as fully aromatic.

The anion B₁₇⁻ is an exceptional case with a high thermodynamic stability involving 10 π electrons,⁵⁰ but its geometry does not involve a high symmetry. It features a four-boron ring which is not a preferred form for boron clusters. Furthermore, B₁₇⁻ also displays a local paratropic ring currents around this, as shown in Fig. S1 (ESI† file). An AdNDP analysis reported by Sergeeva et al.⁵⁰ also indicated that the π electrons of B₁₇⁻ do not exhibit a global delocalization such as the case in 3a. Electronic distribution of the anion B₁₇⁻ also demands an in-depth investigation to thoroughly explain the origin of its high stability.

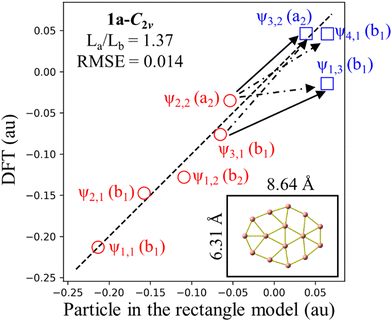
Because π-MO shapes of 1a-C_2v exhibit similarities with the eigenfunctions of the rectangle model, a survey assessing the suitability of RM for 1a-C_2v reveals an RMSE value of 0.014 as shown in Fig. 7. Although 1a-C_2v deviates from an elongated structure and is noticeably less rectangular, the small RMSE value suggests that an explanation of the electronic properties of 1a-C_2v based on the RM model is appropriate. The ratio of L_a/L_b for 1a-C_2v (1.37) is closer to 1 than the L_a/L_b ratio for 3a (1.62), leading to the ψ_1,3 eigenfunction approaching the ψ_3,1 eigenfunction. As a result, ψ_1,3 becomes the first unoccupied π MO, holding the highest weight in the antiaromaticity of 1a-C_2v, which is due to the ψ_2,2 → ψ_1,3 transition. Thus, the properties of a structure depend not only on the occupied MOs but also on the unoccupied MOs, or more precisely on the frontier MOs. An analogy between boron clusters and hydrocarbons solely based on the occupied MOs is thus insufficiently comprehensive.

Fig. 7 Correlation between DFT (PBE/6-311+G(d)) orbital energies of 1a-C_2v and eigenvalues of the particle in a rectangle box. Dimensions of the rectangle are drawn in proportion to its size. Red circles indicate the occupied levels while the blue squares indicate the unoccupied levels. Solid arrows indicate translational transition while dash-dotted arrows stand for allowed translational and rotational transition.

When explaining the antiaromaticity of 1a and the aromaticity of 3a, another question arises as to for why 3a becomes less stable than 1a. The aromaticity of an isomer is just one of the factors influencing its stability, and geometric shape is another significant factor. While boron clusters prefer seven-membered rings, comprising a ring of 6 atoms around a central atom, the eight-membered form is not their preferred geometry. Isomer 1a has an eight-membered ring, while 3a has two; therefore, the stability of 3a is improved as compared to its cation counterpart 3c but it is apparently not enough to surpass 1a.

And finally, there is still one factor influencing the stability of B₁₅⁻. The LUMO of 1a-C_2v is a σ* MO with an energy of only 0.07 eV higher than the HOMO. A narrow frontier orbital energy gap is often the cause leading to a multi-reference character of a structure.⁶⁷ Indeed, Fig. 8 shows that upon stabilization of the wavefunctions of 1a-C_2v, the shapes of its HOMO and LUMO undergo significant changes that are also similar to those of 1a (after geometry relaxation from 1a-C_2v). Such a shape transformation leads to a similarity making it difficult to distinguish between π and σ character for both HOMO and LUMO in 1a, and consequently, it is challenging to assign separated π and σ contributions to its aromatic character.

Fig. 8 Transformation of the HOMO and LUMO shapes from (a) unstable wavefunctions structure to (b) stable wavefunctions structure, and the transformation of HOMO and LUMO shapes during relaxation from (a) to (c).

Overall, the present study identifies two main reasons contributing to the diminished aromaticity of the B₁₅⁻ anion. Firstly, the 10 π electrons do not follow the aromaticity criterion according to the Hückel rule, a phenomenon explainable through both disk and rectangle models. From a DM perspective, a disk-shaped structure with 10 electrons would distort it to a lower symmetry and induce a reduced aromaticity due to similarities in the MO shapes among the frontier MOs. The RM also brings in similarities in the MO shapes among the frontier MOs as the rectangular shape becomes compressed closer to a square. Furthermore, the emergence of a σ* LUMO and a very small HOMO–LUMO gap leads to electron exchange between HOMO and LUMO, diminishing the aromaticity of B₁₅⁻.

In summary, both the RM and DM provide us with a similar perspective on the electronic structure of the B₁₅⁻ anion which leads to its reduced aromaticity. It is not in line with the classical electron count rule that the 10 π electrons must lead to a fully aromatic character.

4. Concluding remarks

A comprehensive examination of the B₁₅^q isomers in three charge states, cationic, neutral and anionic, was meticulously conducted. First, we carried out a benchmark on the accuracy of a series of DFT functionals that has been verified with respect to (U)CCSD(T)/aug-cc-pVTZ single point electronic energy calculations. Through the study of B₁₅^+/0/−, a number of important findings emerge as follows:

– For the cation B₁₅⁺, both 1c and 2c isomers can be considered as degenerate global minima whereas 3c is only slightly higher than 1c by ∼3 kcal mol⁻¹. The 3D isomer 4c is ∼10 kcal mol⁻¹ higher in energy than 1c, providing a better explanation for why this 3D isomer was not discovered in the previous Oger et al.'s experiments.

– A stringent benchmark relying solely on isomers with low spin contamination demonstrated the high reliability of the PBE and BPBE functionals in accurately predicting the relative energies for boron isomers. The accuracy of PBE is attributed to its ability to differentiate between 2D and 3D structures in agreement with CCSD(T) results. The TPSSh, PBE0 and HSE06 functionals still provide a good accuracy but need careful reconsideration regarding the competition in stability between 2D and 3D isomers. The present study also highlighted that functionals previously recommended from benchmarks based on coupled-cluster computations on systems having high-spin contamination tend to lead to large errors. Consequently, much caution is again suggested when treating structures bearing high spin contamination.

– Both cationic isomers 1c and 3c are π antiaromatic with 8 π electrons. However, as extra electrons are successively added, 3c is gradually transiting towards an aromatic character, while 1c undergoes a distortion and fails to acquire a high stability upon electron addition, even with 10 π electrons in the anionic state (1a-C_2v). The 10 electron rule originates from solution of the secular determinants for naphthalene. The rectangle model provides us with a similar solution, but it is easier to solve it than equations of secular determinants, and it can be applied to any rectangle-shaped molecule. The antiaromaticity of 3c and aromaticity of 3a were clearly understood from the rectangle model.

– The 1a-C_2v geometry is closer to a disk shape than a rectangle. Notably, the 10 π electrons according to the Hückel rule are observed in ring-like structures but not in disk-like counterparts. A disk model analysis showed that the ψ_1δ and ψ_2σ levels have similar energy levels, and if ψ_1δ is split into ψ_1δ− and ψ_1δ+, the shape of ψ_1δ+ becomes similar to ψ_2σ. Therefore, these three energy levels can be considered as degenerate, and while these 10 electrons do not confer a higher thermodynamic stability, the 12 electrons do.

– The 1a-C_2v is also examined from the perspective of the RM. The early appearance of ψ_1,3 is the reason behind the antiaromatic character of 1a-C_2v. This highlights the role of an appropriate geometry model for explaining the electron configuration and demonstrates that the shape of frontier MOs greatly influences the stability of the structure considered.

– Another factor contributing to a decreased stability of 1a is the emergence of a σ* LUMO, and a very small HOMO–LUMO gap which leads to an electron exchange between HOMO and LUMO when the 1a is relaxed from the more symmetrical 1a-C_2v.

Conflicts of interest

There is no conflict of interest to declare.

Acknowledgements

This research has been funded by Scientific Research Deanship of the University of Hail, Saudi Arabia through project number GR-22 092.

References

1. D. M. Schubert, Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015, pp. 1–32.
2. J. A. Berson, Chemical Creativity: Ideas from the Work of Woodward, Hückel, Meerwein, and Others, Wiley, 1999.
3. E. Steiner and P. W. Fowler, Ring currents in aromatic hydrocarbons, Int. J. Quantum Chem., 1996, 60, 609–616.
4. J.-S. M. Lee, Benzene, coronene, circumcoronene, Nat. Rev. Mater., 2023, 8, 223.
5. B. Kiran, G. G. Kumar, M. T. Nguyen, A. K. Kandalam and P. Jena, Origin of the unusual stability of B12 and B13+ clusters, Inorg. Chem., 2009, 48, 9965–9967.
6. D. Y. Zubarev and A. I. Boldyrev, Comprehensive analysis of chemical bonding in boron clusters, J. Comput. Chem., 2007, 28, 251–268.
7. O. B. Oña, J. J. Torres-Vega, A. Torre, L. Lain, D. R. Alcoba, A. Vásquez-Espinal and W. Tiznado, Chemical bonding analysis in boron clusters by means of localized orbitals according to the electron localization function topology, Theor. Chem. Acc., 2015, 134, 28.
8. L. Rincon, R. Almeida, J. E. Alvarellos, D. Garcia-Aldea, A. Hasmy and C. Gonzalez, The Σ delocalization in planar boron clusters, J. Chem. Soc., Dalton Trans., 2009, 3328–3333.
9. R. Breslow, J. T. Groves and G. Ryan, Cyclopropenyl cation, J. Am. Chem. Soc., 1967, 89, 5048.
10. H. J. Zhai, L. S. Wang, A. N. Alexandrova, A. I. Boldyrev and V. G. Zakrzewski, Photoelectron Spectroscopy and ab Initio Study of B₃⁻ and B₄⁻ Anions and Their Neutrals, J. Phys. Chem. A, 2003, 107, 9319–9328.
11. T. B. Tai, V. T. T. Huong and M. T. Nguyen, Topics in Heterocyclic Chemistry, Springer, Berlin, Heidelberg, 2014, pp. 161–187.
12. T. B. Tai, N. M. Tam and M. T. Nguyen, Structure of boron clusters revisited, B_n with n = 14–20, Chem. Phys. Lett., 2012, 530, 71–76.
13. T. B. Tai, N. M. Tam and M. T. Nguyen, The Boron conundrum: The case of cationic clusters B_n⁺ with n = 2–20, Theor. Chem. Acc., 2012, 131, 1–15.
14. Y.-J. Wang, X.-R. You, Q. Chen, L.-Y. Feng, K. Wang, T. Ou, X.-Y. Zhao, H.-J. Zhai and S.-D. Li, Chemical bonding and dynamic fluxionality of a B15+ cluster: a nanoscale double-axle tank tread, Phys. Chem. Chem. Phys., 2016, 18, 15774–15782.
15. H.-J. Zhai, B. Kiran, J. Li and L.-S. Wang, Hydrocarbon analogues of boron clusters—planarity, aromaticity and antiaromaticity, Nat. Mater., 2003, 2, 827–833.
16. L. S. Wang, Photoelectron spectroscopy of size-selected boron clusters: from planar structures to borophenes and borospherenes, Int. Rev. Phys. Chem., 2016, 35, 69–142.
17. M. Khatun, P. Sarkar, S. Panda, L. T. Sherpa and A. Anoop, Nanoclusters and nanoalloys of group 13 elements (B, Al, and Ga): benchmarking of methods and analysis of their structures and energies, Phys. Chem. Chem. Phys., 2023, 25, 19986–20000.
18. L. Liu, Z. Wei, Q. Chen, C. Shen, T. Shen, X. Tian and S. Li, Benchmarking boron cluster calculations: Establishing reliable geometrical and energetic references for B_n (n = 1–4), J. Comput. Chem., 2024, 45, 159–169.
19. A. P. Sergeeva, I. A. Popov, Z. A. Piazza, W.-L. Li, C. Romanescu, L.-S. Wang and A. I. Boldyrev, Understanding Boron through Size-Selected Clusters: Structure, Chemical Bonding, and Fluxionality, Acc. Chem. Res., 2014, 47, 1349–1358.
20. E. Oger, N. R. M. Crawford, R. Kelting, P. Weis, M. M. Kappes and R. Ahlrichs, Boron cluster cations: Transition from planar to cylindrical structures, Angew. Chem., Int. Ed., 2007, 46, 8503–8506.
21. Y. Yang, D. Jia, Y.-J. Wang, H.-J. Zhai, Y. Man and S.-D. Li, A universal mechanism of the planar boron rotors B₁₁⁻, B₁₃⁺, B₁₅⁺, and B₁₉⁻: inner wheels rotating in pseudo-rotating outer bearings, Nanoscale, 2017, 9, 1443–1448.
22. R. B. King, Planar Networks of Boron Triangles: Analogies to Benzene and Other Planar Aromatic Hydrocarbons, J. Phys. Chem. A, 2022, 126, 901–909.
23. H. T. Pham, L. V. Duong, B. Q. Pham and M. T. Nguyen, The 2D-to-3D geometry hopping in small boron clusters: The charge effect, Chem. Phys. Lett., 2013, 577, 32–37.
24. M. Saunders, Stochastic search for isomers on a quantum mechanical surface, J. Comput. Chem., 2004, 25, 621–626.
25. F. Avaltroni and C. Corminboeuf, Identifying clusters as low-lying mimina-efficiency of stochastic and genetic algorithms using inexpensive electronic structure levels, J. Comput. Chem., 2012, 33, 502–508.
26. V. N. Staroverov, G. E. Scuseria, J. Tao and J. P. Perdew, Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes, J. Chem. Phys., 2003, 119, 12129–12137.
27. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170.
28. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A, 1988, 38, 3098–3100.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654.
31. G. Monaco, F. F. Summa and R. Zanasi, Program Package for the Calculation of Origin-Independent Electron Current Density and Derived Magnetic Properties in Molecular Systems, J. Chem. Inf. Model., 2021, 61, 270–283.
32. R. Zanasi, Coupled Hartree-Fock calculations of molecular magnetic properties annihilating the transverse paramagnetic current density, J. Chem. Phys., 1996, 105, 1460–1469.
33. P. W. Fowler, R. Zanasi, B. Cadioli and E. Steiner, Ring currents and magnetic properties of pyracylene, Chem. Phys. Lett., 1996, 251, 132–140.
34. D. Y. Zubarev and A. I. Boldyrev, Developing paradigms of chemical bonding: Adaptive natural density partitioning, Phys. Chem. Chem. Phys., 2008, 10, 5207–5217.
35. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, et al., Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT.
37. N. Shen, Y. Fan and S. Pamidighantam, E-science infrastructures for molecular modeling and parametrization, J. Comput. Sci., 2014, 5, 576–589.
38. R. Dooley, K. Milfeld, C. Guiang, S. Pamidighantam and G. Allen, From proposal to production: Lessons learned developing the computational chemistry Grid cyberinfrastructure, J. Grid Comput., 2006, 4, 195–208.
39. J. C. Rienstra-Kiracofe, W. D. Allen and H. F. Schaefer, C₂H₅ + O₂ reaction mechanism: High-level ab initio characterizations, J. Phys. Chem. A, 2000, 104, 9823–9840.
40. L. V. Duong, N. N. Tri, N. P. Hung and M. T. Nguyen, Boron Silicon B2Si3q and B3Si2p Clusters: The Smallest Aromatic Ribbons, J. Phys. Chem. A, 2022, 126, 3101–3109.
41. L. V. Duong, N. T. Si, N. P. Hung and M. T. Nguyen, The binary boron lithium clusters B₁₂Li_n with n = 1–14: in search for hydrogen storage materials, Phys. Chem. Chem. Phys., 2021, 23, 24866–24877.
42. J. Lv, Y. Wang, L. Zhu and Y. Ma, B₃₈: an all-boron fullerene analogue, Nanoscale, 2014, 6, 11692–11696.
43. A. P. P. Sergeeva, Z. A. A. Piazza, C. Romanescu, W.-L. L. Li, A. I. I. Boldyrev and L.-S. S. Wang, B22- and B23-: All-boron analogues of anthracene and phenanthrene, J. Am. Chem. Soc., 2012, 134, 18065–18073.
44. K. C. Lau, M. Deshpande and R. Pandey, A theoretical study of vibrational properties of neutral and cationic B₁₂ clusters, Int. J. Quantum Chem., 2005, 102, 656–664.
45. M. Atiş, C. Özdoğan and Z. B. Güvenç, Structure and energetic of B_n (n = 2–12) clusters: Electronic structure calculations, Int. J. Quantum Chem., 2007, 107, 729–744.
46. T. Janda and C. Foroutan-Nejad, Why is Benzene Unique? Screening Magnetic Properties of C₆H₆ Isomers, ChemPhysChem., 2018, 19, 2357–2363.
47. C. Foroutan-Nejad, Magnetic Antiaromaticity—Paratropicity—Does Not Necessarily Imply Instability, J. Org. Chem., 2023, 88, 14831–14835.
48. A. P. Sergeeva, D. Y. Zubarev, H.-J. Zhai, A. I. Boldyrev and L.-S. Wang, A Photoelectron Spectroscopic and Theoretical Study of B₁₆⁻ and B₁₆²⁻: An All-Boron Naphthalene, J. Am. Chem. Soc., 2008, 130, 7244–7246.
49. L. V. Duong, D. T. T. Mai, M. P. Pham-Ho and M. T. Nguyen, A theoretical approach to the role of different types of electrons in planar elongated boron clusters, Phys. Chem. Chem. Phys., 2019, 21, 13030–13039.
50. A. P. Sergeeva, B. B. Averkiev, H. J. Zhai, A. I. Boldyrev and L. S. Wang, All-boron analogues of aromatic hydrocarbons: B₁₇⁻ and B₁₈⁻, J. Chem. Phys., 2011, 134, 224304.
51. R. McWeeny, Ring currents and proton magnetic resonance in aromatic molecules, Mol. Phys., 1958, 1, 311–321.
52. J. D. Roberts, Notes on Molecular Orbital Calculations, W. A. Benjamin, 1961.
53. E. Hückel, Quantentheoretische Beiträge zum Benzolproblem, Z. Phys., 1931, 70, 204–286.
54. G. Frenking, Perspective on “Quantentheoretische Beiträge zum Benzolproblem. I. Die Elektronenkonfiguration des Benzols und verwandter Beziehungen”, Theor. Chem. Acc., 2000, 187–189.
55. A. G. Arvanitidis, T. B. Tai, M. T. Nguyen and A. Ceulemans, Quantum rules for planar boron nanoclusters, Phys. Chem. Chem. Phys., 2014, 16, 18311–18318.
56. T. A. Keith and R. F. W. Bader, Calculation of magnetic response properties using a continuous set of gauge transformations, Chem. Phys. Lett., 1993, 210, 223–231.
57. S. Coriani, P. Lazzeretti, M. Malagoli and R. Zanasi, On CHF calculations of second-order magnetic properties using the method of continuous transformation of origin of the current density, Theor. Chim. Acta, 1994, 89, 181–192.
58. N. C. Baird, Quantum Organic Photochemistry. II. Resonance and Aromaticity in the Lowest ³ππ* State of Cyclic Hydrocarbons, J. Am. Chem. Soc., 1972, 94, 4941–4948.
59. H. Ottosson, Exciting excited-state aromaticity, Nat. Chem., 2012, 4, 969–971.
60. M. Solà and F. M. Bickelhaupt, Particle on a Ring Model for Teaching the Origin of the Aromatic Stabilization Energy and the Hückel and Baird Rules, J. Chem. Educ., 2022, 99, 3497–3501.
61. C. Liu, Y. Ni, X. Lu, G. Li and J. Wu, Global Aromaticity in Macrocyclic Polyradicaloids: Hückel's Rule or Baird's Rule?, Acc. Chem. Res., 2019, 52, 2309–2321.
62. M. K. Cyrański, R. W. A. Havenith, M. A. Dobrowolski, B. R. Gray, T. M. Krygowski, P. W. Fowler and L. W. Jenneskens, The phenalenyl motif: A magnetic chameleon, Chem. – Eur. J., 2007, 13, 2201–2207.
63. T. B. Tai, R. W. A. Havenith, J. L. Teunissen, A. R. Dok, S. D. Hallaert, M. T. Nguyen and A. Ceulemans, Particle on a Boron Disk: Ring Currents and Disk Aromaticity in B₂₀²⁻, Inorg. Chem., 2013, 52, 10595–10600.
64. T. B. Tai, A. Ceulemans and M. T. Nguyen, Disk aromaticity of the planar and fluxional anionic boron clusters B₂₀^−/2−, Chem. – Eur. J., 2012, 18, 4510–4512.
65. T. B. Tai, L. V. Duong, H. T. Pham, D. T. T. Mai and M. T. Nguyen, A disk-aromatic bowl cluster B₃₀: toward formation of boron buckyballs, Chem. Commun., 2014, 50, 1558–1560.
66. T. K. Zywietz, H. Jiao, P. V. R. Schleyer and A. De Meijere, Aromaticity and Antiaromaticity in Oligocyclic Annelated Five-Membered Ring Systems, J. Org. Chem., 1998, 63, 3417–3422.
67. S. Grimme and A. Hansen, A Practicable Real-Space Measure and Visualization of Static Electron-Correlation Effects, Angew. Chem., Int. Ed., 2015, 54, 12308–12313.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp00077c

---