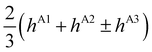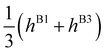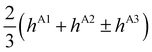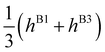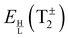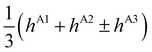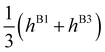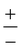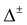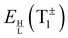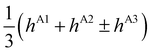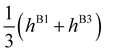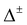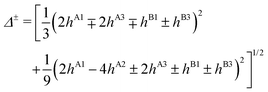Tunneling splittings in the vibrationally excited states of water trimer
Mihael
Eraković
a and
Marko T.
Cvitaš
 *b
*b
aDepartment of Physical Chemistry, Ruđer Bošković Institute, Zagreb, Croatia. E-mail: merakov@irb.hr
bDepartment of Physics, University of Zagreb Faculty of Science, Zagreb, Croatia. E-mail: mcvitas.phy@pmf.hr
First published on 1st April 2024
Abstract
Tunneling splitting (TS) patterns in vibrationally excited states of the water trimer are calculated, taking into account six tunneling pathways that describe the flips of free OH bonds and five bifurcation mechanisms that break and reform hydrogen bonds in the trimer ring. A tunneling matrix (TM) model is used to derive the energy shifts due to tunneling in terms of the six distinct TM elements in symbolic form. TM elements are calculated using the recently-developed modified WKB (Wentzel–Kramers–Brillouin) method in full dimensionality. Convergence was achieved for the lowest six excited vibrational modes. Bifurcation widths of the pseudorotational quartets are shown to be of comparable size to the ground-state widths, obtained using instanton theory, or increased for some particular modes of vibration. The largest increase is obtained for the excited out-of-phase flip of two adjacent water monomers with free OH bonds pointing in opposite directions relative to the ring plane. Bifurcation widths in (D2O)3 are found to be two orders of magnitude smaller than in (H2O)3. Geometrical arguments were used to explain the order of states in some TS multiplets in vibrationally excited water trimers.
1 Introduction
Extensive studies of small water clusters over several decades aimed to quantify their structure, interactions and dynamics in order to develop an accurate molecular description of liquid water.1,2 Interactions that govern the cooperative hydrogen-bond dynamics in water also control the tunneling rearrangements between equivalent minima of water clusters.2–4 These rearrangements produce splittings in rovibrational spectra that can be measured using high-resolution far-infrared spectroscopies.2,5–9 Tunneling splittings, which vary over many orders of magnitude, are thus a sensitive probe of intermolecular water interactions at far-from-equilibrium geometries. They were first measured for the dimer10 and trimer11,12 and, subsequently, for other water clusters up to the decamer.7,13–18 Computational modeling of vibrational spectra provides a means to interpret the measurements19–21 and assists in spectral assignments.8,9The water trimer is the smallest cyclic water cluster. It displays rich hydrogen bond dynamics of the flips of free hydrogens and bifurcations, in which a hydrogen bond that forms the ring is broken and reformed with the previously free hydrogen.22,23 Similar dynamics is also present in larger clusters24 such as the water pentamer.25 Tunneling splitting (TS) patterns of homoisotopic trimers, (H2O)3 and (D2O)3, have been observed for both the torsional (flip) states and also bifurcations.5,12,20,26,27 Partially deuterated trimers have also been studied11 and produce qualitatively different TS patterns.28 Recently, a drastic increase in TS due to bifurcations in vibrationally excited states was observed in water dimer8,29 (40×), trimer9,29 (400×) and pentamer30 (4000×).
State-of-the-art calculations of tunneling spectra usually proceed by solving the nuclear Schrödinger equation in the electron potential. Recent water potentials are based on a fit to ab initio electronic energies and employ a many-body expansion of monomer potentials. The commonly used potentials are the so-called CC-pol,31 WHBB4,32,33 and MB-pol34–36 and contain a contribution of three-body interactions. The exact full-dimensional quantum treatments of water dimer8,37,38 on the above electronic potentials achieve a reasonable agreement with experiment. The full quantum treatment of the water trimer is probably also within reach using recently developed methods,39,40 and is expected to yield the TS patterns of torsional states in the near future. Fine splittings of torsional levels due to bifurcations are unlikely to be captured this way.
The calculation of vibrational tunneling spectra of water trimer and larger water clusters with many equivalent minima can be decomposed into a number of smaller tasks using the tunneling matrix (TM) model.22,23 The TM elements represent tunneling transition amplitudes between two minima and can each be calculated separately using quantum or approximate semiclassical methods. TM eigenvalues then provide the spectrum. Formally exact treatments employ diffusion Monte-Carlo41,42 and path-integral molecular dynamics43 (PIMD) methods. The TM model was also recently employed to treat the interactions beyond that of the nearest neighbors in a PIMD approach and was used to calculate the pseudorotational TS pattern in water trimers in excellent agreement with experiment.44 Earlier studies determined and analysed the TS patterns for flips and bifuractions using WKB (Wentzel–Kramers–Brillouin) approximation.45–47 More recently, the semiclassical instanton theory48 was applied in full dimensionality in a series of studies of water clusters.6,17,21,24,25,49 In particular, it was utilized to determine the six dominant rearrangement pathways of flips and bifurcations in water trimer.21 The same paths were also used to interpret qualitatively different TS patterns in some partially deuterated water trimers.28 Prominently, a combined study of instanton theory with experiment revealed the signature of the double hydrogen-bond breaking dynamics in the spectra of the water hexamer prism.6 All TM calculations mentioned above were only concerned with TS in the ground vibrational state.
Multidimensional instanton theory for calculating TS has been derived in continuous form50 and, later, in discrete form.51 They were generalized to treat multi-well systems with asymmetric paths (with no mirror symmetry of the potential along the path) in ref. 21 and, later, by us52 in the continuous version. Both versions are mutually equivalent and are also equivalent to a modified version of WKB theory50,53,54 for the ground-state (GS) TS. In the modified WKB method, the wavefunction is constructed along the minimum action path connecting two minima, which allows one to determine the TM elements using the Herring formula.55,56 The WKB approach provides a route to calculating TM elements in vibrationally excited states,57 which we generalized to multi-well systems.58 Our approach works for asymmetric paths, encountered in the water trimer, and treats longitudinal and transverse excitations on an equal footing.58 The application on malonaldehyde59 showed that the method gives a quantitative agreement with the exact quantum results for TSs in the low-lying vibrational states.
The objective of this paper is to employ the TM model22 using six previously determined rearrangement paths,21,45 shown to be of comparable importance in ref. 21, and perform a full-dimensional calculation and characterization of TS patterns in the low-lying vibrationally excited states of the water trimer. The focus of the paper is on the fine splittings of pseudorotational states induced by the dynamics of bifurcations, which is, to our knowledge, difficult to obtain in the vibrationally excited states using any other method. A dramatic increase of bifurcation splittings in water clusters has recently been observed in experiments.9,29,30 The TM model, as formulated using instanton theory,21 is described in Section 2. We also derive the energy shifts symbolically in terms of TM elements for the six mechanisms. The TM elements are calculated using the recent version of the modified WKB method52,58 and MB-pol potential.34–36 The method, computational details and results are described in Sections 3, 4 and 5, respectively, with conclusions in Section 6.
2 Tunneling dynamics of the water trimer
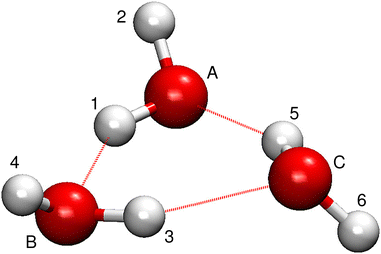
In its equilibrium geometry, the water molecules in a water trimer form a ring, bound by hydrogen bonds.22 Each water molecule has one of its OH bonds inside the ring to uphold the hydrogen bonds. The remaining OH bonds point with their hydrogens either up or down relative to the plane of the ring, as shown in Fig. 1. The oxygen atoms are labeled A, B and C in the direction in which the hydrogens in the in-ring OH bonds point, starting with the first (of the two) up-pointing moiety. Hydrogens inside the ring are labeled using odd number labels and those outside the ring plane using even numbers.There are 48 wells on the potential energy surface (PES) of the water trimer with the minima that are equivalent to the one shown in Fig. 1 and are accessible via dynamics that does not break the covalent bonds or change the orientation of hydrogen bonds inside the ring (in the so-called clockwise–counterclockwise rearrengement5). The low-lying vibrational states of the trimer in different wells interact with each other in the narrow passages inside the barriers via tunneling. These interactions are responsible for the energy splittings that appear in its vibrational spectra. A TM is constructed in which the rows and columns represent different minima. Each TM element quantifies the interactions between the states that are localized in the two minima it connects. The rearrangement processes between the minima have thoroughly been studied in the past.20,45 It has been determined that there are six rearrangements that give rise to the appearance of the ground-state splitting pattern in water trimer.21 TM elements corresponding to the rearrangements can be calculated using accurate methods, such as PIMD,43 or approximate WKB46,47 and instanton methods,21,24 as in the approach we follow below. The eigenvalues of TM are then the energy shifts of vibrational tunneling states.
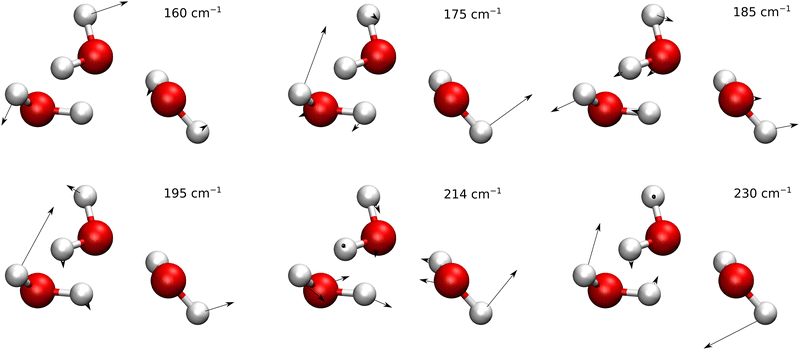
The 48 minima of the water trimer can each be labeled by a symmetry element of the molecular symmetry group G48. The symmetry elements include the cyclic permutations of oxygen atom labels, pairwise transpositions of hydrogen labels on each water monomer and inversion. The character table and irreducible representations of the group have been determined in ref. 22. The six distinct tunneling pathways that form the TS pattern can also be labeled by the symmetry operations of G48 by assigning them the label of the minimum to which the pathway leads starting from the reference structure labeled as in Fig. 1. Different identifications used for the 6 paths are collected in Table 1 and the snapshots of geometries along the paths are shown in Fig. 2.
| Pathway | Dynamics | Symmetry |
|---|---|---|
| F | A | (ACB)(1 5 3)(2 6 4)* |
| B | (ABC)(1 3 5)(2 4 6)* | |
| A1 | ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) + A + A |
(ABC)(1 3 6 2 4 5) |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) + C + C |
(ACB)(1 5 4 2 6 3) | |
| A2 | ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) + B + B |
(ACB)(1 6 4 2 5 3) |
| Ã + C | (ABC)(1 3 5 2 4 6) | |
| A3 | Ã | (ACB)(1 5 3 2 6 4)* |
![[B with combining tilde]](https://www.rsc.org/images/entities/char_0042_0303.gif) |
(ABC)(1 4 6 2 3 5)* | |
| B1 | ![[C with combining tilde]](https://www.rsc.org/images/entities/char_0043_0303.gif) + AB + AB |
(56)* |
| B3 | Ã + BC | (12)* |
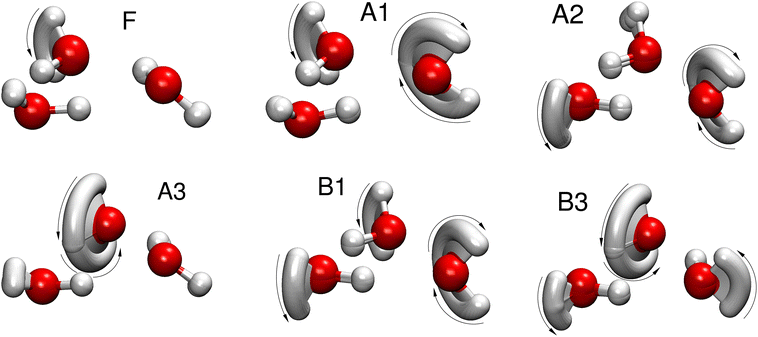 | ||
| Fig. 2 Minimum action paths for 6 rearrangements that are responsible for the formation of the tunneling splitting patterns in the water trimer (H2O)3. Sequential snapshots of the trimer along the path connecting two symmetry-related minima are shown. The pathways are labeled as defined in Table 1. | ||
Rearrangement with the lowest barrier is a flip of a majority monomer, whereby one of the monomers pointing above the ring plane in Fig. 1 rotates around the in-ring OH bond to point below the plane in the final state. Sequential snapshots along the path are shown in Fig. 2 and the potential along the path in Fig. 3, labeled ‘F’. Subsequent flips of the leading majority monomers lead to the initial structure after 6 such flips and are hence termed pseudorotation. The pseudorotations in water trimers form a group that is a direct product of 3 cyclic oxygen permutations, G3, and inversion, and is isomorphic to C3h and forms a subgroup of G48. The dynamics of flips has thoroughly been studied using reduced-dimensionality models,60–64 PIMD,43,44 Monte Carlo methods9,41,42 and instanton theory.21,24
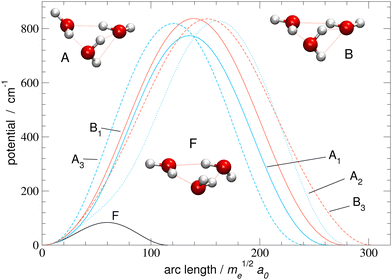 | ||
| Fig. 3 Potential energy curves along minimum action paths of rearrangements listed in Table 1 and shown in Fig. 2. Stationary geometries F, A and B near barrier maxima on paths F, A1–A3, and B1–B3, respectively, are also shown. | ||
TM for the flips is a 6 × 6 matrix. Indices of its rows and columns are labelled by the two minima that the tunneling path connects and the corresponding matrix element is the transition amplitude associated with the rearrangement. TM is thus a Hamiltonian matrix in the basis of 6 degenerate eigenstates of the 6 symmetric wells in the absence of tunneling. We take one local vibrational eigenstate in each well in our basis and neglect its interaction with other vibrational manifolds in our calculations below.
The flip of the out-of-plane OH bond of the leading majority monomer A, labeled by its oxygen atom, starting from the reference version shown in Fig. 1, leads to the version with the leading majority monomer B in the inverted trimer. The flips of A and B monomer are thus the inverse symmetry operations in the group, as shown in Table 1, and the associated TM elements hF are equal in size. We take into account only ‘nearest neighbor’ interactions. Each row of the TM thus has two non-zero entries associated with the A and B monomer flips. The TM can be diagonalized analytically and leads to energies 2hF, hF, −hF and −2hF for states of A+, E−, E+ and A− symmetries, respectively. The inner energy levels E± are doubly degenerate. The eigenvectors of the TM are the expansion coefficients of the vibrational wavefunction in our basis of localized well states. The TM model thus gives a quartet splitting with spacings 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In a recent study,44 a model which takes into account direct interactions between all 6 wells was developed in which the spacings in the quartet no longer follow the same pattern.
1. In a recent study,44 a model which takes into account direct interactions between all 6 wells was developed in which the spacings in the quartet no longer follow the same pattern.
The other five tunneling pathways determined in ref. 21 and shown in Fig. 2 involve bifurcations of water monomers. Bifurcation is the motion in which the in-plane OH bond rotates out of the hydrogen bond and away from the out-of-plane OH, which rotates in the plane of the ring to reform the hydrogen bond. It was found21 that in the dominant rearrangements of water trimer, the bifurcations are always accompanied by one or more flips. The same is true for the water pentamer,25 which also forms an odd-membered ring structure in its ground-state configuration. Bifurcation mechanisms are listed in Table 1 and shown in Fig. 2. We label paths as in ref. 45 in the first column of Table 1 and describe the mechanics of the rearrangement in the second column using symbols. Labels A–C refer to the monomer involved in the flip motion while the letter with ‘∼’ on top refers to a bifuraction of the corresponding monomer. The associated symmetry operation is listed in the third column. Paths labeled A1–A3 are asymmetric, hence the forward and reverse motions are labeled differently because the monomers involved in the motion take on different roles in the two minima they connect. The potential along asymmetric paths does not possess a mirror symmetry. Paths B1 and B3 are symmetric and are associated with the symmetry operation which is its own inverse in Table 1. Bifurcations proceed over significantly higher barriers than the flip, see Fig. 3, because they break hydrogen bonds. They thus produce the fine splittings in each branch of the flip quartet.
The inclusion of a bifurcation mechanism generates paths to all 48 minima on the PES, each of which can be reached in the maximum of 3 such ‘elementary’ steps from any other minimum. The 48 × 48 TM has 10 non-zero elements in each row (or column) with 6 of them different in size. Pathways F (for flips) and A1–A3 produce 8 non-zero TM elements as they are asymmetric so the inverse operation leads to a distinct minimum. B1 and B3 are symmetric and produce the remaining two.
We now proceed to derive the energies of the 48 vibrational tunneling states in terms of TM elements symbolically. For this purpose, we recall the results of ref. 28 in which we studied the ground-state TS pattern of the partially deuterated (PD) water trimer, where either one or two of its monomers are substituted by D2O. The molecular symmetry group of the PD trimer consists of the transpositions of hydrogens on each monomer and the inversion. They together form a subgroup G16 of G48 (bifurcations + inversion without the flips). The group is Abelian, thus all its irreducible representations (irreps) are one-dimensional. Its character table is given in Table 5 of ref. 28. In the PD trimer, the double degeneracy of the inner E± states of the flip quartet is removed (flip is not a symmetry operation) and the flip states form a sextet instead. Bifurcations further split each of the six sextet states into octets, whereby each member state of the octet is of different symmetry species in G16, i.e., 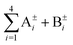 . The energies of these 8 states have been determined in terms of TM elements symbolically in ref. 28 as follows. First, an eigenvector of the desired symmetry (irrep) is constructed using the corresponding projection operator and, then, the associated expectation value of the TM is calculated in symbolic form. The symmetry-adapted vectors are unique since only one state of a particular symmetry lies in each branch of the flip sextet.
. The energies of these 8 states have been determined in terms of TM elements symbolically in ref. 28 as follows. First, an eigenvector of the desired symmetry (irrep) is constructed using the corresponding projection operator and, then, the associated expectation value of the TM is calculated in symbolic form. The symmetry-adapted vectors are unique since only one state of a particular symmetry lies in each branch of the flip sextet.
The PD trimer states converge to the states of homoisotopic trimer in the thought process in which the masses of D atoms are artificially reduced towards the mass of an H atom. Symmetries of G48 irreps in the G16 group are given by the correlation table, Table 6, in ref. 28. For the states of the homoisotopic trimer that appear only once inside a particular branch of the flip quartet, the energy can be determined from the energy expressions in G16, listed in Table S3 of ref. 28 (using the eigenvectors of flip states). In the E± flip branch of the homoisotopic trimer, which splits as E± = 2T±1 + 2T±2 + E±1 + E±2 in G48, the states T±1 and T±2 appear twice. Using descent in symmetry, these states in G48 correlate as T±1 = A±2 + A±3 + B±1, T±2 = A±4 + B±2 + B±3, E±1 = B±4 + B±4 and E±2 = A±1 + A±1 to the states in G16 (left side in G48; right side in G16). The components of two T+1 states that have the same symmetry in G16 belong to different branches of the flip sextet in PD trimer. We need to find two particular linear combinations of flips in the doubly degenerate E+ manifold which, when degeneracy is removed by increasing the hydrogen masses on one monomer, give rise to the pairs of A+2, A+3 and B+1 states, each in a different flip branch of the PD trimer, that originates from E+. Using perturbation theory for degenerate states, we take one pair of states of the same symmetry as a basis, e.g., of A+2 symmetry, and construct a 2 × 2 block of TM in symbolic form. The block is then diagonalized to obtain the energies as 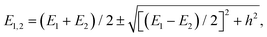 where E1 and E2 are diagonal matrix elements of the block and h is the off-diagonal element. Alternatively, taking A+3 or B+1 states as a basis results in a different 2 × 2 matrix but the same final result. The procedure for determining the energies of T−1 and T±2 states is analogous. Symbolic expressions for the energy levels in terms of TM elements that correspond to rearrangements in Fig. 2 are collected in Table 2. The quadratic form under the square root in Δ± has two non-zero eigenvalues and is expressed in the diagonal representation in Table 2.
where E1 and E2 are diagonal matrix elements of the block and h is the off-diagonal element. Alternatively, taking A+3 or B+1 states as a basis results in a different 2 × 2 matrix but the same final result. The procedure for determining the energies of T−1 and T±2 states is analogous. Symbolic expressions for the energy levels in terms of TM elements that correspond to rearrangements in Fig. 2 are collected in Table 2. The quadratic form under the square root in Δ± has two non-zero eigenvalues and is expressed in the diagonal representation in Table 2.
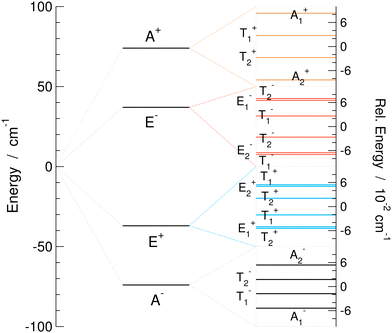 | ||
| Fig. 4 Tunneling splitting pattern for the excited vibrational mode 3 (harmonic frequency 185 cm−1) of the water trimer (H2O)3 on MB-pol PES.34–36 The set of levels on the left is the pseudorotational quartet; insets on the right show the bifurcation splittings of each branch of the quartet. | ||
We are now in the position to analyse the energy-level diagram given by the formulae in Table 2. In the ground vibrational state, all matrix elements hi are negative. Pseudorotational states form a quartet A+ + E− + E+ + A−, as discussed above. Bifurcations split member states of the quartet into finer splittings. State A+ is split into a quartet of equidistant energy levels A+ = A+1 + T+1 + T+2 + A+2. State A− splits similarly into a quartet, equally spaced and of opposite parity. The order of the states in A± is the same as in Table 2, if 2(hA1 + hA2) > ±(2hA3 + hB1 + hB3) and reverse otherwise. The widths of the outer flip states A± are |4(hA1 + hA2 ± hA3) ± 2(hB1 ± hB3)|. With only A1 and A2 mechanisms present, A+ and A− flip manifolds would have equal widths. Generally, for the states that change sign under inversion, with the superscript ‘−’, the matrix elements hA3, hB1 and hB3 change sign relative to the corresponding ‘+’ states in the energy expressions in Table 2. This happens because the symmetry operations, see Table 2, associated with A3, B1 and B3 rearrangements involve inversion.
Bifurcations split the doubly degenerate pseudorotational state E− into a sextet, E−1 + 2T−2 + 2T−1 + E−2. The energy of E−1, the average energy of the two (H/L) T−2 states, that of two T−1 states, and of E−2 are also equidistant. However, the pairs (H/L) of T−2 and T−1 states are set apart by 2Δ−, see Table 2. The E−1,2 states split symmetrically with respect to the origin of the flip state, as do the lower (L) T−2 and upper (H) T−1 states, and the lower T−1 and upper T−2 states. If Δ− > 1/3|E(E−2) − E(E−1)|, T−2 and T−1 states change order with E−1 and E−2 states. The order of the states, therefore, cannot be established in advance although it is not arbitrary. The order of the states in the E− flip manifold is the same as in Table 2, when hA1 + hA2 < ±(−hA3 + hB1 + hB3) and reverse otherwise. If only one bifurcation mechanism was present, E− states would split into a quartet. With B1 or B3 present, the quartet is equally spaced (as in ref. 9 and 20); with A1, A2 or A3 present, the spacings are 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. An analogous analysis applies to the bifurcation splittings of the pseudorotational state E+.
1. An analogous analysis applies to the bifurcation splittings of the pseudorotational state E+.
We note that the energy level diagram in Table 2 uniquely determines the 6 matrix elements h. There are 7 constraints in them: hF is determined from the width of the flip quartet, while the remaining six are the widths of the four branches of the flip quartet and the sizes of Δ± shifts.
3 Tunneling matrix element via modified WKB
The TM element for the interaction between the localized states of two symmetry-related minima i and j, connected by a feasible rearrangement, can be evaluated using the Herring formula,55,56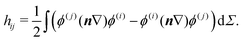 | (1) |
The local wavefunctions ϕi/j are approximated using the standard WKB ansatz (with indices i/j suppressed) as
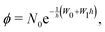 | (2) |
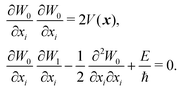 | (3) |
The HJ equation is solved for W0 using the method of characteristics. Momentum is identified with pi = ∂W0/∂xi and the equations of characteristics,
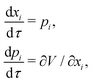 | (4) |
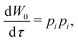 | (5) |
We define a local coordinate system (S, Δx), where S is the arc-length distance from one minimum along the trajectory and Δxi are displacements along the coordinate axes that lie perpendicular to the trajectory. The perpendicular coordinate axes coincide with the normal mode directions of the molecule at minimum and are propagated along the trajectory using parallel transport. Since momentum is tangent to the path, 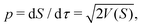 and the trajectory can be reparametrized using S. Characteristic function W0 and the potential V are both expanded to second order in displacements at each point on the characteristic. We then have
and the trajectory can be reparametrized using S. Characteristic function W0 and the potential V are both expanded to second order in displacements at each point on the characteristic. We then have
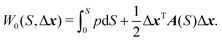 | (6) |
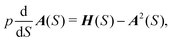 | (7) |
From TE, we immediately obtain W1 on the characteristic in the form
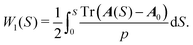 | (8) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A0, where the matrix of frequencies
A0, where the matrix of frequencies 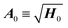 and H0 is the Hessian at minimum. By setting A(0) = A0, the WKB wavefunction in eqn (2) at the minimum coincides with that of the harmonic oscillator if we set the normalization constant N0 = (det
and H0 is the Hessian at minimum. By setting A(0) = A0, the WKB wavefunction in eqn (2) at the minimum coincides with that of the harmonic oscillator if we set the normalization constant N0 = (det![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A0/πf)1/4, where f is the dimensionality of the system.
A0/πf)1/4, where f is the dimensionality of the system.
The excited-state wavefunction with one quantum of excitation in the vibrational mode Ue of frequency ωe is constructed by adding w(S) to W1 in eqn (2), ϕ = N1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[1/ħ(−W0 − W1 − w)], which then satisfies
exp[1/ħ(−W0 − W1 − w)], which then satisfies
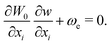 | (9) |
| e−w = F(S) + UT(S)Δx, | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−w)/∂Δxi. Factor F appears in the expression because the MAP in general deviates from the normal mode direction at the distance S = ε from the minimum. From eqn (9), it follows that
exp(−w)/∂Δxi. Factor F appears in the expression because the MAP in general deviates from the normal mode direction at the distance S = ε from the minimum. From eqn (9), it follows that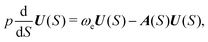 | (11) |
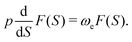 | (12) |
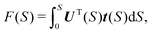 | (13) |
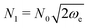 .
.
The dividing plane Σ is chosen to intersect the MAP at S = SΣ, where the potential V(SΣ) has a maximum along the MAP, at the right angle, so that the surface normal n coincides with the tangent t(SΣ) to the MAP at SΣ. The WKB wavefunctions constructed above are inserted into the Herring formula and the normal derivative in eqn (1) brings p(SΣ) in front as the leading order contribution, which is then assumed not to vary appreciably over the width of ϕ in the Σ plane. The integral of the product of wavefunction ϕi and ϕj over the Σ-plane is of Gaussian type and is evaluated analytically. The final expression for the tunneling matrix element between minima i and j with ν excitations (ν is either 0 or 1) reads
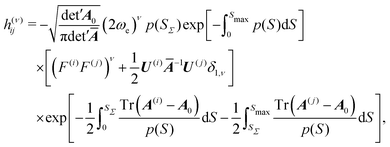 | (14) |
The theory ignores rotations. It is assumed they are decoupled and do not modify the splitting appreciably in the rotational ground state. This is expected to be a good approximation for water trimer.49 The system is treated in full dimensionality but in a harmonic approximation in the directions perpendicular to the MAP. The zero-point motion of perpendicular modes enters the TM element through integrals in the last line of eqn (14). Exact energies of local degenerate well states do not enter the equation, but the normalization to harmonic oscillator states at minima introduces an error through the first factor on the r.h.s. in eqn (14).65 The method performs best for high barriers and small splittings. As described in the next section, the entire theory can be applied in Cartesian coordinates and at a modest computational cost, which allows one to apply it to systems that are out of reach to exact quantum treatments. Using on-the-fly ab initio evaluation of the electronic potential and gradients, the application is limited to systems that allow the evaluation of several thousand gradients with sufficient accuracy.
4 Computational details
The computation of TM elements proceeds as follows. In the first step, one determines the minimum energy geometry, shown in Fig. 1, in Cartesian coordinates. In the next step, we determine the minimum action paths (MAPs) for all rearrangements in Table 1, that are responsible for the formation of the splitting pattern21 through relationships shown in Table 2. The MAP for a particular rearrangement is obtained by applying the corresponding permutation of labels in Table 1 to the minimum geometry and, for the paths F, B1 and B3, the multiplication of all Cartesian coordinates by −1 for the inversion. The two geometries are then aligned with respect to each other to minimize the Euclidean distance in mass-scaled Cartesian coordinates using quaternions66 (or the Kabsch algorithm67). The straight line path that connects the minima in Cartesian coordinates is discretized using N images or beads, in ring-polymer formalism, at equal mass-scaled distances using linear interpolation in each coordinate. The initial path is then optimized using the string method to minimize the Jacobi action along the path as described in ref. 68 and 69. For this purpose, the gradients of the potential are evaluated at all intermediate beads between the two minima at every iteration in order to calculate the discretized gradients of Jacobi action. Geometry update of the intermediate beads is then performed using the LBFG(S) (limited memory Broyden–Fletcher–Goldfarb–Shanno) method70 with the gradients of action projected at directions perpendicular to the path. The end beads are reoriented using a quaternion algorithm to minimize the distance to the closest bead. To ensure that all beads remain equally spaced along the path, reinterpolation of beads along the path is also performed at each iteration. Water trimer MAPs typically give converged matrix elements using N = 30 beads in ≈300 steps with the convergence threshold set at 10−6 a.u. for the largest length of the projected action gradient at a bead. The calculations below use N = 101 to ensure a tight convergence.All subsequent calculations proceed using properties evaluated at the MAP. The potential and Hessians of the potential are evaluated at every bead and the interpolants V(S) and H(S) are constructed in terms of the arc length distance S along the MAP using cubic splines. This allows us to integrate eqn (7) from each minimum up to the dividing plane, at S = SΣ, at both sides of Σ. Matrix A is recorded at predetermined positions, e.g., beads, along the MAP in order to construct the spline interpolants A(S) on each side of the dividing plane Σ. One is then able to solve eqn (11) for U(SΣ) and obtain F(SΣ) from eqn (13) at both sides of the dividing plane and for each vibrational excitation of interest. TM elements are then evaluated using eqn (14).
Integration of eqn (7) and (11) is performed using the adaptive-step Runge Kutta method. There is a singularity in the equations as p = 0 at the minima. The solution is therefore first constructed at S = ε by expansion of A and U in powers of S at S = 0, as described in ref. 52 and 57, and it serves as the initial condition for integration of eqn (7) and (11). The converged TM element has to be independent of the size of ε and it turns out that its dependence on ε is the main indicator of the divergence of WKB. For higher vibrational states, the solution becomes extremely sensitive to the exact form of potential near the minimum, where the classical trajectory spends an infinite amount of time. The results below are obtained using ε = 1me1/2a0.
The normal modes Ui and Uj at the minima i and j must be appropriately aligned in order to avoid errors due to sign ambiguity. The minima at the two ends of the MAP are connected by a permutation–inversion operation and a rotation, which is determined using quaternions. Normal modes are calculated for the reference version at one minimum and the symmetry operation and rotation are then applied to bring them in coincidence with the normal modes of the minimum at the other end of the MAP, which fixes their orientation there.
Finally, a separate 48 × 48 tunneling matrix is constructed for the ground state and each vibrationally excited state of interest. We therefore assume that the states with different number of vibrational quanta do not interact. In general, different branches of pseudorotational quartets in vibrationally excited states interact with each other when they lie close in energy, as observed in ref. 9. Our model, however, cannot predict the occurrence of the situations in which they do. We only have harmonic energies at our disposal to estimate the energy differences between different vibrational manifolds, while the flip matrix elements obtained using WKB, which are of comparable size, are also known to be of poor accuracy for almost barrierless motion.21 Since bifurcation splittings are tiny compared to the energy differences associated with the flip states, it is a safe bet to assume that their sizes are predominantly unaffected by the states belonging to different vibrational manifolds. Robustness of the size of the bifurcation TM elements to the exact form of pseudorotational states was observed in ref. 28.
TM can be diagonalized for each vibrational excitation of interest to obtain the spectrum relative to the degenerate energy of the localized single-well vibrational state. The symmetry of the eigenvector determines the symmetry of the vibrational state (in G48), which allows one to work out the nuclear spin degeneracies and thus the allowed transitions and their intensity pattern, as in ref. 22. However, we have determined the eigen-energies symbolically in Table 2. The additional assumption was to neglect the interaction between the subsets of states belonging to different branches of the flip quartet. The error associated with that is truly negligible resulting in differences in the 5th significant digit. We therefore use Table 2 to determine the energies of 20 substates (48 including vibrational degeneracies) of each vibrational excitation studied below.
5 Results
We now apply the method to (H2O)3 using the MB-pol34–36 PES. Potential energy curves along MAPs for the six pathways in Fig. 2 are shown in Fig. 3 as functions of arc-length distance in mass-scaled coordinates from the reference minimum. Tunneling paths for F (flip) and A1–A3 have a slight asymmetry, with barrier maxima at 51.9%, 51.5%, 56.6% and 49.6% of the full path length, respectively. Paths B1 and B3 are symmetric. Paths vary in length between 115.4me1/2a0 for F path and 284.7me1/2a0 for A2 and 303.7me1/2a0 for B3. The closest stationary points (SP) on the PES to the barrier maxima along the MAPs are shown in the inset pictures in Fig. 3.SP near the F path is of Cs symmetry and at 83.16 cm−1. The barrier maximum along MAP is very close at 83.77 cm−1 suggesting low corner-cutting effects and a minimum-energy path (MEP) close to MAP. Paths A1–A3 pass close to a SP at 757.7 cm−1, with barrier maxima on MAP at 774.3 cm−1, 828.7 cm−1 and 819.2 cm−1, respectively. Paths B1 and B3 pass near a stationary point at 822.6 cm−1 with two negative frequencies. The barrier heights along the path are 837.7 cm−1 and 836.3 cm−1, respectively. As we shall see below, the paths B1, B3 and A2, which are the longest and have the highest barriers along the MAP, unintuitively, give rise to the largest TM elements.
Normal modes of vibration of water trimers are listed in the ESI of ref. 9 and the six lowest-frequency modes are shown in Fig. 5. A visual inspection shows that mode 1, of lowest frequency, is mainly the flip motion of monomer A. Mode 2 and 4 are linear combinations of the bend of angle ABC at oxygen B and in-phase flips of monomers B and C. Mode 3 is mainly the bend of angle BCA at C. Mode 5 is the breathing mode of triangle ABC, while mode 6 is mainly an anti-phase flip of monomers B and C. Modes 7–12 represent librations composed of in-plane and out-of-plane bends of the in-plane OH bonds (the in-ring OH bonds), relative to the plane formed by the three oxygen atoms. Modes 13–21 are high-frequency intramonomer vibrations of water. The convergence of TM elements with ε (see the remarks in the previous section) was achieved for modes 1–6 for all paths. They are listed in Table 3 and shown graphically in Fig. 6 and 7.
| Path | GS | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| F | −49.4 | 169 | 23.5 | 70.5 | −19.5 | −48.7 | −165 |
| [−26] | [90] | [12] | [37] | [−10] | [−26] | [−87] | |
| A1 | −3.46(−3) | −1.32(−2) | 1.73(−2) | −2.37(−4) | 2.42(−2) | 2.29(−3) | −1.65(−3) |
| A2 | −9.65(−3) | −2.31(−2) | −4.93(−2) | 7.60(−3) | −2.58(−2) | 2.81(−2) | 3.13(−1) |
| A3 | −4.37(−3) | 1.15(−2) | 6.04(−3) | 3.56(−3) | 1.89(−3) | −3.22(−3) | −1.16(−2) |
| B1 | −1.18(−2) | 1.07(−1) | −5.32(−3) | 5.76(−2) | −7.00(−2) | −8.40(−4) | 2.29(−1) |
| B3 | −8.07(−3) | −1.07(−1) | 1.29(−1) | 3.87(−3) | 1.82(−1) | 4.36(−2) | 4.83(−1) |
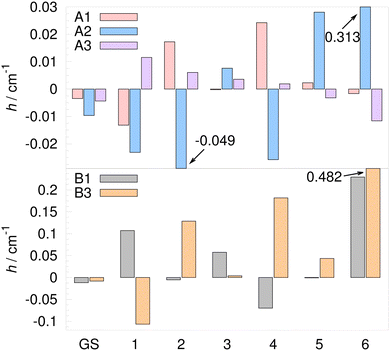 | ||
| Fig. 6 Tunneling matrix elements of the water trimer (H2O)3 on the MB-pol PES34–36 for rearrangement paths A1–A3, B1 and B3 in the vibrational ground state (GS) and the 6 lowest-frequency vibrational modes in cm−1. Exact numbers are given in Table 3. | ||
We first turn our attention to the flip motion. For asymmetric paths, at the ‘left’ side of the dividing surface, the dynamics follows the motion described by the upper row (in the 2nd column) in Table 1; the ‘right’ side is described by the lower row. On the flip (F) path, the longitudinal mode at the left minimum is mode 1. At the right minimum, where what was the flip of monomer A becomes the flip of monomer B, the tangent to the path has large components along both mode 1 and mode 2.
Correspondence between normal modes at minimum and at the transition state is relatively well preserved (only modes 7 and 8 switch order diabatically). The frequencies of modes 2–5 change by between −1 cm−1 and −3.5 cm−1 from minimum to SP, while for modes 7–12, the change is between −11 cm−1 and −45 cm−1 (apart from modes 7 and 8 which together produce a change of −11 cm−1). The stiffness of modes falls towards the SP which contributes to the wavefunction amplitude inside the barrier and the magnitude of the splitting. When the barrier is corrected for the zero-point energy at the minimum and at the saddle, it is equal to −33.32 cm−1, which indicates that the flip motion is above the barrier and free. Transverse vibrational modes (that are perpendicular to MAP) thus significantly affect the splitting. The first factor on the r.h.s. in eqn (14) is affected through the normalization constant and the surface integral over Σ in eqn (1) and contributes a factor 1.12 to the flip TM element compared to the one-dimensional (1D) calculation. The exponential factors in the last line, which account for the change of the zero-point frequencies along the MAP contribute a factor of 1.86. The full-dimensional result is thus a factor of 2.08 larger than the 1D result.
The eigenvalues of matrix A change adiabatically along the MAP; they closely follow the square root of the Hessian eigenvalues for all modes apart from the lowest, longitudinal, mode that correlates with the imaginary frequency mode at the transition state. The eigenvectors of A practically match the eigenvectors of Hessian at TS. The excitation vectors U at both sides of the dividing plane have the largest component along the corresponding eigenvector of A (apart from the (longitudinal) mode 2 on the right side of Σ, which has the largest component along the tangent, the same as (the other longitudinal) mode 1).
The GS TS has been determined using instanton theory in ref. 21 on the WHBB PES4,32,33 and in ref. 24 on the MB-pol PES.34–36 The GS TM element for the flip is 49 cm−1; the formally exact result43 is 26 cm−1 on the same PES, a disagreement by a factor of 0.53. The experimental spacings in the GS pseudorotational quartet are 22.7 cm−1, 42.9 cm−1 and 21.5 cm−1.71 Instanton theory is known to overestimate the splittings51,58 near the barrier top by a factor of ≈2. The flip (F) TM elements for vibrationally excited modes 1–6 are listed in the first row of Table 3. Relative values of observables calculated using instanton theory have often been found to be of better accuracy than the absolute values.28,51 We therefore list the TM elements for the flip scaled by a factor of 0.53, to match the GS TM element of ref. 43, in the second row of Table 3 in brackets.
TSs in vibrationally excited states can be decomposed into the ‘longitudinal’ contribution, given by the ‘F’ term in the 2nd line of eqn (14) in the brackets, and the ‘transverse’ ‘U’ term contribution, given by the second term in brackets, UĀ−1U. The theory of ref. 57 strictly separates the longitudinal and transverse contributions and only one term of the two is present, depending on the nature of the excitation. For the longitudinal excitation in mode 1, TS is expected to come with an even greater error than in the GS, because the wavefunction stretches into the highly anharmonic regions of the PES towards the barrier. Our results are thus interpreted as upper estimates to the splittings.58 TS is predominantly, 93%, determined by the F term in eqn (14), as is expected for a longitudinal mode.
We next note that the TM elements for flip in the excited modes 1–3, in Table 3, come with the opposite sign to that in the GS. For modes 4–6, the sign of hF is again negative as in the GS. From eqn (13), we have that F(ε) = Uet(ε)ε. (ε = 1me1/2a0 in our calculations.) For the excited mode 1, the angle between Ue and t is 167.3° at S = ε, and it is 161.8° at S = SΣ. On the other side of the dividing plane, the angles are 52.8° and 47.0° at S = Smax − ε and SΣ, respectively. F(ε) and F(Smax − ε) therefore have opposite signs at the start. From eqn (12), it follows that F(S(τ)) = F(ε)exp(ωeτ) (and on the other side of the dividing plane accordingly), so that F does not change sign. Hence, the F term in eqn (14) for the excited mode 1 is negative and the TM element is of opposite sign to that in the GS. As a consequence, the quartet states appear in reverse order (to the order given in Table 2) as A−, E+, E− and A+, in the order of increasing energy. Reduced-dimensionality calculations of ref. 62 also predict the reverse order of states for the excitation of mode 1. The excitation of higher vibrational modes involves a change of shape of the ABC triangle formed by the oxygens and cannot be adequately described by the reduced-dimensionality models where its shape is fixed.
For transverse modes, however, we also need to evaluate the U term (UĀ−1U) in eqn (14) to determine the order of the quartet states. Since the evolution of U vectors along the path is largely adiabatic and follows normal modes, as discussed above, the U(i)T⊥U(j)⊥ projection at the dividing plane, where U⊥ is the component of U in the direction perpendicular to the path, coincides with the sign of the U term for the flip. In fact, the sign of the U term also coincides with the overlap between left- and right-minimum modes. It is negative for excited modes 1–4 and positive for modes 5 and 6.
The U term in eqn (14) is expected to be larger than the F term contribution for transverse modes. Indeed, in ref. 57, only the U term is considered and the mixing of transverse and longitudinal modes that arises from the curvature of the path58 is neglected. In water trimers, the U term contributes 95.2%, 26.5%, 38.2%, 86.8% and 16.7% to TS for modes 2–6, respectively. This clearly shows that the F term cannot be neglected for the transverse excitations. The F term signs, deduced from UTet projections at ε, differ from the U term sign only for mode 4 and, unexpectedly, the F term gives a larger contribution resulting in the same order of quartet states as in the GS. The widths of flip quartets in vibrationally excited states (4hF) relative to the GS width are shown in the histogram in the upper panel of Fig. 7. The darker shades of bar color indicate a reverse order of quartet states for modes 1–3. The reverse order of states for mode 3 can also be seen in the TS pattern diagram in Fig. 4. In the recent experiment of ref. 9, the widths of the flip quartets in the excited modes 2 and 3 were found to be of comparable size to the GS (20 cm−1 and 19 cm−1, respectively, with the GS TM element of 22 cm−1).
The evolution of the excitation vector U along the path follows eqn (11). It can be decomposed into the evolution of its norm g and its direction, the unit vector Ũ, as in ref. 57. The time-derivative of g = (UTU)1/2 is
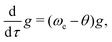 | (15) |
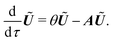 | (16) |
Rearrangements along the A and B paths are tunneling motions. The respective barrier heights corrected for the zero-point energies at the minimum and at the saddle are significantly lowered, at 620.0 cm−1 and 483.8 cm−1, and change their order in energy. The frequencies of modes 2–12 from the minimum to saddle point A are all lowered by between −23 cm−1 and −118 cm−1, apart from mode 8 which changes by +5.7 cm−1. For stationary point B, frequencies of modes 3–12 change by between −24 cm−1 and −135 cm−1, while mode 2 changes by −330 cm−1 and is negative at SP. The adiabaticity of eigenvalues of matrix A is no longer preserved for low frequency modes. Nevertheless, the eigenvectors of Ā and transition-state modes (eigenvectors of H(SΣ)) align relatively well, with direction cosine coefficients of the corresponding transition-state modes equal to 0.7 or larger (with modes 4 and 5 on B1, and modes 3 and 4 on B3 path swapped).
TM elements for A and B paths are listed in Table 3 and shown graphically in Fig. 6. They exhibit large variations in size for different modal excitations; they change sign, and increase and decrease in size compared to the GS TM element. The largest TM elements, in general, appear for paths A2, B3 and B1. The TM element for the B3 path for the excited mode 6 is 60 times larger than in the GS, while for the excited mode 3, it is 2.1 times smaller.
Mode 1 is the longitudinal mode for B1 and B3 paths on both sides of Σ as the paths are symmetric. Mode 1 is also predominantly longitudinal at one end of the A1–A3 paths (left for A1 and A3, right for A2), while mode 2 is longitudinal at the other end. The theory of ref. 57, that strictly separates modes into longitudinal and transverse, predicts zero TM elements for the longitudinal–transverse excitations in the excited modes 1 and 2 on A1–A3 paths.
For the A1 path and all excitations (in modes 1–6), the F term is larger than the U term and determines the sign of the TM element. For mode 4, it gives 99% contribution to the splitting. For mode 3, it gives 53% and comes with the opposite sign to the U term which results in an almost complete cancellation, as shown in Fig. 6. Significant projections of modes 1–3 on the path tangent near the left minimum and of modes 2, 1 and 4 near the right minimum (with coefficients >0.1) are amplified in eqn (12) by a factor that increases with the modal frequency as exp(ωeτ). The net result is large TM elements for the excited modes 1, 2 and 4 on the A1 path. For modes 3, 5 and 6, F and U terms come with opposite signs and the TM elements are smaller, as shown in Fig. 6.
The sign of the U term on the A1 path cannot be predicted using overlaps of left-minimum and right-minimum modes (wrong for mode 6 on A1 path) or U(i)T⊥U(j)⊥ (wrong for mode 4 on the A1 path). Excitation vector U has significant components over several transition-state modes at Σ. The U-term contribution to the TM element can be decomposed over eigenvectors of Ā (where mode 1 of Ā is the tangent t and does not contribute). The decomposition reveals that for the excited modes 1–6 on the A1 path, transition-state modes 3, 2, (2, 4), (2, 5), 6 and (6, 7), respectively, make the largest contribution to the TM element (UĀ−1Uωe > 0.2 contributions listed). Clearly, the sign and size of U term contributions is difficult to predict without fully solving eqn (7) and (11).
On the A2 path, the F term determines the sign of the TM element only for mode 1. Large projections of t on modes 1–4 and 6 (>0.1) at ε near the left minimum and a large path segment with a negative Hessian eigenvalue serve to bring down the value of θ in eqn (15) and to rotate U towards low-frequency modes. Similar behavior is observed on paths B1 and B3. The decomposition of U term contributions over eigenvectors of Ā shows that mode 2 at the transition state dominates for almost all excitations on paths A2, B1 and B3 (exceptions are for the excited mode 1 on the A2 path and mode 2 on B3). The frequency of mode 2 of Ā is 48.8 cm−1, 16.0 cm−1 and 35.6 cm−1 on A2, B1 and B3 paths, respectively (while it is 156.7 cm−1 and 139.2 cm−1 on A1 and A3 paths), which is low in comparison with ωe (see Fig. 5). This behavior signals a large spread of the wavefunction over that mode at the transition state and results in a large U term contribution.
The sole F term gives the TM elements with 25% accuracy for the mode 1 excitations on all paths, and also for modes 2 and 4 on the A1 path. The sole U term gives results with 25% accuracy for modes 2, 5 and 6 on A2, modes 3 and 6 on A3, mode 6 on B1 and modes 2, 4 and 6 on B3. Small TM elements for modes 2 and 5 on B1, for mode 3 on B3, and modes 4 and 5 on A3, are a consequence of the cancellation of F and U terms. On B1 and B3 paths, all U terms are negative and are of opposite sign from F terms and also from the overlap of left- and right-minimum modes.
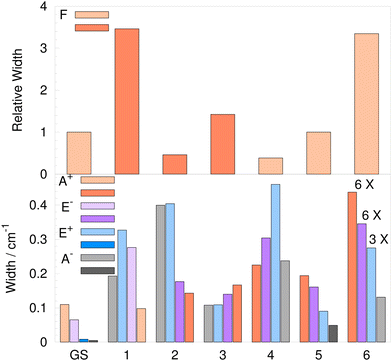
TM elements in Table 3 combine using relationships shown in Table 2 to produce TS patterns in Table 4. Vibrational-tunneling energies in Table 4 refer to bifurcation splittings and are given relative to the energies of the corresponding branches of the flip quartet. The widths of the vibrational splitting patterns are shown in Fig. 7. The upper panel shows the flip quartet widths for excited modes 1–6 relative to the GS, as already discussed. The lower panel shows the widths of the branches of the flip quartet due to bifurcations. The darker shades of bar colors refer to the ‘reverse’ order of states to that in Table 2.
| GS | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | A−1 | 0.239 | A+2 | 4.888 | A+1 | 7.140 | A+1 | 8.333 | A−2 | 11.866 | A−1 | 2.446 | A−2 | 6.550 |
| 19 | T−1 | 0.080 | T+2 | 1.629 | T+1 | 2.380 | T+1 | 2.778 | T−2 | 3.955 | T−1 | 0.815 | T−2 | 2.183 |
| 18 | T−2 | −0.080 | T+1 | −1.629 | T+2 | −2.380 | T+2 | −2.778 | T−1 | −3.955 | T−2 | −0.815 | T−1 | −2.183 |
| 17 | A−2 | −0.239 | A+1 | −4.888 | A+2 | −7.140 | A+2 | −8.333 | A−1 | −11.866 | A−2 | −2.446 | A−1 | −6.550 |
| 16 | T+2 | 0.416 | T−1 | 13.809 | T−2 | 8.829 | T−2 | 6.988 | T+1 | 23.013 | T+1 | 4.508 | E+2 | 41.219 |
| 15 | T+1 | 0.257 | T−2 | 10.662 | E−1 | 8.534 | E−1 | 6.527 | T+2 | 15.583 | T+2 | 3.470 | T+1 | 38.392 |
| 14 | E+1 | 0.239 | E−2 | 4.720 | T−1 | 3.139 | T−1 | 2.636 | E+2 | 11.144 | E+2 | 1.557 | T+2 | 10.913 |
| 13 | E+2 | −0.239 | E−1 | −4.720 | T−2 | −3.139 | T−2 | −2.636 | E+1 | −11.144 | E+1 | −1.557 | T+1 | −10.913 |
| 12 | T+2 | −0.257 | T−1 | −10.662 | E−2 | −8.534 | E−2 | −6.527 | T+1 | −15.583 | T+1 | −3.470 | T+2 | −38.392 |
| 11 | T+1 | −0.416 | T−2 | −13.809 | T−1 | −8.829 | T−1 | −6.988 | T+2 | −23.013 | T+2 | −4.508 | E+1 | −41.219 |
| 10 | T−1 | 3.254 | T+1 | 16.340 | T+1 | 20.201 | T+1 | 5.443 | T−2 | 15.193 | T−2 | 8.037 | E−1 | 103.587 |
| 9 | E−2 | 2.861 | T+2 | 14.644 | E+2 | 14.947 | E+2 | 5.055 | E−1 | 10.835 | E−1 | 7.631 | T−2 | 101.396 |
| 8 | T−2 | 1.347 | E+2 | 2.544 | T+2 | 10.237 | T+2 | 2.073 | T−1 | 7.970 | T−1 | 2.949 | T−1 | 32.337 |
| 7 | T−1 | −1.347 | E+1 | −2.544 | T+1 | −10.237 | T+1 | −2.073 | T−2 | −7.970 | T−2 | −2.949 | T−2 | −32.337 |
| 6 | E−1 | −2.861 | T+1 | −14.644 | E+1 | −14.947 | E+1 | −5.055 | E−2 | −10.835 | E−2 | −7.631 | T−1 | −101.396 |
| 5 | T−2 | −3.254 | T+2 | −16.340 | T+2 | −20.201 | T+2 | −5.443 | T−1 | −15.193 | T−1 | −8.037 | E−2 | −103.587 |
| 4 | A+2 | 5.483 | A−2 | 9.640 | A−2 | 19.965 | A−2 | 5.388 | A+1 | 11.247 | A+1 | 9.701 | A+1 | 131.287 |
| 3 | T+2 | 1.828 | T−2 | 3.213 | T−2 | 6.655 | T−2 | 1.796 | T+1 | 3.749 | T+1 | 3.234 | T+1 | 43.762 |
| 2 | T+1 | −1.828 | T−1 | −3.213 | T−1 | −6.655 | T−1 | −1.796 | T+2 | −3.749 | T+2 | −3.234 | T+2 | −43.762 |
| 1 | A+1 | −5.483 | A−1 | −9.640 | A−1 | −19.965 | A−1 | −5.388 | A+2 | −11.247 | A+2 | −9.701 | A+2 | −131.287 |
TM elements of mechanisms B1 and B3, as well as A1 and A2 always add up in energy expressions in Table 2, except in the Δ± splitting of T±1,2 levels. A large decrease of widths of the quartet branches with energy, from A+ to A−, is observed in the GS.21 The excited mode 5 and 6 exhibit a similar pattern. For mode 5, bifurcation widths are largely determined by the TM elements for paths A2 and B3, see Table 3, since 2hA2 and hB3 are the largest and similar in size. Likewise, for mode 6, 2hA2 and hB1 + hB3 figure prominently in determining the shape of the TS pattern. For modes 3 and 4, hB1 and hB3, respectively, control the qualitative look of the TS pattern so that A+ and A− branches have comparable widths. For the excited mode 1, TM elements A1–A3 determine the TS pattern, as hB1 and hB3 almost completely cancel out. Bifurcation widths of the E± quartets are governed by the T±1,2 energies in Table 2 for all excited modes, apart from mode 6 where the outer states are of E±1,2 symmetry, as shown in Table 4.
The TS pattern for the excited mode 3 is singled out in Fig. 4 as a representative example of the water trimer TS patterns in excited states. It features a reverse order of pseudorotational states relative to the GS, as hF is positive, and also the reverse order of states in A+ and E−. All bifurcation widths of quartet branches are ≈0.1 cm−1, similar to the width of A+ in the GS.
The width of A+ increases up to 2× in the excited modes 1–5, apart from mode 2, where it decreases by ≈11%. The largest width we obtained is for the A+ state in the excited mode 6 (2.6 cm−1), a 24-fold increase compared to the GS (0.11 cm−1). In other excited modes 1–5, the widths of all quartet branches are below 0.5 cm−1.
TSs due to bifurcations have also been measured in experiment.20 The GS splitting of the A+ state was found to be an equally-spaced quartet12 with a width of 2.89 × 10−2 cm−1, 3.8× smaller than the instanton results of ref. 21 and 24, which we reproduce here. A decrease of widths of the GS quartet branches with energy is a feature of the TM model. All TM elements are negative in the GS and they add up in the lowest branch, while they come with different signs in the higher branches, see Table 2, resulting in a marked decrease shown in Fig. 7 and first observed in ref. 21. An analysis in ref. 20 concludes that the widths of higher branches are similar in size. Further research is needed in order to resolve the discrepancies. Recent experiments9,29 measured a dramatic increase in bifurcation splittings of the A+ state in the excited mode 11, with a width of ≈15 cm−1 and unequal spacings. Our method diverges beyond mode 6, which suggests that the TSs are larger. Unequal spacings cannot be accommodated by our model and suggests that the interactions beyond that of the nearest neighbors contribute significantly.44 Bifurcation splittings were also measured9 for the excited modes 8 and 10 with spacings of 4 cm−1 and 7 cm−1, respectively. The experimental resolution in the helium nanodroplet isolation experiments using free-electron lasers was ≈0.5–2 cm−1, which means that the calculated TSs above fall below the detection limit.
We now briefly analyse the TS calculations in the deuterated water trimer. MAPs for the six tunneling processes in Table 1 exhibit similar asymmetries as in the H-trimer. The barriers on MAPs are slightly lower, within 6 cm−1 of H-trimer barriers, while the paths are longer due to mass-scaling with the heavier D mass. The shortest is the F path, 155.1me1/2a0; the longest is B3, 411.3me1/2a0. The longest paths with highest barriers are again A2, B1 and B3, even though they exhibit some of the largest TM elements.
Normal modes of vibration have frequencies 119 cm−1, 133 cm−1, 164 cm−1, 173 cm−1, 178 cm−1 and 205 cm−1. Mode 1 is a flip of monomer A, mode 2 is an in-phase flip of B and C, mode 3 is an out-of-phase flip of B and C, mode 4 and 5 are bends of angle at C and B, respectively, and mode 6 is the breathing mode of the ABC triangle. There is thus a loose correspondence between H- and D-trimer modes 1 ↔ 1, 3 ↔ 4, 5 ↔ 6 and 6 ↔ 3, but qualitative differences and differences in energy ordering point to disparate TS patterns in the H- and D-trimer.
Stationary points F, A and B, corrected for the zero-point motion at the minimum and at the saddle, are all lowered, at −3.62 cm−1, 593.0 cm−1 (lower than in the H-trimer) and 502.1 cm−1 (higher than in the H-trimer), respectively. Frequencies of vibrations in modes 2–6 between the minimum and saddle point F change between −7.0 cm−1 and +4.1 cm−1. Librations, in modes 7–12, change more, between −8.1 cm−1 and −32 cm−1, apart from mode 8 which changes by +13 cm−1. For stationary points A and B, all positive normal mode frequencies change with respect to the minimum between −0.6 cm−1 and −82 cm−1, and −14 cm−1 and −100 cm−1, respectively. The stationary point B has 2 negative frequencies.
TM elements for the D-trimer in the GS and the excited modes 1–6 are listed in Table 5 and shown graphically in Fig. 8. The TM element for the flip (relative to the GS) is shown in the upper panel of Fig. 9 (pseudorotational widths are 4hF). The TM element for the flip of monomer A/B in the GS is −20.8 cm−1, in agreement with ref. 21 and 24; scaled by 0.53 as above, it is −11 cm−1 (scaled TM elements for F are shown in brackets in Table 5). The experimental value12 is −10.27 cm−1 (the full quartet width is 41.1 cm−1). Since the flipping of hydrogens is essentially free motion in the D-trimer as well, the TM elements obtained using modified WKB are upper estimates. The largest error is expected for the longitudinal excitation, which promotes the barrier penetration. For the flip motion in the D-trimer, the longitudinal mode on the left is mode 1, while a mix of modes 1 and 2 gives the path tangent on the right, the same as in the H-trimer.
| Path | GS | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| F | −20.8 | 106 | −4.63 | −78.0 | 14.9 | 3.92 | −23.5 |
| [−11] | [56] | [−2.5] | [−37] | [7.9] | [2.1] | [−12] | |
| A1 | −1.60(−5) | −1.01(−4) | 2.49(−4) | 9.93(−6) | −1.13(−5) | 9.28(−5) | −2.27(−5) |
| A2 | −2.93(−5) | −1.52(−5) | −1.55(−4) | 8.69(−4) | 4.10(−5) | 1.39(−4) | −3.67(−4) |
| A3 | −2.51(−5) | 9.07(−5) | 4.60(−5) | 1.74(−5) | 2.11(−5) | −9.92(−6) | −4.54(−5) |
| B1 | −3.33(−5) | 1.22(−4) | −4.29(−4) | 4.66(−4) | 5.21(−5) | 1.05(−4) | −1.57(−4) |
| B3 | −1.55(−5) | −3.40(−4) | 3.71(−4) | 5.65(−4) | 4.60(−5) | 4.37(−5) | −2.77(−4) |
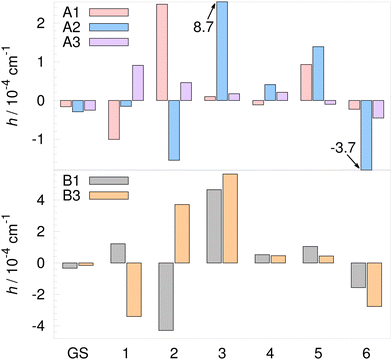 | ||
| Fig. 8 Tunneling matrix elements of the deuterated water trimer (D2O)3 on the MB-pol PES34–36 for rearrangement paths listed in Table 1 in the vibrational ground state (GS) and the 6 lowest-frequency excited vibrational modes. Exact numbers are given in Table 5. | ||
For the H-trimer, we analysed the TM elements in terms of F and U contributions in eqn (14) and tried to predict their sign using geometrical arguments. The evolution of A on the F path in the D-trimer is approximately adiabatic and the normal modes at transition state align well with the eigenvectors of Ā(SΣ). The evolution of U follows the normal modes along the MAP to a lower degree than in the H-trimer. The U term sign on the F path still corresponds to the sign of overlap between left- and right-minimum normal modes and to the sign of U(i)T⊥U(j)⊥ at Σ, as in the H-trimer.
In the D-trimer, large F term contributions are present in the excited modes 1 and 3 and they give rise to large TM elements in Fig. 9. Mode 1 is the longitudinal mode with 96% contribution of the F term. Large TM elements for mode 3 in the D-trimer and mode 6 in the H-trimer, shown in the upper panels of Fig. 7 and 9, are related. They both correspond to the out-of-phase flip of B and C monomers. This is not a longitudinal mode, but the F path alignment with this mode near minima is nevertheless large enough to produce a substantial TM element in both cases.
Reverse order of pseudorotational states in the D-trimer (compared to the order given in Table 2) is found in the excited modes 1, 4 and 5. For the excited mode 1, this result is in agreement with the reduced-dimensionality models of ref. 62 and 64. Modes 1 and 4 in the D-trimer visually correspond to the motions in modes 1 and 3 in the H-trimer, which also exhibit a reverse order of states. A negative U term is responsible for the reverse order of states in mode 5 (which does not have a clear analogue among the H-trimer modes). The sign of U term in eqn (14) is negative for modes 1, 2, 4 and 5. These modes visually correspond to modes 1–4 in the H-trimer, where negative U terms are observed as well. This suggests that the sign is largely determined by geometry. The small flip TM elements for the excited modes 2 and 5 in Fig. 9 arise due to the cancellation of F and U terms in the D-trimer.
On A and B paths, the sign and behavior of TM elements is difficult to predict without fully solving eqn (11). The signs of U terms do not adhere to the signs of overlaps between left- and right-minimum modes. Longitudinal modes are either mode 1 or mode 2 on all paths, the same as in the H-trimer. The only difference is observed on the A2 path, where mode 1 is longitudinal at both ends (it is mode 2 at the left minimum in the H-trimer). On the B1 path, even for the excited longitudinal mode 1, the U term is larger and has the opposite sign of the F term (tangent at ε = 1me1/2a0 has mode-1 and mode-2 components of 0.83 and 0.55, respectively).
Qualitative similarities between normal modes of the H- and D-trimer often correlate with the sizes of the corresponding TM elements. On the A1 path, large TM elements due to the F term in modes 1, 2 and 5 in the D-trimer relate to the large TM elements in modes 1, 2 and 4 in the H-trimer. On the A3 path, similarly, large TM elements in mode 1 have the same cause. On the A2 path, mode 3 in the D-trimer and mode 6 in the H-trimer both correspond to a large U term for the out-of-phase flip of B and C monomers.
Large TM elements on paths A2, B1 and B3 are again driven by the large segment of negative-frequency normal modes along the MAPs, which brings down the value of θ in eqn (15). A major contributor is also a large spread of the wavefunction at the transition state along the lowest non-zero mode of Ā, as discussed above for the H-trimer. The frequency of mode 2 of Ā is 37.4 cm−1, 12.1 cm−1 and 28.6 cm−1 on A2, B1 and B3 paths, respectively. For F, A1 and A3, it is 132 cm−1, 123 cm−1 and 109 cm−1.
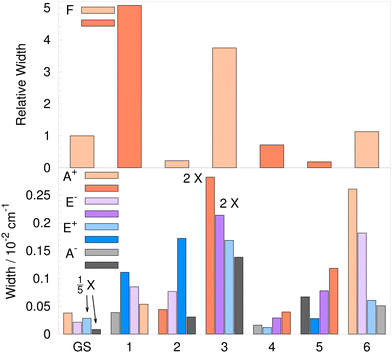
The size of TM elements on the F path is a factor of ≈2 smaller than in the H-trimer. On A paths, the ratio is ≈100, while on B paths, it can be as high as ≈1000 for some TM elements. TS patterns of D-trimer, labelled by irreps of G48, are given in Table 6 relative to the closest branch of the flip quartet. The widths of quartet branches due to bifurcations are shown in the lower panel of Fig. 9. Darker color bars are associated with the reverse order of states, as discussed above. The GS width of A+ is 3.8 × 10−4 cm−1, 24% smaller that the experimental value12 of 5.0 × 10−4 cm−1. A decrease of widths with energy, from A+ to A−, is observed for the excitations in modes 1, 3 and 6, which relates to the decrease in the H-trimer for modes 1, 5 and 6. The width of A+ is significantly increased for the excited modes 3, 5 and 6. The largest width is 5.6 × 10−3 cm−1 in the excited mode 3; the widths of pseudorotational states in all other excited modes are lower than 3 × 10−3 cm−1.
| GS | 1 | 2 | 3 | 4 | 5 | 6 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 20 | A−1 | 0.084 | A+2 | 2.691 | A−1 | 1.541 | A−1 | 6.919 | A+1 | 1.994 | A+1 | 5.917 | A−2 | 2.556 |
| 19 | T−1 | 0.028 | T+2 | 0.897 | T−1 | 0.514 | T−1 | 2.306 | T+1 | 0.665 | T+1 | 1.972 | T−2 | 0.852 |
| 18 | T−2 | −0.028 | T+1 | −0.897 | T−2 | −0.514 | T−2 | −2.306 | T+2 | −0.665 | T+2 | −1.972 | T−1 | −0.852 |
| 17 | A−2 | −0.084 | A+1 | −2.691 | A−2 | −1.541 | A−2 | −6.919 | A+2 | −1.994 | A+2 | −5.917 | A−1 | −2.556 |
| 16 | T+1 | 0.285 | E−2 | 4.253 | T+2 | 8.608 | T+1 | 8.429 | T−2 | 1.454 | E−1 | 3.898 | T+1 | 3.035 |
| 15 | E+2 | 0.216 | T−1 | 3.993 | T+1 | 7.287 | T+2 | 7.532 | E−1 | 1.067 | T−2 | 3.414 | T+2 | 3.022 |
| 14 | T+2 | 0.141 | T−2 | 1.158 | E+1 | 1.981 | E+2 | 1.346 | T−1 | 0.743 | T−1 | 0.815 | E+2 | 0.020 |
| 13 | T+1 | −0.141 | T−1 | −1.158 | E+2 | −1.981 | E+1 | −1.346 | T−2 | −0.743 | T−2 | −0.815 | E+1 | −0.020 |
| 12 | E+1 | −0.216 | T−2 | −3.993 | T+2 | −7.287 | T+1 | −7.532 | E−2 | −1.067 | T−1 | −3.414 | T+1 | −3.022 |
| 11 | T+2 | −0.285 | E−1 | −4.253 | T+1 | −8.608 | T+2 | −8.429 | T−1 | −1.454 | E−2 | −3.898 | T+2 | −3.035 |
| 10 | T−1 | 1.073 | T+2 | 5.559 | T−1 | 3.842 | T−2 | 21.378 | T+1 | 0.595 | T+2 | 1.405 | T−1 | 9.086 |
| 9 | E−2 | 0.690 | T+1 | 4.268 | T−2 | 3.774 | E−1 | 18.920 | E+2 | 0.474 | T+1 | 0.915 | E−2 | 7.778 |
| 8 | T−2 | 0.613 | E+1 | 1.937 | E−2 | 0.102 | T−1 | 8.765 | T+2 | 0.279 | E+1 | 0.735 | T−2 | 3.900 |
| 7 | T−1 | −0.613 | E+2 | −1.937 | E−1 | −0.102 | T−2 | −8.765 | T+1 | −0.279 | E+2 | −0.735 | T−1 | −3.900 |
| 6 | E−1 | −0.690 | T+2 | −4.268 | T−1 | −3.774 | E−2 | −18.920 | E+1 | −0.474 | T+2 | −0.915 | E−1 | −7.778 |
| 5 | T−2 | −1.073 | T+1 | −5.559 | T−2 | −3.842 | T−1 | −21.378 | T+2 | −0.595 | T+1 | −1.405 | T−2 | −9.086 |
| 4 | A+2 | 1.896 | A−2 | 1.942 | A+1 | 2.217 | A+1 | 28.230 | A−2 | 0.809 | A−1 | 3.349 | A+2 | 13.040 |
| 3 | T+2 | 0.632 | T−2 | 0.647 | T+1 | 0.739 | T+1 | 9.410 | T−2 | 0.270 | T−1 | 1.116 | T+2 | 4.347 |
| 2 | T+1 | −0.632 | T−1 | −0.647 | T+2 | −0.739 | T+2 | −9.410 | T−1 | −0.270 | T−2 | −1.116 | T+1 | −4.347 |
| 1 | A+1 | −1.896 | A−1 | −1.942 | A+2 | −2.217 | A+2 | −28.230 | A−1 | −0.809 | A−2 | −3.349 | A+1 | −13.040 |
The results in Tables 3 and 5 come with large uncertainties. The approach we used to calculate the TS patterns here gives a quantitative agreement with the exact quantum results for malonaldhyde.59 There are, however, several reasons why the accuracy of the present results is substantially lower. A shallow well for the flip motion is one source of error already discussed above. Another source is the anharmonic potential in directions perpendicular to the path. An indication of the large anharmonicity comes from large changes in the normal mode frequencies along the paths. Moreover, low eigenfrequencies of Ā indicate a large spread of the wavefunction at the transition state, into the regions where the harmonic approximation of the potential is likely to be invalid. The error in eqn (14) also comes from the normalization of the significantly modified wavefunctions to the harmonic oscillator. The analysis that comes from the geometrical considerations, however, is expected to be of significance in the more accurate calculations as well, and the qualitative TS patterns and the widths of pseudorotational states represent the best estimates for the water trimer. The estimate of anharmonic effects using, e.g., perturbation theory as in ref. 72, are needed to quantify the reliability of the present results and are going to be the subject of future work.
6 Conclusions
We calculated the TS patterns of the water trimer, (H2O)3 and (D2O)3, in vibrationally excited states including the fine splittings of pseudorotational states due to bifurcations. The splittings are obtained using a TM model that takes into account nearest-neighbor processes that represent rearrangements between equivalent minima. Six such rearrangements with sufficiently low action integral were determined in ref. 21 and taken into account in the TM model here. They represent a flip of free OH bonds and five different bifurcation mechanisms, which break and reform hydrogen bonds that form the trimer ring. We derived the energy shifts due to tunneling symbolically in terms of the six TM elements using group theory. TM elements were calculated using the recently-developed modified WKB method58 in full dimensionality. Our approach is equivalent to the instanton theory for calculating tunneling splittings in the ground vibrational state.In the modified WKB method,58 TM elements are obtained from the wavefunction that is constructed along the minimum action path that connects two symmetry-related minima. The potential away from the path is treated in a harmonic approximation. Vibrationally excited states are calculated along the same paths as for the ground-state TS and come at little additional computational cost. We have shown that the convergence can be achieved for the six lowest-frequency normal modes of the water trimer, which include the excitations into torsional and shape modes of the trimer ring. The excitations into the higher-frequency modes, that correspond to librations of hydrogen bonds that form the ring, result in the divergence of WKB, and possibly larger splittings in accord with experiment.
The calculated widths of quartet branches in modes 1–6 are similar in size to the GS or increased in some particular modes of vibration. Largest widths are obtained in the excited mode 6 and mode 3 in (H2O)3 and (D2O)3, respectively, which corresponds to the excitation of the out-of-phase flip of monomers B and C in Fig. 1. The widths are of the order of a few cm−1 for (H2O)3 and two orders of magnitude smaller for (D2O)3. Spacings in the bifurcation TS patterns have recently been measured in the excited modes 8, 10 and 11 at 3–8 cm−1 with a detection limit of 0.5–2 cm−1. The sizes of TM elements and the order of states in the TS patterns were analysed in terms of projections of the normal modes of vibration on the tunneling paths near minima.
The obtained results are semi-quantitative; they are expected to give the right order of magnitude, show trends and identify important modes that are responsible for the appearance of the TS patterns. Pseudorotational quartets in vibrationally excited states have energies close to the barrier top and our results only give upper estimates to its widths. The widths of the quartet branches due to bifurcations are tunneling processes but they proceed over some highly anharmonic regions of the potential. The presence of anharmonicity degrades the accuracy, by 2× even in the GS.43 Future studies will concentrate on improving the accuracy of the present approach using, e.g., perturbation theory72 or higher-order WKB approaches,73 which will also allow us to estimate the accuracy of the results.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was fully supported by Croatian Science Foundation Grant no. IP-2020-02-9932.References
- K. Liu, J. D. Cruzan and R. J. Saykally, Science, 1996, 271, 929–932 CrossRef CAS.
- F. N. Keutsch and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 10533–10540 CrossRef CAS PubMed.
- M. Ceriotti, W. Fang, P. G. Kusalik, R. H. McKenzie, A. Michaelides, M. A. Morales and T. E. Markland, Chem. Rev., 2016, 116, 7529–7550 CrossRef CAS PubMed.
- Y. Wang, X. Huang, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2011, 134, 094509 CrossRef PubMed.
- N. Pugliano and R. J. Saykally, Science, 1992, 257, 1937 CrossRef CAS PubMed.
- J. O. Richardson, C. Pérez, S. Lobsiger, A. A. Reid, B. Temelso, G. C. Shields, Z. Kisiel, D. J. Wales, B. H. Pate and S. C. Althorpe, Science, 2016, 351, 1310–1313 CrossRef CAS PubMed.
- C. Pérez, S. Lobsiger, N. A. Seifert, D. P. Zaleski, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Chem. Phys. Lett., 2013, 571, 1–15 CrossRef.
- R. Schwan, C. Qu, D. Mani, N. Pal, L. van der Meer, B. Redlich, C. Leforestier, J. M. Bowman, G. Schwaab and M. Havenith, Angew. Chem., 2019, 58, 13119–13126 CrossRef CAS PubMed.
- R. Schwan, C. Qu, D. Mani, N. Pal, G. Schwaab, J. M. Bowman, G. S. Tschumper and M. Havenith, Angew. Chem., 2020, 59, 11399–11407 CrossRef CAS PubMed.
- T. R. Dyke, K. M. Mack and J. S. Muenter, J. Chem. Phys., 1977, 66, 498 CrossRef CAS.
- K. Liu, M. G. Brown, M. R. Viant, J. D. Cruzan and R. J. Saykally, Mol. Phys., 1996, 89, 1373–1396 CAS.
- K. Liu, J. G. Loeser, M. J. Elrod, B. C. Host, J. A. Rzepiela, N. Pugliano and R. J. Saykally, J. Am. Chem. Soc., 1994, 116, 3507–3512 CrossRef CAS.
- J. D. Cruzan, L. B. Braly, K. Liu, M. G. Brown, J. G. Loeser and R. J. Saykally, Science, 1996, 271, 59–62 CrossRef CAS PubMed.
- H. A. Harker, M. R. Viant, F. N. Keutsch, E. A. Michael, R. P. McLaughlin and R. J. Saykally, J. Phys. Chem. A, 2005, 109, 6483–6497 CrossRef CAS PubMed.
- K. Liu, M. G. Brown and R. J. Saykally, J. Phys. Chem. A, 1997, 101, 8995–9010 CrossRef CAS.
- C. Pérez, M. T. Muckle, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Science, 2012, 336, 897–901 CrossRef PubMed.
- J. O. Richardson, D. J. Wales, S. C. Althorpe, R. P. McLaughlin, M. R. Viant, O. Shih and R. J. Saykally, J. Phys. Chem. A, 2013, 117, 6960–6966 CrossRef CAS PubMed.
- C. Pérez, D. P. Zaleski, N. A. Seifert, B. Temelso, G. C. Shields, Z. Kisiel and B. H. Pate, Angew. Chem., 2014, 53, 14368–14372 CrossRef PubMed.
- Y. Watanabe, T. Taketsugu and D. J. Wales, J. Chem. Phys., 2004, 120, 5993 CrossRef CAS PubMed.
- F. N. Keutsch, R. J. Saykally and D. J. Wales, J. Chem. Phys., 2002, 117, 8823–8835 CrossRef CAS.
- J. O. Richardson, S. C. Althorpe and D. J. Wales, J. Chem. Phys., 2011, 135, 124109 CrossRef PubMed.
- D. J. Wales, J. Am. Chem. Soc., 1993, 115, 11180–11190 CrossRef CAS.
- J. E. Fowler and H. F. Schaefer III, J. Am. Chem. Soc., 1995, 117, 446–452 CrossRef CAS.
- M. T. Cvitaš and J. O. Richardson, in Molecular Spectroscopy and Quantum Dynamics, ed. R. Marquardt and M. Quack, Elsevier, 2020, ch. 10 Search PubMed.
- M. T. Cvitaš and J. O. Richardson, Phys. Chem. Chem. Phys., 2019, 22, 1035–1044 RSC.
- M. G. Brown, F. N. Keutsch and R. J. Saykally, J. Chem. Phys., 1998, 109, 9645–9647 CrossRef CAS.
- S. Suzuki and G. A. Blake, Chem. Phys. Lett., 1994, 229, 499–505 CrossRef CAS PubMed.
- M. Eraković and M. T. Cvitaš, Phys. Chem. Chem. Phys., 2021, 23, 4240–4254 RSC.
- F. N. Keutsch, R. S. Fellers, M. R. Viant and R. J. Saykally, J. Chem. Phys., 2001, 114, 4005–4015 CrossRef CAS.
- W. T. S. Cole, R. S. Fellers, M. R. Viant and R. J. Saykally, J. Chem. Phys., 2017, 146, 014306 CrossRef PubMed.
- U. Góra, W. Cencek, R. Podeszwa, A. van der Avoird and K. Szalewicz, J. Chem. Phys., 2014, 140, 194101 CrossRef PubMed.
- Y. Wang and J. M. Bowman, Chem. Phys. Lett., 2010, 491, 1–10 CrossRef CAS.
- Y. Wang, B. C. Shepler, B. J. Braams and J. M. Bowman, J. Chem. Phys., 2009, 131, 054511 CrossRef PubMed.
- V. Babin, C. Leforestier and F. Paesani, J. Chem. Theory Comput., 2013, 9, 5395–5403 CrossRef CAS PubMed.
- V. Babin, G. R. Medders and F. Paesani, J. Chem. Theory Comput., 2014, 10, 1599–1607 CrossRef CAS PubMed.
- S. K. Reddy, S. C. Straight, P. Bajaj, C. Huy Pham, M. Riera, D. R. Moberg, M. A. Morales, C. Knight, A. W. Götz and F. Paesani, J. Chem. Phys., 2016, 145, 194504 CrossRef PubMed.
- C. Leforestier, K. Szalewicz and A. van der Avoird, J. Chem. Phys., 2012, 137, 014305 CrossRef PubMed.
- X.-G. Wang and T. Carrington Jr, J. Chem. Phys., 2018, 148, 074108 CrossRef PubMed.
- X.-G. Wang and T. Carrington, J. Chem. Phys., 2023, 158, 084107 CrossRef CAS PubMed.
- H. R. Larsson, M. Schröder, R. Beckmann, F. Brieuc, C. Schran, D. Marx and O. Vendrell, Chem. Sci., 2022, 13, 11119–11125 RSC.
- D. Blume and K. B. Whaley, J. Chem. Phys., 2000, 112, 2218–2226 CrossRef CAS.
- J. K. Gregory and D. C. Clary, J. Chem. Phys., 1995, 102, 7817 CrossRef CAS.
- C. L. Vaillant, D. J. Wales and S. C. Althorpe, J. Phys. Chem. Lett., 2019, 10, 7300–7304 CrossRef CAS PubMed.
- Y.-C. Zhu, S. Yang, J.-X. Zeng, W. Fang, L. Jiang, D. H. Zhang and X.-Z. Li, J. Am. Chem. Soc., 2022, 144, 21356–21362 CrossRef CAS PubMed.
- T. R. Walsh and D. J. Wales, J. Chem. Soc., Faraday Trans., 1996, 92, 2505–2517 RSC.
- T. Taketsugu and D. J. Wales, Mol. Phys., 2002, 100, 2793–2806 CrossRef CAS.
- M. Takahashi, Y. Watanabe, T. Taketsugu and D. J. Wales, J. Chem. Phys., 2005, 123, 044302 CrossRef PubMed.
- A. I. Vainshtein, V. I. Zakharov, V. A. Novikov and M. A. Shifman, Sov. Phys. Uspekhi, 1982, 25, 195 CrossRef.
- C. Vaillant and M. T. Cvitaš, Phys. Chem. Chem. Phys., 2018, 20, 26809–26813 RSC.
- G. V. Mil'nikov and H. Nakamura, J. Chem. Phys., 2001, 115, 6881–6897 CrossRef.
- J. O. Richardson and S. C. Althorpe, J. Chem. Phys., 2011, 134, 054109 CrossRef PubMed.
- M. Eraković, C. L. Vaillant and M. T. Cvitaš, J. Chem. Phys., 2020, 152, 084111 CrossRef PubMed.
- A. Garg, Am. J. Phys., 2000, 68, 430–437 CrossRef.
- V. A. Benderskii, S. Y. Grebenshchikov and G. V. Mil'nikov, Chem. Phys., 1995, 194, 1–18 CrossRef CAS.
- L. D. Landau and E. M. Lifshitz, Quantum Mechanics: Non-Relativistic Theory, Pergamon Press, Oxford, 2nd edn, 1965 Search PubMed.
- C. Herring, Rev. Mod. Phys., 1962, 34, 631–645 CrossRef CAS.
- G. V. Mil'nikov and H. Nakamura, J. Chem. Phys., 2005, 122, 124311 CrossRef PubMed.
- M. Eraković and M. T. Cvitaš, J. Chem. Phys., 2020, 153, 134106 CrossRef PubMed.
- M. Eraković and M. T. Cvitaš, J. Chem. Theory Comput., 2022, 18, 2785–2802 CrossRef PubMed.
- M. Schütz, T. Bürgi, S. Leutwyler and H. B. Bürgi, J. Chem. Phys., 1993, 99, 5228–5238 CrossRef.
- A. van der Avoird, E. H. T. Olthof and P. E. S. Wormer, J. Chem. Phys., 1996, 105, 8034–8050 CrossRef CAS.
- D. Sabo, Z. Bačić, T. Bürgi and S. Leutwyler, Chem. Phys. Lett., 1995, 244, 283–294 CrossRef CAS.
- M. G. Brown, M. R. Viant, R. P. McLaughlin, C. J. Keoshian, E. Michael, J. D. Cruzan, R. J. Saykally and A. Van der Avoird, et al. , J. Chem. Phys., 1999, 111, 7789–7800 CrossRef CAS.
- A. van der Avoird and K. Szalewicz, J. Chem. Phys., 2008, 128, 014302 CrossRef PubMed.
- V. A. Benderskii, E. V. Vetoshkin, L. Von Laue and H. P. Trommsdorff, Chem. Phys., 1997, 219, 143–160 CrossRef CAS.
- C. F. Karney, J. Mol. Graph., 2007, 25, 595–604 CrossRef CAS PubMed.
- W. Kabsch, Acta Crystallgr. A, 1976, 32, 922–923 CrossRef.
- M. T. Cvitaš and S. C. Althorpe, J. Chem. Theory Comput., 2016, 12, 787–803 CrossRef PubMed.
- M. T. Cvitaš, J. Chem. Theory Comput., 2018, 14, 1487–1500 CrossRef PubMed.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef.
- F. N. Keutsch, J. D. Cruzan and R. J. Saykally, Chem. Rev., 2003, 103, 2533–2578 CrossRef CAS PubMed.
- J. E. Lawrence, J. Dušek and J. O. Richardson, J. Chem. Phys., 2023, 159, 014111 CrossRef CAS PubMed.
- E. Pollak and J. Cao, J. Chem. Phys., 2022, 157, 074109 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2024 |