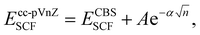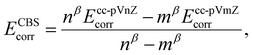Axial–equatorial equilibrium in substituted cyclohexanes: a DFT perspective on a small but complex problem

Abstract

In Chemistry, complexity is not necessarily associated to large systems, as illustrated by the textbook example of axial–equatorial equilibrium in mono-substituted cyclohexanes. The difficulty in modelling such a simple isomerization is related to the need for reproducing the delicate balance between two forces, with opposite effects, namely the attractive London dispersion and the repulsive steric interactions. Such balance is a stimulating challenge for density-functional approximations and it is systematically explored here by considering 20 mono-substituted cyclohexanes. In comparison to highly accurate CCSD(T) reference calculations, their axial–equatorial equilibrium is studied with a large set of 48 exchange–correlation approximations, spanning from semilocal to hybrid to more recent double hybrid functionals. This dataset, called SAV20 (as Steric A-values for 20 molecules), allows to highlight the difficulties encountered by common and more original DFT approaches, including those corrected for dispersion with empirical potentials, the 6-31G*-ACP model, and our cost-effective PBE-QIDH/DH-SVPD protocol, in modeling these challenging interactions. Interestingly, the performance of the approaches considered in this contribution on the SAV20 dataset does not correlate with that obtained with other more standard datasets, such as S66, IDISP or NC15, thus indicating that SAV20 covers physicochemical features not already considered in previous noncovalent interaction benchmarks.

---

1. Introduction

The heuristic validation of new exchange–correlation functionals, leading to a more accurate evaluation of chemical properties, has a relevant role within Density Functional Theory (DFT). Up to now, a large number of properties have been targeted. Among them, we count thermochemistry, molecular structures, ionization potentials, absorption and emission spectra, just to mention a few of them (see for instance ref. 1–3). This huge benchmarking effort is necessary to estimate the typical error on the prediction of a selected property associated to a given functional, thus increasing the number and range of accurate chemical applications for DFT models. Taking also into consideration their excellent ratio between accuracy and required computational resources, it is then not surprising that DFT approaches have become a very widespread computational tool beyond the boundaries of theoretical and computational chemistry.

While a number of properties are actually reproduced (or predicted) with the desired accuracy, often referred to as “chemical accuracy”, still some of them are trickier to describe and require additional care. This is the case, for instance, for weak non-covalent interactions (NCIs), whose relevance in Chemistry is longstanding and unquestionable.^4–6

If, generally speaking, functionals based on Generalized Gradient Approximations (GGAs), such as PBE⁷ and BLYP,^8,9 cannot correctly reproduce the energies associated with NCIs (over- and under-binding respectively for these two examples),² better performances are obtained by functionals including a fraction of Exact Exchange (EXX), leading to the family of so-called Global Hybrids (GHs).¹⁰ Lower deviations can be obtained especially if NCI energy properties are included in the training set for functional parameterization (e.g. M06-2X). DFT approaches specifically developed for weak interactions should be also mentioned, but their performances on other chemical properties are not necessarily exceptional.

Yet, the most significant step towards a greater accuracy for NCIs is represented by the coupling of standard exchange–correlation functionals with empirical dispersion corrections based on classical additive potentials.^11,12 These simple models are widely used since they combine a physically-sound model at negligible computational cost to get (very) low errors on weak-interaction energies. The side effect is the increase of the number of empirical parameters added to the computing approach since the pairwise functions depend on the atom types involved in the interactions and on the exchange–correlation functional to which they are coupled.

An interesting alternative is represented by the so-called Double Hybrids (DHs). They are hybrid functionals containing also a second-order perturbative (PT2) term that improves the treatment of the electronic correlation.^13,14 Indeed, DHs lead to a systematic improvement with respect to GHs on a considerably large number of properties.^13–15 Nevertheless, NCIs are still affected by significant errors at the DH level, even if these are reduced with respect to those obtained with GHs.^2,15 Also in this case, the pairing with empirical potentials, is beneficial^16,17 and, indeed, particular DHs integrate them in their construction (as in DSD-PBEP86 and its variants, for instance)^18,19 still with the need for specific parameterization.

In this context, up to here briefly sketched, we have recently developed a basis set, called DH-SVPD, appositely tailored to deal with NCIs and DHs.²⁰ When this small basis set is coupled with our latest nonempirical DH, PBE-QIDH,²¹ errors comparable to those by the most refined DFT approaches, including DHs paired with large triple- or quadruple-ζ basis set and empirical potentials, are obtained. This fact was proven in a large number of tests, from medium-size molecules such as those contained in the S22²² and S66²³ benchmark sets, to the large systems included in the L7²⁴ and CiM13²⁵ (up to 1000 atoms) datasets.^26–28 Beyond the gain in computing time, as this small basis set allows a roughly 4-times faster calculations with respect to larger quadruple-ζ basis, this combination also implies the definition of a completely nonempirical model, PBE-QIDH/DH-SVPD, a feature that is particularly novel and interesting within the field.

Moving away from the standard benchmarks mentioned above, more complex properties and systems are often considered in literature as “stress” tests for DFT approaches. The aim tackling these systems is therefore to push further the limits of modern functionals and expand their field of applicability. For instance, anharmonic frequencies are a step beyond harmonic vibrations²⁹ and a high accuracy in UV-vis band shape can be considered as an improvement with respect to the benchmarking of simple vertical transitions (λ_max).³⁰ This effort allows to have a better evaluation of complex systems and properties of interest for Chemists. Complexity here is not necessarily related to large chemical systems, but also in properties where the concurrent effects of different factors, distinct in origin and opposite in action, are present in a subtle yet key balance.

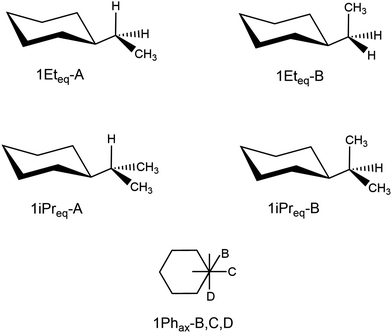
Very recently, a number of articles shed light on some fundamental issues concerning a textbook example, the equilibrium between the axial and equatorial conformation of monosubstituted cyclohexane (see Fig. 1).^31,32 The context is clearly related to the assessment of the role played by NCIs in Chemistry, notably concerning the stabilization of supramolecular complexes or complex molecular structures, for which these interactions play a crucial role (see for instance ref. 33 and 34). Monosubstituted cyclohexanes have, of course, the advantage of being small in size, which allows the deployment of refined post-Hartree–Fock methods for a very precise quantification of the intramolecular NCIs. Furthermore, they have been largely studied at the experimental level and estimations are available for the Winstein–Holness parameter, also known as A-value, that is the free energy difference, often estimated from NMR data, between the axial and equatorial form.^35,36 The equatorial conformer is typically the most stable one, and the textbook explanation is based on the larger contribution of the steric hindrance between the substituent and the close axial hydrogens in the axial form (see Fig. 1 and ref. 37 for a short discussion). However, Schreiner and co-workers pointed out that London dispersion (LD) interactions significantly affect the axial–equatorial equilibrium in monosubstituted cyclohexanes.³¹ They give an estimation of the ratio between the LD and steric contributions to the relative energies of the two forms that ranges between 19% (R = CI₃) and 95% (R = CN), depending on the R-substituent to the cyclohexane ring. This interplay of steric and LD interactions also induces strains into the molecular structure. It should be noted that previous works have already shown the relevance of LD on the conformational equilibrium of mono-substituted cyclohexanes.^38,39

Fig. 1 Sketch of the substituted cyclohexanes considered in the present paper. According to textbooks, the axial conformer should always be higher in energy than the equatorial one, due the dominant steric repulsion.

Starting from this analysis and without entering into details on the nature of different contributions to the relative stabilities³⁹ (that could depend on the energy-partition method used, as other examples show), these monosubstituted cyclohexanes likely represent an example of those small systems discussed above, where one can find a complex balance of effects that escapes the range of structure–property relationships covered by traditional benchmark datasets. Furthermore, they represent an ideal test case since they provide a clear example of a fundamental problem in Chemistry, while still maintaining an affordable dimension from a computational point of view (up to 21 atoms in the cases considered here).

Therefore, we believe that it is interesting to verify if a number of commonly-used DFT methods are able to correctly describe the axial–equatorial equilibrium in substituted cyclohexanes and to reproduce the subtle Chemistry associated to the balance of steric and LD components. To this end, the 20 mono-substituted cyclohexane analyzed by Schreiner and co-workers are considered here and their conformational energies are computed with 48 functionals, including GGAs, GHs, DHs as well as Range Separated Hybrids (RSH). Coupled Cluster (CC) high-quality energies are taken as references; the obtained results nicely illustrate the complexity of this chemical problem and its difference from benchmarks commonly employed for the assessment of NCI interactions.

2. Computational details

A set of 28 exchange–correlation functionals, selected among those more used in literature, listed in Table 1 is considered along this study. Some of them are paired with D3 and D3(BJ) and potentials, using the appropriate parametrizations, for a total number of 48 different DFT approaches. The D4 model⁶⁵ was also considered for selected functionals, taking the parameters from literature⁶⁵ or specifically optimizing them for the PBE-QIDH functional (see Table S1, ESI†).

Table 1 List of the exchange–correlation functionals considered in this work, ranked according to the casted percentage of the exact-like exchange (EXX) and second-order perturbation theory (PT2) correlation contributions

Functional	% EXX	% PT2	Ref.
a Min/max for range separated hybrids. b This functional is a combination of 41.1% B3PW91 (20% EXX exchange) and 58.9% PBE0 (25% EXX exchange).
GGA and metaGGA
BLYP	0	0	8 and 9
PBE	0	0	7
M06-L	0	0	40
revM06-L	0	0	41
B97M-V	0	0	42
TPSS	0	0	43
B97	0	0	44
B97M-V	0	0	45
VV10	0	0	46
Global hybrids
B3LYP	20	0	47 and 48
PBE0	25	0	49
M06	27	0	50
revM06	40.4	0	51
BMK	42	0	55
MN15	44	0	52
M06-2X	54	0	50
M06-HF	100	0	50 and 53
APF^b	22.945	0	54
Range-separated hybrids^a
ωB97M-V	15/100	0	56
ωB97X-V	16.7/100	0	57
CAM-B3LYP	19/65	0	58
ωB97X-D	22/100	0	59
M11	42.8/100	0	60
Double hybrids
PBE0-DH	50	12.5	61
B2-PLYP	53	27	62
mPW2-PLYP	55	25	63
DSD-PBEP86	69	22/52	18
PBE-QIDH	69.336	33.333	64

---

Single-point energy calculations are carried out using the def2-TVPP basis set on the molecular structures of the monosubstituted cyclohexanes optimized at the MP2/aug-cc-pVTZ level of theory and retrieved from ref. 31. This set of data is expanded to include those obtained using the DH-SVPD basis set. As reported in ref. 20, the latter was developed in a nonempirical fashion by minimizing recursively a combination of the PBE-QIDH energy contributions of a set of dimers in NCI and their respective monomers with respect to few atomic basis set exponents. Therefore, the DH-SVPD basis set is not trained on any specific external data coming, for instance, from post-HF interaction energies.

In addition to these approaches, we also considered the methods proposed by DiLabio and co-workers for an accurate evaluation of NCIs, based on the coupling of so-called atom-centered potentials (ACP) with the small 6-31-G(d) basis set (called 6-31G*-ACP).⁶⁶ These ACPs are parametrized on more than 118 000 energies, including about 19 000 NCIs. Only 3 functionals, namely BLYP, M06-2X and CAM-B3LYP are considered in this approach as well as few atomic elements, not including Br and I atoms. Therefore, the 6-31G*-ACP model is not applied to 4 molecules of our cyclohexanes set, namely R = Br, I, CBr₃ and CI₃, thus reducing the number of tested molecules from 20 to 16.

The def2-TZVPP and DH-SVPD basis sets as well as the 6-31G*-ACP model are also considered for the structure optimization and subsequent Gibbs free-energy calculations at DFT level. All DFT calculations are carried out with the Gaussian program.⁶⁷

The CCSD(T) “gold standard” method is selected to compute reference relative energy values.⁶⁸ The complete basis set (CBS) limit is further reached by running a two-point extrapolation with the cc-pVnZ Dunning correlation consistent basis set, n being the ‘cardinal number’ of the basis set. Within this scheme, the convergence of the self-consistent field (SCF) exchange energy to the CBS limit is assumed to follow

with A and α, two constants, the former being determined with the two-point extrapolation scheme and the latter taken as an optimally tuned basis set constant.⁶⁹ It is assigned to α_2/3 = 4.42 (α_3/4 = 5.46) for a 2/3 (3/4) extrapolation scheme. On the other hand, the convergence of the correlation energy is assumed to follow the expression
with β, another tabulated constant which is assigned to β_2/3 = 2.46 or β_3/4 = 3.05 for a 2/3 or 3/4 extrapolation scheme, respectively.⁷⁰ The total CBS energy is then obtained by summing the exchange and correlation energies extrapolated at the basis set limit such as

E^CBS_total = E^CBS_SCF + E^CBS_corr

For domain based local pair natural orbitals (DLPNO) cost-effective methods, a three-point extrapolation scheme (EP3), consisting in adding a correction to the 3/4 extrapolated correlation energy term with the canonical method at cc-pVDZ level has been considered. For instance, an EP3 extrapolation with DLPNO-CCSD(T) level writes

E^EP3_{total-DLPNO-CCSD(T)} = E^CBS(3/4)_SCF + E^CBS(3/4)_{corr-DLPNO-CCSD(T)} + E^cc-pVDZ_corr-CCSD(T) − E^cc-pVDZ_{corr-DLPNO-CCSD(T)}

Following previous suggestions, very tight settings are used in the DPLNO calculations.^71,72

As comparison with CCSD(T), the 2nd order Möller–Plesset perturbation theory (MP2) is also employed in its Spin-Component Scaled (SCS-)MP2 variant⁷³ together with the same sequence of cc-pVnZ basis set (n = D, T, Q) and the corresponding extrapolation to the CBS(2/3) and CBS(3/4) limit.

All CCSD(T) and MP2 calculations have been carried out with the ORCA program.⁷⁴

3. Results and discussion

3.1. High-quality axial–equatorial energy differences

As discussed above, the axial–equatorial energy differences taken as reference are the ones computed at the CCSD(T)/CBS(3,4) level. They are reported in the last column of Table 2. The corresponding Mean Energy Difference (MED) for the whole molecular set, that is the average value of the energy difference between axial and equatorial isomers, amounts to 2.2 kcal mol⁻¹. As expected, all the equatorial conformations, except one, are more stable than the axial ones due to dominant steric effects. The values range between 6.23 kcal mol⁻¹ (R = CI₃) and 0.13 kcal mol⁻¹ (R = F), with the single exception represented by the CN derivative, where the two conformers are computed to be almost isoenergetic (ΔE_ax-eq = −0.03 kcal mol⁻¹). These data well agree with the qualitative analysis of Schreiner and co-workers carried out at the B3LYP-D3(BJ) level of theory.

Table 2 Energy differences (kcal mol⁻¹) between the axial and equatorial conformers of substituted cyclohexanes, computed at the CCSD(T) level using different basis sets and approximations (see (Fig. 2) for labelling)

R	2-ζ		4-ζ		CBS(3/4)
	DLPNO^a	Canonical	DLPNO^a	Canonical	DLPNO^a	Canonical
a Tight settings.
F	−0.358	−0.377	0.082	0.106	0.105	0.134
Cl	0.374	0.355	0.39	0.401	0.357	0.382
Br	0.558	0.508	0.402	0.41	0.342	0.369
I	0.569	0.824	0.343	0.319	0.187	0.178
CCH	0.013	−0.02	0.263	0.248	0.302	0.278
CN	−0.206	−0.225	−0.053	−0.049	−0.048	−0.03
Me	1.87	1.844	1.758	1.758	1.773	1.78
Et-A	1.741	1.691	1.636	1.628	1.657	1.648
Et-B	0.918	0.892	0.79	0.806	0.793	0.816
iPr-A	1.467	1.409	1.391	1.348	1.418	1.38
iPr-B	1.531	1.485	1.374	1.334	1.398	1.356
tBu	5.132	5.1	4.875	4.845	4.878	4.851
Ph-B	3.002	2.922	2.773	2.7	2.77	2.697
Ph-C	4.046	3.98	4.052	4.033	4.066	4.053
Ph-D	3.233	3.149	3.034	2.971	3.027	2.988
CF3	1.691	1.602	2.285	2.27	2.262	2.267
CCl3	5.112	5.051	4.849	4.845	4.732	4.769
CBr3	6.022	5.93	5.563	5.549	5.455	5.454
CI3	6.949	7.164	6.484	6.508	6.214	6.266
SiMe3	2.271	2.209	2.288	2.263	2.288	2.276
MAE	0.254	0.263	0.048	0.043	0.026

---

Fig. 2 Sketch of the ethyl-, isopropyl- and phenyl-cyclohexanes (1Et_eq,ax, 1iPR_eq,ax and 1Ph_ax, respectively). Axial phenyl-cyclohexane is shown from above the cyclohexane ring, with the bold lines representing the three possible orientations of the phenyl ring plane (i.e., conformers B, C and D)

Let us start our discussion from the canonical CCSD(T) calculations. Here the deviations from the reference values systematically decrease going from the 2-ζ to the 4-ζ basis set, namely from 0.26 to 0.05 kcal mol⁻¹. This variation corresponds to a shift of the error from 11.8% to 2.3% on the 2.2 kcal mol⁻¹ average value (MED). An analysis of the results collected in Table 2 shows that they follow the expected trends, with few exceptions. For instance, the stability of the equatorial form of the F-cyclohexane is overestimated at the CCSD(T)/2ζ level of theory (ΔE_ax-eq = −0.38 kcal mol⁻¹) together with that of R = CN (ΔE_ax-eq = −0.22 kcal mol⁻¹) and R = CF₃ (ΔE_ax-eq= 1.60 kcal mol⁻¹) derivatives. While in this latter case the energy difference is positive, thus suggesting the correct reproduction of the interplay between steric and LD interactions, the negative sign for R = F and R = CN suggests an overestimation of the dispersion interactions. The two isomers are predicted to be, instead, isoenergetic for R = CCH (ΔE_ax-eq = −0.02 kcal mol⁻¹), always for the same computational model.

In Fig. 3 are reported the Mean Absolute Error (MAE) obtained for the other post-HF approaches considered in this work. For instance, a MAE of 0.11 kcal mol⁻¹ is obtained with the 3-ζ basis set, about one half of the deviation computed with the smaller basis set. The CBS(2,3) approach provides, instead, an error slightly larger than that obtained with the 3-ζ basis (0.12 kcal mol⁻¹). These two methods restore the correct trends on the energy values (see also Table S2, ESI†).

Fig. 3 Mean Absolute Errors (MAE, kcal mol⁻¹) for the CCSD(T) methods considered in the present paper. The MAEs are computed with respect to CCSD(T)/CBS(3,4) values and the acronym CC in the x-axis refers to CCSD(T) calculations.

More in general, the cyclohexanes with aliphatic substituents (Me, Et, tBu) or the SiMe₃ group are quite insensitive to the method, showing only small fluctuations with the basis set size or the extrapolation scheme (maximum variation of 0.2 kcal mol⁻¹). In contrast, larger variations are found for halogenated groups, as above discussed. This behaviour is well illustrated in Fig. 4 (left), where the CCSD(T) values, computed using different basis set, extrapolation schemes and localized orbitals, are plotted as functions of the reference canonical CCSD(T)/CBS(3,4) energies. The outliers, labelled with the substituent groups, are indeed all halogenated systems.

Fig. 4 Correlations between CCSD(T)/CBS(3,4) energy differences (ΔE^ref, kcal mol⁻¹) and corresponding values computed with: (left) CCSD(T) and (right) MP2 methods. The acronym CC in legend refers to CCSD(T) calculations. The outliers with respect to the identity line are noted with the R substituent to the cyclohexane ring (see Table 2 for a complete list).

Following referee's suggestion, the original two-point extrapolation scheme of Helgaker⁷⁵ was also considered for the CCSD(T) calculations. The differences on the MAE for the CBS(3,4) extrapolation with respect to the scheme using modified coefficients is less than 0.002 kcal mol⁻¹ (see Table S2, ESI†). We have also considered larger basis sets, of aug-cc-pVnZ quality, but, unfortunately, this basis set did not provide converged results for most of the molecules of the data set and it was, therefore, discharged.

The consideration of the DLPNO scheme does not significantly affect the computed MAEs (see Fig. 3 and Table S3, ESI†). Indeed, only small variations (<0.01 kcal mol⁻¹) are observed between the canonical CCSD(T) calculations and their DLPNO counterparts with the 2-, 3- and 4-ζ basis set, thus well confirming the accuracy of that orbital localization scheme. A larger, but still acceptable, difference (ΔMAE = 0.02/0.03 kcal mol⁻¹) is however evaluated with the CBS approaches, corresponding to about 1% of the MED. The error is, however, sizeable at the CCSD(T)/EP3, being about 0.08 kcal mol⁻¹, that is about 4% of the MED. This scheme is supposed to be superior to the more traditional CBS in modelling weak interactions in the S66 dataset, but, apparently, it is not at its best on cyclohexane conformers.

The SCS-MP2 calculations reflect the trends of canonical CCSD(T) ones, with the 2ζ basis set providing a larger error (0.33 kcal mol⁻¹) decreasing to 0.16 kcal mol⁻¹ for the 4ζ basis set (see Fig. 3 and Table S4, ESI†). Interestingly, the two CBS extrapolation schemes considered, namely CBS(2,3) and CBS(3,4), give the same MAE, slightly lower than that found for the 4ζ basis (about 0.12 kcal mol⁻¹). As for the CCSD(T) approaches, the most problematic groups are those containing halogen atoms, as it is clearly shown in Fig. 4 (left). Indeed, the points most distant from the identity line are the same observed for CCSD(T) calculations, namely R = F, I, CF₃, CBr₃ and CI₃.

Generally speaking, these results are completely aligned with those obtained with the same methods for purely covalent interactions, in particular concerning basis set effects and the DLPNO approximations.^67,76,77 It should also be pointed out that, consideration of non-perturbative triple and perturbative quadruple excitations, giving CCSDT and CCSDT(Q) models, respectively, has a small effect on computed NCIs for small systems (such as water and ammonia dimers), modifying the interactions energies only a few cm⁻¹ (that is 0.01–0.02 kcal mol⁻¹). The huge computational effort associated with these methods is, in our opinion, well beyond the scope of the present paper.

3.2. DFT benchmarks

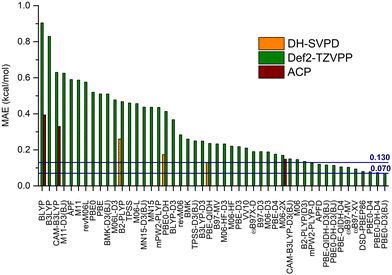
The next step is to identify the most suitable functionals to model the axial–equatorial equilibrium in the set of monosubstituted cyclohexanes. The MAEs for the functionals collected in Table 1 (with and without dispersion corrections) are reported in Fig. 5. The 48 DFT methods have very different behaviors, with MAEs ranging from 0.90 to 0.07 kcal mol⁻¹ for BLYP and PBE0-D3(BJ), respectively, that is between 41% and 4% of the reference MED (2.2 kcal mol⁻¹). Besides the two worst-performing approaches (BLYP and B3LYP), about one half of the functionals provides an error between 0.6 and 0.4 kcal mol⁻¹, while for the others the range is between 0.3 and 0.1 kcal mol⁻¹. As expected, GGA functionals, such as BLYP, PBE and M06-L, are in the first group, while GHs and DHs, eventually corrected for dispersion, are in the second one. Indeed, all the best performers (MAE < 0.14 kcal mol⁻¹) incorporate some form of dispersion correction, from the original Grimme's proposal,¹² to VV10,⁴⁶ through Becke–Johnson⁷⁸ and Spherical Atom Dispersion Term⁵² models.

Fig. 5 Mean Absolute Errors (MAE, kcal mol⁻¹) for the energy differences between axial and equatorial form of the 20 substituted cyclohexanes, computed using the 48 DFT approaches considered in the present paper. The MAEs are calculated with respect to CCSD(T)/CBS(3,4) values. The two lines reported on the bar plot refer to the MAEs of the best approach (PBE0-D3(BJ)/def2-TZVPP, 0.070 kcal mol⁻¹) and to our model (PBE-QIDH/DH-SVPD, 0.130 kcal mol⁻¹).

The best performer is a GH, namely PBE0, coupled to the D3(BJ) potential that provides an error as low as 0.07 kcal mol⁻¹. It is slightly better than the related PBE0-DH functional corrected with the D4 potential (PBE0-DH-D4, 0.074 kcal mol⁻¹) and 3 semi-empirical functionals, namely ωB97X-V, ωB97M-V and DSD-PBEP86, that show deviations of 0.09, 0.10 and 0.11 kcal, respectively. These last three functionals include dispersion corrections and are explicitly developed including NCIs in the training set, e.g., the S22, S66 or NC15 datasets, used to optimize their intrinsic parameters. Indeed, these errors are comparable to those obtained, for instance, on the NC15 data set, at least for ωB97X-V and ωB97M-V.⁷⁹

Other interesting trends can be inferred from the MAEs values. First, functionals including PBE model perform better than those using BLYP. For instance, BLYP, B3LYP (and CAM-B3LYP) are the worst performing methods, with deviations of 0.90 and 0.83 kcal mol⁻¹ (and 0.63 kcal mol⁻¹), respectively, whereas PBE and PBE0 provide 0.51 and 0.52 kcal mol⁻¹. In both cases, it is interesting to notice the negligible role played by the EXX, with GGAs and GHs providing very close deviations. This is not the case for other weak-interacting systems, such as those contained in the S22 or S66 datasets. The two corresponding DHs, B2-PLYP and PBE-QIDH, confirm this behavior, their MAEs being 0.47 and 0.24 kcal mol⁻¹ respectively.

For these two families of functionals, specifically, dispersion corrections have a significant impact, reducing the MAEs between 0.3 and 0.5 kcal mol⁻¹, depending on the specific functional. This is the case, for instance, for B2-PLYP/B2-PLYP-D3 (from 0.47 to 0.14 kcal mol⁻¹) and PBE-QIDH/PBE-QIDH-D3(BJ) (from 0.24 to 0.12 kcal mol⁻¹). Other functionals display the same behavior upon the addition of empirical potentials, such as APF and APFD (from 0.59 to 0.12 kcal mol⁻¹) or mPW2-PLYP and mPW2-PLYP-D (from 0.44 to 0.13 kcal mol⁻¹).

It should be also remarked that the consideration of the most recent D4 correction in place of the D3(BJ) model, marginally affects the MAE for PBE0 (+0.008 kcal mol⁻¹) and the related DH functional, PBE-QIDH (−0.010 kcal mol⁻¹, see Fig. 5 and Table S5, ESI†). Such limited variations in going from the D3(BJ) to the D4 correction for functionals of the PBE family was already reported in literature.^80,81

While the data well highlights the overall contribution of the NCIs, they do not allow to quantify the relative weight of steric and LD interactions. Appropriate analysis tools, based on electron density or energy partition, can be used,³⁹ but this goes beyond the scope of this paper and, in addition, the answer is likely to be method-dependent.

The most accurate dispersion-uncorrected functional is M06 with a MAE of 0.15 kcal mol⁻¹, about two-times that of the best performing functional, PBE0-D3(BJ), but significantly better than other approaches including dispersion corrections, such as ωB97X-D or B3LYP-D3. Interestingly, most of the Minnesota functionals considered here are quite insensitive to the addition of a dispersion potential. For instance, the MAE for M06-D3 is 0.19 kcal mol⁻¹, even higher than the deviation for the bare M06 model. Similar values are also found for M06-HF and M06-HF-D3 (0.22 vs. 0.23 kcal mol⁻¹). These results are in contrast with data in the literature suggesting that empirical dispersions are also beneficial for Minnesota functionals,⁸² thus giving further indications that the set of monosubstituted cyclohexanes are complementary to other commonly employed benchmarks.

Some interesting features appear from a deep analysis of the single energy values collected in Table S5 (ESI†). The functionals involving PBE or BLYP models, pure GGA, GHs or DHs and with or without dispersion corrections, always give energy differences with the correct positive sign, with the axial form being always higher in energy than the equatorial one. The only exception is PBE-QIDH-D3(BJ) that gives −0.10 kcal mol⁻¹ for the CN derivative to be compared to the −0.03 kcal mol⁻¹ for the reference CCSD(T)/CBS(3,4) value.

More in general, the largest deviations are observed with the pure BLYP or PBE functionals, and the agreement with the reference data increases going to the corresponding GHs (B3LYP and PBE0) and then DHs (B2-PLYP and PBE-QIDH). The addition of the D3(BJ) correction further reduces the deviations and leads to an inversion on the quality scale between PBE0-D3(BJ) and PBE-QIDH-D3(BJ). Larger improvements along this scale (from GGAs to DHs and with/without dispersion corrections) are observed for aliphatic or aromatic substituents (such as tBu or Ph) than for halogenated ones (CX₃, X = Cl, Br, I), thus suggesting that, in these molecules, the LDs are less relevant.

A different picture emerges for the Minnesota functionals. Here M11, MN15 and M06-L prefer the equatorial form for the mono-halogenated (R = F, Cl, Br, I), CN and CCH substituted species, even upon addition of a dispersion correction. Correct trends are, instead, obtained for M06, M06-2X and M06-HF, with the small variation, already discussed, from the D3 correction. Functional involving the B97 model (B97M-V, ωB97M-V and ωB97X-V) are, as discussed, in excellent agreement with the reference data for all the 20 molecules.

In Fig. 5 are also reported the MAEs computed with the 6-31G*-ACP model and the 3 functionals for which it was developed, that is BLYP, CAM-B3LYP and M06-2X as well as the results obtained with the DH-SVPD basis set and 3 DHs (B2-PLYP, PBE0-DH and PBE-QIDH). The 6-31G*-ACP model, representing an excellent compromise between cost and accuracy, significantly reduces the MAE for BLYP (from 0.90 to 0.39 kcal mol⁻¹, −56%) and CAM-B3LYP (from 0.63 to 0.33 kcal mol⁻¹, −58%). It has, however, a limited impact on M06-2X (from 0.17 to 0.15 kcal mol⁻¹), thus reproducing the behavior already observed for Minnesota functionals and empirical correction.

More in details, from the data reported in Table S6 (ESI†), one can clearly conclude that the ACP model represents a significant improvement in the description of all the 20 axial–equatorial energy differences with respect to the uncorrected BLYP and CAM-B3LYP, reducing the gap between the energies of the two conformers. For M06-2X, the effect is in the opposite direction, the axial–equatorial difference increases for most of the molecules. The alkyne (CCH) and cyano (CN) substituents represent, however, an exception with the equatorial form being excessively stabilized by the 6-31G*-ACP model, leading to comparable negative energy differences (about −0.5 kcal mol⁻¹).

Finally, the DH-SVPD basis set reduces the overstabilization observed when the PBE-QIDH functional is used with a large basis set, thus systematically increasing the agreement with the reference values, as shown by the data reported in Table S7 (ESI†). This effect is systematic for all the 20 molecules, whose stabilities have the right trend (all positive except CN) at this level of theory. Indeed, the MAE is 0.13 kcal mol⁻¹, thus placing the PBE-QIDH/DH-SVPD model at the twelve place in the ranking of Fig. 5, at 0.06 kcal mol⁻¹ from the best performer.

All these trends are summarized in Fig. 6, where the computed energy differences, obtained with methods selected among those discussed above in details, are reported. In particular the effects of dispersion corrections are clear for the BLYP functionals, while the M06-2X model provides several values far from the identity line, notably those related to halogenated molecules (R = CF₃ and CI₃). The other functionals are among the most accurate ones and their values are, generally speaking, closer or on a similar line.

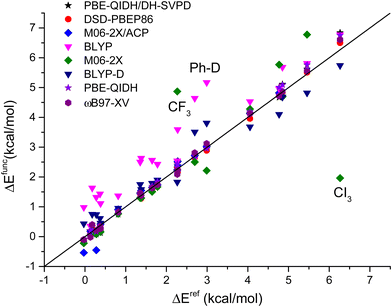Fig. 6 Correlations between CCSD(T)/CBS(3,4) energy differences (ΔE^ref, kcal mol⁻¹) and corresponding values computed with selected DFT approaches. The outliers with respect to the identity line are noted with the R substituent to the cyclohexane ring (see Table 2 for a complete list).

In short, an excellent accuracy of about 0.1 kcal mol⁻¹ or less, corresponding to an error of about 5% of the reference CCSD(T) MED, can be obtained with several functionals, some recent (and more complex), such as ωB97M-V, DSD-PBEP86 and ωB97X-V, other less recent such as PBE0-D3(BJ), B2-PLYP-D3 and PBE-QIDH-D3(BJ), all of them featuring a specific correction for dispersion interactions. Not far, it is possible to find M06, with the standard def2-TZVPP basis set, PBE-QIDH with the specific DH-SVPD basis, and the M06-2X functional coupled to the ACP-6-31G* model. They give MAEs between 0.13 and 0.15 kcal mol⁻¹ (6 to 7% of the reference MED).

3.3. A-values: DFT, CC and experimental data

The DFT values discussed up to now are evaluated using the same molecular structures for all the functionals. This common practice gives the chance to disentangle structural and electronic effects and to thus assess the intrinsic predictive qualities of the tested DFT methods. However, in most cases, the same exchange–correlation functional is often used at the same level of theory for both structural and energy calculations, as well as for (harmonic) frequency evaluations. Of course, there is no a priori guarantee of good performances on both properties. Indeed, some functionals are shown to be more suitable for evaluating just one of the two.⁸³ This fact calls, naturally, for the definition of accurate reference values for the geometrical parameters (at least bond lengths), a task far from trivial, even for small or medium sized molecules.⁸⁴

To this end, in this study, we have also considered an experimental observable, that is linked to structural and vibrational fingerprints of the molecule, the so-called Winstein–Holness A-value.^35,36 This value is an estimate of the difference between the Gibbs free energies of the axial and equatorial isomers obtained via NMR spectroscopy. Indeed, from the ratio of the signal intensities of the two forms, the K equilibrium constant and then the ΔG value can be derived. It is however worth to note that several experimental factors, such as solvent and temperature effects, limit the accuracy of the constant being measured, thus affecting the evaluation of ΔG.⁸⁵ As it can be seen from the experimental data collected in the first column of Table 3, a large value interval has been determined for the smaller monosubstituted cyclohexanes, thus confirming the experimental uncertainty.

Table 3 Experimental free-energy differences between the axial and equatorial conformers of the substituted cyclohexane (ΔG, kcal mol⁻¹). The mean experimental value (ΔG^av, kcal mol⁻¹) as well as the best theoretical estimate (Ref., kcal mol⁻¹) are also provided. Experimental values are taken from ref. 85

R	ΔG	ΔG^av	Ref.
F	0.25–0.42	0.335	0.208
Cl	0.53–0.64	0.585	0.598
Br	0.48–0.67	0.575	0.594
I	0.47–0.61	0.54	0.365
CCH	0.41–0.52	0.465	0.476
CN	0.2	0.2	0.142
Me	1.74	1.74	2.057
Et-A	1.79	1.79	1.954
Et-B			0.992
iPr-A	2.21	2.21	1.728
iPt-B			1.487
tBu	4.7–4.9	4.8	6.803
Ph-B	2.8, 2.87	2.8	3.275
Ph-C			3.539
Ph-D			4.631
CF3	2.4–2.5	2.45	2.512
CCl3			4.912
CBr3			5.547
CI3			6.233
SiMe3	2.5	2.5	3.272

---

Therefore, following the choice made in ref. 31, the mean values, listed in the second column of Table 3, will be considered in the following as an estimation of the experimental A-values. Table 3 also reports the reference theoretical values, evaluated by correcting the CCSD(T)/CBS(3,4) energies with the MP2 thermodynamic contributions. Clearly there are inconsistencies between the two datasets, especially for the bulky substituents, while the A-values of the cyclohexanes with the smaller substituents are better reproduced. The largest deviation is observed for R = tBu, about 2 kcal mol⁻¹, while the computed values for F, Cl, CCH and CF₃ are within the experimental interval. Overall, the deviation between CCSD(T) and experimental data is large, the MAE is 0.52 kcal mol⁻¹, corresponding to about 30% of the mean experimental A-value (1.8 kcal mol⁻¹). However, as it is observed from Fig. 7, a clear linear relationship (r = 0.98) emerges between experimental data and CCSD(T) values. The outliers are, again, the above-mentioned systems, notably R = tBu, iPr and Ph. This good relationship between computed and experimentally-estimated data is, of course, only qualitative, since the theoretical values have been evaluated on isolated molecules without including any solvent model.

Fig. 7 Plot of the CCSD(T)/CBS(3,4) A-values versus the available experimental data. The values are noted with the R substituent to the cyclohexane ring (see Table 2 for a complete list). The dashed orange line corresponds to the best linear fit.

Inspecting the CCSD(T) values, it is worth to note that the equatorial conformers are more stable in terms of Gibbs free energy differences than ΔE, except for the R = Ph-C and CI₃ molecules. The largest absolute variations are observed for R = tBu (+1.95 kcal mol⁻¹) and R = Ph-D (+1.64 kcal mol⁻¹), with the largest relative variations observed for CN (−574%), and CCH (+71%). The latter values are however, small on the absolute scale (+0.17 and +0.20 kcal mol⁻¹ respectively).

This context leads us to prefer the theoretical A-values for further comparison, also considering the limited number of experimental data, 13 instead of the 20 original systems as well as the large interval of experimental values for some molecules. Similar considerations have been also previously reported in literature.³¹

Fig. 8 reports the MAE for the A-values with respect to the CCSD(T) references, obtained for the DFT approaches being considered here. Of course, these A-values have been computed using the same exchange–correlation functional for structures, energies, and thermal corrections (see also Table S8, ESI† for single values). At first sight, it should be observed that the range of MAEs for A-values is reduced with respect to that found for energies at fixed structures. Indeed, the values in Fig. 8 span over an interval of about 0.4 kcal mol⁻¹ (from 0.21 to 0.67), while the MAE range of the MP2 structures is about twice as large (0.8 kcal mol⁻¹, from 0.07 to 0.90 kcal mol⁻¹).

Fig. 8 Mean Absolute Errors (MAE, kcal mol⁻¹) for the A-values of the 20 substituted cyclohexanes computed using the 48 DFT approaches considered in the present paper. The MAEs are computed with respect to CCSD(T)/CBS(3,4) values. The two lines reported on the bar plot refer to the MAEs of the best approach (DSD-PBEP86/def2-TZVPP, 0.204 kcal mol⁻¹) and to our model (PBE-QIDH/DH-SVPD, 0.230 kcal mol⁻¹).

Globally, the trends observed with fixed geometries are preserved, and only a limited reshuffling in the rank of the functionals is observed. Indeed, 7 of the 10 worst performing functionals (BLYP, B3LYP, CAM-B3LYP, M11-D3(BJ), APF, M11 and BMK-D3(BJ)) are the same as those in fixed MP2 geometry, even if not in the same order. Also 9 of the best performing functionals, out of 10, confirm their performance on the new reference set.

These results are rather reassuring since they clearly indicate a marked consistency between single energy values at given geometry and differences in Gibbs free energies.

Two other points deserve further discussion. First, our PBE-QIDH/DH-SVPD protocol has a MAE that is only 0.03 kcal mol⁻¹ higher than the best functional (0.230 vs. 0.204 kcal mol⁻¹, Table S9, ESI†), thus further confirming its robustness and its ability to reproduce both structure and thermal effects. The second point concerns the performance of the ACP-6-31G* model that leads to comparable results to those obtained with the larger def2-TZVPP basis set for BLYP (a MAE of 0.54 vs. 0.48 kcal mol⁻¹, respectively) and CAM-B3LYP (a MAE of 0.51 vs. 0.46 kcal mol⁻¹, respectively), but, of course, at a fraction of the computational cost. In contrast, a slight increase is found for M06-2X in going from the def2-TZVPP basis to the ACP-6-31G* model (from 0.29 to 0.35 kcal mol⁻¹, respectively). Such behavior is likely related to an overestimation of the attractive dispersion interactions in some of the systems, predicting at the CAM-B3LYP level the axial form as the most stable for R = CCH and CN (see Table S9, ESI†).

In summary, the comparison against Gibbs free energies follows the same trends observed using fixed molecular structures, but it is slightly less discriminating for the functional selection, due to the reduced range of values and the significant role played by thermal and vibrational contributions. Therefore, we believe that the axial–equatorial energy differences, as discussed in paragraphs 3.1 and 3.2, represent an appealing option to be included in the datasets for the systematic benchmarking of DFT approaches. This dataset, including the CCSD(T)/CBS(3/4) energies (last column of Table 2), will be named SAV20, from Steric A-values for 20 molecules, to remark its origin.

3.4. About the utility of another dataset for non-covalent interactions

The final question to be addressed concerns the usefulness of this new dataset, compared to those already present in the literature and largely used for functional benchmarking. To answer this basic question, we compare the performances of selected functionals for three standard datasets probing for NCI energy properties, namely the so-called S66²³ IDISP⁸⁶ and NCI15⁷⁷ set, with those obtained on our SAV20 set. These sets are totally diverse in nature, containing different molecules and covering NCIs with various interaction energies. Indeed, the first set, S66, is a relatively large dataset containing the interactions energies of 66 molecular complexes, generated from 13 different monomers (acetic, acetamide cyclic, cyclopentane, ethene, ethyne, neopentane, n-pentane, methylamine, methanol, N-methylacetamide, pyridine, uracil, and water). This dataset was conceived to be representative of the most common types of NCIs in biomolecules, including both LD, H-bond, and mixed LD/H-bond complexes almost in the same ratio. The CCSD(T)/CBS reference energies ranges from about 2 kcal mol⁻¹ to about 20 kcal mol⁻¹, but most of the complexes have interaction energy around 4 kcal mol⁻¹. The mean interaction energy over the whole set is about 5 kcal mol⁻¹.

IDISP is a small dataset covering intramolecular LDs of large organic systems. These energies are evaluated from 4 reactions, namely the dimerization of anthracene, the hydrogenation reaction of [2.2]paracyclophane yielding p-xylene, the isomerization of n-octane to iso-octane and isomerization of n-undecane to 2,2,3,3,4,4-hexamethylpentane, and from the energy differences between the linear and folded conformers of the C₁₄H₃₀ and C₂₂H₄₆ hydrocarbons. These reactions were identified as problematic for DFT methods (see for instance ref. 2). The IDISP set involves 13 single point calculations and the average energy is 14.1 kcal mol⁻¹.

Both S66 and IDISP sets are part of the large GMTKN55 database, commonly used for benchmarking DFT-based (but not exclusively) methods.²

Finally, the third set is the NC15 proposed by Patkowski and co-workers,⁷⁷ composed by small LD complexes such as rare-gas dimers, water, ammonia, and methane dimers, forming 21 homo- and hetero-NCI dimers (please note that the 15 in the acronym is the year). The CCSD(T)/CBS reference energies span from 0.02 to 48.3 kcal mol⁻¹, with 5 of them being between 1 and 5 kcal mol⁻¹, and 1 at 48.3 kcal mol⁻¹. The average value is 3.3 kcal mol⁻¹. Among the three sets, the last one is the most recent and less widespread, but its average value is the closest to that of SAV20 (2.2 kcal mol⁻¹).

In Fig. 9 are reported the MAEs of the SAV20 set as function of the values obtained (with the same functionals) for the S66, IDISP and NC15 sets. A correlation close to linearity between two sets will indicate that they are mapping similar features and, therefore, they are redundant. Since the aim here is to look for a possible correlation between the different sets, a minimal effort strategy, based on using published data for these sets,^79,87 is largely sufficient. Indeed, the variations from a linear correlation are significantly larger than those related to numerical issues (different computers codes and computational parameters).

Fig. 9 Correlations between the MAEs (kcal mol⁻¹) for the SAV20 dataset and that of the: (left) S66 and IDISP and (right) the NCI15 set. The values are obtained with selected DFT models (see text for details). The lines correspond to the best linear fits.

Concerning the first two sets, S66 and IDISP, the regressions are relatively good (r of about 0.7), but different functionals are significantly far from the linear correlation, as also clearly appears from the spreading of the points on the graphs (Fig. 9, left). In particular, the most significant outliers are PBE, MN15, M11, and their D3-corrected counterparts for the IDISP set, and B3LYP, PBE, M11, M11-D3(BJ), TPSS and BMK for the S66 set. In the first case, however, all the functionals provide significant errors on both IDISP and SAV20 sets (even if the two bad performances are not correlated), while in the second case PBE, M11 and M11-D3(BJ) are (relatively) good on S66 and bad on SAV20. Furthermore, the outliers are not always the same for the two sets. The most relevant outliers for the NC15 set (Fig. 9, right) are BLYP, BMK and BMK-D3, these functionals provide different degrees of accuracy on the NC15 and the SAV20 sets. This non-systematic behavior strongly indicates that there is not a clear correlation between our SAV20 set and the other three benchmark datasets. This absence of correlation clearly suggests that the SAV20 set represents a different portion of the chemical interaction space, that is not considered in other widely used benchmarks, and that it could largely be used to complement the existing sets in the quality assessment of exchange–correlation functionals.

4. Conclusions.

The axial–equatorial equilibrium in 20 mono-substituted cyclohexanes are evaluated using 48 DFT approaches, in some cases corrected with empirical potentials for non-covalent interactions. They are compared to basis-set extrapolated CCSD(T) high-quality energies computed within this investigation and used here as a reference. These simple yet challenging molecules are ruled by the interplay of London dispersion and steric repulsion, acting in opposite direction while defining the relative stabilization of the isomer. They represent, therefore, a complex dataset for modelling structure-energy effects. Indeed, our results show a discrepancy between the performances obtained on this dataset and those reported in literature on others specifically developed for NCIs. This peculiar feature allowed us to define the Steric A-Value (SAV20) dataset, composed by the axial and equatorial monosubstituted cyclohexanes (40 molecules in total) and the associated CCSD(T)/CBS(3,4) reference energies. This dataset comes as an interesting addition to the ones already existing and mostly including effects from single energy components, such as LD. As an interesting byproduct of our analysis, we show how our PBE-QIDH/DH-SVPD model, developed for handling NCIs in the framework of double hybrids at a reduced computational cost, performs remarkably well also on the SAV20 dataset. This result is further confirmation that this model is able to catch the main physics underpinning complex NCIs.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

C. A thanks Dr Michele Turelli (Chimie ParisTech, Paris) for useful discussions and hints on manuscript. Funded by the European Union (ERC, project MaMA, no. 101097351). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. E. B. gratefully acknowledges ANR (Agence Nationale de la Recherche) for the financial support of this work through the MoMoPlasm project (ANR-21-CE29-0003). He thanks also ANR and CGI (Commissariat à l'Investissement d'Avenir) for their financial support of this research through Labex SEAM (Science and Engineering for Advanced Materials and devices) ANR-10-LABX-096, ANR-18-IDEX-000. H. L. acknowledges financial support from the China Scholarship Council (grant no. 201908310062).

References

1. Y. Zhao and D. G. Truhlar, Acc. Chem. Res., 2008, 41, 157–167.
2. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
3. D. Jacquemin, V. Wathelet, E. A. Perpète and C. Adamo, J. Chem. Theory Comput., 2009, 5, 2420–2435.
4. J. Klimeš and A. Michaelides, J. Chem. Phys., 2012, 137, 120901.
5. D. Wu and D. G. Truhlar, J. Chem. Theory Comput., 2021, 17, 3967–3973.
6. J. Řezáč and P. Hobza, Chem. Rev., 2016, 116, 5038–5071.
7. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
8. A. D. Becke, Phys. Rev. A., 1988, 38, 3098–3100.
9. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
10. G. I. Csonka, J. P. Perdew and A. Ruzsinszky, J. Chem. Theory Comput., 2010, 6, 3688–3703.
11. Q. Wu and W. Yang, J. Chem. Phys., 2002, 116, 515–524.
12. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
13. E. Brémond, I. Ciofini, J. C. Sancho-García and C. Adamo, Acc. Chem. Res., 2016, 49, 1503–1513.
14. L. Goerigk and S. Grimme, WIREs: Comput. Mol. Sci., 2014, 4, 576–600.
15. E. Brémond, M. Savarese, A. J. Perez-Jimenez, J. C. Sancho-Garcia and C. Adamo, J. Phys. Chem. Lett., 2015, 6, 3540–3545.
16. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2007, 9, 3397–3406.
17. J. C. Sancho-García, E. Brémond, M. Savarese, A. J. Pérez-Jiménez and C. Adamo, Phys. Chem. Chem. Phys., 2017, 19, 13481–13487.
18. S. Kozuch and J. M. L. Martin, Phys. Chem. Chem. Phys., 2011, 13, 20104.
19. G. Santra, N. Sylvetsky and J. M. L. Martin, J. Phys. Chem. A, 2019, 123, 5129–5143.
20. J. Sanz García, E. B. Rémond, M. C. Ampetella, I. C. Iofini and C. A. Damo, J. Chem. Theory Comput., 2019, 15, 2944–2953.
21. E. Brémond, J. C. Sancho-García, A. J. Pérez-Jiménez and C. Adamo, J. Chem. Phys., 2014, 141, 031101.
22. L. Gráfová, M. Pitoňák, J. Řezáč and P. Hobza, J. Chem. Theory Comput, 2010, 6, 2365–2376.
23. J. Řezáč, K. E. Riley and P. Hobza, J. Chem. Theory Comput, 2011, 7, 2427–2438.
24. R. Sedlak, T. Janowski, M. Pitoňák, J. Řezáč, P. Pulay and P. Hobza, J. Chem. Theory Comput., 2013, 9, 3364–3374.
25. Z. Ni, Y. Guo, F. Neese, W. Li and S. Li, J. Chem. Theory Comput., 2021, 17, 756–766.
26. H. Li, B. Tirri, E. Brémond, J. C. Sancho-García and C. Adamo, J. Org. Chem., 2021, 86, 5538–5545.
27. E. Brémond, I. Ciofini, J. C. Sancho-García and C. Adamo, J. Phys. Chem. A, 2019, 123, 10040–10046.
28. E. Brémond, H. Li, J. C. Sancho-García and C. Adamo, J. Phys. Chem. A, 2022, 126, 2590–2599.
29. M. Biczysko, P. Panek, G. Scalmani, J. Bloino and V. Barone, J. Chem. Theory Comput., 2010, 6, 2115–2125.
30. A. Charaf-Eddin, A. Planchat, B. Mennucci, C. Adamo and D. Jacquemin, J. Chem. Theory Comput., 2013, 9, 2749–2760.
31. E. Solel, M. Ruth and P. R. Schreiner, J. Am. Chem. Soc., 2021, 143, 20837–20848.
32. E. Solel, M. Ruth and P. R. Schreiner, J. Org. Chem., 2021, 86, 7701–7713.
33. A. A. Fokin, T. S. Zhuk, S. Blomeyer, C. Pérez, L. V. Chernish, A. E. Pashenko, J. Antony, Y. V. Vishnevskiy, R. J. F. Berger, S. Grimme, C. Logemann, M. Schnell, N. W. Mitzel and P. R. Schreiner, J. Am. Chem. Soc., 2017, 139, 16696–16707.
34. V. Gorbachev, A. Tsybizova, L. Miloglyadova and P. Chen, J. Am. Chem. Soc., 2022, 144, 9007–9022.
35. S. Winstein and N. J. Holness, J. Am. Chem. Soc., 1955, 77, 5562–5578.
36. F. R. Jensen, C. H. Bushweller and B. H. Beck, J. Am. Chem. Soc., 1969, 91, 344–351.
37. F. A. Carroll, Perspectives on Structure and Mechanism in Organic Chemistry, 3rd edn, John Wiley & Sons, Inc, Hoboken, NJ, USA, 2023.
38. R. Bjornsson and I. Arnason, Phys. Chem. Chem. Phys., 2009, 11, 8689.
39. C. Silva Lopez, O. Nieto Faza, F. De Proft and A. Kolocouris, J. Comput. Chem., 2016, 37, 2647–2658.
40. Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101.
41. Y. Wang, X. Jin, H. S. Yu, D. G. Truhlar and X. He, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 8487–8492.
42. N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111.
43. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
44. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
45. N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2015, 142, 074111.
46. O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103.
47. A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377.
48. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
49. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
50. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
51. Y. Wang, P. Verma, X. Jin, D. G. Truhlar and X. He, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 10257–10262.
52. H. S. Yu, X. He, S. L. Li and D. G. Truhlar, Chem. Sci., 2016, 7, 5032–5051.
53. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600.
54. A. Austin, G. A. Petersson, M. J. Frisch, F. J. Dobek, G. Scalmani and K. A. Throssell, J. Chem. Theory Comput., 2012, 8, 4989–5007.
55. A. D. Boese and J. M. L. Martin, J. Chem. Phys., 2004, 121, 3405–3416.
56. N. Mardirossian and M. Head-Gordon, J. Chem. Phys., 2016, 144, 214110.
57. N. Mardirossian and M. Head-Gordon, Phys. Chem. Chem. Phys., 2014, 16, 9904.
58. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
59. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615.
60. R. Peverati and D. G. Truhlar, J. Phys. Chem. Lett., 2011, 2, 2810–2817.
61. E. Brémond and C. Adamo, J. Chem. Phys., 2011, 135, 024106.
62. S. Grimme, J. Chem. Phys., 2006, 124, 034108.
63. T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 4398.
64. E. Brémond, J. C. Sancho-García, A. J. Pérez-Jiménez and C. Adamo, J. Chem. Phys., 2014, 141, 031101.
65. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, J. Chem. Phys., 2019, 150, 154122.
66. V. K. Prasad, A. Otero-de-la-Roza and G. A. DiLabio, J. Chem. Theory Comput., 2022, 18, 2913–2930.
67. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian GDV, Revision J.01, Gaussian, Inc., Wallingford CT, 2016.
68. J. Řezáč and P. Hobza, J. Chem. Theory Comput., 2013, 9, 2151–2155.
69. F. Neese and E. F. Valeev, J. Chem. Theory Comput., 2011, 7, 33.
70. M. Saitow, U. Becker, C. Riplinger, E. F. Valeev and F. Neese, J. Chem. Phys., 2016, 146, 164105.
71. J. Calbo, J. C. Sancho-García, E. Ortí and J. Aragó, J. Comput. Chem., 2017, 38, 1869–1878.
72. G. Santra and J. M. L. Martin, J. Phys. Chem. A, 2022, 126, 9375–9391.
73. S. Grimme, L. Goerigk and R. F. Fink, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 886–906.
74. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
75. A. Halkier, T. Helgaker, P. Jørgensen, W. Klopper, H. Koch, J. Olsen and A. K. Wilson, Chem. Phys. Lett., 1998, 286, 243–252.
76. I. Sandler, J. Chen, M. Taylor, S. Sharma and J. Ho, J. Phys. Chem. A, 2021, 125, 1553–1563.
77. D. G. A. Smith, P. Jankowski, M. Slawik, H. A. Witek and K. Patkowski, J. Chem. Theory Comput., 2014, 10, 3140–3150.
78. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2007, 127, 154108.
79. N. Mardirossian and M. Head-Gordon, Mol. Phys., 2017, 115, 2315–2372.
80. C. J. Nickerson, K. R. Bryenton, A. J. A. Price and E. R. Johnson, J. Phys. Chem. A, 2023, 127, 8712–8722.
81. J. Řezáč, Phys. Chem. Chem. Phys., 2022, 24, 14780–14793.
82. L. Goerigk, J. Phys. Chem. Lett., 2015, 6, 3891–3896.
83. E. Brémond, M. Savarese, N. Q. Su, A. J. Pérez-Jiménez, X. Xu, J. C. Sancho-García and C. Adamo, J. Chem. Theory Comput., 2016, 12, 459–465.
84. G. Ceselin, V. Barone and N. Tasinato, J. Chem. Theory Comput., 2021, 17, 7290–7311.
85. E. L. Eliel and S. H. Wilen, Stereo Chemistry of Organic Compounds, John Wiley & Sons Inc, New York, 1994, pp. 696–697.
86. S. Grimme, M. Steinmetz and M. Korth, J. Org. Chem., 2007, 72, 2118–2126.
87. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06141h

---