Pressure and temperature dependent kinetics and the reaction mechanism of Criegee intermediates with vinyl alcohol: a theoretical study

Abstract

Criegee intermediates (CIs), the key intermediates in the ozonolysis of olefins in atmosphere, have received much attention due to their high activity. The reaction mechanism of the most simple Criegee intermediate CH₂OO with vinyl alcohol (VA) was investigated by using the HL//M06-2X/def2TZVP method. The temperature and pressure dependent rate constant and product branching ratio were calculated using the master equation method. For CH₂OO + syn-VA, 1,4-insertion is the main reaction channel while for the CH₂OO + anti-VA, cycloaddition and 1,2-insertion into the O–H bond are more favorable than the 1,4-insertion reaction. The 1,4-insertion or cycloaddition intermediates are stabilized collisionally at 300 K and 760 torr, and the dissociation products involving OH are formed at higher temperature and lower pressure. The rate constants of the CH₂OO reaction with syn-VA and anti-VA both show negative temperature effects, and they are 2.95 × 10⁻¹¹ and 2.07 × 10⁻¹³ cm³ molecule⁻¹ s⁻¹ at 300 K, respectively, and the former is agreement with the prediction in the literature.

---

1. Introduction

Criegee intermediates (CIs) are also known as carbonyl oxides, the atmospheric intermediates produced in the oxidation of unsaturated hydrocarbons with ozone. In the ozonolysis reactions, the CI is formed vibrationally excited, and the energized CI will undergo rapid unimolecular decomposition or be stabilized collisionally and eventually be lost through bimolecular reactions or UV photolysis.^1,2

Criegee intermediates may affect the oxidative capacity of the atmosphere by producing OH^3–7 and influencing the tropospheric HO_x budget, and they also play an important role in the formation of atmospheric aerosols^8,9 by reaction with SO₂,^10,11 which is an important gas-phase source of low-volatility sulfuric acid. As a 1,3-bipole radical with zwitterionic character, a Criegee intermediate can react with H₂O,^12–14 (H₂O)₂^14,15 NH₃,^16,17 alkane,^18–20 atmospheric organic and inorganic acids acids^21–26 and alcohols^27–31via an insertion reaction, or react with SO₂,^32,33 carbonyl compounds,^34–37 and alkenes³⁸via a cycloaddition reaction, or be associated with other 1,3-bipoles, such as ozone or carbonyl oxides.^39–42

The major loss paths for Criegee intermediates are assumed to be the reactions with water vapor, which is ubiquitous throughout the troposphere while the CI reaction with H₂O is slow, and the rate constant is about 10⁻¹⁵–10⁻¹⁶ cm³ molecule⁻¹ s⁻¹.^43,44 The reaction of CIs + alcohols has a similar 1,2-insertion mechanism to that of CIs + H₂O, and the measured rate constants³¹ by experiment for the simplest Criegee intermediate (CH₂OO) with methanol, ethanol, and 2-propanol are (1.4 ± 0.4) × 10⁻¹³, (2.3 ± 0.6) × 10⁻¹³, and (1.9 ± 0.5) × 10⁻¹³ cm³ molecule⁻¹ s⁻¹. Vereecken²² investigated the reaction of CH₂OO with HNO₃ and HCOOH, and found that a 1,4-insertion mechanism allows for barrierless reactions with high rate constants up to ∼10⁻¹⁰ cm³ molecule⁻¹ s⁻¹. He determined that the 1,4-insertion mechanism relies on the presence of a double bond in the α-position to the acidic OH group. The reactions of CI with enols were predicated to likewise react through the 1,4-insertion mechanism, with the rate constant exceeding 10⁻¹¹ cm³ molecule⁻¹ s⁻¹. Thus, the CH₂OO reaction with enols by 1,4-insertion will be much faster than with H₂O, methanol, ethanol, etc. using the 1,2-insertion mechanism.

Vinyl alcohol (VA) is the simplest enol, with high reactivity in atmospheric and combustion chemistry;⁴⁵ it has been implicated as a precursor to atmospheric carboxylic acids.^46–49 The main atmospheric decay channel of vinyl alcohol is the reaction with the OH radical, which has been incorporated into the atmospheric chemistry box model estimating the contribution of photo-tautomerization of acetaldehyde to the worldwide formic acid production.⁴⁹ Since organic acids are key species in the formation of secondary organic aerosol, the investigation on the bimolecular reaction of vinyl alcohol is of potential importance. Furthermore, the rate constant of VA + CH₂OO may be comparable or even faster than that of VA + OH (1.48 × 10⁻¹¹).⁵⁰ Under natural conditions, vinyl alcohol has two conformers, syn-VA and anti-VA, and the calculated syn/anti ratio is 85 : 15 at 300 K.⁴⁵ As shown in Scheme 1, both syn-VA and anti-VA display Cs symmetry. Theoretical study shows that the favorable OH-addition site for syn-VA is β-C, while for the anti-VA, the favorable OH-addition site is α-C.⁵⁰ Likewise, are the main reaction channels for CH₂OO with syn-VA and anti-VA both 1,4-insertion, or are there different mechanisms?

Scheme 1 Conformers of syn-VA and anti-VA.

In this work, we studied the detailed reaction mechanism of CH₂OO with vinyl alcohol (syn and anti), including 1,4-insertion over the C=C–OH moiety, 1,2-insertion into the C–H or O–H bond, and cycloaddition across the C=C double bond. The rate constants and products’ branching ratios were calculated using the master equation (ME) method, to determine the product distributions at different temperatures and pressures.

2. Computational method

2.1 Electronic structure calculations

The geometries of the reactants, pre-reactive complexes, transition states, and products of the title reaction were optimized at the M06-2X/def2TZVP level of theory. The harmonic vibration frequency was calculated at the same level of theory to obtain the zero-point energy (ZPE) and to verify the nature (minima or saddle points) of the stationary points. All transition states discussed in this work were verified by intrinsic reaction coordinate (IRC) calculations to identify the reactants and products. The single-point energies of all stationary points were then refined by a higher-level (denoted as HL) single-point energy calculation method. The HL energies were obtained via a combination of coupled cluster calculations with perturbative inclusion of the triplet contribution, CCSD(T),⁵¹ and second order Moller–Plesset perturbation theory (MP2).^52,53 The complete basis set limit energy was estimated by the extrapolation of results obtained for sequences of the correlation-consistent polarized-valence basis sets. The expression for this method can be as follows:

E_HL = E[CCSD(T)/cc-pVTZ] + (E[CCSD(T)/cc-pVTZ] − E[CCSD(T)/cc-pVDZ]) × 0.46286 + E[MP2(FC)/cc-pVQZ] + (E[MP2(FC)/cc-pVQZ] − E[MP2(FC)/cc-pVTZ]) × 0.69377 − E[MP2(FC)/cc-pVTZ] − (E[MP2(FC)/cc-pVTZ] − E[MP2(FC)/cc-pVDZ]) × 0.46286

The HL method has been verified to be accurate for both closed shell and open shell species’ calculations.^54,55 The rate constants of Criegee intermediates with acrolein and C₂H₄ reactions^35,56 based on the HL potential energy surface have been proved to be consistent with experimental results. All the electronic structure and energetic calculations were carried out using the Gaussian 09 program package.⁵⁷

2.2 Kinetic calculations

The rate constant and products’ branching ratios were calculated using the master equation method,^58–62 which is a powerful tool for calculating the temperature and pressure dependent kinetics of a multiple-channel and multiple-well chemical reaction system. Energy transfer is treated with the single exponential down model with ΔE_down = 200 cm⁻¹. The Lennard-Jones (L-J) parameters of the intermediates C₃O₃H₆ (σ = 6.0 Å and ε/k_b = 450 K) are taken from ref. 63 and the L-J parameters of N₂ are taken as σ = 3.9 Å and ε/k_b = 48 K.⁵⁸ In order to evaluate the sensitivity of the results for the L-J parameters of the intermediates, σ = 4.5 Å and ε/k_b = 350 K²² are used to recalculated the rate constant for comparison, and the results show no obvious change. In this study, the master equation was solved by an ordinary differential equation (ODE) solver to develop directly the number population of the species with time.^64–66 The populations of species as functions of time can be obtained directly and the first-order rate constants can be extracted from the reactant population using the “exponential decay” approach. More details and test cases can be found in ref. 55 and 66–68. All the kinetic calculations were carried out by using TheRate program.⁶⁹

3. Results and discussion

3.1. Reaction mechanism of CH₂OO + syn-VA

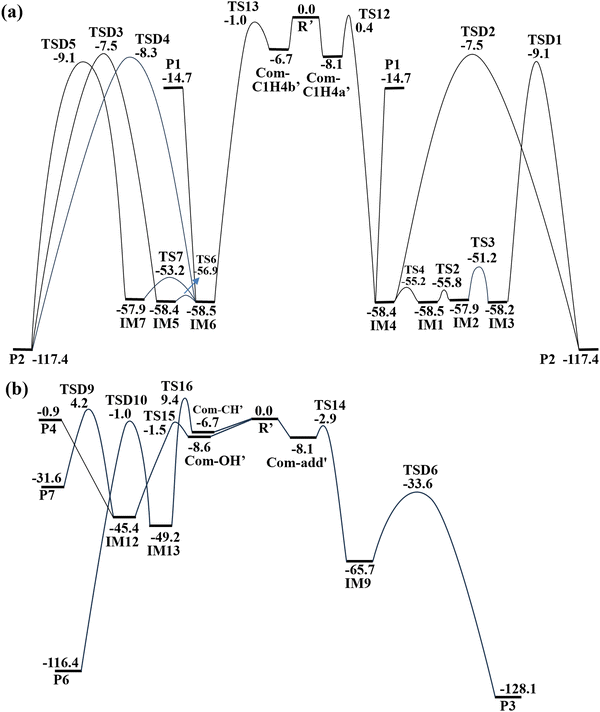
The optimized geometries of pre-reactive complexes, transition states, intermediates, and products are shown in Fig. 1 and 2. The PES for the CH₂OO + syn-VA reaction is portrayed in Fig. 3. All the reaction channels initiate from the pre-reactive complex, and they are named Com-C1H4a (Com-C1H4b) for the 1,4-insertion reaction, Com-add for the cycloaddition reaction, Com-OH and Com-CH for the O–H and C–H 1,2-insertion reaction, respectively.

Fig. 1 The optimized geometries of stationary points in 1,4-insertion reactions for the CH₂OO + syn-VA reaction. (a) Channel initiates from Com-C1H4a; (b) Channel initiates from Com-C1H4b.

Fig. 2 The optimized geometries of stationary points for the CH₂OO + syn-VA reaction. (a) Cycloaddition reaction; (b) 1,2-insertion reaction in O–H and C–H bonds.

Fig. 3 PES of CH₂OO + syn-VA reaction at the HL//M06-2X/def2TZVP level of theory. The relative energies are given in kcal mol⁻¹. (a) 1,4-insertion reaction; (b) cycloaddition and 1,2-insertion reactions in O–H and C–H bonds.

For the 1,4-insertion reaction over the C=C–OH moiety, the CH₂OO carbon atom and the terminal oxygen atom approaches the β-C and the hydroxyl H atom of syn-VA respectively, forming the pre-reactive complexes Com-C1H4a and Com-C1H4b, which are 7.5 and 9.0 kcal mol⁻¹ more stable than the free reactants. In Com-C1H4a, the central oxygen atom (O9) of CH₂OO lies on the same side with hydroxyl O atom (O3) of syn-VA, while in Com-C1H4b, they lie on the opposite side.

As shown in Fig. 1(a) and 3(a), starting from Com-C1H4a, the CH₂OO carbon atom attacks β-C and the hydroxyl H atom shifts to the terminal oxygen of CH₂OO forming the intermediate IM1 (3-hydroperoxy-propanal), the relative energies of TS1 and IM1 are −5.7 and −57.5 kcal mol⁻¹. The energized 3-hydroperoxy-propanal can dissociate directly to CHOCH₂CH₂O + OH (P1, −13.7 kcal mol⁻¹), or it will proceed via two different isomerization and decomposition pathways to form the same product P2 (H₂O + malondialdehyde). Firstly, IM1 isomerizes to IM3 by the rotation of –CHO (TS2, −54.8 kcal mol⁻¹) and –OH groups (TS3, −50.2 kcal mol⁻¹), and then decomposes to P2 by the dissociation of the O9–O10 bond accompanied by H11 shifting from C8 to O10 (TSD1, −8.2 kcal mol⁻¹). Secondly, IM1 isomerizes to IM4 by the molecular skeleton rotation (TS4, −54.3 kcal mol⁻¹) to facilitate the subsequent H1 atom shift from C8 to O10, and then decomposes to P2 by H shift and O–O bond fission (TSD2, −6.5 kcal mol⁻¹). The relative energies of the local minima IM2, IM3, IM4, and P2 are −57.0, −57.2, −57.4, and −116.4 kcal mol⁻¹, respectively. The dissociation to CHOCH₂CH₂O + OH may be energetically more favorable due to the high-energy TSD1 and TSD2 in the formation of H₂O + malondialdehyde.

As shown in Fig. 1(b) and 3(a), starting from Com-C1H4b, the 1,4-insertion of CH₂OO over C=C–OH moiety forms the intermediate IM5 via TS5, the respective relative energy of TS5 and IM5 are −5.6 and −57.4 kcal mol⁻¹. IM5 can isomerize to IM6 (−57.5 kcal mol⁻¹) by rotation of –CHO and –OH (TS6, −55.9 kcal mol⁻¹), and IM6 then isomerizes to IM7 (−57.0 kcal mol⁻¹) by molecular skeleton rotation (TS7, −52.2 kcal mol⁻¹). IM5, IM6, and IM7 can all decompose to H₂O and malondialdehyde, and the relative energies of the corresponding transition state TSD3, TSD4, and TSD5 are −6.5, −7.3 and −8.2 kcal mol⁻¹, respectively. Likewise, IM5 can also form CHOCH₂CH₂O + OH by direct dissociation.

For the cycloaddition reaction on the C=C double bond, the formation of a five-membered adduct IM8 (−62.8 kcal mol⁻¹) needs to overcome an energy barrier of 0.7 kcal mol⁻¹. As shown in Fig. 2(a), IM8 isomerizes to IM9 (−64.7 kcal mol⁻¹) by the –OH group rotation around C–O bond (TS9), and then IM9 decomposes to products aldehyde and formic acid (P3, −127.1 kcal mol⁻¹) by C1–C2 bond breakage and H12 migration from C8 to C1. It is worth mentioning that the electronic energy of TS9 is only 0.02 kcal mol⁻¹ higher than that of IM8, and the PES from IM8 to TS9 is very flat, which leads to the sum of electronic and zero-point energies of TS9 being slightly lower than IM8. Therefore, only the electronic portion is used to compute the relative height of TS9 to IM8 in this work. For clarity, the relative energy values of IM8 and TS9 in Fig. 3 are kept to two decimal places. The vector of the imaginary frequency in TS9 is the OH rotation around the C–O bond (Fig. S1, ESI†), and the dihedral angle C1C2O3H4 is 73.0, 80.8, and 164.2° in IM8, TS9, and IM9, respectively. The Cartesian coordinates of IM8 and TS9 are shown in the ESI† (Table S1).

The 1,2-insertion in the O–H bond is a barrierless pathway leading to IM10 with 42.9 kcal mol⁻¹ exoergicity, IM10 may decompose directly to CH₂CHOCH₂O + OH (P4, 0.1 kcal mol⁻¹), or form CH₂OHCHO + HCHO (P5, −99.3 kcal mol⁻¹) via the O3–C8 bond breakage and O10H4 shift from O9 to C1. The 1,2-insertion in the C–H bond needs to overcome the 9.6 kcal mol⁻¹ energy barrier, so it has a negligible contribution compared to other channels.

Comparing the PESs of all the channels in the CH₂OO + syn-VA reactions (Fig. 3), we found that all the stationary points in the 1,4-insertion reaction lie below the reactants, and the entrance is barrierless for the 1,4-insertion reaction and 1,2-insertion in the O–H bond. So the 1,4-insertion reaction is more competitive than other channels.

3.2. Reaction mechanism of CH₂OO + anti-VA

The optimized geometries of the stationary points in CH₂OO + anti-VA reaction are shown in Fig. 4, and the PES are shown in Fig. 5. Similar to the CH₂OO + syn-VA reaction, all the reaction channels initiate from the pre-reactive complex, and the corresponding complexes are named Com-C1H4a′ (Com-C1H4b′), Com-add′, Com-OH′ and Com-CH′, respectively.

Fig. 4 The optimized geometries of stationary points for the CH₂OO + anti-VA reaction.

Fig. 5 PES of the CH₂OO + anti-VA reaction at the HL//M06-2X/def2TZVP level of theory. The relative energies are given in kcal mol⁻¹. (a) 1,4-insertion reactions; (b) cycloaddition and 1,2-insertion reaction in O–H and C–H bonds.

Starting from Com-C1H4a′ and Com-C1H4b′, the 1,4-insertion of CH₂OO into anti-VA forms the intermediates IM4 and IM6, respectively. Both IM4 and IM6 can dissociate directly to CHOCH₂CH₂O + OH. IM4 can isomerize to IM1, IM2, and IM3 successively, IM6 can isomerize to IM5 or IM7, and then IM3, IM4, IM5, IM6, and IM7 decomposes to the product P2 (H₂O + malondialdehyde). The cycloaddition reaction of CH₂OO + anti-VA forms the adducts IM9 firstly, and IM9 can decompose to the product P3 via TSD6. The optimized structures of IM1–IM9, and their isomerization and dissociation processes have been described in detail in the CH₂OO + syn-VA reaction. The O–H and C–H 1,2-insertion reaction results in the formation of respective intermediates IM12 and IM13 and decomposition to the corresponding products P4 (or P7) and P6.

From Fig. 5 we can see that the energies of the stationary points in the cycloaddition and 1,4-insertion reaction are obviously lower than those in other channels. In addition, TS14 (−2.9 kcal mol⁻¹) in the entrance channel of cycloaddition has lower energy than TS12 and TS13 (0.4 and −1.0 kcal mol⁻¹) in the 1,4-insertion reaction. So, the cycloaddition may be favorable in the CH₂OO + anti-VA reaction, which is different from the CH₂OO + syn-VA reaction.

3.3. Kinetic calculations

The master equation calculations were carried out at the pressure range of 1–760 torr and the temperature range of 200–500 K. According to the reaction PESs, the 1,4-insertion reaction, cycloaddition reaction, and 1,2-insertion reaction in O–H are involved in the master equation calculation, while the 1,2-insertion reaction in C–H bond are excluded because of its higher reaction energy barrier. The calculated TS from the pre-reactive complex is approximately taken as the bottleneck for the present reaction system. The reactants are assumed to be in fast equilibrium with the pre-reactive complex (C), and the rate constant of C → P is much smaller than that of C → CH₂OO + vinyl alcohol, like the treatment in a barrierless entrance reaction system.^70–72

3.3.1 Rate constants. The calculation results show that the rate constants are pressure independent. Fig. 6 portrays the rate constants of CH₂OO + syn-VA and CH₂OO + anti-VA at 200–500 K and 760 torr, and the values are listed in Table 1. We can see that the rate constants decline with the increase of the temperature, i.e., they show negative temperature effects, and this results from their barrierless entrance step. At 300 K and 760 torr, the rate constants of CH₂OO + syn-VA and CH₂OO + anti-VA are 2.95 × 10⁻¹¹ and 2.07 × 10⁻¹³ cm³ molecule⁻¹ s⁻¹, respectively. Vereecken has predicted that the rate constant of CI + VA should easily exceed 1 × 10⁻¹¹ cm³ molecule⁻¹ s⁻¹, which is agreement with our calculation results of CH₂OO + syn-VA. The traditional transition state theory (TST) is used to calculate the rate constants of each entrance channel, and the overall rate constants (Table S2, ESI†) are consistent with those calculated by the master equation method.

Fig. 6 The rate constants of the CH₂OO + syn-VA and CH₂OO + anti-VA reactions at 200–500 K and 760 torr.

Table 1 Values of the rate constants k (in cm³ molecule⁻¹ s⁻¹) for the CH₂OO + VA reaction at 200–500 K and 760 torr

Temperature	200	250	300	350	400	450	500
k (CH2OO + syn-VA)	3.44 × 10^−9	1.92 × 10^−10	2.95 × 10^−11	8.05 × 10^−12	3.14 × 10^−12	3.14 × 10^−12	3.14 × 10^−12
k (CH2OO + anti-VA)	2.15 × 10^−12	5.01 × 10^−13	2.07 × 10^−13	1.17 × 10^−13	8.04 × 10^−14	6.22 × 10^−14	5.23 × 10^−14

---

3.3.2 Products’ branching ratios. For the 1,4-insertion intermediate, the direct dissociation to CHOCH₂CH₂O + OH may be more competitive than the formation of malondialdehyde + H₂O.^22,73 However, this ratio is hard to estimate due to the direct dissociation to CHOCH₂CH₂O + OH without a well-defined transition state. So we located the approximate minimum energy path (MEP) and determined the minima of the TST rate constants along the MEP. The corresponding structure of the minima of TST rate constants was taken as the variational transition state and used to the subsequent master equation calculation to evaluate the product distribution. This is similar to the variational approach applied to the barrierless reactions by Lin et al.^74,75 The location of minimum energy path and the variation of TST rate constants for the dissociation process are given in Fig. S2 (ESI†).

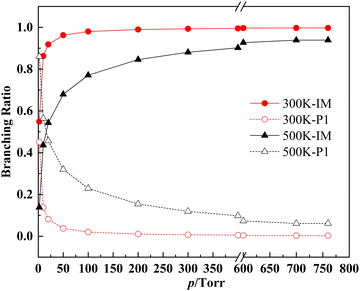
For the CH₂OO + syn-VA reaction, the calculation results show that the both the 1,2-insertion and the cycloaddition reaction are negligible compared to the 1,4-insertion reaction. As shown in Fig. 7 and 8, the domain product is the 1,4-insertion intermediate (3-hydroperoxy-propanal) thermalized in collisions with the bath gas at 300 K and 760 torr. The pressure dependence of the products’ branching ratios is obvious at lower pressure ranges. The intermediates IM1–IM7 are shown in Fig. 7 as a whole for clarity, and the individual branching ratios for IM1–IM7 at 300 K and 1 torr, 100 torr and 760 torr are shown in Fig. 8. The ratios of IM1–IM7 are in the order IM6 > IM1 > IM4 > IM5 > IM3 > IM2 > IM7, which are determined by their relative energies (−57.5, −57.5, −57.4, −57.4, −57.2, −57.0, and −57.0 kcal mol⁻¹). The 1,4-insertion intermediate decomposes to CHOCH₂CH₂O + OH at higher temperature and lower pressure, and the products malondialdehyde + H₂O are negligible.

Fig. 7 The branching ratios of the products for the CH₂OO + syn-VA reaction.

Fig. 8 The branching ratios of the IM1–IM7 in the CH₂OO + syn-VA reaction at 300 K and 1 torr, 100 torr and 760 torr.

The products’ branching ratios of the CH₂OO + anti-VA reaction are shown in Fig. 9. The dominant product is the cycloaddition intermediate IM9, and it dissociates to P3 (aldehyde and formic acid) gradually with the increase of temperature and the decrease of pressure, and, in the meanwhile, the direct dissociation product P4 (CH₂CHOCH₂O + OH) of the O–H 1,2-insertion intermediate IM12 has a significant contribution.

Fig. 9 The branching ratios of the products for the CH₂OO + anti-VA reaction.

Combining the PESs and the kinetic characters of the two reactions, we find that the 1,4-insertion dominated the CH₂OO + syn-VA reaction, while the cycloaddition and O–H 1,2-insertion are more favorable in the CH₂OO + anti-VA reaction. At 300 K and 760 torr, the 1,4-insertion or cycloaddition intermediates are the main products. At higher temperature and lower pressure, the 1,4-insertion intermediate tends to decompose to CHOCH₂CH₂O + OH, so the reaction can be regarded as the OH reservoir, and affect the HO_x budget, thereby having a potential impact on the oxidative capacity of the atmosphere. In addition, the reaction of CH₂OO with vinyl alcohol is significantly faster than CH₂OO + saturated alcohol (∼10⁻¹³ cm³ molecule⁻¹ s⁻¹),³¹ and is comparable to the OH + vinyl alcohol reaction (1.48 × 10⁻¹¹),⁵⁰ due to the zwitterionic character of CH₂OO and special structure of vinyl alcohol, with a double bond in the α-position of the OH group. So this reaction may be an important loss process for both Criegee intermediate and vinyl alcohol.

4. Conclusions

The reaction mechanism of CH₂OO with vinyl alcohol has been investigated at the HL//M06-2X/def2TZVP level of theory. The calculation results of the master equation method reveal the temperature and pressure dependent kinetic characters. The following conclusions can be drawn. (1) The 1,4-insertion reaction is the main channel for the CH₂OO + syn-VA reaction, while the cycloaddition is more competitive in the CH₂OO + anti-VA reaction. (2) The rate constants are 2.95 × 10⁻¹¹ and 2.07 × 10⁻¹³ cm³ molecule⁻¹ s⁻¹ for CH₂OO + syn-VA and CH₂OO + anti-VA reactions at 300 K and 760 torr, and both show negative temperature effects at 200–500 K. (3) The product distribution is temperature and pressure dependent. At 300 K and 760 torr, the 3-hydroperoxy-propanal formed by 1,4-insertion in the CH₂OO + syn-VA reaction and the cycloaddition intermediate in the CH₂OO + anti-VA reaction are main products. At higher temperature and lower pressure, 3-hydroperoxy-propanal dissociates to CHOCH₂CH₂O + OH, and cycloaddition intermediate decomposes to aldehyde and formic acid; in the meanwhile, CH₂CHOCH₂O + OH are formed by the dissociation of 1,2-insertion (in O-H bond) intermediate in CH₂OO + anti-VA reaction.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the National Natural Science Foundation of China (No. 21603152), the Natural Science Foundation of Hebei Province (B2022205022), and the Science Research Project of Hebei Education Department (ZD2022157). We would also like to thank professor S. W. Zhang for providing technical support on the kinetic calculation of the CH₂OO + vinyl alcohol reaction.

References

1. P. Neeb, O. Horie and G. K. Moortgat, J. Phys. Chem. A, 1998, 102, 6778–6785.
2. D. Johnson and G. Marston, Chem. Soc. Rev., 2008, 37, 699–716.
3. K. Samanta, J. M. Beames, M. I. Lester and J. E. Subotnik, J. Chem. Phys., 2014, 141, 134303.
4. F. Liu, J. M. Beames, A. S. Petit, A. B. McCoy and M. I. Lester, Science, 2014, 345, 1596–1598.
5. A. Novelli, L. Vereecken, J. Lelieveld and H. Harder, Phys. Chem. Chem. Phys., 2014, 16, 19941–19951.
6. M. I. Lester and S. J. Klippenstein, Acc. Chem. Res., 2018, 51, 978–985.
7. V. P. Barber, S. Pandit, A. M. Green, N. Trongsiriwat, P. J. Walsh, S. J. Klippenstein and M. I. Lester, J. Am. Chem. Soc., 2018, 140, 10866–10880.
8. Y. Gong and Z. Chen, Atmos. Chem. Phys., 2021, 21, 813–829.
9. F. Bianchi, J. Tröstl, H. Junninen, C. Frege, S. Henne, C. R. Hoyle, U. Molteni, E. Herrmann, A. Adamov, N. Bukowiecki, X. Chen, J. Duplissy, M. Gysel, M. Hutterli, J. Kangasluoma, J. Kontkanen, A. Kürten, H. E. Manninen, S. Münch, O. Peräkylä, T. Petäjä, L. Rondo, C. Williamson, E. Weingartner, J. Curtius, D. R. Worsnop, M. Kulmala, J. Dommen and U. Baltensperger, Science, 2016, 352, 1109–1112.
10. H.-L. Huang, W. Chao and J. J.-M. Lin, Proc. Natl. Acad. Sci., 2015, 112, 10857–10862.
11. L. Vereecken, Science, 2013, 340, 154–155.
12. Y.-J. Wu, K. Takahashi and J. J.-M. Lin, J. Phys. Chem. A, 2023, 127, 8059–8072.
13. B. Long, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2016, 138, 14409–14422.
14. L.-C. Lin, H.-T. Chang, C.-H. Chang, W. Chao, M. C. Smith, C.-H. Chang, J. J.-M. Lin and K. Takahashi, Phys. Chem. Chem. Phys., 2016, 18, 4557–4568.
15. W. Chao, J.-T. Hsieh, C.-H. Chang and J. J.-M. Lin, Science, 2015, 347, 751–754.
16. A. Nazari and V. Saheb, Theor. Chem. Acc., 2022, 141, 66.
17. B. Long, Y. Wang, Y. Xia, X. He, J. L. Bao and D. G. Truhlar, J. Am. Chem. Soc., 2021, 143, 8402–8413.
18. K. Xu, W. Wang, W. Wei, W. Feng, Q. Sun and P. Li, J. Phys. Chem. A, 2017, 121, 7236–7245.
19. T. V. T. Mai, M. v Duong, H. T. Nguyen, K. C. Lin and L. K. Huynh, Chem. Phys. Lett., 2018, 706, 280–284.
20. L. Franzon, J. Peltola, R. Valiev, N. Vuorio, T. Kurtén and A. Eskola, J. Phys. Chem. A, 2023, 127, 477–488.
21. O. Welz, A. J. Eskola, L. Sheps, B. Rotavera, J. D. Savee, A. M. Scheer, D. L. Osborn, D. Lowe, A. Murray Booth, P. Xiao, H. K. M. Anwar, C. J. Percival, D. E. Shallcross and C. A. Taatjes, Angew. Chem., Int. Ed., 2014, 53, 4547–4750.
22. L. Vereecken, Phys. Chem. Chem. Phys., 2017, 19, 28630–28640.
23. E. S. Foreman, K. M. Kapnas and C. Murray, Angew. Chem., Int. Ed., 2016, 55, 10419–10422.
24. R. Chhantyal-Pun, M. R. McGillen, J. M. Beames, M. A. H. Khan, C. J. Percival, D. E. Shallcross and A. J. Orr-Ewing, Angew. Chem., Int. Ed., 2017, 56, 9044–9047.
25. P. Raghunath, Y. P. Lee and M. C. Lin, J. Phys. Chem. A, 2017, 121, 3871–3878.
26. C. A. Chung, J. W. Su and Y. P. Lee, Phys. Chem. Chem. Phys., 2019, 21, 21445–21455.
27. W. Chao, Y.-H. Lin, C. Yin, W.-H. Lin, K. Takahashi and J. J.-M. Lin, Phys. Chem. Chem. Phys., 2019, 21, 13633–13640.
28. S. Enami and A. J. Colussi, J. Phys. Chem. A, 2017, 121, 5175–5182.
29. M. R. McGillen, B. F. E. Curchod, R. Chhantyal-Pun, J. M. Beames, N. Watson, M. A. H. Khan, L. McMahon, D. E. Shallcross and A. J. Orr-Ewing, ACS Earth Space Chem., 2017, 1, 664–672.
30. Y.-H. Lin, C. Yin, W.-H. Lin, Y.-L. Li, K. Takahashi and J. J.-M. Lin, J. Phys. Chem. Lett., 2018, 9, 7040–7044.
31. S. V. Tadayon, E. S. Foreman and C. Murray, J. Phys. Chem. A, 2018, 122, 258–268.
32. L. Vereecken, H. Harder and A. Novelli, Phys. Chem. Chem. Phys., 2012, 14, 14682–14695.
33. N. U. M. Howes, Z. S. Mir, M. A. Blitz, S. Hardman, T. R. Lewis, D. Stone and P. W. Seakins, Phys. Chem. Chem. Phys., 2018, 20, 22218–22227.
34. A. J. Eskola, M. Dontgen, B. Rotavera, R. L. Caravan, O. Welz, J. D. Savee, D. L. Osborn, D. E. Shallcross, C. J. Percival and C. A. Taatjes, Phys. Chem. Chem. Phys., 2018, 20, 19373–19381.
35. C. Sun, S. Zhang, J. Yue and S. Zhang, J. Phys. Chem. A, 2018, 122, 8729–8737.
36. P.-B. Wang, D. G. Truhlar, Y. Xia and B. Long, Phys. Chem. Chem. Phys., 2022, 24, 13066–13073.
37. Y. Wei, Q. Zhang, X. Huo, W. Wang and Q. Wang, Chemosphere, 2022, 296, 133717.
38. Z. J. Buras, R. M. Elsamra, A. Jalan, J. E. Middaugh and W. H. Green, J. Phys. Chem. A, 2014, 118, 1997–2006.
39. L. Vereecken, H. Harder and A. Novelli, Phys. Chem. Chem. Phys., 2014, 16, 4039–4049.
40. Z. J. Buras, R. M. Elsamra and W. H. Green, J. Phys. Chem. Lett., 2014, 5, 2224–2228.
41. L. Vereecken, A. R. Rickard, M. J. Newland and W. J. Bloss, Phys. Chem. Chem. Phys., 2015, 17, 23847–23858.
42. R. Chhantyal-Pun, A. Davey, D. E. Shallcross, C. J. Percival and A. J. Orr-Ewing, Phys. Chem. Chem. Phys., 2015, 17, 3617–3626.
43. D. Stone, M. Blitz, L. Daubney, N. U. Howes and P. Seakins, Phys. Chem. Chem. Phys., 2014, 16, 1139–1149.
44. T. Berndt, R. Kaethner, J. Voigtlander, F. Stratmann, M. Pfeifle, P. Reichle, M. Sipila, M. Kulmala and M. Olzmann, Phys. Chem. Chem. Phys., 2015, 17, 19862–19873.
45. M. F. Shaw, D. L. Osborn, M. J. T. Jordan and S. H. Kable, J. Phys. Chem. A, 2017, 121, 3679–3688.
46. D. U. Andrews, B. R. Heazlewood, A. T. Maccarone, T. Conroy, R. J. Payne, M. J. Jordan and S. H. Kable, Science, 2012, 337, 1203–1206.
47. A. T. Archibald, M. R. McGillen, C. A. Taatjes, C. J. Percival and D. E. Shallcross, Geophys. Res. Lett., 2007, 34, L21801.
48. S. So, U. Wille and G. da Silva, Environ. Sci. Technol., 2014, 48, 6694–6701.
49. M. F. Shaw, B. Sztaray, L. K. Whalley, D. E. Heard, D. B. Millet, M. J. T. Jordan, D. L. Osborn and S. H. Kable, Nat. Commun., 2018, 9, 2584.
50. X. Lei, W. Wang, J. Cai, C. Wang, F. Liu and W. Wang, J. Phys. Chem. A, 2019, 123, 3205–3213.
51. G. E. Scuseria, C. L. Janssen and H. F. Schaefer, III, J. Chem. Phys., 1988, 89, 7382–7387.
52. C. Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622.
53. M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506.
54. J. A. Miller and S. J. Klippenstein, J. Phys. Chem. A, 2003, 107, 2680–2692.
55. C. H. Sun, B. E. Xu and S. W. Zhang, J. Phys. Chem. A, 2014, 118, 3541–3551.
56. C. Sun, B. Xu, L. Lv and S. Zhang, Phys. Chem. Chem. Phys., 2019, 21, 16583–16590.
57. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013.
58. R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell Scientific, Carlton, Australia, 1990.
59. K. A. Holbrook, Michael J. Pilling and S. H. Robertson, Unimolecular Reactions, Wiley, New York, 1996.
60. S. J. Klippenstein and L. B. Harding, J. Phys. Chem. A, 2000, 104, 2351–2354.
61. L. K. Huynh, H. R. Zhang, S. Zhang, E. Eddings, A. Sarofim, M. E. Law, P. R. Westmoreland and T. N. Truong, J. Phys. Chem. A, 2009, 113, 3177–3185.
62. D. R. Glowacki and M. J. Pilling, Chem. Phys. Chem., 2010, 11, 3836–3843.
63. G. da Silva, J. Phys. Chem. A, 2012, 116, 5317–5324.
64. D. W. Chandler and J. A. Miller, J. Chem. Phys., 1984, 81, 455–464.
65. J. A. Miller and D. W. Chandler, J. Chem. Phys., 1986, 85, 4502–4508.
66. J. A. Miller and S. J. Klippenstein, J. Phys. Chem. A, 2006, 110, 10528–10544.
67. J. A. Miller, S. J. Klippenstein and S. H. Robertson, J. Phys. Chem. A, 2000, 104, 7525–7536.
68. L. K. Huynh, H. R. Zhang, S. Zhang, E. Eddings, A. Sarofim, M. E. Law, P. R. Westmoreland and T. N. Truong, J. Phys. Chem. A, 2009, 113, 3177–3185.
69. W. T. Duncan, R. L. Bell and T. N. Truong, J. Comput. Chem., 1998, 19, 1039–1052.
70. G. J. R. Aroeira, A. S. Abbott, S. N. Elliott, J. M. Turney and H. F. Schaefer, Phys. Chem. Chem. Phys., 2019, 21, 17760–17771.
71. L. Chen, Y. Huang, Y. Xue, Z. Shen, J. Cao and W. Wang, Atmos. Chem. Phys., 2019, 19, 4075–4091.
72. N. A. I. Watson, J. A. Black, T. M. Stonelake, P. J. Knowles and J. M. Beames, J. Phys. Chem. A, 2019, 123, 218–229.
73. W.-m Wei, S. Hong, W.-j Fang, R.-h Zheng and Y.-d Qin, Theor. Chem. Acc., 2019, 138, 13.
74. R. S. Zhu and M. C. Lin, J. Phys. Chem. A, 2000, 104, 10807–10811.
75. C. Sun, Y. Liu, B. Xu, Y. Zeng, L. Meng and S. Zhang, J. Chem. Phys., 2013, 139, 154307.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06115a

---