 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Non-monotonic Soret coefficients of aqueous LiCl solutions with varying concentrations†
Namkyu
Lee‡
 ab,
Shilpa
Mohanakumar‡
ab,
Shilpa
Mohanakumar‡
 a,
W. J.
Briels
a,
W. J.
Briels
 *ac and
Simone
Wiegand
*ac and
Simone
Wiegand
 *ad
*ad
aIBI-4:Biomacromolecular Systems and Processes, Forschungszentrum Jülich GmbH, Jülich D-52428, Germany. E-mail: s.wiegand@fz-juelich.de
bDepartment of Mechanical Engineering, Yonsei University, Seoul, Korea. E-mail: nk.lee@yonsei.ac.kr
cUniversity of Twente, Computational Chemical Physics, Postbus 217, Enschede 7500 AE, The Netherlands. E-mail: w.j.briels@utwente.nl
dChemistry Department – Physical Chemistry, University Cologne, Cologne D-50939, Germany
First published on 7th February 2024
Abstract
We investigate the thermodiffusive properties of aqueous solutions of lithium chloride, using thermal diffusion forced Rayleigh scattering in a concentration range of 0.5–2 mole per kg of solvent and a temperature range of 5 to 45 °C. All solutions exhibit non-monotonic variations of the Soret coefficient ST with a concentration exhibiting a minimum at about one mole per kg of solvent. The depth of the minimum decreases with increasing temperature and shifts slightly towards higher concentrations. We compare the experimental data with published data and apply a recent model based on overlapping hydration shells. Additionally, we calculate the ratio of the phenomenological Onsager coefficients 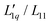 using our experimental results and published data to calculate the thermodynamic factor. Simple linear, quadratic and exponential functions can be used to describe this ratio accurately, and together with the thermodynamic factors, the experimental Soret coefficients can be reproduced. The main conclusion from this analysis is that the minimum of the Soret coefficients results from a maximum in the thermodynamic factor, which appears itself at concentrations far below the experimental concentrations. Only after multiplication by the (negative) monotonous Onsager ratio does the minimum move into the experimental concentration window.
using our experimental results and published data to calculate the thermodynamic factor. Simple linear, quadratic and exponential functions can be used to describe this ratio accurately, and together with the thermodynamic factors, the experimental Soret coefficients can be reproduced. The main conclusion from this analysis is that the minimum of the Soret coefficients results from a maximum in the thermodynamic factor, which appears itself at concentrations far below the experimental concentrations. Only after multiplication by the (negative) monotonous Onsager ratio does the minimum move into the experimental concentration window.
1 Introduction
Temperature gradients occur in many different environments and can lead to interesting coupling effects. In liquid mixtures and suspensions, thermal gradients drive thermodiffusion or thermophoresis, the so-called Ludwig-Soret effect. These are used in numerous applications in biotechnology, chemical engineering, and energy technology.1,2 The coupling of heat and mass flows leads to a concentration profile and plays an essential role in natural and technical transport processes with temperature gradients, e.g., in petrology (rock formation), in oil reservoirs, and separation processes.3–6 Because of its high sensitivity to solvent-water interactions, it is used commercially to characterize the binding affinity between ligands and proteins.7–9 The study of thermal gradients is also considered in the development of thermoelectric fluid cells to convert waste heat into electricity.10–12In an isotropic binary fluid mixture with non-uniform concentration and temperature, the mass flow of the solute ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) contains a contribution stemming from the concentration and one from the temperature gradient,1
contains a contribution stemming from the concentration and one from the temperature gradient,1
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) = −ρDgradc − ρc(1 − c)DTgradT = −ρDgradc − ρc(1 − c)DTgradT | (1) |
So far, no microscopic theory describes the Soret or thermodiffusion coefficients. Several correlations have been observed13–15 and empirical approaches are used to express ST and DT as a function of temperature and/or concentration.16,17
Aqueous salt solutions have been repeatedly studied since the early days of research on the Ludwig-Soret effect.19–23 Recently, systematic studies of ionic solutions have shown that the hydrophilicity of the salt correlates with the thermal diffusion behavior24,25 and that an exchange of the anion has a more decisive influence on the concentration dependence of the Soret coefficient than the replacement of the cation.24,25 One of the unsolved puzzles of the thermodiffusion of aqueous salt solutions is an often observed minimum of the Soret coefficient with concentration.18,22,23,26 Recently, Mohanakumar et al. developed an intuitive picture in which the relevant objects are the fully hydrated salt molecules (FHP), including all water molecules that behave differently from bulk water. For the investigated aqueous iodide salt solutions, they hypothesized that these FHPs form a random close packing at mmin, which implies that the outer hydration shell starts to touch. The preliminary, somewhat sketchy calculations indicate that Soret coefficients begin to rise beyond mmin. At higher concentrations, the approach eventually breaks down, which might be related to cluster formation, which is not considered in the model. Recently, Gittus and Bresme27 performed a Lennard-Jones simulation on a particular set of parameters and found a correlation between the minimum of the thermodynamic factor Γ and the Soret coefficient ST.
Another salt for which a minimum of ST with concentration has been reported is lithium chloride (LiCl). The lithium-ion is the smallest alkali metal ion. Thus, it has the highest charge density and is more strongly hydrated, most probably with a second hydration shell.28 Colombani et al. reported a fairly sharp minimum of ST around mmin = 0.56 mol kg−1,23 whereas authors extrapolated the data from two sources to T = 0 °C. Recently, di Lecce et al. studied the thermodiffusion of LiCl by non-equilibrium molecular dynamics simulations26 at very low temperatures. Simulations showed that the minimum around mmin = 2.5 mol kg−1 disappeared with increasing temperature and seemed to shift slightly towards higher molalities.
In this paper, we perform systematic temperature and concentration-dependent measurements of the thermodiffusive behavior of aqueous LiCl solutions. First, we test whether a recently presented approach to discuss the minimum in ST in the context of overlapping hydration shells can be applied18 and use an empirical equation to describe the Soret coefficient as a function of temperature and concentration. As the hydration model imposes a minimum, we followed a recent approach by Gittus and Bresme,27 who found a correlation between the minimum of the thermodynamic factor and the Soret coefficient. As the thermodynamic data of aqueous solutions of LiCl are well known, we were able to calculate the ratio of the Onsager coefficients, which a simple function can describe.
2 Experimental details
Deionized water from a Millipore filter unit (0.22 μm) was used to prepare the aqueous salt solutions. LiCl was purchased from Sigma Aldrich and used without further purification. The purity of the salt was ≥99% (Sigma–Aldrich). Solutions with a concentration of 0.5–2 mol kg−1 were prepared using a stock solution at a high concentration.An optical quartz cell (Hellma) with an optical path length of 0.2 mm was used for the measurement of the thermodiffusive properties using infrared thermal diffusion forced Rayleigh scattering (IR-TDFRS).29 Prepared solutions were filtered through a 0.2 μm filter (Whatman Anotop 10) and filled into the quartz cell. All measurements were performed in the temperature range between 5 and 45 °C. Since LiCl is a relatively small molecule, the diffraction signal in the TDFRS experiment is quite weak. We conducted a series of six to ten experiments at each temperature and concentration, using different cells and freshly prepared samples for each trial. In every experiment, we collected at least 3000 individual signals, and their average was calculated. We then examined both the on and off phases of each signal, yielding two distinct sets of values for ST and D.29,30 For each specific temperature and concentration, the mean values were derived from the individual data points. Further details of the experimental methods can be found elsewhere.25
The auxiliary parameters, concentration and temperature dependence of the refractive index, were measured independently. The refractive index as a function of concentration was measured using an Abbe refractometer (Anton Paar Abbemat MW) at a wavelength of 632.8 nm. We measured the refractive index for 7 concentrations to determine (∂n/∂c)p,T. The refractive index change in temperature (∂n/∂T)p,c was measured interferometrically.31 All data are shown in the ESI.†
3 Results and discussion
In Fig. 1, we present all our data as a sequence of five Soret coefficient versus concentration plots. The panels correspond to increasing temperatures from left to right; each panel contains data points at eight different concentrations. As a measure of concentration, we use molality, which is the number of moles of LiCl per kilogram of water.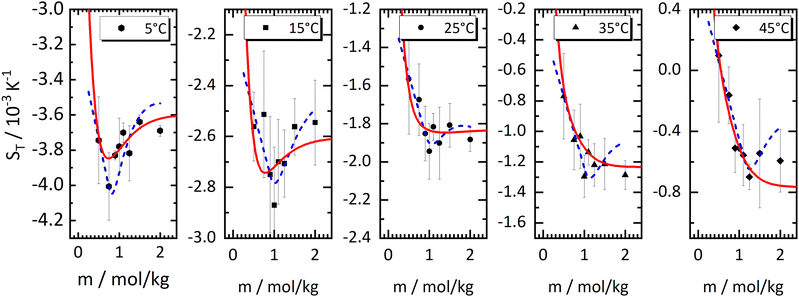 | ||
| Fig. 1 Soret coefficient ST as a function of molality m for five different temperatures. Temperature increases from left to right. The error bars show the measurement uncertainty of the mean. The dashed blue lines have been calculated with a model based on the overlap of hydration shells18 and the red solid lines correspond to an exponential fit according to eqn (2) considering all concentrations individually. Further details are given in the text. | ||
Only a few experimental results on the thermodiffusion of LiCl have been published so far, and these have been collected in the paper by Colombani et al.23 Most of these experiments in our concentration range were conducted at temperatures about ten degrees below our lowest temperature. In order to roughly compare these data with ours, we have extrapolated the fits described in Section 3.1 to the appropriate temperatures and presented the results in Table 1. We found good agreement for molalities near 1 mol kg−1, while for larger concentrations the agreement was reasonable. In their study, the pronounced minimum is shaped by a notably low ST-value at a concentration of 0.56 mol kg−1, a result we have been unable to replicate. At this concentration, we observe our largest discrepancy, amounting to 50%, even though the extrapolation is over a relatively moderate temperature range. This substantial deviation, which in our case results in only a slight minimum, remains unexplained.
| m mol kg−1 | T/°C | S T 23/10−3 K−1 | S T [calc. eqn (S1)]/ 10−3 K−1 | Deviation/% |
|---|---|---|---|---|
| 0.56 | −0.5 | −7.57 | −4.4 | 53 |
| 0.93 | −0.9 | −4.54 | −4.6 | −1 |
| 0.93 | 1.4 | −4.57 | −4.3 | 6 |
| 1.85 | −7.1 | −3.76 | −5.2 | −32 |
| 1.85 | −3 | −3.64 | −4.5 | −23 |
3.1 Temperature dependence and hydrophilicity
The drawn red lines in Fig. 1 are obtained by fitting the data at each individual concentration to the empirical expression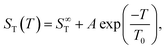 | (2) |
As with all simple ionic salt solutions in water, the exponential function describes the temperature dependence of ST rather well for each individual concentration24 as can be seen in the left panel of Fig. 2, where we show fits at the lowest and highest molalities studied in this paper. All other fits vary monotonously from one curve to the other. At low temperatures, all curves converge more or less to one and the same straight line while at higher temperatures they level off to smaller slopes, with the ones for the larger concentrations leveling off fastest. These findings are in contrast to similar plots for non-ionic solutes,9,32,33 where the slopes change monotonously from positive values at low concentrations to negative values at large concentrations. So, the data reach the plateau from below at low concentrations, while at large concentrations, they do so from above.
 | ||
| Fig. 2 (a) Soret coefficient ST as a function of temperature for the lowest (m = 0.5 mol kg−1) and highest (m = 02.0 mol kg−1) measured molality. The lines represent a fit according to eqn (2). (b) The adjusted amplitude A as a function of concentration. The trend of A at low and high concentrations is highlighted by two light gray dashed lines that intersect around 0.9 mol kg−1. | ||
When fitting the coefficients S∞T, A and T0 as functions of molality, the noise in the data becomes more pronounced as can be seen for example in the plot of A versus molality - see the right panel of Fig. 2. As a result, the overall procedure to fit the data is only modestly successful. A slightly more successful representation of the data is obtained when using the phenomenological expressions of Wittko and Köhler17 (see ESI†) as shown by the drawn lines in Fig. S7 (ESI†).
3.2 Concentration dependence and minimum
The data in Fig. 1, as well as their fitted curves described in the previous section, seem to indicate that at each temperature the Soret coefficient as a function of concentration has a minimum at about 0.9 mol kg−1. This is very similar to our findings with experiments on iodide solutions,18 although the minima for iodides are more pronounced than for LiCl. A look at coefficient A plotted in the right panel of Fig. 2 seems to confirm a change of regime near about the same concentration. At low concentrations, A changes significantly with concentration, while at large concentrations, it is more or less independent of concentration. This is emphasized in Fig. 2(b) by two grey dashed lines which intersect at a concentration of about 0.9 mol kg−1. This is roughly equal to the position of the minima occurring in the fits of the data at the lowest temperatures in Fig. 1.The dashed blue lines in Fig. 1 were calculated using a coarse grain model, from now on called the hydration shell model, that considers each salt molecule together with its strongly attached first hydration shell as a spherically symmetric particle dissolved in equally sized spherically symmetric coarse grain water particles. The first solvation shell of coarse water particles surrounding a coarse salt particle corresponds at the atomistic level to a second, weakly perturbed hydration shell surrounding the salt molecule.34 The weak perturbation of these particles is represented, at the coarse level, by a self-energy attributed to the coarse salt particles, which decreases with increasing overlap of the coarse solvation shells. At concentrations below the minimum, the first regime, the coarse solvation shells do not overlap, while beyond the minimum they do (the second regime). For further details see ref. 18, by lack of other simulation data, the coarse grain salt particles were represented by Lennard-Jones particles and mixed with equally sized coarse water Lennard-Jones particles each representing an unspecified amount of water. This representation allowed us to use the results of simulations of Lennard-Jones mixtures by Artola and Rousseau.35
Although the application of the hydration shell model is less convincing than with the iodides in ref. 18, it describes the data reasonably well for all investigated temperatures. With increasing temperature, the system becomes less thermophilic, the minimum depth is less pronounced, and the concentration where the minimum occurs, mmin, shifts from 0.83 mol kg−1 at T = 5 °C towards 1.3 mol kg−1 at T = 45 °C (cf. Sec. S3.2, ESI†). The depth of the minimum gets smaller with increasing temperature agrees with a recent computer simulation of LiCl.26 In the simulations, the minimum can only be observed below T = −13 °C, and the minimum concentration is ≈2.4 mol kg−1 with a slight tendency to shift towards higher concentrations.
Application of the hydration model as presented above has one somewhat unsatisfactory aspect in that the position of the minimum of Soret is imposed to be able to perform the analysis and is not independently represented by the procedure. With the iodides studied in our previous paper,18 this was no problem since the data clearly indicated where the minimum was to be found. With the present system, the data are clearly less conclusive and the analysis runs the risk of emphasizing a minimum that well may be unphysical. In order to avoid any such risk, we have decided to analyze the data without reference to any microscopic model, but still making use of as much theoretically sound phenomenological input as possible.
3.3 Thermodynamics, heat of transfer and the minimum of the Soret coefficient
In this subsection, we follow the analysis as given in a recent paper by Gittus and Bresme,27 who conducted simulations to study the thermodiffusion of Lennard-Jones mixtures under specific parameter settings. The basis of the analysis is the well-known expression for the Soret coefficient from irreversible-thermodynamics, which, applied to the present case of LiCL solutions, reads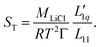 | (3) |
Within the theory of irreversible thermodynamics, this equation is exact. It consists of two factors, the first factor depending on thermodynamical information only and the second factor being the ratio of two Onsager coefficients, also called heat of transfer or L-ratio. Γ in the first factor is proportional to the derivative of the chemical potential of the solute, i.e. LiCl, with respect to its concentration. In the rest of this paper, we use the thermodynamic data for aqueous LiCl solutions published by Pátek and Klomfar.36 For further information, we refer to ESI.† This allows us to concentrate on the precise temperature and concentration dependence of the L-ratio.
In their study of Lennard-Jones mixtures, Gittus and Bresme calculated both factors from their simulations and found that the heat of transfer is constant over the whole concentration range (for the chosen parameter setting). As a result, the minimum observed in their Soret coefficients as a function of concentration is entirely due to a corresponding maximum in the thermodynamic factor, i.e. a minimum in Γ. In a rather bold claim, they promote this finding as a general conjecture. We investigate this claim for LiCl solutions in the rest of this paper. To be precise, we investigate if the minimum in the Soret coefficient is related to an extreme in the thermodynamic factor while the L-ratio behaves monotonously, not necessarily being constant.
In Fig. 3(a), we have plotted the experimental values (symbols) of minus the heat of transfer, i.e. the values of 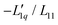 , as a function of concentration for all temperatures studied in this paper. In order to obtain these data, we divided the experimental results for the Soret coefficients by minus the thermodynamic factor in eqn (3), i.e. by −MLiCl/(RT2Γ). This factor was calculated using the thermodynamic data of Pátek and Klomfar36 and is shown in Fig. 3(b). Obviously, taking the product of the data in panels (a) and (b) reproduces the original data. The reason for introducing the two minus signs is that in this representation one easily recognizes how a minimum in Soret coefficient can emerge.
, as a function of concentration for all temperatures studied in this paper. In order to obtain these data, we divided the experimental results for the Soret coefficients by minus the thermodynamic factor in eqn (3), i.e. by −MLiCl/(RT2Γ). This factor was calculated using the thermodynamic data of Pátek and Klomfar36 and is shown in Fig. 3(b). Obviously, taking the product of the data in panels (a) and (b) reproduces the original data. The reason for introducing the two minus signs is that in this representation one easily recognizes how a minimum in Soret coefficient can emerge.
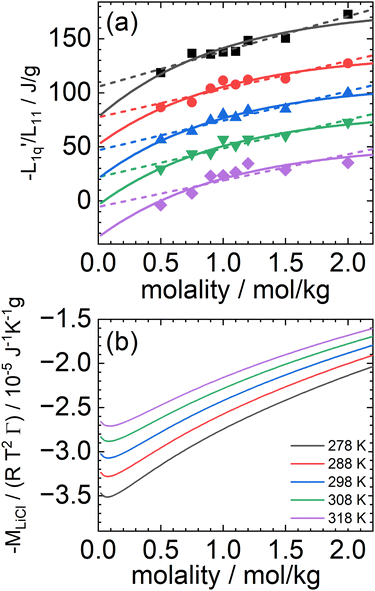 | ||
Fig. 3 (a) The ratio of the phenomenological Onsager coefficients 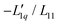 calculated from the experimental data according to eqn (3). The dashed and solid lines are linear and exponential fits, respectively. (b) −MLiCl/(RT2Γ) for different temperatures. calculated from the experimental data according to eqn (3). The dashed and solid lines are linear and exponential fits, respectively. (b) −MLiCl/(RT2Γ) for different temperatures. | ||
A first look at the two panels in Fig. 3 immediately reveals two facts. First, in contrast to the Lennard-Jones case, the heats of transfer are not independent of concentration but seem to smoothly decrease over the whole concentration range (negative values smoothly increase). Second, apart from vertical shifts, the thermodynamic factors hardly depend on temperature. Moreover, the maxima (minima for minus the thermodynamic factors) occur at very low concentrations where they seem to be unrelated to the minima that we have found in the experimental values of the Soret coefficients. Clearly, however, since minus the heat of transfer is always positive and smoothly increasing with concentration, the minimum in Soret coefficient must be a result of a minimum in minus of the thermodynamic factor.
In order to investigate the emergence of the minimum further, we have made fits of the 'experimental' values of the heats of transfer, the symbols in Fig. 3(a), and used these fits together with the thermodynamic factors to reproduce Soret coefficients. We first tried linear fits, shown by the dashed lines in Fig. 3(a). The fits seem to be reasonably accurate, and so are the resulting Soret coefficients shown as light blue lines in Fig. 4. It is promising that our procedure has produced minima in the Soret coefficients that are shifted to larger concentrations than where the minima in the thermodynamic factors occur. On the other hand, the Soret coefficients are badly reproduced at low concentrations, and the minima seem to have moved to larger concentrations way too fast. Moreover, with the larger temperatures, the minima seem to have disappeared altogether. We therefore tried quadratic fits to reproduce the heats of transfer, obtaining the dark blue lines in Fig. 4. Clearly, the Soret coefficients are now much better reproduced, in particular also at low concentrations. At high concentrations and high temperatures, the extrapolated Soret coefficients quickly rise to very large values. One might object now that a quadratic fit induces a maximum in minus the heat of transfer, and that the minimum in Soret coefficient is not a result of a minimum in minus the thermodynamic factor alone. In order to resolve this issue, we decided to perform fits of the heats of transfer using smooth, monotonous functions a−be−cm, with m being molality (see ESI†), the results of which are shown as drawn lines in Fig. 3(a) and in Fig. 5. Note that for all functions, the fits have been performed individually for each temperature. As in Fig. 4, we have extended the concentration axis slightly beyond the range of the experimental data in Fig. 5 in order to better see how the minima develop. It is clearly seen that the extrapolated monotonous fits of the heats of transfer still produce minima in the Soret coefficient, even at the highest temperatures. Compared with the results with the quadratic fits, however, the minima are less pronounced, and the predicted Soret coefficients beyond the minimum increase more slowly with increasing temperature.
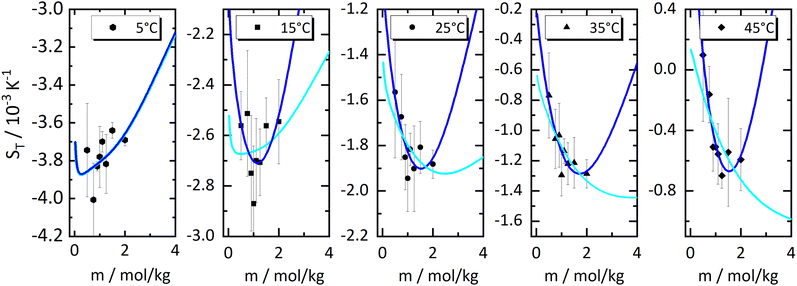 | ||
Fig. 4 The same measured Soret coefficients ST as shown in Fig. 1 together with the calculated Soret coefficient using the thermodynamic function and two approximations of the ratio of the Onsager coefficients 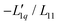 as a function of concentration as displayed in Fig. 3. The solid light blue and dark blue lines are calculated using a linear and quadratic approximation. Further details are given in the text. as a function of concentration as displayed in Fig. 3. The solid light blue and dark blue lines are calculated using a linear and quadratic approximation. Further details are given in the text. | ||
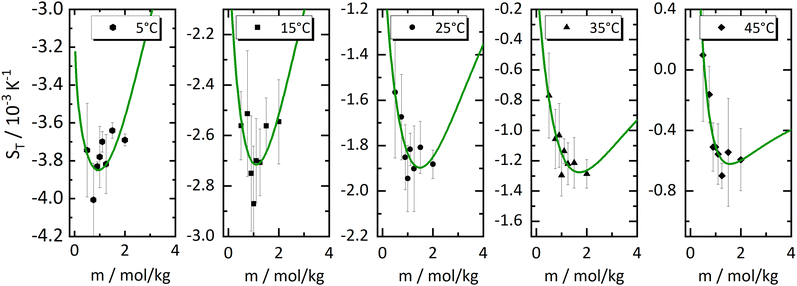 | ||
Fig. 5 Same Soret coefficients ST as shown in Fig. 4. The ratio of the Onsager coefficients 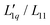 as a function of concentration has been approximated by an exponential function (green solid line). Further details are given in the text. as a function of concentration has been approximated by an exponential function (green solid line). Further details are given in the text. | ||
We finally conclude that the hypothesis that the minima in Soret coefficients are caused by the thermodynamic factor rather than by the ratio of the Onsager coefficients has good chances to be correct, although the experimental data are too noisy to make a definite verdict.
4 Conclusion
This study systematically examines the thermodiffusive properties of aqueous solutions of LiCl. IR-TDFRS was utilized to investigate the system within a concentration range of 0.5 to 2 mole per kg of solvent and a temperature range of 5 to 45 degrees Celsius.The temperature dependence of the Soret coefficient was characterized for all concentrations using eqn (2). Increments of the amplitude A with concentration are very small at large concentrations compared to those at small concentrations (cf.Fig. 2). This observation suggests that fewer hydrogen bonds are available to be broken with increasing concentrations, which is, in rough terms, the principle concept behind the hydration shell model suggested by us in a previous paper. Indeed, we have been able to reproduce the data using that model, observing the minima that were also obtained with empirical fits of the data. The results were nevertheless unsatisfactory for two reasons. First, the analysis makes essential use of the fact that a minimum occurs at a molality of about one mole per kilogram and does not allow the data to independently give rise to such a minimum. Second, in spite of a lot of experimental efforts, the data are still too noisy to justify such an approach.
In order to transform the data into a form more accessible to fitting procedures, and to be able to investigate the origin of emerging minima, we have followed the work by Gittus and Bresme27 and analyzed the Soret coefficients in terms of their two dominant factors, i.e. a thermodynamic factor and the heat of transfer, the latter being the ratio of two Onsager coefficients 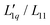 . With all thermodynamic information about aqueous LiCl solutions being available in the literature,36 we have computed the heat of transfer, which is the only remaining unknown factor in eqn (3) and plotted them against concentration for each individual temperature. Our results revealed that the heat of transfer exhibits a very smooth decrease with concentration, which can be described very well by an exponential decay, thereby producing trustworthy fits of the experimental Soret coefficients. The fact that the heats of transfer are rather simple functions of concentration suggests that they provide the most promising ingredients on which to concentrate theoretical analysis. Although the ratio
. With all thermodynamic information about aqueous LiCl solutions being available in the literature,36 we have computed the heat of transfer, which is the only remaining unknown factor in eqn (3) and plotted them against concentration for each individual temperature. Our results revealed that the heat of transfer exhibits a very smooth decrease with concentration, which can be described very well by an exponential decay, thereby producing trustworthy fits of the experimental Soret coefficients. The fact that the heats of transfer are rather simple functions of concentration suggests that they provide the most promising ingredients on which to concentrate theoretical analysis. Although the ratio 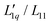 in principle includes both thermodynamic and dynamic ingredients, it is well possible that both factors in the ratio share a common dynamic factor, thereby allowing for a purely thermodynamic description. Finally, we note that, although the experimental Soret coefficients still scatter around the 'predicted' values, the results give strong evidence that the minima result from the minima in minus the thermodynamic factor (i.e. −MLiCl/(RT2Γ)). This finding is at first sight far from obvious since the minima in minus the thermodynamic factors are for all temperatures at very small concentrations, far outside the experimental range of concentrations. With increasing temperatures, the minima are pushed to larger concentrations by the heats of transfer, which are themselves monotonously and only gently increasing with concentration. To develop this approach further and to explore its potential, it would be good to apply the same methodology to systems where comprehensive thermodynamic data are accessible.
in principle includes both thermodynamic and dynamic ingredients, it is well possible that both factors in the ratio share a common dynamic factor, thereby allowing for a purely thermodynamic description. Finally, we note that, although the experimental Soret coefficients still scatter around the 'predicted' values, the results give strong evidence that the minima result from the minima in minus the thermodynamic factor (i.e. −MLiCl/(RT2Γ)). This finding is at first sight far from obvious since the minima in minus the thermodynamic factors are for all temperatures at very small concentrations, far outside the experimental range of concentrations. With increasing temperatures, the minima are pushed to larger concentrations by the heats of transfer, which are themselves monotonously and only gently increasing with concentration. To develop this approach further and to explore its potential, it would be good to apply the same methodology to systems where comprehensive thermodynamic data are accessible.
Data availability
The data for this paper are available at Zenodo https://doi.org/10.5281/zenodo.10666454.Author contributions
All authors conceived and planned the experiments. NL and SM carried out the experiments and analyzed the data. All authors contributed to the interpretation of the results and writing the manuscript. All authors provided critical feedback and helped shape the research, analysis and manuscript.Conflicts of interest
There are no conflicts to declar.Acknowledgements
We thank Fernando Bresme and Jan Dhont for fruitful discussions. We are grateful to Peter Lang for his generous support of our work. SM acknowledges the support of the International Helmholtz Research School of Biophysics and Soft Matter (BioSoft). This research was supported by the Yonsei University Research Fund of 2023-22-0160.References
- S. R. de Groot, Thermodynamics of irreversible processes, North Holland, Amsterdam, 1966 Search PubMed.
- S. Kjelstrup, D. Bedeaux, E. Johannessen and J. Gross, Non-equilibrium thermodynamics for engineers, World Scientific, Hackensack, NJ, 2nd edn, 2017 Search PubMed.
- F. Montel, J. Bickert, A. Lagisquet and G. Galliero, J. Pet. Sci. Eng., 2007, 58, 391–402 CrossRef CAS.
- G. Galliero and F. Montel, Phys. Rev. E, 2008, 78, 041203 CrossRef PubMed.
- W. Köhler and K. I. Morozov, J. Non-Equil. Thermody, 2016, 41, 151–197 Search PubMed.
- H. Pasch, Chromatographia, 2021, 84, 525–530 CrossRef CAS.
- P. Baaske, F. M. Weinert, S. Duhr, K. H. Lemke, M. J. Russell and D. Braun, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 9346–9351 CrossRef CAS PubMed.
- S. A. I. Seidel, P. M. Dijkman, W. A. Lea, G. van den Bogaart, M. Jerabek-Willemsen, A. Lazic, J. S. Joseph, P. Srinivasan, P. Baaske, A. Simeonov, I. Katritch, F. A. Melo, J. E. Ladbury, G. Schreiber, A. Watts, D. Braun and S. Duhr, Methods, 2013, 59, 301–315 CrossRef CAS PubMed.
- D. Niether and S. Wiegand, J. Phys. Condes. Matter, 2019, 31, 503003 CrossRef CAS PubMed.
- T. J. Salez, B. T. Huang, M. Rietjens, M. Bonetti, C. Wiertel-Gasquet, M. Roger, C. L. Filomeno, E. Dubois, R. Perzynski and S. Nakamae, Phys. Chem. Chem. Phys., 2017, 19, 9409–9416 RSC.
- C.-G. Han, X. Qian, Q. Li, B. Deng, Y. Zhu, Z. Han, W. Zhang, W. Wang, S.-P. Feng, G. Chen and W. Liu, Science, 2020, 368, 1091–1098 CrossRef CAS PubMed.
- Y. Jia, Q. Jiang, H. Sun, P. Liu, D. Hu, Y. Pei, W. Liu, X. Crispin, S. Fabiano, Y. Ma and Y. Cao, Adv. Mater., 2021, 33, e2102990 CrossRef PubMed.
- J. Rauch, M. Hartung, A. F. Privalov and W. Köhler, J. Chem. Phys., 2007, 126, 214901 CrossRef CAS PubMed.
- P. Blanco, M. M. Bou-Ali, J. K. Platten, P. Urteaga, J. A. Madariaga and C. Santamaria, J. Chem. Phys., 2008, 129, 174504 CrossRef PubMed.
- D. Niether, H. Kriegs, J. K. G. Dhont and S. Wiegand, J. Chem. Phys., 2018, 149, 044506 CrossRef PubMed.
- S. Iacopini, R. Rusconi and R. Piazza, Eur. Phys. J. E, 2006, 19, 59–67 CrossRef CAS PubMed.
- G. Wittko and W. Köhler, Europhys. Lett., 2007, 78, 46007 CrossRef.
- S. Mohanakumar, H. Kriegs, W. J. Briels and S. Wiegand, PCCP, 2022, 24, 27380–27387 RSC.
- C. Soret, Arch. Geneve, 1879, 3, 48–64 Search PubMed.
- C. C. Tanner, Trans. Faraday Soc., 1927, 23, 75–95 RSC.
- D. R. Caldwell, J. Phys. Chem., 1975, 79, 1882–1884 CrossRef CAS.
- F. S. Gaeta, G. Perna, G. Scala and F. Bellucci, J. Phys. Chem., 1982, 86, 2967–2974 CrossRef CAS.
- J. Colombani, J. Bert and J. Dupuy-Philon, J. Chem. Phys., 1999, 110, 8622–8627 CrossRef CAS.
- S. Mohanakumar, J. Luettmer-Strathmann and S. Wiegand, J. Chem. Phys., 2021, 154, 084506 CrossRef CAS PubMed.
- S. Mohanakumar and S. Wiegand, Eur. Phys. J. E, 2022, 45, 10 CrossRef CAS PubMed.
- S. Di Lecce, T. Albrecht and F. Bresme, PCCP, 2017, 19, 9575–9583 RSC.
- O. R. Gittus and F. Bresme, PCCP, 2023, 25, 1606–1611 RSC.
- J. Mähler and I. Persson, Inorg. Chem., 2012, 51, 425–438 CrossRef PubMed.
- S. Wiegand, H. Ning and H. Kriegs, J. Phys. Chem. B, 2007, 111, 14169–14174 CrossRef CAS PubMed.
- P. Rossmanith and W. Köhler, Macromolecules, 1996, 29, 3203–3211 CrossRef CAS.
- A. Becker, W. Köhler and B. Müller, Phys. Chem. Chem. Phys., 1995, 99, 600–608 CAS.
- Y. Kishikawa, S. Wiegand and R. Kita, Biomacromolecules, 2010, 11, 740–747 CrossRef CAS PubMed.
- A. L. Sehnem, D. Niether, S. Wiegand and A. M. Figueiredo Neto, J. Phys. Chem. B, 2018, 122, 4093–4100 CrossRef CAS PubMed.
- P. D. Mitev, W. J. Briels and K. Hermansson, J. Phys. Chem. B, 2021, 125, 13886–13895 CrossRef CAS PubMed.
- P. A. Artola and B. Rousseau, Phys. Rev. Lett., 2007, 98, 125901 CrossRef PubMed.
- J. Pátek and J. Klomfar, Int. J. Refrig., 2008, 31, 287–303 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06061f |
| ‡ These authors contributed equally to this work. |
| This journal is © the Owner Societies 2024 |
