Modelling the effect of surface charging on plasma synthesis of ammonia using DFT

Abstract

Non-equilibrium plasma has been found to have a synergistic effect on catalytic synthesis of NH₃. The non-equilibrium plasma and catalyst surface together could affect NH₃ synthesis through several mechanisms. Charging of the catalyst surface in the presence of non-equilibrium plasma is one such mechanism. We employed density functional theory (DFT) calculations to understand the effect of surface charge on surface reactivity of γ-Al₂O₃ supported single metal atom catalysts and a metal cluster. We investigated the effect of surface charge on adsorption energies of common adsorbates involved in NH₃ synthesis. It is found that adsorption energy of N, N₂, H, H₂, NH and NH₂ on metal atoms increases by up to ∼1.2 eV, whereas NH₃ desorption is increased by up to 0.45 eV upon surface charging. The present results provide a new mechanism of plasma enhanced catalysis potentially explaining why Ni, Pt and Co have better catalytic performance compared to Ru and Fe in ammonia plasma catalysis. Furthermore, we found that the correlations between adsorption energies of adsorbates change significantly with surface charging. These findings suggest that surface charging might play an important role in plasma synthesis of NH₃.

---

1. Introduction

Ammonia is one of the most important industrial chemicals. The conventional ammonia synthesis method – the Haber–Bosch process – converts N₂ into ammonia using H₂ and metal catalysts. This process employs high pressures (100–200 atm) and high temperatures (700–800 K). These thermodynamic conditions are required to maintain the equilibrium in the favor of producing ammonia as well as to maintain the efficiency of the catalysts.¹ Plasma assisted synthesis of ammonia can overcome these thermodynamic limitations because it produces non-equilibrium molecular excitation as well as space and surface charges. Non-equilibrium plasmas have been shown to synthesize ammonia using N₂ and H₂ at relatively lower temperatures (∼473 K) under atmospheric pressure in the presence of various catalysts.^2–15

The rate limiting step for thermal catalysis of ammonia is the dissociation of N₂ on the catalytic surface. N₂ is a strongly bonded molecule and its dissociative barrier on commonly used catalysts like Fe and Ru is quite high (60–115 kJ mol⁻¹).² This high barrier leads to the requirement of high temperature for thermal-catalytic production of ammonia in an industrial process. Non-equilibrium plasma arguably circumvents high dissociation barrier for N₂ by vibrationally exciting the molecule¹⁴ or creating new reaction pathways to radicals such as NNH.⁷ However, the short lifetime of vibrational excitation states at atmospheric pressure (100–1000 μs for vibrational N₂) means that the vibrational excitation may not be the dominant mechanism and that other plasma induced effects could also play an important role in plasma-assisted catalysis of NH₃.^2,16

In plasma aided ammonia synthesis, in addition to the effects of plasma on the excitation of gas-phase molecules, we also need to consider effects of plasma on catalytic surface. These include surface heating, electric field effects and surface charging effects. Bal et al.¹⁷ reported a ∼35% increase in binding energy of CO₂ on γ-Al₂O₃ surface in the presence of an excess electron on the surface. Surfaces in contact with plasma typically acquires negative charge due to the much higher mobility of electrons in plasma.² An experimental study by Ambrico et al.¹⁸ found that in plasma environments, excess electrons accumulate on alumina surface with energies around 1 eV and a lifetime of several days. The low energy of electron means that they will penetrate only a few nanometers into the surface. Jafarzadeh et al.^19,20 studied the effect of surface charging on CO₂ adsorption on metal clusters as well as pure metal surfaces. They found that the CO₂ adsorption energy increases on Ni and Cu metal clusters on a TiO₂ support, whereas it takes a combination of strong electric field and excess electrons on the surface to alter the adsorption energy of CO₂ on a Cu metal slab. Additionally, the charging of a surface in a plasma environment is dynamic. However, the change in adsorption energy as a function of surface charging strength in not known.

The effect of surface charging on adsorption of typical adsorbates involved in NH₃ synthesis on common catalysts or support materials has not been studied either experimentally or theoretically, to the best of our knowledge. Shah et al. experimentally show that the plasma enhanced zeolite 5A has 50 times higher energy yield than the non-plasma case. They hypothesize that the negative surface charge promotes the nitrogen dissociation.⁶ Chung and Chang found synergistic effects between non-thermal plasma and perovskite ferroelectric in dry reforming of methane. They concluded that the surface charge is beneficial due to the increasing energy density in plasma reactor by surface charge accelerated free electrons.²¹ The synergistic effects of plasma catalysis on ammonia synthesis are largely attributed to the vibrational excitation of N₂ in the gas-phase. However, our current understanding cannot fully explain these synergistic effects.² Although not the sole reason for synergistic effects of plasma synthesis, the changes to the surface chemistry due to surface charging could be an important factor in plasma catalytic synthesis of ammonia. If important, surface charge could provide a mechanism to control the plasma catalytic synthesis process.

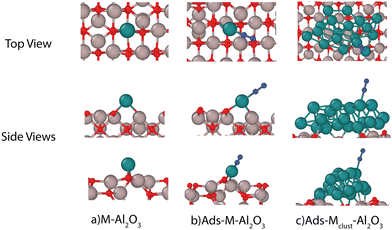
In this work, we explore the effect of surface charge on common catalysts supported by γ-Al₂O₃ using density functional theory (DFT) calculations on single catalyst atom model as it allows us to screen a relatively higher number of catalyst materials. Please note that the use of single metal atoms as catalysts might be challenging, especially under high-temperature plasma conditions. Therefore, considering the challenges involved in using single atom catalysts, we also investigate the effect of surface charge on a metal cluster as well. This work has been arranged as follows: firstly, the methods used in modelling the surface charge as well as their validity is discussed. Then we discuss the effect of surface charge on adsorption of important gas-phase species on a γ-Al₂O₃ surface followed by adsorption of different catalyst atoms on the γ-Al₂O₃ surface. Later we illustrate the effect of surface charge on adsorption energies of several important species involved in NH₃ synthesis on different catalyst atoms. Afterwards, we validate the extent of surface charge effect on a Ru metal cluster supported by γ-Al₂O₃. Finally, we discuss the implications of changes to adsorption energy scaling relationships due to surface charging followed by conclusions of the study.

2. Methods

The DFT calculations of adsorption on a charged surface were performed following the methodology proposed by Bal et al.¹⁷ All calculations are performed using the Quickstep module of the CP2K code.²² The γ-Al₂O₃ structure used in this study is derived following the work of Digne et al.²³ Firstly, the γ-Al₂O₃ 110 surface was optimized using a 2 × 2 anhydrous super cell with 6 aluminum layers (see Fig. 1). The hydrated 110 surface is the most stable termination for γ-Al₂O₃. However, the study of Bal et al.¹⁷ indicates that the effect of surface charge can be effectively modeled with an anhydrous surface. The surface optimization is performed using BFGS scheme while keeping the bottom 2 layers fixed. Additional effects such as presence of O-atom defects could also play an important role in the plasma catalytic processes on the γ-Al₂O₃ surface.^24–28 These effects would be considered as a part of the future work.

Fig. 1 (a) Side view and (b) top view of the γ-Al₂O₃ slab used in the DFT calculations.

The DFT energies are computed using the combined Gaussian and plane wave method. The PBE functional²⁹ is used to determine exchange and correlation. It is supplemented by Grimme's D3 dispersion correction³⁰ in its Becke–Johnson damping form.³¹ Goedecker–Teter–Hutter pseudopotentials are used for the core–valence interactions and a polarized double-ζ (m-DZVP) basis set^32,33 is used to expand the Kohn–Sham valence orbitals. All the calculations are performed at Γ-point only. An energy cutoff of 800 Ry is used for all the calculations. The simulation cell geometry is treated non-periodically in Z-direction. Martyna–Tuckerman Poisson solver³⁴ is used to handle electrostatics of the non-periodic geometry. The adsorption energy is defined as

E_ads = E_{slab+adsorbate} − E_slab − E_adsorbate

For metal cluster calculations, an 18 atom Ru cluster is used. The metal cluster was first geometry optimized on its own before its adsorption on the γ-Al₂O₃ surface. The combined metal cluster and γ-Al₂O₃ geometry was then energy minimized before studying the effect of surface charge on adsorption. The metal cluster consists of two atomic layers Ru atoms (see ESI,† Fig. S5). Several adsorption sites on the top layer were considered while calculating adsorption energies of different adsorbates corresponding to typical adsorption sites considered for adsorption on Ru 0001 surface.³⁵

We also calculated the Gibbs free energies to determine the effects of finite temperatures on adsorption characteristics. The Gibbs free energy calculations also help us improve the compatibility of our calculations with other literature on nitrogen reduction. The Gibbs free energies for the surface–adsorbate systems were calculated using truncated Hamiltonian. We considered adsorbates and their nearest neighbors on the γ-Al₂O₃ slab to calculate the vibrational mode with the commonly made assumption that only the atoms close to the adsorbates have strongly coupled vibrational modes.³⁶ Additional details about these calculations can be found in the ESI,† Section S2.

2.1. Modelling the surface charge

The calculations of the charged system are also performed following the work of Bal et al.¹⁷ Briefly, a proton is fixed far from the γ-Al₂O₃ slab in the Z-direction (40 Å location on the Z-axis). The entire system is then forced to be charge neutral. This introduces an extra electron on the surface. Again, the Martyna–Tuckerman Poisson solver³⁴ is used to handle electrostatics. For the γ-Al₂O₃ geometry used in this work, one extra electron leads to an electron density of −0.06 C m⁻². Spin unrestricted calculations were performed in the case of single metal atom and metal atom cluster. To make sure that correct methodology has been used for the DFT calculations, the calculations were validated using the results in Bal et al.¹⁷ Additional details about the calculations are reported in ESI,† Sections S1–S3.

As mentioned earlier, an experimental study by Ambrico et al.¹⁸ found that in plasma environments, excess electrons accumulate on alumina surface with energies of around 1 eV and a lifetime of several days. Additionally, experimental measurements³⁷ on alumina exposed to a multi-filament atmospheric pressure dielectric barrier discharge (DBD) put the plasma-induced surface electron density in the order of 10¹⁵–10¹⁷ m⁻², equal to the charge density of 10⁻⁴–10⁻² C m⁻², close to values used here. Besides, Q. Zhang et al.³⁸ did simulations on atmospheric pressure dielectric barrier discharge (DBD) to demonstrate that surface charging with an absolute density of 10¹⁷ m⁻², equal to the charge density of 10⁻² C m⁻², can play an important role in the streamer propagation and discharge enhancement inside catalyst pores, and in the plasma distribution along the dielectric surface. For the level of charging with γ-Al₂O₃ geometry used in this work, we introduced an electron density of −0.06 C m⁻², following the work of Bal et al.¹⁷ In the view of these results, the amount of charge we are introducing to the surface in this work is a reasonable approximation. All the geometry parameters as well as partial atomic charges for adsorbed species are provided in the ESI,† Sections S4 and S5.

3. Results and discussions

3.1. Adsorption on γ-Al₂O₃(110)

The adsorption energy of an adsorbate is strongly dependent on the adsorption site. 7 different adsorption sites. These adsorption sites including 2 or 3 coordinated O atoms and 3 or 4 coordinated Al atoms were explored on the γ-Al₂O₃(110) surface (see ESI,† Fig. S2). N and N₂ atom adsorption energies were calculated for all these adsorption sites (see Table S31, ESI†). The adsorption energies from the most stable adsorption site are listed in Table S2. N₂ adsorbs most strongly on the 3-coordinated Al atom on the support. The adsorbed N₂ geometry is in vertical position tilting away from oxygen atoms bonded to the Al atom as shown in Fig. 2.

Fig. 2 Adsorption geometries of most favorable (a) N and (b) N₂ adsorption configurations on γ-Al₂O₃.

This adsorption geometry is similar to that of NO adsorption on γ-Al₂O₃.³⁹ The N-atom prefers the bridge site between 4-coordinated Al and 3-coordinated oxygen. The adsorption energy change for nitrogen adsorbates on other adsorption sites is listed in the ESI,† Table S31. We also found that the optimal adsorption site remains the same even upon surface charging. As these adsorption energies are typically smaller than adsorption energies on single metal atoms, the support would not play an important role in nitrogen species adsorption process unless the metal sites are saturated with nitrogen species.

3.2. Metal atom adsorption on γ-Al₂O₃

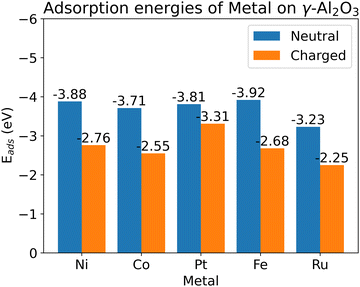
We chose 5 different catalyst candidates to understand the effect of surface charging including Ni, Co, Pt, Fe, and Ru. We chose Fe, Ru, Ni, Co, and Pt to understand the effect of surface charging as these are some of the common catalyst materials used in plasma synthesis of NH₃. Please note that other metals (Ag or Au) have also been shown to be effective catalysts^3,4 for NH₃ synthesis. The optimal metal atom adsorption sites were taken from the literature.¹⁷ The optimum adsorption configuration is the one where the metal atom is coordinated by two oxygen atoms (see Fig. 3). Fig. 4 shows the adsorption energies for all the investigated metals on a charged and neutral support. Surface charging results in the reduction of adsorption energy of around 0.6–1.2 eV for all the metals.

Fig. 3 Typical adsorption geometries obtained using DFT calculations with (a) metal (M: Ru) on support (Al₂O₃), (b) N₂ as adsorbate (Ads) with metal atom on support, and (c) N₂ as adsorbate with metal cluster on support (atom colors: red-oxygen, blue-nitrogen, green-ruthenium, and gray: aluminum).

Fig. 4 Adsorption energies of metal atoms on γ-Al₂O₃ support with and without surface charging.

As pointed out in Bal et al.,¹⁷ metal adsorption on γ-Al₂O₃ support is a redox reaction. Hence, an additional surface electron prevents further reduction of the support through adsorption. Therefore, the metal atom adsorption energy reduces on surface charging. One of the indicators for this hypothesis is that metal–support bonding is mostly ionic in nature. Bal et al. used lack of overlap between the PDOS of metal atoms and the support oxygen to support this hypothesis. Our calculations show (see ESI,† Section S7) that it might not be the case for all the metal atoms. For example, Fe PDOS shows a relatively larger overlap with surface O-atom PDOS. This could result in a metal–surface binding that is not completely ionic in nature. Although all the metal adsorption energies reduce upon surface charging, the metal–surface atom interaction is dependent on the metal atom involved. The metal atoms also become more negatively charged (partial charge) upon surface charging (see ESI,† Section S5).

3.3. N, N₂, and NH₃ adsorption on M–γ-Al₂O₃

Since N₂ adsorption and dissociation reaction is the most important reaction that limits the catalytic synthesis of NH₃, in this study, we chose to focus on the modeling of the charge effect on adsorption energies. The effect of surface charge on the adsorption of 7 different adsorbates (N, N₂, H, H₂, NH, NH₂, and NH₃) involved in NH₃ synthesis on the metal atoms adsorbed on the support is investigated. Later, the surface charge effects are also explored for a metal nanocluster supported by γ-Al₂O₃. We chose Fe, Ru, Ni, Co, and Pt to understand the effect of surface charging although other metals have also been shown to be effective catalysts.^3,4

All the adsorbates investigated in this work show significant changes in adsorption energies on different M–Al₂O₃ systems (Fig. 5). N₂ binds vertically to the metal atom tilting away from the O-atoms coordinated with the metal atom (see Fig. 3(b)). Single metal atoms on the support provide a better adsorption site for N₂ to bind compared to the support sites except in the case of neutral Fe. N₂ and N adsorption energy data on support is provided in the ESI,† Section S4. The N₂ adsorbs most strongly on Pt atom, closely followed by Ru. It adsorbs on Ni, Co, and Fe even less favorably in decreasing order. These adsorption energies are higher than the adsorption energies reported for pure metal surfaces in the literature^35,40–42 as we use a single metal atom model. Interestingly, the trend between Ni and Co as well as the adsorption geometry is also observed by Ma et al.⁴³ in the case of M–WSe₂ system. The adsorption energy increases significantly upon the addition of an extra electron to the M–Al₂O₃ system as shown in Fig. 2(b). The effect of the added charge is not the same for all the metals. Fe, which shows the lowest binding energy on the neutral surface, also shows the highest increase in the binding due to the surface charge. The binding energy of N₂ still decreases in the order of Pt > Ru > Co> Ni > Fe.

Fig. 5 (a) N, (b) N₂, and (c) NH₃ adsorption energies on neutral (blue bars) and charged (orange bars) M–Al₂O₃. M indicates different single metal atoms as specified on the x-axis.

Similarly, in case of atomic N, introduction of the surface charge increases the adsorption energy (see Fig. 2(a)). However, the change in adsorption energy is not as strong as in the case of N₂. Here, N-atom binds most strongly to Ru, followed by Pt and Fe. Introduction of surface charging does not change this order. Again, The N-atom prefers binding exclusively to the metal atom, which means that the substrate is unlikely to play an important role in N-adsorption unless the metal catalysts are saturated with nitrogen. As opposed to all these adsorbates, NH₃ desorption is favored on all the metal atoms by 0.35–0.45 eV due to surface charging. The easier desorption would further promote NH₃ formation in the presence of plasma for all the metals. The surface charge also binds H, H₂, NH, and NH₂ more strongly to the surface by up to ∼1.2 eV except for Pt–H₂ combination (see ESI,† Section S8).

We also performed additional calculations to determine the Gibbs free energies for all the calculations. Our calculations indicate that the effect of surface charge does not change significantly even if we consider Gibbs free energies. Considering most plasma catalysis ammonia synthesis studies are performed in the temperature range of 300–400 K,⁴⁴ the free energy effects are even smaller in magnitude. The detailed results of our calculations have been added in the ESI† (see ESI,† Section S2) for the interested reader.

3.4. Adsorption on Ru cluster

The calculation results discussed above have been obtained using single metal atoms adsorbed on γ-Al₂O₃ as catalysts. However, a better representation of the plasma catalysis process is a metal cluster adsorbed on the γ-Al₂O₃ surface instead of a single metal atom. We also calculated adsorption energies of nitrogen adsorbates on an 18-atom Ru metal cluster with and without the surface charge. We chose Ru as it is the most effective catalyst for thermal catalytic synthesis of NH₃. Fig. 6 shows that the effect of surface charge on a metal cluster could be as strong as the one observed in the single atom calculations. However, we need to be careful while interpreting the results presented with Ru metal cluster. In case of metal clusters, the size and shape of the metal cluster could strongly affect the observed results. For example, the optimal adsorption site with and without surface charge changes in case of N-atom adsorption on the Ru cluster (see ESI,† Section S9). We also assessed the effect of substrate on the metal cluster adsorption energies (see ESI,† Section S11). We calculated the adsorption energies of N, N₂, and NH₃ on pure metal cluster with and without the surface charge. Introduction of surface charge shows similar trends as cluster–adsorbate system. Our calculations show that adsorption energies for N and N₂ increase, whereas the adsorption energy for NH₃ decreases on pure metal cluster as well.

Fig. 6 (a) Adsorption energies of species on a metal cluster with and without charging and (b) comparison between change in adsorption energies due to surface charging on a metal (Ru) cluster and a single metal (Ru) atom on γ-Al₂O₃ support.

Ru is the best catalysts for thermal catalytic ammonia synthesis due to its optimal nitrogen dissociative adsorption energy. Catalysts with lower and higher nitrogen adsorption energy than Ru produce less NH₃ as per the volcano curve.¹ Ni, Co, and Pt all have lower than optimal nitrogen adsorption energies. The overall increase in N-atom adsorption energies mean that these catalysts with lower than optimal nitrogen adsorption energies would become better catalysis candidates. Mehta et al.¹⁰ investigated non-equilibrium plasma synthesis of ammonia using Ru, Fe, Ni, Co, and Pt as catalysts supported on γ-Al₂O₃ using modelling and experiments. Their investigation found that Ni and Co give better site time yield than Ru and Fe, whereas Pt provides a site time yield between that of Ru and Fe. They attribute this effect mainly to the vibrational excitation of the N₂. However, the DFT calculations presented above show that the N-atom adsorption energy increases across the board for all 5 metal atoms along with a decrease in NH₃ desorption energy. This means that Ni, Co, and Pt would become better catalysis candidates compared to Ru and Fe in plasma environments. This agreement with the experimental observations indicates that surface charging could be an important factor behind this observation along with vibrational excitation of N₂.

3.5. Scaling relations changes

The modelling of thermal catalysis of NH₃ relies on scaling relations between key steps involved in the catalysis. For example, a linear relationship can be established between H and N adsorption energies for different metal catalysts.⁴⁵ These linear scaling relations have been established between all the reaction energies and barriers involved in the catalytic synthesis of NH₃ and the dissociative adsorption energy of nitrogen.¹ However, our calculations show that the surface charge effect on adsorption energy is different for different metals. Fig. 7 shows E_ads-H as a function of E_ads-N for charged and neutral surfaces. We do not observe a linear relationship between E_ads-H and E_ads-N for the neutral surfaces as these calculations are performed on a single metal atom catalyst.

Fig. 7 Single metal atom adsorption energy correlations for atomic N and H on a (a) charged and (b) neutral surface.

More importantly though, the change of overall trend upon the introduction of surface charge means that the scaling relations could change due to surface charging. Similar observations have been found for adsorption energies of other intermediates (NH, NH₂, NH₃) important for NH₃ formation (see ESI,† Section S10). As the effect of surface charge is also observed on Ru metal cluster, we believe that the scaling relations could potentially change for larger systems as well. This change in the energy trends means NH₃ formation in plasma catalysis might not have the same dependence on N adsorption energy as thermal catalysis. However, we will need to calculate reaction energies and barriers for all key reactions with and without surface charging with larger metal-substrate models to quantify the effect of change in scaling relations.

3.6. Effect of surface charge on reaction energies

Following table lists the changes to reaction energies for Fe, Ru, Co, Ni, and Pt. Please note that as our simulation system (single metal) is different compared to typical calculation systems (metal slabs), the absolute values are not directly comparable to the literature. Hence, we report the changes to the reaction energies due the surface charge calculated as following:

ΔRE_Charge = RE_Charge − RE_Neutral

This comparison (Table 1) shows three major trends (1) Dissociative adsorption of N and H becomes more favorable across the board whereas 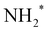and formation less so. (2) desorption also becomes more favorable with surface charging. (3) Following the changes in adsorption energies, reaction energy changes due to surface charge are quantitatively inconsistent across different metals. This behavior also makes changes to the reaction energy of NH* formation inconsistent for different metals. However, these calculations are performed on a relatively simpler model. Additional calculations, involving reaction energies and barriers, on larger metal clusters would be required to quantify the effect of surface charge properly. The current calculations do suggest that surface charging could play an important role in plasma catalysis of ammonia.

Table 1 Difference between reaction energies due to surface charging for different metals. The difference is calculated as ΔRE_Charge = RE_Charge − RE_Neutral

Reaction	Ni	Co	Ru	Pt	Fe
ΔRECharge: N2 → 2N* (eV)	−0.34	−1.44	−0.49	−0.33	−1.27
ΔRECharge: H2 → 2H* (eV)	−1.32	−0.63	−0.23	−1.29	−0.37
ΔRECharge: N* + H* → NH* + * (eV)	0.03	−0.04	−0.20	0.65	0.05
ΔRECharge: NH* + H* → NH2* + * (eV)	1.07	0.71	0.59	0.53	0.24
ΔRECharge: NH2* + H* → NH3* + * (eV)	1.40	1.44	0.63	1.16	1.34
ΔRECharge: NH3* → NH3 + * (eV)	−0.36	−0.44	−0.45	−0.38	−0.44

---

4. Conclusions and future work

In summary, it is found that the introduction of surface charge increases the nitrogen adsorption energies on single metal atoms. Surface charge also facilitates NH₃ desorption and changes the binding energies of H, H₂, NH, and NH₂. It is revealed that the changes in adsorption energies due to surface charging are different for all the metals. However, the predicted higher nitrogen adsorption and easier desorption of NH₃ by surface charge could potentially provide a new mechanism to explain and control the enhanced plasma catalytic performance of Ni, Co, and Pt. Additionally, the effect of surface charge is not the same for all M–Al₂O₃ systems. A comparison of atomic N and H adsorption energy change indicates that scaling relations of adsorption energy could change dramatically due to surface charging effect. As a result, the NH₃ linear scaling relations might not hold in plasma environment. Hence, surface charging could play an important role in and provide a new method to enhance plasma catalytic NH₃ synthesis. However, additional simulations would be required to quantify these effects properly.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Y. J. was supported by the U.S. Department of Energy under Award # DE-SC0023357 and Award # DE-AC0209CH11466. Y. J. also acknowledges support from the U.S. National Science Foundations under Award # EFMA 2029425.

References

1. A. Vojvodic, A. J. Medford, F. Studt, F. Abild-Pedersen, T. S. Khan, T. Bligaard and J. K. Nørskov, Exploring the Limits: A Low-Pressure, Low-Temperature Haber-Bosch Process, Chem. Phys. Lett., 2014, 598, 108–112,  DOI:10.1016/j.cplett.2014.03.003.
2. K. H. R. Rouwenhorst and L. Lefferts, On the Mechanism for the Plasma-Activated N₂ dissociation on Ru Surfaces, J. Phys. D: Appl. Phys., 2021, 54(39) DOI:10.1088/1361-6463/ac1226.
3. T. W. Liu, F. Gorky, M. L. Carreon and D. A. Gómez-Gualdrón, Energetics of Reaction Pathways Enabled by N and H Radicals during Catalytic, Plasma-Assisted NH₃ Synthesis, ACS Sustainable Chem. Eng., 2022, 10(6), 2034–2051,  DOI:10.1021/acssuschemeng.1c05660.
4. M. Iwamoto, M. Akiyama, K. Aihara and T. Deguchi, Ammonia Synthesis on Wool-like Au, Pt, Pd, Ag, or Cu Electrode Catalysts in Nonthermal Atmospheric-Pressure Plasma of N₂ and H₂, ACS Catal., 2017, 7(10), 6924–6929,  DOI:10.1021/acscatal.7b01624.
5. M. L. Carreon, Plasma Catalytic Ammonia Synthesis: State of the Art and Future Directions, J. Phys. D: Appl. Phys., 2019, 52(48) DOI:10.1088/1361-6463/ab3b2c.
6. J. R. Shah, F. Gorky, J. Lucero, M. A. Carreon and M. L. Carreon, Ammonia Synthesis via Atmospheric Plasma Catalysis: Zeolite 5A, a Case of Study, Ind. Eng. Chem. Res., 2020, 59(11), 5167–5176,  DOI:10.1021/acs.iecr.9b05220.
7. H. Zhao, G. Song, Z. Chen, X. Yang, C. Yan, S. Abe, Y. Ju, S. Sundaresan and B. E. Koel, In Situ Identification of NNH and N₂H₂ by Using Molecular-Beam Mass Spectrometry in Plasma-Assisted Catalysis for NH₃ Synthesis, ACS Energy Lett., 2022, 7(1), 53–58,  DOI:10.1021/acsenergylett.1c02207.
8. P. Mehta, P. M. Barboun, Y. Engelmann, D. B. Go, A. Bogaerts, W. F. Schneider and J. C. Hicks, Plasma-Catalytic Ammonia Synthesis beyond the Equilibrium Limit, ACS Catal., 2020, 10(12), 6726–6734,  DOI:10.1021/acscatal.0c00684.
9. P. Barboun, P. Mehta, F. A. Herrera, D. B. Go, W. F. Schneider and J. C. Hicks, Distinguishing Plasma Contributions to Catalyst Performance in Plasma-Assisted Ammonia Synthesis, ACS Sustainable Chem. Eng., 2019, 7(9), 8621–8630,  DOI:10.1021/acssuschemeng.9b00406.
10. P. Mehta, P. Barboun, F. A. Herrera, J. Kim, P. Rumbach, D. B. Go, J. C. Hicks and W. F. Schneider, Overcoming Ammonia Synthesis Scaling Relations with Plasma-Enabled Catalysis, Nat. Catal., 2018, 1(4), 269–275,  DOI:10.1038/s41929-018-0045-1.
11. A. Bogaerts, X. Tu, J. C. Whitehead, G. Centi, L. Lefferts, O. Guaitella, F. Azzolina-Jury, H. H. Kim, A. B. Murphy, W. F. Schneider, T. Nozaki, J. C. Hicks, A. Rousseau, F. Thevenet, A. Khacef and M. Carreon, The 2020 Plasma Catalysis Roadmap, J. Phys. D: Appl. Phys., 2020, 53(44) DOI:10.1088/1361-6463/ab9048.
12. T. Mizushima, K. Matsumoto, H. Ohkita and N. Kakuta, Catalytic Effects of Metal-Loaded Membrane-like Alumina Tubes on Ammonia Synthesis in Atmospheric Pressure Plasma by Dielectric Barrier Discharge, Plasma Chem. Plasma Process., 2007, 27(1), 1–11,  DOI:10.1007/s11090-006-9034-2.
13. Y. Wang, M. Craven, X. Yu, J. Ding, P. Bryant, J. Huang and X. Tu, Plasma-Enhanced Catalytic Synthesis of Ammonia over a Ni/Al₂O₃ Catalyst at Near-Room Temperature: Insights into the Importance of the Catalyst Surface on the Reaction Mechanism, ACS Catal., 2019, 10780–10793,  DOI:10.1021/acscatal.9b02538.
14. K. H. R. Rouwenhorst, H. H. Kim and L. Lefferts, Vibrationally Excited Activation of N₂ in Plasma-Enhanced Catalytic Ammonia Synthesis: A Kinetic Analysis, ACS Sustainable Chem. Eng., 2019, 7(20), 17515–17522,  DOI:10.1021/acssuschemeng.9b04997.
15. W. Somers, A. Bogaerts, A. C. T. Van Duin and E. C. Neyts, Plasma Species Interacting with Nickel Surfaces: Toward an Atomic Scale Understanding of Plasma-Catalysis, J. Phys. Chem. C, 2012, 116(39), 20958–20965,  DOI:10.1021/jp307380w.
16. W.-C. Chung and M.-B. Chang, Dry Reforming of Methane by Combined Spark Discharge with a Ferroelectric, Energy Convers. Manage., 2016, 124, 305–314,  DOI:10.1016/j.enconman.2016.07.023.
17. K. M. Bal, S. Huygh, A. Bogaerts and E. C. Neyts, Effect of Plasma-Induced Surface Charging on Catalytic Processes: Application to CO₂ Activation, Plasma Sources Sci. Technol., 2018, 27(2) DOI:10.1088/1361-6595/aaa868.
18. P. F. Ambrico, M. Ambrico, A. Colaianni, L. Schiavulli, G. Dilecce and S. De Benedictis, Thermoluminescence Study of the Trapped Charge at an Alumina Surface Electrode in Different Dielectric Barrier Discharge Regimes, J. Phys. D: Appl. Phys., 2010, 43(32) DOI:10.1088/0022-3727/43/32/325201.
19. A. Jafarzadeh, K. M. Bal, A. Bogaerts and E. C. Neyts, CO₂ Activation on TiO₂-Supported Cu5 and Ni5 Nanoclusters: Effect of Plasma-Induced Surface Charging, J. Phys. Chem. C, 2019, 123(11), 6516–6525,  DOI:10.1021/acs.jpcc.8b11816.
20. A. Jafarzadeh, K. M. Bal, A. Bogaerts and E. C. Neyts, Activation of CO₂ on Copper Surfaces: The Synergy between Electric Field, Surface Morphology, and Excess Electrons, J. Phys. Chem. C, 2020, 124(12), 6747–6755,  DOI:10.1021/acs.jpcc.0c00778.
21. W. C. Chung and M. B. Chang, Dry Reforming of Methane by Combined Spark Discharge with a Ferroelectric, Energy Convers. Manage., 2016, 124, 305–314,  DOI:10.1016/j.enconman.2016.07.023.
22. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An Electronic Structure and Molecular Dynamics Software Package -Quickstep: Efficient and Accurate Electronic Structure Calculations, J. Chem. Phys., 2020, 152(19) DOI:10.1063/5.0007045.
23. M. Digne, P. Sautet, P. Raybaud, P. Euzen and H. Toulhoat, Use of DFT to Achieve a Rational Understanding of Acid-Basic Properties of γ-Alumina Surfaces, J. Catal., 2004, 226(1), 54–68,  DOI:10.1016/j.jcat.2004.04.020.
24. S. Liu, Z. Zhou, J. Chen, Y. Fu and C. Cai, Adsorption and Decomposition of CO2 on γ-Al₂O₃(100): First-Principles Investigation, Appl. Surf. Sci., 2023, November 2022, 611,  DOI:10.1016/j.apsusc.2022.155645.
25. X. Wang, C. Cai and G. Zhou, Effect of Water Vapor on Alumina Scale Growth Based on First-Principles Calculations, J. Phys. Chem. C, 2021, 125(18), 9736–9746,  DOI:10.1021/acs.jpcc.1c00941.
26. H. L. Li, F. Q. Dong, L. Bian, T. T. Huo, X. C. He, F. Zheng, Z. Z. Lv, L. M. Jiang and B. Li, Heterogeneous Oxidation Mechanism of SO₂ on γ-Al₂O₃(110) Catalyst by H₂O₂: A First-Principle Study, Colloids Surf., A, 2021, 611, 125777,  DOI:10.1016/j.colsurfa.2020.125777.
27. A. Abbaspour Tamijani, L. J. Augustine, J. L. Bjorklund, J. G. Catalano and S. E. Mason, First-Principles Characterisation and Comparison of Clean, Hydrated, and Defect α-Al₂O₃ and α-Fe₂O₃ (110) Surfaces, Mol. Simul., 2022, 48(3), 247–263,  DOI:10.1080/08927022.2021.2009117.
28. J. Saavedra, C. J. Pursell and B. D. Chandler, CO Oxidation Kinetics over Au/TiO₂ and Au/Al₂O₃ Catalysts: Evidence for a Common Water-Assisted Mechanism, J. Am. Chem. Soc., 2018, 140(10), 3712–3723,  DOI:10.1021/jacs.7b12758.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
30. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15) DOI:10.1063/1.3382344.
31. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465,  DOI:10.1002/jcc.21759.
32. M. Krack, Pseudopotentials for H to Kr Optimized for Gradient-Corrected Exchange-Correlation Functionals, Theor. Chem. Acc., 2005, 114(1–3), 145–152,  DOI:10.1007/s00214-005-0655-y.
33. S. Goedecker and M. Teter, Separable Dual-Space Gaussian Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(3), 1703–1710,  DOI:10.1103/PhysRevB.54.1703.
34. G. J. Martyna and M. E. Tuckerman, A Reciprocal Space Based Method for Treating Long Range Interactions in Ab Initio and Force-Field-Based Calculations in Clusters, J. Chem. Phys., 1999, 110(6), 2810–2821,  DOI:10.1063/1.477923.
35. J. A. Herron, S. Tonelli and M. Mavrikakis, Atomic and Molecular Adsorption on Ru(0001), Surf. Sci., 2013, 614, 64–74,  DOI:10.1016/j.susc.2013.04.002.
36. J. M. P. Martirez and E. A. Carter, First-Principles Insights into the Thermocatalytic Cracking of Ammonia-Hydrogen Blends on Fe(110): 1. Thermodynamics, J. Phys. Chem. C, 2022, 126(46), 19733–19744,  DOI:10.1021/acs.jpcc.2c06003.
37. F. J. J. Peeters, R. F. Rumphorst and M. C. M. Van De Sanden, Dielectric Barrier Discharges Revisited: The Case for Mobile Surface Charge, Plasma Sources Sci. Technol., 2016, 25(3) DOI:10.1088/0963-0252/25/3/03LT03.
38. Q. Z. Zhang, W. Z. Wang and A. Bogaerts, Importance of Surface Charging during Plasma Streamer Propagation in Catalyst Pores, Plasma Sources Sci. Technol., 2018, 27(6) DOI:10.1088/1361-6595/aaca6d.
39. D. Mei, Q. Ge, J. Szanyi and C. H. F. Peden, First-Principles Analysis of NOx Adsorption on Anhydrous γ-Al₂O₃ Surfaces, J. Phys. Chem. C, 2009, 113(18), 7779–7789,  DOI:10.1021/jp8103563.
40. Y. Bai, D. Kirvassilis, L. Xu and M. Mavrikakis, Atomic and Molecular Adsorption on Ni(111), Surf. Sci., 2019, 679, 240–253,  DOI:10.1016/j.susc.2018.08.004.
41. L. Xu, D. Kirvassilis, Y. Bai and M. Mavrikakis, Atomic and Molecular Adsorption on Fe(110), Surf. Sci., 2018, 667, 54–65,  DOI:10.1016/j.susc.2017.09.002.
42. D. C. Ford, Y. Xu and M. Mavrikakis, Atomic and Molecular Adsorption on Pt(111), Surf. Sci., 2005, 587(3), 159–174,  DOI:10.1016/j.susc.2005.04.028.
43. X. Ma, J. Hu, M. Zheng, D. Li, H. Lv, H. He and C. Huang, N2 Reduction Using Single Transition-Metal Atom Supported on Defective WS2 Monolayer as Promising Catalysts: A DFT Study, Appl. Surf. Sci., 2019, 489, 684–692,  DOI:10.1016/j.apsusc.2019.05.022.
44. P. Peng, P. Chen, C. Schiappacasse, N. Zhou, E. Anderson, D. Chen, J. Liu, Y. Cheng, R. Hatzenbeller, M. Addy, Y. Zhang, Y. Liu and R. Ruan, A Review on the Non-Thermal Plasma-Assisted Ammonia Synthesis Technologies, J. Cleaner Prod., 2018, 177, 597–609,  DOI:10.1016/j.jclepro.2017.12.229.
45. A. Vojvodic, A. J. Medford, F. Studt, F. Abild-Pedersen, T. S. Khan, T. Bligaard and J. K. Nørskov, Exploring the Limits: A Low-Pressure, Low-Temperature Haber-Bosch Process, Chem. Phys. Lett., 2014, 598, 108–112,  DOI:10.1016/j.cplett.2014.03.003.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp06050k

---