 Open Access Article
Open Access ArticleTowards understanding the lower CH4 selectivity of HCP-Co than FCC-Co in Fischer–Tropsch synthesis†
Dan
Luo
ab,
Xingchen
Liu
 *bc,
Tong
Chang
a,
Jiawei
Bai
b,
Wenping
Guo
d,
Wentao
Zheng
b and
Xiaodong
Wen
*bc,
Tong
Chang
a,
Jiawei
Bai
b,
Wenping
Guo
d,
Wentao
Zheng
b and
Xiaodong
Wen
 *bcd
*bcd
aShanxi Key Laboratory of Ecological Protection and Resources Utilization of Yuncheng Salt Lake, Department of Applied Chemistry, Yuncheng University, 1155 Fudan West Street, Yuncheng 044000, China
bState Key Laboratory of Coal Conversion, Institute of Coal Chemistry, Chinese Academy of Sciences, Taiyuan, 030001, China. E-mail: liuxingchen@sxicc.ac.cn; wxd@sxicc.ac.cn
cUniversity of Chinese Academy of Sciences, No. 19A Yuquan Road, Beijing, 100049, P. R. China
dNational Energy Center for Coal to Liquids, Synfuels China Co., Ltd, Huairou District, Beijing, 101400, China
First published on 16th January 2024
Abstract
In Fischer–Tropsch synthesis (FTS), the cobalt catalyst has higher C5+ and lower CH4 selectivity in the hcp phase than in the fcc phase. However, a detailed explanation of the intrinsic mechanism is still missing. The underlying reason was explored combining density functional theory, Wulff construction, and a particle-level descriptor based on the slab model of surfaces that are prevalent in the Wulff shape to provide single-particle level understanding. Using a particle-level indicator of the reaction rates, we have shown that it is more difficult to form CH4 on hcp-Co than on fcc-Co, due to the larger effective barrier difference of CH4 formation and C–C coupling on hcp-Co particles, which leads to the lower CH4 selectivity of hcp-Co in FTS. Among the exposed facets of fcc-Co, the (311) surface plays a pivotal role in promoting CH4 formation. The reduction of CH4 selectivity in cobalt-based FTS is achievable through phase engineering of Co from fcc to hcp or by tuning the temperature and size of the particles.
1. Introduction
The ultimate goal for catalysis study is to design catalysts with high stability, activity, and selectivity. Although the design principles for catalysts of high stability and activity have been well-established,1,2 it remains a substantial challenge to understand the relationship between the structure of a catalyst and its selectivity, especially for reactions with complex product distributions. A typical example for which selectivity is intricate is Fischer–Tropsch synthesis (FTS), which converts the simple mixture of CO and H2 (syngas) to a broad spectrum of chemicals (C1–C70+), including methane, paraffins, olefins, and different oxygenated species such as aldehydes, ketones, acids, and alcohols.3 Co-based catalysts are widely used in the low-temperature FTS process, due to their high activity, relatively high selectivity to long-chain paraffins, and low water–gas shift side reactions.4–7 Still, in the FTS process, methanation is the main competing pathway for chain growth.8–10 To date, a great deal of effort has been devoted to controlling the product distribution of FTS by changing the catalyst formulations.11–15It is generally accepted that the catalytic performances of inorganic solids can be tuned by their composition,11,16 crystallographic structure (phase),17,18 size,19,20 shape,21 chelating molecular ligands,22,23 and support.24 Among these factors, the crystalline phase lies at the heart of the structural parameters for solids of given composition. It determines how the constituents (atoms or ions) are arranged in a highly ordered microscopic structure, and governs the electronic structures and surface atomic geometry of catalysts.18,25 Besides the most stable phase, the various metastable phases of the catalysts can usually be stabilized by the reactive gas/liquid and often high-temperature environments,26–29 which makes it possible to modulate the catalytic performances of materials by phase engineering.
Chen et al.30 found that the 4H Cu and 4H/fcc Cu shells exhibit greater CO2 reduction reaction activity and better C2H4 selectivity compared to fcc Cu, demonstrating the crystal phase-dependent C2H4 selectivity of Cu. Alumina with different crystal phases shows that CoMo/θ-Al2O3 has a much higher hydrodesulfurization selectivity than CoMo/γ-Al2O3 and CoMo/δ-Al2O3.31 The sorption and catalytic behavior observed between the alkaline ferrites studied are associated with the crystal structures and alkali composition.32 In FTS, Gnanamani et al.33 used a different catalyst reduction process to obtain distinct phases of cobalt, and found that the hcp phase shows higher CO conversion and lower CH4 selectivity than the fcc phase. Du et al.34 found that the multistep activation process derived catalyst (CoZr/AC-RSCR) with more hcp phase has higher CO conversion and lower CH4 selectivity than the H2 reduction derived catalyst (CoZr/AC-R) with more fcc phase.
However, despite the extensive experimental observations of phase-dependent product selectivity of catalysts, the connection between the crystalline phase of a catalyst and its product selectivity remains obscure. A major obstacle in experiments is that the catalyst particles with known crystal phases are composed of multiple facets, due to which their identity and functioning mechanism may be different. It has been proposed by Zhong et al. that different crystal phases have different surface reactivities because of the distinct intrinsic surface strains.35 It has been demonstrated that the isolated Pd sites on the surfaces of the particles determine the high selectivity in acetylene semi-hydrogenation reaction for intermetallic Pd-X (X = Ga or In) materials with multiple phases.36 Several theoretical studies on the CH4 selectivity of Fe5C2 surfaces also showed that the selectivity is highly facet dependent.37,38
In FTS reactions, the selectivity of products is mainly determined by the competition of the coupling between C + H and C + C.39,40 Due to the interrelated nature of all individual selectivities indicated by the linear relationship between the individual C1–C4 hydrocarbon selectivities and the C5+ selectivity,8–10 CH4 selectivity can be used as an indicator of the product selectivity in FTS.41,42 Hydrogenation of carbon species, which is produced through CO dissociation, is the major pathway to CH4 formation, and it has been well accepted that CH3 + H → CH4 is the rate-determining step.38,41,43 Previously, the CH4 selectivity of a few intuitively selected Co surfaces has been studied, such as the (100), (110), (111) and (311) of fcc-Co by Yu et al.44 and the (0001) of hcp-Co by Cheng et al.45 However, as the overall CH4 selectivity of a Co particle is contributed by all its exposed facets, the fundamental cause for the lower CH4 selectivity of hcp-Co than fcc-Co remains elusive.
In this work, we propose to use a theoretical approach to investigate the correlation between the crystalline phases of Co (hcp and fcc) and their CH4 selectivity at the single particle level using the slab model of surfaces that are prevalent in the Wulff shape. CH4 selectivity of hcp-Co and fcc-Co was evaluated by considering the competition between CH4 formation and C1 + C1 coupling on all the prominent surfaces that covers the exterior of particles based on the Wulff theorem. The facet dependent effective barriers for CH4 selectivity were then integrated into a particle-level energy descriptor46 and compared between hcp and fcc Co. Finally, the conditions for phase transition between hcp and fcc were explored with respect to temperature and nanoparticle size to obtain catalysts with higher performances. We envision that our proposed strategy can effectively scoop out the selectivity information of probe reactions occurring on each facet and thereby reasonably add-up these results to represent those of the single particle level. As such, this approach allows us to understand the difference in the intrinsic selectivity of particles with different crystalline phases. We anticipate that this simplified strategy not only can lessen the gap between theoretical methodology and experimental understanding in cobalt-catalyzed FTS study, but may also be applicable to other catalysis systems to understand the correlation between the crystal phase and product selectivity.
2. Methods and models
2.1 Computational details
All DFT calculations were performed using the Vienna Ab Initio simulation package (VASP).47,48 The electron–ion interaction was described with the projector augmented wave (PAW) method.49,50 The electron exchange and correlation energies were treated within the generalized gradient approximation in the Perdew–Burke–Ernzerhof formalism (GGA-PBE).51 The different cutoff energies are given in Tables S1 and S2 (ESI†); according to the energy and lattice constant of bulk cobalt, the cutoff of plane wave basis set was set up to 450 eV. The Monkhorst–Pack k-point sampling was used. Electron smearing was employed according to the Methfessel–Paxton52 technique, with a smearing width σ = 0.2 eV. Due to the large influence of magnetic properties on the adsorption energies, spin polarization was taken into consideration. To locate transition states, we used the Nudged Elastic Band (NEB) method.53 A vibrational frequency analysis was performed to verify whether a transition state is associated with a single imaginary frequency.2.2 Model
Slab models of surfaces that are prevalent in the Wulff shapes were utilized as proxies of the cobalt particles. For the hcp-Co and fcc-Co surfaces, the optimized lattice constants of hcp-Co (a = b = 2.49 Å and c = 4.03 Å) with a 13 × 13 × 7 k-point agree well with the experimental (a = b = 2.51 Å, c = 4.06 Å)54 and calculated (a = b = 2.49 Å, c = 4.03 Å)55 values, which are given in Table S1 (ESI†). The optimized lattice constants of fcc-Co (a = b = c = 3.52 Å) with a 13 × 13 × 13 k-point also agree with the experimental (a = b = c = 3.54 Å)56 and the calculated (a = b = c = 3.52 Å)57 values, which are given in Table S2 (ESI†). We adopted the equilibrium shape of the hcp-Co and fcc-Co particles using Wulff construction at ab initio accuracy reported in the previous work (Fig. 1 and Table S3, ESI†).18 The hcp-Co particles are predicted to be covered by surfaces of (10−11), (10−10), (0001), (10−12), (11−20), and (11−21), while the fcc-Co particles are covered by the surfaces of (111), (100), (311), and (110). We choose unit cells p(4 × 4) for hcp-Co (0001), (11−21), fcc-Co (100), and (111), and p(4 × 2) unit cells for hcp-Co (10−10), (10−11), (10−12), (11−20) and fcc-Co (110), (311), as shown in Fig. 1 and Fig. S1 (ESI†). A 3 × 3 × 1 k-point sampling was used for all surfaces. The atoms in the top two layers of the slab models for hcp-Co and fcc-Co are fully allowed to relax while the bottom two layers atoms are fixed. | ||
| Fig. 1 Wulff construction and the utilized slab models of the prevalent surfaces of hcp-Co and fcc-Co in the Wulff shapes. | ||
2.3 The adsorption energy and reaction barrier
The adsorption energy of C-containing species on cobalt surfaces was calculated according to the equation| Eads = Eslab/X − Eslab − EX, | (1) |
The reaction barrier Ea and the reaction energy Er were calculated according to the equations:
| Ea = ETS − EIS | (2) |
| Er = EFS − EIS | (3) |
To estimate the relative activity of reactions on the particles of different Co phases, we use the concept of particle effective barrier which is a particle-level indicator of the reaction activity defined previously in the literature.45 The particle effective barriers for CH4 formation (Ea_particle,CH4) and the most feasible C1 + C1 coupling (Ea_particle,C1+C1) and the difference of them (ΔEa_particle) were calculated in terms of rates as follows. First, we assume that the overall reaction rate (r) is the sum of the contributions from all the exposed surfaces. This assumption is valid as it has been recently proven unambiguously that in Co-catalyzed FTS reactions, the edges and vertices of the particles are responsible for the CO dissociation, while the C–C and C–H coupling reactions happen mainly on the flat surfaces of the catalyst particles.58,59
Based on the Arrhenius formula, the reaction rate r on a particle with i surfaces can be calculated according to the equation46,60
 | (4) |
 | (5) |
2.4 Phase transition calculation
To obtain the conditions of phase transition between hcp and fcc, the influence of temperature and size on the Gibbs free energy (G) of bulk Co phases was considered. The Gibbs free energy for the solid phase particle is defined as the summation of the Gibbs free energy in the bulk and the surface.61,62 The Gibbs free energy of bulk hcp-Co and fcc-Co was calculated according to the equation in the literature63,64| G = EDFT + Evib+ Esurf | (6) |
| Esurf = γmAm | (7) |
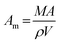 | (8) |
3. Results and discussion
3.1 CH4 formation
We first study the elementary steps of CH4 formation on cobalt surfaces: C + H → CH, CH + H → CH2, CH2 + H → CH3, and CH3 + H → CH4. The methanation potential energy surfaces are given in Fig. 2. The structures of the initial state (IS), transition state (TS), and final state (FS) for the elementary steps are provided in Fig. S1 and S2 (ESI†) and the reaction barriers and reaction energies of hcp-Co and fcc-Co are listed in Tables S4–S6 (ESI†). As shown in Fig. 2, the total energy of the TS has an increasing tendency along the hydrogenation reaction coordinate on most hcp-Co and fcc-Co surfaces, and the addition of the fourth hydrogen is usually the rate-limiting step, which is consistent with previous studies.42,55,67 The increase of the reaction barrier illustrates that C hydrogenation becomes more and more difficult on cobalt surfaces to form CH4. But on (10−12) and (311), the step with the highest barrier is CH2 hydrogenation, which is different from the result of Qin et al.68 and Yu et al.44 This is likely due to the absence of zero point energy corrections in these studies.Following the approach of Cheng,42,69 the effective barriers of CH4 formation (Ea_eff,CH4) were used to evaluate the catalytic activity of the Co surfaces to produce CH4. As CH4 formation happens by stepwise C hydrogenation, the rate-determining step is (CH3 + H → CH4) on most of the Co surfaces. Before the rate-determining step, the preceding hydrogenation steps may reach quasi-equilibrium. Thus, the rate of CH4 formation can be calculated as the rate of the rate-liming step:
rCH4 = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Ea,4/RT]θCH3θH = A exp[−Ea,4/RT]θCH3θH = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(Ea,4 + Er,3)/RT](θCθ*)3θCθH exp[−(Ea,4 + Er,3)/RT](θCθ*)3θCθH | (9) |
Here, A is the pre-exponential factor. θCH3, θC, θH, and θ* are the coverage of CH3, C, H, and the free site on the surface, respectively. R is the ideal gas constant and T is the reaction temperature. Ea,4 is the reaction barrier of CH3 hydrogenation, and Er,3 is the reaction energy for C + 3H → CH3. From eqn (10), it is evident that the effective barrier of CH4 formation (Ea_eff,CH4) can be calculated as (Ea,4 + Er,3), which is essentially the difference between the highest TS energy of CH4 formation (ETS4) and the initial state with one atomic carbon, one atomic oxygen and four atomic hydrogens adsorbed on cobalt surfaces (EC+4H+O)38,41,42 (Fig. 2c).
| Ea_eff,CH4 = Ea,4 + Er,3 = ETS4 − EC+4H+O | (10) |
However, the difference between the barrier from CH3 + H + O toward TS3 is higher than that toward TS4 by 0.53 eV on hcp-Co (10−12), and 0.21 eV on fcc-Co (311), respectively. Since the ratio of hydrogen to the free site coverage θH/θ* is about 1 to 10 under typical reaction conditions (assuming equivalent coverages of H and free site *), the higher barrier of CH3 + * → CH2 + H than CH3 + H → CH4 causes r−3 = k−3θCH3θ* ≪ r4 = k4θCH3θH. Thus, the reaction of CH2 + H → CH3 is irreversible and becomes the rate-determining step on (10−12) and (311), and the rate of CH4 formation on these two surfaces should be calculated as:
RCH4 = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Ea,3/RT]θCH2θH = A exp[−Ea,3/RT]θCH2θH = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(Ea,3 + Er,2)/RT](θH/θ*)2θCθH exp[−(Ea,3 + Er,2)/RT](θH/θ*)2θCθH | (11) |
The effective barrier of CH4 formation (Ea_eff,CH4) on (10−12) and (311) surfaces therefore is determined as the difference between the highest TS energy of CH4 formation (ETS3) and the initial state (EC+4H+O) (Fig. 2d).
| Ea_eff,CH4 = Ea,3 + Er,2 = ETS3 − EC+4H+O | (12) |
To assess the activity of the Co surfaces for CH4 formation, the Ea_eff,CH4 values for all the studied surfaces of hcp and fcc Co are obtained and are plotted in Fig. 3(a). Surprisingly, the CH4 formation activity on hcp is not always lower than that on fcc. The Ea_eff,CH4 of fcc-Co (110), which is the lowest one on fcc-Co, is slightly smaller than that of hcp-Co (0001) and hcp-Co (11−20). The rank of effective barriers is hcp-Co (10−11) > fcc-Co (100) > hcp-Co (10−10) > hcp-Co (11−21) > hcp-Co (10−12) > fcc-Co (311) > hcp-Co (11−20) ≈ fcc-Co (111) ≈ hcp-Co (0001) ≈ fcc-Co (110). It shows that hcp-(0001), hcp-(11−20), fcc-(111) and fcc(110) are all active and have similar catalytic activities in CH4 formation. The rank of the effective barrier for CH4 formation is consistent with previous ab initio studies.44,66
To assess the overall catalytic activity of hcp-Co and fcc-Co phases for CH4 formation, we further calculated the particle effective barriers (Ea_particle,CH4) of CH4 formation on hcp-Co and fcc-Co Wulff particles, assuming that the overall rate of reaction on the catalyst particle is the sum of the rates from all its exposed surfaces (see the Methods section). On hcp-Co, Ea_particle,CH4 is 1.11 eV and on fcc-Co it is 1.02 eV (Fig. 3(a) and Table S7, ESI†). The results indicate that hcp-Co and fcc-Co have similar intrinsic catalytic activity to form CH4.
A weak linear relationship was discovered between Ea_eff,CH4 of the Co surface and the sum of adsorption energies of a C atom and 4 H atoms on it (Eads_C+4H) with R2 of 0.73 on ten surfaces, irrespective of the crystal phase (Fig. 3(b) and Table S8, ESI†). With the adsorption of C and 4 H atoms becoming stronger, the acquired Ea_eff,CH4 follows a downhill trend on the cobalt surfaces, and the higher values of Eads_C+4H are associated with lower Ea_eff,CH4. This linear correlation allows the fast estimation of the effective barrier of CH4 formation on cobalt surfaces, as long as the adsorption energies of C and H are given (Ea_eff,CH4 = −1.10Ead_C+4H − 8.56).
3.2 C1 + C1 coupling
The carbon chain elongation process in FTS was investigated through the carbide mechanism70 (CHi + CHj → CHiCHj, i, j = 0–3) and CO-insertion mechanism71 (CHi + CO → CHiCO, i = 0–3). The structures of the C1 + C1 coupling for IS, TS, FS are shown in Fig. S3–S12 (ESI†), and the reaction barriers and energies are given in Tables S5 and S6 (ESI†).In the carbide mechanism, the CHi + CHj coupling rate is expressed as:
rCHi+CHj = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Ea,i+j/RT]θCHiθCHj = A exp[−Ea,i+j/RT]θCHiθCHj = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(Ea,i+j + Ei + Ej)/RT]θC2(θH/θ*)i+j exp[−(Ea,i+j + Ei + Ej)/RT]θC2(θH/θ*)i+j | (13) |
In the CO-insertion mechanism, the CO + CHj coupling rate is expressed as
rCOi+CHj = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−Ea,CO+j/RT]PCOθCHj = A exp[−Ea,CO+j/RT]PCOθCHj = A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−(Ea,CO+j + Ej)/RT]PCOθC(θH/θ*)j exp[−(Ea,CO+j + Ej)/RT]PCOθC(θH/θ*)j | (14) |
It turns out that the coupling of CHi + CHj, and CHi + CO on ten cobalt surfaces resembles each other, and we hereby use the hcp-Co (0001) surface as an example to demonstrate the most feasible C1 + C1 coupling reaction. The energy profiles of the C1 + C1 coupling reaction on hcp-Co (0001) are shown in Fig. 4. The Ea_eff,i+j of C + CH (0.41 eV), C + CH2 (0.86 eV), and C + CH3 (1.28 eV) gradually increase with the hydrogenation of the carbon atom, indicating that the coupling ability of carbon species will be reduced, due to the increase of the coordination number of the C atom. A similar increasing trend of Ea_eff,+j is observed for CH + CH (0.10 eV), CH + CH2 (0.52 eV), and CH + CH3 (1.38 eV).
We take the hcp-Co (0001) as an example to discuss the C1 + C1 coupling reaction. Since CH4 formation competes with C1 + C1 coupling, if the barrier of a particular C1 + C1 coupling reaction is higher than CH4 formation, then the C1 species will be directly hydrogenated and this C1 + C1 coupling reaction will not be likely to happen. We found that the carbide mechanisms of C + C, C + CH, C + CH2, CH + CH, CH + CH2 reactions are all feasible on hcp-Co (0001), due to their lower Ea_eff,i+j than Ea_eff,CH4. However, the CO-insertion mechanism of C + CO, CH + CO, CH2 + CO, and CH3 + CO coupling reaction all has higher Ea_eff,CO+j than Ea_eff,CH4, indicating that the CO-insertion mechanisms are not favorable on hcp-Co (0001). Among the feasible carbide mechanisms, the CH + CH coupling has the lowest Ea_eff,i+j, and is probably the most favorable pathway among all the C1 + C1 coupling reactions on the hcp-Co (0001) surface.45
For the other hcp-Co and fcc-Co surfaces, the most feasible C1 + C1 coupling pathways are divergent. It is CH + CH on hcp-Co (10−10), (10−12), (11−21), fcc-Co (110), (111), C + CH3 on fcc-Co (311), C + CO on hcp-Co (10−11), fcc-Co (100), and CH + CO on hcp-Co (11−20), as shown in Table 1 and Fig. S13 (ESI†). For most of the surfaces, the reaction of CH + CH coupling is the most favorable pathway among all of the C1 + C1 coupling reactions, which is in line with the findings in ref. 44 and 73.
| (10−10) | (10−11) | (10−12) | (11−20) | (11−21) | (100) | (110) | (111) | (311) | |
|---|---|---|---|---|---|---|---|---|---|
| C1 + C1 | CH + CH | C + CO | CH + CH | CH + CO | CH + CH | C + CO | CH + CH | CH + CH | C + CH3 |
| E a_eff,i+j/Ea_eff,CO+j | 0.05 | 1.42 | 1.21 | 0.18 | 0.67 | 1.05 | 0.20 | −0.01 | 0.77 |
3.3 CH4 selectivity
As Cheng42,72 and Yin, et al.41 have proven, the CH4 selectivity in FTS can be approximately evaluated based on the effective barrier difference of CH4 formation and C1 + C1 coupling.: ΔEa_eff= Ea_eff,CH4 − Ea_eff,C1+C1, where Ea_eff,CH4 is the effective barrier of CH4 formation, and Ea_eff,C1+C1 is the effective barrier of the most feasible C1 + C1 coupling. The CH4 selectivity is thus negatively associated with the value of ΔEa_eff (Fig. 5). | ||
Fig. 5 The effective barrier difference (ΔEa_eff = Ea_eff,CH4 − Ea_eff,C1+C1, the columns) and the particle effective barrier difference (ΔEa_particle, the dashed lines) between CH4 formation and the most feasible C1 + C1 coupling on hcp-Co (0001), (10−10), (10−11), (10−12), (11−20), (11−21), fcc-Co (100), (110), (111), (311), and Fe5C2 (510), (![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 11), (010), (11 11), (010), (11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), (111). The ΔEa_eff of Fe5C2 (510), ( ), (111). The ΔEa_eff of Fe5C2 (510), (![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 11), (010), (11 11), (010), (11![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ), (111) is from ref. 36. ), (111) is from ref. 36. | ||
It is worth noting that the CH4 selectivity in hcp is not always lower than in fcc. Among the ten Co surfaces, hcp-Co (10−10) has the largest ΔEa_eff (2.13 eV), indicating the lowest CH4 selectivity, whereas fcc-Co (311) has the smallest ΔEa_eff (0.55 eV) and the highest CH4 selectivity. However, the ΔEa_eff values of hcp-Co (0001), (10−12), and (11−20) are even lower than those of fcc-Co (100) and fcc-Co (111), implying higher CH4 selectivity of these surfaces on hcp-Co. The ranks of the CH4 selectivity of all the Co surfaces are shown in Fig. 5. To confirm the validity of our prediction, comparisons are made with the available experiments. Qin et al. have synthesized three types of hcp-Co particles exposing only one type of facet each. Comparison of their CH4 selectivity shows that (10−11) has the lowest CH4 selectivity, followed by (0001) and (11−20). Our calculated ΔEa_eff values on (10−11), (0001), and (11−20) are 1.92 eV, 0.92 eV, and 0.87 eV, respectively, with the rank of CH4 selectivity to be (10−11) < (0001) < (11−20), which is in excellent agreement with the experiments.68
The overall CH4 selectivities of hcp-Co and fcc-Co phases are defined by the particle effective barrier difference (ΔEa_particle) between CH4 formation (Ea_eff,CH4) and the most feasible C1 + C1 coupling (Ea_eff,C1+C1) on hcp-Co and fcc-Co Wulff particles, assuming that the overall rate of reaction on the catalyst particle is the sum of the rates from all its exposed surfaces. (See the Methods section). The ΔEa_particle on hcp-Co and fcc-Co surfaces is 0.86 eV and 0.60 eV, respectively. Therefore, the CH4 selectivity in FTS is higher on fcc-Co than on hcp-Co, which is consistent with the experimental observations.33,74,75 Notably, the (311) surface of fcc-Co plays a pivotal role in determining the overall CH4 selectivity of the fcc phase. Moreover, our results suggest that the CH4 selectivity can be suppressed by decreasing the exposure ratio of the facets that are prone to form CH4: (0001), (10−12), and (11−20) on hcp-Co and (110) and (311) on fcc-Co.
In FTS, Co-based FTS generally has higher CH4 selectivity than Fe-based FTS.42,76 Herein, we compare the ΔEa_eff of exposed facets of hcp and fcc Co with those of χ-Fe5C2 particles,36 the most widely accepted active phase in iron-catalyzed FTS.11,23,37 Most of the χ-Fe5C2 surfaces have large ΔEa_eff, with the exception of Fe5C2(111), which has lower ΔEa_eff than the cobalt surfaces of (10−10), (10−11), (11−21), and (100). The overall CH4 selectivity of χ-Fe5C2, hcp-Co, and fcc-CO can be compared using ΔEa_particle (Fig. 5, dashed lines and Table S9, ESI†). The ΔEa_particle (1.20 eV) of Fe5C2 particles is larger than that of hcp-Co and fcc-Co, indicating that the Co particle of both phases has higher CH4 selectivity than the χ-Fe5C2 particle. This is probably the reason why Co-based FTS generally shows higher CH4 selectivity than Fe-based FTS.41
3.4 Tuning of the phase transition between hcp and fcc Co
On the basis of the understanding of the activity and selectivity for CH4 and C2+ production on the cobalt phases, one can further use the knowledge for catalyst design through phase engineering. Operando characterization shows that in FTS, the cobalt catalyst can exist in both hcp and fcc phases.77,78 In order to get more hcp phase which has lower CH4 selectivity and higher C5+ selectivity, the thermodynamic conditions for the modulation of the ratio of hcp and fcc Co phases by changing the temperature and particle size are explored.The thermodynamic stability of the Co particles of different phases can be evaluated using the Gibbs free energy per cobalt atom, which involves the energy, phonon energies at certain temperature, and surfaces energies at a given particle size.55–58 The details of the theory and calculation methods are shown in Section 2.4. The temperature and particle sizes in which the Gibbs free energy difference is zero represent the condition of phase transition between hcp-Co and fcc-Co, which is given in Fig. 6 and Table S10 (ESI†). The black solid curve corresponds to the conditions of phase transition of bulk cobalt. At 718 K, a phase transition from hcp-Co to fcc-Co happens, which is very close to the experimental transition temperature of 695 K.79,80 This shows that bulk hcp-Co is more stable than bulk fcc-Co below 718 K, and keeping a low operating temperature (<718 K) is beneficial for stabilizing the hcp-Co phase. On the other hand, the particle size also plays an important role in the phase transition as shown in Fig. 6. The transition temperatures of different particle sizes (10 nm, 15 nm, 20 nm, 25 nm, and 30 nm) are 1059 K, 946 K, 890 K, 855 K, and 833 K, respectively. With the increase in the size of cobalt particles, the phase transition temperature gradually decreases until it approaches the bulk transition temperature. When the particle size is larger than 30 nm, hcp-Co is stable only at a relatively narrow temperature window between 718 K and 833 K. Therefore, the ratio of hcp phase particles could be maximized by controlling the operating temperature below 718 K and size of the Co particles as small as possible within the range of 10–30 nm, which will likely lower CH4 selectivity and improve C5+ selectivity of the FTS process as observed experimentally.81
 | ||
| Fig. 6 Calculated Gibbs free energy difference for hcp-Co and fcc-Co phases as a function of temperature at different particle sizes. | ||
4. Conclusion
In this work, we proposed a strategy combining DFT, Wulff construction, and a particle-level energy descriptor to understand the relationship between the crystal phase and their catalytic selectivity, using the CH4 formation on hcp-Co and fcc-Co as an example. Hcp-Co has lower intrinsic catalytic activity than fcc-Co to form CH4, due to the higher Ea_particle,CH4. A linear relationship was discovered between Ea_eff,CH4 of a Co surface and the sum of adsorption energies of a C atom and 4H atoms on it (Eads_C+4H), which provides an efficient way of predicting the intrinsic catalytic activity of Co surfaces for CH4 formation. The most feasible C1 + C1 coupling pathway is CH + CH on hcp-Co (0001), (10−10), (10−12), (11−21), fcc-Co (110), (111), C + CH3 on fcc-Co (311), C + CO on hcp-Co (10−11), fcc-Co (100), and CH + CO on hcp-Co (11−20). The CH4 selectivity, represented by the effective barrier difference between CH4 formation and the most feasible C1 + C1 coupling, decreases in the sequence of surfaces (311) > (110) > (10−12) > (11−20) > (0001) > (111) > (11−21) > (100) > (10−11) > (10−10). The lower CH4 selectivity of hcp-Co than fcc-Co can be well explained by its higher ΔEa_particle. Tuning the CH4 selectivity of the Co catalyst can be achieved not only by controlling the morphology of the particles to avoid the active facets for CH4 formation such as (0001), (10−12), (11−20) on hcp-Co and (110), (311) on fcc-Co, but is also achievable through engineering the crystal phases by controlling the temperature and particle size. Our research provides a pathway to understand the phase-selectivity relationship for complex reactions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful for the financial support from the National Science Fund for Distinguished Young Scholars of China (Grant no. 22225206), the National Key R&D Program of China (2022YFA1604103), the National Natural Science Foundation of China (No. 21972160, 21972157, 22372187), CAS Project for Young Scientists in Basic Research (YSBR-005), Key Research Program of Frontier Sciences CAS (ZDBS-LY-7007), Major Research plan of the National Natural Science Foundation of China (92045303), Informatization Plan of Chinese Academy of Sciences, (Grant no. CAS-WX2021SF0110), Youth Innovation Promotion Association CAS (2020179), the Doctoral Research Funds in Shanxi (QZX-2023012), the Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi (2023L304), the Doctoral Research Funds of Yuncheng University (YQ2023025), and the Autonomous Research Project of SKLCC (Grant no. 2023BWZ005).References
- Y. Liu and W. E. Mustain, J. Am. Chem. Soc., 2013, 135, 530–533 CrossRef CAS PubMed
.
- Y. Jiao, T. Chen, L. Wang, P. Yao, J. Zhang, Y. Chen, Y. Chen and J. Wang, Ind. Eng. Chem. Res., 2020, 59, 4338–4347 CrossRef CAS
.
- W. Shafer, M. Gnanamani, U. Graham, J. Yang, C. Masuku, G. Jacobs and B. Davis, Catalysts, 2019, 9, 259 CrossRef CAS
.
- E. Iglesia, Appl. Catal., A, 1997, 161, 59–78 CrossRef CAS
.
- J. H. den Otter, S. R. Nijveld and K. P. de Jong, ACS Catal., 2016, 6, 1616–1623 CrossRef CAS
.
- V. Subramanian, K. Cheng, C. Lancelot, S. Heyte, S. Paul, S. Moldovan, O. Ersen, M. Marinova, V. V. Ordomsky and A. Y. Khodakov, ACS Catal., 2016, 6, 1785–1792 CrossRef CAS
.
- L. Zhang, Y. Dang, X. Zhou, P. Gao, A. P. van Bavel, H. Wang, S. Li, L. Shi, Y. Yang, E. I. Vovk, Y. Gao and Y. Sun, Innovation, 2021, 2, 100170 CAS
.
- Ø. Borg, N. Hammer, B. C. Enger, R. Myrstad, O. A. Lindvåg, S. Eri, T. H. Skagseth and E. Rytter, J. Catal., 2011, 279, 163–173 CrossRef
.
- E. Rytter, N. E. Tsakoumis and A. Holmen, Catal. Today, 2016, 261, 3–16 CrossRef CAS
.
- S. Rane, Ø. Borg, E. Rytter and A. Holmen, Appl. Catal., A, 2012, 437–438, 10–17 CrossRef CAS
.
- T. A. Wezendonk, X. Sun, A. I. Dugulan, A. J. F. van Hoof, E. J. M. Hensen, F. Kapteijn and J. Gascon, J. Catal., 2018, 362, 106–117 CrossRef CAS
.
- P. Wang, W. Chen, F. K. Chiang, A. I. Dugulan, Y. Song, R. Pestman, K. Zhang, J. Yao, B. Feng, P. Miao, W. Xu and E. J. M. Hensen, Sci. Adv., 2018, 4, eaau2947 CrossRef CAS PubMed
.
- W. Chen, Z. Fan, X. Pan and X. Bao, J. Am. Chem. Soc., 2008, 130, 9414–9419 CrossRef CAS PubMed
.
- Q. Zhang, J. Kang and Y. Wang, ChemCatChem, 2010, 2, 1030–1058 CrossRef CAS
.
- W. Li, J. Liu, J. Gu, W. Zhou, S. Yao, R. Si, Y. Guo, H. Su, C. Yan, W. Li, Y. Zhang and D. Ma, J. Am. Chem. Soc., 2017, 139, 2267–2276 CrossRef CAS PubMed
.
- H. Tian, X. Li, L. Zeng and J. Gong, ACS Catal., 2015, 5, 4959–4977 CrossRef CAS
.
- E. de Smit, F. Cinquini, A. M. Beale, O. V. Safonova, W. van Beek, P. Sautet and B. M. Weckhuysen, J. Am. Chem. Soc., 2010, 132, 14928–14941 CrossRef CAS PubMed
.
- D. Luo, X. C. Liu and R. Gao,
et al.
, J. Phys. Chem. C, 2020, 124, 18576–18586 CrossRef CAS
.
- O. Kitakami, H. Sato, Y. Shimada, F. Sato and M. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 13849–13854 CrossRef CAS
.
- N. Fischer, E. van Steen and M. Claeys, Catal. Today, 2011, 171, 174–179 CrossRef CAS
.
- L. Zhong, F. Yu, Y. An, Y. Zhao, Y. Sun, Z. Li, T. Lin, Y. Lin, X. Qi, Y. Dai, L. Gu, J. Hu, S. Jin, Q. Shen and H. Wang, Nature, 2016, 538, 84–87 CrossRef CAS PubMed
.
- V. Lyaskovskyy and B. de Bruin, ACS Catal., 2012, 2, 270–279 CrossRef CAS
.
- R. Nakano, L. W. Chung, Y. Watanabe, Y. Okuno, Y. Okumura, S. Ito, K. Morokuma and K. Nozaki, ACS Catal., 2016, 6, 6101–6113 CrossRef CAS
.
- Z. Li, S. Ji, Y. Liu, X. Cao, S. Tian, Y. Chen, Z. Niu and Y. Li, Chem. Rev., 2020, 120, 623–682 CrossRef CAS PubMed
.
- X. Zhang, R. A. van Santen and E. J. M. Hensen, ACS Catal., 2014, 5, 596–601 CrossRef
.
- G. Sun and P. Sautet, J. Am. Chem. Soc., 2018, 140, 2812–2820 CrossRef CAS PubMed
.
- Z. Zhang, B. Zandkarimi and A. N. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458 CrossRef CAS PubMed
.
- P. Ann Lin, B. Natarajan, M. Zwolak and R. Sharma, Nanoscale, 2018, 10, 4528–4537 RSC
.
- M. S. Spencer, Nature, 1986, 323, 685–687 CrossRef CAS
.
- Y. Chen, Z. Fan, J. Wang, C. Ling, W. Niu, Z. Huang, G. Liu, B. Chen, Z. Lai, X. Liu, B. Li, Y. Zong, L. Gu, J. Wang, X. Wang and H. Zhang, J. Am. Chem. Soc., 2020, 142, 12760–12766 CrossRef CAS PubMed
.
- J. Cao, J. Xia, Y. Zhang, X. Liu, L. Bai, J. Xu, C. Yang, S. Zheng, T. Yang, K. Tang, C. Zhang and C. Zhou, Fuel, 2021, 289, 119843 CrossRef CAS
.
- J. F. Gómez-García, J. A. Mendoza-Nieto, A. Yañez-Aulestia, F. Plascencia-Hernández and H. Pfeiffer, Fuel Process. Technol., 2020, 204, 106404 CrossRef
.
- M. K. Gnanamani, G. Jacobs, W. D. Shafer and B. H. Davis, Catal. Today, 2013, 215, 13–17 CrossRef CAS
.
- H. Du, M. Jiang, H. Zhu, C. Huang, Z. Zhao, W. Dong, W. Lu, T. Liu, Z. Conrad Zhang and Y. Ding, Fuel, 2021, 292, 120244 CrossRef CAS
.
-
L. Zhong, Doctoral thesis, Nanyang Technological University, Singapore, 2020
.
- M. Armbruster, K. Kovnir,M. Behrens, D. Teschner, Y. Grin and R. Schlogl, J. Am. Chem. Soc., 2010, 132, 14745–14747 CrossRef PubMed
.
- J. Yin, X. Liu, X. Liu, H. Wang, H. Wan, S. Wang, W. Zhang, X. Zhou, B. Teng, Y. Yang, Y. Li, Z. Cao and X. Wen, Appl. Catal., B, 2020, 278, 119308 CrossRef CAS
.
- T. H. Pham, Y. Qi, J. Yang, X. Duan, G. Qian, X. Zhou, D. Chen and W. Yuan, ACS Catal., 2015, 5, 2203–2208 CrossRef CAS
.
- G. P. van der Laan and A. A. C. M. Beenackers, Catal. Rev.: Sci. Eng., 1999, 41, 255–318 CrossRef CAS
.
- M. E. Dry, Catal. Today, 2002, 71, 227–241 CrossRef CAS
.
- J. Yin, Y. He, X. Liu, X. Zhou, C. F. Huo, W. Guo, Q. Peng, Y. Yang, H. Jiao, Y. W. Li and X. D. Wen, J. Catal., 2019, 372, 217–225 CrossRef CAS
.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2009, 113, 8858–8863 CrossRef CAS
.
- X. Q. Gong, R. Raval and P. Hu, J. Chem. Phys., 2005, 122, 024711 CrossRef PubMed
.
- M. Yu, L. Liu, Q. Wang, L. Jia, J. Wang, D. Li and B. Hou, J. Phys. Chem. C, 2020, 124, 11040–11049 CrossRef CAS
.
- J. Cheng, X. Gong, P. Hu, C. Lok, P. Ellis and S. French, J. Catal., 2008, 254, 285–295 CrossRef CAS
.
- P. Zhao, Z. Cao, X. Liu, P. Ren, D. Cao and H. Xiang,
et al.
, ACS Catal., 2019, 9, 2768–2776 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed
.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed
.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS PubMed
.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS
.
-
D. Lide and H. Kehiaian, CRC Handbook of Chemistry and Physics, CRC Press, BocaRaton, FL, 1994 Search PubMed
.
- J. X. Liu, H. Y. Su and W. X. Li, Catal. Today, 2013, 215, 36–42 CrossRef CAS
.
- J. Häglund, A. Fernández Guillermet, G. Grimvall and M. Körling, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 11685–11691 CrossRef PubMed
.
- W. Luo and A. Asthagiri, J. Phys. Chem. C, 2014, 118, 15274–15285 CrossRef CAS
.
- B. Böller, K. M. Durner and J. Wintterlin, Nat. Catal., 2019, 2, 1027–1034 CrossRef
.
- C. J. K. Weststrate, D. Sharma, D. Garcia Rodriguez, M. A. Gleeson, H. O. A. Fredriksson and J. W. H. Niemantsverdriet, Nat. Commun., 2020, 11, 750 CrossRef CAS PubMed
.
- G. F. Wei and Z. P. Liu, Chem. Sci., 2015, 6, 1485–1490 RSC
.
- G. J. Kaptay, Nanosci. Nanotechnol., 2012, 12, 2625–2633 CAS
.
- N. Wu, X. Ji, R. An, C. Liu and X. Lu, AIChE J., 2017, 63, 4595–4603 CrossRef CAS
.
- B. Singh, M. K. Gupta, R. Mittal and S. L. Chaplot, Phys. Chem. Chem. Phys., 2018, 20, 12248–12259 RSC
.
- A. Navrotsky, C. Ma, K. Lilova and N. Birkner, Science, 2010, 330, 199–201 CrossRef CAS PubMed
.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef
.
- A. Navrotsky, ChemPhysChem, 2011, 12, 2207–2215 CrossRef CAS PubMed
.
- C. Chen, Q. Wang, G. Wang, B. Hou, L. Jia and D. Li, J. Phys. Chem. C, 2016, 120, 9132–9147 CrossRef CAS
.
- C. Qin, B. Hou, J. Wang, Q. Wang, G. Wang, M. Yu, C. Chen, L. Jia and D. Li, ACS Catal., 2018, 8, 9447–9455 CrossRef CAS
.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2010, 114, 1085–1093 CrossRef CAS
.
- F. Fischer and H. Tropsch, Brennst. Chem., 1926, 7, 97–104 CAS
.
- H. Pichler and H. Schulz, Chem. Ing. Tech., 1970, 12, 1160–1174 Search PubMed
.
- J. Cheng, P. Hu, P. Ellis, S. French, G. Kelly and C. M. Lok, J. Phys. Chem. C, 2008, 112, 6082–6086 CrossRef CAS
.
- P. Zhai, P. Chen and J. Xie,
et al.
, Faraday Discuss., 2017, 197, 207–224 RSC
.
- G. Xiao, J. Yan, J. Du, Y. Han, F. Sun, Y. Zhang, J. Li and J. Hong, Fuel, 2019, 254, 115577 CrossRef CAS
.
- L. Nie, Z. Li, T. Kuang, S. Lyu, S. Liu, Y. Zhang, B. Peng, J. Li and L. Wang, Chem. Commun., 2019, 55, 10559–10562 RSC
.
- W. Ma, G. Jacobs, D. E. Sparks, B. Todic, D. B. Bukur and B. H. Davis, Catal. Today, 2020, 343, 125–136 CrossRef CAS
.
- L. J. Garces, B. Hincapie, R. Zerger and S. L. Suib, J. Phys. Chem. C, 2015, 119, 5484–5490 CrossRef CAS
.
- H. Karaca, J. Hong, P. Fongarland, P. Roussel, A. Griboval-Constant, M. Lacroix, K. Hortmann, O. V. Safonova and A. Y. Khodakov, Chem. Commun., 2010, 46, 788–790 RSC
.
- T. Nishizawa and K. Ishida, Bull. Alloy Phase Diagrams, 1983, 4, 387–390 CrossRef
.
- J. Sort, J. Nogués, S. Suriñach, J. S. Muñoz and M. D. Baró, Mater. Sci. Eng., A, 2004, 375–377, 869–873 CrossRef
.
- G. L. Bezemer, J. H. Bitter, H. P. Kuipers, H. Oosterbeek, J. E. Holewijn, X. Xu, F. Kapteijn, A. J. van Dillen and K. P. De Jong, J. Am. Chem. Soc., 2006, 128, 3956–3964 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed data about the CH4 formation and C1 + C1 coupling on hcp-Co and fcc-Co surfaces. See DOI: https://doi.org/10.1039/d3cp06041a |
| This journal is © the Owner Societies 2024 |



