Energy renormalization for temperature transferable coarse-graining of silicone polymer

Abstract

The bottom-up prediction of thermodynamic and mechanical behaviors of polymeric materials based on molecular dynamics (MD) simulation is of critical importance in polymer physics. Although the atomistically informed coarse-grained (CG) model can access greater spatiotemporal scales and retain essential chemical specificity, the temperature-transferable CG model is still a big challenge and hinders widespread application of this technique. Herein, we use a silicone polymer, i.e., polydimethylsiloxane (PDMS), having an incredibly low chain rigidity as a model system, combined with an energy-renormalization (ER) approach, to systematically develop a temperature-transferable CG model. Specifically, by introducing temperature-dependent ER factors to renormalize the effective distance and cohesive energy parameters, the developed CG model faithfully preserved the dynamics, mechanical and conformational behaviors compared with the target all-atomistic (AA) model from glassy to melt regimes, which was further validated by experimental data. With the developed CG model featuring tremendously improved computational efficiency, we systematically explored the influences of cohesive interaction strength and temperature on the dynamical heterogeneity and mechanical response of polymers, where we observed consistent trends with other linear polymers with varying chain rigidity and monomeric structures. This study serves as an extension of our proposed ER approach of developing temperature transferable CG models with diverse segmental structures, highlighting the critical role of cohesive interaction strength on CG modeling of polymer dynamics and thermomechanical behaviors.

---

1. Introduction

Silicone polymers, also known as polysiloxanes, refer to a class of polymers constituted by a relatively flexible siloxane backbone with two organic functional groups attached to the silicon atoms.¹ The highly stable silicon–oxygen bond imparts excellent thermal stability, chemical resistance, and dielectric properties to silicone polymers, and the presence of silicon atoms contributes to their low surface energy and hydrophobicity.^2–4 The versatile properties of silicone polymers enable their widespread applications in automotive, aerospace, electronics, and construction industries.^5–7 Polydimethylsiloxane (PDMS) belongs to the family of silicone polymers, characterized by methyl (–CH₃) as the functional groups. In addition to the virtues of silicone polymers, PDMS is also known for its high mechanical flexibility, excellent biocompatibility and adhesion associated with its viscoelasticity, making it an ideal candidate for coatings, lubricants, adhesives, biomedical and flexible electronic devices.^8,9 It is worth mentioning that PDMS exhibits remarkably low glass transition temperatures (T_g) of around 150 K, which signifies a strong temperature-dependence in its dynamic responses and properties for its practical usages.¹⁰

Typically, the relationship between structural morphology and dynamical characterizations can be experimentally assessed. However, in many cases, the macroscopic experiments may prove to be laborious and inefficient to provide a molecular-level understanding of materials’ behaviors. Coarse-grained (CG) modelling and simulation present compelling prospects for the design and prediction of materials at the mesoscale level, which is achieved by treating a cluster of atoms as a single super bead, referred to as a CG bead. The CG model excels in efficiently simulating large molecular systems over extended spatiotemporal scales by integrating out unessential degrees of freedom upon coarse-graining.^11–14 Several coarse-graining approaches have previously been explored to overcome the spatiotemporal limitation and sustain the key chemical features of the underlying all-atomistic (AA) system, such as force matching,¹⁵ inverse Monte Carlo,¹² inverse Boltzmann method,¹⁶ top-down mapping,¹⁷ or hybrid CG modelling.¹⁸ However, it has been reported that coarse graining using these strategies also results in the reduction of fluid configurational entropy (S_c) and atomic friction due to the elimination of detailed atom information of AA models.^19,20 This reduction is associated with the loss of atomistic fluctuations and simplification of the energy landscape, which subsequently leads to artificial fast dynamics in CG models and considerable discrepancies of activation free energy between the AA and CG models.^21,22 Even though a few previous studies have introduced additional constraints,²³ coefficients,²⁴ or an improved force field²⁵ to calibrate the dynamics of CG models, achieving full temperature transferability in CG models remains a long-standing challenge in modelling and understanding the dynamics and thermomechanical behaviors of temperature-dependent polymer materials.²⁶

To date, only a few attempts have been made to develop a broadly applicable CG model of PDMS. Johnson et al. employed the Martini 2 force field to study the morphology and chain packing structures in the CG peptidic/PDMS triblock copolymer system.²⁷ Building upon this effort, Cambiaso et al. employed a more recent Martini 3 force field to validate the scaling laws for PDMS conformation in melt and dilute condition considering both good and bad solvent environments.²⁸ Although the improved Martini force field was successful in reproducing the wetting and phase behaviors of the triblock copolymers, both CG models were established at a specific fixed temperature of 300 K, limiting their applications at other thermodynamic states as the transferability of these CG models under different temperatures remained untested. Varun Ullal et al. utilized Williams–Landel–Ferry (WLF) equation, which was more credible in describing diffusion and viscosity than the Arrhenius equation near the glass transition, to capture the role of temperature in un-crosslinked and end-linked PDMS networks.¹⁸ Another temperature transferable CG model for chemically crosslinked PDMS was achieved by conducting a grid-based search to minimize the error function between CG and united-atoms (UA) models, while the transferability of the UA model was derived from its accurate prediction of vapor-liquid equilibrium properties.²⁹ However, those investigations were largely limited in exploring the O₂ diffusion and rheological properties of PDMS, and more fundamental thermomechanical and conformational properties of the UA models were not tested in their study. Huang et al. systematically examined the density, surface tension, T_g, radius of gyration (R_g), and solubility parameter of PDMS in a wide range of thermodynamic states.³⁰ However, the transferrable force field parameters in their CG model were determined by ideally combining both bottom-up and top-down approaches together, taking advantage of temperature-dependent non-bonded functional forms and a rich supply of experimental data in the training set, which made the modelling rather complicated. Despite the few CG models mentioned above having shown validity in specific applications, it is important to note that their testing temperature range typically fell within the range of 250 K to 400 K. Given the exceptionally low T_g of PDMS, it is crucial to extend the temperature coverage well below room temperature, allowing for a more comprehensive approximation of the thermodynamics of PDMS across a broader temperature range, especially the glassy regime below T_g.

A coarse-graining strategy called energy renormalization (ER) was recently proposed by Xia and co-workers to address the temperature transferability issues of CG modelling of polymers,^31,32 wherein the cohesive interactions of the polymer system were dynamically adapted to compensate for the decrease in S_c and atomic friction upon coarse graining. This approach was inspired by Adam-Gibbs³³ and generalized entropy theories,³⁴ both of which confirmed the crucial effect of S_c in characterizing the polymer dynamics and mechanical properties.³⁵ In the ER approach, the entropy differences between AA and CG models are compensated by parameterizing the cohesive energy parameter ε in the nonbonded potential such as Lennard-Jones (LJ) potentials as a function of temperature. Another key interaction parameter σ is rescaled simultaneously to capture the atomistic density of the polymer system. Thus, the CG model using the ER approach is feasible for retaining the dynamics and thermomechanical properties of the AA counterpart over an extensive temperature range, encompassing high-temperature Arrhenius behaviors, low-temperature supercooled states, and even the glassy regime, which has not yet been fulfilled in previous CG models. The effectiveness of the ER approach has been demonstrated in the development of temperature transferable CG models for a few glass-forming systems, including molecular glass formers,³⁶ linear-chain polymers,³⁷ thermosetting polymers,³⁸ and conjugated polymers.³⁹ However, the ER method has not been specifically applied to silicone polymers which possess high chain flexibility and mobility along with remarkably low T_g.

In this study, we employed the ER approach in developing a temperature transferable CG model for a representative silicone polymer, specifically PDMS. In practice, the nonbonded potential parameters ε and σ in the CG model were dynamically varied by incorporating temperature-dependent ER factors to eliminate the deviations in the Debye–Waller factor 〈u²〉 and density between the CG and AA models. The 〈u²〉 and density were selected as metrices since they directly reflect the mobility of molecules and overall system volume or packing density, which are critical parameters governing the dynamic behaviors of the polymer system.⁴⁰ The results showed that the CG model developed by the ER approach successfully captured the T_g, conformational behaviors, and modulus of elasticity of the AA model over a wide temperature range. The influences of temperature and cohesive interaction strength on the dynamic heterogeneity and thermomechanical properties of PDMS were systematically discussed. This study provides evidence for the significant potential of the proposed ER approach in the development of temperature transferable CG models of silicone polymers. The promising application of the ER approach presents innovative insights into predicting and tailoring the thermomechanical properties of polymer materials through CG modelling.

2. Method

2.1. Overview of all-atomistic model

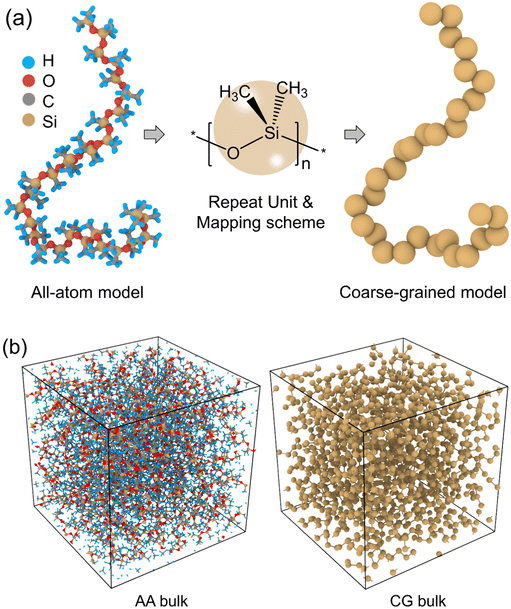
We started with building an AA PDMS model (Fig. 1(a)) using Materials Studio software⁴¹ and the Dreiding force field was chosen for describing the bonded and nonbonded interactions in the AA model.^42,43 The Gasteiger method was employed to calculate system atomic charges for electrostatic interactions.⁴⁴ For computational expediency, we chose a single chain of PDMS AA model with 30 monomers and a monomer liquid system containing 800 PDMS monomers to obtain the target bonded interactions and initial estimation of nonbonded interactions.^45,46 Firstly, the AA PDMS system was initialized with Gaussian randomly distributed velocity at temperature of 300 K and then minimized using the conjugate gradient algorithm.⁴⁴ Afterwards, the AA system underwent a series of annealing processes in the isothermal–isobaric (NPT) ensemble with temperature ramping from 1000 K to 300 K and pressure ramping from 1000 bar to 1 bar for 4 ns, respectively. Finally, the system was gradually cooled to the desired temperature at a rate of 0.2 K ps⁻¹. After the system reached the equilibrium state, additional dynamics run under the NPT ensemble was conducted for 2 ns to obtain the atomistic trajectories for further statistics analysis. Regarding the AA system, the timestep was 1 fs, and damping parameters for temperature and pressure were 100 fs and 1000 fs, respectively. The periodic boundary conditions (PBC) were applied to the cubic simulation box in all three dimensions and the box length was about 60 Å.

Fig. 1 (a) Schematic illustration showing the mapping from AA model (left) to CG model (right) of a linear PDMS polymer chain. The force center of each CG bead (middle) was located at the silicon atom. (b) The snapshots of the equilibrated AA and CG bulk PDMS systems.

2.2. Energy-renormalization coarse-graining strategy

To coarse-grain the AA PDMS model, a one-bead-per-monomer coarse graining mapping scheme was employed. In the CG PDMS model, the silicon atom along with the two attached methyl groups and the oxygen atom in the backbone were clustered into one CG bead resulting in a linear PDMS chain as displayed in Fig. 1(a). Given that the mass of a silicon atom is substantially larger than the other atoms, the force centre of each bead was positioned at the silicon atom to simplify the AA-to-CG mapping. The CG PDMS model consisted of 660 chains with the same chain length of 30 monomers as the AA model, resulting in 19 800 beads. Similar sampling approach, energy minimization, and NPT annealing procedures were performed upon the CG model to those specified in the AA model. The timestep of the CG model was set as 4 fs, and the damping parameters for temperature and pressure were 400 fs and 4000 fs, respectively. The adjustment of timestep and damping parameters for the CG model was made to maintain the stable and proper behaviors for the CG dynamics while optimizing the computational resources for large systems and longer simulation timescales. The simulation box of the CG model was still periodic with a box length of approximately 110 Å, as depicted in Fig. 1(b). All the AA and CG simulations were carried out using large-scale atomic/molecular massively parallel simulator (LAMMPS)⁴⁷ and visualized by the OVITO software.⁴⁸

2.3. Derivation of CG force field parameters

Regarding the PDMS CG model, the bonded interaction terms were directly derived from the AA system through the iterative Boltzmann inversion (IBI) method.^49–51 Specifically, the bonded interactions of bond stretching and angle bending in the CG model were described in a harmonic function, while potential energy of dihedral rotation was fitted in a multipeak harmonic form. After two rounds of IBI, the bonded distributions of CG model were reasonably consistent with the target AA model. The probability distributions of bonds, angles, and dihedrals in both AA and CG models are shown in Fig. 2a–c, and the corresponding potential parameters are presented in Table 1. As illustrated in Fig. 2a–c, the probability distributions of each bonded interaction in the CG model closely aligned with the peaks and patterns exhibited in the AA counterpart.

Fig. 2 The probability distribution of bonded interactions in AA and CG PDMS models: (a) bond; (b) angle; (c) dihedral; (d) radial distribution functions (RDF) g(r) between effective bead centers (located at silicon atoms) and their potentials. The bonded interactions of the AA model were recorded between silicone atoms to make comparisons with the CG model.

Table 1 Potential forms and parameters of bonded interactions for PDMS CG model

Interaction	Potential form	Parameters
Bond	U bond(l) = k(l − l0)^2	k = 115.41 kcal mol^−1 Å^−1
		l 0 = 2.801 Å
Angle	U angle(θ) = k(θ − θ0)^2	k = 64.62 kcal mol^−1·rad^−2
		θ 0 = 116.62°
Dihedral		A 1 = 3.280 kcal mol^−1, A2 = −0.590 kcal mol^−1
		A 3 = 1.991 kcal mol^−1, A4 = 3.310 kcal mol^−1

---

A GROMACS style 12-6 LJ functional form was selected for the nonbonded interaction of the CG breads:

where r is the intermolecular distance, ε is defined as the depth of the potential energy well in the LJ potential, quantifying the cohesive strength of the intermolecular interaction or the Van del Waals attraction between particles, and σ represents the characteristic length scale of the nonbonded interaction and denotes to the distance at which the potential energy between particles is zero. The energy switching function S_LJ was employed to mitigate abrupt changes in the LJ potential at the cutoff distance at which the potential energy transition from the attractive to repulsive regime. R₁ and R_C are inner and outer cutoff distance, with the values being 12 Å and 15 Å, respectively.

In the ER approach, the ε and σ parameters were renormalized by introducing temperature-dependent ER factors α(T) and β(T). Thus, the temperature transferable LJ parameters α(T) and β(T) at each specific temperature were expressed as:

ε(T) = α(T)ε₀ (3)

σ(T) = β(T)σ₀ (4)

where ε₀ and σ₀ were the initial estimates of the LJ parameters which were obtained by fitting the RDF of the AA system using direct Boltzmann methods:

U_nonbonded⁰(r) = −k_BTln[g(r)] (6)

where k_B is Boltzmann constant, T is absolute temperature. Fig. 2(d) shows the RDF g(r) between effective bead centres and their potentials. With the eqn (5) and (6), the initial estimates ε₀ and σ₀ were determined as 0.351 kcal mol⁻¹ and 4.950 Å, respectively. As reported previously, the atomic friction and configurational entropy are inevitably lost upon coarse graining, causing the insufficient cohesive interaction between CG beads, and further influencing the thermodynamics and mechanical properties of CG model, especially when temperature is varied. To address this issue, the energy-renormalization method was introduced, which declared that the σ and ε governed the thermodynamics and dynamics properties of CG model, respectively. Additionally, previous studies indicate that the Debye–Waller factor 〈u²〉 can be treated as an indicator of dynamic property of a polymer glass forming. Therefore, we derived α(T) by preserving the dynamics of the CG model to be consistent with target AA system.^31,36 Similarly, β(T) was obtained by matching the temperature-dependent density ρ of the CG model with that of the AA counterpart. Simmons et al.⁵² and Betancourt et al.³⁵ have both identified the direct correlation between 〈u²〉 at picosecond (ps) timescale and long-time scale structural dynamics. Experimentally, 〈u²〉 can be measured or calculated from X-ray scattering⁵³ and electron diffraction methods.⁵⁴ In MD simulation, 〈u²〉 is defined as the characteristic value of mean-squared displacement (MSD) 〈r²(t)〉 of all the monomers at t = 4 ps which corresponds to a caging coefficient. Here the MSD is calculated as:

〈r²(t)〉 = 〈|r_i(t) − r_i(0)|²〉 (7)

where r_i(t) is the position of the centre of the i_th monomers at time t, while 〈…〉 is the average value of all the monomers. Therefore, by determining the α(T) and β(T) in a wide range of temperature, the PDMS CG model established through the proposed ER approach was expected to exhibit temperature transferability and precisely retain the dynamics and thermomechanical properties of the PDMS AA system over wide temperature range.

2.4. Experimental measurement

To validate the simulation results of the developed CG model, several standard experimental tests were conducted on “Sylgard 184” and lab produced silicone elastomers. Sylgard 184 is a heavily used industrial product, which comes as two components (prepolymer and crosslinker). The two components are mixed at some weight ratio (typically 10 to 1) and cured at some temperature to create a particular elastomer. Altering ratio, cure temperature or cure time can lead to different elastomers. In this case we created a 10 to 1 ratio Sylgard by mixing prepolymer and crosslinker for 5 minutes before degassing the mixture in a vacuum oven. When bubbles were no longer present, the mixture was heated to 70–80 °C for 1 hour, before being allowed to cool down to room temperature.

Because there are several unknowns associated with the complete chemical make-up of Sylgard, we also produced some “simple” silicone elastomers in house. In this case, DMS-V31 (di-vinylterminated polymethylsiloxane, M_w = 28 000 g mol⁻¹) polymer is cross-linked with HMS-151 (15%–18% methylhydrosiloxane-dimethylsiloxane copolymer, trimethylsiloxane terminated, M_w = 1900–2000 g mol⁻¹) in the presence of a platinum catalyst SIP6830.3 (3% Pt catalyst in vinyl terminated PDMS, M_w = 475 g mol⁻¹) and moderator, SIT7900 (1,3,5,7-tetvinyl -1,3,5,7 tetramrthylcycloetrasiloxane, M_w = 345 g mol⁻¹, molecular formula: C₁₂H₂₄O₄Si₄). All components were used as received from Gelest Inc. (PA, USA). In this case, a ratio between polymer and crosslinker of 1 : 1.3 was used. Samples were mixed with a speed-mixer and cured at room temperature for one week prior to use.

A TA Instruments Discovery DMA850 was used to collect dynamic moduli from each elastomer sample. Both temperature ramp and frequency ramp experiments were performed, but here we only made note of the temperature runs. In this case, temperature ranged from −150 °C to 100 °C, at a rate of 5 °C min⁻¹ while the experimental oscillation had an amplitude of 15 μm, a frequency of 1.0 Hz, and a peak load of 0.1 N.

A modulated DSC Q2000 (TA) was used to collect differential scanning calorimetry data (DSC) on each of the PDMS samples. Samples were heated/cooled at 10 °C min⁻¹ in aluminum pans. We cycled the samples over the range of −150 °C to 100 °C twice under helium flow (50 mL min⁻¹). The second run was used for measurement.

3. Results and discussion

3.1. Development of ER factors for coarse-graining

In this study, the ER approach was built upon the previous findings which closely linked the cohesive interaction strength and dynamics of polymer materials.^36,55 It is presumed by appropriately parametrizing the ER factor α(T), the PDMS CG model could be temperature transferable, facilitating the compensation of the entropy loss resulting from coarse-graining and the recovery of the dynamics exhibited in the AA system. To verify this hypothesis, the cohesive interaction strength ε(T) in the LJ parameters were progressively varied by incrementally changing the α(T) over a wide temperature range. Fig. 3(a) show the 〈u²〉 as a function of temperature T for the PDMS AA and CG model and with varying α as the cohesive interaction strength parameter. As shown in Fig. 3(a), it is not surprising to find that the 〈u²〉 exhibited an increasing trend as the elevation of T for both the AA and CG model, while keeping the α value constant. This phenomenon is commonly observed in silicone polymers, which can be attributed to the improved thermal motion and flexibility of the polymer chains at higher temperatures.^18,56 On the other hand, at a certain T, the 〈u²〉 decreased as the increase of α, indicating that the stronger cohesive interaction imposed higher restrictions on the mobility of the monomers. Furthermore, it was noted that none of the curves with a fixed α value were able to precisely reproduce the 〈u²〉 behaviors of the AA model over the entire T range, which highlighted the importance of applying ER approach on coarse graining. In the ER approach, a specific value of α was determined for each T to perfectly preserve the 〈u²〉 of the AA model. By combining these α at each T, the T dependent α(T) was derived, which was found to be well-fitted in a sigmoidal function:where α_A and α_G are lower and upper limits of the α values, respectively. k is a parameter controlling the rate or steepness of the transition between α_A and α_G. T_T stands for the inflection point of this sigmoidal curve. This sigmoidal function has been broadly reported in the literature, describing the influence of cohesive energy in several other linear polymers.^32,57

Fig. 3 (a) 〈u²〉 as a function of temperature T for the PDMS AA and CG model with varying α reflecting the cohesive interaction strength. Inset: The shifting trajectory of α(T) for the CG model determined by matching 〈u²〉 of the AA model. (b) Density as a function of T for the PDMS AA and CG model with varying σ as length scale parameter between monomers. Inset: The shifting trajectory of β(T) for the CG model determined by reproducing the density of the AA model.

Similar ER procedures were also performed on the length scale parameter σ in CG system to capture the AA density with the increase of T, as shown in Fig. 3(b). Previous studies have demonstrated the usage of linear or polynomial relationships in fitting the T dependent β(T) for various polymer systems.^31,36 As clearly displayed in Fig. 3(b), the shifting trajectory of β(T) as a function of T was captured by a linear function. We adopted a linear function to simplify the fitting potential form. The fitting parameters in α(T) and β(T) are summarized in Table 2.

Table 2 Potential forms and parameters of ER factors for PDMS CG model

ER factor form	Parameters
	α A = 1.47; αG = 6.25; k = 0.00758 K^−1; TT = 186 K
β(T) = β1T + β0	β 1 = −0.00785 × 10^−5 K^−1; β0 = 1.27858

---

3.2. Validation of CG PDMS model

After parameterizing the T dependent ER factors α(T) and β(T), the subsequent renormalization of the LJ parameters ε and σ compensated for the entropy loss and enable T transferability in the CG model, which was expected to effectively reproduce the kinetic and thermodynamic properties of the polymer system across a wide T range. Fig. 4(a) compares the density of the AA and CG models at a T range from 25 K to 400 K. As observed in Fig. 4(a), the density of the PDMS AA system underwent a smooth transition from high-temperature Arrhenius behaviors to low-temperature supercooled regimes. Unlike other common glass-forming polymers, PDMS did not exhibit any sharp jump or sudden change, indicating the absence of a distinct glass transition. This phenomenon was consistent with experimental findings and typically observed in silicone polymers.^58,59 Regarding the developed CG model, the implementation of the renormalized nonbonded interaction parameters resulted in a satisfactory preservation of the density of the AA model to a good approximation throughout the entire T regimes. Although the glass transition of PDMS occurs gradually, the T_g could still be approximately estimated from the density curve by identifying the T at which the two most distinct slopes intersect. As demonstrated in Fig. 4(a), the estimated T_g for AA and CG models were remarkably close to each other, with the values of 153 K and 154 K, respectively, which also showed a good consistency with the experimental measurements (around 150 K).^9,28 Although the CG model faithfully captured the density of the target AA model, the density at 300 K was higher than the experimental value, which may be attributed to the limitation of force field parameters.^60,61 Additionally, the experimental density of PDMS at 300 K can be obtained by rationalizing the β, which is elaborated in Fig. S1 in ESI.† It should be noted that the derived β based on the high-resolution AA results showed a discrepancy compared to the β based on the experimental measurement at 300 K. If all the experimental densities of the PDMS in the temperature range are available, the presented ER approach can be directly applied to recalibrating the ER factors to match the experimental data.

Fig. 4 Comparisons of the density, MSD 〈r²(t)〉, and 〈u²〉 for the PDMS AA and CG model. (a) Density as a function of temperature. The intersection of two distinct slopes indicates T_g. (b) 〈r²(t)〉 as a function of time, determining the 〈u²〉. (c) 〈u²〉 as a function of temperature.

MSD along with its derived quantity, 〈u²〉, provides valuable insights into the free volume and mobility of polymer materials by capturing the average fluctuations and displacements of the polymer segments. Fig. 4(b) shows the comparison of the MSD 〈r²(t)〉 for the AA and CG models, demonstrating the ER-corrected CG model faithfully captured the AA dynamics under different temperatures. Additionally, we derived 〈u²〉 for the AA and CG models over a wide range of T, as shown in Fig. 4(c). It is evident that as the increase of T, the 〈u²〉 values for the CG model tightly followed the changing trace of the atomistic values. Moreover, the close good agreement of density and 〈u²〉 between the AA and CG simulations provides robust evidence of the validation of the developed CG model in capturing the essential thermodynamic properties of the PDMS system.

The conformation of a polymer refers to the spatial arrangement or shape of the polymer chain. In addition to dynamic properties, understanding the conformational behaviors of polymer materials is also of vital importance for predicting and even tailoring their properties. In this study, the radius of gyration (R_g) and end-to-end distance (R_ee) were selected as the representative parameters to describe the conformational behaviors of PDMS systems, where the former stands for the root square distance of all the monomers from the center of mass in a polymer chain, and the latter is the spatial separation between two distinct ends of a polymer chain. Fig. S2(a and b) in the ESI,† demonstrates the probability distributions of R_g and R_ee for the PDMS CG system at different temperatures. It is observed in Fig. S2(a and b) (ESI†) that regardless of temperature, both R_g and R_ee followed an approximate normal distribution pattern. Although the peak values of both R_g and R_ee slightly increased with elevating the temperature from glassy to Arrhenius regimes, the overall differences observed were rather indistinct.

Given that the conformational behaviors of the PDMS were not highly temperature-sensitive, to validate the coarse-graining approach, the R_g and R_ee for both AA and CG models were compared with different molecular weights M_n, as shown in Fig. 5(a and b). The M_n is defined as the sum of atom masses in each chain, which is directly related to chain length. As displayed in Fig. 5(a and b), the AA and CG models yielded a reasonable consistency for both R_g and R_ee. The relationship between the two conformational behaviors and molecular weight for the CG model could be described in power law scaling relationships, R_g ∝ M_n^v and R_ee ∝ M_n^ve, which is a common characteristic in many polymer systems.^62,63 The mass scaling exponents ν and ν_e identified in the power law relationships, were estimated as 0.603 and 0.745, respectively. According to the theoretical prediction conducted by Flory et al.,⁶⁴ Freed et al.⁶⁵ and Guida et al.,⁶⁶ the approximation of the mass scaling exponents for R_g and R_ee are around 0.588 and 0.75 for flexible polymers swollen by excluded volume interactions, and this result has also been confirmed by experimental measurements for a variety of copolymers.^67,68 Generally speaking, the exponent may depend on various factors, especially the branching density.^69,70 Regarding PDMS as a lightly branched polymer with linear backbone, the exponents in this study were consistent with theoretical estimates in ideal conditions. In addition, it is noted that the molecular mass of PDMS in real conditions can vary from several hundred to several hundred thousand g mol⁻¹. In this study, we mainly focused on low molecular mass to avoid long equilibrium and capitalize on the benefits of coarse-graining's fast dynamics, since the computational efficiency is directly scaled with the chain length or molecular mass in MD simulation.

Fig. 5 Comparisons of conformational behaviors as a function of molecular mass for the PDMS AA and CG model. (a) R_g and (b) R_ee.

Due to the extraordinarily low T_g of PDMS, at a room temperature or a temperature above T_g, PDMS always exhibits a relatively low tensile strength and Young's modulus, giving rise to high data variability in experimental measurements or large fluctuations in simulation results.^71–73 To address this issue, the mechanical properties of PDMS were tested at a supercooled temperature below T_g where the polymer was in a more rigid and glassy state, the fluctuations associated with the temperature-dependent transition are minimized. Fig. 6(a) shows the tensile stress–strain curves of the PDMS AA and CG models at a temperature of 100 K. The Young's modulus, E was defined as the slope of linear fitting of the stress–strain curves in elastic deformation stage from 0 to 4% strain. As illustrated in Fig. 6(a), the stress–strain curve of the CG model was closely aligned with that of the AA model in the elastic regime. However, in the following plastic deformation stage, some deviations emerged between the AA and CG systems, where the CG model yielded a slightly higher tensile stress compared to the AA model. Moreover, the developed CG model produced a tensile modulus of 4.68 ± 0.18 GPa, which closely matched the value of 4.45 ± 0.49 GPa obtained from the AA model. Although several experimental studies have confirmed the weak mechanical performance of PDMS, there have been very limited investigations concerning its mechanical performance at low temperatures, except for an experimental study by Zhang et al.⁷⁴ In their research, they carried out PDMS compression tests at 123 K and reported an experimental compressive modulus of 1.16 ± 0.10 GPa.

Fig. 6 (a) Tensile stress–strain curves for the PDMS AA and CG models at 100 K. The colored solid lines refer to the stress–strain curves after smoothing, while the corresponding light grey lines are the original curves obtained directly from the simulation. Dashed lines stand for the slope of the elastic deformation state within 4% strain, where E was determined. (b) The scaling relationship of E as a function of 1/〈u²〉 for AA and CG models from 100 K to 200 K.

To further validate our simulation results, we conducted differential scanning calorimetry (DSC) and dynamic mechanical analysis (DMA) on the PDMS material. DSC identified a glass transition for both PDMS samples, Sylgard at 149 K and the in-house PDMS at 153 K, which were in good agreement with our modeling results. Below 153 K, a storage modulus of approximately 2 GPa was noted for the in-house PDMS and of 7 GPa for the Sylgard PDMS sample. Variation of crosslinker-density did not significantly alter the glassy modulus, making it suitable for model validation and comparison purpose. As temperatures warmed, the storage modulus fell for both samples. Notably, the in-house sample showed a slow change until the crystallization temperature above which its modulus fell more quickly (Sylgard showed a smooth change in modulus over the same range). Notably, these experimental results aligned closely with our simulation findings. Although the current loading protocol in this study has been proved valid in several previous MD simulation works, the experimental strain rate was regrettably beyond the reach of MD simulation due to the computational limitations.^31,39,75,76 However, the E of the CG model still fell within the same order of magnitude as with the experimental measurements, and the disparity would not affect any conclusions drawn in this study.

To evidently explore the impact of loading rate, Fig. S3(a) (ESI†) displays the stress–strain curves of the PDMS CG model at fixed temperature of 100 K but different strain rates. According to Fig. S3(a) (ESI†), the E at strain rates of 5 ns⁻¹, 0.5 ns⁻¹, and 0.05 ns⁻¹ were 5.19 ± 0.06 GPa, 4.68 ± 0.18 GPa, and 4.12 ± 0.27 GPa, respectively. As expected, the mechanical performances of the PDMS system were fundamentally influenced by the strain rate. Both modulus and yield strength showed an insignificant increase with the strain rate at a glassy state. Moreover, the elastic deformation stage in the stress–strain curve may also alter the E. The stress–strain curves of the PDMS CG model with different identified elastic strain regimes are shown in Fig. S3(b) (ESI†). As derived from Fig. S3(b) (ESI†), the E of 3%, 4%, and 5% strain ranges were 4.97 ± 0.24 GPa, 4.68 ± 0.18 GPa, and 4.32 ± 0.30 GPa, respectively. The 5% strain fitting was obviously the secant of the stress–strain curves instead of the tangent, while 3% and 4% strain fittings were relatively close in matching the elastic regime of the stress–strain curve. For clarity and consistency, the following mechanical tests were conducted at a strain rate of 0.5 ns⁻¹ and with an elastic strain range of 4%. Additionally, the stress–strain curves of the CG models with different system sizes are demonstrated in Fig. S3(c) (ESI†). It was observed in Fig. S3(c) (ESI†) that the CG models with different system sizes yielded similar stress–strain curves. The E of 9900-, 19800-, and 29700-bead systems were 4.59 ± 0.21 GPa, 4.68 ± 0.18 GPa, and 4.66 ± 0.27 GPa, respectively. These results indicated that the mechanical behaviors of the CG model were not affected by the system size, which aligned with the findings of our previous study.⁷⁷

As mentioned in the previous discussion, 〈u²〉 is widely recognized as a metric for assessing the local free volume within the polymer system.^52,78 Consequently, it inversely serves as an indicator of the local molecular stiffness. It has been acknowledged that there is a direct correlation between molecular stiffness and the mechanical behaviors of the polymeric material.^79–81Fig. 6(b) and Table S1 (ESI†) illustrates the scaling relationship between 1/〈u²〉 and E for AA and CG models at a T range from 100 K to 250 K. As the decrease of T and increase of 1/〈u²〉, the E of both AA and CG models exhibited an upward tendency, which could be well perceived by a power law relationship. Several existing studies have found that the modulus of glass-forming polymers with flexible linear chain are believed to linearly scaled with 1/〈u²〉,^76,82 which was apparently not applicable to the PDMS system. This discrepancy could be attributed to the relative position between T_g and the tested T range. The empirical linear relationships reported in the literature were primarily established within the glassy regime below T_g. However, our study encompassed a broader T range, spanning from the glassy regime below T_g (100–150 K) to the rubbery regime above T_g (150–250 K). While the linear relationship may hold true in the glassy regime for the PDMS system, a noticeable change in slope occurred after passing through the glass transition, leading to a power law scaling across the entire temperature range. Synthesizing all the findings obtained in Fig. 6, the CG model satisfactorily retained the mechanical behaviors of the PDMS system.

Furthermore, the computational efficiencies of the PDMS AA and CG models were evaluated and compared. The current AA and CG models contained 19 200 atoms and 19 800 beads, respectively. With 10 CPU cores, the average computational speed and CPU performance of the CG model were around 59.55 hours and 0.12 hours ns⁻¹, which were 67-fold and 84-fold more efficient than the AA counterparts with similar system size (0.88 hours and 10.02 hours ns⁻¹), respectively. Moreover, we also constructed a CG model with only 1920 beads, covering the same number of atoms (19 200 atoms) as the AA model. This CG model achieved an even higher computational efficiency, with the computation speed and CPU performance reaching 327.8 hours and 0.03 hours ns⁻¹, which were roughly 372-fold and 345-fold compared to the AA counterparts. The developed PDMS CG model not only faithfully preserved the dynamics behaviors of the AA model, but also offered superior computational advantages.

3.3. Influences of cohesive interaction strength

It has been known that the dynamics and mechanical properties of glass-forming polymers are largely governed by the cohesive interaction strength of the materials. In the ER approach, the cohesive interaction strength is adjusted with different T, leading to a substantial variation in the ER factor, α. Additionally, in practical applications of PDMS and other polymer materials, a variety of additives are often integrated in these polymers to create composites with advanced properties, rather than relying solely on the polymer itself.^83,84 The inclusion of the additives may also significantly alter the cohesive interaction strength of the matrix polymer. Therefore, the question arises on the influence of cohesive interaction strength on the dynamics and thermomechanical properties of the PDMS system.

Dynamical heterogeneity refers to the spatial variation in the dynamics or movement of individual components within a complex system. Fig. 7(a–c) display the spatial distribution of 1/〈u²〉 as a measure of local molecular stiffness with different fixed α values (α = 2–6), revealing the influence of cohesive interaction strength on dynamical heterogeneity of the current PDMS CG model. In the color maps, red regions indicate the molecules had notably low mobility and high stiffness, while cyan regions refer to high molecular mobility and softness. Based on the literature and previous discussions, it was not surprising to find that the cohesive interaction strength exerted a critical influence on the local molecular stiffness, thereby directly impacting the dynamical heterogeneity. As the ER factor α increased from 2 to 6, a conspicuous amplification in the 1/〈u²〉 were observed for the PDMS CG models. Considering that the cohesive interaction strength controls the intermolecular interaction, it was anticipated that higher cohesive interaction strength would result in greater molecular stiffness. Specifically, when α = 2, the PDMS system displayed a rather homogenous distribution of local molecular stiffness, suggesting a limited degree of dynamical heterogeneity. As α increased to 6, the difference of 1/〈u²〉 within the PDMS system became more pronounced, indicating an escalated level of dynamical heterogeneity.

Fig. 7 (a)–(c) Representative color maps of 1/〈u²〉 for PDMS CG model with different fixed α values at a 100 K. (a): α = 2; (b) α = 4; (c) α = 6; (d) Probability distributions of 1/〈u²〉 for the PDMS CG model with different fixed α values at a 100 K. As α increases, the 1/〈u²〉 becomes wider and the mean value becomes larger, indicating strong dynamical heterogeneity with increasing cohesive energy.

To quantitively evaluate the dynamic heterogeneity of the PDMS CG model, the probability distribution of 1/〈u²〉 with different α values is presented in Fig. 7(d). As depicted in Fig. 7(d), all the distribution curves could be accurately characterized by normal distribution patterns. In the case of the lowest cohesive interaction strength α = 2, the 1/〈u²〉 yielded the lowest mean value of 4.55 Å⁻² and exhibited a tightly constrained probability distribution, implying the least molecular stiffness and greatest homogeneity in dynamics for the PDMS system. As the increase of α value, the probability distribution of 1/〈u²〉 became remarkably broader showing the higher dynamic heterogeneity. For the mean value of 1/〈u²〉, an ascending trend was evidently observed as the increase of cohesive interaction strength. Specifically, the mean values were 6.42, 8.54, 10.65, and 12.97 Å⁻² for α values of 3 to 6, respectively. In addition to cohesive interaction strength, the dynamic heterogeneity of the PDMS CG model was also examined at different temperatures (T = 100, 150, 200, 250 K) as shown in Fig. S4(a–e) (ESI†). The elevation of T resulted in lower molecular stiffness and lower level of dynamic heterogeneity, which had the similar effect as reducing the cohesive interaction strength.

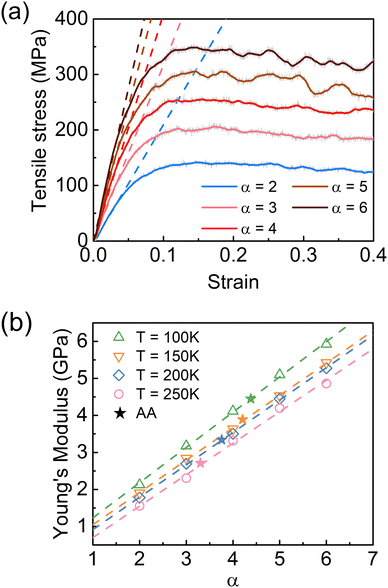
The influence of cohesive interaction strength was further assessed in terms of mechanical properties by varying the ER factor α. Fig. 8(a) shows the stress–strain curves of the PDMS CG model with different fixed α values at 100 K. It was observed in Fig. 8(a) that the mechanical performances of the PDMS system were strongly dominated by cohesive interaction strength. The yield stress and Young's modulus were significantly enhanced with the increase of the α value. The tensile tests were also conducted at different temperatures, and the correlations between Young's modulus and α value at 100, 150, 200, and 250 K are summarized in Fig. 8(b). As the α value rose from 2 to 6, the Young's modulus increased almost linearly, while the linear fittings at each temperature are marked as the dash lines in the figure. The increasing trend remained valid for the system across all the temperatures, implying the strong dependence of the mechanical performance on the cohesive interaction strength. Moreover, by comparing the Young's modulus with the same α values but at different temperatures, the higher Young's modulus was expected to be obtained at lower temperatures. Consistent with the results of dynamic heterogeneity, the mechanical performances of the PDMS CG model responded similarly to both increased cohesive interaction strength and reduced temperature, which undoubtedly emphasized the decisive role of cohesive interaction strength on dynamics and thermomechanical properties of the polymer system. On the other hand, the Young's modulus of the PDMS AA model at identical temperatures is also indicated as pentagram symbols in Fig. 8(b). As illustrated in Fig. 8(b), the Young's modulus of the AA model lay near the corresponding linear fittings. At each temperature, there was a unique α value to allow the match between the AA and CG models, highlighting the necessity of introducing ER factors to renormalize the cohesive energy in the coarse-graining.

Fig. 8 (a) Tensile stress–strain curves for the PDMS CG models with different ER factor α at 100 K. (b) Tensile modulus as a function of the α values at different temperatures. Dash lines serve as visual aid. Pentagrams are the Young's modulus of the AA model at different temperatures.

4. Conclusion

In this study, a temperature transferable PDMS CG model was developed based on the bottom-up strategy accomplished by utilizing a recently proposed coarse-graining strategy of energy-renormalization where the cohesive energy was renormalized with the variation of temperature. By preserving the density and 〈u²〉 of the AA model as a function of temperature, the developed CG model faithfully reproduced the dynamics, conformational and mechanical behaviors of the AA counterpart to a good approximation, spanning over a wide temperature range, which was further validated by experimental data. The crucial influence of cohesive interaction strength was evidently highlighted by varying the ER factor α. It was found that the dynamical heterogeneity and mechanical responses of the PDMS system were considerably enhanced with the increase of cohesive interaction strength or the reduction of temperature. Our proposed ER approach holds promise for application to other silicone polymers, ensuring temperature transferability across various polymer systems. The established CG modeling framework in this study thus contributes to the broader field of materials science, opening avenues for tailoring silicone polymers based on their dynamic and mechanical responses to temperature changes.

Conflicts of interest

The authors declared no conflict of interest.

Acknowledgements

The authors acknowledge the support from the U.S. Office of Naval Research (Award No. N00014-20-1-2817 and N00014-22-1-2129). W. Xia also acknowledges support from the Department of Aerospace Engineering and College of Engineering at Iowa State University.

References

1. S. C. Shit and P. Shah, A review on silicone rubber, Natl. Acad. Sci. Lett., 2013, 36, 355–365.
2. L. G. Hanu, G. P. Simon and Y. B. Cheng, Thermal stability and flammability of silicone polymer composites, Polym. Degrad. Stab., 2006, 91, 1373–1379.
3. A. L. Skov and L. Yu, Optimization Techniques for Improving the Performance of Silicone-Based Dielectric Elastomers, Adv. Eng. Mater., 2018, 20, 1–21.
4. M. J. Owen, Silicone Hydrophobicity and Oleophilicity, Silicon, 2017, 9, 651–655.
5. J. Sołoducho, D. Zając, K. Spychalska, S. Baluta and J. Cabaj, Conducting silicone-based polymers and their application, Molecules, 2021, 26, 2012.
6. M. Zielecka and E. Bujnowska, Silicone-containing polymer matrices as protective coatings: Properties and applications, Prog. Org. Coatings, 2006, 55, 160–167.
7. E. Yilgör and I. Yilgör, Silicone containing copolymers: Synthesis, properties and applications, Prog. Polym. Sci., 2014, 39, 1165–1195.
8. I. Miranda, A. Souza, P. Sousa, J. Ribeiro, E. M. S. Castanheira, R. Lima and G. Minas, Properties and applications of PDMS for biomedical engineering: A review, J. Funct. Biomater., 2022, 13, 2.
9. M. P. Wolf, G. B. Salieb-Beugelaar and P. Hunziker, PDMS with designer functionalities—Properties, modifications strategies, and applications, Prog. Polym. Sci., 2018, 83, 97–134.
10. P. A. Klonos, Crystallization, glass transition, and molecular dynamics in PDMS of low molecular weights: A calorimetric and dielectric study, Polymer, 2018, 159, 169–180.
11. J. T. Padding and W. J. Briels, Systematic coarse-graining of the dynamics of entangled polymer melts: The road from chemistry to rheology, J. Phys.: Condens. Matter, 2011, 23, 233101.
12. S. Riniker, J. R. Allison and W. F. van Gunsteren, On developing coarse-grained models for biomolecular simulation: a review, Phys. Chem. Chem. Phys., 2012, 14, 12423–12430.
13. Z. Li, Y. Wang, A. Alesadi, L. A. Ruiz Pestana and W. Xia, Chapter Three - Particle-Based Mesoscale Modeling and Coarse-Graining Methods, ed. W. Xia and S. M. Ruiz Pestana, Elsevier, 2023, pp. 75–111.
14. S. O. Nielsen, C. F. Lopez, G. Srinivas and M. L. Klein, Coarse grain models and the computer simulation of soft materials, J. Phys.: Condens. Matter, 2004, 16, R481.
15. S. Izvekov, M. Parrinello, C. J. Bumham and G. A. Voth, Effective force fields for condensed phase systems from ab initio molecular dynamics simulation: A new method for force-matching, J. Chem. Phys., 2004, 120, 10896–10913.
16. F. Müller-Plathe, Coarse-graining in polymer simulation: from atomistic simulations to the mesocopic scale and back, Chem. Phys. Chem., 2002, 3, 755–769.
17. S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, The MARTINI force field: Coarse grained model for biomolecular simulations, J. Phys. Chem. B, 2007, 111, 7812–7824.
18. V. Ullal and D. E. Spearot, Molecular dynamics simulation of O2 diffusion in polydimethylsiloxane (PDMS) and end-linked PDMS networks, Mol. Simul., 2014, 40, 976–986.
19. C. Peter and K. Kremer, Multiscale simulation of soft matter systems, Faraday Discuss., 2009, 144, 9–24.
20. M. Grmela and H. C. Öttinger, Dynamics and thermodynamics of complex fluids. I. Development of a general formalism, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 6620–6632.
21. H. A. Karimi-Varzaneh, N. F. A. Van Der Vegt, F. Müller-Plathe and P. Carbone, How good are coarse-grained polymer models? A comparison for atactic polystyrene, ChemPhysChem, 2012, 13, 3428–3439.
22. P. K. Depa and J. K. Maranas, Speed up of dynamic observables in coarse-grained molecular-dynamics simulations of unentangled polymers, J. Chem. Phys., 2005, 123, 094901.
23. I. Y. Lyubimov and M. G. Guenza, Theoretical reconstruction of realistic dynamics of highly coarse-grained cis-1,4-polybutadiene melts, J. Chem. Phys., 2013, 138, 12A546.
24. A. Davtyan, J. F. Dama, G. A. Voth and H. C. Andersen, Dynamic force matching: A method for constructing dynamical coarse-grained models with realistic time dependence, J. Chem. Phys., 2015, 142, 154104.
25. W. Shinoda, R. Devane and M. L. Klein, Zwitterionic lipid assemblies: Molecular dynamics studies of monolayers, bilayers, and vesicles using a new coarse grain force field, J. Phys. Chem. B, 2010, 114, 6836–6849.
26. G. R. Kneller, Quasielastic neutron scattering and relaxation processes in proteins: analytical and simulation-based models, Phys. Chem. Chem. Phys., 2005, 7, 2641–2655.
27. J. C. Johnson, L. T. J. Korley and M. Tsige, Coarse-grained modeling of peptidic/PDMS triblock morphology, J. Phys. Chem. B, 2014, 118, 13718–13728.
28. S. Cambiaso, F. Rasera, G. Rossi and D. Bochicchio, Development of a transferable coarse-grained model of polydimethylsiloxane, Soft Matter, 2022, 18, 7887–7896.
29. A. Khot, R. K. Lindsey, J. P. Lewicki, A. Maiti, N. Goldman and M. P. Kroonblawd, United atom and coarse grained models for crosslinked polydimethylsiloxane with applications to the rheology of silicone fluids, Phys. Chem. Chem. Phys., 2023, 25, 9669–9684.
30. H. Huang, F. Cao, L. Wu and H. Sun, All-atom and coarse-grained force fields for polydimethylsiloxane, Mol. Simul., 2017, 43, 1513–1522.
31. W. Xia, N. K. Hansoge, W. S. Xu, F. R. Phelan, S. Keten and J. F. Douglas, Energy renormalization for coarse-graining polymers having different segmental structures, Sci. Adv., 2019, 5, 1–8.
32. J. Song, D. D. Hsu, K. R. Shull, F. R. Phelan, J. F. Douglas, W. Xia and S. Keten, Energy Renormalization Method for the Coarse-Graining of Polymer Viscoelasticity, Macromolecules, 2018, 51, 3818–3827.
33. G. Adam and J. H. Gibbs, On the temperature dependence of cooperative relaxation properties in glass-forming liquids, J. Chem. Phys., 1965, 43, 139–146.
34. J. Dudowicz, K. F. Freed and J. F. Douglas, Fragility of glass-forming polymer liquids, J. Phys. Chem. B, 2005, 109, 21350–21356.
35. B. A. Pazmiño Betancourt, P. Z. Hanakata, F. W. Starr and J. F. Douglas, Quantitative relations between cooperative motion, emergent elasticity, and free volume in model glass-forming polymer materials, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2966–2971.
36. W. Xia, J. Song, N. K. Hansoge, F. R. Phelan, S. Keten and J. F. Douglas, Energy Renormalization for Coarse-Graining the Dynamics of a Model Glass-Forming Liquid, J. Phys. Chem. B, 2018, 122, 2040–2045.
37. M. Dunbar and S. Keten, Energy Renormalization for Coarse-Graining a Biomimetic Copolymer, Poly(catechol-styrene), Macromolecules, 2020, 53, 9397–9405.
38. A. Giuntoli, N. K. Hansoge, A. van Beek, Z. Meng, W. Chen and S. Keten, Systematic coarse-graining of epoxy resins with machine learning-informed energy renormalization, npj Comput. Mater., 2021, 7, 168.
39. Y. Wang, Z. Li, K. Niu and W. Xia, Energy renormalization for coarse-graining of thermomechanical behaviors of conjugated polymer, Polymer, 2022, 256, 125159.
40. H. X. Cao and L. M. Peng, Parameterization of the temperature dependence of the Debye-Waller factors, Acta Crystallogr., Sect. A: Found. Crystallogr., 1999, 55, 926–932.
41. BIOVIA, Dassault Systèmes, Materials Studio, 2021, San Diego, Dassault Systèmes, 2021.
42. S. L. Mayo, B. D. Olafson and W. A. Goddard, DREIDING: A generic force field for molecular simulations, J. Phys. Chem., 1990, 94, 8897–8909.
43. M. E. Fortunato and C. M. Colina, SoftwareX pysimm: A python package for simulation of molecular systems, SoftwareX, 2017, 6, 7–12.
44. J. Gasteiger and M. Marsili, Iterative partial equalization of orbital electronegativity-a rapid access to atomic charges, Tetrahedron, 1980, 36, 3219–3228.
45. E. Matteoli and G. Ali Mansoori, A simple expression for radial distribution functions of pure fluids and mixtures, J. Chem. Phys., 1995, 103, 4672–4677.
46. B. G. Levine, J. E. Stone and A. Kohlmeyer, Fast analysis of molecular dynamics trajectories with graphics processing units-Radial distribution function histogramming, J. Comput. Phys., 2011, 230, 3556–3569.
47. S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19.
48. A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool, Model. Simul. Mater. Sci. Eng., 2009, 18, 015012.
49. V. Botan, V. D. Ustach, K. Leonhard and R. Faller, Development and Application of a Coarse-Grained Model for PNIPAM by Iterative Boltzmann Inversion and Its Combination with Lattice Boltzmann Hydrodynamics, J. Phys. Chem. B, 2017, 121, 10394–10406.
50. B. Bayramoglu and R. Faller, Coarse-grained modeling of polystyrene in various environments by iterative Boltzmann inversion, Macromolecules, 2012, 45, 9205–9219.
51. V. Agrawal, G. Arya and J. Ostwald, Simultaneous iterative Boltzmann inversion for coarse-graining of polyurea, Macromolecules, 2014, 47, 3378–3389.
52. D. S. Simmons, M. T. Cicerone, Q. Zhong, M. Tyagi and J. F. Douglas, Generalized localization model of relaxation in glass-forming liquids, Soft Matter, 2012, 8, 11455–11461.
53. F. D. Vila, J. J. Rehr, H. H. Rossner and H. J. Krappe, Theoretical x-ray absorption Debye-Waller factors, Phys. Rev. B - Condens. Matter Mater. Phys., 2007, 76, 1–11.
54. X. H. Sang, A. Kulovits and J. M. K. Wiezorek, Determination of Debye - Waller factor and structure factors for Si by quantitative convergent-beam electron diffraction using off-axis multi-beam orientations, Acta Crystallogr., Sect. A: Found. Crystallogr., 2010, 66, 685–693.
55. F. W. Starr, J. F. Douglas and S. Sastry, The relationship of dynamical heterogeneity to the Adam-Gibbs and random first-order transition theories of glass formation, J. Chem. Phys., 2013, 138, 12A541.
56. W. Lou, C. Xie and X. Guan, Understanding radiation-thermal aging of polydimethylsiloxane rubber through molecular dynamics simulation, npj Mater, Degrad, 2022, 6, 84.
57. A. Alesadi and W. Xia, Understanding the Role of Cohesive Interaction in Mechanical Behavior of a Glassy Polymer, Macromolecules, 2020, 53, 2754–2763.
58. J. Qu, K. Gao, G. Hou, L. Zhang, Y. Lu and J. Liu, Molecular dynamics simulation of glass transition and thermal stability of novel silicone elastomer and its nanocomposites, Mater. Today Commun., 2022, 33, 104517.
59. N. Bosq, N. Guigo, J. Persello and N. Sbirrazzuoli, Melt and glass crystallization of PDMS and PDMS silica nanocomposites, Phys. Chem. Chem. Phys., 2014, 16, 7830–7840.
60. S. N. Korobeynikov, V. V. Alyokhin and A. V. Babichev, Simulation of mechanical parameters of graphene using the DREIDING force field, Acta Mech., 2018, 229, 2343–2378.
61. K. Sasaki and T. Yamashita, Modification and Validation of the DREIDING Force Field for Molecular Liquid Simulations (DREIDING-UT), J. Chem. Inf. Model., 2021, 61, 1172–1179.
62. W. Zhang, F. Vargas-Lara, S. V. Orski, K. L. Beers and J. F. Douglas, Modeling short-chain branched polyethylenes in dilute solution under variable solvent quality conditions: Basic configurational properties, Polymer, 2021, 217, 123429.
63. F. M. Mirabella and J. F. Johnson, Polymer Configurational and Compositional Variables as a Function of Molecular Weight, J. Macromol. Sci. Part C, 1975, 12, 81–108.
64. J. Naghizadeh and K. A. Dill, Statistical Mechanics of Chain Molecules at Interfaces, Macromolecules, 1991, 24, 1768–1778.
65. K. F. Freed, Functional Integrals and Polymer Statistics, 2007, 22, 1–128.
66. A. C. Petkou, V. Model, C. Yuan and L. Zhi-bing, Critical exponents of the N-vector model, J. Phys. A: Math. Gen., 1998, 31, 8103.
67. P. Brant, C. J. Ruff and T. Sun, Effect of tacticity on the dilute solution coil dimensions of poly(α-olefin)s, Macromolecules, 2005, 38, 7181–7183.
68. J. C. Le Guillou and J. Zinn-Justin, Critical exponents for the n-vector model in three dimensions from field theory, Phys. Rev. Lett., 1977, 39, 95–98.
69. R. L. Lescanec and M. Muthukumar, Configurational Characteristics and Scaling Behavior of Starburst Molecules: A Computational Study, Macromolecules, 1990, 23, 2280–2288.
70. A. Chremos and J. F. Douglas, A comparative study of thermodynamic, conformational, and structural properties of bottlebrush with star and ring polymer melts, J. Chem. Phys., 2018, 149, 044904.
71. F. C. P. Sales, R. M. Ariati, V. T. Noronha and J. E. Ribeiro, Mechanical characterization of PDMS with different mixing ratios, Procedia Struct. Integr., 2021, 37, 383–388.
72. T. Han, Y. Sun, Z. Zhao and X. Chen, The effect of strain rate on the mechanical property of PDMS and PDMS/graphene: A molecular dynamics study, J. Phys. Conf. Ser., 2022, 2184, 012046.
73. M. Liu, J. Sun and Q. Chen, Influences of heating temperature on mechanical properties of polydimethylsiloxane, Sens. Actuators, A, 2009, 151, 42–45.
74. G. Zhang, Y. Sun, B. Qian, H. Gao and D. Zuo, Experimental study on mechanical performance of polydimethylsiloxane (PDMS) at various temperatures, Polym. Test., 2020, 90, 106670.
75. Z. Li and W. Xia, Coarse-grained modeling of nanocellulose network towards understanding the mechanical performance, Extrem. Mech. Lett., 2020, 40, 100942.
76. W. Xia, J. Song, C. Jeong, D. D. Hsu, F. R. Phelan, J. F. Douglas and S. Keten, Energy-Renormalization for Achieving Temperature Transferable Coarse-Graining of Polymer Dynamics, Macromolecules, 2017, 50, 8787–8796.
77. Y. Wang, Z. Li, D. Sun, N. Jiang, K. Niu, A. Giuntoli and W. Xia, Understanding the thermomechanical behavior of graphene-reinforced conjugated polymer nanocomposites via coarse-grained modeling, Nanoscale, 2023, 15, 17124–17137.
78. F. W. Starr, S. Sastry, J. F. Douglas and S. C. Glotzer, What do we learn from the local geometry of glass-forming liquids?, Phys. Rev. Lett., 2002, 89, 4.
79. J. F. Douglas, B. A. P. Betancourt, X. Tong and H. Zhang, Localization model description of diffusion and structural relaxation in glass-forming Cu-Zr alloys, J. Stat. Mech.: Theory Exp., 2016, 5, 054048.
80. J. H. Van Zanten and K. P. Rufener, Brownian motion in a single relaxation time Maxwell fluid, Phys. Rev. E - Stat. Physics, Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 5389–5396.
81. Z. Li, Y. Liao, Y. Zhang, Y. Zhang and W. Xia, Microstructure and dynamics of nanocellulose films: Insights into the deformational behavior, Extrem. Mech. Lett., 2022, 50, 101519.
82. F. Puosi and D. Leporini, The kinetic fragility of liquids as manifestation of the elastic softening, Eur. Phys. J. E, 2015, 38, 87.
83. R. Ariati, F. Sales, A. Souza, R. A. Lima and J. Ribeiro, Polydimethylsiloxane composites characterization and its applications: A review, Polymers, 2021, 13, 1–21.
84. M. D. Jia, K. V. Pleinemann and R. D. Behling, Preparation and characterization of thin-film zeolite-PDMS composite membranes, J. Memb. Sci., 1992, 73, 119–128.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05969c

---