Open Access Article
Open Access ArticleFull control of the orientation of non-symmetric molecules using weak and moderate electric fields
Rosario
González-Férez
 a and
Juan J.
Omiste
a and
Juan J.
Omiste
 *b
*b
aInstituto Carlos I de Física Teórica y Computacional and Departamento de Física Atómica, Molecular y Nuclear, Universidad de Granada, 18071 Granada, Spain
bDepartamento de Química Física, Universidad Complutense de Madrid, 28040 Madrid, Spain. E-mail: jomiste@ucm.es
First published on 10th January 2024
Abstract
We investigate the full control over the orientation of a planar non-symmetric molecule by using moderate and weak electric fields. Quantum optimal control techniques allow us to orient any axis of 6-chloropyridazine-3-carbonitrile, which is taken as prototype example here, along the electric field direction. We perform a detailed analysis by exploring the impact on the molecular orientation of the time scale and strength of the control field. The underlying physical phenomena allowing for the control of the orientation are interpreted in terms of the frequencies contributing to the field-dressed dynamics and to the driving field by a spectral analysis.
1 Introduction
The interaction of external fields with molecules creates coherent superpositions of field-free rotational states1,2 with plethora of applications in a wide range of areas from stereodynamics,3–5 high precision measurements6 and quantum information processing.7,8 This interaction allows for the creation and control of highly rotating molecular states, namely superrotors,9–11 the manipulation12–15 and separation16,17 of chiral molecules, the orientation of proteins,18,19 the isotopic separation,20 and the controlled manipulation of enantiomers of chiral molecules.21The orientation of a molecule requires the angular confinement of a molecule-fixed axis along a laboratory-fixed one and a preferred direction of the electric dipole moment.22–24 For asymmetric molecules, the 3D orientation implies that the all three molecular axes of inertia are confined to laboratory fixed ones and a well defined direction of the electric dipole moment.25,26 Certain complex molecular systems, such as the planar molecule 6-chloropyridazine-3-carbonitrile and the chiral one bromochlorofluoromethane (CHBrClF), possess a permanent dipole moment which does not coincide with any inertia axis. For these systems, it may be necessary to control the orientation of a specific molecular axis different from the one defined by the electric dipole moment. Therefore, it is mandatory to design an specific protocol beyond brute force orientation27 or standard mixed-field orientation22,24 to accurately restrict the position of a given axis, i.e., a given atom. Such a task could benefit from long-established algorithms, as the quantum optimal control (QOC)28 to accurately drive the molecular dynamics, which is one of the most relevant and promising quantum control algorithms in many active areas of research.29,30
The fundamental concept of QOC involves designing a driving field that optimizes a certain expectation value or a state population in a quantum system. This is done by solving a self-consistent set of equations, for which several algorithms have been developed.31,32 QOC constitutes a powerful tool for manipulating the dynamics of quantum systems,28,32,33 including the control of qubits,34 population of vibrational states,35 and coupled spin dynamics,36 among others. Regarding molecular orientation control, the Krotov algorithm31,37,38 is used to design terahertz laser pulses,39 or to manipulate the permanent dipole orientation of molecular ensembles, as reported in various studies.40–43 In addition, this algorithm has been used to optimize alignment of molecules immersed in a thermal bath.44,45
In this work, we consider a non-symmetric molecule, and apply the QOC algorithm to optimize the orientation along several molecular directions. Nevertheless, this methodology may be applied to any molecular axis contained in the molecular plane. Our study provides physical insights into the design of driving fields for this purpose. In particular, we provide a deeper understanding of the mechanisms underlying the control by means of a spectral analysis of the field-dressed wavepacket and of the driving field. This paper is organized as follows. Section 2 provides the Hamiltonian in an electric field, and a brief overview of the QOC theory with the corresponding equations of motion. In Section 3, we present the QOC results for the planar molecule 6-chloropyridazine-3-carbonitrile (CPC), taken here as a prototype example, orienting its permanent dipole moment and principal axes of inertia within the molecular plane, while varying the control field strength and duration. Finally, Section 4 summarizes the main findings of the study and presents a short outlook.
2 Theory and methods
2.1 The Hamiltonian
In this work we investigate the orientation of a planar molecule without rotational symmetry by means of an external time-dependent electric field![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t), which is taken parallel to the Laboratory Fixed Frame (LFF) Z-axis. We work within the Born–Oppenheimer and the rigid rotor approximation; therefore, the molecular system is described by the Hamiltonian:
(t), which is taken parallel to the Laboratory Fixed Frame (LFF) Z-axis. We work within the Born–Oppenheimer and the rigid rotor approximation; therefore, the molecular system is described by the Hamiltonian:| H(t) = Hrot + HE(t), | (1) |
![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) along the k axis of the molecular fixed frame (MFF). The field-free rotational states are denoted by JKa,KcM,46 where J is the total angular momentum number and M the magnetic quantum number, i.e., the projection of
along the k axis of the molecular fixed frame (MFF). The field-free rotational states are denoted by JKa,KcM,46 where J is the total angular momentum number and M the magnetic quantum number, i.e., the projection of ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) along the LFF Z-axis, and Ka and Kc are the projection of
along the LFF Z-axis, and Ka and Kc are the projection of ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) along the MFF z-axis in the prolate and oblate limiting cases, respectively.
along the MFF z-axis in the prolate and oblate limiting cases, respectively.
The coupling of the molecular electric dipole moment ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) with an electric field parallel to the LFF Z-axis27,47 reads
with an electric field parallel to the LFF Z-axis27,47 reads
 | (2) |
![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) and the LFF Z-axis, and θZk the Euler angle between the molecular k axis and LFF Z-axis.48 The effect of this interaction is to orient the electric dipole moment along the electric field direction, which we characterize by 〈cos
and the LFF Z-axis, and θZk the Euler angle between the molecular k axis and LFF Z-axis.48 The effect of this interaction is to orient the electric dipole moment along the electric field direction, which we characterize by 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉, in this work, we also explore the orientation of the MFF z and x axes along this LFF Z-axis in terms of 〈cos
θZμ〉, in this work, we also explore the orientation of the MFF z and x axes along this LFF Z-axis in terms of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 and 〈cos
θZz〉 and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉, respectively.
θZx〉, respectively.
2.2 Quantum optimal control
The goal of this work is to optimize the orientation of any molecular axis of an asymmetric planar molecule by using the quantum optimal control (QOC) methodology to design a time-dependent electric field while imposing certain restrictions. To do so, we define the following functional31 | (3) |
 , guarantees that the time-dependent Schrödinger equation is fulfilled by introducing the Lagrange multiplier χ(t):
, guarantees that the time-dependent Schrödinger equation is fulfilled by introducing the Lagrange multiplier χ(t): | (4) |
 reads as
reads as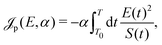 | (5) |
 maximizes the expectation value of the operator O at the final time t = T:
maximizes the expectation value of the operator O at the final time t = T: | (6) |
 and maximizes (minimizes)
and maximizes (minimizes)  . To achieve the latter, the values of α and the function S(t) must be carefully chosen such that the contribution of the fluence of E(t) is small compared to 〈O〉.
. To achieve the latter, the values of α and the function S(t) must be carefully chosen such that the contribution of the fluence of E(t) is small compared to 〈O〉.
The QOC equations31 are obtained by solving the Euler equation associated with the functional 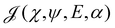 eqn (3) and are given by
eqn (3) and are given by
| i∂tψ(t) − H(t)ψ(t) = 0, | (7) |
| i∂tχ(t) − H(t)χ(t) = 0, | (8) |
| χ(T) = Oψ(T), | (9) |
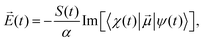 | (10) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZk〉 and to ensure the convergence of the algorithm, we set O = cos
θZk〉 and to ensure the convergence of the algorithm, we set O = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZk + 1. Let us remark that by maximizing the orientation we also ensure a high degree of alignment, since
θZk + 1. Let us remark that by maximizing the orientation we also ensure a high degree of alignment, since  .
.
In order to describe the dynamics, we solve the time dependent Schrödinger equation associated with the Hamiltonian in eqn (1). A basis set expansion of the wavefunction Ψ(Ω,t) is done in terms of the Wigner matrix elements,48 and their most relevant properties and the matrix elements required are given in detailed elsewhere.48 In this basis expansion, we take into account that magnetic quantum number M is conserved, because the electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) (t) is parallel to the LFF Z-axis. For the time propagation, we apply the short iterative Lanczos scheme.50
(t) is parallel to the LFF Z-axis. For the time propagation, we apply the short iterative Lanczos scheme.50
3 Results
As an example of non-symmetric planar molecules, we use 6-chloropyridazine-3-carbonitrile, with rotational constants Bx = 717.42 MHz, By = 639.71 MHz and Bz = 5905 MHz.51 This molecule is characterized by having its electric dipole moment not parallel to any principal axis of inertia, as shown in Fig. 1, with μ = 5.20 D and components μx = 4.37 D and μz = 2.83 D.51 We focus on the field-dressed dynamics of the rotational ground state. To provide a deeper physical insight into the QOC mechanism, we explore the orientation along the driving field direction of the permanent dipole moment,![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) , and the principal axes of inertia in the molecular plane x and z. Note that the orientation may be maximized along any direction in the molecular plane.
, and the principal axes of inertia in the molecular plane x and z. Note that the orientation may be maximized along any direction in the molecular plane.
 | ||
Fig. 1 Sketch of the molecular structure of 6-chloropyridazine-3-carbonitrile (CPC). The molecular geometry and the dipole moment, ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) , are taken from ref. 51. , are taken from ref. 51. | ||
For the mask function of the electric field, we use a Gaussian envelope 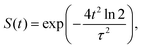 with τ being the Full Width at Half Maximum (FWHM). The time interval is set to [T0,T] = [−2.53τ,2.53τ], taking
with τ being the Full Width at Half Maximum (FWHM). The time interval is set to [T0,T] = [−2.53τ,2.53τ], taking  for computational convenience. The field-dressed dynamics is analyzed in terms of transition between field-free rotational states involved in the optimal control process. The most relevant transitions and their frequencies are collected in Table 1. These frequencies also allow us to interpret the structure of the driving field in the forthcoming sections.
for computational convenience. The field-dressed dynamics is analyzed in terms of transition between field-free rotational states involved in the optimal control process. The most relevant transitions and their frequencies are collected in Table 1. These frequencies also allow us to interpret the structure of the driving field in the forthcoming sections.
| Transition | Frequency (GHz) | Transition | Frequency (GHz) |
|---|---|---|---|
| 0000 ↔ 1010 | 1.35 | 4040 ↔ 5050 | 6.76 |
| 1100 ↔ 2020 | 2.47 | 1010 ↔ 2110 | 7.81 |
| 1100 ↔ 2110 | 2.63 | 2020 ↔ 3120 | 9.05 |
| 1010 ↔ 2020 | 2.71 | 2200 ↔ 3120 | 11.87 |
| 2020 ↔ 3030 | 4.06 | 8080 ↔ 9180 | 15.84 |
| 3030 ↔ 4040 | 5.41 | 1100 ↔ 2200 | 18.40 |
| 0000 ↔ 1100 | 6.53 | 2200 ↔ 3300 | 30.27 |
3.1 Quantum optimal control for the fixed penalty parameter α
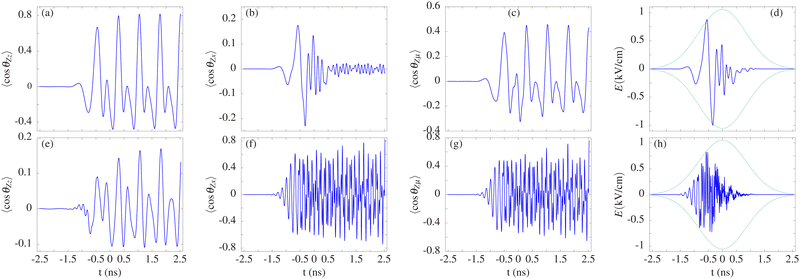
In this section, we set α = 106 for the driving electric field, which is equivalent to fixing its maximum allowed strength given by μ/α, and consider two different FWHMs τ. For a 1 ns-FWHM field, the results obtained when the expectation value 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 is optimized are presented in Fig. 2(a)–(d). The driving field designs a wavepacket populating rotational states and adjusting their relative phases. The time-evolution of the quantum interferences between these populated states provokes that 〈cos
θZz〉 is optimized are presented in Fig. 2(a)–(d). The driving field designs a wavepacket populating rotational states and adjusting their relative phases. The time-evolution of the quantum interferences between these populated states provokes that 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 reaches a maximum at the final T as shown in Fig. 2(a). During the time-evolution, the orientation varies between 〈cos
θZz〉 reaches a maximum at the final T as shown in Fig. 2(a). During the time-evolution, the orientation varies between 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 = −0.48 and 〈cos
θZz〉 = −0.48 and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 = 0.824, and its oscillation pattern indicates that only a few states are involved in the dynamics. A spectral analysis of 〈cos
θZz〉 = 0.824, and its oscillation pattern indicates that only a few states are involved in the dynamics. A spectral analysis of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 encounters three main frequencies 1.38, 2.77 and 4.15 GHz, associated with the transitions 0000 ↔ 1010, 1010 ↔ 2020 and 2020 ↔ 3030, respectively, see Table 1. These rotational states are linked by the selection rules ΔJ = ±1 and ΔM = 0, imposed by the operator cos
θZz〉 encounters three main frequencies 1.38, 2.77 and 4.15 GHz, associated with the transitions 0000 ↔ 1010, 1010 ↔ 2020 and 2020 ↔ 3030, respectively, see Table 1. These rotational states are linked by the selection rules ΔJ = ±1 and ΔM = 0, imposed by the operator cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz48,52 in eqn (2). For this optimization, the driving electric field in Fig. 2(d) is mostly relevant before t = 0 finding two main peaks at t = −0.56 ns and t = −0.35 ns with intensity 0.87 kV cm−1 and −1 kV cm−1, respectively, being very weak afterwards. This control field is also mainly formed by these transition frequencies, as illustrated by the square of its Fourier Transform
θZz48,52 in eqn (2). For this optimization, the driving electric field in Fig. 2(d) is mostly relevant before t = 0 finding two main peaks at t = −0.56 ns and t = −0.35 ns with intensity 0.87 kV cm−1 and −1 kV cm−1, respectively, being very weak afterwards. This control field is also mainly formed by these transition frequencies, as illustrated by the square of its Fourier Transform  in Fig. 3. Note that
in Fig. 3. Note that  is normalized so its maximum value is 1. The wide peaks of the τ = 1 ns field are due to the duration imposed in the optimization algorithm. One can distinguish the frequencies 1.35, 4.06 and 5.41 GHz, associated with the transitions 0000 ↔ 1010, 2020 ↔ 3030 and 3030 ↔ 4040, respectively. Note that the contribution of the latter in the orientation pattern is negligible. The frequency 2.77 GHz from the 1010 ↔ 2020 transition is blurred due to the overlap with the preceding peaks. Despite the field being designed to optimize 〈cos
is normalized so its maximum value is 1. The wide peaks of the τ = 1 ns field are due to the duration imposed in the optimization algorithm. One can distinguish the frequencies 1.35, 4.06 and 5.41 GHz, associated with the transitions 0000 ↔ 1010, 2020 ↔ 3030 and 3030 ↔ 4040, respectively. Note that the contribution of the latter in the orientation pattern is negligible. The frequency 2.77 GHz from the 1010 ↔ 2020 transition is blurred due to the overlap with the preceding peaks. Despite the field being designed to optimize 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉, we encounter a moderate orientation of the molecular x-axis in Fig. 2(c) due to the coupling through μx. The orientation 〈cos
θZz〉, we encounter a moderate orientation of the molecular x-axis in Fig. 2(c) due to the coupling through μx. The orientation 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 faithfully follows the external field until t ≈ 0.5 ns. From there on the field is very small, and 〈cos
θZx〉 faithfully follows the external field until t ≈ 0.5 ns. From there on the field is very small, and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 oscillates with a small amplitude reaching 〈cos
θZx〉 oscillates with a small amplitude reaching 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 = −0.028 at t = T. Reaching this almost zero orientation is possible since the time scale required for the x-axis dynamics is shorter than the period of oscillation of the electric field. Hence the impact of the driving field averages out due to the rapid oscillation of the molecule. The frequency of the x axis orientation is determined by the rotational constants of the orthogonal axes, namely By and Bz, which have an average value of approximately 3.27 GHz. This frequency is greater than the oscillation frequency of the driving field, which is around 1.6 GHz. The spectral analysis of 〈cos
θZx〉 = −0.028 at t = T. Reaching this almost zero orientation is possible since the time scale required for the x-axis dynamics is shorter than the period of oscillation of the electric field. Hence the impact of the driving field averages out due to the rapid oscillation of the molecule. The frequency of the x axis orientation is determined by the rotational constants of the orthogonal axes, namely By and Bz, which have an average value of approximately 3.27 GHz. This frequency is greater than the oscillation frequency of the driving field, which is around 1.6 GHz. The spectral analysis of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 confirms that the states 1100, 2110 and 3120 are also populated in the field-dressed dynamics. For the sake of completeness, we present 〈cos
θZx〉 confirms that the states 1100, 2110 and 3120 are also populated in the field-dressed dynamics. For the sake of completeness, we present 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉 in Fig. 2(c), which shows a similar behaviour to 〈cos
θZμ〉 in Fig. 2(c), which shows a similar behaviour to 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉.
θZz〉.
The driving field and the dressed rotational dynamics are highly complex when the QOC technique is applied to the orientation of the molecular x-axis. In Fig. 2(f), 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 shows a complex oscillatory behaviour, which is due to the different time scale associated with the dynamics along this axis. At t = T a large orientation is reached 〈cos
θZx〉 shows a complex oscillatory behaviour, which is due to the different time scale associated with the dynamics along this axis. At t = T a large orientation is reached 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 ≈ 0.83. The driving field is presented in Fig. 2(h), E(t) rapidly oscillates for t ≲ 0.5 ns, which contrasts with the slow oscillations of field optimizing 〈cos
θZx〉 ≈ 0.83. The driving field is presented in Fig. 2(h), E(t) rapidly oscillates for t ≲ 0.5 ns, which contrasts with the slow oscillations of field optimizing 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 in Fig. 2(d). This behaviour agrees with the rapid rotational dynamics of the MFF x-axis indicated above, and 〈cos
θZz〉 in Fig. 2(d). This behaviour agrees with the rapid rotational dynamics of the MFF x-axis indicated above, and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 follows the field oscillations in Fig. 2(f). The Fourier Transform of 〈cos
θZx〉 follows the field oscillations in Fig. 2(f). The Fourier Transform of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 shows three main frequencies, namely, 6.45 GHz, 18.47 GHz and 30.40 GHz, associated with the transitions 0000 ↔ 1100, 1100 ↔ 2200 and 2200 ↔ 3300, respectively. Now, the orientation of the dipole moment along the LFF Z-axis 〈cos
θZx〉 shows three main frequencies, namely, 6.45 GHz, 18.47 GHz and 30.40 GHz, associated with the transitions 0000 ↔ 1100, 1100 ↔ 2200 and 2200 ↔ 3300, respectively. Now, the orientation of the dipole moment along the LFF Z-axis 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉, see Fig. 2(g) follows a similar behaviour to 〈cos
θZμ〉, see Fig. 2(g) follows a similar behaviour to 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉, and a significant value is reached at t = T with 〈cos
θZx〉, and a significant value is reached at t = T with 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉 = 0.76.
θZμ〉 = 0.76.
In contrast, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 is incapable of adjusting to the rapidly changing driving field as observed in Fig. 2(e). Indeed, the control field in Fig. 2(h) imprints short transfers of momentum at each cycle, similar to the impulsive alignment described for short laser pulses.1 As a consequence, the amplitude of 〈cos
θZz〉 is incapable of adjusting to the rapidly changing driving field as observed in Fig. 2(e). Indeed, the control field in Fig. 2(h) imprints short transfers of momentum at each cycle, similar to the impulsive alignment described for short laser pulses.1 As a consequence, the amplitude of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 cannot be efficiently reduced at the final time in general. To bypass this effect, the algorithm fine tunes all the relative quantum phases within the wavepacket, seeking for reducing the orientation of the z-axis, i.e., approaching it to zero, at the final time t = T. However, if the pulse duration is short compared to the time characteristic of the z-axis dynamics, the oscillation may not vanish. This is the case in Fig. 2(e), where the orientation of the molecular z-axis is not negligible, i.e., 〈cos
θZz〉 cannot be efficiently reduced at the final time in general. To bypass this effect, the algorithm fine tunes all the relative quantum phases within the wavepacket, seeking for reducing the orientation of the z-axis, i.e., approaching it to zero, at the final time t = T. However, if the pulse duration is short compared to the time characteristic of the z-axis dynamics, the oscillation may not vanish. This is the case in Fig. 2(e), where the orientation of the molecular z-axis is not negligible, i.e., 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 ≈ 0.16, at t = T, which is due to the short FWHM, τ = 1 ns, of the driving field.
θZz〉 ≈ 0.16, at t = T, which is due to the short FWHM, τ = 1 ns, of the driving field.
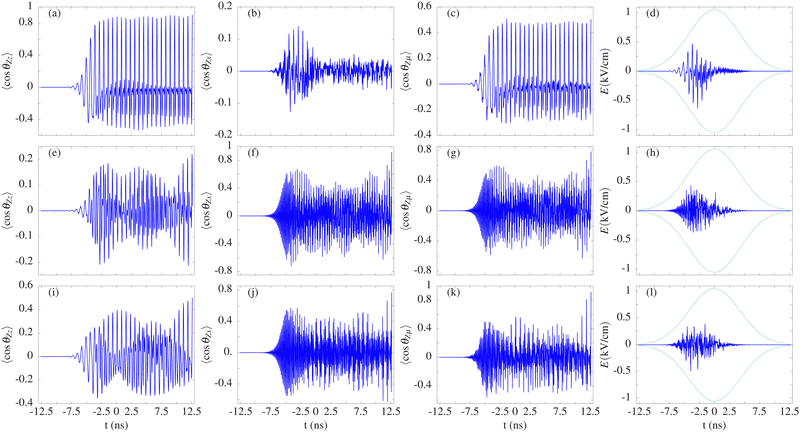
We now consider an optimizing field with τ = 5 ns FWHM and explore the results of the QOC algorithm applied to the three possible orientation axes. Compared to the 1 ns pulse in Fig. 2(a), 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 exhibits faster oscillations with large amplitude, which increase up to the maximal value 〈cos
θZz〉 exhibits faster oscillations with large amplitude, which increase up to the maximal value 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 = 0.9 at t = T. The optimized electric field, see Fig. 4(a), also possesses rapid oscillations mainly for t ≲ 0 ns when the rotational wavepacket is created. In particular, for t ≲ −3.5 ns, 〈cos
θZz〉 = 0.9 at t = T. The optimized electric field, see Fig. 4(a), also possesses rapid oscillations mainly for t ≲ 0 ns when the rotational wavepacket is created. In particular, for t ≲ −3.5 ns, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 follows this driving field. The spectral analysis given by the Fourier Transform of the field in Fig. 3 presents clearly defined and well separated peaks. This larger FWHM allows the population of highly excited rotational states associated with the additional frequency 6.76 GHz of the 4040 ↔ 5050 transition. Panels (b) and (c) of Fig. 4 present the orientation of the MFF x axis and
θZz〉 follows this driving field. The spectral analysis given by the Fourier Transform of the field in Fig. 3 presents clearly defined and well separated peaks. This larger FWHM allows the population of highly excited rotational states associated with the additional frequency 6.76 GHz of the 4040 ↔ 5050 transition. Panels (b) and (c) of Fig. 4 present the orientation of the MFF x axis and ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) along the LFF Z-axis. As in the previous case, the behaviour of 〈cos
along the LFF Z-axis. As in the previous case, the behaviour of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉 resembles 〈cos
θZμ〉 resembles 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉, but reaching smaller final value with 〈cos
θZz〉, but reaching smaller final value with 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉 = 0.502 at t = T. In contrast, 〈cos
θZμ〉 = 0.502 at t = T. In contrast, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 shows rapid oscillations of small amplitude for t > 0 ns, and at t = T 〈cos
θZx〉 shows rapid oscillations of small amplitude for t > 0 ns, and at t = T 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 = 0.015.
θZx〉 = 0.015.
The results obtained when 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 is optimized are shown in Fig. 4(e)–(h). The driving field in Fig. 4(h), presents a more complex structure with faster and narrower oscillations compared to the previous field in Fig. 4(d). The number of rotational states contributing to the field-dressed dynamics is enhanced, as it is manifested in the irregular oscillations of 〈cos
θZx〉 is optimized are shown in Fig. 4(e)–(h). The driving field in Fig. 4(h), presents a more complex structure with faster and narrower oscillations compared to the previous field in Fig. 4(d). The number of rotational states contributing to the field-dressed dynamics is enhanced, as it is manifested in the irregular oscillations of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉, 〈cos
θZz〉, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 and 〈cos
θZx〉 and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉 in Fig. 4(e), (f) and (g), respectively. During the time evolution, 〈cos
θZμ〉 in Fig. 4(e), (f) and (g), respectively. During the time evolution, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 shows moderate values, but the field is adjusted to reduce it at t = T attaining 〈cos
θZz〉 shows moderate values, but the field is adjusted to reduce it at t = T attaining 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 ≈ 0.019. In contrast, the orientation of the MFF x-axis is significantly enhanced to 〈cos
θZz〉 ≈ 0.019. In contrast, the orientation of the MFF x-axis is significantly enhanced to 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 ≈ 0.92 at t = T, and 〈cos
θZx〉 ≈ 0.92 at t = T, and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉 presents a similar behaviour.
θZμ〉 presents a similar behaviour.
For completeness, we present the optimization of the orientation of the dipole-moment axis in Fig. 4(i)–(l). In this case, the quantum interference is constructive for 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 and 〈cos
θZx〉 and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉, having both a local maximum at t = T 〈cos
θZz〉, having both a local maximum at t = T 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 ≈ 0.50 and 〈cos
θZz〉 ≈ 0.50 and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 ≈ 0.77, whereas 〈cos
θZx〉 ≈ 0.77, whereas 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉 ≈ 0.92. This illustrates that the orientation of the permanent dipole moment is largely dominated by its x component. The spectral analysis of E(t) shows that the transitions collected in Table 1 are relevant for the QOC, i.e., these rotational states build up the control dynamics and maximal orientation of
θZμ〉 ≈ 0.92. This illustrates that the orientation of the permanent dipole moment is largely dominated by its x component. The spectral analysis of E(t) shows that the transitions collected in Table 1 are relevant for the QOC, i.e., these rotational states build up the control dynamics and maximal orientation of ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) .
.
3.2 Quantum optimal control for varying the penalty factor α
In this section, we investigate the QOC orientation for different values of α, i.e., the maximum allowed strength of the control field, which is represented by the factor μ/α. For τ = 1 and 5 ns, we present in Fig. 5 the final optimized orientation as a function of the penalty factor α. Our analysis reveals that for a given α and τ, optimizing 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 results in a larger orientation compared to 〈cos
θZx〉 results in a larger orientation compared to 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉. This finding supports the idea that QOC is more effective when the natural timescale of the degree of freedom being optimized is smaller than the field duration, as discussed in Section 3.1. Moreover, for a given α, the larger the FWHM the better the optimized orientation is, for both 〈cos
θZz〉. This finding supports the idea that QOC is more effective when the natural timescale of the degree of freedom being optimized is smaller than the field duration, as discussed in Section 3.1. Moreover, for a given α, the larger the FWHM the better the optimized orientation is, for both 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 and 〈cos
θZx〉 and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉.
θZz〉.
Our analysis also reveals that, for the values of α considered, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 decreases as a function of α, meaning that stronger fields result in larger optimized orientations. Note that for both FWHMs, 〈cos
θZx〉 decreases as a function of α, meaning that stronger fields result in larger optimized orientations. Note that for both FWHMs, 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 is very similar for α = 105 and 106, i.e., the orientation saturates beyond certain intensities of the driving field. Since the orientation is not increasing, the functional
θZx〉 is very similar for α = 105 and 106, i.e., the orientation saturates beyond certain intensities of the driving field. Since the orientation is not increasing, the functional  is maximized by minimizing the fluence of the field, involved in the penalty functional,
is maximized by minimizing the fluence of the field, involved in the penalty functional,  . This saturation of 〈cos
. This saturation of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 with α can be explained in terms of the brute force orientation occurring at these strong fields, combined with the larger frequencies along the MFF x-axis facilitating that the molecule follows the driving field. Furthermore, for α = 105, that is, the stronger field case, the population transfer may not be understood in terms of one-photon transition, but as a strong field process.
θZx〉 with α can be explained in terms of the brute force orientation occurring at these strong fields, combined with the larger frequencies along the MFF x-axis facilitating that the molecule follows the driving field. Furthermore, for α = 105, that is, the stronger field case, the population transfer may not be understood in terms of one-photon transition, but as a strong field process.
In contrast, the orientation of the MFF z-axis decreases as α decreases, i.e., as the maximal field strength increases. This is due to the strong dependence of the controllability of the orientation of this axis on the process for the suppression of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 imposed by the QOC equations. Note that the faster dynamics of the x axis and the larger component of
θZx〉 imposed by the QOC equations. Note that the faster dynamics of the x axis and the larger component of ![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) along x also play an important role against reducing 〈cos
along x also play an important role against reducing 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉. Thus, achieving this suppression requires finely tuned quantum phases among the rotational states, as small changes can result in different outcomes. Besides, the QOC algorithm aims to maximize
θZx〉. Thus, achieving this suppression requires finely tuned quantum phases among the rotational states, as small changes can result in different outcomes. Besides, the QOC algorithm aims to maximize  as discussed in Section 2.2. However, due to the limited control of
as discussed in Section 2.2. However, due to the limited control of  a better approach to the stationary point is reached for smaller
a better approach to the stationary point is reached for smaller 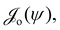 and larger
and larger 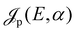 .
.
Finally, we perform a spectral analysis of the optimization along the x, z, and μ axes for the impact parameter α = 105 and 107 and τ = 5 ns. The Fourier transforms of the QOC fields are shown in Fig. 6, together with the frequencies of the main transitions between field-free rotational states, which are also collected in Table 1. In the weak field regime, α = 107, shown in Fig. 6(a), we observe well-defined isolated frequencies for all the optimized orientation observables. The frequencies of E(t) obtained from the optimization of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 and 〈cos
θZz〉 and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 are different due to the different selection rules ΔK = 0 and ΔK = ±1 imposed by the operators μz and μx, respectively. For the initial state 0000, the relevant transitions for the optimization of the z-axis orientation are 0000 ↔ 1010, 1010 ↔ 2020, and 2020 ↔ 3030, which are characterized by frequencies of 1.35, 2.71, and 4.06 GHz, respectively. However, the optimization of 〈cos
θZx〉 are different due to the different selection rules ΔK = 0 and ΔK = ±1 imposed by the operators μz and μx, respectively. For the initial state 0000, the relevant transitions for the optimization of the z-axis orientation are 0000 ↔ 1010, 1010 ↔ 2020, and 2020 ↔ 3030, which are characterized by frequencies of 1.35, 2.71, and 4.06 GHz, respectively. However, the optimization of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 is dominated by the frequencies mixing K, specifically 0000 ↔ 1100 (6.53 GHz), 1100 ↔ 2020 (2.47 GHz), 2020 ↔ 3120 (9.05 GHz). The relatively low value of 〈cos
θZx〉 is dominated by the frequencies mixing K, specifically 0000 ↔ 1100 (6.53 GHz), 1100 ↔ 2020 (2.47 GHz), 2020 ↔ 3120 (9.05 GHz). The relatively low value of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 at t = T, see Fig. 5, can be explained in terms of the relevant frequencies in E(t) for the orientation of 〈cos
θZx〉 at t = T, see Fig. 5, can be explained in terms of the relevant frequencies in E(t) for the orientation of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 being below the frequency required to transfer the population from 0000 to 1100, which is the first excited state coupled by μx. In contrast, the transition frequencies of 0000 ↔ 1100 and 2020 ↔ 3120 are above the main transitions. This results in the impulsive orientation of the molecular Z-axis as discussed in Section 3.1. Additional frequencies are observed in Fig. 6(a) when the orientation of the permanent dipole moment is optimized, with two new peaks at 2.63 and 7.81 GHz due to 1100 ↔ 2110 and 1010 ↔ 2110, respectively.
θZz〉 being below the frequency required to transfer the population from 0000 to 1100, which is the first excited state coupled by μx. In contrast, the transition frequencies of 0000 ↔ 1100 and 2020 ↔ 3120 are above the main transitions. This results in the impulsive orientation of the molecular Z-axis as discussed in Section 3.1. Additional frequencies are observed in Fig. 6(a) when the orientation of the permanent dipole moment is optimized, with two new peaks at 2.63 and 7.81 GHz due to 1100 ↔ 2110 and 1010 ↔ 2110, respectively.
 | ||
Fig. 6 For a pulse duration of τ = 5 ns, the absolute squared Fourier transform,  of the optimized electric field is shown for (a) α = 107 and (b)–(d) α = 105. The Fourier transform plotted corresponds to optimization of 〈cos of the optimized electric field is shown for (a) α = 107 and (b)–(d) α = 105. The Fourier transform plotted corresponds to optimization of 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZz〉 (solid black), 〈cos θZz〉 (solid black), 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZx〉 (blue dashed), and 〈cos θZx〉 (blue dashed), and 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θZμ〉 (red dot-dashed) and taking as initial state 0000. The vertical lines correspond to the transition frequencies shown in Table 1. Note that θZμ〉 (red dot-dashed) and taking as initial state 0000. The vertical lines correspond to the transition frequencies shown in Table 1. Note that  is normalized so that the absolute maximum equals 1. is normalized so that the absolute maximum equals 1. | ||
For a strong control field with α = 105, the spectrum becomes more complex due to two main reasons. Firstly, the contribution of more excited rotational states, such as the peak at 15.84 GHz corresponding to the transition 8080 ↔ 9180, which appears for the orientation of the MFF x-axis along the LFF Z-axis. Secondly, the brute force orientation mediated by the large amplitude of the field, as reported in previous studies.22,27 Therefore, the driving field cannot be simply described as the contribution of several frequencies, i.e., as population transfer mediated by absorption of several photons, due to the high intensity of the driving field, as we discussed in Section 3.2.
4 Conclusions and outlook
In this work, we have demonstrated the feasibility of fully controlling the orientation of non-symmetric planar molecules along several axes, i.e., the principal axes of inertia x and z and![[small mu, Greek, vector]](https://www.rsc.org/images/entities/i_char_e0e9.gif) , by means of quantum optimal control. The driving field is composed of just a few frequencies corresponding to transitions among several field-free states, and its temporal profile and strength can be reached experimentally. For a mask function with FWHM and weak strength, our findings show limited control due to the small population transfer stimulated by the interaction with the field. In contrast, the electric field cannot be described by isolated components for strengths above 1 kV cm−1, since the number of transitions among the involved states increases and they overlap due to their spectral width. This effect is further enhanced for short pulses. This work shows the efficiency, flexibility and potential of QOC for the rotational dynamics control of non-symmetric molecules and provides valuable physical insights into the conditions required for it. In addition, we have checked that the orientation may be maximize along any direction in the molecular plane.
, by means of quantum optimal control. The driving field is composed of just a few frequencies corresponding to transitions among several field-free states, and its temporal profile and strength can be reached experimentally. For a mask function with FWHM and weak strength, our findings show limited control due to the small population transfer stimulated by the interaction with the field. In contrast, the electric field cannot be described by isolated components for strengths above 1 kV cm−1, since the number of transitions among the involved states increases and they overlap due to their spectral width. This effect is further enhanced for short pulses. This work shows the efficiency, flexibility and potential of QOC for the rotational dynamics control of non-symmetric molecules and provides valuable physical insights into the conditions required for it. In addition, we have checked that the orientation may be maximize along any direction in the molecular plane.
Here, we focus on the stereodynamics of the ground state of CPC, and without loss of generality, the results could be extended to excited states. To tackle more realistic experimental conditions, and to face the difficulties of creating samples of ground-state molecules, we aim to generalize our study to thermal ensembles by means of the Von Neumann formalism. In this work, the QOC methodology has been applied to a near prolate molecule, but the main findings also hold for oblate molecules or any asymmetric top. Consequently, the frequencies of the driving field will vary according to the field-free spectrum of the considered molecular system. Furthermore, the rotational dynamics has been controlled by means of the orientation of a certain molecular axis, and analogous procedure might be followed if such control is exerted in terms of the alignment.
Hence, this technique provides an alternative strategy to the mixed-field orientation method, which, in the case of CPC, was shown to attain full control of only one molecular axis.51,53 Experimentally, it is still challenging to produce and control complex electric fields in the order of GHz. However, we have shown that only a limited number of frequencies are involved in the case of weak electric fields, simplifying the design and creation of these control fields, as it is the case of three-wave mixing experiments.13 Indeed, for driving fields involving less frequencies, the control process is more robust. In addition, the optimal orientation is sensitive to the control field parameters, which might be subject to experimental errors. We have checked that small perturbations of the control field diminish this optimal orientation, but are still high, i.e., reaching orientation values above 0.75.
Summing up, we have demonstrated that QOC is a powerful technique to control the orientation of any planar molecule without rotational symmetry, with a dipole moment not parallel to any molecular axis. We expect that our methodology is also efficient for the general molecular species, and it would be subject to further investigation. This class of molecules includes the enantiomers, whose manipulation, control and selection of chiral molecules14,17,54,55 could have an enormous impact, for instance, on the pharmaceutical industry, where the spatial arrangement of the atoms in one enantiomer may determine the biological activity of a drug, as the remarkable case of thalidomide.56 Moreover, creating optimally designed chiral electric fields could be used to efficiently create oriented superrotor states.12
Author contributions
J. J. O. proposed the research idea and formulated the theoretical framework. J. J. O. also developed the computational code for solving the Schrödinger equation and the Krotov algorithm and analyzed the results. R. G. F. and J. J. O. contributed equally to write the manuscript and to interpret the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. J. O. acknowledges the funding by the Madrid Government (Comunidad de Madrid Spain) under the Multiannual Agreement with Universidad Complutense de Madrid in the line Research Incentive for Young PhDs, in the context of the V PRICIT (Regional Programme of Research and Technological Innovation) (Grant: PR27/21-010), Projects PID2019-105458RB-I00 and PID2021-122839NB-I00 (MICIN). R. G. F. gratefully acknowledges financial support by the Spanish projects PID2020-113390GB-I00 (MICIN), PY20-00082 (Junta de Andalucía), and A-FQM-52-UGR20 (ERDF-University of Granada) and the Andalusian research group FQM-207. We would also like to thank Ignacio Solá and Fernando Troyano for fruitful discussions.Notes and references
- H. Stapelfeldt and T. Seideman, Rev. Mod. Phys., 2003, 75, 543–557 CrossRef CAS.
- C. P. Koch, M. Lemeshko and D. Sugny, Rev. Mod. Phys., 2019, 91, 035005 CrossRef CAS.
- D. R. Herschbach, Eur. Phys. J. D, 2006, 38, 3–13 CrossRef CAS.
- V. Aquilanti, M. Bartolomei, F. Pirani, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2005, 7, 291–300 RSC.
- D. Yang, D. Xie and H. Guo, J. Phys. Chem. Lett., 2022, 2022, 1777–1784 CrossRef PubMed.
- I. Kozyryev and N. R. Hutzler, Phys. Rev. Lett., 2017, 119, 133002 CrossRef PubMed.
- D. DeMille, Phys. Rev. Lett., 2002, 88, 067901 CrossRef CAS PubMed.
- V. V. Albert, J. P. Covey and J. Preskill, Phys. Rev. X, 2020, 10, 031050 CAS.
- A. Korobenko, A. A. Milner and V. Milner, Phys. Rev. Lett., 2014, 112, 113004 CrossRef PubMed.
- A. Korobenko and V. Milner, Phys. Rev. Lett., 2016, 116, 183001 CrossRef CAS PubMed.
- A. A. Milner, A. Korobenko and V. Milner, Phys. Rev. A, 2016, 93, 053408 CrossRef.
- I. Tutunnikov, L. Xu, R. W. Field, K. A. Nelson, Y. Prior and I. S. Averbukh, Phys. Rev. Res., 2021, 3, 013249 CrossRef CAS.
- D. Patterson and J. M. Doyle, Phys. Rev. Lett., 2013, 111, 023008 CrossRef PubMed.
- M. Leibscher, E. Pozzoli, C. Pérez, M. Schnell, M. Sigalotti, U. Boscain and C. P. Koch, Commun. Phys., 2022, 5, 110 CrossRef CAS.
- W. Sun, D. S. Tikhonov, H. Singh, A. L. Steber, C. Pérez and M. Schnell, Nat. Commun., 2023, 14, 934 CrossRef CAS PubMed.
- K. Banerjee-Ghosh, O. B. Dor, F. Tassinari, E. Capua, S. Yochelis, A. Capua, S. H. Yang, S. S. Parkin, S. Sarkar, L. Kronik, L. T. Baczewski, R. Naaman and Y. Paltiel, Science, 2018, 360, 1331–1334 CrossRef CAS PubMed.
- A. Yachmenev, J. Onvlee, E. Zak, A. Owens and J. Küpper, Phys. Rev. Lett., 2019, 123, 243202 CrossRef CAS PubMed.
- E. G. Marklund, T. Ekeberg, M. Moog, J. L. P. Benesch and C. Carleman, J. Phys. Chem. Lett., 2017, 8, 4540–4544 CrossRef CAS PubMed.
- A. Sinelnikova, T. Mandl, H. Agelii, O. Grånäs, E. G. Marklund, C. Caleman and E. De Santis, Biophys. J., 2021, 120, 3709–3717 CrossRef CAS PubMed.
- Y. Kurosaki, K. Yokoyama and Y. Ohtsuki, AIP Conf. Proc., 2022, 2611, 20010 CrossRef CAS.
- C. Saribal, A. Owens, A. Yachmenev and J. Küpper, J. Chem. Phys., 2021, 154, 71101 CrossRef CAS PubMed.
- H. J. Loesch and A. Remscheid, J. Chem. Phys., 1990, 93, 4779 CrossRef CAS.
- J. M. Rost, J. C. Griffin, B. Friedrich and D. R. Herschbach, Phys. Rev. Lett., 1990, 68, 1299–1302 CrossRef PubMed.
- B. Friedrich and D. R. Herschbach, J. Chem. Phys., 1999, 111, 6157 CrossRef CAS.
- I. Nevo, L. Holmegaard, J. H. Nielsen, J. L. Hansen, H. Stapelfeldt, F. Filsinger, G. Meijer and J. Küpper, Phys. Chem. Chem. Phys., 2009, 11, 9912 RSC.
- J. S. Kienitz, K. Długołecki, S. Trippel and J. Küpper, J. Chem. Phys., 2017, 147, 024304 CrossRef PubMed.
- J. Bulthuis, J. Miller and H. J. Loesch, J. Phys. Chem. A, 1997, 101, 7684–7690 CrossRef CAS.
- D. J. Tannor, R. Kosloff and S. A. Rice, J. Chem. Phys., 1986, 85, 5805–5820 CrossRef CAS.
- C. Brif, R. Chakrabarti and H. Rabitz, New J. Phys., 2010, 12, 075008 CrossRef.
- C. P. Koch, U. Boscain, T. Calarco, G. Dirr, S. Filipp, S. J. Glaser, R. Kosloff, S. Montangero, T. Schulte-Herbrüggen, D. Sugny and F. K. Wilhelm, EPJ Quantum Technol., 2022, 9, 19 CrossRef.
- J. Werschnik and E. K. U. Gross, J. Phys. B: At., Mol. Opt. Phys., 2007, 40, R175–R211 CrossRef CAS.
- C. P. Koch, J. Phys.: Condens. Matter, 2016, 28, 213001 CrossRef PubMed.
- R. Kosloff, S. A. Rice, P. Gaspard, S. Tersigni and D. J. Tannor, Chem. Phys., 1989, 139, 201–220 CrossRef CAS.
- Q. Ansel, J. Fischer, D. Sugny and B. Bellomo, Phys. Rev. A, 2022, 106, 043702 CrossRef CAS.
- L. H. Delgado-Granados, C. A. Arango and J. G. López, Phys. Chem. Chem. Phys., 2022, 24, 21250–21260 RSC.
- N. Khaneja, T. Reiss, C. Kehlet, T. Schulte-Herbrüggen and S. J. Glaser, J. Magn. Reson., 2005, 172, 296–305 CrossRef CAS PubMed.
- V. F. Krotov and I. N. Feldmann, Eng. Cybern., 1983, 21, 123–130 Search PubMed.
- D. J. Tannor, V. Kazakov and V. Orlov, in Time-Dependent Quantum Molecular Dynamics, ed. J. Broeckhove and L. Lathouwers, Springer US, Boston, MA, 1992, pp. 347–360 Search PubMed.
- E. Dmitriev and N. Bukharskii, Photonics, 2023, 10, 803 CrossRef.
- L. H. Coudert, J. Chem. Phys., 2017, 146, 024303 CrossRef CAS PubMed.
- A. Beer, R. Damari, Y. Chen and S. Fleischer, J. Phys. Chem. A, 2022, 126, 3732–3738 CrossRef CAS PubMed.
- R. Damari, A. Beer, D. Rosenberg and S. Fleischer, Opt. Express, 2022, 30, 44464–44471 CrossRef CAS PubMed.
- L. H. Coudert, J. Chem. Phys., 2018, 148, 094306 CrossRef.
- A. Pelzer, S. Ramakrishna and T. Seideman, J. Chem. Phys., 2008, 129, 134301 CrossRef PubMed.
- J. Salomon, C. M. Dion and G. Turinici, J. Chem. Phys., 2005, 123, 144310 CrossRef PubMed.
- J. J. Omiste, M. Gärttner, P. Schmelcher, R. González-Férez, L. Holmegaard, J. H. Nielsen, H. Stapelfeldt and J. Küpper, Phys. Chem. Chem. Phys., 2011, 13, 18815–18824 RSC.
- W. Kong and J. Bulthuis, J. Phys. Chem. A, 2000, 104, 1055–1063 CrossRef CAS.
- R. N. Zare, Angular Momentum: Understanding Spatial Aspects in Chemistry and Physics, John Wiley and Sons, New York, 1988 Search PubMed.
- Y. Ohtsuki, G. Turinici and H. Rabitz, J. Chem. Phys., 2004, 120, 5509–5517 CrossRef CAS PubMed.
- T. J. Park and J. C. Light, J. Chem. Phys., 1986, 85, 5870–5876 CrossRef CAS.
- J. L. Hansen, J. J. Omiste, J. H. Nielsen, D. Pentlehner, J. Küpper, R. González-Férez and H. Stapelfeldt, J. Chem. Phys., 2013, 139, 234313 CrossRef PubMed.
- J. J. Omiste, R. González-Férez and P. Schmelcher, J. Chem. Phys., 2011, 135, 064310 CrossRef CAS PubMed.
- L. V. Thesing, J. Küpper and R. González-Férez, J. Chem. Phys., 2017, 146, 244304 CrossRef PubMed.
- M. H. Goerz, D. Basilewitsch, F. Gago-Encinas, M. G. Krauss, K. P. Horn, D. M. Reich and C. P. Koch, SciPost Phys., 2019, 7, 80 CrossRef.
- M. Leibscher, E. Pozzoli, A. Blech, M. Sigalotti, U. Boscain and C. P. Koch, arXiv, preprint, 2023, arXiv:2310.11570 DOI:10.48550/arXiv.2310.11570.
- T. Eriksson, S. Bjöurkman, B. Roth, Å. Fyge and P. Höuglund, Chirality, 1995, 7, 44–52 CrossRef CAS PubMed.
Footnote |
| † Note that we omit any spatial dependency in the functions for the sake of clarity. |
| This journal is © the Owner Societies 2024 |