Transition mechanism of the coverage-dependent polymorphism of self-assembled melamine nanostructures on Au(111)

Abstract

Molecular self-assembled films have recently attracted increasing attention within the field of nanotechnology as they offer a route to obtain new materials. However, careful selection of the molecular precursors and substrates, as well as exhaustive control of the system evolution is required to obtain the best possible outcome. The three-fold rotational symmetry of melamine molecules and their capability to form hydrogen bonds make them suitable candidates to synthesize this type of self-assembled network. In this work, we have studied the polymorphism of melamine nanostructures on Au(111) at room temperature. We find two coverage-dependent phases: a honeycomb structure (α-phase) for submonolayer coverage and a close-packed structure (β-phase) for full monolayer coverage. A combined scanning tunnel microscopy and density functional theory based-calculations study of the transition regime where both phases coexist allows describing the mechanism underlying this coverage driven phase transition in terms of the changes in the molecular lateral tension.

---

1. Introduction

The physico-chemical and biological properties of organic materials are highly influenced by their molecular arrangement, which can effectively lead to the fruitful and conceptual design and development of a wide range of applications in multidisciplinary fields such as (opto)electronics, photonics, catalysis or biomedicine, among others.^1–5 However, the possibility of establishing a reliable correlation between the molecular structure and long-range organization turns into a considerable challenge. This difficulty arises from the fact that the structure of molecular solids is usually driven by intermolecular weak non-covalent interactions that have to compete with molecule–substrate interactions.^6–8

To gain a deeper understanding of the delicate energy balance that governs a specific molecular organization, extensive efforts have been recently devoted towards the optimal design of molecules that serve as models for the study in the field of crystal engineering.^9,10 Whilst this topic has been extensively explored in three-dimensional (3D) structures, it has also garnered significant attention in the realm of two-dimensional (2D) molecular organization on surfaces.^11–13 In this context, the molecule–substrate interactions assume great relevance due to the confinement of molecules within a 2D molecular environment. These interactions dictate the chemical nature of the molecule–substrate anchoring (usually physisorption) of organic materials, and must be considered in the structural characterization.¹⁴ Hence, in order to predict, design and control these non-covalent structures, an adequate and careful choice of the molecule and the substrate is particularly important for future applications.

Supramolecular 2D self-assembly is an excellent strategy used in a wide range of applications for the synthesis of novel functional materials, and has emerged as a powerful tool to acquire better control over molecular organization. On this basis, hydrogen bonding has proven to be a valuable protocol due to its higher energy and directionality compared to other non-covalent interactions.¹⁵ Consequently, the strategic placement of hydrogen bonding sites within a molecule can be leveraged to regulate the thermodynamics of intermolecular interactions, exerting partial influence over the growth of molecular nanostructures through a bottom-up approach.^16–18

Melamine, a non-chiral molecule with a triazine structure and three terminal amino groups, is an excellent precursor for carbon nitride networks and other related carbon nitride nanostructures that are photocatalysts in the visible range.^19–22 A large variety of melamine structures have already been studied in past works.^23–34 In ultra-high vacuum environments, melamine has been evaporated on highly reactive surfaces like Pd(111),²³ Ni(111)²⁴ or Cu(111),^25–27 showing an upright adsorption geometry and a partial dehydrogenation of the amino groups laying close to the substrate. Contrary, on weakly reactive surfaces such as Ag(111), melamine remains flat and parallel to the substrate forming different hydrogen-bonded self-assembled structures.²⁸ A similar behaviour has been found on Au(111) substrates,^29,30 where two main coverage-dependent polymorphs are present. A hexagonal ordered structure for low coverage and a closed-packed structure for high coverage. Although there is an agreement regarding the structure of the polymorphs, the theoretical modelling and orientation of the melamine molecules with respect to the substrate is still controversial.^29,33,34 In addition, the transition mechanism between the two self-assembled phases has not been established yet.

In this work, we present a combined study of Scanning Tunneling Microscopy (STM) together with Density Functional Theory (DFT) based-simulations to elucidate the phase transition mechanism from the low coverage (α-phase) to the high coverage (β-phase) of melamine molecules on a Au(111) substrate at room temperature. We propose a coverage-driven mechanism produced by the increment in the molecular lateral tension that forces a re-arrangement of the molecules from a honeycomb structure (in the submonolayer range) with a hexagonal unit cell, to a closed-packed structure with a rectangular unit cell, where the molecules are no longer flat but slightly tilted.

2. Experimental methods

2.1. Experimental details

All experiments have been carried out in an ultra-high vacuum (UHV) chamber with a base pressure of 1.0 × 10⁻¹⁰ mbar, equipped with a flow-cryostat STREAM STM (Scienta Omicron GmbH) operated at 7 K and a LEED optic (Scienta Omicron GmbH). The Au(111) single crystal (Mateck) has been cleaned with several cycles of argon ion sputtering and annealing at 763 K. Melamine molecules (Sigma-Aldrich, 99% purity) were sublimated from a quartz crucible installed in a 6-fold organic evaporator (Mantis GmbH) at 440 K and deposited on the Au(111) substrate kept at room temperature (RT). STM images were processed and analysed with WSxM.³⁵ We define the monolayer (ML) as a single layer of melamine molecules arranged in an ordered structure fully covering the surface of the Au(111) substrate. The coverage has been calibrated with the STM images.

2.2. Computational details

All ab-initio calculations were carried out by using DFT as implemented within the plane-wave CASTEP³⁶ and the local-orbital FIREBALL³⁷ atomistic simulation packages. In the CASTEP code, one electron wave-functions were expanded by plane-waves with a kinetic energy cut-off of 500 eV. Electronic exchange and correlation (XC) effects were considered by means the GGA-PBE functional.³⁸ The modelling of the ion-electron interaction within the H, C, N and Au atoms have been carried out by adopting ultrasoft pseudopotentials.³⁹ In order to add dispersive energies and forces to conventional DFT functionals, which are of particular relevance in the present case, Tkatchenko-Scheffler semi-empirical dispersion correction scheme⁴⁰ has been used to account for van der Waals (vdW) interactions in all the interfacial systems. All the calculations have been performed within a spin-polarized model, with no structural and energy differences w.r.t. the unpolarized calculations. Brillouin zones have been sampled by optimal [4 × 4 × 1] and [2 × 4 × 1] Monkhorst–Pack (MP) grids⁴¹ for the α- and β-phases, and the α/β mix phase, respectively, and atomic positions have been optimized until the maximum net force acting on each atom was <0.02 eV Å⁻¹, and the self-consistent electron density converged up to a precision in the total energy <10⁻⁷ eV.

2.3. Transition state search

Minimum reaction paths and energy barriers have been computed by performing an LST/Optimization calculation followed by a QST maximization.⁴² Subsequently, conjugate gradient minimization is performed, and the procedure is repeated until a stationary point is located.^43,44 The convergence threshold for the norm of the force orthogonal to the reaction path has been set at 0.05 eV Å⁻¹.

2.4. Structural modelling of the systems

The Au(111) surface was modelled in a repeated slab geometry: (i) a slab of four physical in-plane-periodic metal layers (sufficient to obtain perfectly converged results) with a minimum distance ∼20 Å of vacuum between neighbouring cells along the axis perpendicular to the surface; as well as (ii) full periodic boundary conditions representing an infinite Au(111) substrate. The two topmost metal layers were free to relax along all the geometrical optimization processes, whilst the atomic positions of the two bottommost ones were frozen. The resulting sizes of the different unit cells used in calculations, with perfect commensuration between the molecular adlayers and the metal substrate, are 0.95, 0.86 and 1.76 nm² for the α-, β- and mixed α/β-phases, respectively, yielding on-surface molecular densities of 2.11, 2.34 and 2.27 molecules nm⁻². In a first step, pristine gas-phase melamine molecule was pre-optimized to get a suitable geometrical starting-point before forming the large battery of different interfacial systems computationally tested, which were constructed on the basis of the experimental evidence to closely mimic adlayer lattice parameters and angles.

2.5. Theoretical STM-imaging

The efficient local-orbital code FIREBALL³⁷ has been used to simulate the theoretical STM images on the basis of the established interfacial geometries for the different phases. FIREBALL package takes advantage of a local-orbital formulation, in such a way that electronic self-consistency is implemented on the orbital occupation numbers, which were calculated using the orthonormal Löwdin orbitals.⁴⁵ To boost the convergence with no accuracy sacrifice, in these calculations we used a basis set of optimized single and double numerical atomic orbitals (NAOs): sp³d⁵ for C, N and Au, and ss* for H. This local-orbital formulation has been adopted for the STM-imaging simulations, where tunnelling currents for the STM images have been computed within the Keldysh-Green function formalism, together with the first-principles tight-binding Hamiltonian obtained from the FIREBALL code, as explained in full detail elsewhere.^37,46 The major strength of our STM theoretical simulation framework is based in the inclusion of a detailed description of the electronic properties of both the W-tip and the sample simultaneously. All computed theoretical STM images have been obtained at constant-current scanning conditions, where the W-tip moves perpendicularly to the sample in each STM scanning-step to search a pre-selected fixed value of the tunnel current, in order to mimic the experimental procedure.

3. Results and discussion

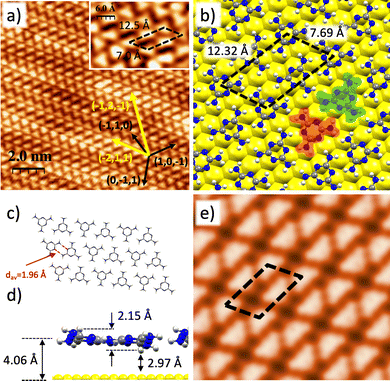
Fig. 1a shows an STM image of a submonolayer coverage (0.4 ML) of melamine molecules on a Au(111) substrate. For this coverage, melamine molecules form islands on the Au(111) surface and within the islands they arranged in a self-assembled honeycomb structure, hereafter called α-phase. The unit cell, marked as a black dashed rhomboid on the inset of Fig. 1a, contains two melamine molecules with lattice parameter of d_exp = (10.1 ± 0.7) Å and an angle α = 59° ± 1°, in excellent agreement with previous studies.²⁹ It can be observed that the herringbone reconstruction of Au(111) is preserved, which indicates a weak molecule–substrate interaction. In this chiral structure, each hexagon is formed by six melamine molecules that are not perfectly aligned along the high symmetry directions of the Au(111) single crystal (marked with black arrows in Fig. 1a) but rotated by approximately 19° w.r.t (1,0,−1). Actually, this alignment differs from others found in literature,²⁹ confirming the weak molecule–substrate interaction.

Fig. 1 (a) STM image (V = 1.0 V, I = 0.05 nA) of the α-phase of melamine molecules on Au(111) for a submonolayer coverage. Black arrows point to the main high symmetry directions of Au(111). Inset: Zoom of the STM image in panel a showing the honeycomb structure of the α-phase and its unit cell represented as a black dashed rhomboid. (b) Top view, (c) chemical sketch, where the average N⋯NH₂ bond-length, d_av, is indicated, and (d) side view of the DFT optimized model of the melamine on Au(111). Red and green highlighted melamine molecules in panel b correspond to “on-top” and “on-hollow” on-surface adsorption sites, respectively. (e) Simulated STM image of the α-phase of the melamine on Au(111) (V = 1.0 V, I = 0.1 nA). In all panels, unit cells are represented as black dashed rhomboids.

To gain more insight about the α-phase of the melamine/Au(111), we have performed a set of DFT-based calculations. Previous studies have incorporated theoretical calculations of the self-assembled nanoarchitecture;^29,33 nonetheless, a careful investigation about the on-surface positioning of the molecular adlayer or its interaction with the Au(111) substrate is still deeply unexplored. Fig. 1b shows the optimized DFT-computed model of the configuration as extracted from STM results in Fig. 1a. In this model, yielding a three-folded molecular coordination, there exist 6 stabilizing N⋯NH₂ bonds per molecule, where one of the H atoms in each of the three amino groups interacts with one of the pyridinic N atoms of the triazine core of the neighbouring molecules; being the average of the N⋯NH₂ bond-length 1.86 Å. These bonds are the main responsible for the adlayer stabilization (see below), with a minor contribution from a number of intermolecular H⋯H bonds with bond-lengths ranging between 2.5 and 3.5 Å. Besides, the almost perfect planarity of the molecules forming this phase, together with the high symmetry of the molecular adlayer, yields a null intermolecular dipole moment. Furthermore, each molecule is alternatively twisted 180° with respect to its closest neighbour, and the centres of adjacent molecules alternate “on-top” (shadowed in red) and “on-hollow” (shadowed in green) on-surface adsorption sites of the Au(111) substrate. It should be noticed that the geometrical position of the molecules with respect to the surface will have an important role in the rationalization of the phase transition. The lattice parameter and angle (d_theory = 10.49 Å, α = 60°) of the unit cell of the α-phase (black dashed rhomboid in Fig. 1b) are in good concordance with the experimental evidence. Fig. 1c depicts a chemical sketch of the molecular adlayer without the substrate for a better visualization, while Fig. 1d shows a side view of the model, where melamine molecules lie flat and parallel to the Au(111) surface, yielding an adsorption distance of 3.61 Å, revealing a clear physisorption ruled by a weak molecule–substrate van der Waals interaction. Fig. 1e illustrates the computed constant-current STM image at I = 0.1 nA and V = +1 V, in excellent agreement with the experimental image.

When the coverage is increased up to the monolayer, instead of ordering into a multilayer structure, the melamine molecules rearrange in a completely different long-range structure, called β-phase, as depicted in the STM image of Fig. 2a. In contrast with the α-phase (Fig. 1a), this structure is highly packed and does not present any pores, maximizing the surface molecular density. As it can be seen in the inset of Fig. 2a, the unit cell (a_exp = (12.5 ± 0.7) Å and b_exp = (7.0 ± 0.7) Å, angle = 53° ± 7°) is aligned along the (1̄21̄) and (2̄11) directions of the single crystal. Fig. 2b shows the computed model of the β-phase structure. The unit cell dimensions (a_theory = 12.32 Å and b_theory = 7.69 Å) are in good agreement with the experimental results. As shown, adjacent inequivalent molecules still preserve the alternation of “on-top” and “on-hollow” on-surface adsorption sites, shadowed again in red and green, respectively.

Fig. 2 (a) STM image (V = −1.0 V, I = 0.05 nA) of the β-phase of melamine molecules on Au(111). Black and yellow arrows point to the main symmetry directions of Au(111) and of the β-phase adlayer, respectively. Inset: Zoom of the STM image in panel a showing the structure of the unit cell of the β-phase represented as a black dashed rhomboid. (b) Top view, (c) chemical sketch, where the average N⋯NH₂ bond-length, d_av, is indicated, and (d) side view of the DFT optimized β-phase model of the melamine on Au(111). Red and green highlighted melamine molecules in panel b correspond to “on-top” and “on-hollow” on-surface adsorption sites, respectively. (e) Simulated constant-current STM image of the β-phase of the melamine on Au(111) (V = −1.0 V, I = 0.1 nA). In all panels, unit cells are represented as black dashed rhomboids.

Fig. 2c depicts the chemical sketch of the β-phase molecular adlayer without the substrate for a better visualization. In contrast with the α-phase, here the density of molecules per unit of area has been increased and, as it is shown in Fig. 2d, they have lost the planarity to accommodate the structure, featuring this more densely packed phase and the intermolecular interaction. This effect is reflected in an increased averaged molecular adsorption distance up to 4.06 Å and an out-of-plane molecular adlayer buckling of 2.15 Å. Fig. 2e shows the theoretical STM image of the β-phase at constant current (I = 0.1 nA and V = −1 V), exhibiting a good concordance with the experimental STM image of the Fig. 2a.

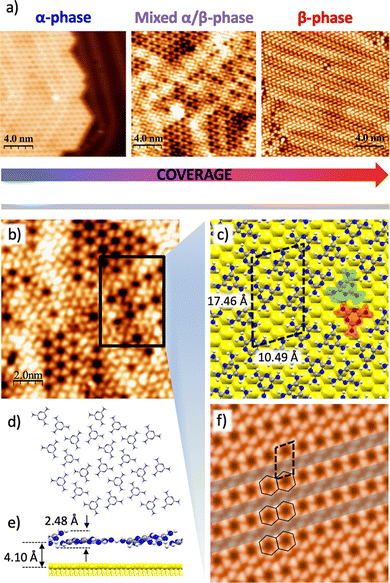
In the line of all the above mentioned, the ultimate purpose of this work consists in unveiling the transition mechanism of the coverage-dependent polymorphism of melamine self-assembled nanostructures (α-phase and β-phase) on Au(111). In order to do that, a thorough study of the transition regime where both phases coexist has been performed. Fig. 3a shows three STM images capturing the shed of this transition (middle image) from the α-phase (left image) towards the formation the β-phase (right image). Within this transient regime, the β-phase intercalates with the α-phase in consecutive arrays, suggesting that the phase-transition takes places correlatively line by line. An increase in the lateral tension of the honeycomb arrays appears as a result of the accommodation of new molecules in the same row (Fig. 3b). DFT calculations predict also this transition regime as can be seen in Fig. 3c. The dimension of the unit cell featuring this regime is a_theory = 10.49 Å and b_theory = 17.46 Å, forming an angle θ = 73.8°, in this case with four melamine molecules per unit cell. Fig. 3d depicts the chemical sketch of the molecular adlayer in this mixed phase without the substrate for a better visualization. In the side view of the model of Fig. 3e, it is possible to appreciate that some molecules are slightly tilted like in the β-phase of the Fig. 2c, meanwhile others remain almost parallel to the surface like in the α-phase of the Fig. 1c. The averaged molecular adsorption distance is, in this case, 4.10 Å and the out-of-plane molecular adlayer buckling increases up to a value of 2.48 Å. It is worth to highlight that the accommodation of the different molecules of the unit cell along the phase transition is reflected, firstly, in an almost perfect molecular planarity in the α-phase, passing through its maximum buckling value in the mixed phase, to finally reach the β-phase upon a slight molecular accommodation, result of an optimal structural and energetic balance. The computed STM image of the mixed phase is shown on Fig. 3f.

Fig. 3 (a) STM images of the transition from the α- to the β-phase of melamine on Au(111) as a function of the coverage. (I = 0.05 nA, V = 1.0 V). (b) STM image of the transition regime where both, α- and β-phases coexist (I = 0.05 nA, V = 1.0 V). (c) Top view, (d) chemical sketch and (e) side view of the DFT optimized model for the transition regime. The molecular tilt observed in the simulations produces a maximum adlayer corrugation of 2.5 Å. (f) Simulated constant-current STM image of the transition regime model (I = 0.1 nA, V = 1.0 V). The porous honeycomb structure (black hexagons) and the close-packed structure (light-grey shadowed stripes) are highlighted. In (c) and (f) the unit cell is represented by a dashed black line rhomboid.

For this β-phase, with a 6-folded molecular coordination, there also exist 6 stabilizing N⋯NH₂ bonds per molecule, like in the α-phase. Nonetheless, for this case, 4 of these 6 bonds are formed involving the two hydrogens of the same amino group in two neighbouring molecules, being the average of the N⋯NH₂ bond-length 1.96 Å. Again, these bonds are the main responsible for the adlayer stabilization; however, the denser packing of these phase, as compared with the one in the α-phase, topologically increases the number of intermolecular H⋯H bonds, with shorter bond-lengths ranging between 2.0 and 3.4 Å and yielding a higher contribution to the adlayer stabilization. The intermolecular H⋯H bonds additional contribution to the stabilization of an adlayer involving molecules on a metal connected by N⋯NH₂ bonds has been recently reported.⁴⁷ It is important to mention that the slight molecular distortion, different for each inequivalent molecule within the unit cell, originates a non-null dipole moment, which can further contribute to stabilize the molecular adlayer w.r.t. the α-phase via intercell dipolar interactions.

Interestingly, in both α- and β-phases, intermolecular stabilization of the adlayers is mainly driven by complementary donor–acceptor N⋯NH₂ hydrogen bonds between adjacent molecules with average N⋯NH₂ distances of 1.86 and 1.96 Å, respectively (see Table 1). This slight difference of around 0.1 Å between both phases arises from the co-planarity of the hydrogen bonds in the α-phase. In contrast, in the β-phase this efficient directionality does not occur due to the tilt/distortion experienced by the molecules. Nevertheless, the stabilization energy per molecule is significantly higher for the β-phase due to a higher contribution of the H⋯H bonds w.r.t. the α-phase. For the α/β mixed phase it is possible to observe N⋯NH₂ distances ranging between 1.88–1.96 Å, due to the coexistence of regions corresponding to each phase.

Table 1 Computed average N⋯NH₂ bond-length, d_N–NH2 in Å, adsorption energy per molecule, E_ads in eV, and intermolecular bond network energy per molecule, E_network in eV, for the on-surface molecular adlayer in the α-, β- and α/β mix phases

Molecular phase	d N⋯NH2 (Å)	E ads (eV per molecule)	E network (eV per molecule)
α-phase	1.86	−0.37	−0.47
β-phase	1.96	−0.30	−0.84
α/β mix phase	1.88–1.99	−0.32	−0.67

---

Energetics of the optimized α- and β-phases predicted by the DFT-based simulations shed some light into the rationalization of the experimentally observed coverage-induced α → β phase transition. In order to evaluate the adsorption strength of molecules on the metal substrate, we have computed, for each phase, the adsorption energy per molecule, E_ads(α/β-phase)/mol, defined as:

where E_tot (α/β-phase) is the total energy of the optimized interface, E_tot (molecule) and E_tot (surface) are the total energies of the gas-phase melamine molecule and the optimized metal surface, respectively, and n the number of molecules per unit cell. Computed E_ads (α/β-phase)/mol for the α- and β-phases result in −0.37 and −0.30 eV per molecule, respectively, manifesting a clear physisorption regime ruled by vdW interactions. Similarly, in order to evaluate the intermolecular strength within each molecular adlayer, we have computed the intermolecular bond network energy per molecule, E_network (α/β-phase)/mol, defined as:where E_tot (α/β-adlayer) and E_tot (molecule) are the total energies of the molecular adlayer and of each gas-phase molecule, respectively, being n the number of molecules per unit cell. Computed E_network (α/β-phase)/mol for the α- and β-phases result in −0.47 and −0.84 eV per molecule, respectively. Results of E_ads and E_network for the α- and β-phases evidence that, indeed, the intermolecular interaction and intrinsic stabilization of the molecular adlayer in β-phase increases around a 43% keeping almost unaltered the binding energy of the two phases (−0.37 and −0.30 eV, respectively). Before further analyses, energy values in Table 1 provide a valuable information by evidencing that, since adsorption energy per molecule seems to be independent of the specific phase, any morphological phase-transition should be associated to channels altering the intermolecular interaction.

Once obtained the main energy quantities describing the stability of both phases, it is interesting to mention that, as experimentally evidenced, the α → β phase transition occurs with the increasing molecular coverage but not with the increase of the temperature. Actually, above 400 K melamine molecules completely desorb and there are no structural changes observed (from α to β or any other structure). In order to evaluate the effect of the temperature in the adsorption of the molecules to form both phases we have adopted the Gibbs formalism to obtain Gibbs adsorption free energies per molecule up to 400 K by additional vibrational calculations, which permits to account for the zero-point energy and the TS term (being T the temperature and S the entropy). The result of these calculations reveals that even at 300 K the molecular adsorption is exothermic, whilst at 400 K theory predicts the adsorption switching to endothermic, which excellently agrees with the experimental evidence, where the molecules desorb at that temperature range.

It is possible to energetically compare the energetics of the β-phase with that of a hypothetical second layer formed above the α-phase. For that purpose, we have computed the optimized structure and energetics of a hypothetical second molecular layer above the α-phase in three different configurations (see Fig. 4a): (i) with each molecule of the second layer lying in the same on-surface position and orientation than those of the first layer (eclipsed configuration I/AA stacking), (ii) with each molecule of the second layer lying in the same on-surface position but azimuthally rotated by 180° w.r.t. those in the first layer (configuration II/AA stacking), and (iii) with one molecule in the unit cell of the second layer lying on the hexagonal “hollow” created by the hexagonal molecular adlayer of α-phase (staggered configuration/AB stacking). We find that configurations (i) and (ii) result non-bounded (yielding positive binding energies), mainly due to the π–π repulsion, while configuration (iii) results bounded to the bottom layer with an average intermolecular bond network energy of −0.39 eV per molecule, lower than the −0.84 eV per molecule predicted for the β-phase (see Table 1). Besides, in this new scenario with two molecular layers, the adsorption energy per molecule in the first layer reduces from −0.37 to −0.32 eV per molecule, and the adsorption energy per molecule of the second layer w.r.t. the first one is −0.07 eV per molecule. These results predict a higher stability and stronger anchoring to the surface in the β-phase over a second molecular adlayer which justifies the fact that instead of a multilayer regime the emerging of the β-phase with the increasing coverage is observed in the experiments. Kinetically, the small binding energy value per molecule obtained for the second layer translates into that the evaporated molecules laying on top the first molecular layer will easily diffuse/slide until reaching a phase boundary, finally lying on the metal surface to continue the completion of the first layer.

Fig. 4 (a) DFT optimized models for the bilayer of melamine molecules on Au(111): (i) and (ii) eclipsed AA and (iii) staggered AB interlayer stacking configurations. (b) Proposed phase-transition restructuration between the α- and β-phases of melamine molecules on Au(111) with increasing coverage. Green and red highlighted melamine molecules represent “on-hollow” and “on-top” on-surface adsorption sites respectively. The numbering of molecules in both phases permits to observe the consistency along the topological restructuration. Arrows of the middle sketch represent diffusion and rearrangement movements that molecules must undergo across the phase transition preserving the original and final geometrical molecular on-surface positions w.r.t. the surface.

Once theory predicts the preferable formation of the β-phase over the multilayer as evidenced by the experiment, we need to understand how the α → β phase transition occurs. Topologically, it is important to notice that both the α and β-phases consist in on-surface molecular arrangements with two molecules per unit cell (each of them with its centre of mass lying on a “hollow” and a “top” adsorption sites) but with significantly different surface molecular densities of 2.11 and 2.34 molecules per nm², respectively. The α → β phase transition can be seen as topologically transforming in a sequential way a 6-molecules hexagon in the α-phase into a 6-molecules rectangle in the β-phase, where the molecules maintain the local adsorption configuration (azimuth and site; see Fig. 4b).

For the α → β phase transition to occur it has to overcome different energy barriers. The first one is that related to the different adsorption energy per molecule in both phases passing from −0.37 to −0.30 eV (see Table 1) by displacement of the molecules from the α- to the β-phase, which essentially is a feasible process at RT considering that computed molecular diffusion energy barriers on the surface range from 0.1 to 0.12 eV. On the other hand, the molecules in the α-phase exhibit a completely flat disposition, whilst in the β-phase, the molecules are slightly tilted, which reduces their adsorption energy as already explained, and show a slight distortion of the ring and the –NH₂ terminal groups. The difference in energy between the perfectly flat configuration in the α-phase and the distorted one is 0.28 eV in gas-phase, with an associated breathing normal mode (phonon) of around 1000 cm⁻¹. According to the Boltzmann distribution, the time required to overcome this barrier will be around 10⁻⁷ s, a feasible process at RT but not so fast as the on-surface diffusion of the molecules to adopt the β-phase arrangement. An explanation to overcome these barriers beyond the thermal bath can be rationalized in terms of the pressure induced by extra molecules arriving to the surface particularly at the phase-boundaries, which can add an extra edging-pressure favouring the reorganization of the molecules into the β-phase. The kinetic energy of the new molecules incorporating to the adlayer boundaries with the increasing coverage push from the edges the α-adlayer favouring, together with the effect of the temperature, the reorganization into the β-phase.

An alternative model that intuitively comes to mind to rationalize the coverage-induced α → β phase-transition is that whereby the melamine molecules landing on the α-phase monolayer are able to accommodate within the hexagonal pore of this molecular adlayer. Nonetheless, this model can be easily discarded mainly due to: (i) the steric hindrance: there is no physical space in the pore to accommodate an extra molecule; besides, the possibility of the molecules incorporating within the pore inducing a lattice expansion is directly hindered since they would prefer to diffuse on the molecular adlayer instead of inducing a lattice accommodation, which would be of a much higher energetically cost, and (ii) in the case that the inclusion of the molecules within the pore were possible, the resulting adlayer configuration would not match the topology with alternating “on-hollow”/“on-top” on-surface adsorption sites of the molecules in the β-phase.

4. Conclusions

This study proposes a plausible mechanism that explains the transition between the two phases observed for melamine molecules on Au(111). We have shown by STM and DFT that, for submonolayer coverages, melamine molecules arrange in a honeycomb structure (α-phase), exhibiting a flat disposition with a surface molecular density of 2.11 molecules per nm². When the coverage reaches the monolayer, melamine molecules re-arrange into a close-packed structure, the β-phase, instead of undergoing into a multilayer regime. Unlike the α-phase, the density of molecules per unit of area increases (2.34 molecules per nm²) and the molecules are not fully flat or parallel to the gold substrate, but slightly twisted. Nonetheless, in both phases the alternation between hollow and top position of the molecules w.r.t the Au(111) is preserved. The intermediate regime sheds light into this transition mechanism. The increment of the coverage on the surface produces an increase of the intermolecular lateral tension forcing to the rearrangement of the melamine molecules from an hexagonal unit cell into a rectangular one, as DFT-based simulations rationalize. This transition mechanism is purely coverage-dependent and no other sources of energy (such as temperature) or time are needed for it to occur.

Author contributions

J. M. Z.-S.: experiments, analysis of the data and writing. J. M. G.-F.: experiments. C. S.-S: discussion. M. F. L: discussion. J. I. M: performed the DFT calculations, discussion and writing. J. A. M.-G.: conceptualization, analysis and discussion. I. P.: conceptualization, design of the experiments, discussion, analysis and writing.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors acknowledge financial support from projects PID2020-113142RB-C21, PID2021-12509OA-I00, TED2021-129999B-C31 and TED2021-129416A-I00 funded by MCIN/AEI/10.13039/501100011033 and EUR2021-122006. Spanish MICIN PLEC2021-007906 (Sol-future) and CAM Y2020/NMT-6469 (Fotosurf). JMZS acknowledges grant PRE2018-086165 funded by the Spanish Science and Innovation Ministry MCIN/AEI/10.13039/501100011033 and by “ESF Investing in your future”.

References

1. A. Jain and S. J. George, New Directions in Supramolecular Electronics, Mater. Today, 2015, 18(4), 206–214.
2. J. D. Tovar, Supramolecular Construction of Optoelectronic Biomaterials, Acc. Chem. Res., 2013, 46(7), 1527–1537.
3. M. Raynal, P. Ballester, A. Vidal-Ferran and P. W. N. M. Van Leeuwen, Supramolecular Catalysis. Part 1: Non-Covalent Interactions as a Tool for Building and Modifying Homogeneous Catalysts, Chem. Soc. Rev., 2014, 43(5), 1660–1733.
4. L. Wang, P.-P. Yang, X.-X. Zhao and H. Wang, Self-Assembled Nanomaterials for Photoacoustic Imaging, Nanoscale, 2016, 8(5), 2488–2509.
5. N. Kwon, H. Kim, X. Li and J. Yoon, Supramolecular Agents for Combination of Photodynamic Therapy and Other Treatments, Chem. Sci., 2021, 12(21), 7248–7268.
6. S. L. Price and J. G. Brandenburg, in Molecular Crystal Structure Prediction, Non-Covalent Interactions in Quantum Chemistry and Physics, Elsevier, 2017, ch. 11, pp. 333–363.
7. K. Takahashi and L. Takahashi, Creating Machine Learning-Driven Material Recipes Based on Crystal Structure, J. Phys. Chem. Lett., 2019, 10(2), 283–288.
8. Modern Methods of Crystal Structure Prediction, ed. Oganov, A. R., Wiley, 1st edn, 2010.
9. C. B. Aakeröy, N. R. Champness and C. Janiak, Recent Advances in Crystal Engineering, CrystEngComm, 2010, 12(1), 22–43.
10. L. Sun, Y. Wang, F. Yang, X. Zhang and W. Hu, Cocrystal Engineering: A Collaborative Strategy toward Functional Materials, Adv. Mater., 2019, 31(39), 1902328.
11. K. S. Mali, N. Pearce, S. De Feyter and N. R. Champness, Frontiers of Supramolecular Chemistry at Solid Surfaces, Chem. Soc. Rev., 2017, 46(9), 2520–2542.
12. L. Sosa-Vargas, E. Kim and A.-J. Attias, Beyond “Decorative” 2D Supramolecular Self-Assembly: Strategies towards Functional Surfaces for Nanotechnology, Mater. Horiz., 2017, 4(4), 570–583.
13. S. K. Park, J. H. Kim and S. Y. Park, Organic 2D Optoelectronic Crystals: Charge Transport, Emerging Functions, and Their Design Perspective, Adv. Mater., 2018, 30(42), 1704759.
14. T. Tian and C.-J. Shih, Molecular Epitaxy on Two-Dimensional Materials: The Interplay between Interactions, Ind. Eng. Chem. Res., 2017, 56(38), 10552–10581.
15. J. W. Steed and J. L. Atwood, Supramolecular Chemistry, John Wiley & Sons, Ltd, Chichester, UK, 2009.
16. M. J. Mayoral, N. Bilbao and D. González-Rodríguez, Hydrogen-Bonded Macrocyclic Supramolecular Systems in Solution and on Surfaces, ChemistryOpen, 2016, 5(1), 10–32.
17. A. G. Slater, L. M. A. Perdigão, P. H. Beton and N. R. Champness, Surface-Based Supramolecular Chemistry Using Hydrogen Bonds, Acc. Chem. Res., 2014, 47(12), 3417–3427.
18. E. D. Głowacki, M. Irimia-Vladu, S. Bauer and N. S. Sariciftci, Hydrogen-Bonds in Molecular Solids – from Biological Systems to Organic Electronics, J. Mater. Chem. B, 2013, 1(31), 3742.
19. A. Akhundi, A. Badiei, G. M. Ziarani, A. Habibi-Yangjeh, M. J. Muñoz-Batista and R. Luque, Graphitic Carbon Nitride-Based Photocatalysts: Toward Efficient Organic Transformation for Value-Added Chemicals Production, Mol. Catal., 2020, 488, 110902.
20. T. S. Miller, A. B. Jorge, T. M. Suter, A. Sella, F. Corà and P. F. McMillan, Carbon Nitrides: Synthesis and Characterization of a New Class of Functional Materials, Phys. Chem. Chem. Phys., 2017, 19(24), 15613–15638.
21. M. Majdoub, Z. Anfar and A. Amedlous, Emerging Chemical Functionalization of G-C ₃ N ₄: Covalent/Noncovalent Modifications and Applications, ACS Nano, 2020, 14(10), 12390–12469.
22. P. Ren, T. Zhang, N. Jain, H. Y. V. Ching, A. Jaworski, G. Barcaro, S. Monti, J. Silvestre-Albero, V. Celorrio, L. Chouhan, A. Rokicińska, E. Debroye, P. Kuśtrowski, S. Van Doorslaer, S. Van Aert, S. Bals and S. Das, An Atomically Dispersed Mn-Photocatalyst for Generating Hydrogen Peroxide from Seawater via the Water Oxidation Reaction (WOR), J. Am. Chem. Soc., 2023, 145(30), 16584–16596.
23. J. Greenwood, H. A. Früchtl and C. J. Baddeley, Self-Assembly of Upright, Partially Dehydrogenated Melamine on Pd(111), J. Phys. Chem. C, 2013, 117(44), 22874–22879.
24. J. Greenwood, H. A. Früchtl and C. J. Baddeley, Ordered Growth of Upright Melamine Species on Ni{111}: A Study with Scanning Tunnelling Microscopy and Reflection Absorption Infrared Spectroscopy, J. Phys. Chem. C, 2012, 116(11), 6685–6690.
25. Y.-P. Lin, O. Ourdjini, L. Giovanelli, S. Clair, T. Faury, Y. Ksari, J.-M. Themlin, L. Porte and M. Abel, Self-Assembled Melamine Monolayer on Cu(111), J. Phys. Chem. C, 2013, 117(19), 9895–9902.
26. B. Schulze Lammers, N. López-Salas, J. Stein Siena, H. Mirhosseini, D. Yesilpinar, J. Heske, T. D. Kühne, H. Fuchs, M. Antonietti and H. Mönig, Real-Space Identification of Non-Noble Single Atomic Catalytic Sites within Metal-Coordinated Supramolecular Networks, ACS Nano, 2022, 16(9), 14284–14296.
27. V. Lanzilotto, C. Grazioli, M. Stredansky, T. Zhang, L. Schio, A. Goldoni, L. Floreano, A. Motta, A. Cossaro and C. Puglia, Tailoring Surface-Supported Water–Melamine Complexes by Cooperative H-Bonding Interactions, Nanoscale Adv., 2021, 3(8), 2359–2365.
28. C. H. Schmitz, J. Ikonomov and M. Sokolowski, Two Commensurate Hydrogen-Bonded Monolayer Structures of Melamine on Ag(111), Surf. Sci., 2011, 605(1–2), 1–6.
29. F. Silly, A. Q. Shaw, M. R. Castell, G. A. D. Briggs, M. Mura, N. Martsinovich and L. Kantorovich, Melamine Structures on the Au(111) Surface, J. Phys. Chem. C, 2008, 112(30), 11476–11480.
30. L. Wang, H.-X. Shi, W.-Y. Wang, H. Shi and X. Shao, Identifying the Hydrogen Bonding Patterns of Melamine and Melem Self-Assemblies on Au(111) Surface, Acta Phys. Chim. Sin., 2017, 33(2), 393–398.
31. S. Uemura, M. Aono, T. Komatsu and M. Kunitake, Two-Dimensional Self-Assembled Structures of Melamine and Melem at the Aqueous Solution−Au(111) Interface, Langmuir, 2011, 27(4), 1336–1340.
32. H.-M. Zhang, Z.-X. Xie, L.-S. Long, H.-P. Zhong, W. Zhao, B.-W. Mao, X. Xu and L.-S. Zheng, One-Step Preparation of Large-Scale Self-Assembled Monolayers of Cyanuric Acid and Melamine Supramolecular Species on Au(111) Surfaces, J. Phys. Chem. C, 2008, 112(11), 4209–4218.
33. M. Mura, N. Martsinovich and L. Kantorovich, Theoretical Study of Melamine Superstructures and Their Interaction with the Au(111) Surface, Nanotechnology, 2008, 19(46), 465704.
34. M. Šimėnas and E. E. Tornau, A Model of Melamine Molecules Ordering on Metal Surfaces, J. Chem. Phys., 2014, 141(5), 054701.
35. I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, WSXM: A Software for Scanning Probe Microscopy and a Tool for Nanotechnology, Rev. Sci. Instrum., 2007, 78(1), 013705.
36. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, First Principles Methods Using CASTEP, Z. Kristallogr. - Cryst. Mater., 2005, 220(5–6), 567–570.
37. J. P. Lewis, P. Jelínek, J. Ortega, A. A. Demkov, D. G. Trabada, B. Haycock, G. Adams, J. K. Tomfohr, E. Abad, H. Wang and D. A. Drabold, Advances and Applications in the FIREBALL Ab Initio Tight-Binding Molecular-Dynamics Formalism, Phys. Status Solidi B, 2011, 248(9), 1989–2007.
38. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
39. D. Vanderbilt, Soft Self-Consistent Pseudopotentials in a Generalized Eigenvalue Formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892–7895.
40. A. Tkatchenko and M. Scheffler, Accurate Molecular van der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data, Phys. Rev. Lett., 2009, 102(7), 073005.
41. J. D. Pack and H. J. Monkhorst, “Special Points for Brillouin-Zone Integrations”—a Reply, Phys. Rev. B: Solid State, 1977, 16(4), 1748–1749.
42. N. Govind, M. Petersen, G. Fitzgerald, D. King-Smith and J. Andzelm, A Generalized Synchronous Transit Method for Transition State Location, Comput. Mater. Sci., 2003, 28(2), 250–258.
43. G. Henkelman, B. P. Uberuaga and H. Jónsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. The, J. Chem. Phys., 2000, 113(22), 9901–9904.
44. G. Henkelman and H. Jónsson, Improved Tangent Estimate in the Nudged Elastic Band Method for Finding Minimum Energy Paths and Saddle Points. The, J. Chem. Phys., 2000, 113(22), 9978–9985.
45. A. A. Demkov, J. Ortega, O. F. Sankey and M. P. Grumbach, Electronic Structure Approach for Complex Silicas, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52(3), 1618–1630.
46. J. M. Blanco, C. González, P. Jelínek, J. Ortega, F. Flores and R. Pérez, First-Principles Simulations of STM Images: From Tunneling to the Contact Regime, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70(8), 085405.
47. L. M. Rodríguez, P. Gómez, M. Más-Montoya, J. Abad, A. Tárraga, J. I. Cerdá, J. Méndez and D. Curiel, Synthesis and Two-Dimensional Chiral Surface Self-Assembly of a Π-Conjugated System with Three-Fold Symmetry: Benzotri(7-Azaindole), Angew. Chem., Int. Ed., 2021, 60(4), 1782–1788.

---