Azido-mediated intermolecular interactions of transition metal complexes

Abstract

The coordinated azido ligand has a variety of ways to establish intermolecular contacts whose nature is computationally analysed in this work on dimers of the [N₃–Hg(CF₃)] complex with different interactions involving only N⋯N contacts, or with an additional Hg⋯N contact. The applied tools include the molecular electrostatic map of the monomer, an energy decomposition analysis (EDA), a topological AIM analysis of the electron density and the study of NCI (non-covalent interactions) isosurfaces. The interactions between two azido ligands are found to be weakly stabilizing (by 0.2 to 2.7 kcal mol⁻¹), topology-dependent and require dispersion forces to complement orbital and electrostatic stabilization. Those interactions are supplemented by the formation of simultaneous Hg⋯N secondary interactions by about −1 kcal mol⁻¹, and by the ability of the monomer to simultaneously interact with several neighbours in the crystal structure.

---

Introduction

Azides are a versatile class of chemical compounds containing the N₃⁻ anion or the –N₃ functional group attached to an element or radical through one of the terminal nitrogen atoms. Most inorganic^1–4 and organic^5,6 azido compounds are highly explosive and toxic and thus must be handled with extreme caution. Despite the hazards associated with their use (or perhaps even because of them), these molecules have many applications in the fields of synthetic chemistry, biology, and biomedicine. For instance, the ionic sodium azide (NaN₃) is used as a propellant in airbags⁷ and as a precursor to other inorganic⁸ and organic⁹ azide compounds. Heavy metal azides, such as Pb(N₃)₂, are used as shock-sensitive detonators.¹⁰ Organic azides are essential components in azide–alkyne “click” reactions^11–13 and bioorthogonal chemistry.^14,15 They are also important precursors to amine¹⁶ and nitrene¹⁷ compounds. Furthermore, several azide-containing drugs have an important pharmaceutical application as enzyme inhibitors.¹⁸

Transition metal azido complexes are relatively stable compounds containing one or more coordinated azido ligands.¹ They are of increasing importance for their use in catalysis,^1,19–24 luminescence,^25,26 magnetism,^1,27–29 inorganic “click” reactions,^30–32 bioorthogonal chemistry,³³ and pharmaceuticals.^34,35 Although the azide anion is often found as a bridging ligand in polynuclear complexes, in this work we are concerned only with complexes in which it is coordinated in a terminal mode to only one metal atom. Compared to the linear anionic azides (N₃⁻),³⁶ all covalent azides of both main group and transition metals display a slightly bent configuration with a N_α–N_β–N_γ bond angle of approximately 172 ± 3° and two different N–N bond lengths,^1–3 where N_α refers to the coordinated nitrogen atom. 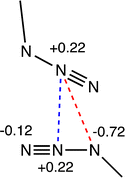One of these bonds (N_α–N_β, 1.18(2) Å from 2742 structural data in the Cambridge Structural Database (CSD) with no disorder and R ≤ 5%) is shorter than a typical N–N single bond (1.44 Å) while the other (N_β–N_γ, 1.16(3) Å) is slightly longer than a N≡N triple bond in the N₂ molecule (1.10 Å).³⁷ The observed values are in agreement with the resonance Lewis structures a and b shown in Scheme 1, with a higher weight of structure a bearing two N=N double bonds and some contribution of structure b, which accounts for the small differences between the two N–N bond lengths. Resonance form c is expected to have a small weight because the negative charge at N_γ is not stabilized via coordination to the metal atom, as is the case for a and b. This expectation is confirmed by the analysis of the CSD structural data, since the M–N–N bond angle distribution is centred at around 125°, and only a few examples are found with angles close to 180° that would be consistent with Lewis structure c (Fig. S1, ESI†). Formal charges indicate the presence of an electron-poor atom (N_β) as well as two electron-rich atoms (N_α and N_γ).

Scheme 1 Lewis resonance structures for the azide anion coordinated to a transition metal.

For the subsequent discussion, it is useful to correlate the charge distribution and the N–N bond orders with a simple MO scheme of the π system of the azide anion (Fig. 1). The occupation of the bonding and antibonding MOs (π and π*) is consistent with the formal bond order of the two N–N bonds in Lewis structure a. On the other hand, the charge distribution of this resonance form correlates with the topology of the π MOs, with a higher electron density concentration at the N_α and N_γ atoms, and an electron density depletion at the central N_β atom. The resonance form b requires mixing of the n_π and π* orbitals of the azide, made possible by the lowering of symmetry induced by coordination to the metal atom. Moreover, both the N_α and N_γ atoms bear a σ-type lone pair that can also participate in donor–acceptor interactions, notably as a 1,1- or 1,3-bridging ligand in many di- and polynuclear complexes, but conceivably also in noncovalent interactions when it is acting as a terminal ligand.

Fig. 1 Schematic depiction of the π molecular orbitals of an independent N₃⁻ anion. The three analogous perpendicular orbitals are not shown for simplicity.

Recent studies have evaluated the ability of azide compounds, specifically of its central nitrogen atom (N_β), to act as electron density acceptors in pnictogen bonds. Regarding organic azides (N₃-R), Bursch and co-workers³⁷ have studied 44 intermolecular model systems containing an azide moiety in close contact with pnictogen, chalcogen, and halogen atoms, respectively. The nature of such interaction was attributed to dispersion forces, with an important electrostatic contribution. However, the same authors found NBO evidence for the interaction of the O-lone pair of carbonyl groups in several compounds with the π* orbital of an azide.³⁸ O⋯N_β interactions are strong enough to dictate the conformation of molecules in the solid-state, which may be used to freeze the otherwise free-rotating azide group in a conformation suitable for its reaction with an alkyne via topochemical cycloaddition.³⁹ Scheiner has investigated, among others, the bonding between a Lewis base and two covalent azides, N₃–F and N₃–CN. The molecular electrostatic potentials (MEPs) of the N₃–X molecules show a π-hole equatorial belt enveloping the N_β atom which can electrostatically interact with the lone pairs of an incoming nucleophile.⁴⁰ The azido unit can also act as an electron density donor via the lone pair of the N_γ atom with an H–N moiety to form an intermolecular hydrogen bond.⁴¹

In this work, we aim at studying the intermolecular interactions that terminal azido complexes can establish with each other in their crystalline phases. In the light of the charge distribution of azido ligands, one can envision a rich supramolecular chemistry with different types of interactions. By means of a comprehensive structural and computational analysis we will try to discern the nature and strength of azido⋯azido interactions associated with several interaction topologies. We believe that understanding and manipulating these interactions is essential for tailoring the properties of azido-containing transition metal complexes for various potential applications in catalysis and inorganic chemistry.

Results and discussion

Structural study

A search in the Cambridge Structural Database (CSD)⁴² for experimental structures containing azides coordinated to transition metals has identified several intermolecular contacts between the azido moieties with N⋯N distances shorter than twice the nitrogen van der Waals radius (3.32 Å).⁴³Scheme 2 represents schematically the different azido⋯azido (dashed lines) interaction topologies found, their abundance (pie charts) and the fraction of supported (red) and unsupported (green) contacts, respectively. The prefix “c-” (cyclo-) indicates that two N⋯N contacts form pseudocycles. Note that c-N_α⋯N_γ also exhibits a N_β⋯N_β interaction.

Scheme 2 Interaction topologies (1–9) for azido⋯azido short contacts (dashed lines) in transition metal azido complexes. For the pie charts, the size of the circle is adjusted to the number of contacts found for each topology, whereas the red and green areas represent supported and unsupported contacts, respectively. The empty circles represent N atoms. The subscripts (α, β, and γ) indicate the position of each N relative to the metal. The prefix “c-” (cyclo-) indicates that a pseudocycle is formed via two or three N⋯N contacts.

For the N_γ⋯N_α and N_γ⋯N_β contacts, the distribution of the relative positions of the two interacting azides, calibrated by the torsion angle τ (inset in Fig. 2), presents a higher probability at τ ≈ 90 and 180°. For torsion angles of 90° or smaller, the N_γ atom gets close to Hg, allowing for a secondary bonding interaction and for that reason we will report in what follows calculations with different interaction topologies (Scheme 2) and the two most representative values of τ, 90 and 180°.

Fig. 2 Distribution of the dihedral angle τ (as defined in the structures) for contacts with (a) N_γ⋯N_α and (b) N_γ⋯N_β interaction topologies. The empty circles represent N atoms, and the dashed lines the azido⋯azido contacts.

According to the above discussion on the Lewis structures (Scheme 1) and a simplified MO diagram (Fig. 1) of the π system of the azide anion, and assuming that the MEP (Molecular Electrostatic Potential) maps of N₃–M are similar to those found for NNN-F and NNN-CN⁴⁰ (see also Fig. 3 below), it is expected that N_α⋯N_β, N_γ⋯N_β, c-N_α⋯N_β, and c-N_β⋯N_γ contacts (i.e., topologies 2, 5, 7 and 9) might be attractive, since regions of electrostatic potential of opposite sign would be close to each other. The electrophilic region surrounding the central N_β atom would act as a binding site for the lone pairs of the incoming nucleophiles (N_α or N_γ), thus forming a π-hole interaction. Indeed, for all interaction topologies, except for c-N_α⋯N_γ, one can find examples of compounds with only intermolecular azido⋯azido contacts, and no additional supporting secondary interaction. Some interaction topologies (1, 3, 4, 6 and 8) seem disfavoured from a Coulombic point of view, according to the Lewis structures, yet they appear in our structural database search, and a more detailed analysis of those interactions is needed. For that reason, we undertook a combined structural and computational analysis of azido⋯azido short contacts with all the interaction topologies found for these short contacts.

Fig. 3 MEP maps for [N₃–Hg(CF₃)],⁴⁴ calculated at M06-2X/def2-TZVP level and plotted in two different orientations on the van der Waals electron density isosurface (s = 0.001 Å). Energies are given in kcal mol⁻¹. Dark red and blue colours indicate the most negative and most positive MEP values, respectively.

Making use of a simple transition metal azido complex, namely trifluoromethyl-azido-mercury(II) (FMHGAZ),⁴⁴ we have designed two sets of models of its dimer with the different interaction topologies shown in Scheme 3. We selected a dicoordinated linear complex in order to focus in azido-involving contacts while minimizing all other metal–ligand and ligand–ligand interactions. This complex was fully optimized before building up the dimers. In both N_α⋯N_β systems (2a and 2b) the N_β⋯N_α–N_β bond angle was arbitrarily fixed at 130°. Because of the free rotation of the Hg–N single bond and the fact that the V_s,max is located around the Hg atom (see Fig. 3), all dimers were partially optimized to preserve the azides in the desired conformations. In each of these calculations, only the distances of the intermolecular N⋯N contacts were optimized while the rest of the structure was frozen at the given bonding pattern. To further investigate the nature and the strength of the interaction we have performed molecular electrostatic potential (MEP), energy decomposition analyses (EDA), quantum theory of atom in molecules (QTAIM) and noncovalent interaction indices (NCI) of the selected models.

Scheme 3 Interaction topologies for the azido⋯azido short contacts (dashed lines) in the [N₃–Hg(CF₃)]₂ model dimers. For each topology, model a has a dihedral angle τ of 180°, and model b corresponds to τ = 90°.

Molecular electrostatic potential

As a first approach to the rationalisation of the azido⋯azido short contacts we can look at the MEP map of the optimized structure of the trifluoromethylazido-mercury(II) monomer (Fig. 3).

As expected, the MEP map of the monomer is similar to those reported earlier for the related molecules NNN-F and NNN-CN.⁴⁰ An electron-poor region of the azide unit is found near the central N_β atom, and its shape resembles the π-hole equatorial belt that those covalent inorganic azides exhibit. Such a feature is due to the nodal properties of the occupied n_π orbital of the azide ion (Fig. 1). This small and slightly positive electron-deficient region is surrounded by two highly electron-rich regions of the N_α and N_γ atoms. In particular, the most negative region of the isosurface is located at the terminal N_γ atom, associated to the σ lone pair, with a minimum MEP value (V_s,min) of −22 kcal mol⁻¹, but a similarly high negative potential region appears in the π region of N_α. On the other hand, the most positive region surrounds the Hg atom, with a maximum MEP value (V_s,max) of 42 kcal mol⁻¹. The MEP map also shows the existence of a σ-hole located at the extension of the Hg–C bond (Fig. 3(b)). If the electrostatic contribution is the main driving force for the interaction, only those dimers in which the electron-rich areas of one monomer are directed to the electron-poor areas of the other are expected to be stable. It is worth mentioning that, given the tendency of the negative electrostatic potential regions to interact with the most positive one, a total optimization of the dimers would favour the intermolecular N⋯Hg interaction over any of the N⋯N interactions, since V_s,max is located near the metal atom.

Interaction energies and interatomic distances

We have first optimized (see Methodology section for further details) the [N₃–Hg(CF₃)] dimers with different functionals to test the effect on the interatomic equilibrium distances and the associated interaction energies. The complete results can be found in the ESI.† Interestingly, the optimized N⋯N and N⋯Hg distances are very similar for all functionals with standard deviations between 0.03 and 0.12 Å (Tables S3 and S4, ESI†). As for the interaction energies, although all interactions are attractive, more differences are found, with standard deviations ranging from 0.22 to 0.40 kcal mol⁻¹ (with the exception of dimer 1b, for which the standard deviation was 0.60 kcal mol⁻¹). Among the six tested functionals, we selected the M06-2X because it yielded the smallest interaction energy values, probably because of the absence of an explicit dispersion correction term. In this manner, we can guarantee conservative values for the interaction strength.

The main results calculated at the M06-2X level are shown in Table 1. No local minima were found for compounds 3a, 8a and 9a. As can be inferred from Fig. 3, these dimers are probably unstable due to electrostatic repulsion since the electrostatic potential regions of the same sign in the two monomers are facing each other. MO arguments also predict strong repulsion between the occupied π orbitals of one azide and the σ lone pair of the other one in model 3a, and between the π orbitals of the two azides in 8a.

Table 1 Key geometrical parameters including distances in Å, penetrations (pen.) in % and interaction energies (kcal mol⁻¹) for all studied interaction topologies of the [N₃–Hg(CF₃)] dimers, calculated at the M06-2X/def2-TZVP level^a

Compd.	ϕ (°)	N contact	N⋯N	Pen.	N–Hg cont.	N⋯Hg^b	pen.	ΔEINT
a No local minima were found for dimers 3a, 8a and 9a. b Only Hg⋯N distances shorter than 4.5 Å.
1a	180	Nα⋯Nα	3.062	14				−1.10
2a	180	Nα⋯Nβ	2.846	25	Nγ⋯Hg	3.533	28	−2.74
4a	180	Nβ⋯Nβ	3.045	14				−0.87
5a	180	Nγ⋯Nβ	3.072	13				−0.10
6a	180	Nγ⋯Nγ	3.138	10				−0.22
7a	180	Nα⋯Nβ	3.161	8				−1.08
		Nβ⋯Nα	3.161	8
1b	90	Nα⋯Nα	3.082	12	Nβ⋯Hg	3.540	27	−2.20
2b	90	Nα⋯Nβ	2.823	26	Nγ⋯Hg	3.561	26	−3.71
3b	90	Nγ⋯Nα	3.463	−8	Nγ⋯Hg	4.019	4	−0.63
4b	90	Nβ⋯Nβ	2.936	20	Nγ⋯Hg	3.764	17	−2.52
5b	90	Nγ⋯Nβ	3.064	14	Nγ⋯Hg	4.198	−4	10.59
6b	90	Nγ⋯Nγ	3.133	10				−0.75
7b	90	Nα⋯Nβ	3.067	13	Nγ⋯Hg	3.440	32	−2.71
		Nβ⋯Nα	3.067	13
8b	90	Nα⋯Nγ	3.730	−22	Nγ⋯Hg	4.242	−6	−0.75
		Nβ⋯Nβ	3.782	−24
		Nγ⋯Nα	3.730	−22
9b	90	Nβ⋯Nγ	3.153	9	Nγ⋯Hg	4.264	−7	−0.88
		Nγ⋯Nβ	3.153	9

---

The calculated short N⋯N contacts vary from 2.823 to 3.730 Å, and the corresponding N⋯N penetration indices are positive (between 8 and 26%) except for structures 3b and 8b. Interestingly, all structures with a torsion angle τ of 90° (1b–9b) exhibit in addition short N⋯Hg contacts that cover a wide range of penetration indices, from small negative values (distances slightly longer than the VdW sum) up to positive values as high as 32%, comparable to those found for weak hydrogen bonds.⁴⁵

To analyse the calculated interaction energies, let us consider first the a-type models, for which we can in principle consider the net attraction to be due only to azide⋯azide interactions, disregarding 2a because it has indeed a short Hg⋯N contact that could be responsible for its much higher interaction energy. In all other a-type models there is an attraction that varies between −0.10 and −1.12 kcal mol⁻¹. Assuming that in 7a each of the two N_α⋯N_β interactions contributes one half of the interaction energy, a plot of the interaction energies as a function of the N⋯N penetration indices (Fig. 4) shows that the interaction energy becomes more attractive as the penetration increases, a trend that can be roughly expressed via the least-squares linear relationship, ΔE_int = 0.781 − 0.136 p_NN (r² = 0.93). Such a correlation holds for the systems in which the interactions involve π orbitals of the two azido anions, while 5a, which involves a π–n_σ interaction deviates more significantly from the linear trend.

Fig. 4 Interaction energies between two molecules of [N₃–Hg(CF₃)] in dimeric topologies with torsion angles of 180° (1a and 4a-7a, Scheme 3 and Table 1) as a function of the N⋯N penetration indices at the energy minima (filled circle for 5a, empty circles for the rest), and estimated contribution (see text) of the Hg⋯N contacts to the interaction energy in topologies with τ = 90° (1b, 2b, and 4b–7b) as a function of the Hg⋯N penetration index (triangles).

If we compare now the interaction energies of each topology with the two different torsion angles τ (i.e., Na and Nb models), we see that the attraction between the two monomers in the b model is in all cases higher than in its a partner by a factor of approximately 2 or greater. We interpret the enhanced attraction as due to the N⋯Hg contacts that appear for the smaller torsion angles of the b topologies. To have a rough idea of the contribution of those interactions, we subtract the estimated N⋯N contribution from the least-squares equation given in the previous paragraph from the calculated interaction energy in b models. The resulting Hg⋯N energetic contributions are plotted as a function of the corresponding penetration indices in Fig. 4, showing a fair linear dependence, E_int = 0.759 − 0.075 p_HgN (r² = 0.90). We must be careful, however, not to extrapolate the observed behaviour to lower and negative penetrations, since dispersion forces can predominate at such low penetrations.

Although we focus on the interactions between azido ligands in the solid state, we have further investigated the effect that the presence of a common solvent has on the strength of these interactions. Accordingly, we have reoptimized systems 1–9 in water (full results can be found in Table S3, ESI†). Two important observations can be made: (i) equilibrium interatomic distances lengthen in all cases, showing negative penetration indices for all systems except for 4a, 2b, 4b and 7b. (ii) Interaction energies weaken for all systems (except for 4a, which remains practically the same) but, remarkably, they remain attractive in all cases (ΔE_INT < 0).

Energy decomposition analysis

To investigate the physical origin of the attractive interactions, we performed an energy decomposition analysis (EDA) of the 8 dimers in which the N⋯N intermolecular contacts are shorter, and the Hg⋯N distances longer, than the corresponding VdW radii sums (including dimers with single and double N⋯N contacts). The results are summarized in Table 2.

Table 2 Energy decomposition analysis of the intermolecular interactions in [N₃–Hg(CF₃)] dimers with N⋯N as the only intermolecular contact shorter than the sum of the van der Waals radii, calculated at the M06-2X/def2-TZVP level. Energies are given in kcal mol⁻¹

Cpd.	Contact	τ (°)	ΔEPAULI	ΔEELEC	ΔEPOL	ΔECT	ΔEDISP	ΔEINT
1a	Nα⋯Nα	180	2.82	−1.41	−0.15	−0.15	−2.19	−1.10
4a	Nβ⋯Nβ	180	2.73	−0.50	−0.16	−0.09	−2.84	−0.87
5a	Nγ⋯Nβ	180	1.70	−0.14	−0.14	−0.09	−1.42	−0.10
6a	Nγ⋯Nγ	180	1.49	−0.20	−0.07	−0.07	−1.37	−0.22
7a	c-Nα⋯Nβ	180	3.42	−1.64	−0.17	−0.03	−2.65	−1.08
5b	Nγ⋯Nβ	90	1.81	−0.45	−0.20	−0.17	−1.57	−0.59
6b	Nγ⋯Nγ	90	1.64	−0.77	−0.11	−0.08	−1.43	−0.75
9b	c-Nβ⋯Nγ	90	2.56	−0.67	−0.23	−0.22	−2.33	−0.88

---

Our first observation is that the Pauli repulsion is large and only partially counterbalanced by the attractive electrostatic and orbital (charge transfer and polarization) components. In second place, there is no correlation at all between the N⋯N contact distance (or, equivalently in this case, the penetration index) and the components of the interaction energy, an unsurprising result given the very different interaction topologies considered. Nevertheless, there seems to be some relationship between the Pauli repulsion and the Coulombic attractive term (Fig. 5(a)), as noted earlier by us for other intermolecular interactions.⁴⁵ In this case, the correlation is somewhat poor because not only the interpenetration of the VdW crusts vary from one molecule to another, but there are also important topological differences in the contacts. The clearest conclusion that can be drawn from the analysis of the results of the EDA analysis of several models of azide⋯azide interactions is that its attractive nature is due to the London dispersion forces, which are quantitatively predominant, between 4 and 13-fold times stronger than the orbital term, although in the case of 5a the dispersion term is not enough by itself to counteract the Pauli repulsion, and the small electrostatic and orbital contributions (−0.14 and and −0.23 kcal mol⁻¹, respectively) become crucial to make the whole interaction attractive. Notice that, in this case, the orbital-based contribution overweighs the electrostatic component, a fact that can be qualitatively explained by (1) the small electron depletion region located at the N_β atom that is surrounded by two regions of large negative potential, and (2) the delocalization of the lone pair of the incoming nucleophile to the antibonding π* orbital also centred at the N_β atom.^39,40

Fig. 5 (a) Pauli repulsion in [N₃–Hg(CF₃)] dimers with only N⋯N contacts represented as a function of the electrostatic term, as obtained from an EDA analysis. The upper red section of the plot comprises all points for which the repulsion term predominates, and the lower green section corresponds to the cases for which the electrostatic attraction term would predominate. (b) Evolution of the interaction energy (solid line) and of the different contributions (dotted lines) with the N⋯N penetration for model dimer 4a. The vertical dashed line marks the energy minimum.

A complementary view consists in focusing on a single model and analyse the evolution of contributions to the interaction energy as the two monomers approach each other (Fig. 5(b)). We discuss here the case of the model 4a (N_β⋯N_β contact) and similar results found for 1a and 5a can be found as ESI.† Let us consider first the long distance (negative penetration) region, and then we will look at the zone near the energy minimum (p = 14%). At negative penetrations the dispersion interaction is already relevant (ca. −1.0 kcal mol⁻¹), and the only other contribution that is non negligible is the electrostatic component (0.2 kcal mol⁻¹), which is slightly repulsive, as could be expected for the interaction between the two positively charged N_β atoms. The net result is an attractive interaction dominated by the dispersion term, nearly constant for penetrations between −20 and +15%. Consistently, a dozen of crystal structures^46–54 were found with a clear 4b topology, with N_β⋯N_β penetration indices between −8 and +17%, while more negative penetrations are excluded by the limit imposed to the N_β⋯N_β distance in the structural searches. As a representative example, two neighbouring molecules in the [OMo(bipy)(N₃)₃] complex⁴⁶ are linked by two N_β⋯N_β contacts at 2.996 Å (p = 17%).

At positive penetrations of about 15% the Pauli repulsion equals the dispersion attractive term, but small orbital and electrostatic contributions join forces to make the net interaction still attractive. more so than the orbital contribution, and its value increases rapidly for higher penetrations. An issue that seems counterintuitive at first sight is the fact that the electrostatic component is attractive at those distances, given the charge distribution expected from the Lewis structures (Scheme 1) as well as from the molecular electrostatic potential of the monomer (Fig. 3). A more detailed geometrical analysis of model 4b indicates that besides the Coulombic repulsive N_β⋯N_β interaction (at 2.996 Å in the case of [OMo(bipy)(N₃)₃]), there are N_β⋯N_α, N_β⋯N_γ, N_α⋯N_β and N_β⋯N_γ contacts between atoms of opposed charge. Even if the distances are somewhat longer, ideally sqrt(d² + b²) vs. d, where d is the N_β⋯N_β intermolecular distance and b is the N_α–N_β or N_β–N_γ bond distance, simple calculations of the q_Aq_B/d_AB Coulombic terms assuming either the charge distribution pattern in Scheme 1(a), that from MEP analysis, or the one found in a natural population analysis (NPA) of 4a shown in Scheme 4, indicate that the four attractive contributions overweigh the repulsive one. Considering the NPA charge distribution, for instance, the product of α and β charges is 3 times the product of the two β charges, whereas the α–β distance is barely 1.1 times the β–β one, making the N_β⋯N_α and N_α⋯N_β contacts the dominant Coulombic interactions.

Scheme 4 NPA atomic charges in interacting system 4a.

Topology of the electron density

In this section we analyse the topology of the electron density of all dimers by means of a QTAIM study, to facilitate comparison with studies carried out by other authors in a variety of noncovalent interactions. The resulting topological properties at the bond critical point (BCP) for N⋯N contacts in the [N₃–Hg(CF₃)] dimers are collected in Table 3.

Table 3 Topological data at the N⋯N BCP for all [N₃–Hg(CF₃)] dimers, calculated at M06-2X/def2-TZVP level of theory. All topological parameters^a are given in atomic units

Cpd.	τ (°)	N⋯N (Å)	ρ BCP	∇^2ρBCP	V BCP	G BCP	H BCP	V BCP/GBCP
a ρ: electron density; ∇^2ρ: Laplacian of the electron density; V and G: local potential and kinetic electron energy, respectively; H: total local electron energy.
1a	180	3.062	0.009	0.030	−0.005	0.006	0.001	0.817
1b	90	3.082	0.009	0.031	−0.006	0.007	0.001	0.828
2a	180	2.846	0.011	0.049	−0.008	0.010	0.002	0.810
2b	90	2.823	0.012	0.051	−0.009	0.011	0.002	0.825
3b	90	3.463	0.004	0.014	−0.002	0.003	0.001	0.662
4a	180	3.045	0.006	0.033	−0.004	0.006	0.002	0.695
4b	90	2.936	0.008	0.041	−0.006	0.008	0.002	0.744
5a	180	3.072	0.006	0.030	−0.004	0.006	0.002	0.684
5b	90	3.064	0.006	0.030	−0.004	0.006	0.002	0.702
6a	180	3.138	0.006	0.025	−0.003	0.005	0.001	0.718
6b	90	3.133	0.007	0.026	−0.004	0.005	0.001	0.730
7a	180	3.161	0.006	0.026	−0.004	0.005	0.001	0.727
		3.161	0.006	0.026	−0.004	0.005	0.001	0.727
7b	90	3.067	0.007	0.031	−0.005	0.006	0.001	0.764
		3.067	0.008	0.034	−0.005	0.007	0.002	0.775
8b	90	3.730	0.002	0.008	−0.001	0.001	0.000	0.668
		3.730	0.002	0.008	−0.001	0.002	0.001	0.660
9b	90	3.153	0.006	0.027	−0.003	0.005	0.002	0.669
		3.153	0.006	0.027	−0.003	0.005	0.002	0.669

---

For all intermolecular N⋯N contacts, we observe that (1) the computed electron density at the bond critical points (ρ_BCP) is low, ranging from 0.002 to 0.012 a.u., typical of weak bonds; (2) the sign of the Laplacian of the electron density (∇²ρ_BCP) is positive, indicating an electron charge depletion in the bonding region;⁵⁵ (3) the local electron kinetic energy (G_BCP) dominates the local electron potential in absolute value (|V_BCP|), leading to an overall positive but small total energy density (H_BCP), and (4) the |V_BCP|/G_BCP ratio is lower than 1, which is characteristic of dispersion-bound systems.^56,57 These topological parameters support the classification of the azido⋯azido contacts as noncovalent “closed–shell” interactions, whose dispersion-dominated nature has been shown in the previous section. Exponential relationships are found between the intermolecular N⋯N penetration and ρ_BCP, ∇²ρ_BCP, |V_BCP| and G_BCP, respectively, which are consistent with the contact distance dependence of other weak interactions^56,58,59 (Fig. 6).

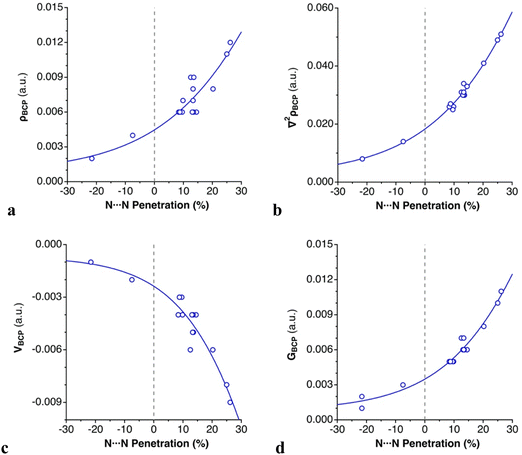Fig. 6 Dependence on the N⋯N penetration of (a) ρ_BCP, (b) ∇²ρ_BCP, (c) |V_BCP|, and (d) G_BCP in the dimers of [N₃–Hg(CF₃)] (Scheme 3 and Table 2).

All these four topological parameters increase as the distances shorten. There is a positive correlation between the ρ_BCP, |V_BCP| and G_BCP. A higher ρ_BCP is related to a higher accumulation of electrons at that point (|V_BCP|), which in turn implies higher repulsion between them (G_BCP).⁵⁶ The absence of BCPs for N⋯Hg contacts in all dimers prevents applying a similar analysis to that used for N⋯N contacts.

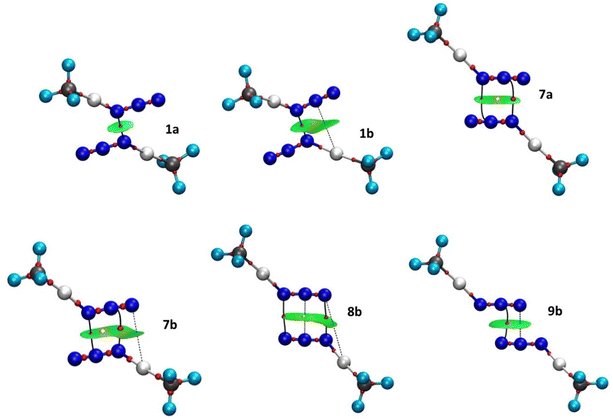
Although the existence of a bond path (BP) and a BCP between two atoms is generally associated with the presence of an attractive interaction, the opposite is not true.^60,61 For this reason, we present the molecular graph of the dimers complemented with NCI isosurfaces, to find other NCIs that remain undetected due to the stringent BCP criterion of QTAIM theory. The NCI method offers advantages in its specific focus on non-covalent interactions, providing visually intuitive representations and efficiently capturing weak forces. NCI is particularly useful for identifying weak and subtle interactions, such as dispersion forces, which may not be as effectively captured by other electron density-based methods such as QTAIM. Therefore, it provides a more nuanced understanding of the intermolecular forces at play. Six examples of molecular graphs are depicted in Fig. 7 (for the molecular graphs of all compounds see Fig. S2 in the ESI†). A total of eleven systems involve a single interaction (compounds 1a-3b and 4b–6b), and the topological analysis of their electron densities reveals a single BP and the corresponding BCP connecting the shortest N⋯N contacts. These interactions appear in the NCI plots as green pill-shaped isosurfaces (compounds 1a, 4a and 5a–6a) or as flat almond-shaped bicoloured green-yellow isosurfaces (compounds 1b, 2b, 2a and 3b). In both cases, the green portion is surrounding the BCP and is aligned with the N⋯N contacts indicating weak stabilizing interactions, as expected from the low ρ_BCP values (0.004–0.012 a.u.). In the latter group, there is a second green portion assigned to weak stabilizing interactions between the N atom of one monomer and the Hg atom of the other. No topological descriptors are found for these N⋯Hg contacts (Fig. 7(b), dashed lines) and, thus, this interaction remains undetected by the QTAIM topology. The same isosurface exhibits a yellow part, which indicates steric strain induced by the formation of the intermolecular four-membered pseudoring. No ring critical point (RCP) is associated with the destabilizing region. The QTAIM topology is also blind to this steric hindrance. Especially noteworthy is that structures 2a and 2b (see Fig. S2c and d, ESI†), which possess the shortest N⋯N distances and the highest ρ_BCP values (0.011–0.012 a.u.), show a dark-green isosurface between the azido⋯azido contacts, indicating a stronger interaction.

Fig. 7 Molecular graphs and NCI isosurfaces (s = 0.4) for several topologies of dimers of [N₃–Hg(CF₃)]. The isosurfaces are coloured according to a BRG scheme from −0.035 < sign(λ₂)ρ < 0.030 a.u. Small spheres represent BCPs (red) and RCPs (yellow). The solid lines represent the azido⋯azido BP and the dashed lines indicate the secondary N⋯Hg interaction.

Regarding compounds 7a and 7b, two BPs and two BCPs that interconnect the N_α⋯N_β and N_β⋯N_α atom pairs, respectively, were identified (Fig. 4). A ring critical point (RCP) is found at the centre of the four-membered pseudo-ring formed by the BPs. Both structures exhibit similar NCI green-yellow isosurfaces. The green areas appear around each N⋯N BCP, whereas the yellow ones are surrounding the RCPs. In compound 7b, the isosurface is extended to incorporate the N_γ⋯Hg interaction, forming a second four-membered pseudo-ring that links the two monomers. The green colour indicates VdW-type interactions (ρ_BCP = 0.006–0.008 a.u.), namely N⋯N and N⋯Hg, whereas the yellow ones indicate steric strain within the pseudo-rings.

The pseudo-cyclic structure 8b (Fig. 7) shows a BP and a BCP at each of the N_α⋯N_γ and N_γ⋯N_α contacts. In addition, an RCP is found in the middle of the N_β⋯N_β contact, at the centre of the intermolecular six-membered pseudo-ring formed by the BPs, indicating some steric repulsion within the ring. Although in the QTAIM analysis we found no critical point between the two N_β atoms, the NCI index analysis shows that all N⋯N (and N⋯Hg) contacts are of VdW type, separated by two barely discernible yellow regions. The absence of a BCP between the N_β atoms might be explained by the flatness of the electron density inside the ring (ρ_BCP = 0.001–0.002 a.u.).

In compound 9b, N_β⋯N_γ and N_γ⋯N_β contacts have the same distance. One thus expects both to show a BP and the corresponding BCP in the molecular graph. Nevertheless, only the former contact exhibits these topological descriptors. Significantly, the BCP is displaced towards the centre of the bonding region. The NCI index method indicates that both contacts are weakly attractive interactions, as expected due to the low ρ_BCP value (0.006 a.u.). There is a yellow region in the middle of the isosurface, indicating a destabilizing crowding effect within the four-member pseudoring.

Conclusions

In this work, we have investigated the intermolecular N⋯N interaction between terminal azido ligands in dimers of the [N₃–Hg(CF₃)] complex. A MEP analysis of the monomer has disclosed an electron-poor region near the central N_β atom, surrounded by two electron-rich regions near the N_α and N_γ atoms. The MEP map is consistent with the qualitative MO and valence-bond description of the azide anion and is useful for predicting the relative stability of different interaction topologies from an electrostatic point of view. No local minima were found for the coplanar (τ = 180°) systems 3a, 8a and 9a. All other dimers are found to be stable, with interaction energies ranging from −0.10 to −3.71 kcal mol⁻¹. The secondary N⋯Hg interaction in the perpendicular (τ = 90°) arrangement of the dimers plays an important role in stabilizing topologies 3b, 8b and 9b, despite the unfavourable azido⋯azido contacts that cannot stabilize the corresponding perpendicular analogues 3b, 8b and 9b. Similar N⋯Hg interactions contribute also to make dimers 1b, 2b, 2a, 4b, and 7b the most stable ones.

The subsequent EDA analysis has shed light on the physical nature of the interaction. As in other cases, the electrostatic and orbital contributions counterbalance only in part the Pauli exchange repulsion, and dispersion is the main attractive force in all cases studied here. Furthermore, the EDA analysis of dimer 4a at different intermolecular distances indicates that the electrostatic component is not dictated by the repulsion involving the two positively charged N_β atoms at a short distance, but by the N_β⋯N_α and N_α⋯N_β attractive interactions at a slightly longer distance. This case warns us of how simple electrostatic arguments based on formal charges of Lewis structures or molecular electron potential maps may in some cases be misleading.

The combined QTAIM and NCI index analyses confirm the closed–shell, dispersion-dominated nature of the azido⋯azido contacts. Almost all the N⋯N short contacts exhibit a BP and the corresponding BCP, which are associated with the existence of an attractive interaction. However, regardless of the presence or absence of BCP, a region of weak attractive interaction (property conventionally associated with the green colour) is found for both types of contacts. In addition, the yellow isosurfaces denote steric strain induced by the formation of intermolecular pseudo-rings in the azido bonding region in dimers 7–9.

Until now, only interactions between azido groups and pnictogen, chalcogen, and halogen atoms or N–H hydrogen bonds have been reported in the literature,^32,39,40,42 This work, in summary, shows that also weak azido⋯azido attractive interactions do exist, covering a range of interaction energies between −0.1 and −1.1 kcal mol⁻¹, that can be further enhanced by around 1 kcal mol⁻¹ through secondary azido⋯metal intermolecular interactions, and by establishing more than one contact per molecule. As occurs in most molecular crystals, the stability of [N₃–Hg(CF₃)] in the solid state is the result of the cooperative effect of several weak interactions. We can see in Fig. 8 that a reference molecule A establishes a type 8 azido⋯azido interaction with its neighbouring molecule B with a penetration of −15%, but also a semicoordinating Hg⋯N interaction with molecule D with a much higher penetration (52%) and two with molecule C (66%).

Fig. 8 Some of the several short contacts established by a molecule of [N₃–Hg(CF₃)] in its crystal structure. N⋯N contacts indicated by dashed lines and Hg⋯N contacts by multiband cylinders.

Methodology

Structural searches were carried out in the Cambridge Structural Database (CSD) version 5.43,⁴² November 2021 + 4 updates. Only crystal structures with three-dimensional (3D) coordinates determined, non-disordered, with no errors, not polymeric, and with R < 0.1 were allowed in searches. We used standard sets of covalent and van der Waals radii.^43,62 DFT calculations were performed using the Gaussian 16 package⁶³ with the M06-2X functional and the def2-TZVP basis set for all atoms, with the corresponding quasi-relativistic pseudopotentials for heavy atoms. Previously, benchmark calculations were carried with different functionals, namely M06-2X, ωB97xD, BP86-D3, B3LYP-D3, B2PLYP-D3 and PBE0-D3. We selected the M06-2X functional because it gave the smallest interaction energy values (see Table S2 in the ESI†) and interatomic distances in very good agreement with all other functionals (Tables S3 and S4 in the ESI†). Moreover, previous comprehensive benchmarking studies have demonstrated that M06-2X shows a good performance for the analysis of noncovalent interactions.^64,65 The structure of the trifluoromethyl-azido-mercury(II) model (FMHGAZ)⁶⁶ was fully optimized and confirmed to be minima of the potential energy surface by frequency calculations. All dimers were partially optimized, i.e., only the distances of the intermolecular N⋯N contacts were optimized while the rest of the structure was frozen to preserve the azides in a specific conformation. Interaction energies were calculated via the supermolecule approach and corrected for the BSSE using the counterpoise method.⁶⁷ Optimizations in water (ε = 78.3553) were made with the polarizable continuum model (PCM) as implemented in Gaussian16. MEP maps were built on the 0.001 Å isosurface with the GaussView 6 program⁶⁸ on the molecular geometry of the FMHGAZ monomer. EDA analyses were carried out with Q-Chem 5.3 software⁶⁹ employing the second-generation ALMO-EDA method.⁷⁰ The QTAIM and NCI Index analyses were carried out with the Multiwfn 3.7 software based on promolecular densities.⁷¹ The NCI isosurfaces were generated for s = 0.4 a.u., coloured according to a BRG scheme and visualized by the VMD 1.9.4 program.⁷² These isosurfaces have been used to identify regions of different interactions by simply examining their colours (blue, strongly attractive interaction; green, VdW interactions; yellow, weak repulsive interactions and red, strong repulsive interactions).^73,74

The penetration index for an A–B contact has been calculated from the interatomic distance d_AB, according to eqn (1), where v_A and v_B are the van der Waals radii,⁴³ and r_A and r_B are the covalent atomic radii.^62,75

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the Spanish Ministry of Economy and Competitiveness (PGC2018-093863-B-C21 and PID2019-109119GA-I00), the Spanish Structures of Excellence María de Maeztu program (grant MDM-2017-0767) and the Generalitat de Catalunya—AGAUR (grant 2017-SGR-1289). The allocation of computer time at the CSUC is also acknowledged. J. E. is grateful to the Spanish MICCIN for a Ramón y Cajal research contract (RYC-2017-22853), to Gobierno de Aragón-ESF (Research Group E07_23R) and to the HPC-Europa3 programme (INFRAIA-2016-1-730897) for funding a stay in Amsterdam.

References

1. W. P. Fehlhammer and W. Beck, Z. Anorg. Allgem. Chem., 2013, 639, 1053–1082.
2. W.-K. Seok and T. M. Klapötke, Bull. Korean Chem. Soc., 2010, 31, 781–788.
3. I. C. Tornieporth-Oetting and T. M. Klapötke, Angew. Chem., Int. Ed. Engl., 1995, 34, 411–520.
4. I. C. Tornieporth-Oetting and T. M. Klapötke, Combustion Efficiency and Air Quality, Springer, Boston, MA, 1995, pp.51–62.
5. S. Bräse, C. Gil, K. Knepper and V. Zimmermann, Angew. Chem., Int. Ed., 2005, 44, 5188–5240.
6. S. Bräse and K. Banert, Organic Azides: Syntheses and Applications, John Wiley & Sons, Nashville, TN, 2011.
7. E. A. Betterton, Crit. Rev. Environ. Sci. Technol., 2003, 33, 423–458.
8. J. Biegańska, Materials, 2021, 14, 2818–2829.
9. J.-J. Li, Synlett, 2007, 0505–0506.
10. H. Bock and R. Dammel, Angew. Chem., Int. Ed. Engl., 1987, 26, 504–526.
11. C. Wang, D. Ikhlef, S. Kahlal, J.-H. Saillard and D. Astruc, Coord. Chem. Rev., 2016, 316, 1–20.
12. M. S. Singh, S. Chowdhury and S. Koley, Tetrahedron, 2016, 72, 5257–5283.
13. H.-K. Li, J.-Z. Sun, A.-J. Qin and B. Z. Tang, Chin. J. Polym. Sci., 2012, 30, 1–15.
14. N. J. Agard, J. M. Baskin, J. A. Prescher, A. Lo and C. R. Bertozzi, ACS Chem. Biol., 2006, 1, 644–648.
15. M. Gutmann, E. Memmel, A. C. Braun, J. Seibel, L. Meinel and T. Lühmann, ChemBioChem, 2006, 17, 866–875.
16. P. T. Nyffeler, C.-H. Liang, K. M. Koeller and C.-H. Wong, J. Am. Chem. Soc., 2002, 124, 10773–10778.
17. Y.-C. Wang, X.-J. Lai, K. Huang, S. Yadav, G. Qiu, L. Zhang and H. Zhou, Org. Chem. Front., 2021, 8, 1677–1693.
18. B. M. Jönsson, K. Håkanson and A. Liljas, FEBS Lett., 1993, 322, 186–190.
19. C. Blandy, D. Gervais and M. S. Cardenas, J. Mol. Catal., 1986, 34, 39–46.
20. C. Blandy, R. Choukroun and D. Gervais, Tetrahedron Lett., 1983, 24, 4189–4192.
21. J. A. López-Sánchez, C. Morisse, J. M. Winfield, B. Krumm, T. M. Klapötke and D. Lennon, Z. Anorg. Allgem. Chem., 2015, 641, 594–698.
22. H. Hennig, K. Ritter and R. Billing, J. Prakt. Chem., 1996, 338, 604–613.
23. H. Hennig, Coord. Chem. Rev., 1999, 182, 101–123.
24. D. Kurz, H. Hennig and J. Reinhold, Z. Anorg. Allg. Chem., 2001, 627, 1895–1900.
25. J. Ohata, F. Vohidov, A. Aliyan, K. Huang, A. A. Mart and Z. T. Ball, Chem. Commun., 2015, 51, 15192–15195.
26. J.-D. Lin, Y. Li, H. J. Xu, G. F.-K. Zheng, G.-C. Guo, R.-X. Lv, W.-C. He, Z.-N. Huang and J.-F. Liu, J. Solid State Chem., 2018, 265, 42–49.
27. Y. Ma, Y.-Q. Wen, J.-Y. Zhang, E.-Q. Gao and C.-M. Liu, Dalton Trans., 2010, 39, 1846–1854.
28. M. Ghosh, P. P. Chakrabarty, A. D. Jana, D. Schollmeyer, H. Sakiyama, M. Mikuriya, R. Debnath, P. Brandão, D. Mal and S. Saha, Inorg. Chim. Acta, 2022, 531–537, 120713.
29. A. Escuer and G. Aromí, Eur. J. Inorg. Chem., 2006, 4721–4736.
30. E. Evangelio, N. P. Rath and L. M. Mirica, Dalton Trans., 2012, 41, 8010–8021.
31. C. C. Beto, C. J. Zeman, Y. Yang, J. D. Bullock, E. D. Holt, A. Q. Kane, T. A. Makal, X. Yan, L. Ghiviriga, K. S. Schanze and A. S. Veige, Inorg. Chem., 2020, 59, 1893–1904.
32. Y.-H. Shen, A. M. Esper, I. Ghiviriga, K. A. Abboud, K. S. Schanze, C. Ehm and A. S. Veige, Dalton Trans., 2021, 50, 12681–12691.
33. M. He, F. Chen, D. Shao, P. Weis, Z. Wei and W. Sun, Biomaterials, 2021, 275, 120915.
34. A. Toscani, C. Hind, J. Clifford, S.-H. Kim, A. Gucic, C. Woolley, N. Saeed, K. M. Rahman, J. M. Sutton and D. Castagolo, Eur. J. Med. Chem., 2021, 213, 113172.
35. U. Müller, Struct. Bonding, 2005, 14, 141–172.
36. C. F. Campana, F. Y.-K. Lo and L. F. Dahl, Inorg. Chem., 1979, 18, 3060–3064.
37. M. Bursch, L. Kunze, A. M. Vibhute, A. Hansen, K. M. Sureshan, P. G. Jones, S. Grimme and D. B. Werz, Chem. – Eur. J., 2021, 274627.
38. M. C. Madhusudhanan, H. Balan, D. B. Werz and K. M. Sureshan, Angew. Chem., Int. Ed., 2021, 60, 22797–22803.
39. S. Scheiner, J. Phys. Chem. A, 2021, 125, 10419–10427.
40. Z. Setifi, F. Setifi, C. Glidewell, D. M. Gil, A. V. Kletskov, J. Echeverría and M. Mirzaei, J. Mol. Struct., 2021, 1235, 130155.
41. A. Chakraborty, L. S. Rao, A. K. Manna, S. K. Pati, J. Ribas and T. K. Maji, Dalton Trans., 2013, 42, 10707–10714.
42. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
43. S. Alvarez, Dalton Trans., 2013, 42, 8617–8636.
44. C. F. Matta and R. J. Boyd, in The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wiley-VCH, Weinheim, 2007, pp.1–34.
45. J. Echeverría and S. Alvarez, Chem. Sci., 2023, 14, 11647–11688.
46. R. Haiges, J. Skotnitzki, Z. Fang, D. A. Dixon and K. O. Christe, Angew. Chem., Int. Ed., 2015, 54, 15550–15555.
47. E. Schweda and J. Strähle, Z. Naturforsch., B: J. Chem. Sci., 1980, 35, 1146–1149.
48. E. Schweda and J. Strähle, Z. Naturforsch., B: J. Chem. Sci., 1981, 36, 662–665.
49. L. Hao and X. Liu, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2008, 64, m1499.
50. J. Honzíček, M. Erben, I. Císařová and J. Vinklárek, Appl. Organomet. Chem., 2005, 19, 102–103.
51. R. P. Sharma, R. Sharma, R. Bala, U. Rychlewska, B. Warzajtis and V. Ferretti, J. Mol. Struct., 2005, 753, 182–189.
52. J. Carranza, C. Brennan, J. Sletten, J. M. Clemente-Juan, F. Lloret and M. Julve, Inorg. Chem., 2003, 42, 8716–8727.
53. Y. Zhao, J. A. Woods, N. J. Farrer, K. S. Robinson, J. Pracharova, J. Kasparkova, O. Novakova, H.-K. Li, L. Salassa, A. M. Pizarro, G. J. Clarkson, L. Song, V. Brabec and P. J. Sadler, Chem. – Eur. J., 2013, 19, 9578–9591.
54. E. Schuh, S. Werner, D. Otte, U. Monkowius and F. Mohr, Organometallics, 2016, 35, 3448–3451.
55. D. Cremer and E. A. Kraka, Croat. Chem. Acta, 1984, 57, 1259–1281.
56. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170–173.
57. S. J. Grabowski, W. A. Siokalski and J. Leszzynski, Chem. Phys., 2007, 337, 68–76.
58. G. Sánchez-Sanz, I. Alkorta and J. Elguero, Molecules, 2017, 22, 227–242.
59. C. Trujillo, I. Alkorta, J. Elguero and G. Sánchez-Sanz, Molecules, 2019, 24, 308–320.
60. J. Contreras-García, W. Yang and E. R. Johnson, J. Phys. Chem. A, 2011, 115, 12983–12990.
61. J. R. Lane, J. Contreras-García, J.-P. Piquemal, B. J. Miller and H. G. Kjaergaard, J. Chem. Theory Comput., 2013, 9, 3263–3266.
62. B. Cordero, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Dalton Trans., 2008, 2832–2838.
63. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. CScalmani, V. Barone, G. A. Petersson, X. Nakatsuji, M. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, 2016.
64. A. Bauzá, I. Alkorta, A. Frontera and J. Elguero, J. Chem. Theory Comput., 2013, 9, 5201–5210.
65. S. Kozuch and J. M. L. Martin, J. Chem. Theory Comput., 2013, 9, 1918–1931.
66. D. J. Brauer, H. Bürger, G. Pawelke, K. H. Flegler and A. Haas, J. Organomet. Chem., 1978, 160, 389–401.
67. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
68. R. Dennigton, T. A. Keith and J. M. Millam, 2016.
69. Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kus, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. Hung Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neil, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Oschenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215.
70. P. R. Horn, Y. Mao and M. Head-Gordon, Phys. Chem. Chem. Phys., 2016, 18, 23067–23079.
71. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
72. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.
73. E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506.
74. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
75. J. Vogt and S. Alvarez, Inorg. Chem., 2014, 53, 9260–9266.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05798d

---