Assessing the importance of multireference correlation in predicting reversed conductance decay

Abstract

In a classical electronic resistor, conductance decays as the device length increases according to Ohm's Law. While most molecular series display a comparable exponential decay in conductance with increasing molecular length, a class of single-molecule device series exists where conductance instead increases with molecular/device length, a phenomenon called reversed conductance decay. While reversals of conductance decay have been repeatedly theoretically predicted, they have been far more difficult to demonstrate experimentally. Previous studies have suggested that theoretical multi-reference(static) correlation errors may be a major cause of this discrepancy, yet most single-molecule transport methods are unable to treat multireference correlation. Using our unique multireference transport method based on non-equilibrium Green's function and multiconfigurational pair-density functional theory (NEGF-MCPDFT), we examined a previously predicted case of reversed conductance decay in systems of linear chains of phenyl rings with varying lengths and electrode designs. We compare our NEGF-MCPDFT results to those of non-multireference NEGF methods to quantify the exact role of static correlation in conductance decay reversals and clarify their relative importance to geometric and electrode design/coupling considerations.

---

1. Introduction

Single-molecule devices display excellent potential both as electronic components and as a platform for investigating electron transport in molecules more generally.^1–4 A key draw of these single-molecule devices is their non-classical transport characteristics. By virtue of their molecular character, conductance through single molecules is affected by a wide variety of quantum properties such as electronic spin, vibrational interactions, and electronic interference. The recent rise of quantum electronics, in particular, has led to renewed efforts to develop molecular devices for a variety of applications including qubits and molecular quantum sensors.^5,6

One such unique quantum transport property can be seen in molecular wires/resistor series. For a typical molecular series such as alkane chains, conductance can be expected to decay exponentially as molecular length increases acting analogously to a classical resistor.⁷ These devices, however, do not work on a traditional length scale with their conductance governed by Ohm's Law, but rather on a quantum one. Therefore, it is possible to create a reverse in the exponential decay of the conductance, a phenomenon most commonly referred to as reversed conductance decay. This non-classical transport effect has seen a surge in interest recently due to its potential to create molecular wires that enable long-range charge transport.^8–21 While it was historically more difficult to demonstrate it experimentally than would be expected from theoretical predictions, in recent years experimentalists have made notable strides in designing molecular series that demonstrate the phenomena.^8–12,21 One key question that remains unaddressed is the relative importance of multireference correlation in predicting conductance decay reversals theoretically. Considering that a major design element of most molecular wire series with predicted conductance decay reversals is the presence of degenerate orbitals close in energy to the electrode Fermi level, it is reasonable to suspect that multireference correlation could play a role in predicting conductance decay reversals. A series of studies by Mandado and collaborators between 2019 and 2021 gave a compelling demonstration that multi-configurational electronic structure effects could play a key role in determining whether a molecular wire series will display non-exponential conductance decay behaviors with increasing length.^16–18

While these studies strongly demonstrate that multi-configurational effects are important when modeling conductance decay reversals, a key follow-up question is the relative importance of multi-configurational effects as compared to other proposed determining factors such as molecule-electrode coupling.¹⁵ When assessing whether a theoretical trend will be replicated experimentally, this is a vital consideration as electrode–molecule coupling is well-known to be critical in determining transport patterns in general and potentially for conductance reversals in particular. To examine the relative importance of multireference effects in creating conductance decay reversals, we employ Multiconfiguration Pair Density Functional Theory (MC-PDFT) combined with non-equilibrium Green's function theory (NEGF) the combination of which is referred to as NEGF-MCPDFT. This methodology allows for the inclusion of multireference effects through its use of complete active space (CAS) and dynamic correlation outside of the active space through a translated density functional.^22–25 A key advantage of this approach is its ability to include electrode–molecule coupling and NEGF-style model electrodes alongside a balanced description of both types of electron correlation. For this study, we utilize this ability to examine model oligophenyl chains with branched and linear electrodes which were previously established as an effective test system for theoretical evaluation of conductance reversals.^16,17,26 We first examine the previous 1-layer electrode models as a test for NEGF-MCPDFT and then examine new multi-layer versions of the electrodes to quantify the relative importance of multireference character in determining conductance decay reversals.

2. Computational methods

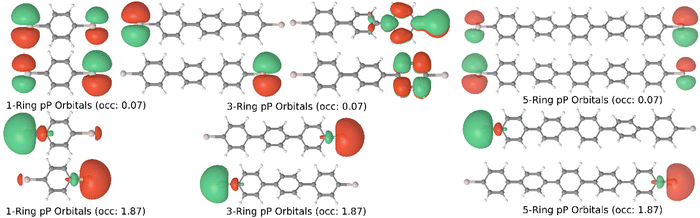
Linear chains with between 1 to 5 phenyl rings were examined for this study and will be referred to as X-ring (ex. 5-ring) systems throughout. Each chain was paired with an electrode on each side consisting of either a single aluminum atom (pP) or a branched electrode consisting of two aluminum atoms bonded to a methylene carbon (pX2). The electrode lengths of 1, 2, 4, and 6 layers were examined. Aluminum was chosen in place of gold used in the previous studies to avoid the use of effective core potentials which had not been verified to work with MC-PDFT at the time of this study. Geometry optimizations for both the five pP and the five pX2 systems were performed using the Q-Chem quantum chemistry software package.²⁷ The molecular geometries were optimized using the B3LYP functional and a 6-31G basis set. In addition, a five-ringed pX2 system optimized to the higher energy twisted ring state was included to examine the relative importance of molecular conformation. To assist with the convergence of the larger systems, the optimizations were done with hydrogen atoms on the single-layer electrodes, which were removed post-optimization. OpenMolcas was used to perform all of the MC-PDFT calculations, which used a T:PBE functional and the cc-pVDZ basis set.²⁸ Both (8,8) CAS (8 electrons in 8 orbitals) and (12,12) CAS (12 electrons in 12 orbitals) active spaces were used for the 1-layer electrode systems and an (8,8) CAS was used for the 2–6 layer systems. Pictures and occupation numbers for active space orbitals for all calculations can be found in the ESI.† DFT calculations using a PBE functional and the cc-pVDZ basis set were done using OpenMolcas to compare the results to that of MC-PDFT.^29,30 Transmission and conductance calculations were performed using the non-equilibrium Green's functions (NEGF) formalism implementation within the Rowan University Quantum Transport (RUQT) code available on GitHub.³¹ All NEGF calculations used a metal wide band limit approximation for the electrode coupling and a fixed Al Fermi level of −4.42 eV estimated from the HOMO–LUMO energies of a separate linear aluminum chain calculation using PBE/cc-pVDZ.³² The extended molecular and electrode region Green's functions are created by partitioning the effective Hamiltonian and overlap matrices for the entire system.

3. Results and discussion

3.1 Single layer pP vs. pX2 electrodes

3.1.1 Active space. When examining MC-PDFT conductance trends across a wide range of molecular lengths a key consideration is the stability of the active space. For NEGF methods, the character of the HOMO–LUMO orbitals is of particular importance as they are typically close to the electrode's Fermi level and can play an outsized role in determining transport values.³³ For NEGF-MCPDFT, it has been previously observed that the HOMO–LUMO-like orbitals (as determined by orbital occupational numbers) likewise play an outsized role in determining current and conductance. Pictures of these orbitals for the 1-, 3-, and 5- Ring systems with pP and pX2 electrodes can be found in Fig. 1 and 2 respectively. As can be seen in Fig. 1 and 2, the HOMO–LUMO-like active space orbitals between the pP and pX2 systems show clear differences. For the pP electrodes, these orbitals generate orbital pairs that are mostly localized on the electrode regions of the devices. This preference for electrode-centered orbitals when starting from SCF guess orbitals was noted previously for the benzyne radical.¹⁰ A key variance seen is with the 3-Ring system where some additional molecule-centered orbitals are occupationally degenerate with the electrode-centered orbitals. In contrast to the pP orbitals, the orbitals for the pX2 systems change depending on the chain length and display a greater contribution from the phenyl rings. It is also notable that for the pX2 electrodes, the 3 and 5-ring orbitals display a greater degree of delocalization across the molecule compared to the pP electrodes.

Fig. 1 Occupation and orbital trends for the pX2 series using a (12,12) active space.

Fig. 2 Occupation and orbital trends for the pP series using a (12,12) active space.

When compared to the DFT HOMO–LUMO orbitals from the 2019 paper by Gil-Guerrero et al. using gold electrodes, a few notable differences emerge.¹⁶ Compared to the gold pX2 electrodes where gold contributes d-like atomic orbitals to the LUMO/HOMO orbitals, Al contributes a p-like orbital. This leads to increased orbital delocalization across the entire electrode structure due to pi-bonding between the aluminum atoms and the linking carbon atom.

3.1.2 Occupation numbers. The orbital occupancy of the CAS orbitals is a well-known metric for evaluating the degree of multireference character. The occupancy of the active space orbitals in the (12,12) and (8,8) CAS pP systems was consistent across all chain lengths showing limited multi-configurational character. For all (12,12) CAS pP electrode systems, the HOMO-like orbitals have an occupancy of 1.87 and the LUMO-like orbitals have an occupancy of 0.07 which is relatively close to the single-reference SCF values of 2.0 and 0.0 respectively. The occupancies of the active space orbitals of the pX2 systems in contrast display increasing degeneracy as the molecular length increases going from nearly identical occupancies to the pP electrodes for the 1-ring chain (1.87 & 0.07) to almost perfectly degenerate occupations (1.02 & 0.98) for the HOMO–LUMO like orbitals. The occupation numbers also indicate an increasing degree of degeneracy and diradical character for the pX2 systems as the number of phenyl rings increases. This finding is consistent with the previous results for these 1-layer electrode oligophenyl chains.^16,17 Increased diradical character in particular has previously been associated with decreased occurrence of conductance decay reversals when edge state density is not maintained as system length increases.^8,18 This is the behaviour observed for all systems studied so we can expect increasing diradical character to result in fewer occurrences of non-exponential conductance decay.

3.1.3 Transmission. The results of the transmission calculations for the 1 electrode layer pP and pX2 systems using both MC-PDFT (12,12) CAS and PBE are displayed in Fig. 3. In the pP systems with 1-layer electrodes, the trend for the peaks near the Fermi level is similar with both MC-PDFT and DFT with all peaks being off-resonant with the Fermi level. The MC-PDFT method predicts both notably lower overall transmission and less peak alignment with the Fermi level consistent with its previous behavior for the benzyne radical.³³ Each method predicts a cluster of peaks near −2 and 2 eV but the gap between the peak clusters is significantly wider for MC-PDFT compared to PBE. For both methods, the cluster of peaks between −2 and −1 eV peaks show the expected progression toward the Fermi level as the number of rings increases but all systems remain highly off-resonant. For the pX2 systems, the predictions of PBE and MC-PDFT differ with the PBE predicting a cluster of peaks near the Fermi level. The MC-PDFT method in contrast gives two different peak behaviors depending on molecular length with the 1- and 2-ring systems having peaks close to the Fermi level and the peaks for the 3+ phenyl ring chains being again clustered between −1 and −2 eV below the Fermi level. This is likely due to the shift in the character of HOMO–LUMO-like orbitals with molecular length as the more electrode-centered orbitals of the 1 and 2-ring systems generate the peaks near the Fermi level. The behavior is thus somewhat but not entirely active space dependent as seen in Fig. 4 where the (8,8) CAS MC-PDFT results show very similar behaviors to the (12,12) CAS but with the location of 1 and 2 ring peaks near the Fermi level exchanged. Overall, the MC-PDFT and PBE transmission results show reasonable agreement in the 1-layer pP electrode case and stronger variance in the 1-layer pX2 electrode case with the PBE showing a greater degree alignment with the Fermi level overall as well as cases of increased transmission with molecular length. This is in keeping with previous findings that adding additional electron correlation effects (multireference or dynamic) typically results in an increase in peak spacing compared to that of many DFT functionals.^33–37

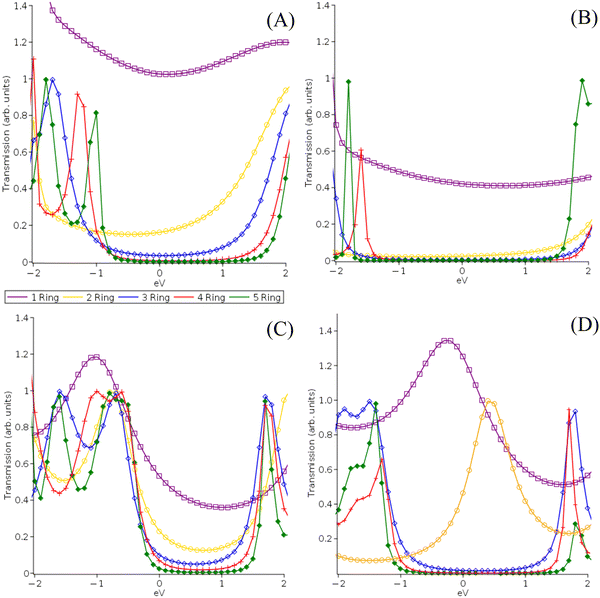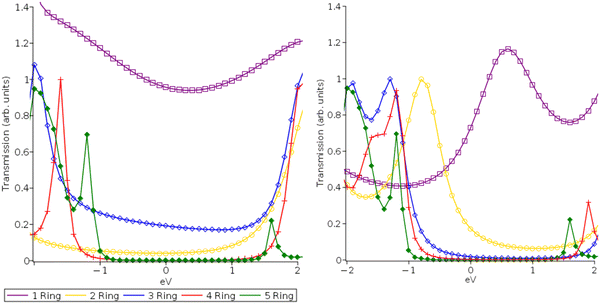
Fig. 3 Transmission functions for DFT-PBE (A) and (C) and MC-PDFT (12,12) CAS (B) and (D) for pP (A) and (B) and pX2 (C) and (D) type electrodes centered at the Fermi level.

Fig. 4 MC-PDFT (8,8) CAS transmission functions for pP (A) and pX2 (B) type electrodes centered at the Fermi level.

3.1.4 Conductance. The conductance trends with the number of phenyl rings at 0.5 and 2.0 V for both PBE and (12,12) CAS MC-PDFT using 1-layer electrodes are displayed in Fig. 5. For a typical molecular resistor, conductance can be expected to decay as an exponential function when compared to molecular length, G(x) = Ae^−βx where x is the number of repeating units, resulting in a linear decay trend on a semi-log plot. As expected, based on their transmission functions, both methods exhibit the expected exponential conductance decay with increasing molecular length for the pP electrode systems at 0.5 V with β coefficient values of 1.6 for PBE (r² = 0.99) and 2.1 for MC-PDFT (r² = 0.88). For the pX2 electrodes, however, the trend predictions for the two methods differ. The MC-PDFT method predicts continued exponential decay overall but with increased variance (r² = 0.71) and a beta coefficient of 2.1. This is likely a result of the previously noted difference in active space orbitals and transmission peak between the 1- and 2-ring systems and the 3–5 ring systems which leads to increased conductance for the 1- & 2-ring systems. The PBE method, in contrast, predicts a beta coefficient of 0.5 (r² = 0.97) indicating non-exponential decay as molecular length increases. This is likely due to the difference in the location of the transmission peaks closest to the Fermi level due to variance in the energetic active space orbitals as the molecular length increases.

Fig. 5 Estimated conductance values in quantum of conductance per number of phenyl rings at 0.5 V (a) and 2.0 V (b). The lines represent the exponential fits for each curve.

In Fig. 5(b), we examine the same systems at 2.0 V. In their original 2019 study, Gil Guerrero et al. noted that the pX2 systems had a multi-configurational character and showed a rise in conductance with the molecular length at 2.0 V. While the quantitative predictive power of a non-self-consistent wideband limit NEGF approach is limited at such high voltages, the high voltage results are still valid for electronic structure method comparison (PBE and MC-PDFT) and examining how their relative peak locations can be expected to impact conductance. At 2.0 V, the predicted conductance shows increasingly non-exponential decay behaviors with increasing molecular length compared to the 0.5 V case allowing transported charges to access them at higher voltages. While the MC-PDFT 2.0 Volt pP results are consistent with the 0.5 V results and similar exponential conductance decay values (β = 1.9), the 5-ring PBE pP system displayed greater conductance than the 4-ring PBE pP system at 2.0 Volts, displaying a reversal of the conductance decay and resulting in a numerical failure of the exponential fit. This result is likely due to the transmission peaks for the PBE being ∼1 eV closer to the Fermi level than those of MC-PDFT. The pX2 systems in contrast exhibit an increased degree of non-exponential conductance decay for both methods. Again, we can see that the tighter transmission peak spacing of the PBE method leads to a nearly flat conductance trend, particularly for the pX2 electrode at 2.0 V beyond 2 Rings with a small reversal seen at the 5-ring system for the pP configuration. MC-PDFT on the other hand continues to exhibit a conductance decay at 2.0 V with a low degree of linearity (r² = 0.70 for pX2 and r² = 0.85 for pP) in the semi-log plots which are relatively close to the 0.5 V values (r² = 0.76 for pX2 and r² = 0.88 for pP). This is again a result of the larger peak spacing and lower Fermi level alignment predicted by MC-PDFT as well as the variance in active space orbitals with system size.

This finding agrees with the follow-up papers to the original 2019 study which found it is more likely that proper multi-configurational corrections would act to decrease conductance and reduce predicted non-exponential decay behaviors rather than increase as originally predicted.^17,18 This is due to an increase in the relative transmission peak spacing a finding which is also consistent with previous results contrasting the impact of including GW electronic correlation corrections in NEGF-DFT calculations.^34,35 While the orbital degeneracies can be expected to be both more prominent and well-described when multi-configurational methods are employed, this does not necessarily translate to tighter peak spacing and Fermi-level alignment in transmission function. This aligns with the tendency of simple GGA DFT functionals such as PBE to underestimate the HOMO–LUMO gap which typically requires further correction (ex. long-range functionals or scissor corrections) to properly describe.^34,38 Our 1-layer can be seen as largely consistent with the previous findings of other studies when taken as a whole and shows that active space size alone is not likely a major determining factor. This suggests that increasing the quality of the multi-configurational description alone is not enough to properly describe conductance decay reversals.

3.2 Multi-layer electrodes

3.2.1 Conductance vs. electrode size. For all NEGF methods and molecular junction transport methodologies more generally, it is well-known that both electrode configuration and the quality of electrode description play a large role in determining conductance.^39–41 This is even evident in the initial test systems where changing to a different electrode configuration results in a significant difference in the displayed conductance patterns. To quantify the relative importance of electrode length versus multi-configurational character when determining transmission and conductance decay patterns we examined pX2 and pP type electrodes with 1,3, and 5 additional layers of Al atoms added on. In the NEGF calculations, the original 1-layer electrodes are included in the extended molecular region with the new layers forming the electrode regions.

3.2.2 Transmission with electrode length. The transmission functions for the pP and pX2 systems with multi-layer electrodes are shown in Fig. 6 and 7 respectively. We examined 2-, 4-, and 6-layer electrodes to contrast with the single-layer electrodes previously studied. From Fig. 6 we can see for the multi-layer pP-type electrodes, the primary difference from the 1-layer case is a decrease in the transmission for the 1-ring system. Otherwise, only a small decrease in the gap between the transmission peaks on either side of the Fermi level is seen as electrode length increases. This would not be expected to impact conductance significantly due to all peaks being highly off-resonant. Fig. 7 in contrast shows significant changes in predicted pX2 transmission spectra as electrode length increases. A large number of resonant peaks move near the Fermi level, and all 2+ ring systems show a large peak at or near the Fermi level. This result is quite striking when compared to the relatively minor difference seen between the different size active spaces for the one-layer pX2 electrodes. While the specific peak alignments shifted when the active space shifted, the overall transmission peak structure did not noticeably change as was previously observed for NEGF-MCPDFT calculations.³³

Fig. 6 Transmission functions for pP electrodes that are 2(A), 4(B), and 6(C) aluminum atoms long.

Fig. 7 Transmission functions for pX2 electrodes that are 2(A), 4(B), and 6(C) aluminum atoms long.

In contrast, the transmission peak character and locations for the pX2 systems significantly change as electrode size increases with the net effect being a large increase in Fermi level-transmission peak alignment. These results suggest that electrode size rather than active space composition or size is likely going to be a more important factor in determining transmission for multiconfigurational transport methods. Considering the well-known dependence of NEGF methods (and charge transport methods more broadly) on electrode description this is not an entirely surprising result. This can be considered a benefit for the NEGF-MCPDFT method as it is capable of describing much larger model electrodes than any similarly advanced multiconfigurational transport methodology.

3.3.3 Conductance with electrode length. As can be expected based on the NEGF methods used, the conductance results align with the transmission analysis. As seen in Fig. 8, the overall trends for the pP electrode systems at both voltages are roughly consistent with the one-layer results although the rate of decline in conductance is lessened (β = 0.78 − 0.83 at 0.5 V). While there is some increased variance between the different lengths, by four or six electrode layers the conductance patterns have mostly converged to the same rate of decay. The 2.0 V pP electrode results are largely consistent with 0.5 V results in contrast to the 1-layer PBE predictions (β = 1.39 − 0.80). For the p2X electrodes (Fig. 9) the addition of electrode layers causes the rate of decay to decline as the electrode length increases with beta values going from 2.18 (1-layer) to 0.16 (6-layer) at 0.5 V. At 2.0 V, we again see increasingly nonlinear conductance decay patterns (β = 1.4 − 0.003) and even an increase in conductance for the 5-ring system with 6-layer electrodes matching the previous PBE result for the one-layer electrodes. In this case, the lessening of the decay rate shows that the increased peak spacing caused by the multi-configurational character of the pX2 systems was effectively overwhelmed by the increase in electrode–molecule interactions. This brings the NEGF-MCPDFT predicted conductance trends for pX2 back to a qualitative agreement with the 1-layer PBE results, especially at 2.0 V. This contrasts with the pP electrodes where a significant difference in overall conductance values is maintained as the number of electrode layers increases and no similar convergence between results is seen.

Fig. 8 Estimated MC-PDFT conductance values for all pP-type electrodes in quantum of conductance per number of phenyl rings at 0.5 V (a) and 2.0 V (b). The lines represent the exponential fits for each curve.

Fig. 9 Estimated MC-PDFT conductance values for all pX2-type electrodes in quantum of conductance per number of phenyl rings at 0.5 V (a) and 2.0 V (b). Lines represent the exponential fits for each curve.

What this suggests is that the electrode description is the more important of the two factors when determining conductance trends. Failing to provide an optimized electrode model will limit the reliability of the conductance trend prediction regardless of the quality of the electronic structure method used or improvements to the correlation recovery characteristics. It is notable though that the results tend to converge as electrode length increases which is an encouraging finding. This suggests that if the model electrode is of sufficient length and quality a definitive theoretical statement about the conductance trends for a multiconfigurational molecular series can be made. With improvements to the electrode descriptions of multiconfigurational transport methods, multiconfigurational contributions to conductance decay reversals can potentially be consistently characterized.⁴²

3.4 Variations in trends with orbital and transport region selection

It is well-known that active space selection can play a major role in property prediction for active space methods like CASPT2 and MC-PDFT. By extension, one might expect it to important contributing factor to the previous transmission and conductance results. However, in the previous investigation of alkane chains and benzyne, active space selection did not prove to be highly important and the energetic criteria proved to be equivalent for treating transport properties when compared to a custom-designed active space which was designed to increase the presence of molecule-centered orbitals.³³ This was because the systems studied displayed a strong preference for specific types of HOMO–LUMO-like orbitals which play an outsized role in determining charge transport at low bias voltages. These preferred HOMO–LUMO-like orbitals were typically centered on the electrodes. This behavior was maintained across a range of active space sizes and orbital reordering attempts. In contrast to the current study, the impact of increasing both electrode and molecule size was not considered. As seen in Fig. 1 and 2, when a small, fixed electrode is used maintaining reasonable active space consistency in terms of the HOMO–LUMO-like orbitals across molecular size increases can be achieved as previously observed. This becomes more challenging, however, when the electrode size is also increased as this alters the relative importance of orbital contributions from the metal atoms in compared to the those of the molecular atoms. When using a localized Gaussian basis set, this results in localized orbitals that struggle to describe the increasingly mixed organometallic system as electrode size increases, yielding variations in active space orbitals and potentially property trends. This is principally seen in a tendency for increasingly electrode-centered orbitals and increased potential for more fragmentary orbitals as system size increases. We examined two potential fixes to this issue the first being an expansion of the extended molecular region so that additional electrode-centered orbitals are included in the transport region and the second being a reoptimization of the active orbitals to include more molecule-centered orbitals rather than using the energetic criteria. For these tests, we reexamined the pX2 systems with the longest electrodes (pX2-6) as they displayed the most orbital fragmentation and variance from the energetic orbital set.

To increase the size of the extended molecular region for the pX2-6 systems, we recalculated the transmission and conductance using only a single pair of aluminum atoms in the electrode region instead of having all aluminum atoms in the electrode region. This means that for the pX2-6 electrodes, the 2 atoms in each electrode region matching the pX2 electrode and previous studies. For the active space optimization test, we aimed to create a balanced active space that maintained consistent molecular and electrode orbitals across the entire series with 4 electrode-centered and 4 molecule-centered orbitals in the active space. Another key goal was to make the HOMO–LUMO-like orbitals molecule centered as was seen in the one-layer electrode case in the previous section. This proved to be only partially achievable with the current basis set due to the tendency of the individual orbitals to fragment and localize into multiple equivalent orbitals as the system size increases. As can be seen in Fig. 10 and the complete orbital sets in the ESI,† the pX2-6 systems using the energetic active space displayed increasingly fragmentary orbitals that centered on the electrodes as the size of the molecules increases. This proved to be only partially reversible by rotating in new orbitals to the active space and re-optimizing in an attempt to achieve the desired mix of molecule- and electrode-centered orbitals. As seen in Fig. 10, rotating in molecule-centered orbitals did result in HOMO–LUMO-like orbitals that were centered on the molecules for the 1-ring (and 2-ring) systems. At three or more rings, attempts to include molecule-centered and non-fragmentary orbitals resulted in limited changes to the preferred HOMO–LUMO-like orbitals. However, overall the new active spaces have an increased number of molecule-centered orbitals when compared to the energetic active spaces, and most of the unpaired fragmentary orbitals were removed or joined by an appropriate orbital pair (see ESI† for all active space orbital pictures). As in the previous NEGF-MCPDFT study, we find a tendency for electrode-centered HOMO–LUMO-like orbitals to be particularly dominant and difficult to rotate out of the active space an optimization behaviour pattern which appears to become stronger as the size of the electrode increases. It should also be noted that orbital degeneracy patterns are maintained when the active spaces are reordered with more variation being seen when the HOMO–LUMO-like orbitals are changed as is the case for the one-ring system which shows modestly fewer degenerate occupations when the fragmentary electrode centered orbitals are replaced with molecular-centered orbitals. Both active spaces also show similar trends in their diradical predications with both predicting diradical behaviour for pX2 system with 3 phenyl rings or more.

Fig. 10 Occupation number and orbital trends for the HOMO–LUMO-like orbitals of the 1, 3, and 5 Ring pX2-6 series using a (8,8) CAS active space.

The transmission curves for both tests can be seen in Fig. 11. Considering the transmission curve for the reoptimized active space, two points of interest appear. The first is that when compared to the original energetic active space for the 3+ ring systems the overall shape and number of peaks are not heavily changed however their locations are highly shifted. This is very much in line with the previous NEGF-MCPDFT study where changes in active space that maintain the same HOMO–LUMO-like orbitals tended to result in similar transmission peaks but with potentially widely shifted transmission energies. The one-ring pX2-6 case in contrast reverts to a single broad peak similar to the (12,12) CAS pX2 1-ring system. This is likely due to the return to more molecule-centered orbitals over the fragmentary electrode orbitals seen in the (8,8) CAS energetic orbital set.

Fig. 11 MC-PDFT (8,8) CAS transmission functions centered at the Fermi level for pX2-6 electrodes with the energetic active space and an enlarged extended molecular region (A) a reordered active space (B) and the energetic active space (C).

Considering the effect of increasing the size of the extended molecular region, overall transmission is decreased and peaks are heavily shifted in transmission energy relative to the Fermi level and decreased in magnitude. This is likely due to the removal of active space orbitals near the Fermi level from the electrode region and placing them into the extended molecular region. This increases the alignment between the electrode and extended molecule orbitals since it places a transmission peak right at the Fermi level for all systems.

The effect that both transport orbital changes have on conductance can be seen in Fig. 12. Considering the expanded molecular region first, we can see that at 0.5 V the a nearly flat and linear conductance trend with a nearly identical decay rate compared to the standard pX2-6 case (β = 0.18 vs. 0.16). Going to 2.0 V in contrast increases the nonlinearity of the curve, decreases the conductance, and increases the decay rate over pX2-6 (β = 0.39 vs. 0.003). This relatively stable conductance can be expected as the transmission graph showed a cluster of small peaks near the Fermi level with the remaining peaks heavily decreasing in magnitude or shifting away. This means that at low voltages you would expect relatively high and consistent conductance due to resonant transport through the aligned transmission peaks.

Fig. 12 Estimated MC-PDFT conductance values for pX2-6 electrodes using an enlarged extended molecular region (px2-6EX) and a reordered active space (pX2-6RE) in quantum of conductance per number of phenyl rings at 0.5 V (a) and 2.0 V (b). Lines represent the exponential fits for each curve.

The conductance of the re-optimized active space orbitals shows a more interesting result. As noted in the transmission results, there was a degree of inconsistency in the peak trends which corresponds to changes in the active space orbitals. Based on the past results for the benzyne diradical, we would expect conductance inconsistencies to emerge only when the HOMO–LUMO-like levels change which did occur for the reoptimized active space to a greater degree than for the energetic active space. This observation is also borne out in the conductance plots where the energetic active space's prediction of a near reversion to PBE results at 0.5 V voltages and a slight reversal of conductance decay/flat conductance at 2.0 V are both reverted to exponential decay with length (β = 0.89 vs. 0.5 V and β = 1.02 at 2.0 V) with increased variability in the overall conductance trend. As noted above, this increased variability is likely due to changes in the HOMO–LUMO-like orbitals as molecular length increases. This reinforces that picking an active space that represents the actual transport orbitals (particularly the HOMO–LUMO-like orbitals) is a key factor for describing transport trends. When combined with the previous results for electrode length, this shows that to predict conductance trend reversals and capture multireference effects consistently both an electrode of sufficient size and a well-chosen set of active space orbitals should be employed. This is an ongoing challenge as there are no active space design principles that currently exist for ensuring a consistent description of charge transport in molecular junctions as few active space methods are commonly used for molecular electronics calculations.

3.5 Role of molecular conformation

Alterations to the molecular configuration are another well-known contributor to conductance trend behaviors. The importance of molecular configuration can be seen in recent efforts to utilize topological states to create conductance decay reversals.⁸ Generally speaking, for phenyl ring-based systems, the alignment of phenyl rings tends to increase conductance, and a potential cause of the increased conductance for pX2 model systems conductance is that the pX2 electrode configuration energetically favors a completely flat ring system over the twisted rings seen in the pP electrode systems. This offers a straightforward check of the relative importance of the molecular configuration by comparing our previous results against those of the twisted pX2 system and those of the p1 systems. As an illustrative example, we examined the twisted five-ring system at multiple electrode lengths. For these calculations, we used the twisted 5-ring geometry from the p1 electrode calculations and then replaced the p1 electrodes with their pX2 equivalents. The transmission results are shown in Fig. 13. We can see from the results that pairing the twisted ring system with the pX2 results in transmission functions that are a mix of the p1 and pX2 results. They display overall increased alignment with the Fermi level compared to the p1 electrodes but with similar overall peak shapes. There is a notable difference in peak alignment between the 4/6 length electrodes and the 1/2 length electrodes. This confirms that a key factor in the pX2 electrode model's conductance reversals at high voltages was the energetic favoring of a flat phenyl ring alignment over a twisted one. This also again confirms that to properly predict conductance decay reversals character a model must at minimum account for all three factors (electrode description, multireference character, and molecular configuration) correctly.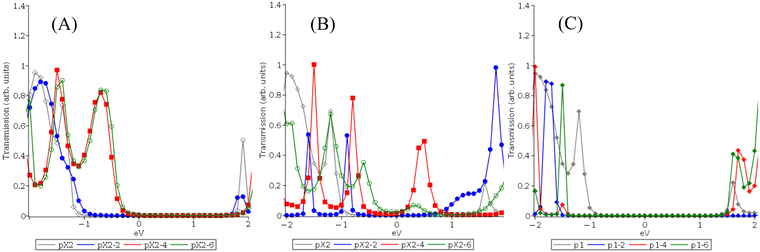

Fig. 13 Transmission functions for the twisted pX2 5-ring system with 1-,2-, 4-, and 6-layer electrodes (A) compared to the previous pX2 results (B) and the p1 electrodes (C).

4. Conclusions

In this study, we sought to clarify the relative importance of multireference/static correlation in determining the appearance of conductance decay reversals in molecular wire series. We examined a model system known to provide a clear case of conductance reversals based on electrode design. Our results match the findings of other groups for the 1-layer model systems and show that NEGF-MCPDFT is consistently capturing multireference correlation effects for these systems. We also showed that this multiconfigurational character is not alone enough to determine conductance decay reversals and that geometric considerations such as electrode configuration and molecular conformations are likely more important. This demonstrates that one needs a robust electrode model paired with a well-designed extended molecular region to make a definitive statement about whether a particular system will display the effect. As shown by the active space test there is also a great need to develop active space design principles for multireference transport methods to ensure that the correct transport orbitals are being used as well as to implement less localized basis sets for use with active space methods. We also find that multireference correlation should be treated as a correction to prevent the miss prediction of conductance decay reversals when other factors (ex. topological states) are in favor of the effect. We hope this provides some guidance for future investigations of the phenomenon. We hope that our findings will aid in the discovery of new devices with enhanced conductance as providing a comprehensive treatment of these factors is particularly important when designing novel systems without experimental guidance.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Erik Hoy would like to acknowledge the funding support provided by National Foundation Grant No. CHE-2154832. This work was supported by the donors of the ACS Petroleum Research Fund under Undergraduate New Investigator Grant 5337-UNI6. Erik Hoy served as Principal Investigator on ACS PRF 5337-UNI6 that provided support for Matthew Tineo. Tanner Cossaboon and Samir Kazmi would like to acknowledge the support provided by The New Jersey Space Grant Consortium Training Grant A18-0090-002 through the Rowan Summer Undergraduate Research Program.

References

1. H. Song, Y. Kim, H. Jeong, M. A. Reed and T. Lee, Coherent Tunneling Transport in Molecular Junctions, J. Phys. Chem. C, 2010, 114, 20431–20435.
2. J. Valdiviezo, P. Rocha, A. Polakovsky and J. L. Palma, Nonexponential Length Dependence of Molecular Conductance in Acene-Based Molecular Wires, ACS Sens., 2021, 6, 477–484.
3. R. Gupta, J. A. Fereiro, A. Bayat, A. Pritam, M. Zharnikov and P. C. Mondal, Nanoscale molecular rectifiers, Nat. Rev. Chem., 2023, 7, 106–122.
4. N. Xin, J. Guan, C. Zhou, X. Chen, C. Gu, Y. Li, M. A. Ratner, A. Nitzan, J. F. Stoddart and X. Guo, Concepts in the design and engineering of single-molecule electronic devices, Nat. Rev. Phys., 2019, 1, 211–230.
5. C.-J. Yu, S. von Kugelgen, D. W. Laorenza and D. E. Freedman, A Molecular Approach to Quantum Sensing, ACS Cent. Sci., 2021, 7, 712–723.
6. P. W. K. Jensen, L. B. Kristensen, C. Lavigne and A. Aspuru-Guzik, Toward Quantum Computing with Molecular Electronics, J. Chem. Theory Comput., 2022, 18, 3318–3326.
7. L. Lafferentz, F. Ample, H. Yu, S. Hecht, C. Joachim and L. Grill, Conductance of a Single Conjugated Polymer as a Continuous Function of Its Length, Science, 2009, 323, 1193–1197.
8. L. Li, S. Louie, A. M. Evans, E. Meirzadeh, C. Nuckolls and L. Venkataraman, Topological Radical Pairs Produce Ultrahigh Conductance in Long Molecular Wires, J. Am. Chem. Soc., 2023, 145, 2492–2498.
9. E. Leary, B. Limburg, A. Alanazy, S. Sangtarash, I. Grace, K. Swada, L. J. Esdaile, M. Noori, M. T. González, G. Rubio-Bollinger, H. Sadeghi, A. Hodgson, T. N. Agraı, S. J. Higgins, C. J. Lambert, H. L. Anderson and R. J. Nichols, Bias-Driven Conductance Increase with Length in Porphyrin Tapes, J. Am. Chem. Soc., 2018, 140, 12877–12883.
10. S. Gunasekaran, D. Hernangómez-Pérez, I. Davydenko, S. Marder, F. Evers and L. Venkataraman, Near Length-Independent Conductance in Polymethine Molecular Wires, Nano Lett., 2018, 18, 6387–6391.
11. W. Xu, E. Leary, S. Sangtarash, M. Jirasek, M. T. González, K. E. Christensen, L. Abellán Vicente, N. Agraït, S. J. Higgins, R. J. Nichols, C. J. Lambert and H. L. Anderson, A Peierls Transition in Long Polymethine Molecular Wires: Evolution of Molecular Geometry and Single-Molecule Conductance, J. Am. Chem. Soc., 2021, 143, 20472–20481.
12. W. Xu, E. Leary, S. Hou, S. Sangtarash, M. T. González, G. Rubio-Bollinger, Q. Wu, H. Sadeghi, L. Tejerina, K. E. Christensen, N. Agraït, S. J. Higgins, C. J. Lambert, R. J. Nichols and H. L. Anderson, Unusual Length Dependence of the Conductance in Cumulene Molecular Wires, Angew. Chem., Int. Ed., 2019, 58, 8378–8382.
13. S. Li, C. K. Gan, Y.-W. Son, Y. P. Feng and S. Y. Quek, Anomalous length-independent frontier resonant transmission peaks in armchair graphene nanoribbon molecular wires, Carbon, 2014, 76, 285–291.
14. Y. Tsuji, R. Movassagh, S. Datta and R. Hoffmann, Exponential Attenuation of Through-Bond Transmission in a Polyene: Theory and Potential Realizations, ACS Nano, 2015, 9, 11109–11120.
15. L. Li, S. Gunasekaran, Y. Wei, C. Nuckolls and L. Venkataraman, Reversed Conductance Decay of 1D Topological Insulators by Tight-Binding Analysis, J. Phys. Chem. Lett., 2022, 13, 9703–9710.
16. S. Gil-Guerrero, N. Ramos-Berdullas, Á. Martín Pendás, E. Francisco and M. Mandado, Anti-ohmic single molecule electron transport: is it feasible?, Nanoscale Adv., 2019, 1, 1901–1913.
17. S. Gil-Guerrero, Á. Peña-Gallego, N. Ramos-Berdullas, Á. Martín Pendás and M. Mandado, Assessing the Reversed Exponential Decay of the Electrical Conductance in Molecular Wires: The Undeniable Effect of Static Electron Correlation, Nano Lett., 2019, 19, 7394–7399.
18. N. Ramos-Berdullas, S. Gil-Guerrero, Á. Peña-Gallego and M. Mandado, The effect of spin polarization on the electron transport of molecular wires with diradical character, Phys. Chem. Chem. Phys., 2021, 23, 4777–4783.
19. Y. X. Zhou, F. Jiang, H. Chen, R. Note, H. Mizuseki and Y. Kawazoe, Quantum length dependence of conductance in oligomers: First-principles calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245407.
20. J. Valdiviezo, P. Rocha, A. Polakovsky and J. L. Palma, Nonexponential Length Dependence of Molecular Conductance in Acene-Based Molecular Wires, ACS Sens., 2021, 6, 477–484.
21. S. Li, H. Yu, J. Li, N. Angello, E. R. Jira, B. Li, M. D. Burke, J. S. Moore and C. M. Schroeder, Transition between Nonresonant and Resonant Charge Transport in Molecular Junctions, Nano Lett., 2021, 21, 8340–8347.
22. G. Li Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, Multiconfiguration Pair-Density Functional Theory, J. Chem. Theory Comput., 2014, 10, 3669–3680.
23. G. L. Manni, S. D. Smart and A. Alavi, Combining the Complete Active Space Self-Consistent Field Method and the Full Configuration Interaction Quantum Monte Carlo within a Super-CI Framework, with Application to Challenging Metal-Porphyrins, J. Chem. Theory Comput., 2016, 12, 1245–1258.
24. L. Gagliardi, D. G. Truhlar, G. Li Manni, R. K. Carlson, C. E. Hoyer and J. L. Bao, Multiconfiguration Pair-Density Functional Theory: A New Way To Treat Strongly Correlated Systems, Acc. Chem. Res., 2017, 50, 66–73.
25. R. K. Carlson, D. G. Truhlar and L. Gagliardi, Multiconfiguration Pair-Density Functional Theory: A Fully Translated Gradient Approximation and Its Performance for Transition Metal Dimers and the Spectroscopy of Re2Cl82–, J. Chem. Theory Comput., 2015, 11, 4077–4085.
26. N. Ramos-Berdullas and M. Mandado, Electronic Properties of p-Xylylene and p-Phenylene Chains Subjected to Finite Bias Voltages: A New Highly Conducting Oligophenyl Structure, Chem. – Eur. J., 2013, 19, 3646–3654.
27. Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Küs, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C. M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. Distasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T. C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S. P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. Oneill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y. C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z. Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J. D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C. P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Advances in molecular quantum chemistry contained in the Q-Chem 4 program package, Mol. Phys., 2015, 113, 184–215.
28. I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. Å. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, OpenMolcas: From Source Code to Insight, J. Chem. Theory Comput., 2019, 15, 5925–5964.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
30. R. K. Carlson, D. G. Truhlar and L. Gagliardi, Multiconfiguration Pair-Density Functional Theory: A Fully Translated Gradient Approximation and Its Performance for Transition Metal Dimers and the Spectroscopy of Re2Cl82–, J. Chem. Theory Comput., 2015, 11, 4077–4085.
31. E. P. Hoy, D. X. Bones, M. Tineo and E. Meyers, Rowan University Quantum Transport (RUQT), Github, 2021, https://github.com/HoyLab-Rowan/RUQT.
32. C. J. O. Verzijl, J. S. Seldenthuis and J. M. Thijssen, Applicability of the wide-band limit in DFT-based molecular transport calculations, J. Chem. Phys., 2013, 138, 094102.
33. A. M. Sand, J. T. Malme and E. P. Hoy, A multiconfiguration pair-density functional theory-based approach to molecular junctions, J. Chem. Phys., 2021, 155, 114115.
34. M. Thoss and F. Evers, Perspective: Theory of quantum transport in molecular junctions, J. Chem. Phys., 2018, 148, 030901.
35. S. Y. Quek, H. J. Choi, S. G. Louie and J. B. Neaton, Length dependence of conductance in aromatic single-molecule junctions, Nano Lett., 2009, 9, 3949–3953.
36. D. X. Bones, J. T. Malme and E. P. Hoy, Examining conductance values in the biphenyl molecular switch with reduced density matrices, Int. J. Quantum Chem., 2021, 121, e26633.
37. E. P. Hoy, D. A. Mazziotti and T. Seideman, Development and application of a 2-electron reduced density matrix approach to electron transport via molecular junctions, J. Chem. Phys., 2017, 147, 184110.
38. A. Yamada, Q. Feng, A. Hoskins, K. D. Fenk and B. D. Dunietz, Achieving Predictive Description of Molecular Conductance by Using a Range-Separated Hybrid Functional, Nano Lett., 2016, 16, 6092–6098.
39. G. Cohen and M. Galperin, Green’s function methods for single molecule junctions, J. Chem. Phys., 2020, 152, 090901.
40. N. Papior, N. Lorente, T. Frederiksen, A. García and M. Brandbyge, Improvements on non-equilibrium and transport Green function techniques: The next-generation transiesta, Comput. Phys. Commun., 2017, 212, 8–24.
41. M. Carlotti, S. Soni, A. Kovalchuk, S. Kumar, S. Hofmann and R. C. Chiechi, Empirical Parameter to Compare Molecule–Electrode Interfaces in Large-Area Molecular Junctions, ACS Phys. Chem. Au, 2022, 2, 179–190.
42. E. P. Hoy and M. Tineo, Python-based Rowan University Quantum Transport (pyRUQT), Github, 2022, https://github.com/HoyLab-Rowan/pyRUQT.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp01110k

---