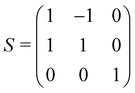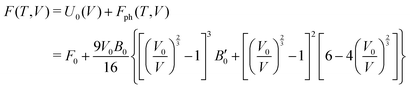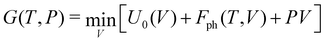Thermodynamics of phase transitions in Zintl clusters from density functional theory: making and breaking of bonds in Ba₃Ge₄

Abstract

Density functional theory, in conjunction with the quasi-harmonic approximation, has been used to study the equilibrium between the orthorhombic and tetragonal phases of Ba₃Ge₄. A transition from the high-temperature tetragonal phase containing isolated Ge₄⁶⁻ units to the low-temperature orthorhombic phase, where precisely half of the Ge₄⁶⁻ units are polymerised along one axis, is predicted at 930 K, somewhat higher than the experimental value of 630 K. An analysis of the phonon density of states shows that the lower entropy of the orthorhombic phase is not associated directly with the polymerisation of the Ge₄⁶⁻ units, but rather with the contraction of the unit cell, which raises the frequencies of ion–ion modes involving the relative motions of the Ba²⁺ and Ge₄⁶⁻ units. Calculations also predict that a third, as yet unobserved, p-tetragonal phase, where all of the Ge₄⁶⁻ units are polymerised to form two separate chains running in orthogonal directions, might be accessible at pressures close to 1 GPa.

---

Introduction

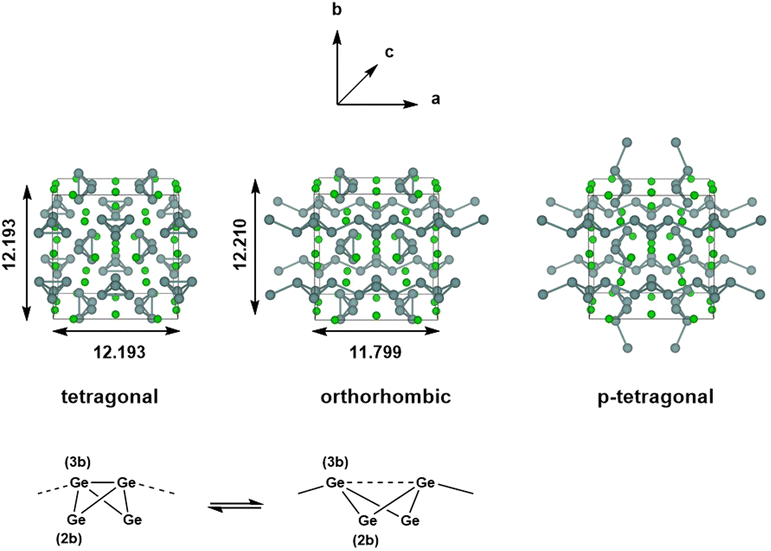
The chemistry of Zintl ions continues to present fascinating challenges in electronic structure theory.^1–6 Much of the work in the field of computational cluster chemistry has focussed on isolated Zintl ions, either in the gas phase or where the ions are separated in the solid state by encapsulated metal cations, such as [M[2·2·2]crypt]⁺. In the so-called Zintl phases, in contrast, the cations are ‘naked’, leading to much smaller separations between the cluster anions.^7–9 Simple examples of this class would be the binary silicides and germanides such as NaSi,¹⁰ which contains tetrahedral E₄⁴⁻ units, isoelectronic with P₄. The relatively close proximity of the cluster anions in these phases admits the possibility of forming additional inter-cluster bonds, and indeed, in LiSi and LiGe, the very small Li⁺ cation allows the tetrel atoms to form an extended network rather than a lattice of discrete E₄⁴⁻ tetrahedra.¹¹ Changes in temperature and/or pressure can also induce structural modifications, as for example in Quesada-Cabrera et al.'s report of the pressure-induce amorphisation of NaSi above 15 GPa, which may involve the oxidative formation of Si–Si bonds between Si₄ clusters with concomitant reduction of Na⁺ to Na.¹⁰ The pressure dependence of phase equilibria for BaGe₂ has been studied extensively: at ambient pressure, BaGe₂ adopts the BaSi₂-type orthorhombic structure with discrete Si₄⁴⁻ tetrahedra,¹² but at high temperatures and pressures, the ThSi₂-type tetragonal lattice is preferred, where the Ge atoms are connected in a 3-dimensional network.¹³ Similar behaviour emerges in the high-pressure (>10 GPa) metastable phases of EuGe₃ and SrGe₆ which have 2-, 3- and 4-connected networks, in marked contrast to the discrete tetrahedra in the MGe₂ decomposition products found at ambient pressures.^14,15 Wang et al. have explored the phase transition in BaGe₂ in some detail using density functional theory, establishing a pathway connecting the orthorhombic and tetragonal phases via flattening of the E₄ tetrahedra and inter-cluster bond formation, with a barrier of 0.35 eV per atom.¹⁶

In this paper, we focus on a more Ba-rich region of the Ba-Si/Ge phase diagrams,^17–19 and specifically on Ba₃Si₄ and Ba₃Ge₄, where E₄ units are again present but now in the more reduced 6-state (Fig. 1). The silicon compound, first characterised by Eisenmann et al. in 1969,²⁰ has a tetragonal unit cell (P4₂/mnm) and contains isolated Si₄⁶⁻ units aligned in two orthogonal chains that run parallel to the crystallographic a and b axes. The Si₄ units adopt a butterfly-type structure where a single Si–Si bond of the tetrahedron has been cleaved, as might be anticipated for a Si₄⁶⁻ unit based on the Zintl–Klemm concept. There are two distinct atom types in each cluster: the atoms on the wing-tips of the butterfly that are bonded to two other atoms and carry a formal charge of 2- (denoted henceforth as ‘(2b)E’ in Fig. 1) and the atoms that constitute the body of the butterfly that are bonded to three others and carry a formal charge of 1- (denoted ‘(3b)E’). The (3b)Si–(3b)Si and (3b)Si–(2b)Si bond lengths were reported to be 2.29 Å and 2.34 Å, respectively, in Eisenmann's original paper, but a subsequent re-evaluation by Grin and co-workers in 2008 revised these to 2.4183(6) Å and 2.4254(3) Å, respectively.²¹ The Ba₃Si₄ phase is weakly conducting (a ‘bad metal’), consistent with band structure calculations that indicate substantial mixing of the Si 3p and the Ba 5d orbitals and a non-zero density of states at the Fermi level. Above 630 K, the Ge analogue Ba₃Ge₄ adopts a tetragonal phase that is structurally very similar to Ba₃Si₄, with isolated Ge₄⁶⁻ anions and (3b)Ge–(3b)Ge and (3b)Ge–(2b)Ge bond lengths of 2.78 Å and 2.59 Å, respectively (the tetragonal phase).²² Below this temperature, however, a first-order transition to a different, orthorhombic, phase, where precisely half of the Ge₄ units polymerise along the crystallographic a-axis (designated (Ba²⁺)₆[Ge₄]⁶⁻¹_∞[Ge₄]⁶⁻), with concomitant cleavage of the intra-cluster (3b)Ge–(3b)Ge bond. Polymerisation causes contraction along the a-axis (11.799 Å vs. 12.193 Å) and a ∼ 2% reduction in cell volume. The Zintl–Klemm concept is equally applicable to both tetragonal and orthorhombic phases: the (3b)Ge centres remain bonded to three others in both cases. The second chain of Ge₄⁶⁻ units aligned along the crystallographic b-axis is largely unaffected by the phase transition, as is the lattice parameter b. There has, as yet, been no evidence reported for a putative third phase (which we label p-tetragonal) where the Ge₄ units polymerise along both the a and b axes ((Ba²⁺)_6¹∞[Ge₄]⁶⁻¹_∞[Ge₄]⁶⁻), a transition that would restore tetragonal symmetry. In a subsequent study, Pani and Palenzona reproduced the low-temperature orthorhombic phase of Ba₃Ge₄ but all attempts to isolate the high-temperature tetragonal phase by quenching the melts were unsuccessful.¹⁷ A weak feature in the differential thermal analysis at ∼610 K was, however, consistent with the transition temperature identified by Zürcher and Nesper.²²

Fig. 1 Optimised structures of the tetragonal, orthorhombic and (as yet unknown) p-tetragonal phases of Ba₃Ge₄ (all distances in Å). The chains of Ge₄ units are polymerised along the a-axis in the orthorhombic phase and along both a and b axes in the p-tetragonal phase.

A number of non-stoichiometric members of the Ba₃Si_xGe_4−x series that interpolate between the limiting forms Ba₃Si₄ and Ba₃Ge₄ have also been characterised,²³ and the polymerised orthorhombic phase is found only for the most Ge-rich of these (x = 0.3 or lower). It is likely that the size of the cation plays an important role in determining the different behaviours of Si- and Ge-rich phases, just as it does in the LiSi/NaSi comparison made above. Nesper and co-workers have argued that while the Ba²⁺ cation is large enough to separate the Si₄⁶⁻ anions from the point where the inter-cluster bond formation is not possible, the more diffuse nature of the valence 4p orbitals of Ge makes the polymerised orthorhombic phase accessible.²³ In that sense, the temperature-dependent behaviour of Ba₃Ge₄ mirrors many of the important features of the pressure-dependent behaviour of BaGe₂.

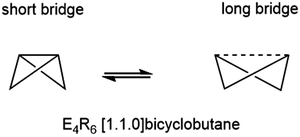
The E₄⁶⁻ unit is valence iso-electronic with the E₄R₆ bicyclo[1.1.0]butanes and heavier analogues, which has been central to the discussion of bond-stretch isomerism, the phenomenon where two or more isomers differ primarily in the length of one or more bonds.^24–32 In the case of bicyclo[1.1.0]butanes, the two isomers in question differ in the length of the E–E bond along the body of the butterfly (Fig. 2).³³ Schleyer and co-workers identified bond-stretch isomers of bicyclo[1.1.0]tetra-silane, Si₄H₆, that differ by almost 0.5 Å at the multi-configurational SCF level.³⁴ Calculations by Koch and co-workers using density functional theory (B3LYP functional) have explored both the impact of different substituents, R, and the switch from Si to Ge, on the potential energy surface.^35,36 The heavier Ge₄R₆ analogues appear to favour the isomer with a long (3b)Ge–(3b)Ge bond to the extent that the short isomer does not even constitute a stable minimum on the potential energy surface. The equilibrium between the tetragonal and orthorhombic phases of Ba₃Ge₄ is clearly more complex in the sense that the cleavage of the intra-cluster Ge–Ge bond is intimately coupled to the polymerisation of the chain; however, nevertheless, the greater tendency to favour the ‘long’ isomer for Ge vs. Si in a molecular context correlates with the apparently greater stability of the orthorhombic phase in Ba₃Ge₄vs. Ba₃Si₄. The relative stabilities of the two phases are, of course, determined by the free energy rather than the internal energy or enthalpy, and so the change in entropy is an important consideration. In a molecular context, we might anticipate that polymerisation results in a loss of entropy, but in a solid state context, there is no translational entropy loss, in which case entropy changes are a more complex function of the phonon modes. With this in mind, we present here an analysis of the thermodynamics of the orthorhombic, tetragonal and p-tetragonal phases of Ba₃Si₄ and Ba₃Ge₄, computed using density functional theory in conjunction with the quasi-harmonic approximation.

Fig. 2 Bond-stretch isomerism in E₄R₆ clusters.

Computational techniques

The calculations reported in this paper were performed using plane-wave pseudopotential density functional theory (DFT) with periodic boundary conditions (PBC) as implemented in the Vienna ab initio Software Package (VASP).^37–42 In the majority of cases, the exchange–correlation energy was modelled using the optB86b-vdW functional,^43,44 but we have also explored the impact on the lattice parameters of alternative formulations including PBE,⁴⁵ SCAN,⁴⁶ and a combination of r²SCAN⁴⁷ and the revised Vydrov–van Voorhis (rVV10) functional,⁴⁸ r²SCAN + rVV10.⁴⁹ The valence electron configurations are 3s²3p² for Si, 3d¹⁰4s²4p² for Ge and 5s²5p⁶6s² for Ba, with the core electrons treated using PAW pseudopotentials. The plane-wave cut-off was set to 400 eV, and the Brillouin zone was sampled on a 6 × 6 × 4 Γ-centred grid. The structural relaxation was considered to converge when the Hellmann–Feynman force decreased below 10⁻⁴ eV Å⁻¹, while the SCF convergence criterion was 10⁻⁸ eV. Wannierisation was performed with a set of occupied valence bands using the Wannier90 software package.⁵⁰ The minimum energy path between the orthorhombic and tetragonal phases was determined using the solid-state climbing-image nudged elastic band (NEB) approach as implemented in the VTST code^51–53 with 8 intermediate images between the two phases and a spring constant of 5 eV Å⁻² between images. The total force was minimised below 10⁻³ eV Å⁻¹ in these calculations. Harmonic phonon dispersion curves are calculated using the finite difference method implemented in Phonopy.^54,55 Force constants were computed with atomic displacements of 0.01 Å in a supercell described by the following transformation of the primitive vectors (Table 1):
k-point sampling was performed on a Γ-centred 4 × 4 × 4 grid. The phonon DOS curves and thermodynamic properties were then calculated by interpolation onto a 12 × 12 × 8 q-mesh applied to the primitive cell. Quasi-harmonic calculations were carried out by performing phonon calculations on optimised structures with up to 6% compression and 8% expansion of the cell volume relative to the equilibrium structures, or until imaginary phonons emerged, at which point the structure became dynamically unstable. The Helmholtz free energy, F(T,V), the sum of the electronic energy, U₀(V), and the phonon free energy, F_ph(T,V), for a given temperature is then fitted to a third-order Birch–Murnaghan equation of states:⁵⁶
where V₀ and B₀ are the reference volume and bulk modulus, respectively, and 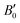is the derivative of the bulk modulus with respect to the pressure. The Gibbs free energy of a phase for a given temperature and pressure is then obtained by determining the volume that minimises the sum of the lattice internal energy U₀(V), the harmonic phonon Helmholtz free energy F_ph(T,V) and the PV term.
The range of temperature and pressures considered were 0–1200 K and 0–1.5 GPa for orthorhombic and tetragonal phases and 0–300 K and 0–1.5 GPa for the p-tetragonal phase: the lower limit for the latter reflects the emergence of dynamic instability at lower temperatures (see ESI,† Fig. S1 and S2). A full summary of the QHA calculations can be found in the ESI.†

Table 1 Summary of optimised energies and structural parameters for the orthorhombic, tetragonal and p-tetragonal phases of Ba₃Si₄ and Ba₃Ge₄. d1 is the intra-cluster (b3)Ge–(b3)Ge distance and d2 is the inter-cluster (b3)Ge–(b3)Ge distance. Distances are given in Å, volumes in ų per formula unit (f.u.) and energies in eV per f.u. 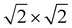Note that the a (= b) parameters for the tetragonal cells (the tetragonal and p-tetragonal phases) are expansions of the primitive unit cells. We were unable to converge on p-tetragonal-like structures for Ba₃Si₄ – all attempts were reverted instead to the more stable tetragonal phase

		a	b	c	V/f.u.	d1	d2	ΔE/f.u.
Ba3Ge4
X-ray	Tetragonal	12.193		12.032	223.6	2.71	3.63
	Orthorhombic	11.799	12.210	12.097	217.8	3.27	2.87
	p-Tetragonal	No data
optB86b-vdW	Tetragonal	12.093		12.064	220.5	2.65	3.63	0
	Orthorhombic	11.799	12.201	12.096	216.8	3.29	2.86	−0.027
	p-Tetragonal	11.892		12.129	214.4	3.16	3.03	−0.013
PBE	Tetragonal	12.250		12.215	229.1	2.64	3.72	0
	Orthorhombic	11.909	12.321	12.252	224.7	3.30	2.91	−0.003
	p-Tetragonal	12.019		12.295	222.0	3.14	3.10	0.027
SCAN	Tetragonal	12.161		12.123	224.1	2.61	3.69	0
	Orthorhombic	11.822	12.261	12.144	220.0	3.24	2.90	0.013
	p-Tetragonal	Not converged
r^2SCAN + rVV10	Tetragonal	12.175		12.071	223.6	2.57	3.75	0
	Orthorhombic	11.799	12.250	12.113	218.8	3.27	2.87	0.007
	p-Tetragonal	11.911		12.185	216.1	3.13	3.05	0.060
Ba3Si4
X-ray	Tetragonal	12.053		11.832	214.9	2.42	3.81
	Orthorhombic	No data
	p-Tetragonal	No data
optB86b-vdW	Tetragonal	12.020		11.857	214.2	2.44	3.77	0
	Orthorhombic	11.507	12.236	11.845	208.5	3.37	2.63	0.022
PBE	Tetragonal	12.135		11.959	220.2	2.43	3.83	0
	Orthorhombic	11.562	12.393	11.937	213.8	3.43	2.61	0.053
SCAN	Tetragonal	12.157		11.901	219.8	2.39	3.88	0
	Orthorhombic	11.553	12.317	11.977	213.0	3.36	2.54	0.091
r^2SCAN + rVV10	Tetragonal	12.122		11.889	218.4	2.40	3.85	0
	Orthorhombic	11.529	12.360	11.883	211.7	3.42	2.60	0.090

---

Results and discussion

Potential energy surfaces for Ba₃Si₄ and Ba₃Ge₄ at 0 K

Optimised structural parameters at 0 K for the three phases of interest in Ba₃Ge₄, the orthorhombic and tetragonal phases and the third, as-yet unknown, p-tetragonal phase where all of the Ge₄ units are polymerised in both orthogonal directions, are summarised in Table 1, where the available experimental data are also shown for comparison. With the optBP86b-vdW functional, the optimised lattice parameters are broadly consistent with the crystallographic data, most strikingly in the orthorhombic phase of Ba₃Ge₄, where the a, b and c lattice parameters are within 0.01 Å of the experiment. The experimentally observed ∼0.2 Å contraction of a in the orthorhombic phase is reproduced in all cases, as is the ∼2% decrease in the unit cell volume. This trend continues to the p-tetragonal phase, where a further 1.1% reduction in volume is associated with polymerisation of the second chain of Ge₄ units along the b-axis. The relative energies are also consistent with the experimental results in that the orthorhombic phase is predicted to be the most stable at 0 K, lying at 0.027 eV per f.u. below the tetragonal alternative, which is, as noted in the Introduction section, stable only above 630 K. The energy of the p-tetragonal phase, which has not been observed under any condition, is intermediate between orthorhombic and tetragonal, lying at 0.014 eV per f.u. above the former. These relative energies are, however, somewhat sensitive to the choice of functional, and all of PBE, SCAN and r²SCAN + rVV10 predict a relative stabilisation of the tetragonal phase relative to orthorhombic, to the extent that the two phases are almost iso-energetic with PBE and orthorhombic is predicted to be more stable for both SCAN and r²SCAN + rVV10. The p-tetragonal phase is not predicted to be the most stable for any of the chosen functionals. PBE predicts lattice parameters that are systematically ∼0.1 Å longer than optBP86b-vdW, while the SCAN-type functionals also overestimate the lattice parameters, but to a lesser degree. Very similar patterns are observed in the data for Ba₃Si₄, although in this case, the tetragonal phase is systematically stabilised by ∼0.06 eV per f.u. relative to orthorhombic, as a result of which the tetragonal phase is the most stable for all functionals tested in this work. The structural differences between the tetragonal and orthorhombic phases also follow the experimental trend, with polymerisation of the Si₄ chains along a causing a 2.5% decrease in the cell volume. All attempts to locate a local energy minimum for the p-tetragonal phase of Ba₃Si₄ relaxed instead of the experimentally characterised tetragonal alternative.

The potential energy surfaces connecting the tetragonal and orthorhombic phases of Ba₃Ge₄ and Ba₃Si₄, computed using the nudged elastic band method and the optBP86b-vdW functional, are shown in Fig. 3. For Ba₃Si₄, the transition state separates the tetragonal phase from its less stable orthorhombic counterpart by a barrier of ∼0.05 eV per f.u. The transition structure is confirmed to be a first-order saddle point by the presence of a single imaginary phonon mode at the Γ point, and has a geometry intermediate between the two phases. There is significant elongation of the intra-cluster bonds (2.88 Å vs. 2.44 Å in orthorhombic) and concomitant contraction of the inter-cluster bonds (3.18 Å vs. 3.77 Å in orthorhombic). The correspondence between the intra-cluster Si–Si bond length of 2.88 Å at the transition structure and the value of 2.86 Å reported by Koch et al. in the ‘long’ bond-stretch isomers in molecular Si₄R₆ is quite striking.³⁵ It appears, then, that the Si₄⁶⁻ units are indeed effectively isolated in Ba₃Si₄, and the cleavage of the intra-molecular Si–Si is almost complete at the transition state. For the Ba₃Ge₄ system (purple line in Fig. 3), the reaction is almost barrierless, with the transition structure being only 0.003 eV per f.u. above the tetragonal phase. Consistent with the exothermicity of the forward reaction, the transition structure shown in Fig. 3(b) is ‘early’, with a marginally elongated Ge–Ge bond along the body of the butterfly (2.76 Å vs. 2.65 Å in the tetragonal phase), and very marginally shortened intra-cluster distance of 3.49 Å vs. 3.63 Å in the tetragonal phase. Even for the Ba₃Si₄ case, the barrier to rearrangement is an order of magnitude smaller than those reported by Wang et al. for the orthorhombic–tetragonal phase transition in BaGe₂,¹⁶ the difference probably reflecting the relative weakness of the bonds in the Si₄⁶⁻ and Ge₄⁶⁻ tetrahedra, and also the fact that the phase transitions in Ba₃E₄ involve only the cleavage/formation of E–E bonds along a single axis rather than the complete collapse of the tetrahedral units into a 3-dimensional network. The evolution of the electronic structure across the potential energy surface has been discussed extensively by Nesper and co-workers,^22,23 and our analysis of the density of states is fully consistent with those reported previously. The making and breaking of Ge–Ge bonds can be tracked through the maximally localised Wannier functions (MLWFs) shown at the bottom of Fig. 3, which show the intra-cluster σ-bond in the tetragonal phase and the inter-cluster σ-bond in the orthorhombic phase. These MLWFs show delocalisation tails on the Ba²⁺ ions surrounding the cluster, consistent with Nesper and co-workers’ observation that the Ba 5d levels are substantially populated in Ba₃Si₄.²² An analysis of the Bader charges, shown in ESI,† Table S1, indicates that polymerisation induces no significant changes in the charges of the ions.

Fig. 3 Potential energy curve (optB86b-vdW) for the concerted phase transition from the tetragonal to the orthorhombic phase in Ba₃Ge₄ and Ba₃Si₄. Maximally localised Wannier functions corresponding to the intra- and inter-molecular bonds of the tetragonal and orthorhombic phases, respectively, are also shown.

Phonon modes and thermodynamic properties at a finite temperature

Given the rather delicate energetic balance between the orthorhombic and tetragonal phases of Ba₃Ge₄ in Table 1, we now consider the relative Gibbs free energies, which require computation of the vibrational entropy. To do this, we use the quasi-harmonic approximation (QHA)⁵⁷ as implemented in phonopy to allow for volume relaxation at a finite temperature. The relative free energies (computed with the optB86b-vdW functional) of the orthorhombic and tetragonal phases as a function of temperature are shown in green and magenta in Fig. 4(a), respectively, while the p-tetragonal phase is shown in cyan. All energies are reported relative to the tetragonal phase. Note that the values at 0 K correspond to U₀(V), the data points in Table 1, and the stability of the phases decreases in the order orthorhombic < p-tetragonal < tetragonal. The free energy of the p-tetragonal phase is truncated at 300 K because, beyond this temperature, the minimum energy point on the Helmholtz free energy surface corresponds to a structure with very low or imaginary harmonic frequencies that render it dynamically unstable. As the temperature is increased, the orthorhombic phase is destabilised relative to the tetragonal phase, leading, ultimately, to a crossover at ∼930 K, beyond which the tetragonal phase becomes thermodynamically stable. This value is 300 K, which is higher than the experimental value of ∼630 K, implying over-stabilisation of the low-temperature (α) phase. We can identify a number of possible reasons for the discrepancy between the experimental and computed transition temperatures, the most obvious being the strong functional dependence of the electronic energies, U₀(V), as shown in Table 1. The values of U₀(V) correspond to the intercepts in Fig. 4(a); therefore, a relative stabilisation of the β phase at 0 K, as observed in all functionals other than optB86b-vdW, would necessarily raise the intercepts and therefore decrease the computed transition temperature. Deringer et al. have identified the density functional as a potential source of error in the calculated transition temperature for the orthorhombic–cubic phase transition in GeSe.⁵⁸ Another potential source of error is the approximate treatment of anharmonicity offered by the QHA approach. Several previous studies using the QHA have noted the overestimation of thermal expansion coefficients and lattice constants at elevated temperatures.^59,60 In such circumstances, the harmonic phonon free energy, F_ph(T,V), often becomes markedly non-linear as a function of T due to the presence of soft phonons at expanded volumes, causing a divergence in the thermal expansion coefficients (see the ESI,† Fig. S1 and S2) and inaccuracies in the calculated thermodynamic parameters. The anharmonicity can, in principle, be explicitly included using computationally intensive methods such as self-consistent phonon theory (SCPH), which has been shown to improve the wurtzite to rocksalt phase boundary in GaN.^61–63 In another recent study of phase transitions in SnS and SnSe, Pallikara and Skelton noted a ∼350 K over-estimation of transition temperatures between Pnma and Cmcm phases, which could be corrected, albeit by only ∼20 K, by renormalising the selected imaginary modes by numerical solution of the Schrödinger equation on the corresponding 1-dimensional potential energy surface.⁶⁴ The dynamic instability of the p-tetragonal phase above 300 K prevents an exact determination of the crossover temperature with the tetragonal phase; however, by extrapolation of the low-volume region,⁵⁸ we can be confident that there is no point in the ambient-pressure phase diagram where it is the global minimum.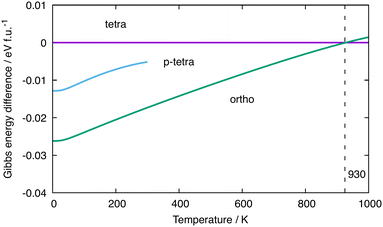

Fig. 4 Relative Gibbs free energies (optB86b-vdW) of different phases of Ba₃Ge₄. The reference value is set as that of the tetragonal phase.

The root cause of the temperature dependence in Fig. 4 is the much lower intrinsic entropy for the orthorhombic and p-tetragonal phases of Ba₃Ge₄ compared to the tetragonal phases, as summarised in Table 2, where the tetragonal phase is again taken as the reference value. The total change in harmonic phonon entropy, ΔS_total, for the transition from orthorhombic to tetragonal phases is −0.042 meV K⁻¹ f.u.⁻¹ (∼0.5 k_B, within the usual range of 0–5 k_B for phase transitions).⁶³ For the orthorhombic to p-tetragonal transition, it is even lower at −0.054 meV K⁻¹ f.u.⁻¹.

Table 2 Harmonic phonon contributions to entropy changes, ΔS, between the tetragonal β phase of Ba₃Ge₄ and the alternative orthorhombic (α) and p-tetragonal phases, calculated at 300 K. The total entropy difference is decomposed as ΔS_total = ΔS_stretch + ΔS_ion−ion, where ΔS_stretch and ΔS_ion−ion are the changes in entropy due to the phonon modes in the high-(>3.9 THz) and low-frequency (<3.9 THz) regions respectively. The values are given in meV K⁻¹ f.u.⁻¹

Ba3Ge4
	Orthorhombic - Tetragonal	p-Tetragonal - Tetragonal
ΔStotal	−0.042	−0.054
ΔSstretch	0.005	0.013
ΔSion−ion	−0.046	−0.067
	Ba3Si4
	Orthorhombic - Tetragonal
ΔStotal	−0.007
ΔSstretch	0.018
ΔSion−ion	−0.025

---

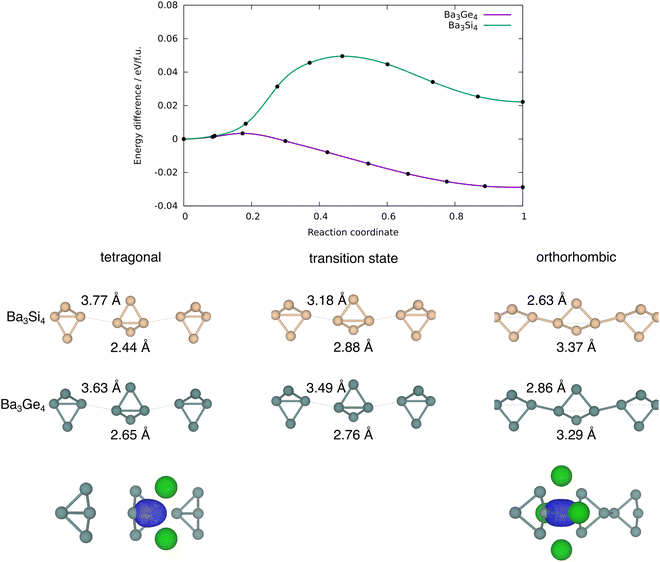
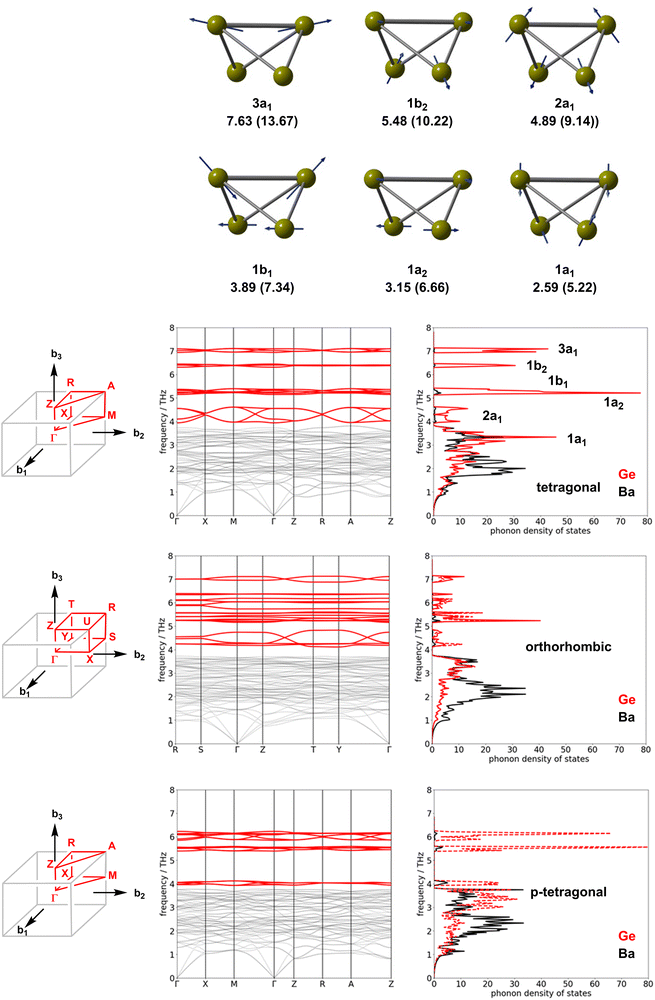
The trends in ΔS_total summarised in Table 2 are at least qualitatively consistent with the idea that an increasing degree of polymerisation of the Ge₄ chains should lead to a loss in entropy. However, as we noted in the Introduction section, there is no loss of translational entropy associated with the linking of the clusters in the solid state, as there would be in a molecular version of polymerisation, and the formation of inter-cluster Ge–Ge bonds in the orthorhombic phase is in any case offset, at least partially, by the cleavage of the intra-molecular bonds. The vibrational entropy, and therefore the free energy, is in fact a complex function of all the phonon modes of the lattice. Fig. 5 shows the phonon dispersion curves and phonon density of states for the orthorhombic, tetragonal and p-tetragonal phases of Ba₃Ge₄. The density of state plots are projected onto the Ge atoms (red) and the Ba²⁺ ions (grey). Each Ge₄⁶⁻ unit has 3N − 6 = 6 vibrational modes, of which 5 correspond to Ge–Ge stretches and the sixth to a wagging motion of the wingtips of the Ge₄ ‘butterfly’. These six vibrational modes are illustrated in the top panel of Fig. 5 for the isolated Ge₄⁶⁻ cluster: they range in frequency from 7.63 THz (a stretching mode of the (3b)Ge–(3b)Ge bond) to 2.59 THz (the wagging motion of the wing-tips noted above). The corresponding frequencies for the Si₄⁶⁻ cluster, shown in parentheses, are higher, reflecting the stronger Si–Si bonds and the lower mass of Si. The phonon modes of the Zintl phases can be separated into those involving the relative motion of the cations and anions in the lattice, found at low frequencies, and those related to the six internal vibrational modes of each Ge₄⁶⁻ unit. There are four Ge₄ units per unit cell; thus, each of the fundamental modes generates four linear combinations in the dispersion curve, giving 24 modes in total. The high-frequency regions of the phonon dispersion curves for both phases are dominated by the five linear combinations of the Ge–Ge stretches, 3a₁, 1b₂, 1b₁, 1a₂ and 2a₁, as shown in red. In the tetragonal phase, these internal modes appear around 7.0 THz, 6.3 THz, 5.2 THz, 5.0 THz and 4–5 THz, respectively, and the marked dispersion between 4 and 5 THz reflects the coupling between the 2a₁ modes where the largest amplitude of motion is aligned along the directions of the Ge₄ chains. The wagging mode lies in the lower frequency region, where it is strongly coupled to the motions of the Ba²⁺ ions. The impact of polymerisation on the formation of the orthorhombic phase is found primarily in the 4–5 THz region, where the dispersion of the 2a₁ fundamental mode is now seen only in two of the four linear combinations, corresponding to the vibrations of the unpolymerised Ge₄⁶⁻ clusters along the b-axis. The 2a₁ fundamentals of the polymerised chain along a instead form a narrow band around 4.2 THz. Similarly, the two linear combinations of the 3a₁ modes of the unpolymerised chain remain at 7.0 THz, but the corresponding two modes for the polymerised chain shift to around 6.0 THz. In the p-tetragonal phase, the dispersion collapses almost entirely as the second chain polymerises along the b direction, leading to very sharp peaks in the phonon density of state curve at 4.0 THz.

Fig. 5 Phonon dispersion curves and densities of states for the tetragonal, orthorhombic and p-tetragonal phases of Ba₃Ge₄. The density of phonon states is projected onto the unpolymerised (full red line) and polymerised (dashed red line) chains of the Ge₄ units. The vibrational modes of the isolated C_2v-symmetric Ge₄⁶⁻ anions, computed with density functional theory with a localised Slater-type basis (ADF package, PBE functional, high-dielectric COSMO solvent model (ε = 100) are used to approximate the confining effect of the cation lattice), are shown for comparison. Frequencies are given in THz and the values for Si₄⁶⁻ are shown in brackets.

The clean separation between the internal stretching modes of the Ge₄ unit and the vibrations of the ionic lattice at lower frequency allows us to assess the relative importance of these different modes to the overall entropy change. By integrating the partition function over the frequency range of 0–3.9 THz, we can compute the contribution of the low-frequency region containing the ionic motions, and the wagging mode of the Ge₄ butterfly (which we anticipate will be broadly unchanged by polymerisation) to the entropy (identified as ΔS_ion−ion in Table 2). The difference between this and the total ΔS obtained by integrating over the entire energy range can then be associated with the contribution of the Ge–Ge stretches, ΔS_stretch. The data in Table 2 show very clearly that the subtle changes in the high-frequency modes linked directly to polymerisation make negligible contributions to the total entropy difference, which is, instead, dominated by changes in the densely packed low-frequency region associated with the relative motions of the Ba²⁺ and Ge₄⁶⁻ ions. The most significant factor in determining the relative entropies appears, therefore, not to be the polymerisation of the Ge₄ units per se, but rather the accompanying ∼2% compression of the unit cell, which causes the modes to harden due to the enforced close approach of the ion cores.^65,66 To validate this assertion, we have recomputed the entropy and its components for the orthorhombic phase with the cell volume constrained at 220.5 ų f.u.⁻¹ (the optimised value for the tetragonal phase), and indeed we find that the difference in entropy almost vanishes (0.005 meV K⁻¹ f.u.⁻¹).

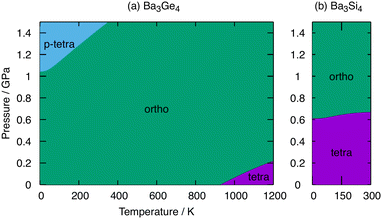
Pressure–temperature phase diagram

Fig. 6 shows phase diagrams for Ba₃Ge₄ and Ba₃Si₄ as functions of pressure and temperature. At ambient pressure, the orthorhombic phase of Ba₃Ge₄ is stable up to 930 K, above which the tetragonal phase emerges, precisely as shown in one dimension in Fig. 4. At elevated pressures, the contraction of the lattice parameters associated with polymerisation increasingly stabilises the orthorhombic and particularly the p-tetragonal phases because of the PV term in the Gibbs free energy. At 0 K, a transition from the orthorhombic to the p-tetragonal phases is predicted just above 1.0 GPa, increasing to ∼1.5 GPa at 375 K. The critical pressure of ∼1 GPa is accessible, and indeed modest, compared to the computed values of ∼4 GPa for the orthorhombic to tetragonal phase transition in BaGe₂,¹⁶ again reflecting the more substantial structural changes involved in that case as well as the intrinsically weaker Ge–Ge bonds in Ge₄⁶⁻vs. Ge₄⁴⁻. For Ba₃Si₄, in contrast, the tetragonal phase remains stable until ∼0.6 GPa, above which the orthorhombic phase forms. Our analysis of Ba₃Si₄ is restricted to temperatures of up to 300 K, above which the dynamic instability of the orthorhombic phase limits the application of the QHA. In the accessible regime, the gradient of the orthorhombic-tetragonal phase boundary is close to zero, which is a result of the smaller differences in ΔS_total in Table 2 for the Si cluster.

Fig. 6 The pressure–temperature phase diagrams of (a) Ba₃Ge₄ and (b) Ba₃Si₄ constructed from Gibbs free energy calculated within the QHA. Green, magenta and cyan indicate the regions of stability of the orthorhombic, tetragonal and p-tetragonal phases, respectively. The temperature range in Ba₃Si₄ is truncated at 300 K, beyond which the orthorhombic phase becomes dynamically unstable.

Summary and conclusions

In this paper, we have explored the electronic origins of bistability in the Zintl phase Ba₃Ge₄, where experiments show a transition at 630 K from a tetragonal phase to an orthorhombic one, where half of the Ge₄ tetrahedra are polymerised in a 1-dimensional chain. The energetic balance between the two phases is delicate, with the competing effects of making and breaking Ge–Ge bonds, along with changes in cation/anion interactions, combined to make the overall internal energy change less than 0.11 eV per f.u. The challenges in accurately capturing these competing effects are illustrated by the functional dependence of the relative energies of the orthorhombic and tetragonal phases. The optBP86b-vdW functional correctly predicts the orthorhombic form to be the most stable at 0 K, but others predict that either the phases are effectively iso-energetic or even the tetragonal phase is more stable. In contrast, analogous calculations for the corresponding silicon compound, Ba₃Si₄, show a strong preference for the (unpolymerised) tetragonal phase, which is indeed the only phase that has been observed experimentally. An analysis of the phonon modes for Ba₃Ge₄ confirms that the tetragonal phase, where the Ge₄ units are not linked, is entropically favoured over the other isomers, leading to a predicted transition temperature of 930 K compared to 630 K measured experimentally. The phonon spectrum can be separated into five Ge–Ge stretching modes at a relatively high frequency (above 3.9 THz) and modes involving the relative motion of the cations and anions at lower frequencies. The making and breaking of Ge–Ge bonds appear to have only a minor impact on the differences in entropy, the major contribution coming instead from changes in the frequencies of the anion/cation vibrations caused by the contraction of the lattice upon polymerisation.

Author contributions

YZ performed the calculations and contributed to the writing of the manuscript. JEM conceived the project and contributed to the writing of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202), this work used the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/T022213/1, EP/W032260/1 and EP/P020194/1).

Notes and references

1. J. Zhao, Q. Du, S. Zhou and V. Kumar, Chem. Rev., 2020, 120, 9021–9163.
2. B. Weinert and S. Dehnen, in Binary and Ternary Intermetalloid Clusters, ed. S. Dehnen, Springer International Publishing, Cham, 2017, pp. 99–134.
3. D. M. P. Mingos, in Electron Counting Rules for Gold Clusters Which Are Stereochemically Non-rigid and Exhibit Skeletal Isomerism, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2021, pp. 1–67.
4. F. Gam, J. Wei, S. Kahlal, J.-Y. Saillard and J.-F. Halet, in Electron Counting in Ligated High Nuclearity Late Transition Metal Clusters, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2021, pp. 69–102.
5. W. Klein, A. Schier and T. F. Fässler, in Molecules Meet Solids: From Wade-Mingos Clusters to Intermetalloid Clusters, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2021, pp. 149–195.
6. F. Pan, B. Weinert and S. Dehnen, in Binary Zintl Anions Involving Group 13–15 (Semi-)Metal Atoms, and the Relationship of Their Structures to Electron Count, ed. D. M. P. Mingos, Springer International Publishing, Cham, 2021, pp. 103–148.
7. S. M. Kauzlarich, Chem. Mater., 2023, 35, 7355–7362.
8. S. M. Kauzlarich, Z. Ju, E. Tseng and J. Lundervold, Chem. Soc. Rev., 2021, 50, 13236–13252.
9. S. Fang, J. Li, K. Zou, H. Shuai, L. Xu, W. Deng, G. Zou, H. Hou and X. Ji, Chem. Eng. J., 2022, 433, 133841.
10. R. Q. Cabrera, A. Salamat, O. I. Barkalov, O. Leynaud, P. Hutchins, D. Daisenberger, D. Machon, A. Sella, D. W. Lewis and P. F. McMillan, J. Solid State Chem., 2009, 182, 2535–2542.
11. C. Lorenz, S. Gärtner and N. Korber, Crystals, 2018, 8, 276.
12. J. Vaughey, G. J. Miller, S. Gravelle, E. Alejandro Leon-Escamilla and J. D. Corbett, J. Solid State Chem., 1997, 133, 501–507.
13. A. W. J. Evers and G. Oehlinger, Z. Naturforsch. B, 1980, 35, 397.
14. R. Castillo, A. I. Baranov, U. Burkhardt, Y. Grin and U. Schwarz, Z. Anorg. Allg. Chem., 2015, 641, 355–361.
15. U. Schwarz, R. Castillo, J. M. Hübner, A. Wosylus, Y. Prots, M. Bobnar and Y. Grin, Z. Naturforsch. B, 2020, 75, 209–216.
16. J.-T. Wang, C. Chen and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 054107.
17. M. Pani and A. Palenzona, J. Alloys Compd., 2008, 462, L9–L11.
18. R. Benhafid, A. Belgacem Bouzida, Y. Djaballah, A. Candan, A. İyigör and G. Uğur, J. Phase Equilib. Diffus., 2019, 40, 195–205.
19. J. Shi, W. Cui, J. A. Flores-Livas, A. San-Miguel, S. Botti and M. A. L. Marques, Phys. Chem. Chem. Phys., 2016, 18, 8108–8114.
20. B. Eisenmann, K. H. Janzon, H. Schäfer and A. Weiss, Z. Naturforsch. B, 1969, 24, 457–458.
21. U. Aydemir, A. Ormeci, H. Borrmann, B. Böhme, F. Zürcher, B. Uslu, T. Goebel, W. Schnelle, P. Simon, W. Carrillo-Cabrera, F. Haarmann, M. Baitinger, R. Nesper, H. G. von Schnering and Y. Grin, Z. Anorg. Allg. Chem., 2008, 634, 1651–1661.
22. F. Zürcher and R. Nesper, Angew. Chem., Int. Ed., 1998, 37, 3314–3318.
23. F. Zürcher, S. Leoni and R. Nesper, Z. Kristallogr. – Cryst. Mater., 2003, 218, 171–177.
24. W. D. Stohrer and R. Hoffmann, J. Am. Chem. Soc., 1972, 94, 1661–1668.
25. W. D. Stohrer and R. Hoffmann, J. Am. Chem. Soc., 1972, 94, 779–786.
26. V. C. Gibson and M. McPartlin, J. Chem. Soc., Dalton Trans., 1992, 947–956.
27. M.-M. Rohmer and M. Bénard, Chem. Soc. Rev., 2001, 30, 340–354.
28. J. E. McGrady, Angew. Chem., Int. Ed., 2000, 39, 3077–3079.
29. J. A. Labinger, C. R. Chim, 2002, 5, 235–244.
30. B. Hammann, C. Chen, U. Flörke, R. Hauptmann, E. Bill, S. Sinnecker and G. Henkel, Angew. Chem., Int. Ed., 2006, 45, 8245–8249.
31. J. M. Mayer, Angew. Chem., Int. Ed. Engl., 1992, 31, 286–287.
32. P. R. Remya and C. H. Suresh, J. Comput. Chem., 2017, 38, 1704–1711.
33. F. Breher, Coord. Chem. Rev., 2007, 251, 1007–1043.
34. P. V. R. Schleyer, A. F. Sax, J. Kalcher and R. Janoschek, Angew. Chem., Int. Ed. Engl., 1987, 26, 364–366.
35. R. Koch, T. Bruhn and M. Weidenbruch, J. Mol. Struct.: THEOCHEM, 2004, 680, 91–97.
36. R. Koch, T. Bruhn and M. Weidenbruch, J. Mol. Struct. THEOCHEM, 2005, 714, 109–115.
37. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
38. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
39. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
40. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
41. G. Román-Pérez and J. M. Soler, Phys. Rev. Lett., 2009, 103, 096102.
42. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
43. J. Klimeš, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131.
44. M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. J. Sun, A. Ruzsinszky and J. P. Perdew, Phys. Rev. Lett., 2015, 115, 036402.
47. J. W. Furness, A. D. Kaplan, J. Ning, J. P. Perdew and J. Sun, J. Phys. Chem. Lett., 2020, 11, 8208–8215.
48. R. Sabatini, T. Gorni and S. de Gironcoli, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 041108.
49. J. Ning, M. Kothakonda, J. W. Furness, A. D. Kaplan, S. Ehlert, J. G. Brandenburg, J. P. Perdew and J. Sun, Phys. Rev. B, 2022, 106, 075422.
50. G. Pizzi, V. Vitale, R. Arita, S. Blügel, F. Freimuth, G. Géranton, M. Gibertini, D. Gresch, C. Johnson, T. Koretsune, J. Ibañez-Azpiroz, H. Lee, J.-M. Lihm, D. Marchand, A. Marrazzo, Y. Mokrousov, J. I. Mustafa, Y. Nohara, Y. Nomura, L. Paulatto, S. Poncé, T. Ponweiser, J. Qiao, F. Thöle, S. S. Tsirkin, M. Wierzbowska, N. Marzari, D. Vanderbilt, I. Souza, A. A. Mostofi and J. R. Yates, J. Phys.: Condens. Matter, 2020, 32, 165902.
51. D. Sheppard, P. Xiao, W. Chemelewski, D. D. Johnson and G. Henkelman, J. Chem. Phys., 2012, 136, 074103.
52. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
53. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
54. A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys.: Condens. Matter, 2023, 35, 353001.
55. A. Togo, J. Phys. Soc. Jpn., 2023, 92, 012001.
56. F. Birch, Phys. Rev., 1947, 71, 809–824.
57. R. Stoffel, C. Wessel, M.-W. Lumey and R. Dronskowski, Angew. Chem., Int. Ed., 2010, 49, 5242–5266.
58. V. L. Deringer, R. P. Stoffel and R. Dronskowski, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 094303.
59. J. M. Skelton, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205203.
60. J. Tsuchiya, T. Tsuchiya and R. M. Wentzcovitch, J. Geophys. Res.: Solid Earth, 2005, 110, B02204.
61. T. Tadano and S. Tsuneyuki, J. Phys. Soc. Jpn., 2018, 87, 041015.
62. B. Sadovyi, M. Wierzbowska, S. Stelmakh, S. Boccato, S. Gierlotka, T. Irifune, S. Porowski and I. Grzegory, Phys. Rev. B, 2020, 102, 235109.
63. K. Tolborg, J. Klarbring, A. M. Ganose and A. Walsh, Digital Discovery, 2022, 1, 586–595.
64. I. Pallikara and J. M. Skelton, Phys. Chem. Chem. Phys., 2021, 23, 19219–19236.
65. J. M. Ziman, Electrons and Phonons: The Theory of Transport Phenomena in Solids, OUP, Oxford, 2001.
66. M. T. Agne, S. Anand and G. J. Snyder, Research, 2022, 1–11.

---

Footnote

† Electronic supplementary information (ESI) available: Phonon band structure and PDOS for the tetragonal, orthorhombic and p-tetragonal phases of Ba₃Si₄. See DOI: https://doi.org/10.1039/d3cp05713e

---