Ab initio investigations of circularly polarised luminescence in Samarium(III)-based complexes

Abstract

The present study aims to gain insight into the circularly polarised luminescence (CPL) of lanthanide complexes through the angle of one of their elements, namely Samarium. The simulation of luminescent properties of Samarium(III) complexes remains a challenge for computational chemistry, considering the multiconfigurational character of the electronic structure, the importance of the spin–orbit coupling and the fact that its emissive level is high in energy and preceded by numerous states of various multiplicity. Herein, a methodology based on CASSCF/RASSI-SO calculations is exposed and applied to simulate the CPL properties of two different Samarium(III) complexes, presenting either a rigid or a flexible architecture around the centre ion.

---

1 Introduction

Once a light emitter compound is chiral, the light that it emits is circularly polarised with different left- and right-handed polarisation intensities. This phenomenon is called circularly polarised luminescence (CPL) and is a feature of chiral compounds. Usually, it is described as the difference in intensity of the left- and right-handed polarised emitted lights.¹ The first reported measurements can be attributed to Samoilov for a crystal of sodium uranyl acetate in 1948² and to Emeis and Oosterhoff for a bicyclic ketone in 1967.³ Since, noteworthy improvements have been made in experimental measurements^4,5 and the research field on CPL has steadily progressed, bringing many applications in its wake. Among them, one can mention circularly polarised light-emitting diodes,⁶ probes of chiral environments⁷ and security inks.⁸

Lanthanide complexes emerged as a significant class of compounds in this field, by exhibiting stronger CPL signals than transition-metal complexes or organic compounds.⁹ To characterise CPL signals, the dissymmetry factor is usually used and corresponds to g_lum = 2(I_L − I_R)/(I_L + I_R) where I_L and I_R stand for the intensity of the left- and right-handed circular emission.^10,11 The highest value reported to date, g_lum = 1.38, is still ascribed to the ⁵D₀ → ⁷F₁ transition at room temperature (RT) and at 598 nm for the Cesium tetrakis(3-heptafluoro-butylryl-(+)-camphorato) Europium(III) complex.¹² This transition is particularly well-suited since it satisfies the magnetic-dipole selection rule.¹³ Nevertheless, two limiting mechanisms are steadily mentioned to explain a non-vanishing electric dipole transition moment for lanthanide complexes: static coupling and dynamic coupling.^14,15 The first implies a mixing between the 4f and the nd and ng orbitals to provide odd-parity interconfigurational character to overcome the parity rule. It is possible when the organisation of the first coordination sphere around the lanthanide ion is at the origin of the chirality.¹⁶ The second refers to the induction of electric dipole moments in the surrounding ligands by the electric quadrupole transition moment centred at the lanthanide ion. As such, ligand-centred electric dipole moments couple with one another and the component of the coupling can constructively interact with lanthanide-centred magnetic dipole transition moment to give rise to the CPL signal.¹⁷ Beforehand, it is also necessary to mention the multiconfigurational character of the electronic description of lanthanide complexes as well as the dominance of the spin–orbit (SO) coupling in comparison with the effect of the crystal field. All of these points can make the interpretation of CPL spectra tricky, and theoretical chemistry can help to provide insight into the observed photophysics. However, the theoretical description suffers also from the complexity of the involved phenomena and requires a high level of calculations.

Among the visible-emitting 4f-elements, the CPL of Europium(III)^12,18–23 and Terbium(III)^24–26 has been more widely studied than other lanthanide ions.⁹ The main reason is the fact that the luminescence of these two ions is less sensitive to vibrational deactivation by high-energy oscillators, and, consequently, presents the largest quantum yields. However, Samarium(III), with Dysprosium(III), are the next two ions usually recognised for emitting visible light in the 4f series.²⁷ Thus, it appeared relevant to dedicate a first theoretical analysis of the CPL of this element. The characteristic ⁴G_5/2 → ⁶H_J (with J = 5/2, 7/2, and 9/2) transitions of Samarium(III) all fall within the 18 100 − 15 200 cm⁻¹ region and the crystal-field components of these three ⁶H_J sextets lead to non-overlapping emission manifolds, allowing each level-to-level transitions to be separately characterised and analysed. According to Richardson's selection rules, transitions to J = 5/2 and 7/2 should have a stronger CPL signal than the transition to ⁶H_9/2 and all of them have a stronger dependence of the SO than of the CF.¹³ Among the available experimental studies,^{19,25,26,28–36} we retained our attention on two complexes.^37,38 The first complex, [Sm^III(cryptate)]³⁺ (Fig. 1a), is a Samarium(III) cryptate 8-coordinated by two bipyridine units and one tether derived from a N-N′-dioxide bipyridine unit modified by the attachment of (S,S)-2,3-butanediol.³⁷ It is charged +3 (neutralised by chloride counter-ions) and interestingly its structure is rigid and acts like a shielding for the Sm(III) ion from the surrounding molecules. The second complex, Sm^III(hfac)₃(ⁱPr-PyBox) (Fig. 1b), is 9-coordinated and made of three achiral hexafluoroacetylacetonate (hfac) units and a pyridine bisoxazoline (PyBox) which is turn on chiral by the addition of two iso-propyl groups, i.e. the (X)-2,6-bis(4-isopropyl-2-oxazolin-2-yl) pyridine with X = R, S (ⁱPrPyBox).³⁸ The complex is neutral and highly flexible. Both Sm(III)-based complexes are structurally different while both exhibited intense CPL signal at RT in solution, with a characteristic g_lum value of +0.13 at 560 nm and +0.18 at 595 nm for the first and second complex, respectively.

Fig. 1 Structures of [Sm^III(cryptate)]³⁺ (a) and Sm^III(hfac)₃(ⁱPr-PyBox) (b) obtained from DFT structural optimisation, computed at ZORA-PBE0/TZP. Colour code: sea-green, Sm; red, O; blue, N; grey, C; lightgreen, F; white, H.

We propose in this article to simulate the CPL of these two complexes. Previous theoretical studies on Eu(III) and Yb(III) let developing us a methodology to simulate the CD and CPL of lanthanoid complexes.^39–42 It implies Complete Active Space Self-Consistent Field (CASSCF) and Restricted Active Space SCF (RASSCF) calculations and homemade post-treatment to simulate the chiroptical properties.^43,44 A first focus will be made on the number of configurations required in the description of the electronic structure of the [Sm^III(cryptate)]³⁺ complex. Calculations for the mentioned analysis were done in gas phase and the influence of the solvent will be discussed shortly based on applied dielectric models. Next, physical interpretations of the recorded spectrum will be presented in the light of the calculations. Lastly, with the established results for the quite rigid [Sm^III(cryptate)]³⁺, a similar procedure will be applied to the Sm^III(hfac)₃(ⁱPr-PyBox) complex, in order to gain insight into its CPL signals as well.

2 Computational details

The two studied systems have been optimised using Density Functional Theory (DFT) through Amsterdam Density Functional software package (AMS version 2022.103).^45–47 The geometry of the complex [Sm^III(cryptate)]³⁺ has been built on the basis of previous DFT optimisations⁴⁸ but adapted for a tether derived from a (S,S)-2,3-butanediol. Following the nomenclature of this previous study, our guess geometry corresponds to the (R, R, R_a) conformation. DFT optimisations were performed with the zeroth order regular approximation (ZORA)^49,50 along with the hybrid functional PBE0^51,52 with 25% of exact exchange and the atomic basis set corresponding to the triple-ζ polarised Slater-type orbital (STO) all-electron basis set with one set of polarisation functions for all atoms (TZP).⁵³ Once the geometry of the [Sm^III(cryptate)]³⁺ complex was obtained in gas phase, it has been optimised in a solvent model of methanol. To do so, we used the COSMO model implemented in ADF i.e. a molecule-shaped cavity of a dielectric medium reproducing methanol.^54,55 For the Sm^III(hfac)₃(ⁱPr-PyBox) complex, the starting geometry for the DFT optimisation was the X-ray structure of the Terbium(III) version of the complex published by Yuasa et al. and for which we have replaced Tb(III) by Sm(III).¹⁹ The same level of DFT as for [Sm^III(cryptate)]³⁺ has been applied for the optimisation. Nevertheless, the dielectric constant of the dichloromethane was used instead of the methanol to mimic the effect of the solvent on the geometry of the complex.

For evaluating CPL properties on these geometries, state-average (SA) complete-active space (CAS)^56,57 and restricted-active space (RAS)^58,59 self-consistent field (SCF) approaches were used with the OpenMolcas software package (version 19.11).⁶⁰ The all electron atomic natural orbital relativistic with core correlation (ANO-RCC) basis sets have been employed with the following contraction for Sm [25s22p15d11f4g2h/8s7p4d3f2g1h], for O and N [14s9p4d3f2g/4s3p2d], for C [14s9p4d3f2g/3s2p1d], for F [14s9p4d3f2g/3s2p], and for H [8s4p3d1f/2s].^61–63 For a given spin multiplicity the calculations were first performed at the scalar relativistic (SR) level using the second-order Douglas–Kroll–Hess scalar relativistic Hamiltonian.^64–67 The SO coupling was then introduced by a state interaction (SI) within the basis of spin–orbit free states using the restricted active space state interaction (RASSI) approach⁶⁸ and based on SO coupling integrals calculated using the atomic mean-field integrals (AMFI) approximation.⁶⁹ The number of configuration state functions (CSFs) to take into account in the RASSI approach is studied in section 3.1 for the [Sm^III(cryptate)]³⁺ complex. The group of CSFs from the three different spin multiplicities (sextet, quartet and doublet for Sm(III)) were built on energetic consideration. SA-CAS(5,7)SCF/RASSI-SO calculations have been realised by including in the active space five electrons spanning the seven 4f orbitals of Sm(III) (represented in Fig. S1 in ESI†). These calculations were extended by RASSCF calculations through the inclusion of a π and a π* orbital (Fig. S2 in ESI†) of the tether (SA-RAS[7,1,1,1,7,1]SCF/RASSI-SO), the inclusion of two π and two π* orbitals (Fig. S3 in ESI†) of bipyridine units (SA-RAS[9,1,1,2,7,2]SCF/RASSI-SO) and by the inclusion of the five 5d orbitals of Sm(III) (Fig. S4 in ESI†) (SA-RAS[5,0,1,0,7,5]SCF/RASSI-SO). The notation used is RAS[n,l,m,i,j,k] where i, j and k correspond to the number of orbitals in the RAS1, RAS2 and RAS3 spaces, respectively, n is the number of active electrons, and l and m are the number of holes and particles created in the RAS1 and RAS3 spaces, respectively.^58,59 Based on the adapted number of CSFs retained for [Sm^III(cryptate)]³⁺ complex, similar SA-CAS(5,7)SCF/RASSI-SO have been done for the Sm^III(hfac)₃(ⁱPr-PyBox) complex.

These CASSCF and RASSCF calculations let us obtain the transition dipole moments required to calculate the rotatory strength proportional to the CPL signal.^43,44 For an isotropic sample, the rotatory strength between an initial state i and a final state f corresponds to the scalar product between the electric dipole transition moment μ_if and the magnetic dipole transition moment m_fi. With the electric dipole operator expressed like and the magnetic dipole operator like , the expression of the rotatory strength in the length representation is:⁷⁰

R_if = 〈i|[small mu, Greek, circumflex]|f〉〈f|m̂|i〉 (1)

Following eqn (1), rotatory strengths were calculated at 0 K. To mimic the influence of the temperature, a Boltzmann averaging of the calculated rotatory strengths was carried out using the calculated energies of the three Kramers doublets of the emissive spectroscopic level ⁴G_5/2 by solving the following equations:

Lastly, to provide a shape to the simulated spectra, rotatory strengths were scaled with the following Gaussian function:

using a full width at half maximum of 228 cm⁻¹ for the [Sm^III(cryptate)]³⁺ complex and 76 cm⁻¹ for the Sm^III(hfac)₃(ⁱPr-PyBox). This allows an easier comparison to the experimental spectra and the difference of full width at half maximum originates in the different resolutions of their experimental spectrum. For comparison between calculated and experimental spectra, where relevant, energetic shifts have been applied to align a selected transition and thus facilitate comparison between spectra.

3 Results & discussions

3.1 Setting up of the methodology for [Sm^III(cryptate)]³⁺ number of CSFs required from CASSCF calculations

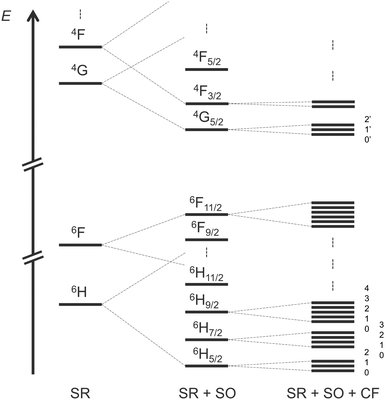
To simulate the CPL of a compound, you need at least to obtain the electronic description of the emissive states. For Sm(III) complexes that corresponds to the three m_J sublevels of ⁴G_5/2 at room temperature (RT) (see Scheme 1). To achieve the description of excited states there is no rule concerning the number of configuration state functions (CSFs) that you are supposed to consider in the RASSI procedure of multiconfigurational self-consistent field calculations. In the present section, we propose to analyse this issue on the rigid [Sm^III(cryptate)]³⁺ complex at SA-CAS(5,7)SCF/RASSI-SO level of theory first, including a comparison with experimental data.

Scheme 1 Schematic diagram of the energetic splittings of the lowest states of a 4f⁵ Sm(III) complex with successive adding of scalar relativistic (SR), spin–orbit (SO) and crystal-field (CF) interactions.

The electronic states of Sm(III) complexes take three spin values (5/2, 3/2, and 1/2) which require a CASSCF procedure for each of them, as detailed in the Computational Details. In the case of a CAS(5,7)SCF calculation 21 sextets, 224 quartets and 490 doublets can be described by CSFs. Based on energetic considerations three selections have been used in the RASSI approach to simulate the CPL of the complex (Table 1). The first one (RASSI 1) consists of 18 sextets, 48 quartets and no doublets. That could make sense because the target transitions involve only sextet and quartet Kramers doublets at first glance if one forgets SO coupling. Then, if one wants to consider more sextets and quartets for Sm(III), it appears important to consider doublets at least because they start to complete the electronic state diagram in higher energy. Thus, the compositions of 21, 108, 32 (RASSI 2) and 21, 163, 238 (RASSI 3) were also considered and compared to a last RASSI approach made by all possible CSFs (RASSI 4). A spectral comparison, energetically shifted to be compared with the experimental spectrum, is drawn in Fig. 2 (row spectra are available in ESI† Fig. S5). It appears clearly that doublets need to be added to establish electronic states at SR-SO-CF level. The results from RASSI 2 are closer to the ones of RASSI 1, and both are different from RASSI 3 and 4 as well as the experimental spectrum. Nevertheless, all CSFs did not need to be computed to achieve a reliable description of the electronic structure able to simulate the targeted optical properties of the Samarium(III) complex. Indeed, the simulated CPL of RASSI 3 is similar to that of RASSI 4 and good agreement with experimental data is achieved at least for wavelengths under 590 nm.

Table 1 Number of CSFs considered by spin multiplicity in the various CAS(5,7)SCF calculations performed on [Sm^III(cryptate)]³⁺

Spin multiplicity	RASSI 1	RASSI 2	RASSI 3	RASSI 4
6	18	21	21	21
4	48	108	163	224
2	0	32	238	490

---

Fig. 2 Simulated CPL spectra at SA-CAS(5,7)SCF/RASSI-SO level of [Sm^III(cryptate)]³⁺ with various numbers of CSFs for each spin multiplicity: RASSI 1 (orange) RASSI 2 (red) RASSI 3 (blue) RASSI 4 (green). Calculated rotatory strengths indicated as “stick” spectra. Experimental spectrum in black dotted lines. Energetic shifts of 3775 cm⁻¹ for orange and red and of 4613 cm⁻¹ for blue and green spectra have been applied.

CASSCF vs. RASSCF calculations. While it is possible to compute all CSFs at the CAS(5,7)SCF level regardless of their spin multiplicity, this tends to quickly exceed the computational resources for RASSCF calculations. Three different RASSCF calculations were done (see Computational details) and following a similar procedure to the CASSCF one, several selections of multiplets led to different RASSI calculations for each RASSCF. For all these calculations, the simulated CPL spectra are presented in Fig. S6–S8 (ESI†) and the different numbers of CSFs kept in the calculations are specified in the caption. The selected numbers of CSFs were close to these presented in Table 1 and similar evolutions of the CPL spectra have been found regarding the numbers of CSFs. Thereby, to simulate the CPL of this Sm(III) system, at least one hundred doublets and the according number of sextets and quartets seem required to achieve a correct description. Indeed, spectra in orange and red in Fig. S6–S8 (ESI†) with either no or 32 doublets behave similarly as RASSI 1 and 2 in Fig. 2 while they highly differ with calculations including more doublets.

It is interesting that all performed CASSCF and RASSCF calculations do not lead to major changes in the results, once an adequate inclusion of CSFs has been made and individualised energetic shift applied (Fig. 3). If all simulated CPL spectra are normalised to 1 for the transition at 554 nm (Fig. S9 in ESI†) it is even clearer that no distinctions can be discussed. The motivation for these RASSCF calculations attempted to consider the static¹⁶ (RAS[5,0,1,0,7,5]SCF) or dynamic¹⁷ (RAS[7,1,1,1,7,1]SCF and RAS[9,1,1,2,7,2]SCF) coupling mechanism usually employed to explain the process giving rise to CPL activity.^13,15 Thereby, notwithstanding that our methodology was already able to distinguish both mechanisms for Europium(III) and Ytterbium(III)-based complex (underlining the added value of RASSCF calculations instead of CASSCF),^43,44 any mechanisms seem to predominate the process for the CPL of [Sm^III(cryptate)]³⁺. This is in accordance with the Richardson's rules since the rotatory strength of the studied transition of Sm(III) depends squared to the SO Hamiltonian and only linearly on the CF Hamiltonian affecting the static and dynamic coupling mechanism.¹³

Fig. 3 Simulated CPL spectra at SA-RAS[5,0,1,0,7,5]SCF/RASSI-SO (blue), SA-RAS[7,1,1,1,7,1]SCF/RASSI-SO (red), SA-RAS[9,1,1,2,7,2]SCF/RASSI-SO (green) and SA-CAS(5,7)SCF/RASSI-SO (yellow) level of theory. Calculated rotatory strengths indicated as “stick” spectra. Experimental spectrum in black dotted lines. Energetic shifts of 4587 cm⁻¹ for blue, of 2793 cm⁻¹ for red, of 3533 cm⁻¹ for green and of 3726 cm⁻¹ for yellow spectrum have been applied. Experimental spectrum in black dotted lines.

Influence of the solvent. The influence of the solvent has been only considered by optimising the complex at the DFT level with the COSMO model (see Computational Details). As expected, the structural modifications are tiny. In methanol, the two bipyridine units are slightly further from each other by an increase of 2.3° between two hydrogen atoms regarding the Sm(III) centre. For the tether the atoms of oxygen are slightly further from each other while the methyl group are slightly closer (see Table S1 and Fig. S10 in ESI†). Consequently, the variations in the CPL spectra due to the solvent are negligible. Spectra are shown in Fig. 4 and the simulation done on the optimised structure in methanol is red-shifted by 83 cm⁻¹ in average (e.g. 74 cm⁻¹ for the 0′ → 0 transition; Table S2 in ESI†). The reader should notice that the methodology is not yet able to provide quantitative rotatory strength values and in that sense, the two spectra are relatively similar in terms of intensity (Table S2 in ESI†). Therefore, the inclusion of a dielectric solvent model in the structural optimisation has minor effects and does not change the qualitative physical interpretations that can be made for this complex.

Fig. 4 Simulated CPL spectra at SA-CAS(5,7)SCF/RASSI-SO level of [Sm^III(cryptate)]³⁺ with a number of CSFs corresponding to RASSI 3 on the optimised structure in gas phase (blue) and in a solvent model of methanol (red). According optimised based-structures are superimposed in the right-down corner. Calculated rotatory strengths indicated as “stick” spectra. No energetic shift has been applied.

3.2 Physical interpretation of the CPL measurement of [Sm^III(cryptate)]³⁺

Based on the previous section, CASSCF and RASSCF calculations computed with the geometry optimised in gas phase can be used to interpret the CPL of the studied complex. For the following analysis, calculations based on SA-RAS[7,1,1,1,7,1]SCF/RASSI-SO including π and π* orbitals have been retained. This choice is made because it has the medium description among the obtained variations between all performed CASSCF and RASSCF calculations (Fig. 3). Indeed, its rotatory strengths are relatively higher such as the one of RAS[7,0,1,0,7,5]SCF but the simulated ⁴G_5/2 → ⁶H_7/2 transition is slightly more in accordance with CAS(5,7)SCF and RAS[7,1,1,2,7,2]SCF calculations.

Since the experimental measurements were done at RT, the observed CPL comes from the various multiplets of the emissive ⁴G_5/2 level. This level is composed of three Kramers doublets refer as 0′, 1′ and 2′ hereinafter (Scheme 1). The energetic difference between 0′–1′ and 0′–2′ is 82 and 275 cm⁻¹ respectively (see Table S3 in ESI†). Accordingly, the Boltzmann population of these three states is 51, 35 and 14% for 0′, 1′ and 2′ respectively at RT (see Table S4 in ESI†). Thus, it appears essential to sum the contribution of all the multiplets of ⁴G_5/2 to describe the CPL of the complex at RT (results in Table S5 in ESI†). The CPL spectra from the three states are obtained independently at 0K (spectra Fig. 5b) and can be combined for a given temperature using the Boltzmann population as weight for the rotatory strength (eqn (2)). Thus, the evolution of the CPL spectrum with the temperature can be evaluated and is presented in Fig. 4a. The blue-shift of 2793 cm⁻¹ originates from the difference between the calculated and the experimental energetic level of the emissive ⁴G_5/2 level, expected around 18 100 cm⁻¹ but calculated around 21 000 cm⁻¹ (see Table S3 in ESI†).

Fig. 5 Simulated CPL spectra as a function of the temperature (a) and with different absolute contributions of the Kramers doublets from the emissive level ⁴G_5/2 (b). Calculations done at SARAS[7,1,1,1,7,1]SCF/RASSI-SO level for [Sm^III(cryptate)]³⁺ complex with the 7 4f orbitals of Sm in RAS2 and 1 π and 1 π* orbital of dioxide bipyridine in RAS1 and RAS3, respectively. Calculated rotatory strengths indicated as “stick” spectrum. Energetic shift of 2793 cm⁻¹ have been applied. Experimental spectrum in black dotted lines.

The comparison with the experimental CPL is especially satisfactory for the ⁴G_5/2 → ⁶H_5/2 transition. The simulation clearly accesses the negative band at 545 nm to the emission of the highest Kramers doublet 2', emerging at high temperature (≥120 K). The positive CPL band at 560 nm is ascribed to the two other Kramers doublets 0′ and 1′. Interestingly, the shoulder at 577 nm emerges with the temperature and belongs to the ⁴G_5/2 → ⁶H_7/2 electronic transition. Again, it is explained by the emission from 2′, suggesting that the energy gap ΔE_2′−0′ is correctly estimated and used in the Boltzmann statistics rationalising the spectrum at RT. However, the main shape of this transition, i.e. a negative band followed by a positive band at higher wavelengths, is not correctly reproduced from 590 to 610 nm. This may be due to the high accuracy required to calculate five transitions in a short energetic range of 200 cm⁻¹. Both the energetic positions and the rotatory strengths must be correctly estimated. Nevertheless, a deeper analysis of Fig. 5b might suggest an erroneous description of the higher state number 3 of ⁶H_7/2. Indeed, the transitions to this state give rise to high values of rotatory strength, but in the issued range of the spectrum the transitions 0′ and 1′ → 3 do not match the observed sign. Thus, a modification in the transition moments implying the state 3 of ⁶H_7/2 could improve the description. Notwithstanding, among all the various CASSCF and RASSCF calculations done, such a modification was not achieved. Lastly, the experimental ⁴G_5/2 → ⁶H_9/2 transition is less resolved than the two other level-to-level transitions. This precludes a fine comparison with the simulations, but transitions with low intensities in agreement with the experiment have been nevertheless calculated. These transitions are also at the right wavelengths when the energetic position of the emissive states is corrected, suggesting that the spectroscopic level ⁶H_9/2 is overall well positioned in terms of energy with respect to ⁶H_5/2.

Thus, even if the experimental agreement was not perfectly achieved due to the precision required (as illustrated by the ⁴G_5/2 → ⁶H_7/2 level-to-level transition), that encouraged us to apply our methodology to another Samarium(III) complex.

3.3 Study of Sm^III(hfac)₃(ⁱPr-PyBox)

We applied the methodology on the more flexible nine-coordinated Sm^III(hfac)₃(ⁱPr-PyBox) complex. For this compound, the experimental spectrum has been recorded in dichloromethane at RT and presents narrower bands than the CPL spectrum of [Sm^III(cryptate)]³⁺.³⁸ Calculations were done at SA-CAS(5,7)SCF/RASSI-SO level of theory, based on a geometry optimised in dichloromethane (Computational details). No further RASSCF calculations were attempted regarding the results already obtained and the weak difference observed for [Sm^III(cryptate)]³⁺. The energetic splitting (available in ESI† Table S6) is too high in energy to agree with the experimental narrow band (Fig. 6a). Nevertheless, qualitative results were already achieved using Boltzmann population (Tables S7 and S8 in ESI†) and meaningful physical interpretation can be done by analysing Fig. 6b. For the ⁴G_5/2 → ⁶H_5/2 measured transition, the two positive bands and the negative one at 572 nm can be attributed to the emission of 0′ Kramers doublet of ⁴G_5/2, while the negative bands at 550 and 560 nm are due simultaneously to the 1′ and 2′ Kramers doublets. For the ⁴G_5/2 → ⁶H_7/2 transition, the two first bands are also due to these two higher Kramers doublets of ⁴G_5/2, with a contribution from only 2′ for the positive band at 582 nm, and from both at 590 nm. These two bands should disappear by decreasing the temperature of the sample during the spectral acquisition. Then, the three dominating bands of the CPL spectrum seem to benefit from the emission of all states composing the ⁴G_5/2 level. This cumulative effect explains the origin of the high CPL signal and g_lum values of this compound. That implies that the high g_lum value at 595 nm cannot be attributed to an isolated m_J state and underlines the temperature dependence of such characterisation given to CPL measurements. Lastly, as far as it is possible to be confident in the analysis of ⁴G_5/2 → ⁶H_9/2 transition, the main constitutive negative band seems to originate from transitions of the 0′ Kramers doublets.

Fig. 6 Simulated CPL spectra as a function of the temperature (a) and with different absolute contributions of the Kramers doublets from the emissive level ⁴G_5/2 (b). Calculations done at SA-CAS(5,7)SCF/RASSISO level for Sm^III(hfac)₃(ⁱPr-PyBox) complex. Calculated rotatory strengths indicated as “stick” spectrum. Energetic shift of 3975 cm⁻¹ has been applied. Experimental spectrum in black dotted lines.

4 Conclusions

The first simulations of CPL centred on the f–f transitions of Samarium(III) complexes have been done. This achievement is thanks to the extension of an already established procedure for Eu(III) and Yb(III) based on CASSCF and RASSCF calculations. The present study established that a minimal requirement of a hundred CSFs with the spin multiplicity two is required to correctly describe the states involved in the CPL phenomenon of Sm(III) complexes, although they do not seem to be formally implied in the ⁴G_5/2 → ⁶H_J transitions (with J = 5/2, 7/2 and 9/2). For [Sm^III(cryptate)]³⁺ complex, it reveals also that static or dynamic coupling mechanisms cannot be distinguished. Indeed, CAS(5,7)SCF calculations provided already good qualitative CPL simulation for both rigid and flexible complexes and both eight- and nine-coordinated compounds. Detailed attributions of the experimental bands have been made from m_J sublevels for both [Sm^III(cryptate)]³⁺ and Sm^III(hfac)₃(ⁱPr-PyBox) complexes. Lastly, this study underlines the key influence of temperature in the description of CPL signals, recently highlighted with collaborators for an Yb(III) complex.⁷¹ Nevertheless, the calculated electronic structure could certainly be improved to correct some discrepancies. Preliminary structural optimisation using conducting model of solvent reveals that the effect of the solvent on the CD and CPL properties is negligible at this level of calculations. One of the next step in the methodology to improve the description of the system is the use of an explicit modelling of solvent molecules with the analysis of different geometries by means of molecular dynamics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Dr Grégoire David for relevant discussions, the French National Research Agency (ANR) through SMMCPL (ANR-19-CE29-0012-02) and Rennes Métropole for financial supports as well as the French GENCI/IDRIS-CINES centers for high-performance computing resources.

References

1. L. D. Barron, Molecular Light Scattering and Optical Activity, Cambridge University Press, Cambridge, 2nd edn, 2004.
2. B. N. Samoilov, J. Exp. Theor. Phys., 1948, 18, 1030–1040.
3. C. Emeis and L. Oosterhoff, Chem. Phys. Lett., 1967, 1, 129–132.
4. B. Baguenard, A. Bensalah-Ledoux, L. Guy, F. Riobé, O. Maury and S. Guy, Nat. Commun., 2023, 14, 1065–1076.
5. W. R. Kitzmann, J. Freudenthal, A. P. M. Reponen, Z. A. VanOrman and S. Feldmann, Adv. Mater., 2023, 2302279.
6. D.-W. Zhang, M. Li and C.-F. Chen, Chem. Soc. Rev., 2020, 49, 1331–1343.
7. R. Carr, N. H. Evans and D. Parker, Chem. Soc. Rev., 2012, 41, 7673–7686.
8. L. E. MacKenzie and R. Pal, Nat. Rev. Chem., 2021, 5, 109–124.
9. L. Arrico, L. Di Bari and F. Zinna, Chem. – Eur. J., 2021, 27, 2920–2934.
10. W. Kuhn, Trans. Faraday Soc., 1930, 26, 293–308.
11. H. Tanaka, Y. Inoue and T. Mori, ChemPhotoChem, 2018, 2, 386–402.
12. J. L. Lunkley, D. Shirotani, K. Yamanari, S. Kaizaki and G. Muller, J. Am. Chem. Soc., 2008, 130, 13814–13815.
13. F. S. Richardson, Inorg. Chem., 1980, 19, 2806–2812.
14. F. S. Richardson and T. R. Faulkner, J. Chem. Phys., 1982, 76, 1595–1606.
15. F. Zinna and L. Di Bari, Chirality, 2015, 27, 1–13.
16. B. R. Judd, Phys. Rev., 1962, 127, 750–761.
17. S. F. Mason, R. D. Peacock and B. Stewart, Mol. Phys., 1975, 30, 1829–1841.
18. M. Seitz, E. G. Moore, A. J. Ingram, G. Muller and K. N. Raymond, J. Am. Chem. Soc., 2007, 129, 15468–15470.
19. J. Yuasa, T. Ohno, K. Miyata, H. Tsumatori, Y. Hasegawa and T. Kawai, J. Am. Chem. Soc., 2011, 133, 9892–9902.
20. F. Zinna, U. Giovanella and L. Di Bari, Adv. Mater., 2015, 27, 1791–1795.
21. Y. Zhou, H. Li, T. Zhu, T. Gao and P. Yan, J. Am. Chem. Soc., 2019, 141, 19634–19643.
22. Y. B. Tan, Y. Okayasu, S. Katao, Y. Nishikawa, F. Asanoma, M. Yamada, J. Yuasa and T. Kawai, J. Am. Chem. Soc., 2020, 142, 17653–17661.
23. P. Stachelek, L. MacKenzie, D. Parker and R. Pal, Nat. Commun., 2022, 13, 553.
24. S. Wada, Y. Kitagawa, T. Nakanishi, K. Fushimi, Y. Morisaki, K. Fujita, K. Konishi, K. Tanaka, Y. Chujo and Y. Hasegawa, NPG Asia Mater., 2016, 8, e251–e251.
25. S. Petoud, G. Muller, E. G. Moore, J. Xu, J. Sokolnicki, J. P. Riehl, U. N. Le, S. M. Cohen and K. N. Raymond, J. Am. Chem. Soc., 2007, 129, 77–83.
26. B.-A. N. Willis, D. Schnable, N. D. Schley and G. Ung, J. Am. Chem. Soc., 2022, 144, 22421–22425.
27. J.-C. G. Bünzli, Coord. Chem. Rev., 2015, 293–294, 19–47.
28. R. C. Carter, C. E. Miller, R. A. Palmer, P. S. May, D. H. Metcalf and F. S. Richardson, Chem. Phys. Lett., 1986, 131, 37–43.
29. J. L. Lunkley, D. Shirotani, K. Yamanari, S. Kaizaki and G. Muller, Inorg. Chem., 2011, 50, 12724–12732.
30. T. Güden-Silber, C. Doffek, C. Platas-Iglesias and M. Seitz, Dalton Trans., 2014, 43, 4238–4241.
31. C. R. Wright, L. VandenElzen and T. A. Hopkins, J. Phys. Chem. B, 2018, 122, 8730–8737.
32. D. E. Barry, J. A. Kitchen, L. Mercs, R. D. Peacock, M. Albrecht and T. Gunnlaugsson, Dalton Trans., 2019, 48, 11317–11325.
33. D. Cotter, S. Dodder, V. J. Klimkowsk and T. A. Hopkins, Chirality, 2019, 31, 301–311.
34. K. M. Ayers, N. D. Schley and G. Ung, Inorg. Chem., 2020, 59, 7657–7665.
35. M. Deng, N. D. Schley and G. Ung, Chem. Commun., 2020, 56, 14813–14816.
36. L. Arrico, C. De Rosa, L. Di Bari, A. Melchior and F. Piccinelli, Inorg. Chem., 2020, 9, 5050–5062.
37. E. Kreidt, L. Arrico, F. Zinna, L. Di Bari and M. Seitz, Chem. – Eur. J., 2018, 24, 13556–13564.
38. M. Górecki, L. Carpita, L. Arrico, F. Zinna and L. Di Bari, Dalton Trans., 2018, 47, 7166–7177.
39. A. Abhervé, M. Mastropasqua Talamo, N. Vanthuyne, F. Zinna, L. Di Bari, M. Grasser, B. Le Guennic and N. Avarvari, Eur. J. Inorg. Chem., 2022, e202200010.
40. F. Gendron, S. Di Pietro, L. A. Galán, F. Riobé, V. Placide, L. Guy, F. Zinna, L. Di Bari, A. Bensalah-Ledoux, Y. Guyot, G. Pilet, F. Pointillart, B. Baguenard, S. Guy, O. Cador, O. Maury and B. Le Guennic, Inorg. Chem. Front., 2021, 8, 914–926.
41. M. Atzori, K. Dhbaibi, H. Douib, M. Grasser, V. Dorcet, I. Breslavetz, K. Paillot, O. Cador, G. L. J. A. Rikken, B. Le Guennic, J. Crassous, F. Pointillart and C. Train, J. Am. Chem. Soc., 2021, 143, 2671–2675.
42. K. Dhbaibi, M. Grasser, H. Douib, V. Dorcet, O. Cador, N. Vanthuyne, F. Riobé, O. Maury, S. Guy, A. Bensalah-Ledoux, B. Baguenard, G. L. J. A. Rikken, C. Train, B. Le Guennic, M. Atzori, F. Pointillart and J. Crassous, Angew. Chem., Int. Ed., 2023, 62, e2022155.
43. F. Gendron, B. Moore II, O. Cador, F. Pointillart, J. Autschbach and B. Le Guennic, J. Chem. Theory Comput., 2019, 15, 4140–4155.
44. F. Gendron, M. Grasser and B. Le Guennic, Phys. Chem. Chem. Phys., 2022, 24, 5404–5410.
45. R. Rüger, M. Franchini, T. Trnka, A. Yakovlev, E. van Lenthe, P. Philipsen, T. van Vuren, B. Klumpers and T. Soini, AMS 2022.1, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2022, https://www.scm.com.
46. E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, O. Baseggio, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, C. Cappelli, L. Cavallo, C. Daul, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, F. Egidi, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, A. Förster, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. Goez, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, Z. Hu, C. R. Jacob, H. Jacobsen, L. Jensen, L. Joubert, J. W. Kaminski, G. van Kessel, C. König, F. Kootstra, A. Kovalenko, M. V. Krykunov, P. Lafiosca, E. van Lenthe, D. A. McCormack, M. Medves, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, H. Ramanantoanina, P. Ramos, W. Ravenek, M. Reimann, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, D. Schlüns, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solà, M. Stener, M. Swart, D. Swerhone, V. Tognetti, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF 2022.1, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2022, https://www.scm.com.
47. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
48. T. Güden-Silber, C. Doffek, C. Platas-Iglesias and M. Seitz, Dalton Trans., 2014, 43, 4238–4241.
49. E. v Lenthe, E. J. Baerends and J. G. Snijders, J. Phys. Chem., 1993, 99, 4597–4610.
50. E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Phys. Chem., 1999, 110, 8943–8953.
51. M. Ernzerhof and G. E. Scuseria, J. Chem. Phys., 1999, 110, 5029–5036.
52. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
53. E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
54. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
55. C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396–408.
56. B. O. Roos, Int. J. Quantum Chem., 1980, 18, 175–189.
57. B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173.
58. J. Olsen, B. O. Roos, P. Jørgensen and H. J. A. Jensen, J. Chem. Phys., 1988, 89, 2185–2192.
59. P. A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482.
60. I. Fdez. Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. González, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovačević, E. Källman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Sørensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesołowski, P.-O. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964.
61. P.-O. Widmark, P.-A. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291–306.
62. B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858.
63. B. O. Roos, R. Lindh, P.-A. Malmqvist, V. Veryazov and P.-O. Widmark, J. Phys. Chem. A, 2005, 109, 6575–6579.
64. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155.
65. B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 32, 756–763.
66. B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748.
67. A. Wolf, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 9215–9226.
68. P.-A. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240.
69. B. A. Heß, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371.
70. F. S. Richardson and J. P. Riehl, Chem. Rev., 1977, 77, 773–792.
71. A. Sickinger, M. Grasser, B. Baguenard, A. Bensalah-Ledoux, L. Guy, A. T. Bui, Y. Guyot, V. Dorcet, F. Pointillart, O. Cador, S. Guy, O. Maury, B. Le Guennic and F. Riobé, 2024, submitted.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05695c

---