Self-propelled motion controlled by ionic liquids

Abstract

We studied the self-propulsion of a camphor disk floating on a water surface using two types of ionic liquids (hexylammonium-trifluoroacetate (HHexam-TFA) and hexylethylenediaminium-trifluoroacetate (HHexen-TFA)). Bifurcation between continuous, oscillatory, and no motion was observed depending on the concentration of the ionic liquid. The bifurcation concentration between oscillatory and no motion for HHexam-TFA was lower than that for HHexen-TFA. The different bifurcation concentrations are discussed in relation to the surface tension and Fourier transform infrared spectra of the mixtures of camphor and ionic liquids. These results suggest that the interaction between the ionic liquid molecules at the air/water interface is weakened by the addition of camphor molecules and the features of self-propulsion vary due to the change in the driving force.

---

1. Introduction

Inanimate self-propelled objects have been investigated for transferring materials or themselves in small spaces.^1–4 There are two types of driving forces. One is the electrophoresis or bubbles produced from the surface of noble metals, such as a nanorod and a Janus particle.^5–13 The other one is the difference in the interfacial tension around the object.^14–20 Most inanimate self-propelled objects exhibit random or uni-directional motion depending on the initial internal or external conditions, and the direction and speed of motion are controlled by the external field, e.g., electro-magnetic field.^10,20–23 In contrast, animate self-propelled objects, such as bacteria, exhibit characteristic features of motion while responding to the environment.²⁴ Introduction of nonlinearity into the inanimate self-propelled system is one of the strategies to not only enhance the autonomy but also induce characteristic features of motion.^{18–20,25–28}

On the other hand, ionic liquids (ILs) composed of anionic and cationic parts have been investigated as solvents or electrolytes.^29,30 The nature of the melting point, viscosity, and electrical conductivity can be changed by the size of the polar group, length of the alkyl chain, and anionic species.³¹ E. Hua et al. previously reported the self-propulsion of a camphor disk or a camphor boat on water or surfactant aqueous solutions such as sodium dodecyl sulfate (SDS).^20,27 In this paper, we utilized ILs (hexylammonium-trifluoroacetate (HHexam-TFA) and hexylethylenediaminium-trifluoroacetate (HHexen-TFA)) to control the nature of self-propulsion from the viewpoint of the nature of the solvent and surface activity.^32,33 The chemical structures of the ILs are shown in Scheme 1. A camphor disk as a self-propelled object was placed on an aqueous solution of HHexam-TFA or HHexen-TFA. Mode bifurcation among continuous motion, oscillatory motion, and no motion was observed as a function of the IL concentration. The difference in the bifurcation concentration between HHexam-TFA and HHexen-TFA is discussed in relation to the surface tension, FTIR spectra, and numerical calculations based on density functional theory (DFT) with the B3LYP method and the 6-311G(d,p) basis set. These results suggest that the characteristic features of motion can be created based on the interaction between the source of self-propulsion and ionic liquid molecules.

Scheme 1 Chemical structures of the ionic liquids and camphor used in this study.

2. Experimental section

Protic ionic liquids HHexam-TFA (C₈H₁₆NO₂F₃) and HHexen-TFA (C₁₀H₂₁N₂O₂F₃) shown in Scheme 1 were synthesized based on the previous papers (see Fig. S1 and Table S1, ESI†).^32,33 The purity of the protic ILs was identified by ¹³C-NMR measurement with a Bruker 400 MHz spectrometer and CHN elemental analysis with a Vario EL instrument of Elementar Analysensysteme GmbH. (+)-Camphor (C₁₀H₁₆O, purity >96%, CAS 76-22-2) in Scheme 1 was purchased from Shanghai Macklin Biochemical Technology Co., Ltd (Shanghai, China). Two types of ILs were used, as shown in Scheme 1. A camphor disk (diameter: 6.0 mm, thickness: 1.0 mm, and mass: ∼30 mg) as a self-propelled object was manufactured using a pellet die set for Fourier transform infrared spectroscopy (inner diameter: 6 mm, depth: 15 mm). A glass Petri dish (inner diameter: 120 mm; depth: 15 mm) was used as the water chamber. The camphor disk was floated on the aqueous phase, including HHexam-TFA or HHexen-TFA (volume: 40 mL, depth: 4 mm). The water was purified using an ultrapure water system (Ningbo Dansboton Environmental Protection Technology Co., Ltd, Ningbo, China). At least, three examinations were performed under each experimental condition to confirm the reproducibility of the results. The motion of the camphor disk was monitored using a digital video camera (Olympus, STYLUS XZ-2, Tokyo, Japan; minimum time resolution: 1/30 s) in an air-conditioned room at 298 ± 2 K and then analyzed using an image-processing system (ImageJ, National Institutes of Health, MD, USA). The surface tension at the air/aqueous interface was measured using a Surface Tensiometer (BZY-2; Shanghai Heng Ping Instrument Factory, Shanghai, China). The FT-IR spectra of the ILs were measured using an FT-IR spectrophotometer (FTIR-650, Tianjin GANGDONG SCI. & TECH. Co., Ltd, Tianjin, China) at 298 ± 2 K. The spectral resolution was 1 cm⁻¹ and the cumulative number was 100. The intermolecular interaction energy of the IL-camphor was obtained by the Gaussian 09W software package³⁴ with DFT calculations at the B3LYP/6-311G(d,p) level. Justification of the DFT calculations is described in the ESI.†

3. Results

First, we observed the self-propulsion of a camphor disk on water at different concentrations of HHexam-TFA and HHexen-TFA, as shown in Fig. 1 and 2. The camphor disk exhibited continuous motion on water without IL (Fig. 1a and 2a). The oscillatory motion between rest and motion was observed with 3 and 7 mM HHexam-TFA and HHexen-TFA, respectively (Fig. 1b, c and 2b, c). The frequency of the oscillatory motion decreased with an increase in the concentrations of HHexam-TFA and HHexen-TFA (Fig. 1, 2 and Fig. S2a, ESI†). The locations of the oscillatory motion were random for 3 and 7 mM HHexam-TFA and 3 mM HHexen-TFA (Fig. 1b1, b2 and c1). In contrast, reciprocal oscillatory motion was observed in the presence of 7 mM HHexen-TFA (Fig. 1c2). The concentration dependencies of the maximum speed of motion for HHexam-TFA and HHexen-TFA are shown in Fig. S2b (ESI†). The Marangoni flow for the IL using a visualization particle was observed (Movie S1, ESI†). The nature of Marangoni flow was similar to that for SDS in the place of IL.

Fig. 1 Trajectories on the center position of a camphor disk on (a) water without additives, (b) HHexam-TFA, and (c) HHexen-TFA at t = 0–20 min (top view). The concentrations of the ILs were (1) 3 and (2) 7 mM. The time interval of the center position was 1/30 s. The movies of motion in (a), (b1), (b2), (c1), and (c2) are provided in ESI† as Movies S2, S3, S4, S5, and S6, respectively.

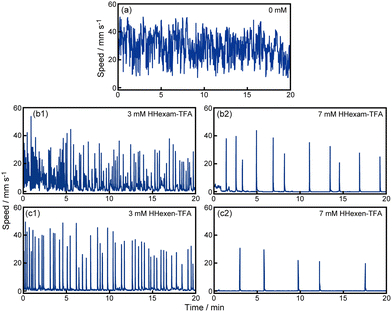Fig. 2 Time variation of the speed for camphor motion on (a) water without additives, (b) HHexam-TFA aqueous solution, and (c) HHexen-TFA aqueous solution. The concentrations of the ILs were (1) 3 and (2) 7 mM. The data of (a), (b1), (b2), (c1), and (c2) in Fig. 2 correspond to those in Fig. 1, respectively.

Fig. 3 shows a phase diagram of the self-propelled camphor disk as a function of the concentration of HHexam-TFA or HHexen-TFA in the aqueous phase, C_il. Here, we considered no motion when the speed of motion was less than 0.5 mm s⁻¹. Oscillatory motion was classified when the peak-to-peak amplitude of the speed of oscillation was larger than 10 mm s⁻¹ and the speed at the resting state was lower than 1 mm s⁻¹. The bifurcation concentration between the continuous and oscillatory motions of HHexam-TFA (1–2 mM) was the same as that of HHexen-TFA. In contrast, the bifurcation concentration between the oscillatory motion and no motion for HHexam-TFA (10–11 mM) was lower than that of HHexen-TFA (14–15 mM).

Fig. 3 Phase diagram on the features of camphor motion depending on the concentrations of HHexam-TFA (upper) and HHexen-TFA (lower), C_il. C, O, and N denote continuous, oscillatory, and no motion, respectively. The dotted points in the phase diagram denote the examined concentrations.

The measurement of the surface tension of the water phase is important for clarifying the reason for the different bifurcation diagrams between HHexam-TFA and HHexen-TFA. Because the driving force in the present system is determined by the difference in the surface tension around the camphor disk.²⁰Fig. 4 shows the surface tension of HHexam-TFA or HHexen-TFA aqueous solutions, γ, mixed with or without camphor, depending on C_il. Here, we selected 1 and 7 mM camphor as the concentration regions for continuous and oscillatory motion, respectively (see Fig. 3). γ decreased monotonically with an increase in C_il. With the addition of camphor, γ increased in comparison with that for HHexen-TFA and HHexam-TFA only (Fig. 4a). In addition, γ for HHexen-TFA was higher than that for HHexam-TFA at 3 mM < C_il < 15 mM. The lowest value of C_il at γ = 20 mN m⁻¹ shifted to a higher value with increasing camphor concentration. To clarify the effect of camphor molecules on the bifurcation concentration between oscillatory and no motion, the relationship between the lowest value of C_il and the camphor concentration at γ = 20 mN m⁻¹ was plotted, as shown in Fig. S3 (ESI†).

Fig. 4 Surface tension of HHexen-TFA (filled circles) and HHexam-TFA (empty circles) aqueous solutions, γ, mixed with (a) 0, (b) 1, and (c) 7 mM camphor depending on their concentrations, C_il. Error bars represent the standard deviation obtained from three examinations.

FT-IR was used to evaluate the interaction between the IL (HHexam-TFA or HHexen-TFA) and camphor at the functional group level. IR spectra of camphor, HHexam-TFA, HHexen-TFA, the mixture of HHexam-TFA and camphor, and that of HHexen-TFA and camphor over the wavenumber range of 500–4000 cm⁻¹ are shown in Fig. S4 (ESI†). Table 1 shows the IR absorbance peaks arising from the N–H stretching vibration mode for HHexam-TFA and HHexen-TFA, and their mixtures with camphor. Blue shifts in the N–H stretching vibration mode upon the addition of camphor were observed for both HHexam-TFA and HHexen-TFA, and the degree of blue shift for HHexam-TFA was larger than that for HHexen-TFA.

Table 1 Wavenumbers of the IR absorbance peak arising from the N–H stretching vibration mode for HHexam-TFA, HHexen-TFA, the mixture of HHexam-TFA and camphor, and that of HHexam-TFA. The molar ratio of IL and camphor was 1 : 1. The peak value was obtained from Fig. S4 (ESI)

Sample name	Wavenumber of N–H stretching, ṽ/cm^−1
HHexam-TFA	3046
HHexen-TFA	3362
HHexam-TFA + camphor	3444
HHexen-TFA + camphor	3466

---

To understand the blue shift of the N–H group in the IL after the addition of camphor, the interaction between the IL and camphor was calculated. The configurations of the two ILs and two ILs-one camphor molecule were individually optimized at the B3LYP/6-311G(d,p) level of the DFT calculation, as shown in Fig. S5 (ESI†). The intermolecular interaction energy (ΔE^BSSE₀ kJ mol⁻¹) of the configurations of the two HHexam-TFA molecules was lower than that of the two HHexen-TFA molecules, as shown in Table 2. ΔE^BSSE₀ increased when a camphor molecule was combined with the 2ILs, but ΔE^BSSE₀ for HHexam-TFA with the addition of camphor was maintained at a lower level than that for HHexen-TFA. Details of the DFT calculations are described in ESI.†

Table 2 Intermolecular interaction energies for the ILs with or without camphor

Configurations	ΔE^BSSE0 (kJ mol^−1)
(HHexam-TFA)–(HHexam-TFA)	−78
(HHexen-TFA)–(HHexen-TFA)	−63
2(HHexam-TFA)–camphor	−17
2(HHexen-TFA)–camphor	−12

---

4. Discussion

Based on the experimental results and related papers,^18–20,27 we discuss the mechanism of self-propelled motion of a camphor disk floating in an aqueous phase with HHexen-TFA or HHexam-TFA. The driving force of a camphor disk is the difference in the surface tension around the disk as a one-dimensional system, i.e., Δγ = γ_cL − γ_cR, where γ_cL and γ_cR are the surface tensions at the left and right sides of camphor disk, respectively.²⁰ In addition, the difference in the surface tension between near and apart from the camphor disk induces Marangoni flow. The difference in the surface tension generally induces Marangoni flow.^35–40 We have reported Marangoni flow in the camphor system.^20,40–44 Observation of Marangoni flow in continuous motion suggests that the difference in the surface tension around the camphor disk occurs as the driving force of motion.

Continuous motion of both HHexen-TFA and HHexam-TFA at C_il ≤ 1 mM suggests that the camphor disk successively developed to the water surface from the disk to obtain continuous driving force of motion (Fig. 1a, 2a, 3 and 4). In fact, γ at C_il ≤ 1 mM was greater than or equal to that of the saturated camphor aqueous solution (∼ 55mN m⁻¹). The initial direction of motion of the camphor disk is determined by the asymmetric floating state of the disk on the aqueous phase. If the camphor disk starts continuous motion, the difference in the surface tension around the disk remains, and therefore continuous motion is maintained, as indicated in Fig. 2a.²⁰

In contrast, no motion was observed at C_il ≥ 11 mM for HHexam-TFA or C_il ≥ 15 mM for HHexen-TFA (Fig. 3), suggesting that the camphor disk could not obtain the driving force of motion. In these concentration ranges, γ is significantly lower than that of the saturated camphor aqueous solution, i.e., γ ≤ 20 mN m⁻¹. Marangoni flow is suppressed by the IL molecular layer. Actually, Marangoni flow was not observed in the range of no motion.

Fig. 5 shows the schematic illustration of (a) the interaction between HHexen-TFA molecules and the effect of the addition of camphor molecules at the air-aqueous interface and (b) the mechanism of oscillatory motion. The effect of IL on self-propulsion of a camphor disk is clearly different from that of a surfactant, such as SDS.²⁰ That is, the surface tension of the mixture of SDS and camphor reduces the surface tension rather than that of SDS or camphor only, and therefore the driving force of oscillatory motion is due to the decrease in the surface tension of the mixture. In contrast, the surface tension of the mixture of IL and camphor increases the surface tension rather than that of IL only (Fig. 4 and 5a), therefore the driving force of oscillatory motion is due to the increase in the surface tension of the mixture. In other words, oscillatory motion of the IL-camphor system is generated by the recovery to the surface tension of pure water.

Fig. 5 Schematic illustration of (a) suggested interaction between HHexen-TFA molecules (a1) and the effect of the addition of camphor (a2) at the air–aqueous interface and (b) oscillatory motion of a camphor disk between state I, rest (b1), and state II, motion (b2).

In the IL concentration range (2 ≤ C_il ≤ 10 mM for HHexam-TFA or 2 ≤ C_il ≤ 14 mM for HHexen-TFA) of oscillatory motion, γ without camphor was lower than that of the saturated camphor aqueous solution (∼7 mM), that is, 20 < γ < 55 mN m⁻¹ (Fig. 1b, c, 2b, c, 3 and 4). Fig. 4 suggests that camphor molecules are easily localized at the air/aqueous interface rather than IL. Camphor molecules are dissolved into the aqueous phase, resulting in the formation of aggregates by the IL with an increase in IL concentration (Fig. 5a). Although similar oscillatory motion was observed in other already reported systems,^18–20,27 the following different mechanism is suggested due to the effect of the IL.

During the resting state, the disk is suppressed by the lower surface tension of the IL than that of camphor, i.e., an IL molecular layer exists around the disk (state I, see Fig. 5b1). In this stage, no Marangoni flow occurs. The surface tension around the disk is increased with an increase in the concentration of camphor since adsorbed IL molecules on water around the disk are dissolved into the aqueous phase together with camphor molecules dissolved from the disk (state II, see Fig. 5b2). Then, the camphor disk is accelerated by a slight difference in the surface tension around the disk, and Marangoni flow is generated. As the camphor disk moves to the other aqueous surface, the system returns to state I. Thus, oscillatory motion is generated by the repetition between States I and II. The decrease in the frequency of oscillatory motion with an increase in C_il (Fig. S2a, ESI†) also guarantees this mechanism because the duration time for reaching a threshold value of Δγ to accelerate from the resting state is decreased with an increase in C_il due to the mixture of camphor and IL molecules. The similar frequency of HHexam-TFA and HHexen-TFA in the oscillatory motion is consistent with this mechanism because the surface tension of HHexam-TFA without camphor was similar to that of HHexen-TFA without camphor (see Fig. S2, ESI† and Fig. 4a).

The aggregation between IL and camphor molecules as described in the mechanism is revealed by not only surface tension measurements but also FTIR measurements and DFT calculations. No significant change in N–H bending vibration mode for both HHexam-TFA and HHexen-TFA with the addition of camphor (∼3000 cm⁻¹ in Fig. S4, ESI†) suggests that the global structure of the hydrogen-bonding network formed by the hydrophilic group remained after the addition of camphor molecules. In contrast, the significant blue shift of the N–H stretching vibration mode in Table 1 means that the hydrogen bonding interaction between HHexen-TFA molecules (or HHexam-TFA molecules) is weakened by the penetration of camphor molecules into the HHexen-TFA molecular layer (or the HHexam-TFA molecular layer) on water. It suggests that camphor molecules influence the hydrophobic region of the ILs and weaken the N–H stretching vibration without a change in the global structure of the hydrogen-bonding network. The DFT calculations indicate that the intermolecular interaction energies for both HHexam-TFA and HHexen-TFA are destabilized by the addition of camphor (Table 2). The results agree with FTIR measurements.

The difference between HHexen-TFA and HHexam-TFA is also verified by surface tension measurements, FTIR measurements, and DFT calculations as follows. The higher surface tension of HHexen-TFA in comparison with HHexam-TFA upon the addition of camphor is due to its hydrophilicity (see Fig. 4). The stronger hydrophilicity of HHexen-TFA molecules than that of HHexam-TFA molecules leads to easy removal of HHexen-TFA molecules rather than that of HHexam-TFA molecules at the air/water interface after the addition of camphor molecules. The wavenumber of the N–H stretching vibration mode of HHexam-TFA was lower than that of HHexen-TFA (Table 1). The difference is derived from hydrogen bonding formation. The difference in the wavenumber between them is reduced by the addition of camphor because hydrogen bonding between the HHexen-TFA molecules (or HHexam-TFA molecules) is reduced by the addition of camphor. The higher value of N–H bending vibration mode for HHexam-TFA (∼1530 cm⁻¹ in Fig. S4, ESI†) than that for HHexen-TFA (∼1470 cm⁻¹ in Fig. S4, ESI†) suggests that HHexam-TFA has a network structure composed of their molecules rather than HHexen-TFA. The FTIR measurements (Table 1) and the DFT calculations (Table 2) agree that camphor molecules can easily replace HHexen-TFA molecules rather than HHexam-TFA molecules at the air/water interface.

5. Conclusions

In this study, self-propulsion of a camphor disk was found to be sensitive to two types of ionic liquids (HHexam-TFA and HHexen-TFA). In particular, the period of oscillatory motion decreased with increasing concentration. The bifurcation concentration between the oscillatory motion and no motion for HHexam-TFA was lower than that for HHexen-TFA. These different bifurcation concentrations are discussed in relation to the experimental results of the surface tension, FTIR for the mixture of camphor and HHexam-TFA (or HHexen-TFA), and numerical calculations. If we select camphanic acid as the self-propelled object in the place of camphor, different features of motion will be observed since the carboxylic acid ion in camphanic acid may interact with the cation in HHexen and HHexam. On the other hand, if the size of the camphor disk is changed, the nature of motion does not change but the maximum speed of motion will be changed since the amount of camphor molecules developed from the disk depends on the diameter of the disk. These examinations will be performed in future work. The experimental results in this paper suggest that the nature of motion of a self-propelled object, whose driving force is the difference in surface tension, can be designed depending on the physicochemical properties of the ionic liquid; for example, the combination of cationic and anionic compounds, electrical conductivity, and viscosity.

Author contributions

Hua Er: analysis, review & editing. writing & draft preparation. Jun Gao: experimental & analysis, review & editing. Yu Xu: experimental & analysis, review & editing. Muneyuki Matsuo: review & editing. Satoshi Nakata: planning, writing draft preparation, review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was supported by JSPS KAKENHI (Grant no. JP20H02712, JP21H00996, JP22K14657), Iketani Science and Technology Foundation (0351181-A), and the Cooperative Research Program of “Network Joint Research Center for Materials and Devices” (no. 20231004) to S. N. We also gratefully acknowledge the project of a joint master's course student educated by a supervisor from China and a foreign country, MEXT Leading Initiative for Excellent Young Researchers Grant (JPMXS032023L0007) to M. M., and the China Postdoctoral Science Foundation (2023M732856) to Y. X.

References

1. F. Soto, E. Karshalev, F. Zhang, B. E. F. Esteban Fernandez de Avila, A. Nourhani and J. Wang, Smart materials for microrobots, Chem. Rev., 2022, 122, 5365–5403.
2. B. Jurado-Sánchez and J. Wang, Micromotors for environmental applications: A review, Environ. Sci.: Nano, 2018, 5, 1530–1544.
3. F. Peng, Y. Tu and D. A. Wilson, Micro/nanomotors towards: In vivo application: Cell, tissue and biofluid, Chem. Soc. Rev., 2017, 46, 5289–5310.
4. H. Zhou, C. C. Mayorga-Martinez, S. Pané, L. Zhang and M. Pumera, Magnetically driven micro and nanorobots, Chem. Rev., 2021, 121, 4999–5041.
5. Z. Wu, Y. Wu, W. He, X. Lin, J. Sun and Q. He, Self-propelled polymer-based multilayer nanorockets for transportation and drug release, Angew. Chem., Int. Ed., 2013, 52, 7000–7003.
6. Z. Lin, C. Gao, D. Wang and Q. He, Bubble-propelled Janus gallium/zinc micromotors for the active treatment of bacterial infections, Angew. Chem., Int. Ed., 2021, 60, 8750–8754.
7. J. Katuri, X. Ma, M. M. Stanton and S. Sánchez, Designing micro- and nanoswimmers for specific applications, Acc. Chem. Res., 2017, 50, 2–11.
8. M. Gai, J. Frueh, N. Hu, T. Si, G. B. Sukhorukov and Q. He, Self-propelled two dimensional polymer multilayer plate micromotors, Phys. Chem. Chem. Phys., 2016, 18, 3397–3401.
9. Q. Wang and O. Steinbock, Shape-preserving conversion of calcium carbonate tubes to self-propelled micromotors, Phys. Chem. Chem. Phys., 2022, 24, 14538–14544.
10. G. Salinas, K. Tieriekhov, P. Garrigue and N. Sojic, A. Kuhn, Lorentz force-driven autonomous Janus swimmers, J. Am. Chem. Soc., 2021, 143, 12708–12714.
11. Z. Ye, Y. Wang, S. Liu, D. Xu, W. Wang and X. Ma, Construction of nanomotors with replaceable engines by supramolecular machine-based host–guest assembly and disassembly host−guest assembly and disassembly, J. Am. Chem. Soc., 2021, 143, 15063–15072.
12. Y. Wu, T. Si, C. Gao, M. Yang and Q. He, Bubble-pair propelled colloidal kayaker, J. Am. Chem. Soc., 2018, 140, 11902–11905.
13. D. K. Kanti and A. Sen, Chemically propelled molecules and machines, J. Am. Chem. Soc., 2018, 139, 7666–7676.
14. R. Fujita, N. Takayama, M. Matsuo, M. Iima and S. Nakata, Height-dependent oscillatory motion of a plastic cup with a camphor disk floated on water, Phys. Chem. Chem. Phys., 2023, 25, 14546–14551.
15. T. Ban, M. Sugiyama, Y. Nagatsu and H. Tokuyama, Motion-based detection of lanthanides (III) using self-propelled droplets, J. Phys. Chem. B, 2018, 122, 10647–10651.
16. R. Zahorán, P. Kumar, D. Horváth and A. Toth, Self-propulsion of a calcium alginate surfer, Soft Matter, 2023, 19, 8033–8039.
17. R. J. G. Löffler, M. M. Hanczyc and J. Gorecki, A hybrid camphor–camphene wax material for studies on self-propelled motion, Phys. Chem. Chem. Phys., 2019, 21, 24852–24856.
18. S. Nakata, M. Nagayama, H. Kitahata, N. J. Suematsu and T. Hasegawa, Physicochemical design and analysis of self-propelled objects that are characteristically sensitive to environments, Phys. Chem. Chem. Phys., 2015, 17, 10326–10338.
19. N. J. Suematsu and S. Nakata, Evolution of self-propelled objects: From the viewpoint of nonlinear science, Chem. – Eur. J., 2018, 24, 6308–6324.
20. Self-organized motion: Physicochemical design based on nonlinear dynamics, ed. S. Nakata, V. Pimienta, I. Lagzi, H. Kitahata and N. J. Suematsu, The Royal Society of Chemistry, Cambridge, 2019.
21. G. Holló, N. J. Suematsu, E. Ginder and I. Lagzi, Electric field assisted motion of a mercury droplet, Sci. Rep., 2021, 11, 2753.
22. M. You, C. Chen, L. Xu, F. Mou and J. Guan, Intelligent micro/nanomotors with taxis, Acc. Chem. Res., 2018, 51, 3006–3014.
23. H. W. Huang, F. E. Uslu, P. Katsamba, E. Lauga, M. S. Sakar and B. J. Nelson, Adaptive locomotion of artificial microswimmers, Sci. Adv., 2019, 5, eaau1532.
24. K. F. Jarrell and M. J. McBride, The surprisingly diverse ways that prokaryotes move, Nat. Rev. Microbiol., 2008, 6, 466–476.
25. S. Thakur, J. X. Chen and R. Kapral, Interaction of a chemically propelled nanomotor with a chemical wave, Angew. Chem., Int. Ed., 2011, 50, 10165–10169.
26. N. J. Suematsu, Y. Mori, T. Amemiya and S. Nakata, Spontaneous mode switching of self-propelled droplet motion induced by a clock reaction in the Belousov−Zhabotinsky medium, J. Phys. Chem. Lett., 2021, 12, 7526–7530.
27. Y. Xu, N. Takayama, H. Er and S. Nakata, Oscillatory motion of a camphor object on a surfactant solution, J. Phys. Chem. B, 2021, 125, 1674–1679.
28. M. Matsuo, K. Ejima and S. Nakata, Recursively positive and negative chemotaxis coupling with reaction kinetics in self-organized inanimate motion, J. Colloid Interface Sci., 2023, 639, 324–332.
29. A. Krishnan, K. P. Gopinath, D.-V. N. Vo, R. Malolan, V. M. Nagarajan and J. Arun, Ionic liquids, Deep eutectic solvents and liquid polymers as green solvents in carbon capture technologies: A review, Environ. Chem. Lett., 2020, 18, 2031–2054.
30. Q. Q. Ruan, M. Yao, D. Yuan, H. Dong, J. Liu, X. Yuan, W. Fang, G. Zhao and H. Zhang, Ionic liquid crystal electrolytes: Fundamental, applications and prospects, Nano Energy, 2023, 106, 108087.
31. C. S. Buettner, A. Cognigni, C. Schröder and K. Bica-Schröder, Surface-active ionic liquids: A review, J. Mol. Liq., 2022, 347, 118160.
32. H. Er and H. Wang, Properties of protic ionic liquids composed of N-alkyl (= hexyl, octyl and 2-ethylhexyl) ethylenediaminum cations with trifluoromethanesulfonate and trifluoroacetate anion, J. Mol. Liq., 2016, 220, 649–656.
33. H. Er, Y. Xu and H. Zhao, Properties of monoprotic ionic liquids composed of hexylammonium and hexylethylenediaminium cations with trifluoroacetate and bis (trifluoromethylsulfonyl) imide anions, J. Mol. Liq., 2019, 276, 379–384.
34. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria and M. A. Robb, et al., Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford CT, 2013.
35. L. E. Scriven and C. V. Sternling, The Marangoni effect, Nature, 1960, 187, 186–188.
36. H. Kitahata and N. Yoshinaga, Effective diffusion coefficient including the Marangoni effect, J. Chem. Phys., 2018, 148, 134906.
37. T. Bickel, Spreading dynamics of reactive surfactants driven by Marangoni convection, Soft Matter, 2019, 15, 3644–3648.
38. E. Lauga and A. M. J. Davis, Viscous Marangoni propulsion, J. Fluid Mech., 2012, 705, 120–133.
39. V. Vandadi, S. J. Kang and H. Masoud, Reverse Marangoni surfing, J. Fluid Mech., 2017, 811, 612–621.
40. H. Kitahata, S. Hiromatsu, Y. Doi, S. Nakata and M. R. Islam, Self-motion of a camphor disk coupled with convection, Phys. Chem. Chem. Phys., 2004, 6, 2409–2414.
41. Y. Xu, N. Takayama, Y. Komasu, N. Takahara, H. Kitahata, M. Iima and S. Nakata, Self-propelled camphor disk dependent on the depth of the sodium dodecyl sulfate aqueous phase, Colloids Surf., A, 2022, 635, 128087.
42. H. Kitahata, H. Yamamoto, M. Hata, Y. S. Ikura and S. Nakata, Relaxation dynamics of the Marangoni convection roll structure induced by camphor concentration gradient, Colloids Surf., A, 2017, 520, 436–441.
43. Y. Matsuda, N. J. Suematsu, H. Kitahata, Y. S. Ikura and S. Nakata, Acceleration or deceleration of self-motion by the Marangoni effect, Chem. Phys. Lett., 2016, 654, 92–96.
44. Y. S. Ikura, R. Tenno, H. Kitahata, N. J. Suematsu and S. Nakata, Suppression and regeneration of camphor-driven Marangoni flow with the addition of sodium dodecyl sulfate, J. Phys. Chem. B, 2012, 116, 992–996.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05630a

---