Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Comparative study of the reductive decomposition reaction of ethylene carbonate in lithium battery electrolyte: a ReaxFF molecular dynamics study
Jingqi
Gao
,
Ruitian
He
and
Kai H.
Luo
 *
*
Department of Mechanical Engineering, University College London, Torrington Place, London WC1E 7JE, UK. E-mail: k.luo@ucl.ac.uk
First published on 12th August 2024
Abstract
Electrolyte decomposition and subsequent solid electrolyte interphase (SEI) are considered to be the primary cause of degradation of lithium batteries. We investigate the multiple factors that can affect the reductive decomposition pathways of ethylene carbonate (EC) and SEI formation using reactive molecular dynamics. Our simulations reveal the effects of lithium concentration, simulation temperature, and the imposition of external electric field on the decomposition reaction and pathways, respectively. The comparative results reveal the increasing lithium concentration has a strong influence on EC decomposition and its pathway at each temperature. Also, the increasing temperature and imposition of an external electric field have been found to non-electrochemically and electrochemically modify the decomposition pathways of EC. This study provides insights into not only the SEI chemistry in Li-ion batteries but also that in lithium metal batteries, which can potentially contribute to the design and optimisation of future novel battery materials and electrolyte solutions.
1. Introduction
As the demand for energy continues to rise worldwide, the need for high energy density storage systems is becoming increasingly crucial. To address this need, rechargeable lithium batteries (RLB) are being developed for more critical application areas including medical equipment and heavy vehicles. In conventional RLBs, the negative electrode is made of graphite, and forms lithium–graphite intercalation compounds (Li–GICs).1 However, during the initial charging of RLBs, the electrolyte experiences reductive decomposition at the surface of the lithiated graphite anode with the presence of Li-ions and form a passivated solid electrolyte interphase (SEI) film. As a complex mechanism,2 the film is comprised of organic and inorganic decomposition intermediates and products of electrolyte,3,4 and leads to the degradation of both the electrode and the electrolyte, due to the irreversible loss of active lithium and capacities of RLB. The SEI has significant impacts on the performance of RLBs, particularly during cycling at deep discharge and operating at high rates. As a result, it is important to understand its formation mechanisms, in particular the decomposition mechanisms and pathways of electrolyte, in order to design RLBs with high performance and long-lasting life.In the commercial LIB industry, current electrolytes are in the form of liquid solutions of organic carbonates, commonly including aromatic ethylene carbonate (EC), aliphatic ethyl methyl carbonate (EMC), and other lithium salts. It is well known that cyclic esters such as EC play an important role as they have better dielectric properties  , relatively higher viscosity and abilities to form a stable passivating layer over a graphite electrode5,6 or active LME surface.7,8 Various experimental techniques have been utilised in the studies of SEI formation over the last decade both in situ and ex situ, including scanning electron microscopy (SEM), X-ray photoelectron spectroscopy (XPS), X-ray diffraction (XRD), infrared spectroscopy (IR), and transmission electron microscopy (TEM).9–11 Although advances in these surface analysis tools and techniques enable the analysis of parameters of composition and morphology, it is still very challenging to capture and characterize SEI and its initial stage of growth experimentally.
, relatively higher viscosity and abilities to form a stable passivating layer over a graphite electrode5,6 or active LME surface.7,8 Various experimental techniques have been utilised in the studies of SEI formation over the last decade both in situ and ex situ, including scanning electron microscopy (SEM), X-ray photoelectron spectroscopy (XPS), X-ray diffraction (XRD), infrared spectroscopy (IR), and transmission electron microscopy (TEM).9–11 Although advances in these surface analysis tools and techniques enable the analysis of parameters of composition and morphology, it is still very challenging to capture and characterize SEI and its initial stage of growth experimentally.
Quantum chemistry (QC) based methods such as density functional theory (DFT) and ab initio molecular dynamics (AIMD) simulations are able to predict the electrochemistry at a high accuracy, albeit for a limited system size of hundreds of atoms as they are computationally intensive. A number of mechanisms have been proposed in DFT studies for the degradation of EC molecules,12–15 and in these studies, two reduction steps of EC molecules are captured. Firstly, the EC molecule undergoes a ring-opening reaction after transfer of an electron, as the homolytic bond cleavage between an alkoxy oxygen atom and the adjacent ethylene carbon atoms is observed. From this reduction step, lithium ethylene decarbonate (Li2EDC) or lithium butylene decarbonate (Li2BDC) may be formed. Moreover, the second reduction step of the EC radical could lead to the formation of ethylene gas (C2H4) and CO32− as a two-electron mechanism. Furthermore, besides the DFT calculations of single molecules, AIMD simulations are used to model the initial stages of SEI growth by incorporating periodic DFT calculations.16–19 The reduction processes of one-electron and two-electron have been identified in AIMD, in addition to the formation of a diolate with carbon monoxide observed as a new mechanism when ring opening of the reduced EC takes place within the carbonate moiety itself. Leung and co-workers used AIMD simulation to estimate the voltage dependence of the surface charges and the free energy of electrolyte.16,20,21 The surface charge may be adjusted by changing the number of deintercalated Li-ions from the graphite anode, and the deintercalated potential of lithium and degradation potential of EC are estimated. Furthermore, a hybrid Monte Carlo/molecular dynamic method is proposed by Takenaka and co-workers to study the formation mechanism of the solid electrolyte interphase on the graphite anode in lithium and sodium ion batteries,22,23 by pre-defining a known set of chemical reaction, hence the simulation can only reproduce the pre-defined reaction pathways.
In contrast, classical MD methods can drastically extend the system size as well as the timescale for the atomistic simulations. ReaxFF, developed by van Duin and co-workers,24 has been constructed to bridge the gap between ab initio QC and non-reactive empirical force fields. ReaxFF can describe complex chemical reactions, featuring the ability of simulating dissociation, transition, and formation of chemical bonds. ReaxFF has previously been performed to study the formation and dynamics of SEI in LIB chemistries under certain conditions.25–28 However, the detailed effects of lithium density, temperature and electric field are still unclear. It has been found that cycling or aging with increasing temperature can accelerate the formation of SEI.29,30 Besides, the kinetics of the decomposition of electrolytes is highly dependent on the salt concentration (or Li concentration) in the electrolytes, which remains to be thoroughly investigated.
It should be noted that when it comes to interfacial SEI studies, ReaxFF in combination with the adopted charge equilibration method (QEq) has a limitation. Essentially, QEq treats the SEI as an electronic conductor rather than an electronic insulator, as the charges of particles in this region are updated in each MD step. This issue becomes significant as SEI grows thick enough and the electron tunnelling through SEI becomes unphysical. However, this limitation could be alleviated in the initial stage of electrolyte decomposition and SEI formation without an interface configuration. Therefore, ReaxFF could be suitably utilised to simulate electrolyte solvent decomposition reactions.
In this study, we aim to investigate the fundamental decomposition mechanisms of EC molecules during the initial SEI formation in a simplified system with several restrictive assumptions using the ReaxFF molecular dynamics method. The effects of lithium concentration, temperature, and the imposition of an external electric field on the decomposition pathways are discussed. This comparative study enhances understanding of not only the SEI chemistry in Li-ion batteries but also that in lithium metal batteries, which can potentially contribute to the design and improvement of novel battery materials and electrolyte solutions.
2. Simulation details
The ReaxFF adopted in this study was developed to describe the relationship of C/H/O/S/Li/F/N atoms by Bedrov et al.27 It was further parameterised by Islam et al.,28 trained for LIB materials, to reproduce the QC calculations and describe bond dissociation and Li-binding energies for electrolyte molecules. The validity of ReaxFF for investigating the decomposition of electrolyte and formation of SEI has been examined in previous studies,31,32 and is proven to be the set of optimum parameters for this research.The simulation box has dimensions of 35 × 35 × 35 Å3 and details of the studied reactive systems are provided in Table 1. As a fundamental study, the adopted EC density in the simulation setup deviates the typical density of liquid state EC. To improve the chances of electrolyte decomposition reactions within the accessible computational timescale, a higher than practical lithium concentration is used, which contributes to a higher Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) EC ratio and allows for the observation and analysis of electrolyte decomposition mechanisms in ReaxFF MD simulations.
EC ratio and allows for the observation and analysis of electrolyte decomposition mechanisms in ReaxFF MD simulations.
| System | No. of molecules/atoms | Temperature | Electric field strength (V Å−1) | |
|---|---|---|---|---|
| EC | Li | |||
| 1 | 60 | 40 | 300 & 600 K | — |
| 2 | 60 | 60 | ||
| 3 | 60 | 80 | ||
| 4 | 300 K | 0.01 | ||
| 5 | 0.05 | |||
| 6 | 0.1 | |||
| 7 | 0.12 | |||
| 8 | 60 | 40 | 0.14 | |
| 9 | 0.16 | |||
| 10 | 0.18 | |||
| 11 | 0.2 | |||
| 12 | 0.3 | |||
| 13 | 0.5 | |||
Systems 1 to 3 are used to investigate the basic pathways of EC reductive decomposition and mechanisms of SEI formation. With different numbers of lithium atoms at different temperatures, the effects of lithium density and temperature on the decomposition pathway of EC are also investigated. One limitation of the combined ReaxFF and QEq method is that it lacks an explicit electronic degree of freedom, hence it does not simulate electron flow and dynamics. Even though Li ions (Li+) could be included in the initial model construction, QEq will recalculate the charge of Li+ ions in the same way as Li atoms as soon as the MD simulation begins. Therefore, there is no difference in the calculated charges between lithium particles initially configured as either ions or atoms. To avoid ambiguity, we adopted and described the particles as Li atoms. A snapshot of these systems is presented in Fig. 1. The Li atoms are introduced randomly at a distance of more than 5 Å away from the centroids of EC molecules.
Due to the high reactivity of lithium, ethylene carbonate can be spontaneously decomposed with the presence of lithium atoms in ReaxFF MD simulations, even under room temperature. For the purpose of equilibration, each system is relaxed at 1 K for 100 picoseconds. Based on the charge equilibration method, the average charges of Li atoms in the studied system in the equilibration state range from +0.55 to +0.6e. The ReaxFF MD simulations are then carried out at both 300 K and 600 K to study the reduction reaction and its dynamic evolution. The higher temperature of 600 K is achieved by gradually increasing from 300 K in 6 ps (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD iterations and a rate of 0.005 K per step), to accelerate the reaction by enhancing kinetics and allow the observation of the electrolyte chemistry of interest within the shorter timescale in MD simulation.33
000 MD iterations and a rate of 0.005 K per step), to accelerate the reaction by enhancing kinetics and allow the observation of the electrolyte chemistry of interest within the shorter timescale in MD simulation.33
Systems 4–7 use duplications of the equilibrated system 1 after 100 ps 1 K relaxation as the starting point, and different strengths of electric field are applied in the x-direction, ranging from 0.01 to 0.5 V Å−1. The adopted high-intensity electric field is used to speed up the decomposition process within the short timescale of the ReaxFF MD simulation. It is worth noting that the electric field is applied in the form of an external force with the magnitude of F = qE in LAMMPS and is proportional to the charge status allocated to each particle. Topologies of single molecules are created using Avogadro,34,35 and the initial configurations of every system are made using packing optimization for molecular dynamics simulations (PACKMOL).36
We perform all ReaxFF MD simulations using the embedded REAXC37 package in the open source large-scale atomic/molecular massively parallel simulation (LAMMPS) program developed by Plimpton et al.38,39 and Thompson et al.38 The canonical ensemble (NVT) is used, with a constant number of atoms N, volume V and temperature T for all ReaxFF MD simulations, and the temperatures are maintained using the default Nosé–Hoover thermostat. The temperature damping constant has significant influence on the effectiveness of the Nosé–Hoover thermostat; temperature can fluctuate wildly if it is too small, while a longer temperature equilibration time can be expected if it is too large. A good choice for ReaxFF MD models is around 100 timesteps.
All our ReaxFF MD simulations are performed with a time step of 0.1 fs with a damping constant of 10 fs. In order to eliminate artificial effects of the structure, each simulation system undergoes energy minimization steps via a conjugate gradient algorithm. Periodic boundary conditions are enforced in all directions. The bond order cut-off should be carefully selected: too many bonds are included with the choice of low cut-off value and would lead to errors by including unsuccessful events producing every short-lived species. In contrast, fragmented molecules are identified if the cut-off value is too large. For the bonding pairs only involving elements C, H, and O, the bond order cut-off of 0.3 is adopted as in general this value suitably compromises species identification accuracy, as recommended in previous studies.40–42 A bond order cut-off of 0.8 for Li–Li pair, 0.55 for Li–O pair, and 0.3 for Li–C and Li–H pairs interatomic connectivity are adopted, to recognise the molecules and therefore identify the species formed during every step of MD simulations, with the aid of visualization of trajectories.
Three replicas with different initial configurations are constructed for every scenario to simulate a total of 39 systems, and the results are averaged for further analysis. All the parallel ReaxFF MD simulations are carried out on ARCHER2, the UK national supercomputing service. For post-processing of atomic trajectories during MD simulations, the atomic positions and velocities are generated at every 100 MD steps (0.1 ps), while bond information is collected at every 100 MD steps (0.1 ps) for recognising species in order to provide more details on the mechanism of species and intermediates formation. Visualization of the results is conducted using Visual Molecular Dynamics (VMD)43 software and the open visualization tool Ovito.44 Post-processing of MD results is accomplished using a self-developed MATLAB code.
3. Results and discussions
3.1. Time evolution of potential energy
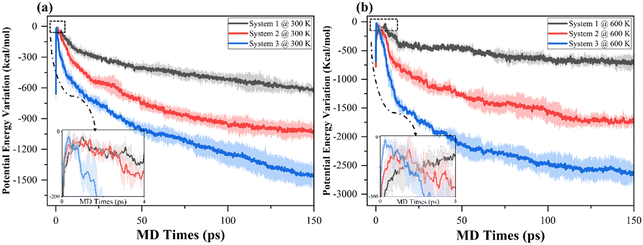
Potential energy profile is used as an indicator of the reliability of the simulating model. In particular, the temporal variation of systematic potential energy is expected to be relatively slight and stable before the end of equilibration runs. The potential energy profiles of the equilibration run for systems 1–3 are stabilized from 40 ps, irrespective of the different lithium density in the systems. Fig. 2 depicts the transient variation in the potential energy of simulation systems 1, 2 and 3 during (a) 300 K, and (b) 600 K NVT MD simulations of ethylene carbonate decomposition. To visualise the difference in the variations of potential energy in each system, the potential energy profiles are shifted vertically to make sure the peaks of the curve reach zero before they start to drop vigorously. The shaded area represents error bands showing the uncertainty of MD simulations as a standard deviation of the three replicas. Due to the fast ramping of simulation temperature from 1 K to the desired value, in all systems the potential energy initially abruptly rises to a local maximum before entering decreasing trajectories when ethylene carbonate undergoes decomposition.The comparisons within Fig. 2(a) and (b) conclude that the higher lithium density not only catalyses the decomposition of EC molecules, but also leads to a more rapid increase and decrease of the magnitudes of potential energy, unveiling the quicker absorption and release of heat energy during NVT MD simulations. Furthermore, the widths of potential energy peak are shortened when there are more lithium atoms in the systems. The result shows the promotion of the reductive decomposition of EC molecules when more lithium atoms are involved.
Fig. 2(b) depicts more drastic variations of magnitudes of the potential energy at 600 K in comparison with those of systems 1–3 at 300 K, implying the promotion of heat releases at the elevated temperature. It is worth noting that, although at both temperatures the amount of absorption of energy (the difference in the starting point to the peak value of the potential energy) is approximately 600 kcal mol−1 before decreasing, the peaks in the systems for the 600 K cases are wider, due to the increasing temperature during the first 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MD iterations which alleviates the release of heat. For system 1, the potential energy drops more vigorously at 600 K in the first 20 ps than at 300 K; however, the variation in the potential energy profile enters a steady and slightly decreasing regime, implying the lithium in system 1 is at a sufficiently saturated density at a high thermodynamic temperature in a 150 ps NVT MD simulation.
000 MD iterations which alleviates the release of heat. For system 1, the potential energy drops more vigorously at 600 K in the first 20 ps than at 300 K; however, the variation in the potential energy profile enters a steady and slightly decreasing regime, implying the lithium in system 1 is at a sufficiently saturated density at a high thermodynamic temperature in a 150 ps NVT MD simulation.
3.2. EC decomposition reaction rate and pathways
Fig. 3(a) and (b) show the number of EC remaining after decomposition and lithium atom consumption. For all systems, the reactions start as soon as the simulations begin, with a faster initial reaction rate. System 1 initially has a steady decomposition reaction involved, then enters a relatively stable regime with very slight variation of species numbers from 50 ps of the MD simulation. In contrast, a similar trend of EC decomposition and lithium consumption is observed during the first 75 ps of MD simulations of system 2 and system 3, before two curves enter different trends. After 75 ps, the EC decomposition reaction with lithium atom can still be observed in system 2, in a steady but slower reaction in comparison to the beginning of the simulation. In contrast, EC in system 3 is decomposed at a similar rate across the entire 150 ps NVT MD simulation, as well as the consumption rate of lithium atoms.
Quantitatively, Fig. 3(a) and (b) show the effect of lithium concentration on EC decomposition, in the way of the decomposition mechanism. 16.67% (10 molecules), 35% (21 molecules), and 51.67% (31 molecules) of EC molecules are involved in the reductive decomposition reaction in systems 1, 2 and 3, respectively. Furthermore, for the lithium atoms, there are 25% (10 atoms), 51.67% (31 atoms), and 65% (52 atoms) consumed by the end of the 150 ps NVT MD simulation of systems 1, 2 and 3, respectively. In system 1, the vast majority of decomposition only involves one EC molecule and one lithium atom. The addition of 20 lithium atoms from system 1 to system 2 and from system 2 to system 3 both results in the additional lithium consumption of approximately 20 atoms while the EC consumption increases with the increment of 10, implying the different decomposition reaction pathways in systems 2 and 3 in comparison with system 1.
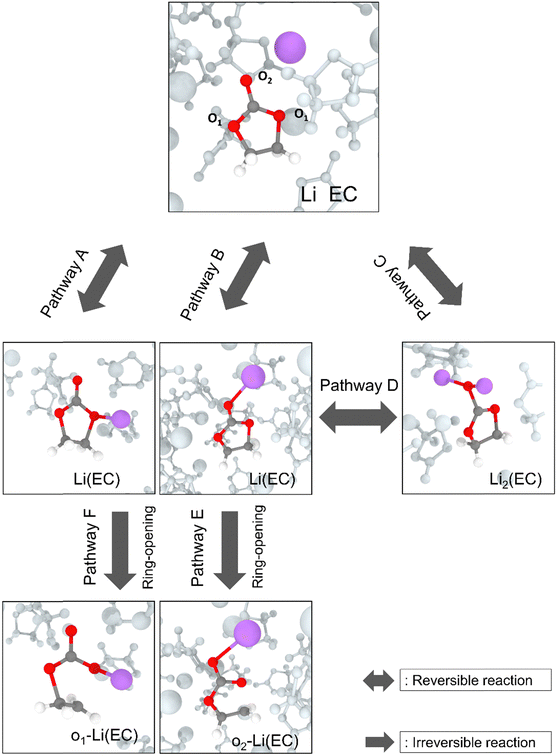
Fig. 4 depicts the primary decomposition pathway of ethylene carbonate when interacting with active lithium atoms. From the ReaxFF MD simulation, the primary decomposition pathway of the EC molecule is found to be initiated by the redox interactions when EC is approached by active lithium atoms, at the sites near either ethereal (pathway A) or carbonyl oxygen (pathway B) atom. The lithium atom is oxidised, which transfers electron to initiate an EC reduction reaction to form a Li(EC) complex. This decomposition pathway agrees with various experimental and simulation studies.12,15,45–49 Furthermore, this complex can interact with an additional lithium atom to form Li2(EC) as shown as pathway C and then follows a reversible pathway D to form Li(EC). Alternatively, Li(EC) can undergo a ring-opening reaction through the cleavage of the bond between ethylene carbon and ethereal oxygen and then forms an o-Li(EC) complex as shown in pathways E and F.
It is important to mention that, although the bond between lithium and oxygen atoms is not necessarily formed in the product of pathways A–F, it is connected in the post-processing visualization step once the lithium atom approaches within 2.5 Å of the ethereal or carbonyl oxygen, to signify the approaching of lithium atoms on the decomposition of EC and the subsequent ring-opening reactions to form o-Li(EC) radicals.
Fig. 5 presents the time evolution of the number of dominant SEI species formed during 150 ps NVT MD simulations of EC decomposition at 300 K. The transient variation of the primary decomposition product Li(EC) is presented in Fig. 5(a), showing a similar overall trend in comparison with lithium consumption in Fig. 3(b). It is worth noting that, although the number of Li(EC) in Fig. 5(a) includes the ring-opening products of the o-Li(EC) complex, this ring-opening complex and pathway E or F are not observed in system 1 at 300 K. However, unlike the higher initial lithium consumption rate in systems 2 and 3, during the beginning of MD simulations the formation of Li(EC) is at a similar rate for all systems, represented by the overlap in curves before 75 ps. This is because the ring-opened o-Li(EC) radical forms as the primary decomposition product and can be treated as an “intermediate” that then undergoes a secondary and further decomposition reaction. This could be explained by the notably lower formation number of Li(EC) compared to its corresponding EC and Li consumption in systems 2 and 3, and the larger height of the shaded area.
Furthermore, the secondary and further decomposition reaction in systems 2 and 3 of Li(EC) is reflected in Fig. 5(b). In the less lithium concentrated system 1, the formation of Li(EC) dominates the consumption of EC and Li-atoms, presenting an “1-EC-to-1-Li” decomposition reaction mechanism, and no further decomposition occurs. Without ring-opening reaction and secondary decomposition occurrence, the total number of SEI species formed in system 1 can match not only the lithium consumption but also the total number of Li(EC) formed, with one additional Li2(EC) observed.
Due to the single-electron transfer mechanism, the lithium atom transfers electron to initiate EC reduction reaction, and form Li(EC). This mechanism is most likely to occur when the lithium density or concentration in the system is low. In contrast, the profile of total species in systems 2 and 3 presents a rapid initial increase, followed by similar trajectories to that of the corresponding lithium consumption. Similarly, the total number of EC decomposition products agrees with the corresponding lithium consumption for systems 2 and 3. In these systems with higher lithium concentrations, the reductive decomposition pathways are different, as the formation of products from the secondary decomposition mechanism contributes to the majority of the total SEI product number rise.
Furthermore, the subtle increase in the number of available EC molecules (decrease in consumption) is observed after 20 ps, due to the fact that a small number of EC molecules are following the irreversible pathways A, B and C. As discussed in the previous section, the overlapped curves of EC decomposition and lithium consumption are observed during the first 75 ps of MD simulations of system 2 and system 3 at 300 K, before the two curves follow different trends. However, at elevated temperature the initial decomposition of EC in system 3 is at a higher rate than that in system 2, and this difference in contrast with 300 K is caused by the effect of thermal decomposition.
Interestingly, the number of available EC molecules for each system at the end of 150 ps tends to converge to that of the replicated system at different simulation temperatures. Due to the fact that the number of available EC molecules serves as the primary indicator of the number of EC involved in the primary decomposition pathways, the observations can reveal the different EC decomposition mechanisms under different simulation temperature, where most EC molecules are chemically and electrochemically decomposed with the presence of lithium and the decomposition rate is affected by the lithium concentration at lower temperatures, while an additional non-electrochemically thermal degradation can be observed at higher temperatures.
Fig. 6(b) shows the time evolution of the number of total SEI species formed during 150 ps NVT ReaxFF MD simulation at 300 K and 600 K. Similar to the EC number variation profiles, the curves for 600 K also show an abrupt change once the system reaches 600 K then transfers into a stable and slightly increasing regime. Furthermore, the number of total decomposition products are further increased by an increment of approximately 20 for all systems due to the thermal decomposition and radical termination of the ring-opened o-Li(EC) complex at a higher simulation temperature, on top of the additional SEI species discovered at higher lithium concentration discussed in the previous section.
The ring-opened o-Li(EC) complex is involved in the radical termination reaction through secondary decomposition pathways, and decomposed into a combination of carbonates, gas, and other SEI species in different phases, including LixO, LixCO3, CO2 and C2H4. These species are commonly attributed to the electrolyte decomposition and the associated SEI formation, and our ReaxFF simulations well reproduced previous computational and experimental results.15,25,45,46,48,50–61 C2H4 and CO2 are found to be the most abundant gas phase decomposition products experimentally, and these have been confirmed through our computational studies. Fig. 7 summaries the pathways leading to the formation of major and key species discovered through ReaxFF MD simulation. The presented pathways agree with experimental findings of the predominant presence of gas phase C2H4, and other organic/inorganic species. Although the bond between lithium and oxygen atoms is not necessarily formed in Li2(EC), o-Li(EC) and products of pathway I and P, the lithium–oxygen bonds are connected in the post-processing visualization step once the lithium atom approaches within 2.5 Å of the ethereal or carbonyl oxygen.
 | ||
| Fig. 7 Snapshots of secondary decomposition pathways and products of EC when interacting with active lithium atoms from the ReaxFF MD simulation. Colour code: C: grey, H: white, O: red, Li: purple. | ||
In previous studies,12,17,45,62–64 the two-electron reduction routes of ethylene carbonate have been identified, especially in lithium concentrated systems. In the ReaxFF MD simulation, this fast two-electron reduction results in the ring opening of EC by the cleavage of the O1–CE bond, which then spontaneously decomposes into carbonic acid CO32− and ethylene gas C2H4 in the presence of lithium atoms. The ReaxFF MD simulation in this study captures these decomposition routes as pathways L and M. After the decomposition, CO32− is found to be negatively charged while C2H4 is shown to be slightly positively charged. Therefore, CO32− subsequently bonds to the active lithium to form lithium carbonate LixCO3 (x = 0, 1, 2, 3), represented by pathways N, O and P. Alternatively, the Li2(EC) complex, as the primary decomposition product of EC, undergoes CC–O2 bond breaking and forms Li2O and a C3H4O2 complex, which is subsequently decomposed in sequence and liberates gas phase ethylene C2H4 and carbon dioxide CO2. This route is less favourable than the previous fast two-electron reduction due to the fact that the number of C3H4O2 complexes is found to be significantly lower than Li(EC) and o-Li(EC).
Fig. 8 shows the time evolution of the number of key species (left column) and its ratio towards the total number of SEI species (right column) during 150 ps NVT MD simulations of EC decomposition at 300 K and 600 K. According to the temporal variation profiles, the decomposition mechanisms and pathways exhibit a big difference from those at lower temperature. In Fig. 8(a) and (b), unlike the results using the lower temperature of 300 K, where the number of Li(EC) increases during the first 75 ps then remains in system 1 or continues to grow in systems 2 and 3, the number of such molecules at 600 K increases vigorously and peaks during the initial 10 ps with a lower count of them captured in the lithium-diluted environment. After that, the decreasing trend is discovered and the amount at the end of the 150 ps MD simulation converges to similar values for systems of different concentrations. This result not only shows that the different amounts of Li(EC) formed at different lithium concentrations are all thermally decomposed, but also concludes the effect of temperature on the decomposition mechanism of EC.
At lower temperature, the electrochemically formed Li(EC) complex tends to be stabilized in a lithium-diluted environment but can undergo further and relatively slower secondary decomposition reaction via chemical and electrochemical mechanisms. However, in addition to the electrochemical mechanism, at higher temperature the primary decomposed product also undergoes nonelectrochemical thermal decomposition, and the effect of lithium concentration is not significant in the remaining amount in the system. The ratio of the Li(EC) complex towards the total SEI species also agrees with the effect of temperature, where the complex acts as the prominent SEI component in 300 K, while the ratio in 600 K shows its insignificance.
Further results also confirm the effect of temperature on the decomposition mechanism. In Fig. 8(c)–(f), the temporal variations for the inorganic species LixCO3 (x = 0, 1, 2, 3) and LixO (x = 1, 2, 3) and their ratios towards total SEI species are shown, respectively. The formation of these two species is not observed in the lithium-diluted environment of system 1 at 300 K, and the effect of lithium concentration on EC decomposition is revealed in the profiles of systems 2 and 3. The increasing lithium concentration donates to the formation of lithium carbonates and lithium oxide through pathways L, G and I, although identical numbers of carbonate-species are discovered in systems 2 and 3 while a higher lithium concentration further stimulates the formation of lithium oxide. By this, it suggests the effect of lithium concentration is specifically more significant on the routes C and G. The steady growth of lithium oxide number correlates to the steady growth in the total SEI species number and forms a noisy ratio curve in 300 K.
Furthermore, the simulation temperature influences the formation of these two species, as they grow rapidly at the beginning of the simulation and then enter a steady trend with decayed formation rates. As mentioned previously, especially at elevated temperature, carbonate-species form through fast two-electron reduction pathways by the cleavage of the O1–CE bond and then spontaneously decompose into carbonic acid CO32− and ethylene gas C2H4 in the presence of lithium atoms. In contrast, lithium oxide is formed through CC–O2 bond breaking which is less favourable than the previous fast two-electron reduction because the number of C3H4O2 complexes is found to be lower than Li(EC) and o-Li(EC). Furthermore, the result of the ratio of lithium carbonates to total species suggests that the elevated temperature has a significant impact on the decomposition pathway of EC, as primary non-electromechanical thermal decomposition products are observed. Nevertheless, the effect of lithium concentration is less important, owing to the fact that the increased lithium concentration only affects electromechanically and causes the increase in the number of carbonate-species formed but not affecting its ratio towards total species.
The liberation of gas phase product carbon dioxide CO2 and ethylene C2H4 is illustrated in Fig. 8(g) and (i) with their ratio towards total SEI species shown in Fig. 8(h) and (j), respectively. Similar to the difference in formation rates found in the inorganic species LixCO3 (x = 0, 1, 2, 3) and LixO (x = 1, 2, 3) and their ratios towards total SEI species, the comparison of the gas formation trend throughout the 150 ps ReaxFF MD simulation also proves the EC molecules are decomposed in favour of the mechanism of the faster two-electron reduction pathways by the cleavage of the O1–CE bond, which then spontaneously decompose into carbonic acid CO32− and ethylene gas C2H4 in the presence of lithium atoms. After the EC decomposition into Li2O and C3H4O2 complexes, the former inorganic product follows a reversible reduction pathway I, and the latter C3H4O2 complex is further reduced following pathways J and K to form gases CO2 and C2H4. The formation of CO2 is not observed at 300 K electrochemically or chemically, and is found to be gradually increasing during the 600 K simulation at a slower rate than that of lithium oxide. From this observation, it suggests the liberation of CO2 is through a non-electrochemical decomposition mechanism and is a thermally decomposed product triggered at higher temperature. Furthermore, identical amounts of CO2 and LixO (x = 1, 2, 3) are found at the end of the 150 ps MD simulation, suggesting all C3H4O2 “intermediates” are thermally decomposed to carbon dioxide, leading to the similar ratio towards total SEI species for all systems with different lithium concentrations.
Moreover, the generation of C2H4 is at the same rate of inorganic species LixCO3 (x = 0, 1, 2, 3), in agreement with the previous observation of the major/favourable secondary decomposition routes that the primary decomposed product would follow at elevated temperature. Its rapid formation reproduces the formation rate of carbonate-species during the initial 10 ps before converting into steady growth regimes, implying pathway M plays a dominant role in the initial process. This observation is confirmed by the small quantity of CO2 in the initial 10 ps as C2H4 forms through pathway K simultaneously with CO2 formed via pathway J. In contrast to the nearly constant quantity of lithium carbonates found from three systems at the later stage, the amount of C2H4 continues to grow steadily to the end at 600 K, and the corresponding ratios toward the total SEI species not only converges below 0.4 but also presents a big discrepancy hence a strong influence of temperature on the C2H4 formation, either in an electrochemical way or more profoundly in a nonelectrochemical way. Overall, while at low temperature the primary decomposed product, the Li(EC) complex, is found to be the prominent SEI species, gas phase products and inorganic lithium carbonates dominate in the formation towards the total SEI species at high temperature.
A summary of the primary and secondary decomposition pathways of EC for each system at 300 K and 600 K is shown below in Tables 2 and 3, respectively. It is worth mentioning that, although lithium ethylene dicarbonate (LEDC) is considered to be the primary SEI component and its formation is observed in previous experimental and simulation studies,15,45,55,56,65–69 in the current ReaxFF MD simulation it is only captured for a few flux during post-processing of bond-order data of millions of MD steps in some of the replica systems when o-Li(EC) is approached by LiCO3−. It is neither stable nor visually captured during visualization. Due to the fact that o-Li(EC) rapidly undergoes spontaneous decomposition into carbonic acid CO32− and ethylene gas C2H4 while LiCO3− can be easily reduced to Li2CO3 in a reversible mechanism, the co-existence of LiCO3− adjacent to o-Li(EC) is unlikely in the timescale of ReaxFF MD simulations.
Furthermore, it is believed that the formation and presence of LEDC favours a low lithium concentration environment, as a lithium concentrated environment promotes the decomposition of LEDC into inorganic salts. Nonetheless, the capture of LEDC is not of particular interest in the current study. The ultimate aim is to investigate the effect of lithium concentration and temperature on the EC decomposition mechanism and the followed pathways, and the findings and conclusions on these effects remain.
3.3. Impact of external electric field on the EC decomposition reaction
An illustration of a simulation system configuration containing 60 EC molecules and 40 Li atoms with an applied external electric field with various strengths is shown in Fig. 9. With this external electric field on the equilibrated system along the x-direction, the impact of the external electric field on the EC decomposition reaction is justified and scrutinized by the variations of the remaining EC numbers and SEI species formed compared with system 1 without the imposition of this e-field. It is worth noting that through conducting several simulation cases by varying the intensity of the electric field from 0.01 to 0.5 V Å−1, it was found that EC would not decompose without the presence of lithium even at the highest voltage used.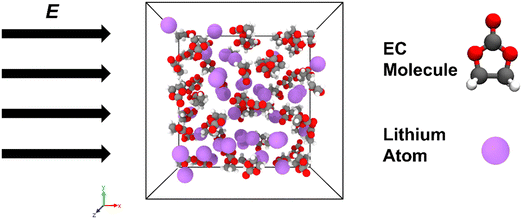 | ||
| Fig. 9 Simulation system configuration containing 60 EC molecules and 40 Li atoms with applied external electric field with various strengths. Colour code: C: grey, H: white, O: red, Li: purple. | ||
Fig. 10 describes the impact of the external electric field of various strengths on EC decompositions. This field affects the transport and reaction of species involved in the SEI formation, and is revealed by the time evolution of undecomposed EC molecules with representative curves shown in Fig. 10(a). In general, the applied external electric field enhances the migration of particles, ions and radicals, and promotes the reduction and decomposition of EC by altering the kinetics of the electrochemical reaction, represented by the increase in the EC consumption number at the end of the simulation. The impact of e-field strength on the amount of undecomposed EC molecules at the end of the 150 ps MD simulation below 0.1 V Å−1 is minimal, although the reversible decomposition is enhanced by the e-field, observed by the fluctuation of the curve.
With increasing the e-field strength to 0.1 V Å−1 and above, the decomposition during the initial 25 ps becomes more prominent, followed by further decomposition and SEI formation. This finding is in agreement with the observation of the number of types of SEI products and intermediates found at the end of 150 MD simulation shown in Fig. 10(b). The linear regime between the e-field strength and EC decomposition is found, where a more non-linear relationship can be found for the type of products and intermediates when the magnitude of the electric field increases. Although a similar amount of EC decomposition is captured between 0 and 0.1 V Å−1, their increasing tendency to undergo electrochemical reactions leads to the additional amount of SEI species and by-products formed electrochemically.
With the increased strength, the larger electric fields further polarize the particles and alter the chemical reaction mechanisms by electrochemical activation, especially in the secondary decomposition pathways. EC molecules are found to be more prone to ring opening, which in turn almost spontaneously decompose into secondary decomposition products. Furthermore, the increasing fragmentation of secondary decomposition products and their recombination is observed with stronger e-field imposition.
To reveal how the electric field influences the secondary decomposition of ethylene carbonate molecules, the generation of key SEI species and the corresponding pathways are scrutinized and compared. Fig. 11 shows the influence of an electric field on the formation of key species. As shown in Fig. 11(a) and (b), the imposition of the electric field starts to promote the electrochemical formation of lithium oxide at the lowest electric field, and the superatomic Li3O, typically formed as an intermediate species through pathways G and I, is the prominent lithium oxide found at low e-field with a strength below 0.12 V Å−1. Beyond this electric field strength, Li2O molecules are formed in favour through pathway G and become the dominant species found in inorganic lithium oxides. Considering the higher formation energy and lower binding energy of Li3O than that of Li2O, the superatomic intermediate Li3O can easily break into Li2O and Li through the reversible pathway I.
In contrast, the higher atomic binding force in Li2O contributes to the higher stability as the Li–O bond is more difficult to break. In this ReaxFF MD simulation, the charge transfer and distribution are performed by the charge equilibration method (QEq), and the effective partial charge in Li2O is computed to be Li2+0.5O−0.7, in agreement with the effective charge in a previous study.70 The imposition of an external electric field with strengths below 0.1 V Å−1 does not promote the generation of lithium carbonates. However, the increasing generation of lithium carbonates is captured in the simulation systems with a higher magnitude of external e-field. As mentioned previously EC molecules are electrochemically activated and more prone to ring opening with a higher e-field strength imposed. Therefore, the number of decomposed EC molecules further increases, by ring-opening reaction and spontaneous decomposition into lithium carbonates and ethylene gas. LiCO3− is found to be the most stable and dominant carbonate decomposition product in the ring-opening reaction through pathway N, and the amount of Li2CO3 and Li3CO3 is found to be low, due to the low Li-density.
The amount of carbon dioxide CO2 and ethylene gas C2H4 for various e-field strengths is shown in Fig. 11(c) and (d). After two lithium atoms bind to the O2 atom and break the CC–O2 bond, the lithium oxide and C3H4O2 complex are formed following pathways G and H, which is further decomposed into two gas phase products. Similar to the findings for the effect of an electric field on lithium carbonates, the generation of these two gas phase products is inhibited in a low e-field environment, while the higher e-field strength boosts the formation of CO2 and C2H4. This can be explained by the fact that the energy barrier of the ring-opening of the C3H4O2 complex is substantially higher than the reaction of pathway G, thus the release of lithium oxide exists earlier than CO2. Furthermore, as the liberation of C2H4 can be tracked from pathways J and M, it is found to be formed simultaneously with carbonate-species at a lower e-field strength. The amount of C2H4 generated through pathway J is identical to the findings in CO2. Similarly, the number of C2H4 is equal to that of lithium carbonates at various e-field strengths. This result validates the decomposition pathway found through current ReaxFF simulations.
4. Conclusion
In summary, the reductive decomposition reaction of ethylene carbonate in lithium battery electrolyte and the subsequent SEI species formation is studied using ReaxFF MD simulations. Our simulations reveal the effect of lithium concentration, temperature, and the imposition of an external electric field on the decomposition reaction and pathways, respectively. By using the potential energy profile as the indicator of the reliability of simulation models, the result indicates the higher lithium concentration not only promotes the reductive decomposition of EC molecules, but also leads to rapid absorption and release of heat energy. Furthermore, the time evolution of the number of key species is analysed. The comparative results reveal the increasing lithium concentration has a strong influence on EC decomposition and its pathway for the same temperature, where the lowest lithium concentration systems have the lowest EC decomposition number, while the highest lithium concentration systems undergo more vigorous EC decomposition reaction. Only primary decomposition of EC is observed in the Li-diluted environment, and the primary decomposition product is found to be further electrochemically reduced in the Li-concentrated environment and contributes to the majority of the total SEI product number rise.By conducting the simulations at higher temperature, the observed different trends in temporal variation between low and high temperature imply different decomposition mechanisms. The results suggest that most EC molecules are electrochemically decomposed with the presence of lithium and the decomposition rate is affected by the lithium concentration at lower temperature, while an additional non-electrochemical thermal degradation can be observed at higher temperature. The temporal variation of key SEI species suggests carbonate-species form through fast two-electron reduction pathways and then spontaneously decompose into carbonic acid CO32− and ethylene gas C2H4, and the ratio of lithium carbonates to the total species suggests the elevated temperature has significant impact on the decomposition pathway of EC.
Furthermore, the results from key SEI species analysis on the imposition of an external electric field with various strengths suggests strong electrochemical impact on the decomposition mechanisms of EC. While the electric field strength below 0.1 V Å−1 only exerts minimal impact on the decomposition reactions, the stronger electric field polarizes the particles and alters the mechanisms by promoting the electrochemical formation of lithium oxides, lithium carbonates, gas phase CO2 and C2H4. In addition, the increasing fragmentation of secondary decomposition products and their recombination are observed with stronger e-field imposition.
The limitation of this ReaxFF MD study is that several organic SEI species are absent due to the short timescale of the ReaxFF MD simulation. Also, we acknowledge that our simulation setups do not fully represent realistic electrolyte conditions and battery operations due to the simplified simulation configurations. However, the findings still provide insights into the effects of key parameters on the EC decomposition mechanism and the followed pathways. This study not only reveals the SEI chemistry in lithium batteries but also provides clues to that in lithium metal batteries. In future research, the electrolyte composition with the presence of novel lithium salts will be studied to further our understanding of the SEI formation.
Author contributions
Jingqi Gao: conceptualization, methodology, software, investigation, data curation, visualization, writing – original draft. Ruitian He: methodology, software, investigation, data curation, writing – review & editing. Kai H. Luo: conceptualization, supervision, resources, investigation, project administration, writing – review & editing.Data availability
All data included in this study are available upon request by contacting the corresponding author.Conflicts of interest
The authors declare that they have no conflicts of interest.Appendices
A. Pathways for the decomposition products of EC
| Pathway | Product | S1 | S2 | S3 | |||
|---|---|---|---|---|---|---|---|
| 300 K | 600 K | 300 K | 600 K | 300 K | 600 K | ||
| A | Li(EC) | 0 | 0 | 1 | 0 | 1 | 2 |
| B | Li(EC) | 3 | 3 | 3 | 3 | 3 | 3 |
| C | Li2(EC) | 3 | 3 | 3 | 3 | 3 | 3 |
| D | Li(EC) | 3 | 3 | 3 | 3 | 3 | 3 |
| E | O1–Li(EC) | 0 | 0 | 0 | 2 | 0 | 1 |
| F | O2–Li(EC) | 2 | 3 | 3 | 3 | 3 | 3 |
| Pathway | Product | S1 | S2 | S3 | |||
|---|---|---|---|---|---|---|---|
| 300 K | 600 K | 300 K | 600 K | 300 K | 600 K | ||
| G | Li2O | 2 | 3 | 3 | 3 | 3 | 3 |
| H | C3H4O2 | 2 | 3 | 3 | 3 | 3 | 3 |
| I | Li3O+ | 0 | 3 | 3 | 3 | 3 | 3 |
| J | CO2 | 0 | 3 | 0 | 3 | 1 | 3 |
| K | C2H4 | 0 | 3 | 1 | 3 | 3 | 3 |
| L | CO32− | 0 | 3 | 2 | 3 | 3 | 3 |
| M | C2H4 | 0 | 3 | 2 | 3 | 3 | 3 |
| N | LiCO3− | 0 | 3 | 1 | 3 | 3 | 3 |
| O | Li2CO3 | 0 | 3 | 1 | 3 | 2 | 3 |
| P | Li3CO3 | 0 | 3 | 0 | 3 | 0 | 3 |
B. Decomposition reaction pathways of EC
Although the bond order relationships and visualisation are used in post-processing as the sole indication for pathways and species identification in current research, Chemical Trajectory AnalYzer (ChemTraYzer, or CTY) script71 is used to aid and assist the analysis of reaction pathways and decomposition mechanisms of ethylene carbonate. Although the CTY script is originally designed for the study of ReaxFF molecular dynamics of fuel in combustion chemistry that is in the gas phase, hence is not suitable in accurately capturing all reaction activities during simulations of current study, this limitation is still realised and the data from CTY is solely used for discovering trends in variations for a variety of simulation scenarios, and compare with the adopted data.The flux value presented in the following tables represents the count of occurrence of corresponding decomposition reaction that is discovered during the studied period of time. The flux value of three replicas of each simulated concentration/temperature is averaged and shown below. Tables 4 and 5 summarise decomposition reactions of ethylene carbonate during NVT ReaxFF MD simulations of EC decomposition at 300 K and 600 K, respectively, while Table 6 includes a summary of pathways for the investigation of selected e-field strength.
| ID | Decomposition reaction | Total flux@300 K | ||
|---|---|---|---|---|
| S1 | S2 | S3 | ||
| R1 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] → [Li]O[C]1OCCO1 C1OCCO1, [Li] → [Li]O[C]1OCCO1 |
2674 | 2116 | 1276 |
| R1* | [Li]O[C]1OCCO1 → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] C1OCCO1, [Li] |
2641 | 2038 | 1193 |
| R2 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li][Li] → [Li], [Li]O[C]1OCCO1 C1OCCO1, [Li][Li] → [Li], [Li]O[C]1OCCO1 |
— | 34 | 82 |
| R2* | [Li], [Li]O[C]1OCCO1 → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li][Li] C1OCCO1, [Li][Li] |
— | 31 | 72 |
| R3 | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → O O)[O] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1 C1OCCO1 |
31 | 68 | 78 |
| R3* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1 → [CH2]COC( C1OCCO1 → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
22 | 56 | 43 |
| R4 | [Li], [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]O[C](O[Li])O[Li] O)[O] → [Li]O[C](O[Li])O[Li] |
— | 5 | 5 |
| R5 | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li]O[C](O[Li])O[Li] O)O[Li] → [Li]O[C](O[Li])O[Li] |
— | 150 | 271 |
| R5* | [Li]O[C](O[Li])O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
— | 149 | 271 |
| R6 | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]OC( O)[O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
— | 121 | 99 |
| R6* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li], [Li]OC( O)O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | 120 | 95 |
| R7 | [Li], [Li]O[C]1OCCO1 → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li][Li] O)[O], [Li][Li] |
— | — | 5 |
| R8 | [Li], [Li]O[C]1OCCO1 → [C]1OCCO1, [Li]O[Li] | — | 292 | 755 |
| R8* | [C]1OCCO1, [Li]O[Li] → [Li], [Li]O[C]1OCCO1 | — | — | 743 |
| R9 | [Li], [Li][O] → [Li]O[Li] | — | — | 6 |
| R10 | [Li], [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]OC( O)[O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 155 |
| R10* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li], [O]C( O)[O] → [Li], [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 148 |
| R11 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → O O)OC[CH2] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] C1OCCO1, [Li] |
18 | 63 | 58 |
| R11* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] → [Li]OC( C1OCCO1, [Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
7 | 46 | 31 |
| R12 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → [CH2]COC( O)OC[CH2] → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] O)[O], [Li] |
6 | 22 | 13 |
| R12* | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] → [Li]OC( O)[O], [Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
6 | 13 | 9 |
| R13 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li], [Li], [O]C( O)O[Li] → [Li], [Li], [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 23 |
| R13* | [Li], [Li], [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]OC( O)[O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
— | — | 18 |
| R14 | [Li]O[C]1OCCO1, [Li][Li] → [Li], [Li], [Li]O[C]1OCCO1 | — | — | 14 |
| R14* | [Li], [Li], [Li]O[C]1OCCO1 → [Li]O[C]1OCCO1, [Li][Li] | — | — | 9 |
| R15 | [Li]O[C]1OCCO1 → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, [Li]OC( C, [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 5 |
| R16 | [Li]O[C]1OCCO1 → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] O)[O], [Li] |
24 | 41 | 57 |
| R16* | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] → [Li]O[C]1OCCO1 O)[O], [Li] → [Li]O[C]1OCCO1 |
16 | 40 | 32 |
| R17 | [Li]O[C]1OCCO1 → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
15 | 88 | 73 |
| R17* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → [Li]O[C]1OCCO1 O)OC[CH2] → [Li]O[C]1OCCO1 |
15 | 56 | 40 |
| R18 | [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] → [Li], [Li]OC( O, [Li]O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
— | — | 9 |
| R18* | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li]O[C] O)O[Li] → [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] O, [Li]O[Li] |
— | — | 8 |
| R19 | [Li]O[Li], [Li]O[Li] → [Li], [Li]O[Li], [Li][O] | — | — | 6 |
| ID | Decomposition reaction | Total flux@600 K | ||
|---|---|---|---|---|
| S1 | S2 | S3 | ||
| R1 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] → [Li]O[C]1OCCO1 C1OCCO1, [Li] → [Li]O[C]1OCCO1 |
3377 | 2260 | 1567 |
| R1* | [Li]O[C]1OCCO1 → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] C1OCCO1, [Li] |
3339 | 2239 | 1524 |
| R2 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li][Li] → [Li], [Li]O[C]1OCCO1 C1OCCO1, [Li][Li] → [Li], [Li]O[C]1OCCO1 |
— | — | 16 |
| R2* | [Li], [Li]O[C]1OCCO1 → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li][Li] C1OCCO1, [Li][Li] |
— | — | 14 |
| R3 | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → O O)[O] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1 C1OCCO1 |
14 | 21 | 21 |
| R3* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1 → [CH2]COC( C1OCCO1 → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
17 | 25 | 18 |
| R4 | [Li], [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]O[C](O[Li])O[Li] O)[O] → [Li]O[C](O[Li])O[Li] |
12 | 15 | 19 |
| R4* | [Li]O[C](O[Li])O[Li] → [Li], [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
17 | 10 | 14 |
| R5 | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li]O[C](O[Li])O[Li] O)O[Li] → [Li]O[C](O[Li])O[Li] |
489 | 480 | 610 |
| R5* | [Li]O[C](O[Li])O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
499 | 489 | 624 |
| R6 | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]OC( O)[O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
495 | 582 | 756 |
| R6* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li], [Li]OC( O)O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
499 | 573 | 743 |
| R8 | [Li], [Li]O[C]1OCCO1 → [C]1OCCO1, [Li]O[Li] | 158 | 159 | 102 |
| R8* | [C]1OCCO1, [Li]O[Li] → [Li], [Li]O[C]1OCCO1 | 153 | 151 | 99 |
| R11 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → O O)OC[CH2] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] C1OCCO1, [Li] |
5 | 20 | 28 |
| R11* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] → [Li]OC( C1OCCO1, [Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
8 | 13 | 22 |
| R12 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → [CH2]COC( O)OC[CH2] → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] O)[O], [Li] |
— | 8 | 8 |
| R12* | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] → [Li]OC( O)[O], [Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
8 | 10 | — |
| R16 | [Li]O[C]1OCCO1 → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] O)[O], [Li] |
9 | 10 | 12 |
| R16* | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] → [Li]O[C]1OCCO1 O)[O], [Li] → [Li]O[C]1OCCO1 |
5 | 11 | 14 |
| R17 | [Li]O[C]1OCCO1 → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
9 | 41 | 48 |
| R17* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → [Li]O[C]1OCCO1 O)OC[CH2] → [Li]O[C]1OCCO1 |
12 | 26 | 14 |
| R18 | [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] → [Li], [Li]OC( O, [Li]O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
75 | 87 | 111 |
| R18* | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li]O[C] O)O[Li] → [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] O, [Li]O[Li] |
84 | 82 | 109 |
| R20 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] → [Li], [Li]OC( O, [Li]O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
9 | 17 | 28 |
| R20* | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → O O)[O] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] O, [Li]O[Li] |
7 | 13 | 23 |
| R21 | [CH2]CO[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → C O → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, O C, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
— | 8 | 10 |
| R22 | [C]1OCCO1 → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, O C, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
— | — | 7 |
| R23 | [C]1OCCO1 → [CH2]CO[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
7 | 17 | 43 |
| R23* | [CH2]CO[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → [C]1OCCO1 O → [C]1OCCO1 |
5 | 11 | 39 |
| R24 | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li], [Li], [Li]OC( O)O[Li] → [Li], [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
9 | — | 9 |
| R24* | [Li], [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li], [Li]OC( O)[O] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
6 | — | 8 |
| R25 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → C O)OC[CH2] → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, [Li]OC( C, [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
7 | 14 | 23 |
| R26 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → O O)O[Li] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] O, [Li]O[Li] |
12 | 18 | 32 |
| R26* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] → [Li]OC( O, [Li]O[Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
9 | 13 | 23 |
| R27 | [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] → [Li]O[C](O[Li])O[Li] O, [Li]O[Li] → [Li]O[C](O[Li])O[Li] |
17 | 13 | 20 |
| R27* | [Li]O[C](O[Li])O[Li] → [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] O, [Li]O[Li] |
7 | 16 | 18 |
| R28 | [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → O O → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, O[Li] O, O[Li] |
— | — | 9 |
| R28* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li] → [Li]O[C] O, [Li] → [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
— | — | 7 |
| R29 | [Li], [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li], [Li]OC( O)[O] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
— | 7 | — |
| ID | Decomposition reaction | Total flux S1@300 K | ||
|---|---|---|---|---|
| E = 0.1 | E = 0.2 | E = 0.3 | ||
| R1 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] → [Li]O[C]1OCCO1 C1OCCO1, [Li] → [Li]O[C]1OCCO1 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 877 877 |
6285 | 5051 |
| R1* | [Li]O[C]1OCCO1 → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] C1OCCO1, [Li] |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 815 815 |
6251 | 5048 |
| R2 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li][Li] → [Li], [Li]O[C]1OCCO1 C1OCCO1, [Li][Li] → [Li], [Li]O[C]1OCCO1 |
13 | 8 | 8 |
| R2* | [Li], [Li]O[C]1OCCO1 → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li][Li] C1OCCO1, [Li][Li] |
18 | 6 | 9 |
| R3 | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → O O)[O] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1 C1OCCO1 |
1993 | 358 | 261 |
| R3* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1 → [CH2]COC( C1OCCO1 → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
1965 | 356 | 271 |
| R4 | [Li], [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]O[C](O[Li])O[Li] O)[O] → [Li]O[C](O[Li])O[Li] |
— | — | 8 |
| R4* | [Li]O[C](O[Li])O[Li] → [Li], [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 8 |
| R5 | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li]O[C](O[Li])O[Li] O)O[Li] → [Li]O[C](O[Li])O[Li] |
— | — | 511 |
| R5* | [Li]O[C](O[Li])O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
— | — | 519 |
| R6 | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]OC( O)[O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
— | 1805 | 3593 |
| R6* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → [Li], [Li]OC( O)O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | 1797 | 3590 |
| R8 | [Li], [Li]O[C]1OCCO1 → [C]1OCCO1, [Li]O[Li] | 1252 | 2176 | 1379 |
| R8* | [C]1OCCO1, [Li]O[Li] → [Li], [Li]O[C]1OCCO1 | 1246 | 2170 | 1371 |
| R9 | [Li], [Li][O] → [Li]O[Li] | — | 61 | 40 |
| R9* | [Li]O[Li] → [Li], [Li][O] | — | 63 | 41 |
| R10 | [Li], [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]OC( O)[O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 19 |
| R10* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li], [O]C( O)[O] → [Li], [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 16 |
| R11 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → O O)OC[CH2] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] C1OCCO1, [Li] |
107 | 42 | 46 |
| R11* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1, [Li] → [Li]OC( C1OCCO1, [Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
100 | 40 | 49 |
| R12 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → [CH2]COC( O)OC[CH2] → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] O)[O], [Li] |
26 | 6 | 16 |
| R12* | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] → [Li]OC( O)[O], [Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
20 | 9 | 16 |
| R15 | [Li]O[C]1OCCO1 → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, [Li]OC( C, [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | 7 | 9 |
| R15* | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, [Li]OC( C, [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]O[C]1OCCO1 O)[O] → [Li]O[C]1OCCO1 |
8 | — | 7 |
| R16 | [Li]O[C]1OCCO1 → [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] O)[O], [Li] |
109 | 45 | 26 |
| R16* | [CH2]COC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li] → [Li]O[C]1OCCO1 O)[O], [Li] → [Li]O[C]1OCCO1 |
89 | 22 | 36 |
| R17 | [Li]O[C]1OCCO1 → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
249 | 177 | 162 |
| R17* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → [Li]O[C]1OCCO1 O)OC[CH2] → [Li]O[C]1OCCO1 |
237 | 174 | 161 |
| R19 | [Li]O[Li], [Li]O[Li] → [Li], [Li]O[Li], [Li][O] | — | 57 | 27 |
| R19* | [Li]O[Li], [Li]O[Li] → [Li], [Li]O[Li], [Li][O] | — | 56 | 27 |
| R20 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] → [Li], [Li]OC( O, [Li]O[Li] → [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | 36 | 67 |
| R20* | [Li], [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → O O)[O] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] O, [Li]O[Li] |
— | 35 | 65 |
| R21 | [CH2]CO[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → C O → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, O C, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
21 | — | — |
| R21* | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, O C, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → [CH2]CO[C] O → [CH2]CO[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
17 | — | — |
| R22 | [C]1OCCO1 → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, O C, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
67 | 14 | — |
| R22* | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, O C, O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → [C]1OCCO1 O → [C]1OCCO1 |
71 | 8 | — |
| R23 | [C]1OCCO1 → [CH2]CO[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
2002 | 601 | 32 |
| R23* | [CH2]CO[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → [C]1OCCO1 O → [C]1OCCO1 |
1999 | 603 | 30 |
| R25 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] → C O)OC[CH2] → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, [Li]OC( C, [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
12 | 9 | 10 |
| R25* | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, [Li]OC( C, [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]OC( O)[O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)OC[CH2] O)OC[CH2] |
7 | 7 | 6 |
| R26 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] → O O)O[Li] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] O, [Li]O[Li] |
— | 33 | 60 |
| R26* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] → [Li]OC( O, [Li]O[Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li] O)O[Li] |
— | 32 | 58 |
| R27 | [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] → [Li]O[C](O[Li])O[Li] O, [Li]O[Li] → [Li]O[C](O[Li])O[Li] |
— | — | 15 |
| R27* | [Li]O[C](O[Li])O[Li] → [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li]O[Li] O, [Li]O[Li] |
— | — | 7 |
| R28 | [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O → O O → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li] O, [Li] |
— | — | 95 |
| R28* | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, [Li] → [Li]O[C] O, [Li] → [Li]O[C]![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
— | — | 90 |
| R30 | O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1 → C C1OCCO1 → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, [O]C( C, [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 8 |
| R30* | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C, [O]C( C, [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → O O)[O] → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C1OCCO1 C1OCCO1 |
— | 5 | 5 |
| R31 | [Li]O[Li], [O] → [Li][O], [Li][O] | — | — | 132 |
| R31* | [Li][O], [Li][O] → [Li]O[Li], [O] | — | 5 | 120 |
| R32 | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li]O[Li] → [Li]OC( O)[O], [Li]O[Li] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li], [Li][O] O)O[Li], [Li][O] |
— | — | 7 |
| R32* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)O[Li], [Li][O] → [Li]OC( O)O[Li], [Li][O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li]O[Li] O)[O], [Li]O[Li] |
— | — | 5 |
| R33 | [Li]O[Li], [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] → [Li]OC( O)[O] → [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li][O] O)[O], [Li][O] |
— | — | 7 |
| R33* | [Li]OC(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O], [Li][O] → [Li]O[Li], [O]C( O)[O], [Li][O] → [Li]O[Li], [O]C(![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O)[O] O)[O] |
— | — | 6 |
Acknowledgements
Support from the UK Engineering and Physical Sciences Research Council under Grant No. EP/T015233/1 and EP/X035875/1 is gratefully acknowledged. This work made use of ARCHER2 and the computational support by CoSeC, the Computational Science Centre for Research Communities, through the UK Consortium on Mesoscale Engineering Sciences (UKCOMES).References
- J. R. Dahn, Phase diagram of LiC6, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(17), 9170–9177 CrossRef CAS PubMed.
- P. Arora, R. E. White and M. Doyle, Capacity Fade Mechanisms and Side Reactions in Lithium-Ion Batteries, J. Electrochem. Soc., 1998, 145(10), 3647 CrossRef CAS.
- P. Verma, P. Maire and P. Novák, A review of the features and analyses of the solid electrolyte interphase in Li-ion batteries, Electrochim. Acta, 2010, 55(22), 6332–6341 CrossRef CAS.
- L. Seidl, S. Martens, J. Ma, U. Stimming and O. Schneider, In situ scanning tunneling microscopy studies of the SEI formation on graphite electrodes for Li+-ion batteries, Nanoscale, 2016, 8(29), 14004–14014 RSC.
- K. Xu, Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries, Chem. Rev., 2004, 104(10), 4303–4418 CrossRef CAS PubMed.
- R. Fong, U. von Sacken and J. R. Dahn, Studies of lithium intercalation into carbons using nonaqueous electrochemical cells, J. Electrochem. Soc., 1990, 137, 7 CrossRef . Available from: https://www.osti.gov/biblio/6393800.
- O. Borodin and G. D. Smith, Quantum Chemistry and Molecular Dynamics Simulation Study of Dimethyl Carbonate: Ethylene Carbonate Electrolytes Doped with LiPF6, J. Phys. Chem. B, 2009, 113(6), 1763–1776 CrossRef CAS PubMed.
- X. You, M. I. Chaudhari, S. B. Rempe and L. R. Pratt, Dielectric Relaxation of Ethylene Carbonate and Propylene Carbonate from Molecular Dynamics Simulations, J. Phys. Chem. B, 2016, 120(8), 1849–1853 CrossRef CAS PubMed.
- X. Wang, G. Pawar, Y. Li, X. Ren, M. Zhang and B. Lu, et al., Glassy Li metal anode for high-performance rechargeable Li batteries, Nat. Mater., 2020, 19(12), 1339–1345 CrossRef CAS PubMed.
- V. Etacheri, O. Haik, Y. Goffer, G. A. Roberts, I. C. Stefan and R. Fasching, et al., Effect of Fluoroethylene Carbonate (FEC) on the Performance and Surface Chemistry of Si-Nanowire Li-Ion Battery Anodes, Langmuir, 2012, 28(1), 965–976 CrossRef CAS PubMed.
- C. Xu, F. Lindgren, B. Philippe, M. Gorgoi, F. Björefors and K. Edström, et al., Improved Performance of the Silicon Anode for Li-Ion Batteries: Understanding the Surface Modification Mechanism of Fluoroethylene Carbonate as an Effective Electrolyte Additive, Chem. Mater., 2015, 27(7), 2591–2599 CrossRef CAS.
- Y. Wang, S. Nakamura, M. Ue and P. B. Balbuena, Theoretical studies to understand surface chemistry on carbon anodes for lithium-ion batteries: reduction mechanisms of ethylene carbonate, J. Am. Chem. Soc., 2001, 123(47), 11708–11718 CrossRef CAS PubMed.
- K. Tasaki, Solvent Decompositions and Physical Properties of Decomposition Compounds in Li-Ion Battery Electrolytes Studied by DFT Calculations and Molecular Dynamics Simulations, J. Phys. Chem. B, 2005, 109(7), 2920–2933 CrossRef CAS PubMed.
- K. Tasaki, K. Kanda, T. Kobayashi, S. Nakamura and M. Ue, Theoretical Studies on the Reductive Decompositions of Solvents and Additives for Lithium-Ion Batteries near Lithium Anodes, J. Electrochem. Soc., 2006, 153(12), A2192 CrossRef CAS.
- M. A. Gialampouki, J. Hashemi and A. A. Peterson, The Electrochemical Mechanisms of Solid–Electrolyte Interphase Formation in Lithium-Based Batteries, J. Phys. Chem. C, 2019, 123(33), 20084–20092 CrossRef CAS.
- K. Leung and J. L. Budzien, Ab initio molecular dynamics simulations of the initial stages of solid–electrolyte interphase formation on lithium ion battery graphitic anodes, Phys. Chem. Chem. Phys., 2010, 12(25), 6583–6586 RSC.
- P. Ganesh, P. R. C. Kent and D. E. Jiang, Solid–Electrolyte Interphase Formation and Electrolyte Reduction at Li-Ion Battery Graphite Anodes: Insights from First-Principles Molecular Dynamics, J. Phys. Chem. C, 2012, 116(46), 24476–24481 CrossRef CAS.
- W. I. Choi, M. S. Park, Y. Shim, D. Y. Kim, Y. S. Kang and H. S. Lee, et al., Reductive reactions via excess Li in mixture electrolytes of Li ion batteries: an ab initio molecular dynamics study, Phys. Chem. Chem. Phys., 2019, 21(10), 5489–5498 RSC.
- Y. Okuno, K. Ushirogata, K. Sodeyama and Y. Tateyama, Decomposition of the fluoroethylene carbonate additive and the glue effect of lithium fluoride products for the solid electrolyte interphase: an ab initio study, Phys. Chem. Chem. Phys., 2016, 18(12), 8643–8653 RSC.
- K. Leung, Predicting the voltage dependence of interfacial electrochemical processes at lithium-intercalated graphite edge planes, Phys. Chem. Chem. Phys., 2014, 17(3), 1637–1643 RSC.
- K. Leung, Electronic Structure Modeling of Electrochemical Reactions at Electrode/Electrolyte Interfaces in Lithium Ion Batteries, J. Phys. Chem. C, 2013, 117(4), 1539–1547 CrossRef CAS.
- N. Takenaka, Y. Suzuki, H. Sakai and M. Nagaoka, On Electrolyte-Dependent Formation of Solid Electrolyte Interphase Film in Lithium-Ion Batteries: Strong Sensitivity to Small Structural Difference of Electrolyte Molecules, J. Phys. Chem. C, 2014, 118(20), 10874–10882 CrossRef CAS.
- N. Takenaka, H. Sakai, Y. Suzuki, P. Uppula and M. Nagaoka, A Computational Chemical Insight into Microscopic Additive Effect on Solid Electrolyte Interphase Film Formation in Sodium-Ion Batteries: Suppression of Unstable Film Growth by Intact Fluoroethylene Carbonate, J. Phys. Chem. C, 2015, 119(32), 18046–18055 CrossRef CAS.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF:
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105(41), 9396–9409 CrossRef CAS.
A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105(41), 9396–9409 CrossRef CAS. - S. P. Kim, A. C. T. van Duin and V. B. Shenoy, Effect of electrolytes on the structure and evolution of the solid electrolyte interphase (SEI) in Li-ion batteries: A molecular dynamics study, J. Power Sources, 2011, 196(20), 8590–8597 CrossRef CAS.
- M. Zhou, C. Feng, R. Xiong, L. Li, T. Huang and M. Li, et al., Molecular Insights into the Structure and Property Variation of the Pressure-Induced Solid Electrolyte Interphase on a Lithium Metal Anode, ACS Appl. Mater. Interfaces, 2022, 14(21), 24875–24885 CrossRef CAS PubMed.
- D. Bedrov, G. D. Smith and A. C. T. van Duin, Reactions of Singly-Reduced Ethylene Carbonate in Lithium Battery Electrolytes: A Molecular Dynamics Simulation Study Using the ReaxFF, J. Phys. Chem. A, 2012, 116(11), 2978–2985 CrossRef CAS PubMed.
- M. M. Islam, V. S. Bryantsev and A. C. T. van Duin, ReaxFF Reactive Force Field Simulations on the Influence of Teflon on Electrolyte Decomposition during Li/SWCNT Anode Discharge in Lithium-Sulfur Batteries, J. Electrochem. Soc., 2014, 161(8), E3009 CrossRef CAS.
- K. Xu and A. von Cresce, Interfacing electrolytes with electrodes in Li ion batteries, J. Mater. Chem., 2011, 21(27), 9849–9864 RSC.
- J. M. Tarascon and M. Armand, Issues and challenges facing rechargeable lithium batteries, Nature, 2001, 414(6861), 359–367 CrossRef CAS PubMed.
- F. Ospina-Acevedo, N. Guo and P. B. Balbuena, Lithium oxidation and electrolyte decomposition at Li-metal/liquid electrolyte interfaces, J. Mater. Chem. A, 2020, 8(33), 17036–17055 RSC.
- S. Bertolini and P. B. Balbuena, Buildup of the Solid Electrolyte Interphase on Lithium-Metal Anodes: Reactive Molecular Dynamics Study, J. Phys. Chem. C, 2018, 122(20), 10783–10791 CrossRef CAS.
- J. Gao, G. Wang and K. H. Luo, Formation of solid electrolyte interphase in Li-ion batteries: Insights from temperature-accelerated ReaxFF molecular dynamics, Appl. Energy, 2024, 371, 123708 CrossRef CAS.
- Avogadro: an open-source molecular builder and visualization tool, [Internet], Avogadro, 2022 [cited 2023 Feb 16], Available from: https://avogadro.cc/.
- M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, Avogadro: an advanced semantic chemical editor, visualization, and analysis platform, J. Cheminf., 2012, 4(1), 17 CAS.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, PACKMOL: A package for building initial configurations for molecular dynamics simulations, J. Comput. Chem., 2009, 30(13), 2157–2164 CrossRef PubMed.
- H. M. Aktulga, J. C. Fogarty, S. A. Pandit and A. Y. Grama, Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques, Parallel Comput., 2012, 38(4–5), 245–259 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown and P. S. Crozier, et al., LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- S. Plimpton, Fast Parallel Algorithms for Short-Range Molecular Dynamics, J. Comput. Phys., 1995, 117(1), 1–19 CrossRef CAS.
- D. Hou, M. Feng, J. Wei, Y. Wang, A. C. T. van Duin and K. H. Luo, A reactive force field molecular dynamics study on the inception mechanism of titanium tetraisopropoxide (TTIP) conversion to titanium clusters, Chem. Eng. Sci., 2022, 252, 117496 CrossRef CAS.
- M. Feng, H. Li, Q. Mao, K. H. Luo and P. Hellier, Fundamental Study on Mechanisms of Thermal Decomposition and Oxidation of Aluminum Hydride, J. Phys. Chem. C, 2019, 123(40), 24436–24445 CrossRef CAS.
- M. Feng, H. Li and K. H. Luo, A molecular dynamics study on oxidation of aluminum hydride (AlH3)/hydroxyl-terminated polybutadiene (HTPB) solid fuel, Proc. Combust. Inst., 2021, 38(3), 4469–4476 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14(1), 33–38 CrossRef CAS PubMed.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2009, 18(1), 015012 CrossRef.
- M. M. Islam and A. C. T. van Duin, Reductive Decomposition Reactions of Ethylene Carbonate by Explicit Electron Transfer from Lithium: An eReaxFF Molecular Dynamics Study, J. Phys. Chem. C, 2016, 120(48), 27128–27134 CrossRef CAS.
- X. Teng, C. Zhan, Y. Bai, L. Ma, Q. Liu and C. Wu, et al., In Situ Analysis of Gas Generation in Lithium-Ion Batteries with Different Carbonate-Based Electrolytes, ACS Appl. Mater. Interfaces, 2015, 7(41), 22751–22755 CrossRef CAS PubMed.
- J. Zhang, J. Yang, L. Yang, H. Lu, H. Liu and B. Zheng, Exploring the redox decomposition of ethylene carbonate–propylene carbonate in Li-ion batteries, Mater. Adv., 2021, 2(5), 1747–1751 RSC.
- K. Leung and J. L. Budzien, Ab initio molecular dynamics simulations of the initial stages of solid–electrolyte interphase formation on lithium ion battery graphitic anodes, Phys. Chem. Chem. Phys., 2010, 12(25), 6583–6586 RSC.
- J. L. Tebbe, T. F. Fuerst and C. B. Musgrave, Degradation of Ethylene Carbonate Electrolytes of Lithium Ion Batteries via Ring Opening Activated by LiCoO2 Cathode Surfaces and Electrolyte Species, ACS Appl. Mater. Interfaces, 2016, 8(40), 26664–26674 CrossRef CAS PubMed.
- K. S. Yun, S. J. Pai, B. C. Yeo, K. R. Lee, S. J. Kim and S. S. Han, Simulation Protocol for Prediction of a Solid-Electrolyte Interphase on the Silicon-based Anodes of a Lithium-Ion Battery: ReaxFF Reactive Force Field, J. Phys. Chem. Lett., 2017, 8(13), 2812–2818 CrossRef CAS PubMed.
- T. Gao and W. Lu, Mechanism and effect of thermal degradation on electrolyte ionic diffusivity in Li-ion batteries: A molecular dynamics study, Electrochim. Acta, 2019, 323, 134791 CrossRef CAS.
- Y. Wang, Y. Liu, Y. Tu and Q. Wang, Reductive Decomposition of Solvents and Additives toward Solid-Electrolyte Interphase Formation in Lithium-Ion Battery, J. Phys. Chem. C, 2020, 124(17), 9099–9108 CrossRef CAS.
- B. B. Berkes, A. Jozwiuk, H. Sommer, T. Brezesinski and J. Janek, Simultaneous acquisition of differential electrochemical mass spectrometry and infrared spectroscopy data for in situ characterization of gas evolution reactions in lithium-ion batteries, Electrochem. Commun., 2015, 60, 64–69 CrossRef CAS.
- J. Young, P. M. Kulick, T. R. Juran and M. Smeu, Comparative Study of Ethylene Carbonate-Based Electrolyte Decomposition at Li, Ca, and Al Anode Interfaces, ACS Appl. Energy Mater., 2019, 2(3), 1676–1684 CrossRef CAS.
- N. Ohba, S. Ogata and R. Asahi, Hybrid Quantum-Classical Simulation of Li Ion Dynamics and the Decomposition Reaction of Electrolyte Liquid at a Negative-Electrode/Electrolyte Interface, J. Phys. Chem. C, 2019, 123(15), 9673–9679 CrossRef CAS.
- L. Alzate-Vargas, S. M. Blau, E. W. C. Spotte-Smith, S. Allu, K. A. Persson and J. L. Fattebert, Insight into SEI Growth in Li-Ion Batteries using Molecular Dynamics and Accelerated Chemical Reactions, J. Phys. Chem. C, 2021, 125(34), 18588–18596 CrossRef CAS.
- T. Momma, H. Nara, S. Yamagami, C. Tatsumi and T. Osaka, Effect of the atmosphere on chemical composition and electrochemical properties of solid electrolyte interface on electrodeposited Li metal, J. Power Sources, 2011, 196(15), 6483–6487 CrossRef CAS.
- X. B. Cheng, R. Zhang, C. Z. Zhao, F. Wei, J. G. Zhang and Q. Zhang, A Review of Solid Electrolyte Interphases on Lithium Metal Anode. Advanced, Science, 2016, 3(3), 1500213 Search PubMed.
- K. Kanamura, H. Tamura, S. Shiraishi and Z. Takehara, XPS Analysis of Lithium Surfaces Following Immersion in Various Solvents Containing LiBF4, J. Electrochem. Soc., 1995, 142(2), 340–347 CrossRef CAS.
- A. Schechter, D. Aurbach and H. Cohen, X-ray Photoelectron Spectroscopy Study of Surface Films Formed on Li Electrodes Freshly Prepared in Alkyl Carbonate Solutions, Langmuir, 1999, 15(9), 3334–3342 CrossRef CAS.
- J. Young and M. Smeu, Ethylene Carbonate-Based Electrolyte Decomposition and Solid–Electrolyte Interphase Formation on Ca Metal Anodes, J. Phys. Chem. Lett., 2018, 9(12), 3295–3300 CrossRef CAS PubMed.
- J. Yu, P. B. Balbuena, J. Budzien and K. Leung, Hybrid DFT Functional-Based Static and Molecular Dynamics Studies of Excess Electron in Liquid Ethylene Carbonate, J. Electrochem. Soc., 2011, 158(4), A400 CrossRef CAS.
- K. Leung, Two-electron reduction of ethylene carbonate: A quantum chemistry re-examination of mechanisms, Chem. Phys. Lett., 2013, 568–569, 1–8 CrossRef CAS.
- M. D. Brennan, M. Breedon, A. S. Best, T. Morishita and M. J. S. Spencer, Surface Reactions of Ethylene Carbonate and Propylene Carbonate on the Li(001) Surface, Electrochim. Acta, 2017, 243, 320–330 CrossRef CAS.
- Y. Xu, H. Wu, H. Jia, M. H. Engelhard, J. G. Zhang and W. Xu, et al., Sweeping potential regulated structural and chemical evolution of solid-electrolyte interphase on Cu and Li as revealed by cryo-TEM, Nano Energy, 2020, 76, 105040 CrossRef CAS.
- P. Mukherjee, A. Lagutchev and D. D. Dlott, In Situ Probing of Solid-Electrolyte Interfaces with Nonlinear Coherent Vibrational Spectroscopy, J. Electrochem. Soc., 2011, 159(3), A244 CrossRef.
- G. V. Zhuang, K. Xu, H. Yang, T. R. Jow and P. N. Ross, Lithium Ethylene Dicarbonate Identified as the Primary Product of Chemical and Electrochemical Reduction of EC in 1.2 M LiPF6/EC:EMC Electrolyte, J. Phys. Chem. B, 2005, 109(37), 17567–17573 CrossRef CAS PubMed.
- K. Xu, Y. Lam, S. S. Zhang, T. R. Jow and T. B. Curtis, Solvation Sheath of Li+ in Nonaqueous Electrolytes and Its Implication of Graphite/Electrolyte Interface Chemistry, J. Phys. Chem. C, 2007, 111(20), 7411–7421 CrossRef CAS.
- I. Hasa, A. M. Haregewoin, L. Zhang, W. Y. Tsai, J. Guo and G. M. Veith, et al., Electrochemical Reactivity and Passivation of Silicon Thin-Film Electrodes in Organic Carbonate Electrolytes, ACS Appl. Mater. Interfaces, 2020, 12(36), 40879–40890 CrossRef CAS PubMed.
- S. Nasu and H. Takeshita, The lattice energy of lithium monoxide, J. Nucl. Mater., 1978, 75(1), 110–114 CrossRef CAS.
- M. Döntgen, M. D. Przybylski-Freund, L. C. Kröger, W. A. Kopp, A. E. Ismail and K. Leonhard, Automated Discovery of Reaction Pathways, Rate Constants, and Transition States Using Reactive Molecular Dynamics Simulations, J. Chem. Theory Comput., 2015, 11(6), 2517–2524 CrossRef PubMed.
| This journal is © the Owner Societies 2024 |