Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing the conformational dynamics of an Ago–RNA complex in water/methanol solution†
Francesco
Porcelli
 a,
Anna Rita
Casavola
a,
Alessandro
Grottesi
b,
Donatella
Schiumarini
a and
Lorenzo
Avaldi
a,
Anna Rita
Casavola
a,
Alessandro
Grottesi
b,
Donatella
Schiumarini
a and
Lorenzo
Avaldi
 a
a
aCNR-Istituto di Struttura della Materia, Area della Ricerca di Roma 1, CP 10 Monterotondo Scalo, Italy. E-mail: Francesco.Porcelli@mlib.ism.cnr.it
bCineca, Via dei Tizii, 6, Rome, Italy
First published on 15th December 2023
Abstract
Argonaute (Ago) proteins mediate target recognition guiding miRNA to bind complementary mRNA primarily in the seed region. However, additional pairing can occur beyond the seed, forming a supplementary duplex that can contribute to the guide–target affinity. In order to shed light on the connection, between protein–RNA interactions and miRNA–mRNA seed and supplementary duplex mobility, we carried out molecular dynamics simulations at the microsecond time-scale using a different approach compared to the ones normally used. Until now, theoretical investigations with classical MD on Ago–RNA complexes have been focused primarily on pure water solvent, which mimics the natural environment of biological molecules. Here, we explored the conformational space of a human Ago2 (hAgo2) bound to the seed + supplementary miRNA–mRNA duplex, using the solvent environment as a molecular probe. MD simulations have been performed in a mixture of water/MeOH at a molar ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30 as well as in pure water for comparison. Our findings revealed that the mixed solvent promotes protein RNA association, principally enhancing salt–linkages between basic amino acid side-chains and acidic phosphates of the sugar–phosphate backbone. The primary effect registered was the restriction of supplementary duplex flexibility and the stabilization of the miRNA 3′ terminus. Interestingly, we observed that the influence of the solvent appears to have almost no impact on the conformation of the seed duplex.
30 as well as in pure water for comparison. Our findings revealed that the mixed solvent promotes protein RNA association, principally enhancing salt–linkages between basic amino acid side-chains and acidic phosphates of the sugar–phosphate backbone. The primary effect registered was the restriction of supplementary duplex flexibility and the stabilization of the miRNA 3′ terminus. Interestingly, we observed that the influence of the solvent appears to have almost no impact on the conformation of the seed duplex.
1. Introduction
MicroRNAs (miRNAs) are a class of small (21–23 nt) non-coding single strained RNAs,1 which interact with complementary target RNAs through the action of the argonaute (AGO) protein, that represents the catalytic part of the RNA-induced silencing complex (RISC).2,3 The AGO protein makes guiding miRNA recognize and locate complementary sequences in the RNA target. These targets are then silenced inducing their suppression or degradation. Among the different kinds of Ago proteins, the human ago2 protein (hAgo2) is known to possess slicer activity in RISC.4 Ago2 is organized in six functional domains: N, L1, PAZ, L2, MID and PIWI.5 Typically, miRNA interacts with the target, pairing 6–8 bases in the seed region (nt 2–8 from the 5′ end), shielding its 3’ end inside the PAZ domain and preventing exonucleases and transferases.6 It is extensively understood that about 80% of target recognition occurs in the seed region, through complementary base pairing with the miRNA.7 However, supplementary base pairing can take place beyond the seed8 enhancing guide–targeting affinity.9 Where extensive base pairing exists, the crystal structure of human Ago2 bound to the miRNA–mRNA duplex can be divided into three macro domains (Fig. 1). The model structure, employed in our simulations, has a seed chamber with complementary base pairing involving nucleotides g2–g8 of miRNA. A central gate consists of four unpaired bases and a supplementary duplex between nucleotides g13 and g16. Although the duplex in the central gate is formed by complementary bases, the pairing between them is forbidden because of the steric clash8 with nearby protein domains. 5′ and 3′ termini of miRNA are directly anchored in MID and PAZ domain respectively, preventing enzymatic attacks which can lead to miRNA degradation.10 The conformational dynamics of the Ago–RNA complex have been widely explored.11–19 However, the role of non-bonded interactions related to complex stability and flexibility has not been fully studied. In particular, our study has investigated the contribution of electrostatic interactions, between positively charged residues on protein side chains and negative phosphates of duplex backbones, related to the conformational dynamics of the selected Ago–RNA complex. Until now, molecular dynamics simulation of the Ago–RNA complexes has been conducted in water, starting from a validated crystallographic structure and inserting targeted mutations at specific RNA residues. The impact of additional base pairs, located beyond the seed region, on the conformational dynamics of an Ago–RNA complex was recently investigated11 examining how different patterns of base pairing and variations in the mRNA length influenced the complex's structure and behavior. In order to explore in more detail, the binding pocket between protein and RNA, we performed MD at the microsecond timescale level, varying the solvent environment from pure water to a water/methanol solution having a molar ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30, corresponding to a volume ratio of 50%.20 It is widely understood that polar organic solvents promote protein precipitation and/or refolding.21–23 For the oligonucleotide counterpart, a solvent with low polarity, can promote base pair opening24 mainly due to the repulsion of the negative charge on a sugar phosphate backbone. In general, for protein complexes, computational studies such as molecular docking and molecular dynamics simulations performed in different solvents, can provide information related to specific site interactions between a protein and small ligand as well as protein and protein, particularly in the field of drug design25–27 or to detect cryptic binding sites in proteins.28–30Considering protein RNA/DNA complexes, the role of amino-acids and nucleobases related to the strength of protein–oligonucleotide interactions, was also investigated using molecular dynamics simulations in methanol.31 Our study provides new insights into the relationship between seed and supplementary duplex mobility. Modifying the solvent environment from water to water/MeOH, the complex experiences a conformational rearrangement produced by stronger Ago and RNA interactions. Interestingly this effect appears to be strongly domain dependent.
30, corresponding to a volume ratio of 50%.20 It is widely understood that polar organic solvents promote protein precipitation and/or refolding.21–23 For the oligonucleotide counterpart, a solvent with low polarity, can promote base pair opening24 mainly due to the repulsion of the negative charge on a sugar phosphate backbone. In general, for protein complexes, computational studies such as molecular docking and molecular dynamics simulations performed in different solvents, can provide information related to specific site interactions between a protein and small ligand as well as protein and protein, particularly in the field of drug design25–27 or to detect cryptic binding sites in proteins.28–30Considering protein RNA/DNA complexes, the role of amino-acids and nucleobases related to the strength of protein–oligonucleotide interactions, was also investigated using molecular dynamics simulations in methanol.31 Our study provides new insights into the relationship between seed and supplementary duplex mobility. Modifying the solvent environment from water to water/MeOH, the complex experiences a conformational rearrangement produced by stronger Ago and RNA interactions. Interestingly this effect appears to be strongly domain dependent.
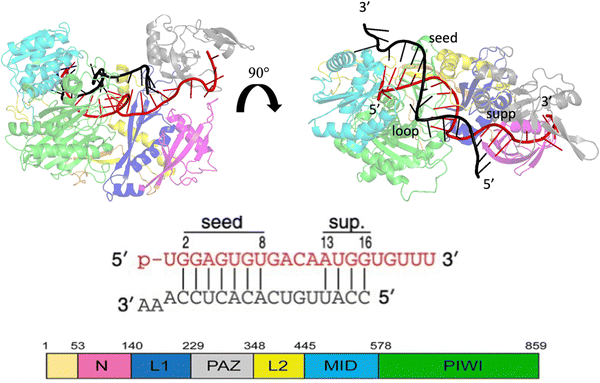 | ||
| Fig. 1 Crystallographic structure of the Human Argonaute2-miR-122 complex (PDB:6N4O), the protein domains are colored as given in the scheme at the bottom left. Guide miRNA is red colored, while target mRNA is black colored. | ||
2. Materials and methods
2.1. Structure preparation
The crystal structure of a seed + supplementary miRNA–mRNA duplex bound with hAGO2 (PDB entry: 6N4O) was selected for the conformational exploration using classical molecular dynamics. Missing residues on protein were supplied with the SWISS-Model webtool database32 except for the first 22 amino acids. The incomplete structure of the RNA duplex was instead separately reconstructed with ModeRNA,33 inserting missing A and U residues at positions 10 and 19 of the guide miRNA and GUC at positions 6–8 of the target RNA as well as UU at the mRNA 3′ terminus. Before complex assembly, the RNA structure with minimum energy was searched using the QRNAS 3.0 package.34 Using the above reported protocol, we obtained a very good agreement between the reconstructed complex structure and the database one, with a RMSD of 0.351 Å calculated between common atoms. This value is almost one order of magnitude less than the reported crystallographic resolution of 2.91 Å for 6N4O, indicating a suitable starting structure for conformational dynamics exploration.2.2 MD protocol
Two systems were considered in our MD protocol, one system in water and a second one immersed in water/MeOH solvent having a molar ratio of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30. The topology was built using Gromacs 2021.535 with the amber99sb-ildn force-field.36 The system was then inserted at the center of a dodecahedron box leaving a distance of 1.0 nm from the box wall to avoid interaction with periodic replica. The TIP3P model37 was employed for the implicit water solvent while the topology of methanol molecules was assigned using a generalized amber force field (GAFF).38 The number of methanol molecules to be added to reproduce the desired water/MeOH ratio was calculated as follows:
30. The topology was built using Gromacs 2021.535 with the amber99sb-ildn force-field.36 The system was then inserted at the center of a dodecahedron box leaving a distance of 1.0 nm from the box wall to avoid interaction with periodic replica. The TIP3P model37 was employed for the implicit water solvent while the topology of methanol molecules was assigned using a generalized amber force field (GAFF).38 The number of methanol molecules to be added to reproduce the desired water/MeOH ratio was calculated as follows: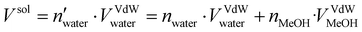 | (1) |
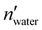 and nwater are the number of water molecules in the box containing only water and water/MeOH respectively. VVdWwater and VVdWmeoh are the Van-der-Waals volumes of water and methanol and nMeOH is the number of methanol molecules in the box containing the water/MeOH solution. By eqn (1), the desired number of methanol molecules in the simulation box, have been randomly inserted using gmx insert-molecules command, at a distance larger than the sum of van der Waals radii of the solute and solvent atoms.30 The solvated box has a total of 21
and nwater are the number of water molecules in the box containing only water and water/MeOH respectively. VVdWwater and VVdWmeoh are the Van-der-Waals volumes of water and methanol and nMeOH is the number of methanol molecules in the box containing the water/MeOH solution. By eqn (1), the desired number of methanol molecules in the simulation box, have been randomly inserted using gmx insert-molecules command, at a distance larger than the sum of van der Waals radii of the solute and solvent atoms.30 The solvated box has a total of 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 950 and 10
950 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 985 molecules of water and methanol respectively, corresponding to a water/MeOH molar ratio of 67% Taking VVdWwater and VVdWMeOH equal to 19.51 and 36.75 Å3 respectively, the mixed solvent box has a water/MeOH volume ratio of ∼50%. After solvation a total of 8 Na+ ions were added to set both systems electrically neutral. The systems of minimum energy were then obtained using steepest descent algorithms. Afterwards, both systems were equilibrated with a simulated annealing of 250 ps where the temperature was gradually increased from 50 to 300 K, followed by 50 ns at 300 K in a canonical ensemble (NVT). Production run consisted of two replicas of 1 μs in the isothermal–isobaric ensemble (NPT) at P = 1 atm, and T = 300 K for a total simulation time of 2 μs in water and water/MeOH. Long range electrostatic interactions were treated using Particle Mesh Ewald (PME) while a 0.9 nm cut-off was employed for short range electrostatic and van der Waals interactions. LINCS algorithm39 was used for the restraining of hydrogen atoms involved in covalent bonding.
985 molecules of water and methanol respectively, corresponding to a water/MeOH molar ratio of 67% Taking VVdWwater and VVdWMeOH equal to 19.51 and 36.75 Å3 respectively, the mixed solvent box has a water/MeOH volume ratio of ∼50%. After solvation a total of 8 Na+ ions were added to set both systems electrically neutral. The systems of minimum energy were then obtained using steepest descent algorithms. Afterwards, both systems were equilibrated with a simulated annealing of 250 ps where the temperature was gradually increased from 50 to 300 K, followed by 50 ns at 300 K in a canonical ensemble (NVT). Production run consisted of two replicas of 1 μs in the isothermal–isobaric ensemble (NPT) at P = 1 atm, and T = 300 K for a total simulation time of 2 μs in water and water/MeOH. Long range electrostatic interactions were treated using Particle Mesh Ewald (PME) while a 0.9 nm cut-off was employed for short range electrostatic and van der Waals interactions. LINCS algorithm39 was used for the restraining of hydrogen atoms involved in covalent bonding.
2.3 Trajectory analysis
Principal component analysis (PCA)40,41 was used to identify the major conformational changes in the simulated trajectories.Starting from the mean-centred trajectory matrix X, with dimensions nframes × 3N, (with N equal to the number of atoms), the related covariance matrix C = XXT is diagonalized as follows:
| C = WΛWT | (2) |
Here Λ represents the diagonal eigenvalues, and W is the matrix associated with the corresponding eigenvectors. Furthermore, the trajectory matrix X is projected along orthogonal directions (principal components) having the largest eigenvalues (representing the largest fluctuations):
| TL = XWL | (3) |
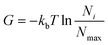 | (4) |
In eqn (4)kb is the Boltzman constant, T is the temperature of the system, and Ni and Nmax are the number of trajectory points in the i-th bin and in the most populated bin respectively. PCA was performed on protein Cα atoms using the Gromacs tools gmx covar and gmx anaeig. FEL was constructed with the command gmx sham. Cumulative modes (eigenvectors) along PC1and PC2 were represented using the pymol modevectors.py script.
Clustering analysis was performed separately on RNA and protein dynamics to retrieve the representative conformations of nucleotide and protein fragments, in the two solvent environments employed. Analysis was carried out using gmx cluster with a RMSD cut-off of 0.2 nm on all atoms of RNA duplex and hAgo2.
To recover general information about base association, the RNA per-residue contact maps were calculated using gmx mdmat. Salt–bridge interactions were evaluated using gmx contact and MD analysis python tool.42 The former was used to calculate the salt–bridge occupancy displayed as red–gray–blue colored surface on O1P and O2P atoms. The latter was employed to recover residue-by-residue interaction. Base pair parameters were determined using amber-cpptraj package.43
3. Results and discussion
The sampled trajectories achieved a satisfactory stationary state, displaying a mean Cα-RMSD ranging from 0.30 to 0.41 nm, with a maximum standard deviation of 0.04 nm (Fig. 2). To exclude transient states, the initial 150 ns from each replica were discarded before the analysis of the trajectories.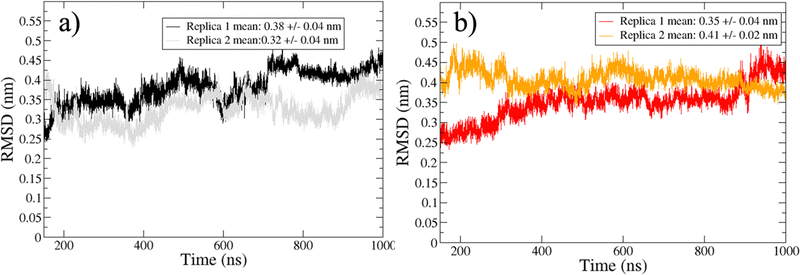 | ||
| Fig. 2 Cα-RMSD for trajectories sampled in water (a) and water/MeOH (b). Mean RMSD and standard deviation of the two independent replicas are showed inside the legend box. | ||
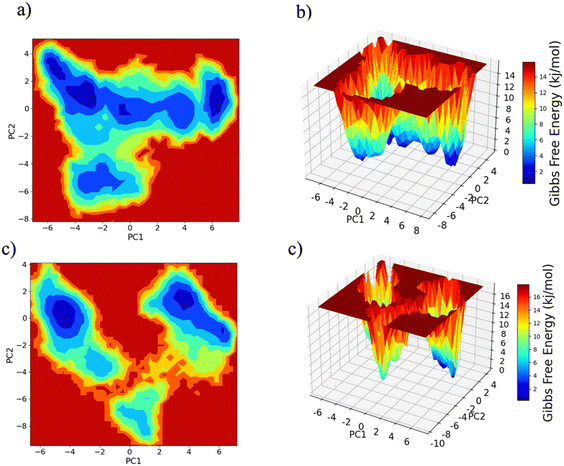
PC1 vs. PC2 free energy landscape (FEL), obtained from MD simulation in water solvent (Fig. 3(a and b)), shows the presence of adjacent local minima separated by a small potential barrier (<8 kJ mol−1). In contrast, the dynamic performed in water/MeOH (Fig. 3(c and d)) exhibits three distinct minima, separated by a high free energy barrier. In the representation of the reduced coordinate system, the magnitude of conformational subspace, spanned by trajectories sampled in the two solvents, is almost the same, as witnessed by the extent of PC1 and PC2 axes. However, the free energy surface computed in water solvent, suggests that protein experiences more rapid conformational rearrangements compared to water/MeOH solution. In water/MeOH, protein seems to possess a limited number of energetically favorable conformations, which do not communicate to each other. Functional domains of Ago are organized in structural scaffold forming two opposite lobes PAZ-N and MID-PIWI44 which undergo a conformational change to accommodate miRNA–mRNA duplex.45 The modes represented along PC1(Fig. 4) calculated from water system, indicate a conformational rearrangement, where the highly mobile PAZ domain19 (Fig. S1, the ESI†) moves in the direction of the MID-PIWI lobe. Along PC2, the collective coordinate motion provides evidence that PAZ and MID increase their distance. Overall, the eigenvectors analysis carried-out on water trajectories, can be contextualized within the biological behavior of human AGO2 bounded to the seed + supplementary duplex. Indeed, to locate duplex with supplementary base pairs, the gate formed by PAZ-L2 and MID-PIWI domain must create sufficient space to accommodate the base-pairs beyond the seed.8,11 Along PC1, collective modes computed in the water/MeOH system revealed a clockwise motion of the PAZ domain which moves toward MID and L2, while the N domain moves in the direction of PAZ with a closure of the PAZ-N pocket. As in water, along PC2, eigenvector analysis indicates the departure of PAZ from the MID domain.
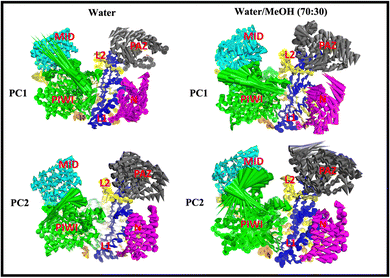 | ||
| Fig. 4 Cumulative modes from first (PC1) and second (PC2) eigenvector computed in water and water/MeOH. The colored arrows indicate the displacement of Cα atoms. | ||
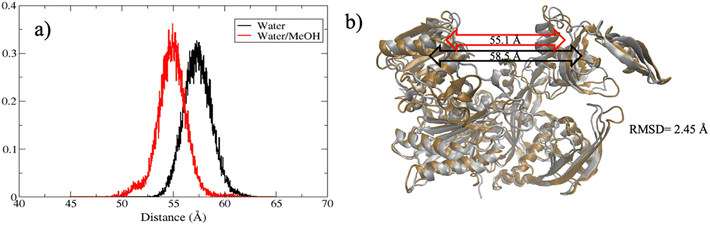
The extent of PAZ motion with respect to MID, measured as distribution of the center of mass distance is reported in Fig. 5(a). Overall, this suggests a much closer contact between PAZ and MID in water/MeOH solvent compared to water system as also supported by the superposition of the middle cluster structures in Fig. 5(b).
From this observation, it is also reasonable to assume a stronger protein–RNA association promoted by the presence of methanol in the solution, compared to pure water solvent. Ago2 protein interacts with RNA mainly through hydrogen bonds and non-base specific salt–bridges.8,46–48 The latter occur via electrostatic attraction between negatively charged phosphates of RNA backbone and the positively charged side chains of LYS and ARG amino acids. Trajectories collected in water/MeOH, registered an increasing number of protein–RNA contacts as highlighted by the comparison of the numbers of hydrogen bonds (Fig. S2(a), ESI†) and salt–bridge interactions (Fig. S2(b), ESI†) in the two simulated systems. The observed differences can be interpreted on the basis of the nature of salt–bridge interactions, which include both electrostatic and hydrogen bond contributions.
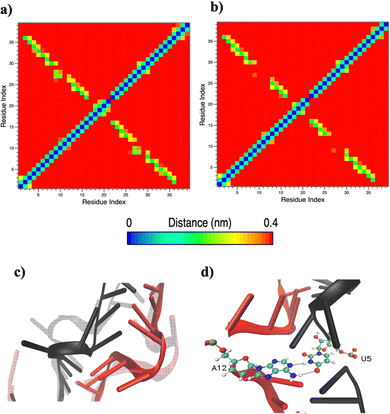
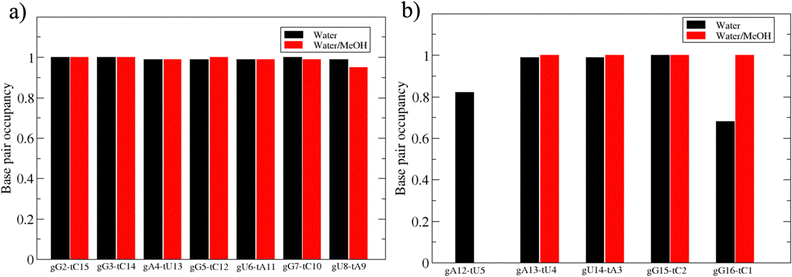
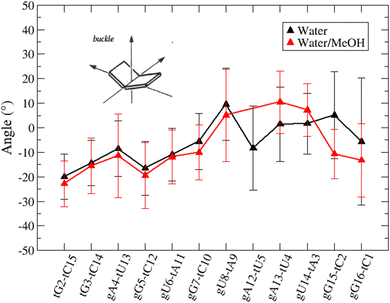
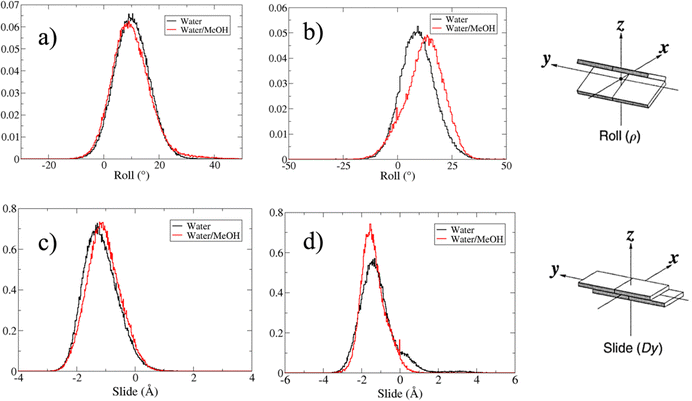
Based on pure water and methanol relative dielectric constant at 25 °C (78.4 and 32.70, respectively), we can assume that the mixed solvent employed in our simulation has a dielectric constant lower than that of water alone49 thereby favoring protein RNA interactions via salt bridges and hydrogen bonds. Considering the dynamics of RNA, excluding the base pair contact in seed and supplementary duplex, inter residue distances between miRNA and mRNA in water (Fig. 6(a)) reveal local interactions occurring in the central gate region. At the same time, nucleotides gA12 and tU5, which are staggered in the starting crystallographic structure (Fig. S3(a), ESI†), adopt a paired conformation in water solution (Fig. 6(d)). In contrast, mean smallest distances calculated from trajectories sampled in water/MeOH, do not exhibit interactions in the central loop within a cut-off of 4 Å (Fig. 6(b)). As can be inferred from the middle structure displayed in Fig. 6(c), the water/MeOH environment induces the central duplex to adopt an open conformation preventing interactions between miRNA and mRNA. Interestingly, in the seed region, contact maps do not show significant variations on the basis of the solution composition, suggesting almost no correlation with supplementary duplex dynamics. Taking the base pair occupancy as a global parameter for duplex mobility, the data in Fig. 7(a) indicate a quasi-complete retention of base association in seed duplex despite the solvent used. On the other hand, supplementary duplex has experienced some conformational rearrangements due to the variation of solvent composition as witnessed by the values of base pair occupancy in Fig. 7(b). Trajectories collected in water solvent, showed an additional base pairing, involving A12 residue of guide miRNA and U5 nucleotide of target mRNA, for at least 80% of the simulation time. Again, in water, the sampled trajectories showed a base pair dissociation involving the gG16-tC1 pair, although nucleotides maintain mutual interaction as indicated by the middle cluster structure provided in Fig. S4 (ESI†). In contrast, in water/MeOH, the duplex conformation retains almost completely the initial base pairing in the supplementary region with an occupancy close to 100%. Although a full complementary exists in the middle region of the RNA duplex (g9–11 and t6–8), the base pairing in this region is hampered because steric clashes in the central gate involving L2 and PIWI loop.8 In order to allow a full guide–target pairing, the central gate has to open destabilizing the tertiary complex.10 As reported in ref. 50 and 6, a high complementarity between miRNA and its target mRNA with stable base pairing in the middle and 3′ regions leads to the unbinding and releasing of the RNA duplex from Ago protein. To estimate the flexibility of base pairing in RNA duplex, we calculated the mean oscillation of the buckle angles across the sampled trajectories, considering only paired nucleotides in the seed and supplementary regions as representative of duplex flexibility. As clearly shown in Fig. 8, all paired bases are not coplanar, displaying a typical behavior of a duplex in a bent conformation.51,52 In the seed duplex, the mean buckle angle values, as well as their average oscillations, are minimally affected by the solvent employed. In contrast, in supplementary duplex, water trajectories exhibit buckle angles values shifted by about ±10–15° from their water/MeOH counterparts. In addition, the water trend shows a quasi-coplanarity of gA13-tU4, gU14-tA3 gG15-tC2 with buckle angles ranging between 0 and 5°. The helix parameters slide and roll have been calculated providing information about translational and rotational motion of stacked bases along their long axes.53 Data in Fig. 9(a) and (c) show a broad distribution with mean values falling within the range of 9 to 10° for roll and between −1.2 and −1.1 Å for slide parameters, respectively. This findings strongly suggest that, in the transition from water environment to water/MeOH mixture, the seed duplex retains its A-form conformation.54 By the comparison of the roll angle distributions of supplementary duplex (Fig. 9(b)) a clear shift of about 6° is observable between water and water/MeOH system. Slide distributions in Fig. 9(d) show, instead, the presence of a second population located around 0.3 Å for water system. Thus, while the dynamics of the seed duplex does not seem to be significantly affected by the mixed solvent employed, the supplementary duplex in water appears to be more flexible than in water/MeOH.
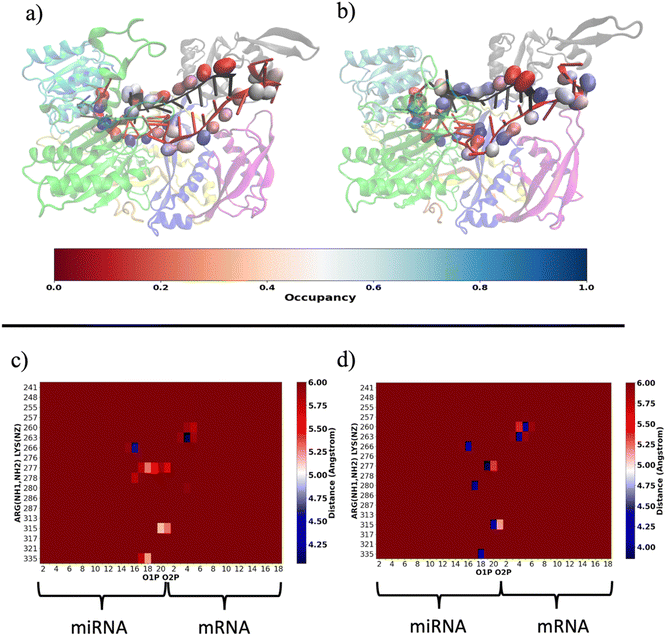
Our results are consistent with those already reported by Gruttadauria et al.8 who stated that supplementary duplex is mobile in the Ago–RNA complex. Based on the information provided so far, we attempted to delve into the potential correlation between Ago–RNA association and duplex flexibility, exploring in more detail the extent of salt–bridge contacts in the two simulated systems. From preliminary data in Fig. S2(b) (ESI†), we explored the salt–bridge network between the RNA backbone and protein side chains. In Fig. 10(a) and (b), we compare the salt–bridge occupancy (the frequency of salt–bridge contacts within a cutoff of 4.5 Å) in the two simulated systems. Main differences are observable in the region located at the 3′ terminus of the miRNA and in the central duplex of the target mRNA. The blue surface on O1P and/or O2P atoms indicates that, in these regions, the water/methanol environment retains protein–RNA salt–bridge interactions for more than 50% of the simulated time (Fig. 10(b)). Conversely, the same analysis performed on the water system suggests a lower tendency of ARG and LYS to interact with phosphates located at the guide 3′ end and mRNA in the central duplex (Fig. 10(a)). The contact map in Fig. S5(a) (ESI†) clearly exhibits the region delimited by MID-PIWI and seed duplex as the most populated salt–linkage region. Conversely, in water/MeOH (Fig. S5(b), ESI†), the majority of salt linkages arise by the proximity of ARG and LYS residues located in PAZ domain with a backbone of the miRNA 3′ tail and mRNA in the central gate. A stronger binding affinity of target 3′ end with MID and PIWI domain is also to be noted. This is attributable to the solvent exposure of 3′ target terminal which, as the miRNA 3′ end, is more subject to the surrounding environment. By a magnification of the PAZ domain region in Fig. 10(c and d) specific residue-by-residue interactions involving LYS260-tU5, ARG277-gU19, ARG280-gU17 and ARG315-gU20 were recognized. The center-of-mass distances distribution between acidic O1P, O2P and basic NH1, NH2 of the selected couples underlines that, the water/MeOH solvent, promotes the association of guide 3′ tail with the PAZ domain (Fig. S6, ESI†). At the same time, U6 of miRNA is much more intimately linked with LYS 260 in the mixed solvent, contributing to the lower flexibility of the central duplex and preventing gA12-tU5 base association. Based on our previous observations, extrapolated from the PCA, we can therefore infer an association between the limited conformational freedom of protein observed in water/MeOH, with the extent of Ago–RNA binding due by salt–bridge interactions.
Moreover, our analysis suggests that the modification of solvent environment seems to have a negligible effect on seed duplex conformation. These findings can be connected with the regulatory properties of Ago2, which mediate target recognition primarily in the seed region.55–58 Indeed, to stabilize miRNA–mRNA interaction, Ago2 provides a screening effect on seed region reducing its exposure to solvent. This favors the miRNA–mRNA interaction preserving the target RNA from dissociation to guide miRNA.59
In summary, in physiological condition, supplementary base-pairing can undergo some conformational interconversion, as evidenced by the dynamical change of complementary base association (Fig. S7, ESI†). In the mixed solvent system, the main effect recorded has been the stronger 3′ tail-PAZ association with the consequent stabilization of paired bases in supplementary region, while preserving the conformation of seed duplex. Another consideration can be done about the dynamics of guide 3′ end. miRNA 3′ terminal, is anchored to PAZ domain via salt–bridges and by π-stacking interactions involving phenylalanine PHE294 with nitrogenous base on 3′ ending nucleotide.10 Simulations performed in water revealed a partial release of the 3′ end of guide nucleotides from the PAZ domain. This is evidenced by the broad peak centered around 13 Å in Fig. 11(a), which indicates the leak of the PHE294-gU21 interaction (Fig. 11(c)). Conversely, in water/methanol, the sharp distribution centered at 6 Å indicates the retention of the PHE294-gU21 interaction(Fig. 11(b)) for the entire collected trajectories. Experimental evidence reported in literature,60–62 have shown that 3′ end of miRNA can dynamically associate/reassociate with PAZ.
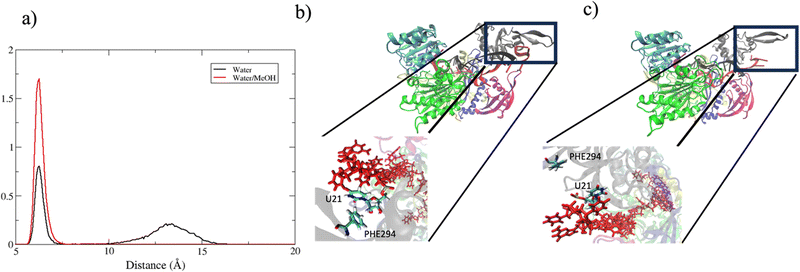 | ||
| Fig. 11 (a) center of mass distance distribution between PHE294 and gU21. (b) and (c) Binding pocket of guide 3′ end with PAZ domain in bound and unbound state respectively. | ||
Wang et al.63 previously discovered that a binding pocket consisting of 14–15 base pairs promotes the releasing of guide 3′ terminal from the PAZ domain while still maintaining guide 5′ end anchored to MID. Our analysis also showed that, in a water solution, salt bridge interactions with 3′ guide terminal are less significant compared to those with seed duplex. Based on information provided by FEL and eigenvectors analyses, we investigated in more detail the structural variations at the different local minima positions. In water solvent (Fig. S8, ESI†) the partial dissociation of 3′ guide from PAZ is depicted by the structural transitions from point 1–2 to 3,4 and 5. These transitions occur with a very low free energy barrier suggesting a reversible interconversion between PAZ-3′ bounded and unbounded conformation. We can interpret these transients status on the basis of the conformational motion of PAZ which, moving in direction of MID can lead to a leak of PAZ guide 3′ interaction. Structures extracted from water/MeOH system (Fig. S9, ESI†) instead, clearly exhibit a stable guide 3′ PAZ association. Thus, the conformational motion of PAZ and guide 3′ is more correlated in water/MeOH system compared to water alone. Because the high mobility of PAZ domain, the transient unbinding of guide 3′ from PAZ can be explained by the missing of cooperative effects due by salt–linkage interactions, present instead in water/MeOH.
4. Conclusions
In this work we have carried out 2-μsec long molecular dynamics simulations of human Ago2 bound to seed + supplementary miRNA–mRNA duplexes, varying the composition of the solvent environment from pure water to water/MeOH at molar concentration of 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30% mol mol−1. Within the limitations of the simulated time range and force-field approximation, our findings revealed that the enhanced contact of the PAZ functional domain with the guide 3′ terminal, as registered in water/MeOH simulations, did not significantly impact the global conformation of the seed duplex. Conversely, the natural mobility of the supplementary duplex in water is restricted in water/MeOH. The enhancement of the attraction of the opposite charges, between basic ARG and LYS residues and acidic phosphates on the RNA backbone, contributed to maintain the stability of the starting base pairs in the supplementary duplex, while preserving the 3′ terminal association with the PAZ domain. We also find that the mobility of the supplementary duplex in water simulation does not affect the stability of the seed-duplex which retains almost completely base pair and helix parameters. Consistently with previous finding,8,46 our data highlight that the specificity of guide–target interaction arises principally in the seed-region. At the same time, the solvent effect on hAgo2–RNA association is attenuated moving from PAZ-N to MID-PIWI lobe. Our study offers a different approach for the theoretical examination of the Ago–RNA complexes and can contribute to the understanding of Ago-mediated guide–target interactions.
30% mol mol−1. Within the limitations of the simulated time range and force-field approximation, our findings revealed that the enhanced contact of the PAZ functional domain with the guide 3′ terminal, as registered in water/MeOH simulations, did not significantly impact the global conformation of the seed duplex. Conversely, the natural mobility of the supplementary duplex in water is restricted in water/MeOH. The enhancement of the attraction of the opposite charges, between basic ARG and LYS residues and acidic phosphates on the RNA backbone, contributed to maintain the stability of the starting base pairs in the supplementary duplex, while preserving the 3′ terminal association with the PAZ domain. We also find that the mobility of the supplementary duplex in water simulation does not affect the stability of the seed-duplex which retains almost completely base pair and helix parameters. Consistently with previous finding,8,46 our data highlight that the specificity of guide–target interaction arises principally in the seed-region. At the same time, the solvent effect on hAgo2–RNA association is attenuated moving from PAZ-N to MID-PIWI lobe. Our study offers a different approach for the theoretical examination of the Ago–RNA complexes and can contribute to the understanding of Ago-mediated guide–target interactions.
Author contributions
F. P. contributed the method, performed data analysis, and wrote the original draft. A. C., A. G & D. S contributed to the conceptualization, method and the writing of the paper. D. S. edited the paper. L. A. performed funding acquisition and edited the paper.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work has been performed in the framework of the project BIOVERSI Regione Lazio “Bando Gruppi di Ricerca 2020” no. A0375-2020_26607. All authors gratefully acknowledge the computational support of CINECA (grant IsCa2_miRNAAgo).References
- L. F. R. Gebert and I. J. MacRae, Regulation of microRNA function in animals, Nat. Rev. Mol. Cell Biol., 2019, 20, 21–37, DOI:10.1038/s41580-018-0045-7.
- G. Meister, Argonaute proteins: functional insights and emerging roles, Nat. Rev. Genet., 2013, 14, 447–459, DOI:10.1038/nrg3462.
- J. Höck and G. Meister, The Argonaute protein family, Genome Biol., 2008, 9, 210, DOI:10.1186/gb-2008-9-2-210.
- J. Liu, M. A. Carmell, F. V. Rivas, C. G. Marsden, J. M. Thomson, J.-J. Song, S. M. Hammond, L. Joshua-Tor and G. J. Hannon, Argonaute2 Is the Catalytic Engine of Mammalian RNAi, Science, 1979, 305, 1437–1441, DOI:10.1126/science.1102513.
- N. T. Schirle and I. J. MacRae, The Crystal Structure of Human Argonaute2, Science, 1979, 336, 1037–1040, DOI:10.1126/science.1221551.
- J. H. Park, S.-Y. Shin and C. Shin, Non-canonical targets destabilize microRNAs in human Argonautes, Nucleic Acids Res., 2017, 45, 1569–1583, DOI:10.1093/nar/gkx029.
- S. Grosswendt, A. Filipchyk, M. Manzano, F. Klironomos, M. Schilling, M. Herzog, E. Gottwein and N. Rajewsky, Unambiguous Identification of miRNA:Target Site Interactions by Different Types of Ligation Reactions, Mol. Cell, 2014, 54, 1042–1054, DOI:10.1016/j.molcel.2014.03.049.
- J. Sheu-Gruttadauria, Y. Xiao, L. F. R. Gebert and I. J. MacRae, Beyond the seed: structural basis for supplementary microRNA targeting by human Argonaute2, EMBO J., 2019, 38, e101153 CrossRef PubMed.
- L. M. Wee, C. F. Flores-Jasso, W. E. Salomon and P. D. Zamore, Argonaute Divides Its RNA Guide into Domains with Distinct Functions and RNA-Binding Properties, Cell, 2012, 151, 1055–1067, DOI:10.1016/j.cell.2012.10.036.
- J. Sheu-Gruttadauria, P. Pawlica, S. M. Klum, S. Wang, T. A. Yario, N. T. Schirle Oakdale, J. A. Steitz and I. J. MacRae, Structural Basis for Target-Directed MicroRNA Degradation, Mol. Cell, 2019, 75, 1243–1255, DOI:10.1016/j.molcel.2019.06.019.
- H. Zhuang, X. Fan, D. Ji, Y. Wang, J. Fan, M. Li, D. Ni, S. Lu, X. Li and Z. Chai, Elucidation of the conformational dynamics and assembly of Argonaute–RNA complexes by distinct yet coordinated actions of the supplementary microRNA, Comput. Struct. Biotechnol. J., 2022, 20, 1352–1365, DOI:10.1016/j.csbj.2022.03.001.
- B. Mallick, A. R. Sharma, S.-S. Lee and C. Chakraborty, Understanding the molecular interaction of human argonaute-2 and miR-20a complex: A molecular dynamics approach, J. Cell. Biochem., 2019, 120, 19915–19924, DOI:10.1002/jcb.29300.
- S. Rinaldi, G. Colombo and A. Paladino, The dynamics of t1 adenosine binding on human Argonaute 2: Understanding recognition with conformational selection, Protein Sci., 2022, 31, e4377, DOI:10.1002/pro.4377.
- Z. Xia, P. Clark, T. Huynh, P. Loher, Y. Zhao, H.-W. Chen, I. Rigoutsos and R. Zhou, Molecular dynamics simulations of Ago silencing complexes reveal a large repertoire of admissible ‘seed-less’ targets, Sci. Rep., 2012, 2, 569, DOI:10.1038/srep00569.
- R. Kong, L. Xu, L. Piao, D. Zhang, T.-J. Hou and S. Chang, Exploring the RNA-bound and RNA-free human Argonaute-2 by molecular dynamics simulation method, Chem. Biol. Drug Des., 2017, 90, 753–763, DOI:10.1111/cbdd.12997.
- L. Zhu, H. Jiang, F. K. Sheong, X. Cui, X. Gao, Y. Wang and X. Huang, A Flexible Domain-Domain Hinge Promotes an Induced-fit Dominant Mechanism for the Loading of Guide-DNA into Argonaute Protein in Thermus thermophilus, J. Phys. Chem. B, 2016, 120, 2709–2720, DOI:10.1021/acs.jpcb.5b12426.
- S. Willkomm and T. Restle, Conformational Dynamics of Ago-Mediated Silencing Processes, Int. J. Mol. Sci., 2015, 16, 14769–14785, DOI:10.3390/ijms160714769.
- Y. Liu, Z. Yu, J. Zhu, S. Wang, D. Xu and W. Han, Why Is a High Temperature Needed by Thermus thermophilus Argonaute During mRNA Silencing: A Theoretical Study, Front. Chem., 2018, 6, 223, DOI:10.3389/fchem.2018.00223.
- M. Kalia, S. Willkomm, J. C. Claussen, T. Restle and A. M. J. J. Bonvin, Novel Insights into Guide RNA 5′-Nucleoside/Tide Binding by Human Argonaute 2, Int. J. Mol. Sci., 2016, 17, 22, DOI:10.3390/ijms17010022.
- J. M. Sutton and M. G. Bartlett, Modeling cationic adduction of oligonucleotides using electrospray desorption ionization, Rapid Commun. Mass Spectrom., 2020, 34, e8696, DOI:10.1002/rcm.8696.
- Y. Yu, J. Wang, Q. Shao, J. Shi and W. Zhu, The effects of organic solvents on the folding pathway and associated thermodynamics of proteins: a microscopic view, Sci. Rep., 2016, 6, 19500, DOI:10.1038/srep19500.
- D. Roccatano, G. Colombo, M. Fioroni and A. E. Mark, Mechanism by which 2,2,2-trifluoroethanol/water mixtures stabilize secondary-structure formation in peptides: A molecular dynamics study, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 12179–12184, DOI:10.1073/pnas.182199699.
- M. S. Searle, R. Zerella, D. H. Williams and L. C. Packman, Native-like β-hairpin structure in an isolated fragment from ferredoxin: NMR and CD studies of solvent effects on the N-terminal 20 residues, Protein Eng., Des. Sel., 1996, 9, 559–565, DOI:10.1093/protein/9.7.559.
- A. M. Ababneh, C. C. Large and S. Georghiou, Solvation of Nucleosides in Aqueous Mixtures of Organic Solvents: Relevance to DNA Open Basepairs, Biophys. J., 2003, 85, 1111–1127, DOI:10.1016/S0006-3495(03)74548-2.
- G. F. Mayol, L. A. Defelipe, J. P. Arcon, A. G. Turjanski and M. A. Marti, Solvent Sites Improve Docking Performance of Protein–Protein Complexes and Protein–Protein Interface-Targeted Drugs, J. Chem. Inf. Model., 2022, 62, 3577–3588, DOI:10.1021/acs.jcim.2c00264.
- J. P. Arcon, L. A. Defelipe, C. P. Modenutti, E. D. López, D. Alvarez-Garcia, X. Barril, A. G. Turjanski and M. A. Martí, Molecular Dynamics in Mixed Solvents Reveals Protein–Ligand Interactions, Improves Docking, and Allows Accurate Binding Free Energy Predictions, J. Chem. Inf. Model., 2017, 57, 846–863, DOI:10.1021/acs.jcim.6b00678.
- P. M. U. Ung, P. Ghanakota, S. E. Graham, K. W. Lexa and H. A. Carlson, Identifying binding hot spots on protein surfaces by mixed-solvent molecular dynamics: HIV-1 protease as a test case, Biopolymers, 2016, 105, 21–34, DOI:10.1002/bip.22742.
- L. Zuzic, F. Samsudin, A. T. Shivgan, P. V. Raghuvamsi, J. K. Marzinek, A. Boags, C. Pedebos, N. K. Tulsian, J. Warwicker, P. MacAry, M. Crispin, S. Khalid, G. S. Anand and P. J. Bond, Uncovering cryptic pockets in the SARS-CoV-2 spike glycoprotein, Structure, 2022, 30, 1062–1074, DOI:10.1016/j.str.2022.05.006.
- R. D. Smith and H. A. Carlson, Identification of Cryptic Binding Sites Using MixMD with Standard and Accelerated Molecular Dynamics, J. Chem. Inf. Model., 2021, 61, 1287–1299, DOI:10.1021/acs.jcim.0c01002.
- I. M. Ilie, C. Ehrhardt, A. Caflisch and G. Weitz-Schmidt, Decrypting Integrins by Mixed-Solvent Molecular Dynamics Simulations, J. Chem. Inf. Model., 2023, 63, 3878–3891, DOI:10.1021/acs.jcim.3c00480.
- A. de Ruiter and B. Zagrovic, Absolute binding-free energies between standard RNA/DNA nucleobases and amino-acid sidechain analogs in different environments, Nucleic Acids Res., 2015, 43, 708–718, DOI:10.1093/nar/gku1344.
- A. Waterhouse, M. Bertoni, S. Bienert, G. Studer, G. Tauriello, R. Gumienny, F. T. Heer, T. A. P. de Beer, C. Rempfer, L. Bordoli, R. Lepore and T. Schwede, SWISS-MODEL: homology modelling of protein structures and complexes, Nucleic Acids Res., 2018, 46, W296–W303, DOI:10.1093/nar/gky427.
- M. Rother, K. Milanowska, T. Puton, J. Jeleniewicz, K. Rother and J. M. Bujnicki, ModeRNA server: an online tool for modeling RNA 3D structures, Bioinformatics, 2011, 27, 2441–2442, DOI:10.1093/bioinformatics/btr400.
- J. Stasiewicz, S. Mukherjee, C. Nithin and J. M. Bujnicki, QRNAS: software tool for refinement of nucleic acid structures, BMC Struct. Biol., 2019, 19, 5, DOI:10.1186/s12900-019-0103-1.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers, SoftwareX, 2015, 1–2, 19–25, DOI:10.1016/j.softx.2015.06.001.
- V. Hornak, R. Abel, A. Okur, B. Strockbine, A. Roitberg and C. Simmerling, Comparison of multiple Amber force fields and development of improved protein backbone parameters, Proteins: Struct., Funct., Bioinf., 2006, 65, 712–725, DOI:10.1002/prot.21123.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935, DOI:10.1063/1.445869.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174, DOI:10.1002/jcc.20035.
- B. Hess, P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation, J. Chem. Theory Comput., 2008, 4, 116–122, DOI:10.1021/ct700200b.
- A. Amadei, A. B. M. Linssen and H. J. C. Berendsen, Essential dynamics of proteins, Proteins: Struct., Funct., Bioinf., 1993, 17, 412–425, DOI:10.1002/prot.340170408.
- Y. Wang, Y. Li, Z. Ma, W. Yang and C. Ai, Mechanism of MicroRNA-Target Interaction: Molecular Dynamics Simulations and Thermodynamics Analysis, PLoS Comput. Biol., 2010, 6, 1–19, DOI:10.1371/journal.pcbi.1000866.
- N. Michaud-Agrawal, E. J. Denning, T. B. Woolf and O. Beckstein, MDAnalysis: A toolkit for the analysis of molecular dynamics simulations, J. Comput. Chem., 2011, 32, 2319–2327, DOI:10.1002/jcc.21787.
- D. R. Roe and T. E. I. I. I. Cheatham, PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data, J. Chem. Theory Comput., 2013, 9, 3084–3095, DOI:10.1021/ct400341p.
- J. Wu, J. Yang, W. C. Cho and Y. Zheng, Argonaute proteins: Structural features, functions and emerging roles, J. Adv. Res., 2020, 24, 317–324, DOI:10.1016/j.jare.2020.04.017.
- H. Jiang, F. K. Sheong, L. Zhu, X. Gao, J. Bernauer and X. Huang, Markov State Models Reveal a Two-Step Mechanism of miRNA Loading into the Human Argonaute Protein: Selective Binding followed by Structural Re-arrangement, PLoS Comput. Biol., 2015, 11, 1–21, DOI:10.1371/journal.pcbi.1004404.
- N. T. Schirle, J. Sheu-Gruttadauria and I. J. MacRae, Structural basis for microRNA targeting, Science, 1979, 346, 608–613, DOI:10.1126/science.1258040.
- C.-D. Kuhn and L. Joshua-Tor, Eukaryotic Argonautes come into focus, Trends Biochem. Sci., 2013, 38, 263–271, DOI:10.1016/j.tibs.2013.02.008.
- L. Zhu, H. Jiang, S. Cao, I. C. Unarta, X. Gao and X. Huang, Critical role of backbone coordination in the mRNA recognition by RNA induced silencing complex, Commun. Biol., 2021, 4, 1345, DOI:10.1038/s42003-021-02822-7.
- P. S. Albright and L. J. Gosting, Dielectric Constants of the Methanol-Water System from 5 to 55°1, J. Am. Chem. Soc., 1946, 68, 1061–1063, DOI:10.1021/ja01210a043.
- N. De, L. Young, P.-W. Lau, N.-C. Meisner, D. V. Morrissey and I. J. MacRae, Highly Complementary Target RNAs Promote Release of Guide RNAs from Human Argonaute2, Mol. Cell, 2013, 50, 344–355, DOI:10.1016/j.molcel.2013.04.001.
- S. B. Dixit, F. Pitici and D. L. Beveridge, Structure and axis curvature in two dA6·dT6 DNA oligonucleotides: Comparison of molecular dynamics simulations with results from crystallography and NMR spectroscopy, Biopolymers, 2004, 75, 468–479, DOI:10.1002/bip.20157.
- J. Hizver, H. Rozenberg, F. Frolow, D. Rabinovich and Z. Shakked, DNA bending by an adenine–thymine tract and its role in gene regulation, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 8490–8495, DOI:10.1073/pnas.151247298.
- R. E. Dickerson, Definitions and Nomenclature of Nucleic Acid Structure Parameters, J. Biomol. Struct. Dyn., 1989, 6, 627–634, DOI:10.1080/07391102.1989.10507726.
- R. E. Dickerson and H.-L. Ng, DNA structure from A to B, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 6986–6988, DOI:10.1073/pnas.141238898.
- S. Grosswendt, A. Filipchyk, M. Manzano, F. Klironomos, M. Schilling, M. Herzog, E. Gottwein and N. Rajewsky, Unambiguous Identification of miRNA:Target Site Interactions by Different Types of Ligation Reactions, Mol. Cell, 2014, 54, 1042–1054, DOI:10.1016/j.molcel.2014.03.049.
- D. P. Bartel, MicroRNAs: Target Recognition and Regulatory Functions, Cell, 2009, 136, 215–233, DOI:10.1016/j.cell.2009.01.002.
- N. Rajewsky, microRNA target predictions in animals, Nat. Genet., 2006, 38, S8–S13, DOI:10.1038/ng1798.
- Z. Xia, T. Huynh, P. Ren and R. Zhou, Large Domain Motions in Ago Protein Controlled by the Guide DNA-Strand Seed Region Determine the Ago-DNA-mRNA Complex Recognition Process, PLoS One, 2013, 8, 1–11, DOI:10.1371/journal.pone.0054620.
- H. Zhuang, D. Ji, J. Fan, M. Li, R. Tao, K. Du, S. Lu, Z. Chai and X. Fan, Mechanistic Insights into the Protection Effect of Argonaute–RNA Complex on the HCV Genome, Biomolecules, 2022, 12, 1631, DOI:10.3390/biom12111631.
- A. Zander, P. Holzmeister, D. Klose, P. Tinnefeld and D. Grohmann, Single-molecule FRET supports the two-state model of Argonaute action, RNA Biol., 2014, 11, 45–56, DOI:10.4161/rna.27446.
- S.-R. Jung, E. Kim, W. Hwang, S. Shin, J.-J. Song and S. Hohng, Dynamic Anchoring of the 3′-End of the Guide Strand Controls the Target Dissociation of Argonaute–Guide Complex, J. Am. Chem. Soc., 2013, 135, 16865–16871, DOI:10.1021/ja403138d.
- S. Willkomm, L. Jakob, K. Kramm, V. Graus, J. Neumeier, G. Meister and D. Grohmann, Single-molecule FRET uncovers hidden conformations and dynamics of human Argonaute 2, Nat. Commun., 2022, 13, 3825, DOI:10.1038/s41467-022-31480-4.
- Y. Wang, S. Juranek, H. Li, G. Sheng, G. S. Wardle, T. Tuschl and D. J. Patel, Nucleation, propagation and cleavage of target RNAs in Ago silencing complexes, Nature, 2009, 461, 754–761, DOI:10.1038/nature08434.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp05530b |
| This journal is © the Owner Societies 2024 |