Is 1-methylcytosine a faithful model compound for ultrafast deactivation dynamics of cytosine nucleosides in solution?

Abstract

1-Methylcytosine (1mCyt) is the base for nucleoside N1-methylpseudodeoxycytidine of Hachimoji nucleic acids and a frequently used model compound for theoretical studies on excited states of cytosine nucleosides. However, there is little experimental characterization of spectra and photo-dynamic properties of 1mCyt. Herein, we report a comprehensive investigation into excited state dynamics and effects of solvents on fluorescence dynamics of 1mCyt in both water and acetonitrile. The study employed femtosecond broadband time-resolved fluorescence, transient absorption, and steady-state spectroscopy, along with density functional theory and time-dependent density functional theory calculations. The results obtained provide the first experimental evidence for identifying a dark-natured ∼5.7 ps lifetime nπ* state in the ultrafast non-radiative deactivation with 1mCyt in aqueous solution. This study also demonstrates a significant effect of the solvent on 1mCyt's fluorescence emission, which highlights the crucial role of solute–solvent hydrogen bonding in altering structures and reshaping the radiative as well as nonradiative dynamics of the 1mCyt's ππ* state in the aprotic solvent compared to the protic solvent. The solvent effect exhibited by 1mCyt is distinctive from that known for deoxycytidine, indicating the need for caution in using 1mCyt for modelling the ultrafast dynamics of Cyt nucleosides in solvents with varying properties. Overall, our study unveils a deactivation mechanism that confers a high degree of photo-stability for 1mCyt in solution, shedding light on the molecular basis for solvent-induced effects on the excited state dynamics of nucleobases and derivatives.

---

Introduction

1-Methylcytosine (1mCyt) is a derivative of cytosine (Cyt), with a methyl substitution at its N1 position (Scheme 1). It is the base for one of the nucleosides, N1-methylpseudodeoxycytidine (Scheme 1), of Hachimoji DNAs that have potential implications for extraterrestrial life.¹ 1mCyt is also a model compound used in high-level quantum mechanical calculations for decreasing the computational cost in analyzing the highly complex excited state potential energy surfaces (PESs) and deactivation dynamics of cytidine (Cyd) and deoxycytidine (dCyd) (Scheme 1).^2,3 There is, however, very limited experimental study regarding excited states of 1mCyt, with only one known investigation using time-resolved IR (TRIR) by Keane et al.⁴ This study reported that both 1mCyt and Cyt, after photo-excitation, exhibit ultrafast decay from their light-absorbing ππ* state with no significant involvement of the nπ* natured state.⁴ However, later studies on Cyt and its canonical N1 derivatives, such as the nucleosides and nucleotides of Cyt (dCyd/Cyd and dCMP/CMP, Scheme 1), showed that both the ππ* state and a low-lying nπ* state, likely associated with the oxygen lone pair,^2,4–9 contribute importantly to their excited state deactivation but with the lifetime of the nπ* state being different.^{2,5,6,10–13} For example, the lifetime of the nπ* state is ∼7.7 ps for Cyt, which is much shorter than the ∼30 ps and ∼34 ps lifetime of the nπ* state for dCyd and CMP in water, respectively.¹⁰

Scheme 1 (left) 1-Methylcytosine (1mCyt) and the nucleoside N1-methylpseudodeoxycytidine, (right) cytosine (Cyt) and its nucleosides and nucleotides.

Moreover, previous studies on the role of solvents in deactivation have observed noticeably different spectra and excited state dynamics of Cyt nucleosides in protic versus aprotic solvents.^{2,6,10,14–17} For instance, steady-state and time-resolved spectroscopy on dCyd reported the observation of a red-shift (by ∼6 nm) in the absorption spectrum whilst a blue-shift (by ∼12 nm) in the fluorescence spectrum from the S₁ ππ* state upon changing the solvent from water to acetonitrile (CH₃CN).² The study also showed a variation in the ππ* state lifetime with the average decay time being ∼0.37 ps in water and ∼0.53 ps in CH₃CN.² This is explained by an effect of water as a typical protic solvent and CH₃CN as an aprotic solvent in modulating differently the energetics and decay dynamics of the ππ* excited state, according to theoretical calculations performed with 1mCyt as a model for dCyd.² There is nonetheless no information from the perspective of experiments on how the change of solvent properties may affect the spectra and deactivation dynamics of 1mCyt, and it remains elusive whether excited state behaviors of 1mCyt could be considered representative for those of the nucleosides and nucleotides of Cyt.

In order to address the open issue on the excited state dynamics and to explore effects of solvents on the excited state dynamics of 1mCyt, as well as to assess whether 1mCyt is a faithful model compound for Cyt nucleosides and nucleotides, we reported here a comparative study on the excited state behaviors of 1mCyt in water and CH₃CN. This study employed a combination of methods including steady-state spectroscopy, femtosecond broadband time-resolved fluorescence (fs-TRF), fs-TRF anisotropy (fs-TRFA), transient absorption (fs-TA), density functional theory (DFT) and time-dependent DFT (TDDFT) calculations. Our work provides concrete and direct experimental evidence for identifying the involvement of the nπ* state and similarities in the deactivation pathways of 1mCyt compared to Cyt and its nucleosides and nucleotides. More importantly, the results we obtained unveil important differences in terms of the energy, excited state lifetimes, and in particular, effects of solvents on the excited state properties between 1mCyt and its canonical counterparts.

Materials and methodology

A. Materials

lmCyt with a purity of 95% was purchased from Bidepharm and used without further purification. CH₃CN and methanol (CH₃OH) of analytical high-performance liquid chromatography (HPLC) grade were purchased from Duksan and used as received. A 50 mM pH 7 aqueous potassium phosphate buffer was prepared for the spectroscopic measurements in water. The buffer solution was prepared by dissolving potassium dihydrogen phosphate (KH₂PO₄) and dipotassium hydrogen phosphate (K₂HPO₄) in 18.2 MΩ double deionized water produced by a MILLIPORE (Milli-Q synthesis) system.

B. Methodology

B1. Steady-state spectroscopy. The UV-vis absorption spectra were recorded using a Hitachi U-3900H spectrometer. The steady-state fluorescence spectra and fluorescence excitation spectra were measured using a Jobin Yvon Fluoromax-4 spectrofluorometer. The fluorescence quantum yield (Φ_f) of the examined systems was determined using a comparative method, with 2′-deoxy-5-methylcytidine in pH 7 aqueous buffer (Φ_f = 5.97 × 10⁻⁴) as the standard.¹⁰

B2. Time-resolved spectroscopy. Time-resolved measurements were performed based on a commercial ultrafast Ti: Sapphire regenerative amplifier laser system (800 nm fundamental laser, 1 kHz repetition rate, ∼35 fs duration) and home-built broadband fs-TRF and fs-TA spectrometers. The details of the spectrometers are illustrated elsewhere.^10,18–21 In brief, the sample solution (∼1.7–2.7 mM) was excited by a femtosecond laser pulse (pump) at 267 nm. The pump pulse was generated in an optical parametric amplifier (OPA) through sum-frequency generation of a portion of the 800 nm fundamental laser. The excited state processes after the excitation were probed by a second laser pulse (probe) to monitor the temporal evolution of the broadband transient fluorescence, fluorescence anisotropy, and transient absorption spectra in the fs-TRF, fs-TRFA, and fs-TA measurements, respectively.

For the fs-TRF and fs-TRFA measurements, the Kerr-gate technique was used.¹⁰ In this method, a Kerr-gate device made of a quartz plate (Kerr medium) with a thickness of 1 mm was sandwiched between a pair of crossed polarizers and driven by the 800 nm fundamental laser to function as an ultrafast shutter to allow the detection of broadband transient fluorescence signals at varied designated pump/probe delays. For the TRF measurement, the polarization direction of the pump laser was set at the magic angle (54.7°) with respect to that of the first polarizer in the Kerr-gate device to avoid the effect of rotational diffusion of the molecule after the excitation. To obtain the fs-TRFA spectra (r(t)), the polarization direction of the pump laser was adjusted to be parallel and perpendicular to that of the first polarizer in the Kerr-gate device. This enabled the recording of the transient fluorescence spectrum of I_para(t) and I_perp(t) at a designated pump/probe time decay, respectively. The r(t) was then obtained using the following equation:²²

r(t) = (I_para(t) − I_perp(t))/(I_para(t) + 2I_perp(t))

For the measurement of fs-TA, a white light continuum (WLC) with wavelengths ranging from approximately 300 to 700 nm was generated from a calcium fluoride (CaF₂) plate which was pumped by a part of the 800 nm fundamental laser. This WLC was then used as the probe pulse to detect the broadband TA signals. The polarization directions of the pump and probe pulses were set at the magic angle (54.7°) to eliminate the effect of rotational diffusion.

For all the time-resolved measurements, the sample solution was measured in a CaF₂ cell with an optical path length of 0.5 mm. Computer-controlled optical delay lines were utilized to control time delays between the pump and probe pulses, which may vary from the tens of femtoseconds to 6 ns after the photo-excitation. A liquid nitrogen-cooled charge-coupled device (CCD) was employed to detect and record the time-resolved spectra. To prevent multi-photon effects, the energy of the pump laser pulse was kept low, with a photon density not greater than approximately 2.69 × 10²⁷ photon per s cm². Given the known propensity for similar pyrimidine compounds to undergo photodegradation,^23–26 the steady-state absorption spectrum of 1mCyt was examined to assess whether there is degradation caused during the time-resolved experiments. The sample solutions were found to display identical absorption spectra before and after the time-resolved experiments (Fig. S1 in ESI†), indicating no degradation during the measurements. All the measurements were conducted at room temperature and atmospheric pressure. The kinetic analysis and decay associated analysis of the time-resolved data, as well as the log-normal functions for simulation of the steady-state and time-resolved spectra, are presented in the ESI.†

B3. Density functional theory (DFT) and time-dependent DFT (TDDFT) calculations. The DFT²⁷ and TDDFT²⁸ calculations were conducted for 1mCyt (Scheme 1) to determine the energy and optimized structures for both the ground state (S₀) and excited state (S₁). These calculations were also used to calculate vertical electronic transition energies, associated oscillation strengths, and Kohn–Sham orbitals for comparison with the experimental absorption and fluorescence spectra. The structural optimization for the ground state was computed using the TPSS functional^29,30 with a basis set of 6-31G+(d,p).³¹ For the excited state structure optimization, the B3LYP functional was employed in conjunction with the basis set of 6-31G+(d,p).³¹ To ensure that the optimized structures represent local minima, frequency calculations were carried out to verify the absence of imaginary frequencies for all the obtained structures. Solvent effects were considered in the computation and described using the integral equation formalism polarizable continuum model (IEFPCM).³² For the calculations in water and methanol, in addition to the implicit non-specific bulk solvent effect simulated by the IEFPCM, a hybrid solvent model that additionally involves the site-specific solute–solvent interaction resulting from hydrogen-bond formation was also employed in the computation by including one water molecule or methanol molecule hydrogen-bonded to the keto oxygen in the pyrimidine ring of 1mCyt. All the calculations were performed using the Gaussian16 package.³³ The calculated energies and atomic coordinates of the optimized structures for 1mCyt at the S₀ and S₁ state under implicit and explicit solvent conditions are given in Tables S1–S7 in the ESI.†

Results

A. Steady-state spectroscopy

The steady-state absorption, fluorescence (λ_ex = 267 nm), and fluorescence excitation spectra (for emission at 330 nm) recorded using 1mCyt in H₂O and CH₃CN are displayed and compared in Fig. 1. The associated key spectral parameters are summarized in Table 1.

Fig. 1 (a) Experimental absorption (solid lines) and fluorescence excitation spectra (dot lines, for emission at 330 nm), and (b) normalized fluorescence spectra (λ_ex = 267 nm) of 1mCyt in H₂O and CH₃CN. The calculated wavelengths of electronic absorption and fluorescence transitions computed using the implicit solvation model in water and CH₃CN and with the additional explicit solvation effect in water are indicated by the vertical solid lines and the vertical dashed lines, respectively. The insets in (a) and (b) represent the Kohn–Sham orbitals calculated for the absorption and fluorescence transition, respectively.

Table 1 Spectral and dynamic parameters obtained for 1mCyt, Cyt, Cyd, dCyd and 5mCyd in different solvents

		λ a /nm	ε max /L mol^−1 cm^−1	λ f /nm	τ 1 /ps	τ 2 /ps	τ 3 /ps	Φ f (× 10^−4)
a Wavelength of the maximum absorbance at the lowest energy absorption band. b Maximum extinction coefficient at the lowest energy absorption band. c Wavelength of the maximum fluorescence intensity with 267 nm excitation. d Decay time constants from TRF measurements. e Decay time constants from TA measurements. f Fluorescence quantum yield with 267 nm excitation. g From ref. 10. h From ref. 34. i From ref. 35. j From ref. 36. k From ref. 2. l From ref. 37.
1mCyt	H2O	274	8213 ± 120	324	0.18 ± 0.01	0.76 ± 0.03	5.7 ± 0.3	0.78 ± 0.05
	CH3CN	280	6177 ± 80	336	0.20 ± 0.01	0.77 ± 0.01		0.88 ± 0.06
Cyt	H2O	267^g	6333^g	322^h	0.20 ± 0.03^g	1.5 ± 0.1^g	7.7 ± 0.6^g	0.82^i
	CH3CN	274^j		334^j
Cyd	H2O	271^g	9199^g	325^g	0.20 ± 0.03^g	1.8 ± 0.1^g	35 ± 2^g	1.02 ± 0.06^g
dCyd	H2O	271^g^k	9807^g	324^g; 323^k	0.20 ± 0.03^g; 0.22 ± 0.01^k	1.1 ± 0.1^g; 0.96 ± 0.07^k	30 ± 2^g	0.89 ± 0.06^g; 0.6^k
	CH3CN	277^k		311^k	0.22 ± 0.02^k	0.91 ± 0.04^k		0.9^k
5mCyd	H2O	278^g^l	8871^g	344^l	0.60 ± 0.05^k	7.6 ± 0.3^k		7.53 ± 0.32^g
	CH3CN	283^l		352^l

---

As shown in Fig. 1a and Table 1, the absorption spectrum in H₂O is different from that in CH₃CN. The lowest energy absorption band, peaking at the wavelength (λ_a) of 274 nm in H₂O, exhibits a red-shift to 280 nm in CH₃CN. Furthermore, the value of the correlated extinction coefficient (ε_max) is larger in H₂O (8213 L mol⁻¹ cm⁻¹) than in CH₃CN (6177 L mol⁻¹ cm⁻¹).

Varying the solvent from H₂O to CH₃CN also results in obvious changes in the fluorescence spectrum of 1mCyt. As can be seen from Fig. 1b and Table 1, the maximum fluorescence intensity wavelength (λ_f) in H₂O at 324 nm exhibits a notable blue-shift of ∼12 nm compared to that of the spectrum in CH₃CN (336 nm). The value of Φ_f was slightly larger in CH₃CN (∼0.88 × 10⁻⁴) than in H₂O (∼0.78 × 10⁻⁴). In addition, the fluorescence spectrum in CH₃CN is considerably broader than that in H₂O, with a bandwidth (Δ) of ∼5731 cm⁻¹ and ∼5129 cm⁻¹ in CH₃CN and H₂O, respectively (Table S8 in the ESI†). Note that both in H₂O and CH₃CN, the fluorescence excitation spectrum matches with the corresponding lowest energy absorption band (Fig. 1a), indicating that the fluorescence emission originates from the same electronic excitation after photo-absorption.

The calculations performed in CH₃CN and H₂O (with and without involving the site-specific hydrogen bonding) observed a common planar structure for the S₀ state of 1mCyt (illustrated in Fig. 2). In CH₃CN, according to the TDDFT computation, both the absorption and fluorescence spectra arise from the lowest energy (S₁) bright ππ* state derived from transitions between the HOMO and LUMO (Fig. 1 inserts, Fig. S2 and S3 in the ESI†), with large oscillation strengths (Tables S9 and S10 in the ESI†) and a significant bonding/anti-bonding character of the C5=C6 double bond. The calculated ππ* state absorption and fluorescence wavelengths, which are 279 and 340 nm in CH₃CN, respectively, agree well with the experimental spectra, indicating the reliability of the computational method (Fig. 1 and Tables S9, S10 in the ESI†). The S₁ ππ* state is also responsible for the spectra in water. However, it should be noted that when considering merely the implicit solvent effect in water, the calculated transitions are at the wavelengths (279 nm for the absorption and 338 nm for the fluorescence) nearly identical to those computed in CH₃CN. In contrast, when explicitly including a water molecule hydrogen-bonded to the keto oxygen (Fig. 2), the calculated transition energies have reproduced nicely the wavelength red-shifts observed experimentally for both the absorption and fluorescence spectra in CH₃CN compared to those in water (Fig. 1). The same trend of red-shift in the absorption transition was also observed in computation done with the commonly used B3LYP functional (Table S9b in the ESI†). However, such computation uniformly overestimated the transition energies (by ∼0.31 eV) under various solvent conditions, analogous to those reported in previous computational studies using this functional for nucleobases and derivatives.^2,5 To this end, the TPSS functional^29,30 has a practical advantage in giving the excellent results for the absorption transition energies with the different solvation models for 1mCyt. This implies that the site-specific solute–solvent inter-molecular hydrogen bonding, presenting solely in the protic solvent, plays an important role in modulating the spectral energy of the ππ* state upon and after the photo-excitation.

Fig. 2 Optimized top-view and side-view structures of 1mCyt at the ground state (S₀) using TPSS/6-31G+(d,p) calculations and at the lowest energy excited state (S₁) using B3LYP/6-31G+(d,p) calculations, with the keto oxygen hydrogen-bonded to one water molecule (left) and under the bulk solvent condition of CH₃CN (right).

Of note, the 1mCyt S₁ ππ* state features a structure that differs significantly from its S₀. Unlike the planar structure in the S₀, the S₁ ππ* state displays a significant non-planar structure (Fig. 2 and Fig. S4 in the ESI†), which is manifested mainly by the out-of-planar distortions at the N1 and C4 of the pyrimidine ring and an obvious lengthening of the C5=C6 bond length (by ∼0.06 Å) due to its anti-bonding character in the S₁ state. These major structural changes on going from the S₀ to the S₁ ππ* state are in line with the literature on 1mCyt^2,38,39 and Cyt.⁵ More importantly, although the solvent effect, implicit or explicit, affects little the conformation in S₀, the inclusion of the site-specific hydrogen bonding in water results in small but clear variations in the S₁ ππ* state structure. For instance, when compared to that in CH₃CN, the S₁ structure, considering the explicit hydrogen bonding between the keto oxygen and water molecule, displays a substantial shortening of the C3–C4 bond length by ∼0.05Å, and more importantly, a moderate decrease in the dihedral angle of C6–C5–C4–N8 and C4–N3–C2–O7 by ∼1.12° and ∼1.17°, respectively. This suggests that there is a higher degree of out-of-planarity in the S₁ ππ* state structure in CH₃CN compared to that in water. Such structural changes, induced by the explicit hydrogen bonding interactions in the protic solvent, may contribute importantly to the altered fluorescence spectrum in CH₃CN compared to that in water.

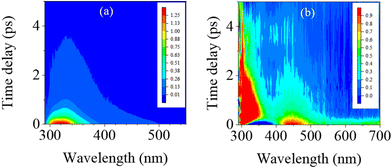
B. Time-resolved spectroscopy in water

Fig. 3 displays the three-dimensional (3D) spectra of fs-TRF and fs-TA from 1mCyt in water recorded with 267 nm excitation, which ascertains the excited state dynamics including both radiative and non-radiative deactivation pathways in water. It can be seen from this figure that both the fs-TRF and fs-TA exhibit spectra that decay on a very rapid timescale. However, the decay of the fs-TA appears to be more complex and proceeds in a longer time region (up to about ten picoseconds) than the case of fs-TRF where the transient fluorescence diminishes and disappears in less than 4 ps after the excitation.

Fig. 3 3D (a) fs-TRF and (b) fs-TA spectra recorded with 267 nm excitation of 1mCyt in H₂O.

B1. Time-resolved fluorescence spectroscopy. To reveal the details of the broadband temporal evolution of the fs-TRF, Fig. 4(a and b) display the 2D spectra of the transient fluorescence and decay profiles of fluorescence intensities at selected emission wavelengths of 309, 330, and 364 nm. As shown in Fig. 4a, the TRF at the very early time features spectra peaking at ∼316 nm, which then exhibits a rapid decay along with spectral narrowing and a gradual red-shift of the intensity maximum to ∼324 nm (Fig. 4a insert). The decay of the TRF intensity is marginally dependent on emission wavelengths, being slightly slower at longer wavelengths (Fig. 4b). It is important to note that during the decay process, there is no rise in the emission intensity across all the emission wavelengths of the TRF detected. Global analysis of the TRF time profiles shows two decay components, with time constants of ∼0.18 ps (τ₁) and ∼0.76 ps (τ₂), respectively. The amplitudes of these time constants vary with emission wavelengths and are given in Table S11 in the ESI.†Fig. 4d shows the decay-associated spectra (DAS) derived from the global analysis for the two time constants. It is clear that the ∼0.18 ps time constant is associated with a strong fluorescence component peaking at ∼316 nm, while the ∼0.76 ps component corresponds to a much weaker fluorescence component peaking at ∼324 nm.

Fig. 4 (a) 2D fs-TRF spectra, (b) experimental (○, □, ◊) and fitted (solid lines) TRF intensity decay profiles, (c) 2D fs-TRFA spectra, and (d) decay-associated spectra (DAS) from global analysis of fs-TRF spectra after 267 nm excitation of 1mCyt in H₂O. The time delays for 2D spectra shown in (a) are 0, 0.05, 0.1, 0.15, 0.2, 0.25, 0.3, 0.35, 0.4, 0.5, 0.6, 0.85, 1.5 and 10 ps. The insert in (a) shows intensity normalized TRF spectra at the denoted time delays.

B2. Time-resolved fluorescence anisotropy spectroscopy. To learn more about the electronic nature of the state underlying the TRF, Fig. 4c presents the fs-TRFA spectra recorded with 267 nm excitation of 1mCyt in H₂O. It can be seen that the fluorescence anisotropy value (r) is almost independent of the emission wavelengths. This indicates that both of the TRF decay time constants are due to a common emitting state, which can be attributed with certainty to the S₁ ππ* state of 1mCyt.

Given that the S₁ ππ* state is also the state responsible for the absorption transition (Fig. 1), the observed TRF spectra (Fig. 3a and 4a) should feature the theoretical anisotropy (r) value of 0.4.²² However, it should be noted that the r value of the TRF at the initial time (∼0.35) is lower than 0.4. This divergence may arise because the 267 nm excitation could populate partially a closely lying higher energy excited state with different polarizations that converted into the S₁ ππ* state at a rate beyond the time-resolution of the measurement.^14,22 Furthermore, as shown in Fig. 4c, the r value displays slight changes as time proceeds, dropping from ∼0.35 at 0 ps to ∼0.3 at 0.6 ps after the excitation. This is attributable to solvent reorientation and the structural rearrangement of the photo-prepared S₁ ππ* state from the early time planar structure in the Franck–Condon (FC) region to the late time out-of-planar conformation in the local minimum of the S₁ ππ* PES.

B3. Transient absorption spectroscopy. To display the temporal evolution of the fs-TA, the spectra recorded at the early (0–0.6 ps) and late (0.6–25 ps) times after the excitation are presented separately in Fig. 5a and b, respectively. Promptly after the excitation, the TA spectrum contains a strong negative signal peaking at ∼340 nm and a broad positive band covering the entire visible region, with the maximum at ∼450 nm. The positive band is from the excited state absorption (ESA), while the negative signal is due to stimulated emission (SE) from the S₁ ππ* state prepared by photo-absorption. In the early time, the ESA and intensity of the SE decay rapidly accompanied by the growth of a higher energy ESA band peaking at ∼330 nm. This spectral evolution produces a well-defined isosbestic point at ∼400 nm. In the late time intervals, the TA spectra are dominated by the newly formed ∼330 nm ESA, along with the relatively weak absorption at ∼450 nm, which decays nearly completely by about 10 ps after the excitation. A careful examination observes a minimal offset at ∼325–500 nm, which persists and remains unchanged in the next ∼6000 ps (Fig. S5 in the ESI†).

Fig. 5 (a) and (b) 2D fs-TA spectra, (c) and (d) experimental (○, □, ◊) and fitted (solid lines) TA intensity decay profiles at the denoted wavelengths in the range of (c) (∼0–3 ps), (d) (∼0–10 ps), representing the early time delays after 267 nm excitation of 1mCyt in H₂O. The time delays for 2D spectra shown in (a) are 0, 0.05, 0.1, 0.15, 0.2, 0.3 and 0.6 ps, while those in (b) are 0.6, 1.25, 2, 3, 6 and 25 ps.

The TA intensity decays, as shown in Fig. 5(c and d), are strongly wavelength-dependent. Global analysis of the decay profiles at representative wavelengths, e.g., 337, 451 and 551 nm, shows dynamics that can be described by a multi-exponential function containing three time components (τ₁, τ₂, and τ₃) and a time-dependent offset (τ₄). The time constants are ∼0.18 ps (τ₁), 0.76 ps (τ₂), and 5.7 ps (τ₃), respectively. The details of the weighting factors for each of the time components are listed in Table S12 in the ESI.† Note that the first two time constants (τ₁ and τ₂) are identical to those for the TRF decays (Fig. 4b and Table 1). This, along with the observation of the SE in the correlated timescale, indicates that both phenomena originate from the brightly emissive S₁ ππ* state. However, the components of τ₃ and τ₄, having no counterparts in the TRF decays, must arise from a non-emissive or very weakly emissive transient state.

The component of τ₃ (∼5.7 ps), which is associated with the TA with the ESAs at ∼330/450 nm (Fig. 5b), can be attributed to the dark-natured nπ* state deactivating into the S₀ State. This assignment is made based on the point that the profile of the ∼330/450 nm ESAs is very similar to the absorption spectra reported for the nπ* state of Cyt, dCyd and Cyd.¹⁰ The attribution is also supported by the previous high-level computations which showed that although the nπ* state lies at an energy higher than the S₁ ππ* state in the FC region, it could be populated during the excitation relaxation and participate in the non-radiative decay via readily accessible conical intersection (CI) into the S₀ state.^2,5,40 In line with this, our TDDFT calculations (Table S9, S10 and Fig. S2, Fig. S3 in the ESI†) showed that the energy of the S₁ ππ* state is close to that of the second-lowest S₂ nπ* state that has a lone pair from the keto oxygen (denoted as n_Oπ*). This agrees with the early theoretical studies indicating the involvement of the n_Oπ* state for the deactivation of 1mCyt, like the case for Cyt and dCyd.^2,4–6,8

In addition, the residual component (τ₄), given its very long-lived feature, is attributable to the triplet state of 1mCyt. The minimal contribution (∼1–5%, Table S12 in the ESI†) of this component implies a minute role of the triplet in the deactivation dynamics. This is analogous to the very low yield of the triplet state (∼0.01) known for Cyt and its nucleotides and nucleotides.^10,41,42

C. Effects of solvents on the fluorescence dynamics

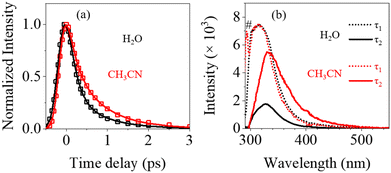
In order to explore the role of solvents in the fluorescence decay and to resolve the cause for solvent effects on the steady-state fluorescence in water versus CH₃CN, comparative fs-TRF and TRFA measurements were conducted with 267 nm excitation for 1mCyt in CH₃CN. The results acquired are displayed in Fig. S6 in the ESI,† and the dynamic parameters derived for the TRF intensity decays are given in Table S11 in the ESI.† The main features of the fs-TRF and TRFA in CH₃CN, such as the rapid TRF decay and the nearly wavelength-independent high values of TRFA, are very similar to those observed in H₂O. This is not surprising, as the fluorescence in both the solvents is due to the common very short-lived S₁ ππ* state, a type of state that is known to be relatively less affected by solvent properties.^2,10

In spite of this, a careful comparison of the TRF spectra and the correlated fluorescence dynamics in the two solvents has unveiled important differences in two aspects. First, the TRF decay appears to be slower in CH₃CN than in H₂O (Fig. 6a). However, according to the global kinetic analysis, the decay profiles in CH₃CN feature two time components with the time constants (τ₁ = 0.20 ps, τ₂ = 0.77 ps, Table 1) being almost equivalent to the values in H₂O. The apparently slower decay in CH₃CN is found due to a substantially increased fractional contribution of the slower component τ₂ (a₂ = 46%) in CH₃CN than the case in H₂O (a₂ = 19%, Table S11 in the ESI†). Therefore, the average fluorescence lifetime (〈τ〉 at 330 nm, see the ESI†) is longer in CH₃CN (∼0.46 ps) compared to that in H₂O (∼0.29 ps). Second, as shown in Fig. 6b, with respect to the DAS of τ₁, the DAS of τ₂ is obviously stronger in CH₃CN than in H₂O. Also, the DAS of τ₂ in CH₃CN peaking at ∼333 nm is clearly broader and red-shifted, especially in the region of long emission wavelengths (∼330–500 nm), when compared to the counterpart spectrum in H₂O. Log-normal simulation of the spectra (Table S8 in the ESI†) shows that for the DAS of τ₂, the spectral bandwidth in CH₃CN (∼5516 cm⁻¹) is greater than that in H₂O (∼4748 cm⁻¹). Conversely, the DASs of τ₁ in the two solvents, both peaking at ∼314 nm, are very similar, featuring nearly identical profiles as shown in Fig. 6b.

Fig. 6 (a) Experimental (□) and fitted (solid lines) TRF intensity decay profiles at 330 nm, and (b) decay-associated spectra (DAS) obtained from the global analysis of fs-TRF spectra after 267 nm excitation of 1mCyt in H₂O and CH₃CN. # due to solvent scattering.

Altogether, these observations reveal that the variation in the percentage contribution and the spectral character, correlating to the ∼0.77 ps time component, is the underlying cause of the steady-state fluorescence spectral red-shift and the greater quantum yield of 1mCyt in CH₃CN (λ_f = 336 nm, Φ_f = ∼0.88 × 10⁻⁴) compared to H₂O (λ_f = 324 nm, Φ_f = ∼0.78 × 10⁻⁴). Given that this relatively slow time constant is associated with the decay of the S₁ ππ* state in the local minimum of its PES, this corroborates nicely the calculated result regarding the crucial role of the explicit inter-molecular hydrogen bonding in regulating the fluorescence energy and dynamics in the water compared to CH₃CN. The broader fluorescence spectrum in CH₃CN is connected to a greater degree of structural variation in S₁ relative to the S₀ state in this solvent than in water.

Discussion

A. Deactivation pathways of 1mCyt in H₂O

Putting together the above experimental and theoretical results allows the construction of the following deactivation pathway for 1mCyt in H₂O. After the photo-excitation, 1mCyt displays two decay channels from the emissive S₁ ππ* state and one additional channel mediated by the dark-natured nπ* state to eliminate the excitation by IC into the S₀ state. The first ππ* decay channel is brought by the photo-populated ππ* state at approximately the FC region featuring the planar structure emitting the ∼316 nm fluorescence with a lifetime of ∼0.18 ps. The second channel of the ππ* decay is from the fraction of the population at its PES local minimum displaying the nonplanar conformation that emanates the ∼324 nm fluorescence emission at the time constant of 0.76 ps. The nπ* state, as indicated by the isosbestic point shown in the fs-TA (Fig. 5a), is populated by a part of the initial ππ* excitation after the photo-excitation, and its decay occurs at the rate of ∼5.7 ps.

The very rapid decay from the S₁ ππ* state agrees with that reported in the earlier TRIR study.⁴ The two channels of the S₁ ππ* non-radiative deactivation are likely achieved through the nearly barrierless (for τ₁) and low-barrier (for τ₂) conical intersections (CIs) as identified by the extensive theoretical descriptions of the PESs between the S₁ ππ* and S₀ for Cyt and 1mCyt.^5,43 The previous sophisticated computational studies have also located readily accessible CIs connecting the nπ* state with S₀,^2,38,39 while our data (Fig. 5) provide the first direct experimental evidence for the participation of nπ* in the non-radiative deactivation of 1mCyt in aqueous solution. Of note, the overall deactivation, driven by the ∼0.18 ps S₁ ππ* decay and completed within the timescale in several picoseconds, provides an effective mechanism to a high degree of photo-stability for 1mCyt after absorption of UV irradiation. On the other hand, with regard to the known proclivity of pyrimidine analogs that undergo photo-degradation due to photo-hydration in an aqueous solution,^23–26 future research to investigate the behavior of 1mCyt excited states in extensive timescale after successive irradiation intervals, beyond the scope of the current study, is essential for evaluating the involvement of any photo-reaction and potential role of the nπ* state in the photochemistry of 1mCyt, whether incorporated into Hachimoji DNA or not.

B. Comparison of the deactivation dynamics of 1mCyt with Cyt and its nucleosides

The deactivation dynamics we derived for 1mCyt share some similarities and also display important differences from those documented for Cyt and its nucleosides and nucleotides.^2,10,14

On the one hand, the non-radiative and radiative channels we described for 1mCyt resemble the deactivating pathways of Cyt and its analogs. These pathways exhibit biexponential S₁ ππ* decay, with the involvement of nπ* for rapidly regenerating the S₀ state after photo-excitation. The time constant of the 1mCyt's early-time S₁ ππ* decay (∼0.2 ps) is very close to the counterpart values of Cyt and the derivatives (Table 1).^2,10,14,16 Additionally, the steady-state and time-resolved absorption and fluorescence spectra of the S₁ ππ* state, as well as the TA from the nπ* state of 1mCyt, are also very similar to those recorded experimentally for Cyt, dCyd, and Cyd (Table 1).^2,6,10 To illustrate such similarity and some differences between Cyt and 1mCyt, provided in Fig. S8 and S9 in the ESI† are, respectively, the fs-TRF and TA spectra acquired for Cyt in water under identical experimental conditions. Furthermore, all these molecules share a common very low yield of the triplet state during their non-radiative processes.^10,41,42 In light of this, 1mCyt might be considered a useful model compound for eliminating the various tautomeric forms (except for the keto form) in the study of the Cyt excited states^44,45 and to reduce the computational cost in the theoretical exploration of the mechanistic details of the dCyd and Cyd deactivation.^2,3

On the other hand, the precise time constants of the S₁ ππ* decay from its PES minimum (τ₂) and the decay of nπ* (τ₃) in 1mCyt are noticeably different from those in Cyt, dCyd and Cyd.^2,10 As shown in Table 1, the value of τ₂ is ∼0.76 ps for 1mCyt in water, which is smaller than the time constant of ∼1.5 ps for Cyt (Fig. S8c, ESI†), ∼1.8 ps for Cyd and ∼1.1 ps for dCyd.^2,10 Besides, the lifetime of the nπ* state, which is ∼5.7 ps with 1mCyt, is close to the ∼7.7 ps nπ* lifetime in Cyt but significantly shorter than the ∼30 and 35 ps lifetime in dCyd and Cyd, respectively.¹⁰ The much longer lifetime of the nπ* state with dCyd and Cyd may originate due to the presence of the ribose (in Cyd) or deoxyribose (in dCyd), which could lead to the substantial stabilization of the energy of nπ* concerning the correlated nπ*/S₀ CI, deferring its decay into the S₀ state.^4,7 It is important to note that whilst glycosylation at N1 in Cyd lengthens substantially the nπ* state's lifetime, the additional methylation at C5 in m5Cyd removes the access of the nπ* state, and its deactivation occurs primarily through the S₁ππ* state that has an increased lifetime of ∼7.6 ps (Table 1).^2,10 The variation in the time constant of the ππ* decay reflects that the exact energy barrier height, involved in reaching the relevant ππ*/S₀ IC from the energy minimum of the ππ* state, is differently affected by N1 methylation in 1mCyt vs. C5 methylation in 5mCyd. It is also altered variably by the substitution at N1 of the methyl group in 1mCyt compared to the hydrogen in Cyt and the deoxyribose and ribose group in dCyd and Cyd, respectively. These observations, put together, demonstrate an intricate impact of the ring substitutions on the electronic properties of the pyrimidine bases, adding insight into the understanding of the complex excited state dynamics and photophysics of nucleobases and their derivatives.^10,46–50

C. Solvent effects on the fluorescence dynamics of 1mCyt and Cyt nucleosides

Using a solvent is a well-known important factor in regulating the energy and dynamics of the nucleobases’ fluorescence emissions. We observe that 1mCyt features very different solvent effects on its fluorescence spectra compared to dCyd. As shown in Fig. 1 and Table 1, when varying the solvent from water to CH₃CN, the fluorescence spectrum of 1mCyt shows a notable red-shift (by ∼12 nm) from 324 to 336 nm, in contrast to the case of dCyd where the fluorescence displays a blue-shift (by ∼12 nm) from 323 to 311 nm.² According to the results we obtained, the solvent effect observed in 1mCyt is caused primarily due to the explicit solute–solvent hydrogen bonding, which is present solely in the protic solvent. Our further steady-state measurements and TDDFT calculations on the fluorescence from 1mCyt in CH₃OH observed a fluorescence spectrum nearly identical to that in water (Fig. S7 and Table S10 in the ESI†). Given that CH₃OH is a protic solvent and has the polarity similar to CH₃CN, this observation lends further support to the importance of the solvent hydrogen bonding and implies little relevance of solvent polarity to the changes in the 1mCyt's fluorescence observed. Besides, it is known that compared to water and CH₃OH being both hydrogen bond donors and acceptors, the aprotic solvent CH₃CN is a hydrogen bond acceptor only. Given this, our result implies that the ability of the protic solvent to be a hydrogen bond donor is the key factor for the altered dynamics of the 1mCyt excited state. Pertinent to this, a previous study found that solvents with hydrogen bond donor capacity significantly influenced the dynamics of photo-induced vibrational cooling in purine derivatives.⁵¹

In this context, it is pertinent that dCyd, containing the deoxyribose group at the N1 atom position, in water, may possess not only the inter-molecular hydrogen bonding with the solvent molecules but also intra-molecular hydrogen bonding interactions between the ribose hydrogen and the nearby carbonyl oxygen of the pyrimidine ring. The additional sugar group-induced intra-molecular hydrogen bonding could override the inter-molecular interactions, leading to the substantial stabilization of its S₁ ππ* state at the PES minimum. This probably contributes to the reported red shift of the dCyd's fluorescence in H₂O compared to CH₃CN. This might also account for the longer ππ* lifetime as well as the slightly greater Φ_f of dCyd when compared to those of 1mCyt in water. The lack of intra-molecular hydrogen bonding in 1mCyt may affect the conformation and the solvation dynamics before and after the photo-excitation in comparison to the case of dCyd. Indeed, in contrast to the much greater fluorescence Stokes’ shift (by ∼2000 cm⁻¹) displayed by dCyd in water than in CH₃CN, the Stokes’ shift of 1mCyt in water is lesser (by ∼320 cm⁻¹) than that in CH₃CN. As a result, 1mCyt shall not be a faithful model compound for dCyd in delineating the effects of solvents and the exact dynamics of its radiative and non-radiative deactivation.

It is pertinent that like 1mCyt, 5-methylcytidine (5mCyd) shows similar red shifts in both the absorption (278 to 283 nm) and fluorescence (344 to 352 nm) spectra when changing the solvent from water to CH₃CN (Table 1).³⁷ Theoretical calculations on 5mCyd suggest that the spectral shifts are due to increased transition energy between the frontier Kohn–Sham orbitals for the spectra which is caused by the presence of solute–solvent hydrogen bonding in water.³⁷ However, for the case of 1mCyt, our data show that the inter-molecular hydrogen bonding in water slightly restrains the out-of-plane distortion of the S₁ ππ* state structure when compared to that in CH₃CN. This explicit solute–solvent interaction also facilitates significantly the most rapid channel of the S₁ ππ* decay from the FC region at the rate of ∼0.18 ps. The greater degree of the structural change, associated with the increased fractional contribution of the S₁ ππ* decay via the relatively slower ∼0.77 ps path, is responsible for the prolonged average ππ* lifetime, higher Φ_f, lower energy, and broader fluorescence spectrum in CH₃CN compared to water. To this end, our result exemplifies that a solvent-induced change in the average fluorescence lifetime does not necessarily imply a variation in the fluorescence lifetime, but is rather a consequence of an altered branching ratio between the different fluorescence time components occurring in the varied solvents involved.

Additionally, it is noted that other pyrimidine bases, such as thymine and uracil, exhibit blue-shifts in the absorption spectra upon changing the solvent from water to aprotic solvents,^52–59 which is opposite to the cases of 1mCyt, dCyd,² and 5mCyd.³⁷ In addition, there are also strong solvent effects on the excited state deactivation of pyrimidine derivatives in terms of spectral shifts, lifetimes and energies, etc.^{10,46,47,57,60,61} Clearly, the excited states of different molecules respond differently to the change of solvent properties, which is governed by their specific electronic and structural characters before and after the photo-excitation.^2,10,37 Given this, caution should be taken when using 1mCyt as a model for the study of the deactivation dynamics of Cyt nucleosides and nucleotides under various solvent conditions.

Conclusion

This study, combining fs-TRF(A), fs-TA, and (TD)DFT, provides a comprehensive characterization of excited state deactivation and the effect of solvents on the fluorescence dynamics of 1mCyt in CH₃CN compared to water. The results reveal a bi-channel sub-picosecond decay from the S₁ ππ* state, and provide the first experimental evidence for the involvement of an additional short-lived dark natured nπ* state in jointly mediating the rapid non-radiative deactivation of 1mCyt. This presents an effective mechanism, allowing a high degree of photo-stability for 1mCyt. The deactivation pathways exhibited by 1mCyt are largely analogous to those known for Cyt, Cyd, and dCyd, while the precise decay rates of the 1mCyt's S₁ ππ* and nπ* states are, however, different from those of the canonical counterparts. More importantly, our study demonstrates a significant solvent effect, arising from the explicit hydrogen bonding with the protic solvent molecules, on altering the structure and the radiative as well as non-radiative dynamics of the S₁ ππ* state of 1mCyt. This solvent effect is distinctive from that for dCyd, indicating a limitation in using 1mCyd as a model compound for exploring the ultrafast deactivation of Cyd and dCyd under various protic and aprotic solvent conditions. The results of this study provide important insights into the subtle and complex dependencies on the substituent and solvent properties of the photo-physics of nucleobases.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors thank the National Natural Science Foundation of China (No. 21773157 and 22073063), the Project of Shenzhen Science and Technology (JCYJ20190808110801662 and JCYJ20210324095210028) and the Research Grants Council of Hong Kong (15303018, 15302319 and 15301721) for financial support.

References

1. S. Hoshika, N. A. Leal, M. J. Kim, M. S. Kim, N. B. Karalkar, H. J. Kim, A. M. Bates, N. E. Watkins, H. A. SantaLucia, A. J. Meyer, S. DasGupta, J. A. Piccirilli, A. D. Ellington, J. SantaLucia, M. M. Georgiadis and S. A. Benner, Science, 2019, 363, 884–887.
2. L. Martinez-Fernandez, A. J. Pepino, J. Segarra-Marti, J. Jovaišaitė, I. Vaya, A. Nenov, D. Markovitsi, T. Gustavsson, A. Banyasz, M. Garavelli and R. Improta, J. Am. Chem. Soc., 2017, 139, 7780–7791.
3. L. Martinez-Fernandez and R. Improta, Photochem. Photobiol., 2023 DOI:10.1111/php.13832.
4. P. M. Keane, M. Wojdyla, G. W. Doorley, G. W. Watson, I. P. Clark, G. M. Greetham, A. W. Parker, M. Towrie, J. M. Kelly and S. J. Quinn, J. Am. Chem. Soc., 2011, 133, 4212–4215.
5. R. Improta, F. Santoro and L. Blancafort, Chem. Rev., 2016, 116, 3540–3593.
6. X. Wang, Z. Zhou, Y. Tang, J. Chen, D. Zhong and X. Jianhua, J. Phys. Chem. B, 2018, 122, 7027–7037.
7. A. J. Pepino, J. Segarra-Marti, A. Nenov, I. Rivalta, R. Improta and M. Garavelli, Phys. Chem. Chem. Phys., 2018, 20, 6877–6890.
8. S. Blaser, M. A. Trachsel, S. Lobsiger, T. Wiedmer, H. M. Frey and S. Leutwyler, J. Phys. Chem. Lett., 2016, 7, 752–757.
9. N. Ismail, L. Blancafort, M. Olivucci, B. Kohler and M. A. Robb, J. Am. Chem. Soc., 2002, 124, 6818–6819.
10. C. Ma, C. C.-W. Cheng, C. T.-L. Chan, R. C.-T. Chan and W.-M. Kwok, Phys. Chem. Chem. Phys., 2015, 17, 19045–19057.
11. P. Wu, X. Wang, H. Pan and J. Chen, J. Phys. Chem. B, 2022, 126, 7975–7980.
12. P. M. Hare, C. E. Crespo-Hernández and B. Kohler, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 435–440.
13. J. B. Nielsen, J. Thøgersen, S. K. Jensen and S. R. Keiding, Chem. Phys. Lett., 2013, 567, 50–54.
14. D. Onidas, D. Markovitsi, S. Marguet, A. Sharonov and T. Gustavsson, J. Phys. Chem. B, 2002, 106, 11367–11374.
15. J. M. L. Pecourt, J. Peon and B. Kohler, J. Am. Chem. Soc., 2001, 123, 10370–10378.
16. A. Sharonov, T. Gustavsson, V. Carre, E. Renault and D. Markovitsi, Chem. Phys. Lett., 2003, 380, 173–180.
17. A. Sharonov, T. Gustavsson, S. Marguet and D. Markovitsi, Photochem. Photobiol. Sci., 2003, 2, 362–364.
18. C. Ma, W. M. Kwok, W. S. Chan, Y. Du, J. T. W. Kan, P. H. Toy and D. L. Phillips, J. Am. Chem. Soc., 2006, 128, 2558–2570.
19. C. Ma, R. C. T. Chan, C. T. L. Chan, A. K. W. Wong and W.-M. Kwok, J. Phys. Chem. Lett., 2019, 10, 7577–7585.
20. C. T.-L. Chan, C. Ma, R. C.-T. Chan, H.-M. Ou, H.-X. Xie, A. K.-W. Wong, M.-L. Wang and W.-M. Kwok, Phys. Chem. Chem. Phys., 2020, 22, 8006–8020.
21. C. C.-W. Cheng, C. Ma, C. T.-L. Chan, K. Y.-F. Ho and W.-M. Kwok, Photochem. Photobiol. Sci., 2013, 12, 1351–1365.
22. J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, Boston, 2006.
23. G. J. Fisher and H. E. Johns, in Photochemistry and Photobiology of Nucleic Acids, ed. S. Y. Wang, Academic Press, 1976, pp. 169–224 DOI:10.1016/B978-0-12-734601-4.50010-0.
24. J. G. Burr, E. H. Park and A. Chan, J. Am. Chem. Soc., 1972, 94, 5866–5872.
25. R. Szabla, H. Kruse, J. Šponer and R. W. Góra, Phys. Chem. Chem. Phys., 2017, 19, 17531–17537.
26. S. J. Hoehn, S. E. Krul, M. M. Pogharian, E. Mao and C. E. Crespo-Hernández, J. Phys. Chem. Lett., 2023, 48, 10856–10862.
27. P. M. W. Gill, B. G. Johnson, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1992, 197, 499–505.
28. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
29. J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401.
30. J. P. Perdew, J. Tao, V. N. Staroverov and G. E. Scuseria, J. Chem. Phys., 2004, 120, 6898–6911.
31. C. R. Legler, N. R. Brown, R. A. Dunbar, M. D. Harness, K. Nguyen, O. Oyewole and W. B. Collier, Spectrochim. Acta A, 2015, 145, 15–24.
32. A. Klamt, C. Moya and J. Palomar, J. Chem. Theory Comput., 2015, 11, 4220–4225.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Wallingford, CT, 2016.
34. L. Blancafort, B. Cohen, P. M. Hare, B. Kohler and M. A. Robb, J. Phys. Chem. A, 2005, 109, 4431–4436.
35. M. Daniels and W. Hauswirth, Science, 1971, 171, 675–677.
36. C. Párkányi, C. Boniface, J.-J. Aaron, M. D. Gaye, R. Ghosh, L. von Szentpály and K. S. RaghuVeer, Struct. Chem., 1992, 3, 277–289.
37. L. Martinez-Fernandez, A. J. Pepino, J. Segarra-Marti, A. Banyasz, M. Garavelli and R. Improta, J. Chem. Theory Comput., 2016, 12, 4430–4439.
38. M. A. Trachsel, T. Wiedmer, S. Blaser, H. M. Frey, Q. S. Li, S. Ruiz-Barragan, L. Blancafort and S. Leutwyler, J. Chem. Phys., 2016, 145, 134307.
39. Q. S. Li and L. Blancafort, Photochem. Photobiol. Sci., 2013, 12, 1401–1408.
40. M. Yaghoubi Jouybari, Y. Liu, R. Improta and F. Santoro, J. Chem. Theory Comput., 2020, 16, 5792–5808.
41. H. Görner, J. Photochem. Photobiol., B, 1990, 5, 359–377.
42. I. G. Gut, P. D. Wood and R. W. Redmond, J. Am. Chem. Soc., 1996, 118, 2366–2373.
43. A. Nakayama, Y. Harabuchi, S. Yamazaki and T. Taketsugu, Phys. Chem. Chem. Phys., 2013, 15, 12322–12339.
44. S. C. Wei, J. W. Ho, H. C. Yen, H. Q. Shi, L. H. Cheng, C. N. Weng, W. K. Chou, C. C. Chiu and P. Y. Cheng, J. Phys. Chem. A, 2018, 122, 9412–9425.
45. J. W. Ho, H. C. Yen, W. K. Chou, C. N. Weng, L. H. Cheng, H. Q. Shi, S. H. Lai and P. Y. Cheng, J. Phys. Chem. A, 2011, 115, 8406–8418.
46. T. Gustavsson, N. Sarkar, E. Lazzarotto, D. Markovitsi, V. Barone and R. Improta, J. Phys. Chem. B, 2006, 110, 12843–12847.
47. P. M. Hare, C. E. Crespo-Hernández and B. Kohler, J. Phys. Chem. B, 2006, 110, 18641–18650.
48. J. P. Villabona-Monsalve, R. Noria, S. Matsika and J. Peon, J. Am. Chem. Soc., 2012, 134, 7820–7829.
49. T. Kobayashi, H. Kuramochi, Y. Harada, T. Suzuki and T. Ichimura, J. Phys. Chem. A, 2009, 113, 12088–12093.
50. H. Kuramochi, T. Kobayashi, T. Suzuki and T. Ichimura, J. Phys. Chem. B, 2010, 114, 8782–8789.
51. Y. Zhang, J. Chen and B. Kohler, J. Phys. Chem. A, 2013, 117, 6771–6780.
52. L. B. Clark and I. Tinoco, Jr., J. Am. Chem. Soc., 1965, 87, 11–15.
53. M. Etinski and C. M. Marian, Phys. Chem. Chem. Phys., 2010, 12, 4915–4923.
54. T. Gustavsson, Á. Bányász, E. Lazzarotto, D. Markovitsi, G. Scalmani, M. J. Frisch, V. Barone and R. Improta, J. Am. Chem. Soc., 2006, 128, 607–619.
55. R. Improta and V. Barone, J. Am. Chem. Soc., 2004, 126, 14320–14321.
56. K. A. Kistler and S. Matsika, J. Phys. Chem. A, 2009, 113, 12396–12403.
57. T. Gustavsson, N. Sarkar, E. Lazzarotto, D. Markovitsi and R. Improta, Chem. Phys. Lett., 2006, 429, 551–557.
58. C. Zazza, A. Amadei, N. Sanna, A. Grandi, G. Chillemi, A. Di Nola, M. D’Abramo and M. Aschi, Phys. Chem. Chem. Phys., 2006, 8, 1385–1393.
59. V. Ludwig, K. Coutinho and S. Canuto, Phys. Chem. Chem. Phys., 2007, 9, 4907–4912.
60. F. Santoro, V. Barone, T. Gustavsson and R. Improta, J. Am. Chem. Soc., 2006, 128, 16312–16322.
61. C. Ma, Q. Xiong, J. Lin, A. K.-W. Wong, M. Wang and W.-M. Kwok, Photochem. Photobiol., 2023 DOI:10.1111/php.13849.

---

Footnote

† Electronic supplementary information (ESI) available: Absorption spectra before and after time-resolved experiments; methods of kinetic analysis of the TRF and TA decay profiles and the log-normal simulation of the time-resolved and steady-state spectra; kinetic parameters for decay profiles from fs-TRF and fs-TA; DFT and TDDFT calculated optimized structures, atomic coordinates, total energies of the optimized structures, and transition energies and Kohn–Sham orbitals for the absorption and fluorescence spectra in different solvents. See DOI: https://doi.org/10.1039/d3cp05509d

---