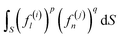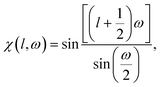Theory of density waves and organization of proteins in icosahedral virus capsids
Olga V.
Konevtsova
 ,
Dmitrii V.
Chalin
and
Sergei B.
Rochal
,
Dmitrii V.
Chalin
and
Sergei B.
Rochal
 *
*
Faculty of Physics, Southern Federal University, 5 Zorge str., 344090 Rostov-on-Don, Russia. E-mail: rochal_s@yahoo.fr
First published on 6th December 2023
Abstract
Understanding the physical principles underlying the structural organization of the proteinaceous viral shells is of major importance to advance antiviral strategies. Here, we develop a phenomenological thermodynamic theory, which considers structures of small and middle-size icosahedral viral shells as a result of condensation of a minimum number of protein density waves on a spherical surface. Each of these irreducible critical waves has icosahedral symmetry and can be expressed as a specific series of the spherical harmonics Ylm with the same wave number l. As we demonstrate, in small viral shells self-assembled from individual proteins, the maxima of one critical density wave determine the positions of proteins, while the spatial derivatives of the second one control the protein orientations on the shell surface. In contrast to the small shells, the middle-size ones are always formed from pentamers and hexamers (referred to as capsomers). Considering all such structures deposited in the Protein Data Bank, we unexpectedly found that the positions of capsomeres in these shells correspond to the maxima of interference patterns produced by no more than two critical waves with close wave numbers. This fact allows us to explain the observed limit size of the icosahedral shells assembled from pentamers and hexamers. We also construct nonequilibrium thermodynamic potentials describing the protein crystallization and discuss the reasons behind the specific handedness of the viral shells.
Introduction
Almost 70 years ago, Frenkel-Konrath and Williams showed that fully infectious rod-like viral particles of the Tobacco Mosaic Virus (TMV) can be spontaneously formed in the water solution of two molecular components: purified genomic RNA and viral coat protein.1 A dozen years later, in a similar experiment, “spherical” Cowpea chlorotic mottle virus (CCMV) was recreated in vitro for the first time.2 Unlike in TMV, 180 copies of CCMV coat protein self-assemble into a shell with icosahedral symmetry (capsid) enclosing viral genome. Later it was found that in some cases, before the capsid self-assembly, identical proteins are combined into symmetrical capsomeres while still in the solution.3–12 Thus, some small capsids (containing N = 240 or less proteins) self-assemble directly from individual proteins, while other small and larger capsids are formed from pre-assembled capsomeres. In both cases, no local energy consumption like ATP hydrolysis is needed and by changing the acidity or salinity of the solution, one can reverse initial stages of the capsid formation.1,13–16 Therefore, as Caspar and Klug (CK) concluded long ago,17 the self-assembly of proteinaceous viral shells is akin to ordinary crystallization, the theory of which was proposed back in 1937 by L.D. Landau.18,19In Landau theory of crystallization and structural phase transitions, these ordering phenomena are considered as condensation of static waves of microscopic density ρ: as a result of a usual structural phase transition from a high-temperature phase, an additional component δρ in the density ρ appears, and the symmetry of the system decreases. L.D. Landau proposed to consider nonequilibrium free energy that is a potential or a functional of the density variation δρ. Within this approach, many interesting structural phase transitions have been studied. For example, Landau theory has allowed to explain the existence and stability of such remarkable objects as quasicrystals,20–23 phase diagrams and properties of various ferroelectric materials,24–26 as well as ordering features in different liquid crystal phases.27
Within the framework of Landau theory, the self-assembly of icosahedral protein shells of small spherical viruses was also considered.28,29 In this modified approach, the crystallization is controlled by the acidity or salinity of the protein solution instead of the temperature, density waves are usual spherical harmonics Ylm28,29 and the positions of individual proteins are located at maxima of the interference patterns formed by harmonics that yield a critical contribution to δρ function.
The authors28,29 assumed that the self-assembly of icosahedral protein shells, like most known structural transitions, is driven by only one irreducible representation (IR). The IRs spanned by spherical harmonics Ylm are indexed by a wave number l that plays a role analogous to the wave vector in the planar case. Examining icosahedral interference patterns produced by spherical harmonics with the same l, the authors28,29 deduced structures of small shells assembled from individual proteins and demonstrated that these assemblies correspond to strictly defined odd values of l. Moreover, if l < 45, then for each permitted l there is only one icosahedral shell. In this context, it is interesting to note that the approach28,29 allowed to rationalize the structures of several shells violating the paradigmatic Caspar and Klug model17 that describes the structures of most icosahedral capsids.
In the subsequent work,30 the geometric meaning of the interference patterns28,29 with the first odd l was revealed. It was found that these patterns correspond to chiral icosahedral spherical lattices (SLs) (also called geodesic icosahedral polyhedra) with excluded nodes located at the icosahedron symmetry axes. The first five of these SLs describe protein positions in small (N ≤ 240) shells formed from individual proteins.30
In ref. 31 and 32 the modified Landau theory analogous to Brazovskii approach33 was proposed. To explain the selectivity in the formation of left- and right-handed structures, the authors proposed a nonequilibrium thermodynamic functional, which lifts the corresponding energy degeneration. It disappeared due to specific interactions between the density waves with close even and odd values of the wave number l. In addition, in contrast to the earlier version of the crystallization theory,28,29 where the maxima of δρ were associated with individual proteins, in ref. 31 and 32, the maxima of this function were considered as positions of capsomer centers.
Let us note, however, that a theory that rationalizes the capsids assembled from individual proteins must predict their coordinates. In addition, the handedness of any real capsid is determined precisely by the chiral shape of its asymmetric proteins, just as the modulus of the chirality vector and, accordingly, the radius of the shell are determined by the intrinsic curvature of structural units (SUs).34 Thus, for such a theory to be considered as a complete one, it must also account for the fact that proteins are asymmetric and extended SUs. Moreover, we argue that if it were possible to synthesize proteins with a handedness, which is opposite to that selected by nature, then all the thermodynamic characteristics of the mirror-symmetric shell would be the same.
In the following, we start our consideration from small icosahedral capsids assembled from individual proteins. Within the framework of the theory of crystallization on a spherical surface, for the first time we consider proteins as non-point SUs and take into account their elongated chiral shape. The protein positions, as in earlier works,28,29 are obtained as maxima of the statistical density distribution function δρ, which is an irreducible critical density wave with icosahedral symmetry and an appropriate wave number. The protein orientation is described by another irreducible critical icosahedral function ξ, whose spatial derivatives determine the basis vectors of the local coordinate system, with respect to which the local orientation of individual proteins remains constant. Within the framework of the proposed thermodynamic theory, we discuss the features of the positional and orientational order in small capsids formed from individual proteins. Then, again applying the approach of critical density waves, we develop a theory that describes the structures of icosahedral capsids assembled from capsomeres. Analyzing all structural types of these middle-size viral shells from the Protein Data Bank archive (PDB),35 we show that the organization of capsomeres in them is determined by no more than two critical icosahedral density waves with close wave numbers.
Results and discussion
Positional and orientational ordering of proteins in the shells of small viruses
Following ref. 28–30, we represent the density distribution of protein molecules on the sphere as| ρ = ρ0 + δρ, | (1) |
Spherical viral shells have mostly icosahedral symmetry, so, we limit our study to this case only. Below, when constructing a phenomenological theory, we a priori assume that δρ has either I or Ih symmetry. Note that unlike ref. 28 and 29, we additionally consider functions δρ with Ih symmetry, since the location of chiral SUs at the maxima of such a function can result in a structure with I symmetry. For the small shells analyzed in this section, we suppose that only one critical IR is substantial, and the contribution of the remaining non-critical degrees of freedom to the value of δρ and crystallization is negligible. For each such IR indexed by the wave number l, the critical variation δρl, which represents an irreducible critical density wave (ICDW), can be written as
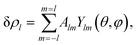 | (2) |
| l = 15i + 10j + 6k, | (3) |
Note that the integrity basis of the group I consists of invariants of the 2nd, 6th, 10th and 15th degrees, while the basis of the group Ih does not include the 15th degree invariant. At the same time, the 2nd degree invariant (which is the radius vector squared) is simply a constant on the sphere. Thus, eqn (3) follows from the properties of the integrity basis considered above.28,29 We emphasize that eqn (3) is equivalent to the well-known Birman criterion, according to which a phase transition from a high-symmetry phase to a low-symmetry phase is possible if and only if the IR of the order parameter (OP), which is restricted to the symmetry group of the low-symmetry phase, contains a totally symmetric representation.36
The number of different solutions (j, k) of eqn (3) for a given wave number l is equal to the parametricity of δρl in the low-symmetry phase. For odd l < 45 and even l < 30, all functions δρl are single-parametric, and the irreducible normalized icosahedral functions fl can be found by simply averaging the spherical harmonics over the group I (see Methods).28,29 In other words, δρl = αlfl, where αl = const and when integrated over the surface of the sphere 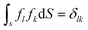 . The first single-parametric irreducible density waves are shown in Fig. 1. For large l, when more than one solution of eqn (3) exists, the function δρl is expressed as
. The first single-parametric irreducible density waves are shown in Fig. 1. For large l, when more than one solution of eqn (3) exists, the function δρl is expressed as 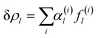 , and the amplitudes α(i)l can be determined by minimizing the appropriate free energy. The functions f(i)l do not depend on the form of the free energy and can be found by averaging Ylm with different values of m.
, and the amplitudes α(i)l can be determined by minimizing the appropriate free energy. The functions f(i)l do not depend on the form of the free energy and can be found by averaging Ylm with different values of m.
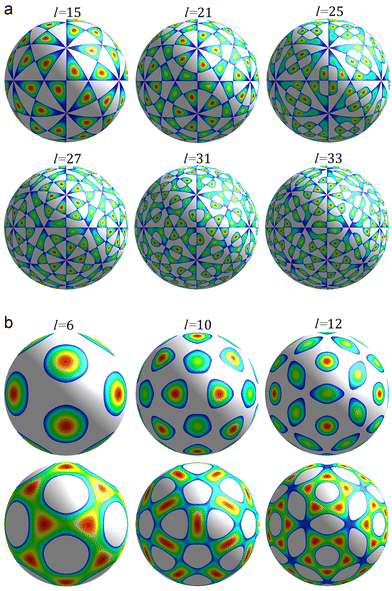 | ||
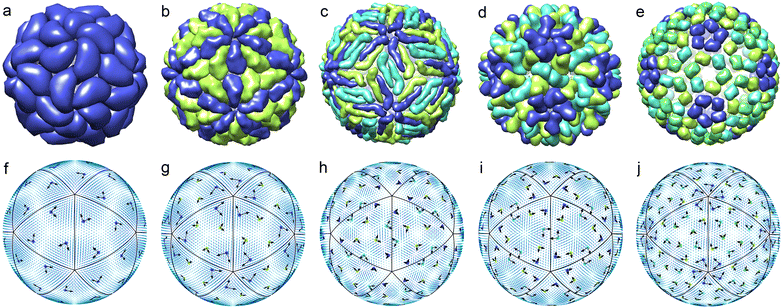
| Fig. 1 First irreducible single-parametric density functions. Only the areas where the functions are positive are shown. The colour change from blue to red corresponds to a growth of the function. Panel (a) shows density waves δρl(θ,φ) with odd l permitted by eqn (4) and wave numbers l = 15, 21, 25, 27, 31, 33. These functions have chiral symmetry I. Panel (b) shows density waves δρl(θ,φ) with Ih symmetry and even numbers l = 6, 10, 12. | ||
To analyze the structures of middle-size viral shells considered in the next section, along with single-parametric solutions, we use two-parametric solutions as well. In this case, the functions f(1)l and f(2)l can be calculated by averaging over the group I the harmonics Yll and Yll−2 (if l is even) or harmonics Yll−1 and Yll−3 (if l is odd) (see Methods). After that, the obtained functions should be normalized, and, if necessary, they can always be orthogonalized (e.g., using Gram–Schmidt process).37 Note that the functions f(1)l and f(2)l used in the next section are normalized, but the orthogonalization procedure for these functions was not performed. We also note that if for a given l, the basis function is unique, then we do not mark fl or αl with a superscript.
The maxima/minima of the functions δρl(θ,φ) with odd l always have trivial symmetry and their positions can be filled with asymmetric SUs, on the contrary, this is not so for δρl with even l.38 In the latter case it is possible to reduce the Ih symmetry of δρl to I symmetry by filling the positions of maxima with suitable chiral n-fold capsomeres. In particular, the 12 maxima of the function f6 (see Fig. 1b, top row) can be filled with pentamers, and one can place 12 pentamers and 20 hexamers32 at the appropriate maxima of the function f10 (see Fig. 1b, top row). For more detail, see the next section.
To account for the orientation of individual proteins, we introduce another icosahedral function ξ(θ,φ) that sets the basis vectors {e1, e2} of the local coordinate system, with respect to which all individual proteins have the same orientation. Suppose that e1 and e2 are parallel to the vectors ∇‖ξ and er × ∇‖ξ, where ∇‖ = eθ∂θ + eφ∂φ/sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ and {er, eθ, eφ} is the local basis of the spherical coordinate system.
θ and {er, eθ, eφ} is the local basis of the spherical coordinate system.
The function ξ(θ,φ) as well as δρ(θ,φ) can be expanded in series of spherical harmonics spanning irreducible representations of O(3). The basis irreducible icosahedral functions fl for both ξl and δρl simply coincide: ξl = βlfl. Note also that the functions ∇‖fl and er × ∇‖fl can be linearly expressed in terms of well-known vector spherical harmonics Ylm = erYlm, Ψlm = ∇Ylm and Φlm = er × ∇Ylm39 with the same value of l. The functions fl and ∇‖fl have the same parity, which is (−1)l, while the parity of the function er × ∇‖fl is (−1)l+1.
Following the standard ideology of Landau theory, we suppose that for a small viral shell, the orientational ordering as well as positional one is driven by only one IR. Then, as we demonstrate below, within this approximation it is possible to rationalize the orientational order of proteins forming the simplest shells of small viruses with N ≤ 240. The top row of Fig. 2 shows five viral shells, in which the mass centers of proteins are located very close to the maxima of the function δρl(θ,φ) with l = 15, 21, 25, 27, 31. The bottom row of Fig. 2 shows icosahedral fields ∇‖fm with m = 6, 6, 15, 10, 12, respectively. At the points coinciding with the maxima of δρl(θ,φ), the local basis vectors e1 and e2 (proportional to the values of ∇‖fm and er × ∇‖fm, respectively) are drawn. One can see that individual proteins of the viral shells presented in the top row of the figure have approximately the same orientation with respect to the local coordinate systems drawn in the bottom row.
The structural analysis presented above was based solely on the symmetry principles. Now, let us discuss a possible construction of thermodynamics within the framework of Landau theory. First of all, we emphasize that proteins are chiral structural units and can be either left-handed or right-handed. In addition, protein synthesis is not a self-assembly process since it is carried out by cellular machinery after infection with a virus. Therefore, the capsid proteins synthesized by the cell have a strictly defined chiral shape which is dictated by the left handedness of amino acids used in all living organisms.
We would like to point out that the origin of chirality in biological nanostructures is still a matter of discussion.40,41 An interesting experiment, providing a possible explanation for biological homochirality, was carried out quite recently.40 The authors40 synthesized enantiomorphically pure (either right-handed or left-handed) crystals on a ferromagnetic substrate from a racemic solution of ribo-aminooxazoline (RAO), which is an important precursor of RNA and directly determines the chirality of the assembled RNA. In the experiments,40 depending on the spin polarization of the substrate, the chirality of the obtained crystals was also different. Similarly, if it were possible to synthesize capsid proteins with the handedness opposing that observed in vivo, then the assembled shells would also have the opposite handedness but the same thermodynamic properties including energy. Consideration of enantiomorphic shells that model viral capsids yields analogous results.42 Thus, although the symmetry group of the homochiral solution of viral proteins is SO(3), the symmetry group of the nonequilibrium Landau free energy must be O(3), which accounts for the virtual possibility of the existence of mirror-symmetric proteins in the solution and naturally results in the same energy (and area at the phase diagram) of enantiomorphic protein shells, one of which is real and the other is virtual.
Suppose that in a small icosahedral shell (see Fig. 2), the positions of proteins are determined by a density wave with the wave number l, and their orientation by a density wave with the wave number m. Then the corresponding nonequilibrium Landau potential can be written in the standard form, typical of the case of one critical and one secondary (improper) order parameters:
| F = a2(T, pH)I2 + a4I4 + a4I4 + ⋯ + b2J2 + cM, | (4) |
Note that for the considered odd values of l, the term I3 (like all other invariants of odd degrees) vanishes identically and the first part of the potential (4), containing terms with coefficients ai, coincides with the nonequilibrium potential from ref. 28 and 29, even though the latter potential28,29 was built as an invariant function with respect to SO(3) group.
Let us stress that self-assembly of even a small viral shell is always a first-order transition,32,43 thus, the potential (4) must contain terms at least up to 6th degree or even higher to ensure the stability of the icosahedral phase. Let us also point out the case when a Landau potential (or a functional) depends not only on δρ but also on the specific spatial derivatives of δρ. Since the term er × ∇‖fl and the function fl have different parities, the degeneracy of the left- and right-handed solutions31,32 can be lifted, and one of the shells becomes more energetically favorable. However, in the light of recent experimental40 and theoretical results,42 we suppose this as unnecessary complication of the theory, although earlier, following the works,31,32 we ourselves discussed38 possible terms in the Landau potential leading to an energy asymmetry in left- and right-handed octahedral shells.
After restricting the symmetry of the eqn (4) to icosahedral one, the simplest effective nonequilibrium potential (describing self-assembly of the shells shown in Fig. 2) can be written as:
| F = a2(T, pH)αl2 + a3αl4 + a4αl6 + ⋯ + b2βm2 + cq1(αl)qβm, | (5) |
A detailed study of such potentials can be found in ref. 44. Here we only point out that for odd l, minimization of eqn (5) with respect to αl and βm leads to a pair of solutions in the form of (αl, βm) and (−αl, −βm) (if m is odd) or a pair of solutions (αl, βm) and (−αl, βm) (if m is even). It occurs since amplitudes with an odd wave number change their sign under spatial inversion, and the amplitudes with an even wave number do not. These two solutions correspond to a virtual and real enantiomorphic shells, which interconverted into each other by spatial inversion. Namely, in the case of odd l (examples of the corresponding shells are shown in Fig. 2), the transformation αl → −αl leads to inversion of positional order. Considering the secondary OP, we note that the unit vectors e1 and e2 are constructed using icosahedral fields with different parity and regardless of the parity of m, the local coordinate system always changes its handedness under spatial inversion; therefore, the proposed OP correctly describes the orientation of chiral proteins in both enantiomorphic shells.
Above, we discussed only the most general thermodynamic properties of the proposed model simply to ensure that there are no contradictions within its framework and, in particular, the energies of enantiomorphic shells are equal. In the future, the model can be developed in the direction of Brazovsky approach,31,32 while maintaining its core ideas that the chirality of a viral shell is determined by the specific shape (and handedness) of proteins. In turn, the handedness of proteins stems from the fact they are produced by cellular machinery using exclusively left-handed amino acids.
In the next section, we will consider the relationship between the concept of ICDWs and the structure of viral shells assembled from capsomeres, which are initially formed in a solution. As we show, using one or at most two icosahedral ICDWs with close wave numbers, one can rationalize arrangement of pentamers and hexamers in all known middle-size virus capsids assembled from these units.
Viral shells assembled from capsomeres and the theory of critical density waves
Individual proteins in an icosahedral shell can occupy general crystallographic positions (60-fold orbits) only, so the total number of proteins N must be equal to 60T, where T is the total number of protein orbits.17 Small capsids with T ≤ 4 can be assembled not only from monomers (individual proteins) but also from capsomeres of the single type, such as dimers, trimers, or pentamers. These symmetrical SUs are initially self-assembled from identical proteins or symmetrically arranged protein domains.For example, T = 2 structures can be self-assembled not only from 120 monomers like Cystoviridae,45 but also from 60 dimers (Partitiviridae) or 12 pentamers composed of dimers (decamers) (Reoviridae and Totiviridae).4,5 The positional order in the shell comprised of 60 identical dimers can be well described by the irreducible icosahedral wave f15 (see Fig. 1a, top row), since all the maxima of f15 belong to the same orbit, which consists of 60 positions. Similarly, SU positions in the shell composed of 12 identical decamers can be well described by the density wave f6 (see Fig. 1b, top row).
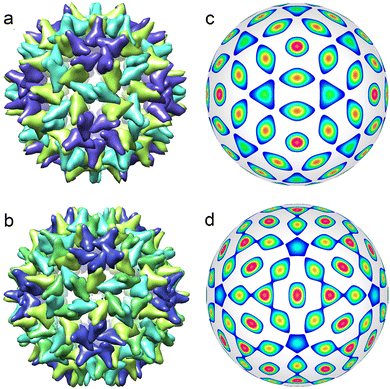
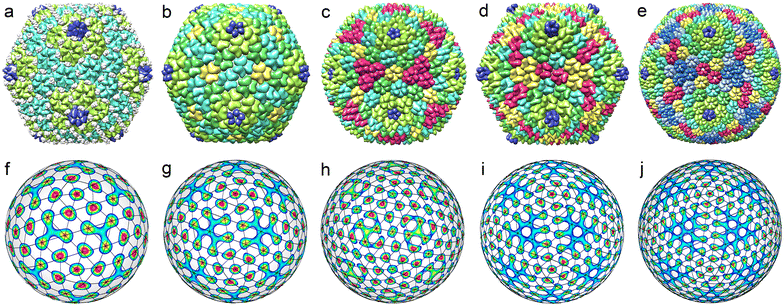
During the formation of some T = 1 structures, individual proteins can self-assemble into pentamers at the first stage of the virus assembly. The AaLS structure of the protein complex12 (described by the ICDW f6) is an example. There are many interesting pseudo-T = 3 structures (Picornaviridae, Dicistroviridae, Flaviridae, Marnaviridae, Secoviridae)46 that are self-assembled from 60 trimers (and described by the ICDW f15). An even more intriguing example of self-assembly is observed in structures composed of dimers, which in turn are organized into trimers.9,10 Such capsomers are also called pseudohexamers. This structural organization is typical of Hepatitis B. Both T = 3 and T = 4 shells of this virus (see Fig. 3a and b) are formed in the cytoplasm during infection, with the majority (approximately 95%) being of T = 4 form.47,48 The structure of both capsids can be rationalized in terms of a honeycomb lattice, at the vertices of which individual proteins are located. When such a lattice is mapped onto a spherical surface, in addition to hexagonal honeycombs, 12 pentagons will appear around 5-fold icosahedron axes. Furthermore, the hexagon centres (as well as the centres of pentagons) will coincide with the maxima of f18 and f20 harmonics describing T = 3 and T = 4 viral shells, respectively (see Fig. 3c and d).
The T = 3 and T = 4 structures that are self-assembled from monomers, can be described by f27 and f31 harmonics,28,29 but the same capsids may well be viewed as shells composed of pentamers and hexamers. If the difference between the capsomeres is neglected, then their location in T = 3 and T = 4 shells can be described by f10 and f12 harmonics.32 Nevertheless, although it is possible to distinguish motifs corresponding to pentamers and hexamers in such structures (see Fig. 2d and e), we are not aware of experimental data confirming the formation of pentamers and/or hexamers at intermediate stages of self-assembly of such small viral capsids.
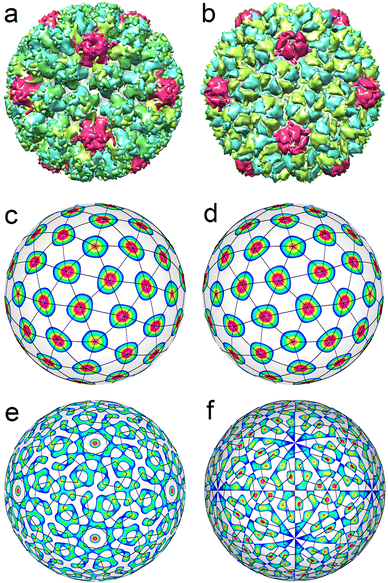
Now, let us consider the larger viral shells with T > 4. First of all, we note that single-shelled capsids with T = 5 are not observed at all. Viral shells with T = 6 belonging to Polyomaviridae and Papillomaviridae families46 always have a similar structure and are assembled from 72 identical pentamers, whose centers form a SL typical of capsids with T = 7 (see Fig. 4a). Due to this fact, a shell composed from 72 identical pentamers is also called a pseudo-T = 7 structure. An ordinary T = 7 structure (see Fig. 4b) is self-assembled from 72 capsomeres, 12 of which are pentamers, and another 60 are hexamers (Siphoviridae, Podoviridae). Fig. 4c and d show that capsomeres in T = 7 and pseudo-T = 7 shells are located at the nodes of two enantiomorphic SLs (2,1) and (1,2). To obtain these SLs, it is necessary to consider a combination of two ICDWs with wave numbers l = 15 and l = 16.32 By changing the sign of the harmonic f15, one can obtain either left-handed or right-handed SL (see Fig. 4c and d).
It is interesting to note that in this and many cases considered below, the coefficients in a linear combination of ICDWs with different but close wave numbers turn out to be close by the absolute value. The latter fact is not surprising, since the icosahedral SLs under consideration are locally similar to an ordinary planar triangular lattice. In the latter case, as is well known,49 if the density function ρ(r) of this lattice is expanded in terms of plane waves as 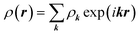 , where k is a reciprocal lattice vector, then the amplitudes ρk of all waves in this expansion turn out to be equal.
, where k is a reciprocal lattice vector, then the amplitudes ρk of all waves in this expansion turn out to be equal.
Spherical structures with T = 6 and T = 7 are transient within the ICDW concept (see Fig. 4e and f). In appropriate interference patterns it is still possible to distinguish motifs related to individual proteins. Note in this context that the P22 capsid is self-assembled from 420 individual proteins, while an ordinary viral shell with T = 7 is formed from capsomers (like HK97 capsid shown in Fig. 4b).50
Fig. 4e shows an interference pattern generated by two harmonics f40 and f41. As can be seen in this figure, the positions of individual proteins in each pentamer match well the maxima of the interference pattern. However, the latter, along with the maxima describing the protein locations, additionally has 12 pronounced maxima at the icosahedron vertices and 60 weak maxima near the 2-fold axes of icosahedron.
Fig. 4f shows the icosahedral function f41. The maxima of this ICDW are arranged similarly to the proteins in the bacteriophage HK97 shell. Their number also coincides with the number of individual proteins (N = 420) in the capsid. However, these maxima form very distorted hexamers. For structures with T ≥ 7, ICDW combinations describing the positions of individual proteins become essentially multicomponent, and, as the result, their utilization loses its significance. However, the simplest combinations of ICDWs still describe the positions of individual capsomers (pentamers, hexamers or pseudohexamers) in the considered capsids, which, in fact, reflects the actual processes of self-assembly of T ≥ 7 structures.
All known middle-size icosahedral capsids, as well as capsids with T = 7, can be described by the Caspar and Klug model.17 Such viral shells are composed of pentamers and hexamers, the centers of which are located at the nodes of appropriate SLs. An SL with indices (h,k) has 10T + 2 nodes, where T = h2 + k2 + hk, and h and k are integers. Twelve of these nodes (which lie on the 5-fold rotational axes) correspond to pentamers, and the entire capsid contains 60T proteins. However, not all middle-size capsids predicted by the CK model have been found.45 In fact, only CK structures corresponding to SLs with (h,k) = (2,1), (3,0), (3,1), (3,3), (4,0), (4,1), (4,2), (5,0), (5,1) and (6,1) are known. The SL (6,1) is characterized by T = 43, whereas the next in size experimentally observed shell has T = 169 and like other large and giant virus capsids46,51 are self-assembled not from pentamers and hexamers, but from large, preassembled clusters, the so-called symmetrons.52,53 Therefore, this and larger shells are out of the scope of this paper.
Below, within the approach of icosahedral ICDWs, we consider all known middle-size structures with 7 < T ≤ 43 and show that considering the maxima of two or even one critical density wave, one can obtain the location of capsomeres in all such shells. For the sake of clarity, the capsids described by achiral and chiral SLs are considered separately.
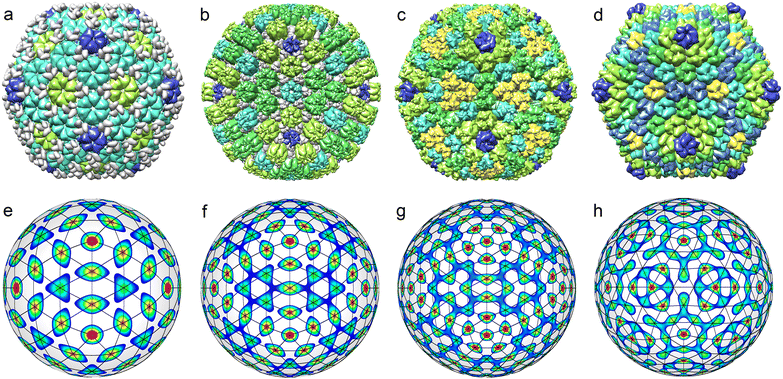
The top row of Fig. 5 shows all known35 middle-size CK capsids, which correspond to achiral SLs. Let us note that achiral SLs are produced by icosahedral density waves with even wave numbers only. Furthermore, the first SLs with indices (h,0) correspond to ICDWs with the wave numbers l = 6h. The SLs with indices (h,h), where h = 1,2, correspond to the density waves f10 and f20. The next analogous SLs with h > 2 resemble the interference patterns produced by a pair of waves with l = 10h and l = 10h + 2. However, only in the case h = 3 (presented in Fig. 5h), the maxima of the interference pattern match relatively well the nodes of the SL (3,3).
Fig. 6 shows all the structural types of middle-size capsids with chiral SLs (with T > 7) that can be found in PDB. Let us point out an interesting trend that we have identified while selecting the structures for Fig. 6. With an increase in the wave number l and a corresponding increase in T, the number of isostructural viral shells diminishes drastically. For example, there are about two dozen different T = 13 capsids, while T = 43 shell is unique.46,51
The limiting factor T = 43 for the existing middle-size icosahedral viral shells can be easily understood within the developed theory. The SLs of both chiral and achiral shells with T > 43 can no longer be generated by one or at most two icosahedral density waves. As T increases, the value of l increases as well. As the result, the intrinsic parametricity (the number of solutions of eqn (3)) of the corresponding icosahedral waves must also increase. Thus, the viral shells observed in nature have the simplest SLs that can be obtained within the density wave approach.
Additionally, besides predicting the positions of capsomer centres, the developed theory can explain the orientationally consistent arrangement of pentamers and hexamers in the SL nodes. Note that SLs obtained have local symmetry elements. In the middle of each SL edge there is a local 2-fold axis, in the center of each SL triangle there is a 3-fold one, while the node itself (depending on its location) lies either on a global 5-fold axis or on a local 6-fold one. If the lattice is formed from asymmetric proteins, then an additional improper OP is required: it breaks these symmetries and, accordingly, describes the orientation of the asymmetric units. In contrast, when the SL is filled with symmetric capsomeres, there is no need to break the local symmetries, and the improper OP is simply redundant. Therefore, the orientations of neighbouring capsomeres in the capsid turn out to be interconnected by the local 2-fold and 3-fold axes of SLs obtained within our theory. In exactly the same way, orientational coordination of neighbouring capsomeres occurs in the CK geometric model.17 Surprisingly, our analysis of the Bovine papillomavirus capsid (with pseudo-T = 7 structure) shows that the orientations of three symmetry inequivalent neighbouring pentamers (one of which is located at the icosahedron vertex) are also coordinated with good precision by the corresponding local 3-fold axis.
Within the framework of the proposed density wave approach, it is also interesting to discuss a perfect match (commensurability) between protein shells in double-layered capsids from the families Cystoviridae and Reoviridae. From the structural point of view, this commensurability manifests itself in the fact that each protein of the T = 2 inner shell is located approximately under the center of the corresponding hexamer of the T = 13 outer shell.30,54 The upper layer of the considered capsids is arranged similarly to the shell shown Fig. 6a and is described by the same combination of f21 and f22 harmonics (see Fig. 6f). The inner layer contains 120 proteins and corresponds to the ICDW f21. Thus, the harmonic f21 turns out to be common for both layers, which demonstrates the commensurability between the layers in terms of density waves.
To conclude this section, let us briefly discuss the construction of effective Landau potentials for the single-layered shells considered in this section. The capsids described by SLs (h,0), where h = 3, 4, 5 and l = 6h, represent the simplest case, which we will consider first. Here, the nonequilibrium effective potential is constructed as a power series expansion in only one amplitude αl. Since this potential contains a cubic invariant, different signs of αl correspond to different solutions, only one of which describes the real viral shell. Note that under spatial inversion, αl does not change its sign and the arrangement of capsomer centers remains the same, however, the capsomeres themselves are transformed into their mirror-symmetric counterparts.
Now, let us proceed to the shells that we have rationalized using two ICDWs. Corresponding effective potential depends on two critical OPs which are the amplitudes of the first and second density wave α(i)l and α(j)n, denoted as A and B, respectively. In all the above considered cases when two ICDWs condense on a spherical surface, their wave numbers l and n turn out to be adjacent in the series of values allowed by icosahedral symmetry. This fact can be easily understood within the ideas originally expressed by Lifshitz. Following ref. 55, we can assume that in a solution of proteins, the effective thermodynamic force, that prevents δρ fluctuations, has a quasi-continuous dependence on the wave number l. Under this rather obvious assumption, it becomes clear that in the Landau potential the quadratic terms corresponding to ICDWs with close values of l should have similar dependences on external thermodynamic parameters and such ICDWs tend to condense concurrently.
In the discussed potential, a term ApBq is symmetrically allowed if and only if the integral
Then, in the case when both wave numbers of the first and second ICDWs are even, the potential can be constructed as follows:
| F = a2A2 + a3A3 + a4A4 + ⋯ + b2B2 + b3B3 + b4B4 + ⋯ + c12AB2 + c21A2B + c22A2B2 + ⋯, | (6) |
In the case when one of the wave numbers is odd (e.g., suppose it's l), the terms containing odd powers of A vanish in the potential (6). Minimization of this potential with respect to A and B will result in a pair of solutions (A, B) and (−A, B). These solutions have the same energy and describe virtual and real enantiomorphic shells interconverted into each other by spatial inversion (which, of course, also changes the capsomer handedness).
Thus, in all the cases considered, which include shells composed of capsomers as well as shells assembled from individual proteins, the effective nonequilibrium potential is invariant with respect to spatial inversion. This fact corresponds to the equality of energies of the real and virtual shells, the latter of which could be constructed using proteins of opposite handedness.
Conclusions
This Article continues the series of studies28–32 devoted to the theory of protein crystallization on a spherical surface. As in our previous works,28–30 to describe the positions of proteins and/or capsomeres in viral shells, we introduce the statistical function δρ(θ,φ), which characterizes the critical variation of density distribution and appears only in the ordered phase. This critical variation can be expanded in a series of irreducible critical density waves (ICDWs), which produce an interference pattern. The maxima of the resulting pattern determine the positions of proteins and/or capsomeres. In the case of small capsids, crystallization is driven by a single irreducible representation, so only one ICDW determines the protein positions in such shells. Since the proteins are extended structural units (SUs), in order to give a more complete description of the capsid structure, one needs to know not only the coordinates of proteins, but also their local orientation. To take into account orientational ordering of SUs, we introduce an additional improper order parameter (OP) associated with the function ξ(θ,φ), whose spatial derivatives set the basis of a local coordinate system with respect to which the orientations of proteins remain the same. As we show, in the case of small virus capsids with T ≤ 4, the orientational ordering is also described by a single irreducible representation. Therefore, the explicit form of the function ξ(θ,φ) coincides with that of an appropriate ICDW. Concluding the symmetry analysis of small capsids, we propose a nonequilibrium thermodynamic potential that depends on two order parameters (OPs): one critical and one secondary (improper) OP, which describe the positional and orientational ordering, respectively.In the article, along with small capsids assembled from individual proteins, we also consider structures of middle-size icosahedral virus shells that are self-assembled from pentamers and hexamers. All known structural types of such shells are characterized by T ≤ 43. The next in size experimentally observed icosahedral capsid has T = 16946,51 and belongs to the group of large and giant viruses, whose shells are formed not from individual capsomeres, but from large preassembled clusters, the so-called symmetrons.52,53 In addition, giant shells are characterized by different principles of the structure assembly and protein packing,56 and, therefore, are not considered in the present study.
In this context, it is also interesting to note that small viruses are always round and giant viruses have a pronounced icosahedral faceting, while the maturation process of middle-size icosahedral viruses is very often accompanied by a change in the shape from practically spherical to faceted icosahedral, although other scenarios are still possible. The appearance of icosahedral faceting in the middle-size shells can be well described within the framework of Landau theory.56,57 The OP of such a transformation is an amplitude of a radial displacement field determined by the function f6. The change in the sign of the OP turns the icosahedral faceting into a dodecahedral one. As have been shown in ref. 58, the OP associated with a radial displacement field proportional to the function f10 can also contribute to the capsid faceting. However, to maintain clarity and conciseness of our paper, here, we do not consider possible shape changes of the middle-size shells but focus on describing the structural organization of capsomers in these capsids.
As we demonstrate, the positional order of capsomere centers in these shells is described by those SLs, which emerge as superpositions of no more than two ICDWs. Furthermore, the orientational improper OP is unnecessary since the local symmetry axes of the SLs are preserved and the 2-fold and 3-fold local axes located between the nearest SL nodes dictate the mutual orientation of capsomers as it occurs in the CK model17 (see also ref. 59).
Thus, in order to describe the structures of all known middle-size icosahedral shells with T ≤ 43, it is sufficient to consider the crystallization with only one or two ICDWs with close symmetry-allowed wave numbers. However, not all icosahedral shells with T ≤ 43 described by Caspar and Klug model are experimentally observed. Among these not observed structures, we have found only one shell (characterized by spherical lattice (3,2) and T = 19) that can be rationalized in terms of two ICDWs [with amplitudes (α25, α26) ≈ (1, −1)]. Therefore, the condensation of no more than two ICDWs seems to be an important general principle governing the structures of middle-size icosahedral shells.
We argue that any nonequilibrium Landau potential describing self-assembly of individual proteins or capsomeres should be invariant with respect to O(3) group rather than SO(3) group. Viral proteins, like the proteins of all other living organisms, are assembled by cellular machinery exclusively from left-handed amino acids. The latter fact explains the absolute selectivity in the formation of naturally occurring left-handed or right-handed biological structures, including viral shells. However, this selectivity bears no relation to the nonequilibrium Landau potential, which describes self-assembly from pre-made SUs. Assembly of a small viral shell from proteins that are already present in a solution is a purely physical process, which does not require the presence of a spherical substrate in the form of a genome.60 Correspondingly, if proteins of opposite handedness were to appear in the solution, we would observe an analogous self-assembly process of a mirror-symmetric shell. Therefore, the binding energy, phase diagram, and other thermodynamic characteristics of the left- and right-handed shells must be exactly the same. The theory developed here explicitly takes this into account and all the nonequilibrium potentials proposed in the current study have two enantiomorphic solutions with equal energy, which correspond to the observed and virtual (mirror-symmetric) viral shells. In this context, the mechanism first proposed in ref. 31 and 32, which explains the prevalence of capsids with a specific chirality by the fact that one of the structures is more energetically favorable, seems unlikely to us.
In conclusion, we have developed a phenomenological thermodynamic model that describes the structures of small and middle-size viral shells. The model develops Landau's theory of crystallization and uses his idea that phase transitions and, in particular, crystallization are driven by a minimum number of critical degrees of freedom. Landau theory is a reliable symmetry-based approach, which allows one to obtain general information about the structural organization of the considered system, without making any assumptions about real interactions between its structural units. This is both an advantage of the theory and its shortcoming. If it is necessary to model details of the internal structure of the capsid, for example the actual chemical bonds between individual proteins or capsomeres, our symmetry approach would be interesting to combine with a patchy particle model, which has had success in modeling many soft matter systems.61–64 Our results may be of interest for a wide range of scientists developing the theory of phase transitions and for specialists involved in rationalizing the structure of protein viral shells for various biotechnological applications and the development of new antiviral strategies.
Methods
Parametricity of a solution
The number η of different icosahedral irreducible density waves with a given l (in other words, parametricity) can be directly found by using the Birman criterion,36i.e. by calculating the number of times the considered representation of O(3) group, restricted to I or Ih group, subduces the identity representation: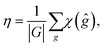 | (7) |
If for a given l, the parametricity η is not zero, this implies that there are η functions with the wave number l that are invariant with respect to I or Ih group. Note that for the considered representations of O(3) with parity (−1)l, the characters χ(ĝ) of both rotational and mirror elements coincide and are found as:
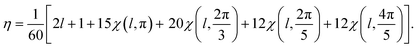 | (8) |
Averaging of spherical harmonics over the group I
After the symmetry-allowed values of the wave number l are established, the spherical harmonics Ylm can be averaged using the following expression: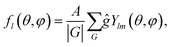 | (9) |
If the parametricity η equals 1 and the wave number l is fixed, then the averaging procedure (9) performed for different m ∈ [−l,l] gives either 0 or, up to an amplitude A, the same function fl(θ,φ). The result of the averaging procedure (9) can be always made real and normalized by choosing an appropriate value of A.
Let us consider first the even values of l. if η = 1, then it is convenient to average a spherical harmonic of the highest order Yll. If η = 2, then in order to obtain f(1)l and f(2)l, we used the following harmonics: Yll and Yll−2. In the case of odd l and η = 1, it is convenient to use the spherical harmonic Yll−1. If η = 2, then to obtain f(1)l and f(2)l, we used the harmonics Yll−1 and Yll−3.
Note that spherical function Ylm can be calculated by repeatedly applying the lowering operator ![[l with combining circumflex]](https://www.rsc.org/images/entities/i_char_006c_0302.gif) − = −z(∂x − i∂y) + (x − iy)∂z to the harmonic Yll = (x + iy)l, where i is the imaginary unit.65
− = −z(∂x − i∂y) + (x − iy)∂z to the harmonic Yll = (x + iy)l, where i is the imaginary unit.65
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support from the Russian Science Foundation, grant no. 22-12-00105.Notes and references
- H. Fraenkel-Conrat and R. C. Williams, Proc. Natl. Acad. Sci. U. S. A., 1955, 41, 690–698 CrossRef CAS PubMed
.
- J. B. Bancroft, G. J. Hills and R. Markham, Virology, 1967, 31, 354–379 CrossRef CAS PubMed
.
-
B. V. V. Prasad and M. F. Schmid, Advances in Experimental Medicine and Biology, in Viral Molecular Machines, ed. M. G. Rossmann and V. B. Rao, Springer, 2012, vol. 726, pp. 7–47 Search PubMed
.
- D. Luque, J. M. González, D. Garriga, S. A. Ghabrial, W. M. Havens, B. Trus, N. Verdaguer, J. L. Carrascosa and J. R. Castón, J. Virol., 2010, 84, 7256–7266 CrossRef CAS PubMed
.
-
M. M. Poranen and D. H. Bamford, Advances in Experimental Medicine and Biology, in Viral Molecular Machines, ed. M. G. Rossmann and V. B. Rao, Springer, 2012, vol. 726, pp. 379–402 Search PubMed
.
- H. S. Savithri and M. R. N. Murthy, Curr. Sci., 2010, 98, 346–351 CAS
.
- D. Sirohi and R. J. Kuhn, J. Infect. Dis., 2017, 216, S935–S944 CrossRef CAS PubMed
.
- Z. Gao, H. Pu, J. Liu, X. Wang, C. Zhong, N. Yue, Z. Zhang, X. B. Wang, C. Han, J. Yu, D. Li and Y. Zhang, Mol. Plant-Microbe Interact., 2021, 34, 49–61 CrossRef CAS PubMed
.
- K. Holmes, D. A. Shepherd, A. E. Ashcroft, M. Whelan, D. J. Rowlands and N. J. Stonehouse, J. Biol. Chem., 2015, 290, 16238–16245 CrossRef CAS PubMed
.
- G. K. Shoemaker, E. Van Duijn, S. E. Crawford, C. Uetrecht, M. Baclayon, W. H. Roos, G. J. L. Wuite, M. K. Estes, B. V. V. Prasad and A. J. R. Heck, Mol. Cell. Proteomics, 2010, 9, 1742–1751 CrossRef CAS PubMed
.
- R. C. Liddington, Y. Yan, J. Moulai, R. Sahli, T. L. Benjamin and S. C. Harrison, Nature, 1991, 354, 278–284 CrossRef CAS PubMed
.
- E. Sasaki, D. Böhringer, M. Van De Waterbeemd, M. Leibundgut, R. Zschoche, A. J. R. Heck, N. Ban and D. Hilvert, Nat. Commun., 2017, 8, 14663 CrossRef PubMed
.
- J. B. Bancroft, Adv. Virus Res., 1970, 16, 99–134 CrossRef CAS PubMed
.
- L. O. Liepold, J. Revis, M. Allen, L. Oltrogge, M. Young and T. Douglas, Phys. Biol., 2005, 2, S166 CrossRef CAS PubMed
.
- R. Lata, J. F. Conway, N. Cheng, R. L. Duda, R. W. Hendrix, W. R. Wikoff, J. E. Johnson, H. Tsuruta and A. C. Steven, Cell, 2000, 100, 253–263 CrossRef CAS PubMed
.
- I. M. Yu, W. Zhang, H. A. Holdaway, L. Li, V. A. Kostyuchenko, P. R. Chipman, R. J. Kuhn, M. G. Rossmann and J. Chen, Science, 2008, 319, 1834–1837 CrossRef CAS PubMed
.
- D. L. D. Caspar and A. Klug, Cold Spring Harbor Symp. Quant. Biol., 1962, 27, 1–24 CrossRef CAS PubMed
.
- L. D. Landau, Zh. Eksp. Teor. Fiz., 1937, 11, 19 Search PubMed
.
- L. D. Landau, Zh. Eksp. Teor. Fiz., 1937, 11, 627 Search PubMed
.
- P. Bak, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 5764–5772 CrossRef CAS PubMed
.
- L. Gronlund and N. D. Mermin, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 38, 3699–3710 CrossRef PubMed
.
- M. V. Jarić, Phys. Rev. Lett., 1985, 55, 607–610 CrossRef PubMed
.
- P. A. Kalugin, A. I. Kitaev and L. S. Levitov, ZhETF Pisma Redaktsiiu, 1985, 41, 119–121 CAS
.
- J. Mangeri, Y. Espinal, A. Jokisaari, S. Pamir Alpay, S. Nakhmanson and O. Heinonen, Nanoscale, 2017, 9, 1616–1624 RSC
.
- M. A. Pavlenko, F. Di Rino, L. Boron, S. Kondovych, A. Sené, Y. A. Tikhonov, A. G. Razumnaya, V. M. Vinokur, M. Sepliarsky and I. A. Lukyanchuk, Crystals, 2022, 12, 453 CrossRef CAS
.
- S. Kondovych, M. Pavlenko, Y. Tikhonov, A. Razumnaya and I. Lukyanchuk, SciPost Phys., 2023, 14, 56 CrossRef CAS
.
- S. Singh, Phys. Rep., 2000, 324, 107–269 CrossRef CAS
.
- V. L. Lorman and S. B. Rochal, Phys. Rev. Lett., 2007, 98, 4–7 CrossRef PubMed
.
- V. L. Lorman and S. B. Rochal, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224109 CrossRef
.
- S. B. Rochal, O. V. Konevtsova, A. E. Myasnikova and V. L. Lorman, Nanoscale, 2016, 8, 16976–16988 RSC
.
- S. Dharmavaram, F. Xie, W. Klug, J. Rudnick and R. Bruinsma, Europhys. Lett., 2016, 116, 26002 CrossRef
.
- S. Dharmavaram, F. Xie, W. Klug, J. Rudnick and R. Bruinsma, Phys. Rev. E, 2017, 95, 62402 CrossRef PubMed
.
- S. Brazovskii, Zh. Eksp. Teor. Fiz., 1975, 68, 175–185 Search PubMed
.
- J. Wagner and R. Zandi, Biophys. J., 2015, 109, 956–965 CrossRef CAS PubMed
.
- H. M. Berman, T. N. Bhat, P. E. Bourne, Z. Feng, G. Gilliland, H. Weissig and J. Westbrook, Nat. Struct. Biol., 2000, 7, 957–959 CrossRef CAS PubMed
.
- J. L. Birman, Phys. Rev. Lett., 1966, 17, 1216–1219 CrossRef CAS
.
- S. J. Leon, Å. Björck and W. Gander, Numer. Linear Algebra Appl., 2013, 20, 492–532 CrossRef
.
- D. V. Chalin and S. B. Rochal, Phys. Rev. B, 2023, 107, 24102 CrossRef CAS
.
- R. G. Barrera, G. A. Estevez and J. Giraldo, Eur. J. Phys., 1985, 6, 287–294 CrossRef
.
- S. F. Ozturk, Z. Liu, J. D. Sutherland and D. D. Sasselov, Sci. Adv., 2023, 9, eadg8274 CrossRef CAS PubMed
.
- N. Globus and R. D. Blandford, Astrophys. J., 2020, 895, L11 CrossRef CAS
.
- S. B. Rochal, O. V. Konevtsova, I. Y. Golushko and R. Podgornik, Soft Matter, 2023, 19, 8649–8658 RSC
.
- J. M. Johnson, J. Tang, Y. Nyame, D. Willits, M. J. Young and A. Zlotnick, Nano Lett., 2005, 5, 765–770 CrossRef CAS PubMed
.
-
Y. A. Izyumov and V. N. Syromyatnikov, Phase transitions and crystal symmetry, Springer Science & Business Media, 1990, vol. 38 Search PubMed
.
- D. Nemecek, E. Boura, W. Wu, N. Cheng, P. Plevka, J. Qiao, L. Mindich, J. B. Heymann, J. H. Hurley and A. C. Steven, Structure, 2013, 21, 1374–1383 CrossRef CAS PubMed
.
- C. Hulo, E. De Castro, P. Masson, L. Bougueleret, A. Bairoch, I. Xenarios and P. Le Mercier, Nucleic Acids Res., 2011, 39, D576–D582 CrossRef CAS PubMed
.
- L. M. Stannard and M. Hodgkiss, J. Gen. Virol., 1979, 45, 509–514 CrossRef CAS PubMed
.
- K. A. Dryden, S. F. Wieland, C. Whitten-Bauer, J. L. Gerin, F. V. Chisari and M. Yeager, Mol. Cell, 2006, 22, 843–850 CrossRef CAS PubMed
.
-
N. W. Ashcroft and N. D. Mermin, Solid State Physics, Holt-Saunders, 1976 Search PubMed
.
- D. Veesler and J. E. Johnson, Annu. Rev. Biophys., 2012, 41, 473–496 CrossRef CAS PubMed
.
- C. M. Shepherd, I. A. Borelli, G. Lander, P. Natarajan, V. Siddavanahalli, C. Bajaj, J. E. Johnson, C. L. Brooks and V. S. Reddy, Nucleic Acids Res., 2006, 34, D386–D389 CrossRef CAS PubMed
.
- N. G. Wrigley, J. Gen. Virol., 1969, 5, 123–134 CrossRef CAS PubMed
.
- V. F. Manyakov, J. Gen. Virol., 1977, 36, 73–79 CrossRef
.
- O. V. Konevtsova, D. S. Roshal, A. Lošdorfer Božič, R. Podgornik and S. Rochal, Soft Matter, 2019, 15, 7663–7671 RSC
.
- E. M. Lifshitz, Zh. Eksp. Teor. Fiz., 1941, 11, 269 Search PubMed
.
- S. B. Rochal, O. V. Konevtsova and V. L. Lorman, Nanoscale, 2017, 9, 12449–12460 RSC
.
- O. V. Konevtsova, V. L. Lorman and S. B. Rochal, Phys. Rev. E, 2016, 93, 52412 CrossRef CAS PubMed
.
- O. V. Konevtsova, D. S. Roshal, R. Podgornik and S. B. Rochal, Soft Matter, 2020, 16, 9383–9392 RSC
.
- V. V. Pimonov, O. V. Konevtsova and S. B. Rochal, Acta Crystallogr., Sect. A: Found. Adv., 2019, 75, 135–141 CrossRef CAS PubMed
.
-
S. J. Flint, L. W. Enquist, R. M. Krug, V. R. Racaniello and A. M. Skalka, Principles of virology: molecular biology, pathogenesis, and control, ASM Press, Washington, D.C., 2000 Search PubMed
.
- Z. Zhang and S. C. Glotzer, Nano Lett., 2004, 4, 1407–1413 CrossRef CAS PubMed
.
- J. P. Doye, A. A. Louis, I. C. Lin, L. R. Allen, E. G. Noya, A. W. Wilber, H. C. Kok and R. Lyus, Phys. Chem. Chem. Phys., 2007, 9, 2197–2205 RSC
.
- H. Liu, S. K. Kumar and F. Sciortino, J. Chem. Phys., 2007, 127, 084902 CrossRef PubMed
.
- D. Fusco and P. Charbonneau, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 012721 CrossRef PubMed
.
-
J. P. Elliott and P. G. Dawber, Symmetry in Physics Vol 1: Principles and Simple Applications, University of Sussex, Brighton, 1987 Search PubMed
.
| This journal is © the Owner Societies 2024 |