Radiolytic evaluation of a new technetium redox control reagent for advanced used nuclear fuel separations

Abstract

Technetium is a problematic radioisotope for used nuclear fuel (UNF) and subsequent waste management owing to its high environmental mobility and coextraction in reprocessing technologies as the pertechnetate anion (TcO₄⁻). Consequently, several strategies are under development to control the transport of this radioisotope. A proposed approach is to use diaminoguanidine (DAG) for TcO₄⁻ and transuranic ion redox control. Although the initial DAG molecule is ultimately consumed in the redox process, its susceptibility to radiolysis is currently unknown under envisioned UNF reprocessing conditions, which is a critical knowledge gap for evaluating its overall suitability for this role. To this end, we report the impacts of steady-state gamma irradiation on the rate of DAG radiolysis in water, aqueous 2.0 M nitric acid (HNO₃), and in a biphasic solvent system composed of aqueous 2.0 M HNO₃ in contact with 1.5 M N,N-di-(2-ethylhexyl)isobutyramide (DEHiBA) dissolved in n-dodecane. Additionally, we report chemical kinetics for the reaction of DAG with key transients arising from electron pulse radiolysis, specifically the hydrated electron (e_aq⁻), hydrogen atom (H˙), and hydroxyl (˙OH) and nitrate (NO₃˙) radicals. The DAG molecule exhibited significant reactivity with the ˙OH and NO₃˙ radicals, indicating that oxidation would be the predominant degradation pathway in radiation environments. This is consistent with its role as a reducing agent. Steady-state gamma irradiations demonstrated that DAG is readily degraded within a few hundred kilogray, the rate of which was found to increase upon going from water to HNO₃ containing solutions and solvents systems. This was attributed to a thermal reaction between DAG and the predominant HNO₃ radiolysis product, nitrous acid (HNO₂), k(DAG + HNO₂) = 5480 ± 85 M⁻¹ s⁻¹. Although no evidence was found for the radiolysis of DAG altering the radiation chemistry of the contacted DEHiBA/n-dodecane phase in the investigated biphasic system, the utility of DAG as a redox control reagent will likely be limited by significant competition with its degradation by HNO₂.

---

Introduction

About 6% of all uranium-235 fission events yield technetium-99 (⁹⁹Tc),^1,2 which for a typical Light Water Reactor (LWR) results in the production of ∼40 kg of ⁹⁹Tc per year.³ This high fission yield, combined with its long half-life (τ_1/2 = 211 000 years), makes ⁹⁹Tc a very important component of used nuclear fuel (UNF) and subsequent waste management.⁴ For example, at the Hanford site in Washington, USA, some 1500 kg of ⁹⁹Tc is present in ∼53 million gallons of waste.⁵ Historically, some of the 177 waste tanks at the Hanford site have leaked and contaminated the local environment.⁶ These events are problematic for many reasons, but especially because of technetium's high mobility in all water environments,⁷ due to its most stable chemical form being the soluble pertechnetate anion (TcO₄⁻).⁸

Technetium is similarly challenging in UNF reprocessing environments. The TcO₄⁻ ion is often coextracted as a counter ion, alongside nitrate ions (NO₃⁻), when forming tributylphosphate (TBP) complexes of hexavalent uranium (UO₂²⁺) and tetravalent plutonium (Pu⁴⁺) under typical Plutonium Uranium Reduction Extraction (PUREX) process conditions:

UO₂²⁺ + 2TBP + TcO₄⁻ + NO₃⁻ ⇌ [UO₂(TcO₄)(NO₃)(TBP)₂], (1)

Pu⁴⁺ + 2TBP + TcO₄⁻ + 3NO₃⁻ ⇌ [Pu(TcO₄)(NO₃)₃(TBP)₂]. (2)

Multiple efforts to date have provided a quantitative foundational, understanding of technetium chemistry under UNF reprocessing conditions.^9–25 However, the challenges of technetium management have been amplified by more recent efforts to simplify the traditional PUREX process, motivated by economics, plutonium proliferation concerns, and neptunium management.^26–28 Some iterations of the PUREX process use hydrazine-stabilized ferrous and uranous nitrates for the reduction and separation of plutonium and neptunium (transuranics) from uranium-loaded organic phases.²⁹ In addition, the hydrazine component acts as a nitrite ion (NO₂⁻) scavenger and facilitates the reduction of the TcO₄⁻ ion to the non-extractable oxide (TcO₂).^26,30,31 Both are useful processes in the management of UNF. However, hydrazine also reacts with nitrous acid (HNO₂), which in the presence of TBP results in the formation of explosive hydrazoic acid.^29,32 Consequently, advanced PUREX formulations aim to use alternative redox control methods for transuranic and technetium management. Diaminoguanidine (DAG, Fig. 1(A)) has recently been identified as a potential candidate for this role in Advanced PUREX processes. Under moderately acidic conditions, DAG has been shown to facilitate the desired redox control of the aforementioned transuranic ions, in addition to the reduction of the TcO₄⁻ ion.^33–35 This is not the case for other proposed substitutes, such as acetohydroxamic acid (AHA).^36–42

Fig. 1 Molecular structure of diaminoguanidine (DAG, A) and N,N-di-(2-ethylhexyl)isobutyramide (DEHiBA, B).

However, the radiation stability of DAG is currently unknown, and yet is a critical factor in determining the feasibility of any chemical employed in a UNF reprocessing flowsheet. The dissolved fuel's inherent ionizing radiation fields promote the destruction of useful process chemicals into a variety of degradation products that are often detrimental to process performance. In the case of DAG, which is expected to be ultimately consumed by its redox control reactions with TcO₄⁻ and transuranic ions, there are two major radiolytic concerns. The first involves the potential competition for DAG between the aforementioned metal ions and accumulated radiolysis products. Both the direct and indirect radiolysis of nitric acid (HNO₃) affords the formation and accumulation of HNO₂:⁴³

NO₃⁻/HNO₃ [long arrow, wavy then straight] e⁻, NO₃˙, NO₂⁻/HNO₂, O, H_aq⁺, (3)

NO₃⁻ + e_aq⁻/H˙ → HNO₂, (4)

The family of aminoguanidines has been shown to react with HNO₂ under mild and strongly acidic conditions.^44–48 Given the fact that HNO₃ radiolysis leads to the accumulation of 10s of micromolar of HNO₂ within only a few kGy,⁴⁹ DAG may be preferentially consumed by HNO₂, thereby inhibiting its redox control of TcO₄⁻ and transuranic ions.

The second radiolytic concern relates to whether the use of excess amounts of DAG affords the formation of hazardous degradation products, from the scavenging of radical and molecular HNO₃ radiolysis products (eqn (3)). For example, explosive products and byproducts have been reported from syntheses involving the reaction of aminoguanidines with HNO₂.^44–50 In addition, degradation products with the capacity to migrate across the interface and negatively impact the longevity of Advanced PUREX process ligands, such as N,N-di-(2-ethylhexyl)isobutyramide (DEHiBA, Fig. 1(B)), could also be created by the HNO₂ reaction.

Based on these concerns, and in support of the continued development of DAG-based technetium management strategies, we have investigated the radiation robustness of DAG. Here, we report the impacts of steady-state gamma irradiation on the radiolysis of DAG in water, aqueous 2.0 M HNO₃, and in a solvent system composed of aqueous 2.0 M HNO₃ in contact with 1.5 M DEHiBA dissolved in n-dodecane. Additionally, we report chemical kinetics for the reaction of DAG and a 1 : 1 perrhenate ion system, [DAG·ReO₄], with key transients arising from the radiolysis of aqueous HNO₃ solution, specifically the hydrated electron (e_aq⁻), hydrogen atom (H˙), and hydroxyl (˙OH) and nitrate (NO₃˙) radicals. We have also directly measured the thermal kinetics for the reaction of DAG with HNO₂ in acidic aqueous media.

Methods

Chemicals

Acetonitrile (≥99.97%), diaminoguanidine hydrochloride (DAG, 98%), hexane (≥99%), iron(III) sulfate heptahydrate (FeSO₄·7H₂O, ReagentPlus®, ≥99%), n-dodecane (≥99% anhydrous), nitric acid (HNO₃, ≥99.999% trace metals basis), parachlorobenzoic acid (pCBA, 99%), perchloric acid (HClO₄, ≥99.999% trace metals basis), potassium thiocyanate (KSCN, ≥99.0% ACS Reagent Grade), sodium chloride (NaCl, 99.999% trace metals basis), sulfuric acid (H₂SO₄, 99.999%), and tertiary butanol (tBuOH, ≥99.5% anhydrous) were obtained from MilliporeSigma (Burlington, Massachusetts, USA). Potassium nitrite (KNO₂, Reagent grade >99%) was supplied by Ward Scientific (Ontario, Canada). N,N-Di-(2-ethylhexyl)isobutyramide (DEHiBA, 99%) was sourced from Marshallton Research Laboratories Inc. (King, NC, USA). Potassium perrhenate (KReO₄, 99% trace metals basis) was supplied by Beantown Chemical Corporation (Hudson, NH, USA). Dibasic phosphate (>99% ACS) was received from Thermo Fisher Scientific (Waltham, MA, USA). Unless otherwise specified, all chemicals were used without further purification. Compressed argon (Ar), nitrogen (N₂), and nitrous oxide (N₂O) gases were purchased from Airgas (Radnor, PA, USA) and Matheson (Irving, TX, USA) with purities ≥99.5%. Ultra-pure water (18.2 MΩ cm) was used to prepare all aqueous solutions.

Time-resolved electron pulse irradiations

Chemical kinetics were measured for the reaction of DAG and a 1 : 1 [DAG·ReO₄] system with radiation-induced transient aqueous radical species, specifically the e_aq⁻, H˙ atom, and ˙OH and NO₃˙ radicals. Reaction kinetics were measured using the Notre Dame Radiation Laboratory (NDRL) linear electron accelerator facility, details for which have been previously reported for both the electron accelerator and transient absorption detection system.^51,52 Dosimetry was determined at the beginning of each day using N₂O saturated solutions of 10 mM KSCN at λ = 475 nm (G_ε = 5.2 × 10⁻⁴ m² J⁻¹),⁵³ affording an average of 6 ± 1 (˙OH and e_aq⁻) and 25 ± 2 Gy per pulse (H˙ and NO₃˙). The DAG molecule was irradiated in aqueous solutions formulated to isolate specific radicals:⁵⁴

• Hydrated electron (e_aq⁻). Direct decay kinetics of the e_aq⁻ were observed at 720 nm using Ar or N₂-saturated aqueous solutions containing 0.5 M tBuOH and 10 mM monobasic phosphate buffer at pH 6.95.

• Hydrogen atom (H˙). Growth kinetics of the transient pCBA-H adduct absorbance was observed at 360 nm using Ar or N₂-saturated solutions containing 10 mM tBuOH, 1 mM HClO₄, and 10 mM monobasic phosphate buffer at pH 3.06.

• Hydroxyl radical (˙OH). Transient growth kinetics of the oxidized DAG/1 : 1 [DAG·ReO₄] species formed at 260 nm were observed using N₂O saturated solutions containing 10 mM monobasic phosphate buffer at pH 7.01.

• Nitrate radical (NO₃˙). Direct decay kinetics of the NO₃˙ radical were observed at 640 nm using N₂O-saturated aqueous solutions containing 5.0 M NaNO₃/1 mM HClO₄ at pH 3.01.

The 1 : 1 [DAG·ReO₄] solutions were prepared by the dissolution of equivalent moles of ReO₄⁻ into the corresponding DAG solution, and then left for 24–36 hours.

The presented kinetic data were generated by averaging 10–15 individual measurements. Quoted errors for the derived second-order reaction rate coefficients (k) are a combination of measurement precision (∼4%) and initial (∼6%) and dilution (<1%) sample concentration errors.

Steady-state cobalt-60 gamma irradiations

Gamma irradiation of single and biphasic DAG solutions was achieved using a Foss Therapy Services Model 812 and a Nordion Gammacell 220E cobalt-60 irradiator at the Idaho National Laboratory (INL) Center for Radiation Chemistry Research, and a Shepherd 109-68R cobalt-60 irradiator at the NDRL. Single phase samples comprised of 50 mM DAG dissolved in either water or 2.0 M HNO₃ solution. Biphasic samples comprised of 100 mM DAG dissolved in 2.0 M HNO₃ solution contacted in a 1 : 1 aqueous-to-organic ratio with 1.5 M DEHiBA dissolved in n-dodecane solvent that had been pre-equilibrated thrice with 2.0 M HNO₃ solution. Both sample solution formulations were irradiated in 20 mL screw-cap scintillation vials: 5 mL for single phase samples, and 10 mL for biphasic samples (5 mL of each phase). Although initially aerated, all samples were considered deaerated upon irradiation due to the radiolytic consumption of dissolved oxygen. Irradiations were performed in triplicate.

Dose rates were determined for each occupied irradiator sample position by chemical dosimetry using Fricke solution (1 mM FeSO₄·7H₂O and 1 mM NaCl in 0.4 M H₂SO₄),⁵⁵ corrected for the radioactive decay of cobalt-60 (τ_1/2 = 5.27 years) throughout the duration of the study. Furthermore, the gamma dose received by the organic phase was derived by accounting for the electron density difference of n-dodecane as compared to Fricke solution: (Z_n-dodecane/A_n-dodecane)/(Z_Fricke/A_Fricke) × (ρ_n-dodecane/ρ_Fricke) = 0.78,⁵⁵ where Z, A, and ρ are the atomic number, mass number, and density, respectively. Previous work showed that the additional volume and height afforded by the 10 mL biphasic samples had a negligible effect (<2.5% higher) on the dose rate relative to that experienced by 5 mL samples.⁵⁶

Aqueous phase analysis by liquid chromatography–mass spectrometry

Post irradiation, biphasic sample phases were separated. All aqueous phases were analyzed for the loss of DAG as a function of absorbed gamma dose and solution composition (water, 2.0 M HNO₃, and 2.0 M HNO₃ : 1.5 M DEHiBA/n-dodecane) at California State University Long Beach. The quantification of DAG was achieved by liquid chromatography–mass spectrometry (LCMS) using an Agilent (Santa Clara, CA, USA) 1260 Infinity II Liquid Chromatography system equipped with a binary solvent pump, an autosampler, and a column oven. Separation was achieved using an Agilent Poroshell 120 EC-C18 reversed-phase column (3.0 mm inner diameter × 50 mm length, 2.7 μm particle size). The sample injection volume was 1 μL and quantification was performed in triplicate. Analytes were detected with an Agilent 6470 triple quadrupole mass spectrometer, operating in the positive electrospray ionization mode with dynamic multiple reaction monitoring. Mass spectrometer parameters were as follows: 300 °C dry N₂ gas temperature, 5 L min⁻¹ dry N₂ gas flow, 45 psi nebulizer pressure, 250 °C sheath N₂ gas temperature, 11 L min⁻¹ sheath N₂ gas flow rate, 3500 V capillary voltage, and 500 V nozzle voltage.

For DAG samples initially dissolved in 2.0 M HNO₃ and 2.0 M HNO₃ : 1.5 M DEHiBA/n-dodecane, the mobile phase consisted of an isocratic mixture of 90% water and 10% acetonitrile with a flow rate of 0.30 mL min⁻¹. The column temperature was maintained at 30 °C. DAG was quantified using a 5-point calibration curve (0.2–1.0 μM) made from DAG in 2.0 M HNO₃. Samples were diluted up to 200 000 times in 2.0 M HNO₃.

For DAG samples dissolved only in water, the HNO₃ method was modified to optimize the peak shape. The mobile phase consisted of an isocratic mixture of 70% water and 30% acetonitrile. The flow rate was 0.45 mL min⁻¹ and the column temperature was 40 °C. A 5-point calibration curve made from DAG in water was used (20–100 nM). Samples were diluted by factors ranging up to 500 000. A blank and a quality control (QC, 100 mM DAG in water) standard were injected after every five samples.

The degradation rates for the radiolysis of DAG in each solution and solvent system are expressed as dose constants (d, kGy⁻¹) derived from fits between 0 and ∼30 kGy.⁵⁷

Organic phase analysis by gas chromatography

Separated organic phases were analyzed at INL for the loss of DEHiBA as a function of absorbed gamma dose. Quantification of DEHiBA was achieved by gas chromatography (GC) using an Agilent 7890A gas chromatograph equipped with an autosampler and a flame ionization detector (FID). Sample organic phases were diluted by a factor of 1 : 20 in hexane. Each dilution replicate was injected four times using the following conditions: an Agilent Technologies HP-5 column (0.32 mm inner diameter × 30 m length × 0.25 μm film thickness) with an injector temperature of 300 °C; an oven temperature of 100 °C for 1 minute, ramped to 250 °C at 30 °C min⁻¹. The split ratio was 40 : 1 with 2.7 mL min⁻¹ flow through the column. The FID temperature was 350 °C. The dilution replicate injection order was randomized to help differentiate systematic instrument drift from real trends in the samples. The quadruple injections per dilution replicates were conducted sequentially to reduce any diluent evaporation. Quantification was performed using a calibration curve with standards prepared from neat DEHiBA dissolved in hexane. Five calibration points and a blank were used to construct calibration curves for each compound on each instrument. Each standard was injected four times and analyzed in order of increasing concentration.

QC standard concentrations at 50 mM DEHiBA/hexane were analyzed at the mid-point of the analysis and at the end to ensure the validity of the calibration curve throughout the entire measurement period. Each QC standard run was a separate aliquot of the QC standard in order to reduce the effects of diluent evaporation.

The radiation-induced degradation rate of DEHiBA is reported as a radiolytic yield (G-value, μmol J⁻¹).

Stop-flow analysis for the reaction of DAG and HNO₂

The reaction kinetics of DAG with HNO₂ in acidic aqueous solutions was studied using a Hi-Tech Scientific (Bradford-on-Avon, UK) SF-61 DX2 double mixing stopped-flow spectrometer. Separate solutions of DAG (4–20 mM) and KNO₂ (5–10 mM) in 2.0 M HNO₃ were mixed at 25.0 °C in a 1 : 1 ratio. Upon mixing, the decay of HNO₂ was directly monitored as a function of time (up to 10 seconds) at 350 nm. An ε₃₅₀ of 18.7 ± 0.3 M⁻¹ cm⁻¹ was determined in this study, which is slightly lower than the literature value of ε₃₅₄ = 22.1 ± 0.22 M⁻¹ cm⁻¹ in HCl solution at pH 1.5.⁵⁸ A HNO₂ concentration of 2.5 mM was chosen to obtain useful absorption changes. However, at this concentration it was difficult to maintain pseudo-first-order concentration kinetic conditions. Hence, the kinetics analyses were performed in two different ways depending on the initial concentration of DAG in 2.0 M HNO₃. For the 5–10 mM DAG we assumed pseudo-first-order conditions and fitted single-exponential decay kinetics:where [HNO₂]_t is the concentration of HNO₂ at time t, [HNO₂]_o is the initial concentration of HNO₂, k′ is the pseudo-first-order rate coefficient (s⁻¹), and t is the time (seconds). For lower DAG concentrations (3–4 mM) we fitted the general second-order expression:⁵⁹to determine the second-order rate coefficient directly, where [DAG]_t and [DAG]_o are the concentrations of DAG at time t and zero, respectively, and k is the second-order reaction rate coefficient (M⁻¹ s⁻¹). Here, the [HNO₂]_t values were determined at each measured time point based on the measured absorption and ε₃₅₀ value, and the [DAG]_t values were calculated by mass balance assuming a 1 : 1 reaction. The average second-order rate coefficient calculated in this manner had larger errors (∼10%) compared to the pseudo-first-order fitted k′ values. However, excellent agreement was obtained for the derived k value from both methods (within fitting error).

Results and discussion

Chemical kinetics

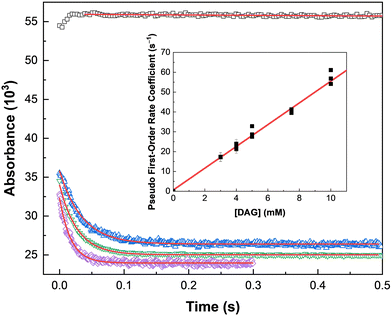
To elucidate the impact of ionizing radiation on DAG-based solvent systems, an understanding of its fundamental reaction kinetics with the expected suite of radiation-induced aqueous radicals is essential. Typical kinetic data are shown in Fig. 2 for the reaction of DAG and a 1 : 1 [DAG·ReO₄] system with the oxidizing ˙OH radical, for which rate coefficients were determined.

Fig. 2 (A) Transient absorption spectra from the reaction of the ˙OH radical with DAG from the electron pulse irradiation of 4.91 mM DAG in 2.0 M HNO₃ () and 2.50 mM of 1 : 1 [DAG·ReO₄] in 2.0 M HNO₃ (), respectively, at 22.7 ± 0.1 °C. Data obtained from limiting absorbance values for the faster exponential growth fits to measured kinetics. All data have had solution blank absorbances subtracted. (B) Transient kinetic growths measured at 260 nm for 4.91 (), 2.48 (), 2.00 (), 1.00 (), and 0.49 () mM DAG dissolved in 2.0 M HNO₃ at 22.6 °C. Solid lines are double-exponential growth kinetics, corresponding to k′ = (9.77 ± 0.14) × 10⁶, (7.96 ± 0.13) × 10⁶, (3.97 ± 0.04) × 10⁶, and (2.02 ± 0.13) × 10⁶ s⁻¹, respectively, for the faster exponential component. Inset: Second-order rate coefficient determination for the ˙OH radical reaction with DAG (■) and the 1 : 1 [DAG·ReO₄] system (). Solid lines are weighted linear fits, corresponding to k(˙OH + DAG) = (3.87 ± 0.05) × 10⁹ M⁻¹ s⁻¹ (R² = 0.98) and k(˙OH + [DAG·ReO₄]) = (4.15 ± 0.07) × 10⁹ M⁻¹ s⁻¹ (R² = 0.98).

The observed absorption growths exhibited double-exponential behavior:

where Abs is the measured absorption change, A₁ and A₂ are the two pre-exponential factors, k₁ and k₂ are corresponding pseudo-first-order rate constants (s⁻¹), and t is time (seconds). The reactivity of the ˙OH radical was taken as the faster (k₁) component of these fits. The corresponding kinetic data and fits for the reaction of DAG/1 : 1 [DAG·ReO₄] with the e_aq⁻, H˙ atom, and NO₃˙ radical are given in the ESI,† and all the derived second-order rate coefficients (k) are summarized in Table 1.

Table 1 Summary of measured second-order rate coefficients for the reaction of the e_aq⁻, H˙ atom, and ˙OH, and NO₃˙ radicals with DAG and the 1 : 1 [DAG·ReO₄] system

Radical	Second-order rate coefficient (k, M^−1 s^−1)
	DAG	1 : 1 [DAG·ReO4]
eaq^−	(1.97 ± 0.06) × 10^8	(1.62 ± 0.03) × 10^10
H˙	(7.25 ± 0.23) × 10^6	(3.19 ± 0.23) × 10^7
˙OH	(3.87 ± 0.05) × 10^9	(4.15 ± 0.07) × 10^9
NO3˙	(2.19 ± 0.03) × 10^9	(2.06 ± 0.03) × 10^9

---

Fast rate coefficients were measured for the reaction of only DAG with both the ˙OH and NO₃˙ radicals, suggesting that this molecule is susceptible to oxidation, which is consistent with its proposed role as a TcO₄⁻ ion reductant. This was further supported by the slower (by orders of magnitude) reactivities measured for the reaction of only DAG with the reducing species from water radiolysis, i.e., the e_aq⁻ and H˙ atom. In addition, the high concentrations (molar) of HNO₃ used under envisioned UNF reprocessing conditions would result in most of these reducing radicals being scavenged (eqn (4)), and thus unavailable for reaction with other solutes. Given these expected reprocessing conditions and the rate coefficient values given in Table 1, the radiolytic longevity of DAG is expected to be determined by its extent of reaction with the ˙OH and NO₃˙ radicals, with their availability dictated by competition kinetics with the other constituents of a UNF reprocessing solvent system.

As the ReO₄⁻ ion is often used as a chemical surrogate for the TcO₄⁻ ion,⁶⁰ the 1 : 1 [DAG·ReO₄] system was chosen with the goal of investigating the chemistry of the rhenium product species (believed to be ReO²⁺) arising from the reduction of ReO₄⁻ by DAG. Insights into the radiation-induced chemical behavior of the ReO²⁺/TcO²⁺ species is also necessary for the continued development of DAG-based reprocessing flowsheets. However, in the presence of the ReO₄⁻ ion we found negligible impact on the reaction of DAG with the ˙OH and NO₃˙ radicals (Table 1), suggesting that either little of the DAG had been consumed through the aforementioned ReO₄⁻ ion reduction process or that the resulting product ReO²⁺ species exhibited negligible reactivity with these two radicals. Confirmation of this chemistry was also provided by the measured rate for the reaction of the 1 : 1 [DAG·ReO₄] system with the e_aq⁻, which gave a coefficient that was almost identical to the single measurement reported for the ReO₄⁻ ion and similar to that reported for TcO₄⁻ ion:^61–64

ReO₄⁻ + e_aq⁻ → ReO₄²⁻ k = 1.5 × 10¹⁰ M⁻¹ s⁻¹, (8)

TcO₄⁻ + e_aq⁻ → TcO₄²⁻ k = (1.3–2.5) × 10¹⁰ M⁻¹ s⁻¹. (9)

These kinetic measurements indicate that little to no ReO₄⁻ was reduced by DAG to the ReO²⁺ ion species within our 24–36-hour timeframe. As such, the measurements made with the 1 : 1 [DAG·ReO₄] system only appear to represent the combined scavenging capacities of the two independent chemical species, and not the ReO²⁺ ion species. The measured kinetics for the H˙ atom for the 1 : 1 [DAG·ReO₄] system also reflects only this radical's chemical reactivity with the ReO₄⁻ ion. This is an interesting finding in itself, as the corresponding reaction for the TcO₄⁻ ion has been reported to be fast:⁶²

TcO₄⁻ + H˙ → TcO₄²⁻ + H_aq⁺ k > 1 × 10¹⁰ M⁻¹ s⁻¹. (10)

Typically, H˙ atom reaction rate coefficients are several orders of magnitude slower than the corresponding e_aq⁻ reaction,⁵⁴ which we find to be consistent for the ReO₄⁻ ion, but not for the TcO₄⁻ ion, suggesting an alternative reaction mechanism may be occurring.

Overall, these kinetic findings are consistent with observations reported by Zalupski et al.,³⁴ who found that the addition of an aliquot of TcO₄⁻ (to a final concentration of 3 mM) to a 0.1 M solution of DAG resulted in an energetic reaction that afforded a reduced technetium product species (believed to be TcO²⁺), as identified by precipitation and a color change of solution. In dilute HNO₃ (pH = 2), a black precipitate formed from the TcO₂ species, while in 2.0 M HNO₃, the initially colorless solution became a yellow hue, denoting the formation of the TcO²⁺ species. A much less energetic reaction was observed for the ReO₄⁻ ion in the presence of DAG, taking multiple days to achieve the same quantitative reduction. The reaction of DAG analogues, such as 1,1′-(ethane-1,2-diyl) diaminoguanidine, also showed similar differences in reactivity with the TcO₄⁻ and ReO₄⁻ ions.

Steady-state irradiations

The changes in DAG concentration upon its gamma irradiation in water, 2.0 M HNO₃, and 2.0 M HNO₃ contacted with 1.5 M DEHiBA/n-dodecane are shown in Fig. 3 and Fig. S4 (ESI†).

Fig. 3 Normalized concentration of DAG as a function of absorbed dose from the gamma irradiation of: 50 mM DAG in water (); 50 mM DAG in 2.0 M HNO₃ (); and 100 mM DAG in 2.0 M HNO₃:1.5 M DEHiBA/n-dodecane () under ambient irradiator temperature conditions. Solid lines are first-order exponential fits to data for dose constant calculation. Non-normalized DAG concentration data given in Fig. S4 (ESI†).

For all three investigated systems, the irradiation of DAG promoted its destruction, affording dose constants (d-values) of up to −31 × 10⁻³ kGy⁻¹, as summarized in Table 2.

Table 2 Summary of calculated dose constant values for the gamma irradiation of DAG in various solvents and solvent systems

Solvent system	d-value (10^−3 kGy^−1, R^2 = 0.99)
H2O	−9.54 ± 0.31
2.0 M HNO3	−30.70 ± 0.88
2.0 M HNO3:DEHiBA/n-dodecane	−24.60 ± 0.97

---

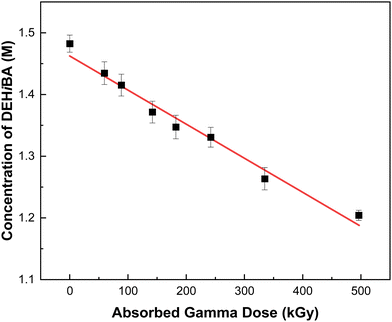
These degradation efficiencies are relatively high compared with other molecules considered for this redox-control role, such as AHA (d ∼ −(5.87 ± 0.61) × 10⁻³ kGy⁻¹).⁵⁶ Further, it is evident from Fig. 3 and the range of d-values in Table 2 that the rate of DAG radiolysis is very dependent upon solution composition, and that it was completely degraded within 100 kGy of absorbed gamma dose in systems containing 2.0 M HNO₃. These observed changes in the rate of DAG radiolysis with solution composition are indicative of a reaction between DAG and HNO₂, the dominant aqueous HNO₃ radiolysis product. Here we measured a rate coefficient of k = 5480 ± 85 M⁻¹ s⁻¹, the kinetic data for which is shown in Fig. 4. This rate coefficient is consistent with the reactivity of DAG with HNO₂ reported by Levering,⁴⁵ where the addition of one equivalent of KNO₂ to a solution of DAG in dilute HNO₃ afforded an exothermic reaction accompanied by a sudden change in solution color from clear to bright orange and eventually yellow, highlighting the speed with which HNO₂/NO₂⁻ (HNO₂ ⇌ NO₂⁻ + H_aq⁺, pK_a = 3.2) reacts with the amine backbone of DAG.

Fig. 4 Stopped-flow kinetic data for the reaction of DAG with HNO₂ in 2.0 M HNO₃ at 25.0 °C: 5.0 mM HNO₂ self-reaction (); 5.0 mM DAG + 2.50 mM HNO₂ (); 7.5 mM DAG + 2.50 mM HNO₂ (); and 10.0 mM DAG + 2.50 mM HNO₂ (). Solid lines are fitted pseudo-first-order exponential decays, corresponding to values of k′ = 0.04 ± 0.05, 22.29 ± 0.23, 39.51 ± 0.39, and 56.83 ± 0.69 s⁻¹, respectively. Inset: Second-order determination for the reaction of DAG with HNO₂ in 2.0 M HNO₃. Solid line is a weighted linear fit, corresponding to k = 5480 ± 85 M⁻¹ s⁻¹, R² = 0.99.

Although DAG was completely consumed within 160 kGy in the biphasic systems, higher gamma dose irradiations were also performed to determine whether the presence of DAG or its degradation products impacted the radiation chemistry of the organic phase. The concentration of DEHiBA as a function of absorbed gamma dose (corrected for the electron density of n-dodecane relative to Fricke solution) from the irradiated biphasic DAG solvent system is shown in Fig. 5. Within the investigated dose range, DEHiBA was found to degrade linearly with absorbed gamma dose, which is consistent with previous findings for the irradiation of DEHiBA under a variety of solvent system conditions.^56,65

Fig. 5 Concentration of DEHiBA as a function of absorbed dose from the gamma irradiation of 100 mM DAG in 2.0 M HNO₃ contacted with 1.5 M DEHiBA/n-dodecane under ambient irradiator temperature conditions. Solid line is a weighted linear fit to data, affording G(DEHiBA) = −0.55 ± 0.02 μmol J⁻¹, R² = 0.94.

A linear fit to the data shown in Fig. 5 gave a G-value of −0.55 ± 0.02 μmol J⁻¹ for the loss of DEHiBA, in excellent agreement with that reported by Drader et al. (−0.53 μmol J⁻¹) for the gamma irradiation of 1 M DEHiBA/n-dodecane contacted with an aqueous HNO₃ phase in the absence of DAG.⁶⁵ Our data clearly show that the presence of DAG and its degradation products have little effect on interfacial radiation chemistry under the investigated conditions, which is consistent with findings for the irradiation of DEHiBA in contact with an AHA containing aqueous HNO₃ phase.⁵⁶ That said, the organic phases developed a green hue, the intensity of which increased with absorbed gamma dose. This was not observed in our previous DEHiBA irradiations in the absence of DAG.⁵⁶

Conclusions

Foundational knowledge for the radiation robustness of DAG has been established in solutions and solvent systems of relevance to UNF reprocessing solvent systems. Reaction kinetic measurements for the suite of transient aqueous HNO₃ radiolysis products (e_aq⁻, H˙ atom, and ˙OH and NO₃˙ radicals) with DAG indicate that the primary path for this molecules’ radiation-induced degradation is via fast reaction with the oxidizing ˙OH (k = (3.87 ± 0.05) × 10⁹ M⁻¹ s⁻¹) and NO₃˙ (k = (2.19 ± 0.03) × 10⁹ M⁻¹ s⁻¹) radicals.

The steady-state gamma irradiation of DAG afforded its complete destruction within a few hundred kilogray, with its observed loss in water being much slower than in the investigated 2.0 M HNO₃ systems. This solution formulation dependence is attributed to an important thermal reaction between DAG and the major HNO₃ radiolysis product, HNO₂, which occurs with a relatively fast rate coefficient of k = 5480 ± 85 M⁻¹ s⁻¹ at 25.0 °C.

These steady-state and time-resolved findings suggest that the effectiveness of DAG as a TcO₄⁻ and transuranic ion redox control reagent will be limited by its competition with HNO₂ and scavenging of oxidizing radicals (˙OH and NO₃˙) from aqueous HNO₃ radiolysis. That said, beyond exhibiting little capacity to interfere with organic phase radiation chemistry, it is currently unclear as to what the impact of DAG degradation products, from both radiolysis and reduction processes, have upon overall process performance.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research has been funded by the U.S. Department of Energy (DOE) Assistant Secretary for Nuclear Energy, under the Material Recovery and Waste Form Development Campaign, DOE-Idaho Operations Office Contract DE-AC07-05ID14517. The NDRL is supported by the Division of Chemical Sciences, Geosciences and Biosciences, Basic Energy Sciences, Office of Science, US-DOE through award no. DE-FC02-04ER15533.

References

1. J. M. Siegel, J. Am. Chem. Soc., 1946, 68, 2411–2442.
2. A. L. Nichols, D. L. Aldama and M. Verdelli, Handbook of Nuclear Data for Safeguards, INDC International Nuclear Data Committee Report INDC(NDS)-0502, International Atomic Energy Agency, Vienna, 2007.
3. K. H. Lieser, Radiochim. Acta, 1993, 63, 5–8.
4. G. Choppin, J.-O. Liljenzin and J. Rydberg, Radiochemistry and Nuclear Chemistry, Butterworth-Heinemann, Woburn, Massachusetts, 2002, ch. 21, p. 593.
5. D. Banerjee, D. Kim, M. J. Schweiger, A. A. Druger and P. Thallapally, Chem. Soc. Rev., 2016, 45, 2724–2739.
6. R. E. Gephart, A Short History of Hanford Waste Generation, Storage, and Release, Report PNNL-13605, Rev. 4, Pacific Northwest National Laboratory, Washington, 2003.
7. J. P. Icenhower, W. J. Martin, N. P. Oafoku and J. M. Zachara, The geochemistry of technetium: A summary of the behavior of an artificial element in the natural environment, Report PNNL-18139, Pacific Northwest National Laboratory, 2008.
8. E. Anders, The Radiochemistry of Technetium, National Academy of Sciences, National Research Council Report NAS-NS 3021, U.S. Atomic Energy Commission, 1960.
9. F. Poineau, B. P. Burton-Pye, A. Maruk, G. Kirakosyan, I. Denden, D. B. Rego, E. V. Johnstone, A. P. Sattelberger, M. Fattahi, L. C. Francesconi, K. E. German and K. R. Czerwinski, Inorg. Chim. Acta, 2013, 398, 147–150.
10. M. H. Campbell, Anal. Chem., 1963, 35(13), 2052–2054.
11. X. Feng and C. Song, Solvent Extr. Ion Exch., 2001, 19(1), 51–60.
12. N. C. Schroeder, M. Attrep Jr. and T. Marrero, Technetium and Iodine Separations in the UREX Process, LA-UR-01-6607, 2001.
13. E. G. Orebaugh, Analysis of Technetium in SRP Uranium Product Streams, DPST-84-835, 1986.
14. E. Vialard and M. Germain, Technetium Behaviour Control in the PUREX Process, Fr. Pat., FR8602443, 1992.
15. S. Tachimori, J. Nucl. Sci. Technol., 2012, 31(5), 456–462.
16. G. D. Jarvinen, K. M. Long, G. S. Goff, W. H. Runde, E. J. Mousolf, K. R. Czerwinski, F. Poineau, D. R. McAlister and E. P. Horwitz, Solvent Extr. Ion Exch., 2013, 31(4), 416–429.
17. M. Ozawa, M. Ishida and Y. Sano, Radiochemistry, 2003, 45(3), 205–212.
18. A. N. Mashkin, K. K. Korchenkin and N. A. Svetlakova, Radiochemistry, 2002, 44(1), 34–40.
19. F. Liu, W.-F. Zheng, Y. Zhang, H. Wang and C.-X. Zhou, J. Radioanal. Nucl. Chem., 2013, 295, 1621–1625.
20. K.-W. Kim, S.-H. Kim, K.-C. Song, E.-H. Lee and S.-H. Yoo, J. Radioanal. Nucl. Chem., 2002, 253, 3–10.
21. E. Aneheim, C. Ekberg, A. Littley, E. Lofstrom-Engdahl and G. Skarnemark, J. Radioanal. Nucl. Chem., 2013, 296, 743–748.
22. P. Moeyaert, T. Dumas, D. Guillaumont, K. Kyashnina, C. Sorel, M. Miguirditchian, P. Moisy and J. F. Durfreche, Inorg. Chem., 2016, 55, 6511–6519.
23. K. Geroge, A. Masters, F. Livens, M. Sarsfield, R. Taylor and C. Sharrad, Hydrometallurgy, 2022, 211, 105892.
24. H. Chen, M. Jobson, R. J. Taylor, D. A. Woodhead, A. J. Masters and C. Sharrad, Ind. Eng. Chem. Res., 2022, 61, 786–804.
25. H. Chen, M. Jobson, R. Taylor, M. Sarsfield, A. Masters, D. Woodhead and C. Sharrad, Prog. Nucl. Energy, 2023, 164, 104856.
26. R. S. Herbst and M. Nilsson, in Advanced Separation Techniques for Nuclear Fuel Reprocessing and Radioactive Waste Treatment, ed. K. L. Nash and G. J. Lumetta, Woodhead Publishing Series in Energy, Cambridge, 2011, vol. II, ch. 6, pp. 141–175.
27. P. Baron, M. Lecomte, B. Boullis, N. Simon and D. Warin, Separation of the Long Lived Radionuclides: Current Status and Future R&D in France, Global, New Orleans, 2003.
28. R. Taylor, G. Mathers and A. Banford, Prog. Nucl. Energy, 2023, 164, 104837.
29. P. Paviet-Hartmann, C. Riddle, K. Campbell and E. Mausolf, Overview of Reductants Utilized in Nuclear Fuel Reprocessing/Recycling, INL/CON-12-28006, United States, 2013.
30. T. J. Kemp, A. M. Thyer and P. D. Wilson, J. Chem. Soc., Dalton Trans., 1993, 2601–2605.
31. J. Garraway and P. Wilson, J. Less-Common Met., 1984, 97, 191–203.
32. E. K. Dukes and R. M. Wallace, Formation of hydrazoic acid from hydrazine in nitric acid solutions, DP-72B, United States, 1962.
33. P. R. Zalupski, T. S. Grimes, C. D. Pilgrim and S. Jansone-Popova, Complete Initial Evaluation of Novel Complexants for Tc Holdback for Simplified Single Cycle Separations, Report INL/RPT-22-69248, Idaho National Laboratory, 2022.
34. P. R. Zalupski, T. S. Grimes, C. D. Pilgrim, S. Jansone-Popova and M. Jopaul, Pertechnetate Recognition by Guanidinium-Based Compounds. Part I. Reagent Screening. Report INL/RPT-23-73272, Idaho National Laboratory, Idaho, 2023.
35. P. R. Zalupski, T. S. Grimes, C. D. Pilgrim, S. Jansone-Popova and J. Mathew, Complete initial demonstration of guanidinium class of complexants for technetium with a goal of reducing the Tc distribution ratio to below 0.2 in the prototypic DEHiBA extraction system, Report INL/RPT-23-74656, Idaho National Laboratory, Idaho, 2023.
36. J. E. Birkett, M. J. Carrott, O. D. Fox, C. J. Jones, C. J. Maher, C. V. Roube, R. J. Taylor and D. A. Woodhead, J. Nucl. Sci. Technol., 2007, 44, 337–343.
37. I. May, R. J. Taylor and G. Brown, J. Alloys Compd., 1998, 271–273, 650–653.
38. R. J. Taylor and I. May, Czech. J. Phys., 1999, 49, 617–621.
39. M. J. Carrott, O. D. Fox, C. J. Maher, C. Mason, R. J. Taylor, S. I. Sinkov and G. R. Choppin, Solvent Extr. Ion Exch., 2007, 25(6), 723–745.
40. M. J. Carrott, O. D. Fox, G. LeGurun, C. J. Jones, C. Mason, R. J. Taylor, F. P. L. Andrieux and C. Boxall, Radiochim. Acta, 2008, 96(6), 333–343.
41. R. J. Taylor, S. I. Sinkov, G. R. Choppin and I. May, Solvent Extr. Ion Exch., 2008, 26(1), 41–61.
42. P. Tkac, B. Matteson, J. Bruso and A. Paulenova, J. Radioanal. Nucl. Chem., 2008, 277(1), 31–36.
43. S. P. Mezyk and D. M. Bartels, J. Phys. Chem. A, 1997, 101, 6233–6237.
44. E. Lieber and G. B. L. Smith, Chem. Rev., 1939, 25(2), 213–271.
45. D. R. Levering, The reaction of diaminoguanidine with nitrous acid, Doctoral Dissertation, Illinois Institute of Technology, 1950.
46. E. Lieber, E. Sherman, R. A. Henry and J. Cohen, J. Am. Chem. Soc., 1951, 73, 2327–2329.
47. E. Lieber and D. R. Levering, J. Am. Chem. Soc., 1951, 73, 1313–1317.
48. J. Wang, M. Cai, F. Zhao and K. Xu, Molecules, 2019, 24(19), 3616.
49. G. P. Horne, C. R. Gregson, H. E. Sims, R. M. Orr, R. J. Taylor and S. M. Pimblott, J. Phys. Chem. B, 2017, 121(4), 883–889.
50. T. M. Klapötke and J. Stierstorfer, J. Am. Chem. Soc., 2009, 131, 1122–1134.
51. K. Whitman, S. Lyons, R. Miller, D. Nett, P. Treas, A. Zante, R. W. Fessenden, M. D. Thomas and Y. Wang, Proceedings of the ’95 Particle Accelerator Conference and International Conference on High Energy Accelerators, IEEE, New Jersey, 1996.
52. G. L. Hug, Y. Wang, C. Schöneich, P. Y. Jiang and R. W. Fessenden, Radiat. Phys. Chem., 1999, 54, 559–566.
53. G. V. Buxton and C. R. Stuart, J. Chem. Soc., Faraday Trans., 1995, 91, 279–281.
54. G. V. Buxton, C. L. Greenstock, W. P. Helman and A. B. Ross, J. Phys. Chem. Ref. Data, 1988, 17, 513–886.
55. J. W. T. Spinks and R. J. Woods, An Introduction to Radiation Chemistry, Wiley Press, New York, 1990.
56. R. E. Umpleby, J. K. Conrad, J. R. Wilbanks, K. D. Schaller and G. P. Horne, Radiat. Phys. Chem., 2023, 207, 110799.
57. B. J. Mincher and R. D. Curry, Appl. Radiat. Isot., 2000, 52, 189–193.
58. G. McKay, B. Sjelin, M. Chagnon, K. P. Ishida and S. P. Mezyk, Chemosphere, 2013, 92, 1417–1422.
59. P. Atkins and J. de Paula, Physical Chemistry, W.H. Freeman and Co., New York, 7th edn, 2001.
60. R. J. Drout, K. Otake, A. J. Howarth, T. Islamoglu, L. Zhu, C. Xiao, S. Wang and O. K. Farha, Chem. Mater., 2018, 30(4), 1277–1284.
61. K. Libson, J. C. Sullivan, W. A. Mulac, S. Gordon and E. Deutsch, Inorg. Chem., 1989, 28, 375–377.
62. L. Heller-Grossman, S. Abrashkin, A. Shafferman, M. A. Davis and R. A. Taube, Int. J. Appl. Radiat. Isot., 1981, 32, 501–506.
63. E. Deutsch, W. R. Heineman, R. Hurst, J. C. Sullivan, W. A. Mulac and S. Gordon, J. Chem. Soc., Chem. Commun., 1978, 1038–1040.
64. A. K. Pikaev, S. V. Kryuchkov, A. F. Kuzina and V. I. Spitsyn, Dokl. Phys. Chem., 1977, 236, 992–995.
65. J. Drader, G. Saint-Louis, J. M. Muller, M.-C. Charbonnel, P. Guilbaud, L. Berthon, K. M. Roscioli-Johnson, C. A. Zarzana, C. Rae, G. S. Groenewold, B. J. Mincher, S. P. Mezyk, K. McCann, S. G. Boyes and J. Braley, Solvent Extr. Ion Exch., 2017, 35, 480–495.

---

Footnote

† Electronic supplementary information (ESI) available. Contains additional chemical kinetic measurement data and non-normalized DAG concentrations vs. absorbed gamma dose data. See DOI: https://doi.org/10.1039/d3cp04987f

---