Pure and Sc-doped diopside (CaMgSi₂O₆) vibrational spectra: modelling and experiments

Abstract

We investigated the structure of pure and Sc-doped synthetic diopside (a monoclinic single-chain silicate nominally CaMgSi₂O₆); in Sc-doped diopside, Sc³⁺ substitutes Mg²⁺ in the structure and, to achieve charge balance, vacancies form at the expense of Ca²⁺. We compared the structure obtained from ab initio modelling techniques at the density functional theory (DFT) level with the structure solved by employing single crystal X-ray diffraction. Furthermore, we compared IR and Raman spectroscopy experiments with vibrational density of states (VDOS) calculated from the Fourier transform of the velocity autocorrelation function obtained using ab initio (DFT) molecular dynamics simulations. In this framework, we developed a computational tool to assign the vibrational mode associated with a specific frequency. This method consists of projecting velocities along a specific set of internal coordinates such as stretching or bending, in cases involving defects or vacancies, to calculate a partial VDOS (pVDOS) that takes into account only the vibrations associated with selected internal modes, aiding the interpretation of the total VDOS and the experimental spectra in a relevant way. The computed data were validated with the experiments and we observed that doping the diopside structure with Sc produces peak broadening and the occurrence of new peaks in the Raman spectra and that site vacancies are associated with the nearby Sc site. The present work constitutes an interesting starting point to exploit the calculated VDOS/pVDOS to characterize experimental vibrational spectra of complex systems containing local vacancies, substitutions or defects as the Sc-doped diopside.

---

1 Introduction

The synthesis of inorganic nanomaterials has experienced growing attention, providing researchers with different tools that can be used for different purposes,¹ for example the synthesis of a nanocrystal prototype to study geological evolution.² The mechanism of trace element incorporation in minerals is of great importance in geosciences and materials sciences because not only the physical properties of materials (and minerals) may change by doping but also the partition coefficient describing the uptake or the release of such elements from/to the environment depends on the solubility of the element in the structure (local structure environment and coupled substitutions to achieve charge neutrality).³ In this framework, spectroscopic techniques are of paramount importance, providing complementary information to highlight local atomic features, which are not accessible via traditional diffraction techniques applied to bulk substances. In fact, the disruption of local atomic symmetry due to the presence of defects or vacancies in materials leads to the activation of vibrational modes which are visible in Raman and/or infrared vibrational spectra in most cases and can be exploited to characterize these materials. For example, Raman spectroscopy represents one of the main characterization techniques for most graphene-based materials to attribute defects, vacancies or chemical functionalisations.^4–7

Diopside, nominally CaMgSi₂O₆, is a monoclinic single-chain pyroxene silicate whose structure is relatively simple but has been proved to be very sensitive to the incorporation of a small amount of transition metals^2,8–10 depending on intensive parameters, like pressure, temperature and oxygen fugacity. This peculiar pyroxene property has been used in geosciences to estimate the pressure of crystallization in magmatic systems,^11,12 and the cooling rate of host rocks.^13,14 Moreover, diopside doped with other elements (Li, Sc, Ti, Ga, and Fe) can often be relatively easily synthesised, and has been studied to probe the incorporation mechanisms and to measure the variation on physical properties.¹⁰ Scandium (Sc) has similar chemical properties to rare earth elements and can easily substitute magnesium in octahedral coordination since their ionic radii differ by only 3%.¹⁵ A series of Sc-doped diopsides have been studied by single-crystal X-ray diffraction (SC-XRD)^2,9 obtaining an average crystal structure that shows the coupled substitution of Sc³⁺ at M1 octahedron. The substitution of a bivalent element by a trivalent one in the structure is charge balanced by a vacancy at the M2 site. Raman and IR spectroscopy may highlight the short-range configuration of Sc doping in the diopside structure provided that modelling and reference spectra are available. Pure diopside Raman spectra are reported as the starting point of high-pressure studies^16,17 and only ref. 18 reports the comparison between ab initio modeling and Raman spectra. Thus, starting from the average XRD structure of a pure and a Sc-doped diopside with a Sc content of 0.168 atoms per formula unit (a.p.f.u.) and a vacancy content of 0.08 a.p.f.u.,² we generated a set of distinct models by using ab initio modelling at the density functional level of theory (DFT).

Here, ab initio modelling is exploited to build pristine pure diopside and a series of prototype structures obtained by scandium (Sc³⁺) substitution at site M1 and creating vacancies by eliminating calcium ions at sites M2 to account for charge compensation. Pristine pure diopside and selected Sc-diopside models are used to carry out ab initio MD simulations. From these, we calculate the Fourier transform of the velocity autocorrelation function (VACF), to obtain the vibrational density of states (VDOS) of the simulated systems.¹⁹ The VDOS displays all the vibrational frequencies, which are accessible, for example, by Raman and IR spectroscopy. The standard method used for the assignment of the peaks on pristine crystalline models is based on the calculation of the vibrational frequencies and of the normal modes in the limit of harmonic approximation by evaluating the second derivatives of the potential of the system with respect to the mass-weighted atomistic displacements (Hessian matrix) and exploiting the symmetry and selection rules.²⁰ However, the presence of defective/doped systems requires large supercells and causes a loss of symmetry. These aspects make the evaluation of the Hessian matrix and the assignment of the normal modes through the use of symmetry cumbersome, completely bypassing the advantages of the standard vibrational analysis. Moreover, the evaluation of IR or Raman intensities requires the calculation of dipole moment and polarizability, which can be computationally challenging for large systems.

The assignment of the VDOS peaks to specific vibrations does not follow as straightforwardly as in the case of classical normal modes analysis.²⁰ To address this shortcoming, which prevents a useful interpretation of the VDOS, we present a protocol based on the projection of Cartesian atomic velocities in a subset of selected internal coordinates (ICs) derived from molecular mechanics²⁰ (e.g., stretchings, bendings and torsions). Indeed, it is generally of interest to identify the dominant character of the vibrations associated with the peaks in terms of these ICs. In particular, using ICs defined on a subset of atoms involved in defects, vacancies, or specific chemical groups highlights the frequencies activated by these local features of the system, which are difficult to grasp by analysing the normal modes. Moreover, with the use of VDOS, it is possible to take into account anharmonic effects, which are not valuable in the harmonic approximation approach. Our approach is inspired by studies on organic molecules recently performed by Lai et al.,²¹ Cardini et al.²² and Pagliai et al.²³ However, in the present study, we extend the computational procedure developed so far^24,25 to treat semi-rigid and rigid molecules to derive the projection procedure and finally resolve the VDOS and experimental vibrational spectra (i.e., IR and Raman spectra) of a complex defected inorganic material such as the Sc-doped diopside. We started from the average SC-XRD structure of Sc-doped diopside and compared our computations with Raman and IR spectra from pure and Sc-doped diopside to achieve full characterization of their vibrational properties.

2 Methods

2.1 Computational details

All calculations were performed with CP2K²⁶ at the density functional level of theory (DFT) by using the mixed Gaussian and plane waves (GPW) approach²⁷ and applying periodic boundary conditions (PBC). The Perdew–Burke–Ernzerhof exchange and correlation functional parameterized for solids (PBEsol) was used.²⁸ The use of PBE-derived functionals in performing the vibrational analysis was established in the work of De la Perre et al.²⁹ The basis sets were the optimized short range double-ζ plus polarization³⁰ (DZVP-MOLOPT-SR) with PBE optimized Goedecker–Teter–Hutter (GTH) pseudopotentials³¹ for all atoms. The energy cutoff for the auxiliary plane-wave basis was set to 1200 Ry.

A supercell for the diopside was modelled as 2 × 2 × 3 starting from the experimental unit cell (CaMgSi₂O₆) as reported in the work of Thompson et al.³² (see Table 1 and Fig. 1). Geometry and cell optimizations for the diopside supercell were carried out using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization algorithm as implemented in CP2K.²⁶ Convergence criteria were 10⁻⁴ Bohr for displacements and 10⁻⁴ Hartree per Bohr for the forces, respectively.

Table 1 Cell parameters calculated at the DFT level of theory and experimental data for pure and Sc-doped diopsides

	a (Å)	b (Å)	c (Å)	β (°)
a This work.
Diopside
PBEsol^a	9.802	8.961	5.28	105.62
PBE^41	9.857	8.995	5.316	106.29
PBE^40	9.910	9.051	5.33	106.51
Exp.^32	9.74	8.917	5.25	105.87
Exp.^42	9.752	8.927	5.253	105.84
Exp.^43	9.741	8.919	5.257	105.97
Sc-doped diopside
PBEsol^a	9.805	8.97	5.286	105.65
Exp.^2	9.741	8.951	5.283	105.95

---

Fig. 1 Diopside, unit cell: Mg²⁺ orange, Ca²⁺ cyan, Si yellow and O red. M1 sites are composed each of six Si=O groups that form a square bipyramidal shape (orange octahedron) accommodating the Mg²⁺ cations. The Ca²⁺ cations, interacting with oxygen of Si–O at the bridge site (Si–O_br) and the nearest Si=O, fill the larger M2 sites (cyan). The SiO₄ tetrahedral groups are in yellow.

2.2 Structure optimization and molecular dynamics simulations

Scandium substitution in the diopside structure was modelled by randomly selecting 4 Mg and 2 Ca from the optimized diopside supercell; thus, Mg atoms were exchanged with Sc atoms and Ca atoms were deleted creating 2 vacancy defects. Exploiting this protocol, 140 models were generated with different and random dispositions of Sc and vacancies; the aim in generating such structures was to generate different (non-isoenergetic) structures that can reasonably represent several lattice conformations. Geometry and the cell of the created Sc-doped diopsides were optimized by using convergence criteria of 10⁻² Hartree per Bohr for the forces and 10⁻² Bohr for the displacements. Of all the systems modelled, the one with the lowest energy was selected and further minimized by employing the same criteria used for pristine diopside (10⁻⁴ Bohr and 10⁻⁴ Hartree per Bohr).

Pristine diopside and the selected Sc-doped diopside were then subjected to ab initio (DFT) MD simulations. All MD simulations were performed in the canonical ensemble (NVT ensemble, T = 300 K) employing a canonical-sampling-through-velocity-rescaling (CSVR) thermostat³³ with a time constant of 500 fs. A single integration time step of 0.5 fs was used. MD simulations were carried out for 77 ps saving the coordinates every 2.5 fs. The total vibrational density of states (VDOS) was obtained by calculating the Fourier transform of the atom's velocity auto-correlation function (VACF)^19,34 taking into account only the last 75 ps of the trajectory. Vibrational frequencies were expressed as the wavenumber in cm⁻¹ and the resolution of all VDOS was lower than 0.5 cm⁻¹. All VDOS were smoothed averaging 4 consecutive points and no quantum scaling factor was applied. All VDOS were normalized and the intensity was expressed in arbitrary units.

2.3 Partial vibrational density of states

Partial vibrational density of states (pVDOS) were obtained by projecting the Cartesian atomic velocities in a subset of molecular coordinates (q^a,…,q^m,…,qⁿ) defined as the displacements of the internal coordinates (R) with respect to a reference (°) of the kind function defined in the book of Wilson et al., namely stretching, bending and torsion;²⁰ the n-th internal coordinate (also known as molecular coordinates) is defined as
where X_is are the Cartesian coordinates and the suffixes i and s represent atoms and components (s = 1, 2, and 3 for x-, y-, and z-axis, respectively), respectively. The Cartesian mass-weighted coordinates are defined as labelled with a unique subscript t = (i − 1)3 + s, where s stands for the components and i stands for the atoms. Considering infinitesimal displacements and adopting the summation convention over repeated literal suffixes, the internal coordinates can be related to the Cartesian mass-weighted coordinates as:
where q^a is the a-th internal coordinate, the quantity 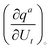can be calculated at a specific point (°) and t is the unique subscript for atoms and components as defined above. The internal coordinates are characterized using a metric tensor where contravariant and covariant components are defined as:
such that 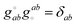, where δ_ab is the Kronecker delta (i.e., δ_ab = 1 if a = b, and δ_ab = 0 if a ≠ b). The Cartesian components along a set of selected internal coordinates, i.e., the projected Cartesian coordinates U^P_t, are therefore:
where is evaluated from
and is obtained by inverting . More details on the projection procedure can be found in ref. 24 and 25. The previous relationships for the internal and projected coordinates, q^a and U^P_t respectively, can be extended to the internal and Cartesian velocities as

After the projection, the new Cartesian velocities (U̇^P_t) are “cleaned” of all contributions other than the contribution along the selected ICs, i.e. only the Cartesian components parallel to ICs remain active. Projected Cartesian velocities (U̇^P_t) are then used to evaluate pVDOS exploiting the same procedure as that used to calculate the VDOS described above (see also the Schematic flow of the algorithm in Fig. S6, ESI†). It is worth noting that in the harmonic approximation (Wilson method), the whole system is defined with 3N-6 orthogonal normal modes, defined as linear combinations of a set of 3N-6 internal coordinates. Normal modes are orthogonal to each other and each one corresponds to one single frequency.²⁰ The selected subset of ICs does not realize a complete set of 3N-6 molecular coordinates necessary to define the entire system and are not orthogonal to each other. Therefore, pVDOS shows multiple contributions in the spectral bands, depending on the choice and definitions of the internal coordinates and their superimposition with the components of the normal modes. Despite some uncertainties arising from the non-orthogonality of the ICs, the projection over the careful choice of ICs helps to understand the main nature of the vibrational modes and characterize the spectral bands in terms of internal coordinates such as stretching, bending and torsion.

The projection procedure tool for the calculation of VACS and VDOS/pVDOS was implemented by ourselves and is freely available upon request.

2.4 Synthetic materials

Here, we measured pure CaMgSi₂O₆ diopside (DiBa8), and a Sc-doped diopside (DiBa19) of composition Ca_0.908 (Mg_0.803Sc_0.168)Si₂O₆. The technique used to synthesize the pure and Sc-doped diopsides used a mixture of BaO and B₂O₃ as a flux, and a mixture of oxides (SiO₂, CaO, and MgO) in a given proportion. Scandium oxide was introduced into the mix to dope the diopside structure.³ 5 g of powder oxides were placed in a platinum crucible covered with a lid and a Pt100/Pt90Rh10 thermocouple was placed near the crucible to control the temperature. Experimental synthesis runs quickly reached 1200-hours, and after 24-hours at this temperature, where components melt and homogenise, they were cooled down to 800 °C at a rate of 2° h⁻¹ and then quenched to room temperature. Up to 1 × 1 × 5 mm well formed idiomorphic crystals were obtained.³ Due to the presence of the boron flux, a very small amount of B entered the diopside structure at the tetrahedral site (B = 0.04 a.p.f.u. for DiBa19).² Nevertheless, the B amount was deemed as negligible and is not considered in the calculation procedure.

2.5 Raman and IR measurements

Raman spectra were collected by means of a Thermo Scientific DXR2 (Madison, WI, USA) supplied with a solid-state laser having emission line wavelength (λ_exc) at 532 nm with a dedicated edge filter for the Rayleigh elastic-tail removal. The scattered radiation was dispersed by custom grating and detected using a Peltier-cooled charge-coupled device (CCD). The custom grating covered a spectral range in the Stokes side from 23 to 1880 cm⁻¹. The average spectral resolution was 3 cm⁻¹ and the lowest resolvable frequency was 30 cm⁻¹. Each measurement was carried out at room temperature, starting from the lowest irradiation power available to each setup and then increased step-wise to higher power levels to select the best condition (3 mW). Spectra were then acquired by setting 30 s exposure for 10 accumulations. After each measurement, the samples were visually inspected in order to discriminate any artefact (i.e. surface damage or phase transformation) eventually occurring after the interaction with the laser.

Unpolarized FTIR absorption spectra were measured using small amounts of powdered sample materials mixed with KBr and pressed into pellets. A Bruker Vertex 70 spectrometer attached to a Hyperion 2000 microscope and equipped with a Globar source, a KBr beam-splitter, and an MCT detector was used to acquire spectra in the wavenumber range of 550–7000 cm⁻¹ with a spectral resolution of 2 cm⁻¹.

3 Results and discussion

3.1 Validation of the computational simulation for pristine pure diopside

The optimized unit cell of pure diopside is reported in Fig. 1. The structure of pure diopside is known at different temperatures and pressures.^{16–18,32,35–39} The SiO₄ tetrahedral groups are linked together to form the base chain structure. Mg²⁺ is accommodated in an octahedral site (M1 site) and interacts with the oxygens double bonded to Si of SiO₄ (Si=O::Mg), whereas Ca²⁺ is located in the centre of a larger and distorted dodecahedron site (M2 site) interacting with bridging oxygen (Si–O_br::Ca) and oxygens double bonded to Si (Si=O::Ca) (see also Fig. S1, ESI†).

After minimization, the average energy per atom is −555.556 eV. The 2 × 2 × 3 supercell parameters are a = 19.603 Å, b = 17.922 Å, c = 15.839 Å, α = 90°, β = 105.62°, and γ = 90° in good agreement with the reported computed^40,41 and experimental data,^37,42,43 confirming the soundness of the present computational set up and in particular of the use of the revised PBE functional for solids (PBEsol)²⁸ instead of the standard PBE parametrization⁴⁴ (see Table 1).

The distances between the metal cations and oxygen atoms at the M1 and M2 sites are reported in Table 2. The distance distribution evaluated for Mg²⁺ and O (Si=O::Mg) shows two distinct peaks of shorter than 3 Å due to the direct bonds between the Si=O groups and the metal cation (top, Fig. S2, ESI†). The presence of the two peaks suggests that the Si=O groups forming the octahedron are not equivalent and interact slightly differently with the cation. The distance distribution for the atomic species involved in the M2 site shows 4 peaks (bottom, Fig. S2, ESI†). Two of these peaks are related to the non-equivalent interaction Si=O::Ca, while the rest are related to the non-equivalent interactions between Ca²⁺ and the two neighbors Si–O_br (Si–O_br::Ca). Calculated data (Table 2) are in agreement with the experimental data reported in ref. 32.

Table 2 Structural parameters relative to the M1 and M2 sites. Computed data (DFT) are extrapolated from the peaks of the distance distributions between oxygen and selected ions (see Fig. S2, ESI); uncertainty in the measurement is ±0.01 Å, taken as the resolution used in the calculation of the distance distribution. The distance distribution between oxygen and Sc³⁺ is a large peak spanning between 1.85 Å and 2.35 Å centered at 2.05 Å (see Fig. S3, ESI); uncertainty in this measure is ±0.05 Å. SC-XRD measured bond lengths for pure diopside are from ref. 32 and for Sc-doped diopside (DiBa19) are from ref. 2

Distance		DFT		Exp.
	Diopside:	Pure	Sc-doped	Pure^32	Sc-doped^2
D(Si=O)		1.62	1.62	—	1.590
D(Si–Obr)		1.70	1.71	—	1.676
M1
D(Si=O::Mg)	M1–OA1	2.08	2.08	2.058(1)	2.076(1)
D(Si=O::Mg)	M1–OA2	2.13	2.13	2.117(1)	2.142(2)
D(Si=O::Sc)		—	2.05	—	—
M2
D(Si=O::Ca)	M2–O1	2.38	2.38	2.349(1)	2.395(1)
D(Si=O::Ca)	M2–O2	2.34	2.36	2.336(1)	2.363(1)
D(Si–Obr::Ca)	M2–O3C1	2.59	2.57	2.559(1)	2.541(1)
D(Si–Obr::Ca)	M2–O3C2	2.69	2.7	2.721(1)	2.741(1)

---

The total and partial vibrational density of states evaluated following the protocol described in the section “Methods and computational details” are reported in Fig. 2; they span from 0 cm⁻¹ to 1150 cm⁻¹, with no bands observed beyond this range.

Fig. 2 Calculated VDOS for pure diopside. (A) VDOS evaluated taking into account all atoms. The colored area highlights the regions of the vibrational spectra of diospside: green 1000–1200 cm⁻¹, yellow 600–1000 cm⁻¹ and red 100–600 cm⁻¹. (B) pVDOS for Si=O stretching involved in two M1 and two M2 selected sites. (C) pVDOS for Si–O_br stretching in the selected sites. (D) pVDOS for stretching between oxygen and the metal cation of M1 (Si=O::Mg²⁺, red line) and M2 (Si=O::Ca²⁺, blue line; Si–O_br::Ca²⁺, green line).

To better characterize the origin of the vibrational modes of the total VDOS (Fig. 2(A)), the Cartesian velocities are projected along the stretching of the Si=O double bond (see Fig. S4, ESI†) and the Si–O_br bond (see Fig. S5, ESI†) resulting in the spectra of Fig. 2(B) and (C). In these specific cases, the internal coordinates are constructed taking into account the atoms of two independent M1 (stretching of Si=O groups) and M2 (stretching of Si=O groups and stretching of Si–O_br) sites. In the first case (Fig. 2(B)), most of the bands lower than 1000 cm⁻¹ disappear or are strongly reduced in intensity. Bands at a wavenumber larger than 1000 cm⁻¹ are enhanced after projection. Some bands between 850 cm⁻¹ and 1000 cm⁻¹ are still present, probably due to the coupling with other lattice vibrations, involving Si–O_br related modes. The pVDOS evaluated for the stretching of Si=O groups involved in the M2 site shows the same features (Fig. S8, ESI†).

In the second case (Fig. 2(C)), projecting over the stretching Si–O_br of M2 sites highlights the peaks between 600 cm⁻¹ and 700 cm⁻¹ and between 775 cm⁻¹ and 950 cm⁻¹. The well-defined peaks at 800 cm⁻¹ and 850 cm⁻¹ suggest a major Si–O_br stretching contribution. The broad band centered at 900 cm⁻¹ shows a certain involvement with more complex lattice modes that are also present in pVDOS evaluated after projection along the Si=O stretching (Fig. 2(B)).

Fig. 2(D) shows the pVDOS obtained by projecting the Cartesian velocities along the stretching ICs between metal cations and oxygen atoms forming the selected M1 and M2 sites. The broad peak associated with the Mg²⁺ cation coordinated by six oxygen atoms of the Si=O group (M1 site) extends from 200 cm⁻¹ to 550 cm⁻¹ and is centered at around 400 cm⁻¹ (red line in Fig. 2(D)). In the M2 site, there are two types of stretching: (a) along the direction between Ca²⁺ and the oxygen atom of the bridge (Si–O_br::Ca) and (b) between the cation and the oxygen of the Si=O groups (Si=O::Ca). Both projections give rise to a broad peak in the region lower than 600 cm⁻¹. The frequencies due to Si=O::Ca²⁺ (blue line in Fig. 2(D)) are centered at around 350 cm ⁻¹, whereas the frequencies due to Si–O_br::Ca²⁺ are centered between 200 cm ⁻¹ and 300 cm⁻¹ showing a prominent peak at 250 cm⁻¹ and a smaller one at 150 cm⁻¹. In all cases, the frequencies above 600 cm ⁻¹ can be traced back to the spurious contribution of the Si=O group and Si–O_br–Si chains.

In conclusion, deconvolution of the total VDOS through the projection procedure allows us to assign the vibrational frequencies to the dominant character of the vibration mode in terms of the selected ICs. Therefore, frequencies higher than 1000 cm⁻¹ are due to the stretching of Si=O groups, when coupled with the stretching vibration related to the bridging oxygens Si–O_br.⁴² The stretching modes due to the bridging bond Si–O_br are between 600 cm⁻¹ and 700 cm⁻¹ and between 800 and 1000 cm⁻¹. The broad peak extending from 100 cm⁻¹ to 600 cm⁻¹ is assigned to Ca::O and Mg::O stretching and complex lattice vibrations.

3.2 Application to Sc-doped diopside

To study the scandium substitution, we use 140 models where 4 Mg atoms are randomly exchanged with Sc atoms and 2 Ca atoms are randomly selected and deleted creating 2 vacancy defects. Among all, only four models shared the same total energy and, therefore, equivalent atomic arrangements, thus generating 137 non-equivalent models. The average energy per atom is −547.643 ± 0.0012 eV, and the difference between the most stable structure and the less stable is negligible being 0.005 eV per atom. However, the most stable model was selected and further minimized (see the Methods and computational details section) and is shown in Fig. 3. Interestingly, in this case, both vacancies are close to scandium. The destabilization energy due to the defects in Sc-doped diopside, in comparison to the pristine form, is 5.62 eV per atom. In agreement with the experimental data,² the substitution of scandium for magnesium at the M1 site and the creation of vacancy at the M2 sites causes a subtle increase of the cell, especially for “b” and “c” lattice parameters (see Table 1). The root mean square deviation (RMSD) evaluated for the Si and O atoms of Sc-doped diopside with respect to the pure diopside is 0.043 Å, showing that the lattice on average does not undergo any noticeable structural changes. Indeed, Sc and Mg have very similar ionic radii and the substitution does not influence very much the volume of the M1 site, but it has an influence on the nearby Mg–M1 and Ca–M2 sites because of different oxygen charge balances (see Table 3). In particular, when, to charge balance the Sc–Mg substitution, a vacancy replaces Ca at M2, a polyhedral volume strongly increases (30.319 vs. 25.781 ų), thus influencing the structure locally. The surrounding M1 and M2 volume values have a higher variability with respect to the similar Sc–Mg–Mg octahedral and Ca–Ca–Ca polyhedral M2 strip distant from the vacancy. b and c lattice directions, perpendicular to and along the M1–M2 polyhedral strip respectively, are thus the most affected by the vacancy substitution induced by Sc-doping.

Fig. 3 Sc-doped diopside supercell, viewed along the c axis: Mg²⁺ orange, Ca²⁺ cyan, Si yellow and O red. The four Sc are in mauve, whereas the two vacancies are highlighted in light green spheres.

Table 3 Polyhedral volumes calculated at the DFT level of theory for pure and Sc-doped diopsides. Volumes are expressed in ų and are calculated using the VESTA software.⁴⁵ We calculated volumes of M1 octahedra and nearby M2 polyhedra of the [001] strip both “near vacancy” (a) and “distant from vacancy” (b) in the Sc-doped and corresponding crystallographic position in the pure diopside

	Sc-diopside			Pure diopside
	a	b		a	b
Sc	12.042	12.005	Mg	12.081	12.106
Mg	11.880	12.167	Mg	12.087	12.105
Mg	12.127	12.164	Mg	12.081	12.103
Ca	25.897	25.600	Ca	25.779	25.795
Ca	25.662	25.701	Ca	25.771	25.803
Vacancy/Ca	30.319	25.600	Ca	25.781	25.804

---

The distance between oxygen and Sc³⁺ (Si=O::Sc) on average is similar to the distances reported for Si=O::Mg in pristine diopside (see Table 2); however, the broad distribution of distances (see Fig. S3, ESI†) strongly suggests a certain degree of distortion/asymmetry of the M1 site. Overall, the calculated structural parameters for the Sc-doped system, as reported in Table 2, and the broadening of the distributions indicate a noticeable level of lattice distortion attributed to the presence of Sc (see Fig. S2, ESI†). Lattice distortion is also suggested by the polyhedral volume distribution (see Table 3).

The VDOS of Sc-doped diopside is shown in black in Fig. 4(A). Comparison with the VDOS of the pristine pure diopside (yellow in Fig. 4(A)) shows small differences highlighted with colored areas in the figure. The differences include: (i) a presence in Sc-doped diopside VDOS of a shoulder around 860 (red, Fig. 4(A)), (ii) a broadening of the amplitude of peaks above 1000 cm⁻¹ (yellow, Fig. 4(A)) and (iii) a small isolated peak at 700 cm⁻¹ (blue, Fig. 4(A) and Fig. S9, ESI†).

Fig. 4 Sc-doped diopside VDOS and pVDOS. (A) VDOS evaluated taking into account all atoms of Sc-diopside (black) and pristine pure diopside(orange). (B) pVDOS for Si=O stretching of M1 involving Sc. (C) pVDOS for Si–O_br stretching in the vacancies of the M2 site. (D) pVDOS for stretching between oxygen and (E) Sc of M1 (Si=O::Sc).

The spectrum obtained by projecting the velocities on the Si=O stretching of the M1 sites containing the Sc³⁺ atom is shown in Fig. 4(B) and has a broad band between 800 cm⁻¹ and 1100 cm⁻¹. The largest contribution is at about 860 cm⁻¹ and gives rise to the small shoulder between the peak at 850 cm⁻¹ and the peak at 900 cm⁻¹ of the VDOS (Fig. 4(A), highlighted in red). The comparison between pVDOS of Si=O of the pristine diopside and Sc-doped diopside (see Fig. 2(B) and 4(B)) highlights the effect of the presence of Sc in M1. In particular, the peak at 1025 cm⁻¹ of pristine diopside disappears, while the prominent peaks between 850 cm⁻¹ and 875 cm⁻¹ present in the pVDOS of Sc-doped diopside (highlighted in red in Fig. 4(B)) are negligible in the pVDOS of the pristine diopside (Fig. 2(B) and comparison in the top of Fig. S7, ESI†). The pVDOS for Si=O involved in the vacancies of M2 sites is shown in Fig. 4(C). The oxygen atoms are not involved in the coordination of Ca²⁺ and the bands are shifted towards higher frequencies (yellow area in Fig. 4(A) and (C), and Fig. S8, ESI†).

Fig. 4(D) shows the pVDOS obtained by projecting the Cartesian velocities along the stretching ICs of Si–O_br of M2 empty sites; in this case, the bridging oxygen atoms are not interacting with Ca²⁺. The pVDOS shows less defined peaks at higher frequencies with respect to the pristine diopside pVDOS as reported in Fig. 2(C). The set of peaks less than 700 cm⁻¹ and the peaks between 775 cm⁻¹ and 950 cm⁻¹ are not defined well, while the peaks at 800 cm⁻¹ and 850 cm⁻¹ are very low compared to the pVDOS of the pristine diopside of Fig. 2(C) (see Fig. S7, ESI† bottom for comparison). Instead, two well-defined peaks appear at 700 cm⁻¹ and around 975 cm⁻¹. The peak at 700 cm⁻¹ is isolated (Fig. 4(A) and (D), highlighted in blue), while the peak at around 975 cm⁻¹ contributes to the broad peak between the prominent peak at 900 cm⁻¹ and 1000 cm⁻¹ of VDOS.

Fig. 4(E) shows the pVDOS obtained by projecting the Cartesian velocities along the stretching between Sc cations and oxygen atoms involved in M1 sites. These projections result in a broad peak in the region lower than 600 cm⁻¹. Three peaks at 550 cm⁻¹, 500 cm⁻¹ and 450 cm⁻¹ and a broad peak between 300 cm⁻¹ and 400 cm⁻¹ appear, but their presence does not affect the profile of the VDOS. The peak at higher frequencies, greater than 600 cm⁻¹, shows a non-negligible involvement with the stretching of Si=O and Si–O_br is the present peak in the region between 600 cm⁻¹ and 700 cm⁻¹ and between 800 cm⁻¹ and 1100 cm⁻¹.

3.3 Comparison with the recorded IR and Raman spectra

Synthetic pure diopside (DiBa8) and Sc-doped diopside (DiBa19 of²) were used to record the Raman spectra in the 200–2000 cm⁻¹ region and IR spectra in the 550–7000 cm⁻¹ region to be compared with the calculation; the direct comparison between VDOS and Raman spectra is presented in Fig. S11 (ESI†). The diopside structure (sp. gr. C2/c) belongs to the 2/m point group and thus Γ_tot = 14A_g + 14A_u + 16B_g + 16B_u. The only IR active modes are 14A_u + 16B_u whereas A_g and B_g are only Raman active modes.

In the IR measured spectra (Fig. 5), diopside displays only the Si–O_br stretching modes at frequencies greater than 800 cm⁻¹ and O=Si=O bending modes between 600 cm⁻¹ and 700 cm⁻¹ (see Fig. S10, ESI†), whereas the M1–O and M2–O stretching (i.e., Si=O::Ca/Mg stretchings) and bending modes occur below 500 cm⁻¹ outside the range of our measurement. We can observe a broadening of the IR peaks at 863 and 1074 cm⁻¹ and a small shift of the 922 cm⁻¹ (to 912 cm⁻¹ in Sc-doped diopside), in good agreement with the calculations that showed a general broadening on amplitude above 1000 cm⁻¹ and an increase in intensity of the peak at 863 cm⁻¹.

Fig. 5 IR spectra of pristine pure diopside (black) and Sc-doped diopside (blue).

The Raman spectrum of Sc-doped diopside matches with that of the pure diopside composition, pointing out the weak effect of doping with 0.8 mol of Sc (Fig. 6). Conversely, the increasing content of Sc provides a substantial modification of the structure mirrored in some spectral regions (see DiBa19 spectra, Fig. 6). The mode assignation (determined by fitting the peak to a pseudo-Voight function) is reported in Table 4. All in all, the centroid values of DiBa8 are almost in line with those of pure diopside from ref. 35, except the hidden A_g mode at about 310 cm⁻¹ (only detectable with an appropriate apparatus and polarization).

Fig. 6 Raman spectra of pristine pure diopside (black) and Sc-doped diopside (blue).

A comparison of pure and Sc-doped diopside spectra outlines that some peaks of the DiBa8 diopside seem to disappear or merge into a single convoluted band in DiBa19. In particular, the B_g peak (165.6 cm⁻¹) originating from the Ca vibrations coupled with chain rotations experiences a dramatic change from tight and sharp in DiBa8 to a very weak shoulder of the stronger 140 cm⁻¹ A_g peak in Sc-doped diopside DiBa19. It is worth to note that the 303.5 cm⁻¹ peak in pure diopside (DiBa8) merges as a shoulder in the 325 cm⁻¹ A_g peak's tail. Similarly, the doublet at 358 and 368 cm⁻¹ in DiBa8 merges into a single broad and asymmetric band at 366.7 cm⁻¹ in DiBa19. Indeed, this frequency range 327–390 cm⁻¹ is dominated by tetrahedral tilting (O_br–O_br–O_br kinking angle increases in value from pure to Sc-doped diopside²) that experiences a topological redistribution around the M1 site which is deformed and distorted by Sc atoms (17% with respect to pure diopside) as demonstrated by SC-XRD.²

Table 4 Experimental normal mode wavenumber (cm⁻¹) for the pristine pure diopside from ref. 35 and this work for pure (DiBa8) and Sc-doped diopside (DiBa19)

	Diopside^35 (Exp.)	DiBa8	DiBa19
* and ** refer to sample 1 and 3 of Table 3 in ref. 35.
Ag	140	140	140
Bg	164	165.6
Ag	181	182.5	183
Bg	194	196	193
Bg	230	231	230.7
Ag	233	234.6
Ag	255	255.8	253.8
Bg	301	303.5
Ag	310
Ag	323	325.2	325.2
Ag, Bg	356	358
Bg	367	368	366.7
Ag	389	391.2	390.3
Bg	464	466	466
Ag	508	509.4	507.5
Bg	515	515.6
Ag	529	530.6
Bg	558	560	561.9
?			579
Ag	667	667	666.1
Bg	708	705.6
?			741
Ag	854	854	854
Bg*	915	915	906
Bg*,**	964 and 971	969.7
Ag	1013	1013	1011.8
Ag,Bg	1047	1047.9	1042

---

The O=Si=O bending motions in the A_g symmetry at 508 and 530 cm⁻¹ do not show any appreciable change in DiBa8 compared with those of the literature,³⁵ as well as the B_g mode originated by the Si–O_br–Si and O_br–Si–O_br vibrations at 515 and 560 cm⁻¹. However, the Sc-doped sample displays broad and weak features in which the 515 cm⁻¹ shoulder (B_g) seems to be convoluted into the slightly broadened A_g peak at 508 cm⁻¹. Analogously, the peak at 530 cm⁻¹ seems involved in the broadening of the 560 cm⁻¹ band of the Sc-doped samples. This could probably be due to a polarization effect combined with a change of the bond bending angle induced by Sc³⁺. Additionally, we noted a shoulder-like feature at about 580 cm⁻¹ in DiBa19. Although it is in the frequency range dominated by A_g (O=Si=O bending motions) and B_g modes (Si–O_br–Si or/and O_br–Si–O_br vibrations), we undoubtedly ascribe it to the presence of Sc³⁺. Interestingly, the Si–O_br symmetric and anti-symmetric stretching modes with peaks at 706 and 970 cm⁻¹ in the DiBa8 sample undergo strong modifications with Sc-doping. Indeed, they seem incorporated into the broad tails of the most intense and neighbouring A_g modes with peaks at 667 and 1013 cm⁻¹. The latter undergoes a backward shift and a FWHM broadening of about 10%, mirroring the broadening of the peaks above 1000 cm⁻¹ predicted by calculations. Finally, we observed a quite weak feature around 741 cm⁻¹ which turns out very weak in the DiBa8 sample but slightly increases its intensity in the Sc-doped sample (DiBa19). This is the only unexpected peak (both from theory and literature) that might fit the calculated one at 700 cm⁻¹ related to the vacancy at the M2 site. Moreover, the observed broadening of about 30% in the A_g and B_g peaks FWHM at 854 and 915 cm⁻¹, respectively, may be related to the calculated shoulder at ca. 860 cm⁻¹.

4 Conclusions

Our experimental study combined with ab initio modeling provides deeper characterization of the structural modifications of the silicate diopside doped with a transition metal (Sc). Calculated structural data and vibrational analysis are validated by the experimental measurements (SC-XRD and IR and Raman spectroscopy). The protocol based on the projection of Cartesian atomic velocities in a subset of selected ICs is presented and exploited to decompose and to analyze the VDOS allowing its resolution in terms of intuitive internal coordinates modes. We applied this protocol to the pure single-chain silicate diopside and to Sc-doped diopside, where the transition metal enters the structure and can be described by the coupled substitution involving Mg²⁺ + Sc³⁺ at the octahedron M1 and Ca²⁺ + [] at the irregular dodecahedron M2 to achieve charge neutrality. The presence of vacancies at the M2 site on one side introduces further complexity to the model, and on the other side allows us to investigate the presence of this local feature in synthetic/natural materials by using spectroscopic and computational techniques. The comparison of the two models suggests that when the diopside structure is doped with Sc, the main effects are the broadening of the peaks above 1000 cm⁻¹ together with a shoulder at ca. 860 cm⁻¹, and the occurrence of a small peak at 700 cm⁻¹, which could be ascribed to the presence of vacancies at M2. This model also suggests that the vacancies are most probably in proximity to the nearby Sc site, in agreement with the distribution of bond valences associated with the trivalent cations substituting the divalent Mg. We speculate that the position of this peak could be related to the average distance between the Sc and the vacancies; however, this topic represents the main object of further investigations. Overall, the computed VDOSs are in good agreement with the measured Raman and IR spectra, and provide a more detailed interpretation of the spectroscopic signature of the samples. In particular, we could correlate the M1 polyhedral distortion due to Sc-doping to the broadening of the low frequency Raman peaks.

In conclusion, we are confident that the application of this method can offer comprehensive characterization of complex systems, such as minerals or nanomaterials. In the case of defective or doped systems, this is particularly valuable, where the need for large supercells and the loss of symmetry essentially nullify the advantages of standard harmonic vibrational analysis and make the computational calculation of IR or Raman intensities particularly demanding.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

L. B. conceived the theoretical and computational parts, carried out the molecular dynamics simulations and developed the software to evaluate the VDOS and pVDOS. M. C. performed the Raman measurements. H. S. synthesised the samples and performed the IR measurements. S. N. and L. B. conceptualised the work. L. B. and S. N. wrote the draft version. L. B., S. N., M. C., and H. S. finalised the final version of the manuscript. All authors wrote and reviewed the manuscript. This research was partially funded by the EU-H2020 FETPROACT, project name LESGO (DOI: 10.3030/952068, agreement No. 952068).

References

1. N. Baig, I. Kammakakam and W. Falath, Mater. Adv., 2021, 2, 1821–1871.
2. S. Nazzareni, H. Skogby and U. Hålenius, Phys. Chem. Miner., 2013, 40, 789–798.
3. U. Hålenius, H. Skogby, M. Edén, S. Nazzareni, P. Kristiansson and J. Resmark, Geochim. Cosmochim. Acta, 2010, 74, 5672–5679.
4. J.-B. Wu, M.-L. Lin, X. Cong, H.-N. Liu and P.-H. Tan, Chem. Soc. Rev., 2018, 47, 1822–1873.
5. N. Melchioni, L. Bellucci, A. Tredicucci and F. Bianco, Surf. Interfaces, 2023, 102662.
6. L. Basta, A. Moscardini, F. Fabbri, L. Bellucci, V. Tozzini, S. Rubini, A. Griesi, M. Gemmi, S. Heun and S. Veronesi, Nanoscale Adv., 2021, 3, 5841–5852.
7. L. Basta, F. Bianco, A. Moscardini, F. Fabbri, L. Bellucci, V. Tozzini, S. Heun and S. Veronesi, J. Mater. Chem. C, 2023, 2630–2639.
8. S. Nazzareni, G. Molin, H. Skogby and A. Dal Negro, Eur. J. Mineral., 2004, 16, 443–449.
9. S. Nazzareni, T. Busà and R. Cristofolini, Eur. J. Mineral., 2003, 15, 81–93.
10. H. Ohashi, X-ray study on Si–O bonding, Maruzen Publishing Service Center, 2003.
11. S. Nazzareni, G. Molin, A. Peccerillo and P. F. Zanazzi, Eur. J. Mineral., 1998, 291–300.
12. S. Nazzareni, V. Barbarossa, H. Skogby, V. Zanon and M. Petrelli, Contrib. Mineral. Petrol., 2020, 175, 1–16.
13. M. Murri, F. Cámara, J. Adam, M. Domeneghetti and M. Alvaro, Geochim. Cosmochim. Acta, 2018, 227, 133–142.
14. E. Brizi, S. Nazzareni, F. Princivalle and P. F. Zanazzi, Contrib. Mineral. Petrol., 2003, 145, 578–584.
15. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
16. A. Chopelas and G. Serghiou, Phys. Chem. Miner., 2002, 29, 403–408.
17. B. J. Moulton, G. S. Henderson, H. Fukui, N. Hiraoka, D. de Ligny, C. Sonneville and M. Kanzaki, Geochim. Cosmochim. Acta, 2016, 178, 41–61.
18. M. Tribaudino, L. Mantovani, D. Bersani and P. P. Lottici, Am. Mineral., 2012, 97, 1339–1347.
19. M. P. Allen and D. J. Tildesley, Computer simulation of liquids, Oxford university press, 2017.
20. E. B. Wilson, J. C. Decius and P. C. Cross, Molecular vibrations: the theory of infrared and Raman vibrational spectra, Courier Corporation, 1980.
21. P.-K. Lai and S.-T. Lin, J. Comput. Chem., 2015, 36, 507–517.
22. G. Cardini and V. Schettino, Chem. Phys., 1990, 146, 147–153.
23. M. Pagliai, G. Cardini, R. Righini and V. Schettino, J. Chem. Phys., 2003, 119, 6655–6662.
24. N. Neto, J. Mol. Struct., 2001, 563, 135–139.
25. N. Neto and L. Bellucci, Chem. Phys., 2006, 328, 259–268.
26. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt and F. Schiffmann, et al. , J. Chem. Phys., 2020, 152, 194103.
27. J. VandeVondele, M. Krack, F. Mohamed, M. Parrinello, T. Chassaing and J. Hutter, Comput. Phys. Commun., 2005, 167, 103–128.
28. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
29. M. De La Pierre, R. Orlando, L. Maschio, K. Doll, P. Ugliengo and R. Dovesi, J. Comput. Chem., 2011, 32, 1775–1784.
30. J. VandeVondele and J. Hutter, J. Chem. Phys., 2007, 127, 114105.
31. M. Krack, Theor. Chem. Acc., 2005, 114, 145–152.
32. R. M. Thompson and R. T. Downs, Am. Mineral., 2008, 93, 177–186.
33. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
34. M. Thomas, M. Brehm, R. Fligg, P. Vöhringer and B. Kirchner, Phys. Chem. Chem. Phys., 2013, 15, 6608–6622.
35. M. Prencipe, L. Mantovani, M. Tribaudino, D. Bersani and P. P. Lottici, Eur. J. Mineral., 2012, 24, 457–464.
36. F. Zou, Z. Wu, W. Wang and R. M. Wentzcovitch, J. Geophys. Res.: Solid Earth, 2018, 123, 7629–7643.
37. P. Richet, B. O. Mysen and J. Ingrin, Phys. Chem. Miner., 1998, 25, 401–414.
38. V. Swamy, L. S. Dubrovinsky and M. Matsui, Phys. Chem. Miner., 1997, 24, 440–446.
39. R. T. Downs, Am. Mineral., 2003, 88, 556–566.
40. A. M. Walker, R. P. Tyer, R. P. Bruin and M. T. Dove, Phys. Chem. Miner., 2008, 35, 359–366.
41. X. Gao, H. Wang, C. Wang, S. Chen, M. Zhao and B. Li, J. Non-Cryst. Solids, 2019, 526, 119701.
42. P. Richet and G. Fiquet, J. Geophys. Res.: Solid Earth, 1991, 96, 445–456.
43. S. Sasaki, K. Fujino, Y. Takeuchi and R. Sadanaga, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1980, 36, 904–915.
44. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
45. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp02324a

---