The role of helicity in PFAS resistance to degradation: DFT simulation of electron capture and defluorination

Abstract

Defluorination of perfluorinated alkyl substances (PFASs) via the direct capture of excess electrons poses a promising path to environmental decontamination. Herein we show that quantum-chemical model optimization methods can be adapted to simulate the changes to molecular geometry that result from electron capture. These reaction pathways demonstrate that the introduction of an additional electron causes a loss of the helical arrangement along linear carbon tail chains. Regaining helicity is sufficiently favourable to enable fluoride release in C7–C10 PFAS chains; shorter chains are enthalpically hindered from degradation while the additional charge is stabilized on longer chains by the greater entropy their flexibility permits. These results suggest that reductive PFAS treatment processes could be made more effective under high pressure or confined conditions.

---

Introduction

Perfluorinated alkyl substances (PFAS) comprise a large class of aliphatic compounds in which all carbon–hydrogen bonds in the non-fluorinated equivalent have been replaced with carbon–fluorine bonds. Fluorination results in increased hydrophobicity and resistance to chemical or physical degradation as compared to their hydrogenated alkyl counterparts.¹ It is due to their structural stability, and to their long-term unregulated industrial production and disposal, that PFAS have become pervasive and persistent environmental pollutants.² This in turn has motivated a rapid rise in efforts to understand PFAS toxicology, decontamination, and destruction.

Perfluorooctanoic acid (PFOA) and perfluorooctane sulfonic acid (PFOS) and their anions are especially widespread and have therefore received relatively high scrutiny from the scientific and regulatory communities. The United States Environmental Protection Agency is empowered to develop non-enforceable, non-regulatory national Health Advisories to identify the “drinking water concentration level of a specific contaminant at or below which exposure for a specific duration is not anticipated to lead to adverse human health effects.” In June 2022, published updated interim Health Advisory values for PFOA and PFOS concluded that the lifetime interim Health Advisory for PFOA³ is 0.004 ng L⁻¹ (4 parts per quadrillion (ppq) – 0.006% of the 0.07 μg L⁻¹ (70 parts per trillion (ppt)) values published in 2016) and for PFOS⁴ is 0.02 ng L⁻¹ (20 ppq–0.03% of the 70 ppt 2016 value). These updated values indicate that in practice there is no safe level of these abundant, ubiquitous, highly stable substances.

Naturally, PFAS degradation and decontamination has also become a high value research domain. Effective techniques are needed, and quickly, to extract and destroy the PFAS that has already infiltrated our water supply. The literature is rich with recent reviews on the current state of the overall field,^5–10 emerging technologies,^11–13 advanced reduction and oxidation methods,^14–16 as well as several specific techniques.^17–22 The focused community effort has generated exciting advances towards effective and efficient PFAS degradation in organic solvents²³ or low/no solvent²⁴ but methods that operate in aqueous solution hold the promise of in situ PFAS groundwater decontamination. One set of techniques for the degradation of dilute PFAS in water is via the capture of hydrated electrons, e_aq⁻. The sources of electrons vary and include the use of electrodes,²⁵ plasmas,^26–29 photochemical interactions with electron donors,^30–33 or radiolysis of the water.^34–36

As a recent review comprehensively covers, theoretical studies to elucidate the defluorination mechanisms complement the experimental work although identification of the elementary steps on the reaction pathway remains as recalcitrant as the molecules themselves.³⁷ Theoretical and experimental studies on the site and rate of electron insertion show that electron capture is independent of the length of the carbon chain or carbon–fluorine bond dissociation energy.^38,39 Bentel's comprehensive study demonstrated a correlation between carbon chain length and degradation rate that remains unexplained by their table of carbon–fluorine bond dissociation energies.⁴⁰ Yamijala's Born–Oppenheimer Molecular Dynamics (BOMD) study found that the initial loading of the additional electron across the carbon chain made the site of defluorination nearly random on an ultrafast (<100 fs) timescale.⁴¹ Simulation of hydrated electron dynamics by Biswas et al. showed polarization of the surrounding water shell before electron capture that affected both insertion point and subsequent C–F bond strengths, altering the relative probability of which fluorine will break its bond to carry the charge away as an anion.⁴² Their subsequent dynamic work on expanded systems further confirmed the behaviours and femto- to picosecond timescale.⁴³ Taken together these studies suggest that the mechanism linking chain length and degradation rate occurs after electron capture. Furthermore, these theoretical studies are consistent in their treatment of bond strength as the decisive factor in the determination of whether and where defluorination will occur and understate the contribution of how those bonds are arranged within the molecular structure.

Structural representations and mental models

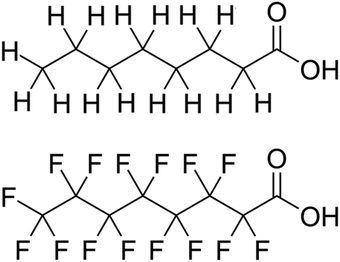
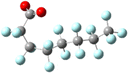
From the beginning, PFAS compounds were discussed in contrast to their non-fluorinated analogues.¹ Even the name “per- and poly-fluorinated alkyl substances” defines the class of compounds by comparison to their hydrogen-only counterparts. The analogy is a useful one and quickly conveys the principal characteristic of the class; however, the convention privileges the similarity in schematic bond connectivity over the differences in molecular geometry created by the H to F exchange. Because the stronger C–F bond dissociation energies are foregrounded they have been the subject of theoretical studies. Conversely, the shorter bond–bond length and the higher electronegativity, higher electron density, and larger atomic radius of the fluorine constituent produce important differences between the PFAS and its H-analogue bond lengths, angles, and dihedrals and the rotational freedom about the C–C backbone.

For a literal illustration of how bond structure becomes privileged, we must consider the structural formulae used to identify the compounds. We use structural formulae to picture the molecules under discussion, and by so doing may easily forget that they are not actually “pictures.” The symbols and connections constitute a pictogram with rules for composition and interpretation. It is a visual language: the structural formula for octanoic acid shown in Fig. 1 is a translation of that name into pictographic form, not an image of the molecule itself. Where the carbon chains appear to be drawn in the trans configuration, we ought to understand that to be fallacious. This is the default conformation in which to display alkyl chains with the understanding that at room temperature CH₂–CH₂ bonds undergo rapid, fluid exchange between the various conformers. However, the barrier to rotational conformation exchange is significantly higher for CF₂–CF₂, so the same assumption of fluidity between conformers is not appropriate and therefore the trans-default representational standard does not apply. If we are to understand both the alkyl and PFAS structural formulas as non-conformer specific, then we can conclude that the structural formulae contain no spatial information.

Fig. 1 Structural formulae of octanoic acid (top) and perfluorooctanoic acid (bottom). The layout seems to convey that the two molecules share the same linear trans conformation; however, these are connectivity schematics only and contain zero geometric information.

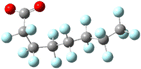
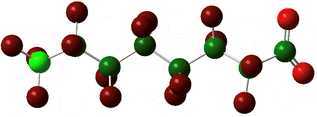
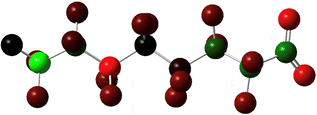
Yet the illusion is compelling enough that one could easily misinterpret the identical line lengths and direction as indicative that the molecular geometries are also identical. In recognizing that it is a connection schematic only, we should also recognize that the effect of H–F exchange on bond length, direction, and rotational freedom are not represented at all. It is far more difficult to notice what is absent than what is present and so the evident similarities are given greater attention than the non-evident differences. This is a problem for two reasons. First, mental modelling is an important tool chemists use to develop and evaluate mechanism diagrams. Second, neglecting the molecular geometry gives the false impression that the molecular geometry can be neglected. In a tightly formed, stable compound the bond lengths, angles, and dihedrals are critical contributors to its chemical behaviour and available reaction pathways (Fig. 2 and 3).

Fig. 2 A picture of an optimized model of PFOA (top) and a second structural formula of PFOA (bottom). The picture depicts molecular connectivity and geometry and thus comparatively greater information content than the Fig. 1 structural formula, despite visual similarity. By contrast, the information content of the PFOA structural formula shown here is identical to that held by the more typical layout in Fig. 1.

Fig. 3 Side and end views of a perfluorooctanoate model with charge on the electron density surface shown in red (negative) at the carboxylate head group progressing toward green (neutral) at the tail. Carbon is shown in grey, fluorine in blue, oxygen in red. The helicity imposed by fluorine–fluorine repulsion is evident.

Molecular geometries of linear PFAS chains

In the specific example of octanoate/perfluorooctanoate, the direct structural analogue takes on new and important features when their geometries are optimized to their ground state. Most notably, PFAS carbon chains twist into a compact helix, in contrast to the straight, linearly-aligned carbon chain of the H-analogue. The more accurate and complete representation also shows the similarities in connectivity but doesn’t overstate its importance, inviting different perspectives on the problem of PFAS resilience. For instance, the helical conformation makes it more obvious that the C–F bond is not only stronger but more difficult to access than the C–H bond, which could impact treatment methods. The compact structure makes the PFAS more rigid than the H-analogue and this mechanical rigidity could affect reactivity. A helical structure creates a persistent conformational chirality which could alter its susceptibility to degradation under treatment conditions. If the compact, helical conformation is the stable conformation: how can the PFAS be induced into a less-stable elongated, linear state? The point of this discussion is not to advocate for 3D ball-and-stick or electron density representations to replace all 2D line drawing as a publication standard (although it would improve our accuracy in graphic communication of our subject molecules) but instead to underline the value of increasing the number and type of (sometimes literal) perspectives on a problem.

Computational details

The level of theory employed in this work, DFT B3LYP-D3(BJ)/6-311+(2p,2d),^44–46 follows from the important experimental validation of the method conducted by Schilberg and coworkers.⁴⁷ They identified stable structural conformers of PFOA by comparing theoretical model predictions to molecular rotational resonance (MRR) spectra, noting that fluorine–fluorine repulsion induces a helical conformation of the carbon tail. This comparison validates the theoretical model used for the systems shown here. While we focus on the conjugate base in this work to better represent the oxidation state of the compounds under environmental conditions, our models correspond with the trends demonstrated in their experimental work.

Bentel and coworkers employed the same model chemistry for their extensive study of bond dissociation energies of per- and polyfluorinated carboxylates and sulfonates at varying chain lengths.⁴⁰ That study, unlike this one, employed the SMD model to provide implicit simulation of solvation in water. We tested the model but ultimately chose not to include it in this work. Critically, the dielectric cavity generated by the implicit model stabilizes a local metastable conformational minimum preceding a critical transition state, clouding the reaction mechanism revealed by the simulation method. In fact, the developers of SMD have shown that it is not well suited for ion dissociation calculations without including a shell of explicit water molecules, an issue observed across ionic solutes expected to have a strong hydrogen bonding interaction with water.^48,49 The PFAS species under investigation here are compact and electron rich, indicating that the intramolecular forces, rather than solvent interactions, are decisive. For these reasons, the high computational expense of computationally-sound explicit aqueous solvation is neither justified nor required for the simulation sets that follow.

That being said, DFT methods using the B3LYP functional are known to overbind certain anion states, predicting a stable or metastable anion where none exists.^50,51 While existing experimental and dynamic simulation results strongly indicate that a −2 oxidation state with a lifespan of at least femtoseconds must be possible, we confirmed key optimizations using the range-separated CAM-B3LYP functional which corrects the energies of long-range exchange interactions and improves the accuracy of energy level calculations.^50,51

Simulating electron capture through optimization

Although the terms are occasionally used interchangeably, molecular modeling and molecular simulation are distinct computational processes. To create a molecular model is to produce a representation of the molecule that suits the purpose for which it was built. By contrast, to perform a simulation is to put a model into action and to study its response to stimulus. In both modeling and simulation, we apply theory to a construction in an attempt to gain or validate insights by extension of the theoretical results onto the real molecule. For models, we might study its atomic geometry, bond strengths and lengths, or electronic structure. Simulations of molecular behaviour could tell us about reaction mechanisms, transport properties, spectroscopic outputs, or intermolecular interactions.

Not all calculation processes are common to modeling and simulation. The process of optimizing the geometry of a molecule, for instance, begins with the set of nuclear charges and their approximate positions and the number of electrons in the system. One tries to make the initial locations of the nuclei a reasonable guess, but in principle the positions are arbitrary. The Born–Oppenheimer Approximation holds that electrons adapt instantaneously to nuclear movement and therefore allows the electronic orbital structure to be calculated on a static landscape.⁵² The total energy of the molecular system can now be determined by application of the appropriate theory. If we were to map all the possible nuclear positions we would find a multidimensional surface whose “height” is determined by the system energy – the potential energy surface (PES). Peaks and valleys on the PES represent nuclear coordinates with particularly high energy (highly strained geometries) or low energy (stable geometries). Geometric optimization is the iterative process of moving the nuclei “downhill” along the PES until coming to rest at the local or global minimum energy, corresponding to physically meaningful metastable or stable states.⁵³ This set of nuclear coordinates and molecular orbitals now form a theoretical model of the molecule under study. Because optimization is a process used in model generation and not application, optimization is typically considered a modeling process and not a simulation process.

However, what if the initial geometry is not arbitrary but is itself a physically meaningful optimized model? Could optimization then simulate a spontaneous chemical process? Most inter- or intramolecular processes rule out this hypothetical by definition: the optimized model is already at its energetically stable geometry and therefore not prone to reaction. Electron capture stands out as an exception. According to the Born–Oppenheimer Approximation, electron motion is instantaneous compared to nuclear motion and so the optimized molecular geometry of the pre-capture state is a physically meaningful initial geometry of the post-capture state. Therefore, optimization of a model generated on the PES of the n oxidation state would move downslope along the PES of the n − 1 oxidation state in a manner that simulates the molecule's response after reduction. Because the starting and end points are physically relevant, the pathway that the optimization follows to connect them represents a mechanism of action.

This study uses optimization methods to simulate the behaviour of PFAS molecules immediately following reduction by electron capture from the −1 to the −2 oxidation state. All carboxylate and sultanate models were optimized to the DFT CAM-B3LYP-D3(BJ)/6-311+G(2d,2p) level of theory at the −1 oxidation state using the Gaussian 16 software package.⁵⁴ The agreement between these models and the experimental geometries supports our claims that the optimized structures can be used as a physically meaningful starting point for simulation of the geometric changes that follow reduction in related compounds.⁴⁷

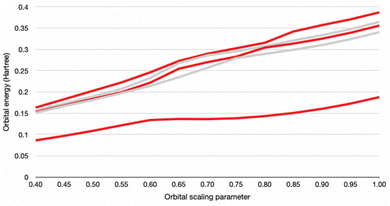
The oxidation state was then set to −2 to place the model on the new, post-electron capture PES. Examination of the calculated orbital energies of the molecular geometries reveal that the additional electron initially lies in at a positive energy level in all cases. The positive orbital energy (or negative electron affinity) indicates that it either does not attach at all, in which case the model is in conflict with experiment, or that the electron attaches via resonance with a metastable orbital. To determine the status of the unbound electron, we examine the parent molecule for the presence of a repulsive Coulomb barrier. If present, an additional electron may tunnel through it into an orbital level that is unbound (positive energy value) yet able to play temporary host to an electron trapped behind the Coulomb barrier.⁵¹ The stabilization method is performed by varying the scaling factor α of the diffuse functions on the atomic centres and then plotting the higher-lying orbital energies as a function of scaling factor. If a Coulomb barrier capable of supporting a metastable anionic state is present, it will be revealed by the presence of “avoided crossings” on the plot – points at which pairs of orbitals sharply change in their sensitivity to the scaling factor – indicating resonance between the α-sensitive exterior state and the α-insensitive attached inside-barrier state (Fig. 4).⁵¹ We applied the orbital exponent stabilization method using DFT CAM-B3LYP-D3(BJ)/6-31+(p,d) on the initial geometries of carboxylate and sulfonate structures.^51,55,56 A smaller basis set is acceptable for the basic test provided that we accept the limitation that the results cannot be used to reproduce the true resonance energies.^51,55 All searches confirmed the presence of avoided crossings, providing evidence that the unbound electron lies in a metastable attached state consistent with existing experimental and theoretical results. Indeed, applying the stabilization method at points along the optimization pathway and at the final geometries shows that the orbital energy decreases towards the bound state as relaxation progresses.

Fig. 4 Stabilization plot of PFOA after electron capture showing the highest occupied and lowest unoccupied orbital energies as a function of the diffuse basis functions’ scaling factor. The rate change in the lowest plot line around (0.60, 0.14) is created by a resonance state indicative of a metastable anion.

With the metastable attachment status of the extra electron established, subsequent simulation of molecular relaxation along the geometry optimization pathway on the reduced PES could be completed using the uncorrected B3LYP functional. In this application, its usual limitation permits a wider search amongst the relevant states in which the electron is retained. These simulations are therefore of the ‘extra electron’ type and do not include the changes to the molecule that could be induced by the approach of an explicit hydrated electron.⁴² The optimization pathway is charted to show metastable and transition states as well as the final stable state of the system after reduction. The orbital stabilization method can provide an estimate of the expected lifetime of the metastable state given energy level and tunnelling barrier information and a crude approximation places the stability timescale in the femtosecond range, consistent with Biswas’ dynamic predictions; however, we can make no claim on the time or rate of reaction. Optimization does not provide time information: a greater or lesser number of steps in the simulations that follow do not in any way indicate a slower or faster process.

Results and discussion

Carboxylate simulation

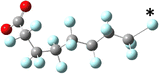
Prior experimental and theoretical work on PFOA has focused on the most linear conformation since that is its lowest energy conformer. Although fluorinated alkyl chains are not as fluid in conformation change as their hydrogenated analogues, some variability in conformer is present in samples.⁴⁷ Conformer search was performed using Avogadro: an open-source builder and visualization tool Version 1.2.0.⁵⁷ The systematic molecular mechanics search used the MMFF94 force field to scan the rotatable bonds and generated 243 geometric isomers.⁵⁸ We then formatted the output files for Gaussian and optimized these geometries to the PM6 semi-empirical level of theory.⁵⁹ The 100 lowest energy non-equivalent conformers were then optimized using DFT B3LYP-D3(BJ)/6-311+G. Eliminating the high strain conformers from this set left 43 non-equivalent conformers remaining, of which the 7 most stable were further serially optimized to DFT B3LYP-D3(BJ)/6-311+(2p,2d) at both the −1 and −2 charge. The results are tabulated in Table 1, below. As mentioned above, simulation of electron capture via the addition of an extra electron does not capture the probability or location of electron insertion so the initial change in energy between the −1 and −2 charge states are reported but are qualitative at best.

Table 1 The results of the search for most stable carboxylate conformers before and after the addition of an extra electron. The total electronic energy (Ee) of each structure is reported in Hartree and normalized in kilojoules per mole to the most stable conformer. The change in energy after electron insertion only reports the geometric relaxation and does not include the cost of capture. The defluorination site is marked by an asterisk

Initial conformation, charge = −1	Post-electron capture, charge = −2
Ee: −1953.682549 Ha	Initial: −1953.574478 Ha
Normalized: 0.00 kJ mol^−1	Final: −1953.609328 Ha
e^− capture: 283.74 kJ mol^−1	Change: −91.50 kJ mol^−1
Ee: −1953.681983 Ha	Initial: −1953.57091 Ha
Normalized: +1.49 kJ mol^−1	Final: −1953.57091 Ha
e^− capture: +291.62 kJ mol^−1	Change: −91.65 kJ mol^−1
Ee: −1953.681236 Ha	Initial: −1953.563853 Ha
Normalized: +3.45 kJ mol^−1	Final: −1953.60162 Ha
e^− capture: +308.19 kJ mol^−1	Change: −99.16 kJ mol^−1
Ee: −1953.681089 Ha	Initial: −1953.56063 Ha
Normalized: +3.83 kJ mol^−1	Final: −1953.605819 Ha
e^− capture: +316.27 kJ mol^−1	Change: −118.64 kJ mol^−1
Ee: −1953.680853 Ha	Initial: −1953.56056 Ha
Normalized: +4.45 kJ mol^−1	Final: −1953.603718 Ha
e^− capture: +315.83 kJ mol^−1	Change: −113.31 kJ mol^−1
Ee: −1953.680818 Ha	Initial: −1953.556774 Ha
Normalized: +4.54 kJ mol^−1	Final: −1953.597001 Ha
e^− capture: +325.68 kJ mol^−1	Change: −105.62 kJ mol^−1
Ee: −1953.680777 Ha	Initial: −1953.562828 Ha
Normalized: +4.65kJ mol^−1	Final: −1953.605804 Ha
e^− capture: +309.68 kJ mol^−1	Change: −112.83 kJ mol^−1

---

The sites of defluorination on these structures give us the first indication of a trend that will continue across the changes to chain length and head group below. The five most stable conformers each terminate in a set of trans carbon–carbon bonds and in each case it is the terminal fluorine that is lost. Conformers six and seven are intersected by a cis bond on the fifth and sixth carbon, respectively. In those cases, it is a fluorine from the lowest numbered carbon on the cis bond that carries away the excess charge. In all structures the carbon–fluorine bond that breaks is the one whose loss enables the reformation of a compact helical structure. The mechanism is most clearly demonstrated by tracking the geometry of the most stable, most linear conformation as it relaxes after electron capture.

In all the PFAS species included in this study, the lowest unoccupied molecular orbital is an anti-bonding orbital spread along the carbons in the tail, as one might expect to find at the centre of a cylinder of highly electronegative C–F bonds. The primary impact of the reduced bond order brought on by the insertion of an additional electron is a weakening and lengthening of the C–C bonds. Greater distance between the carbons also increases the distance between neighbouring fluorines, which reduces their steric repulsion and allows the carbons to relax toward their ideal tetrahedral geometry. As a result, the helix unwinds and the tail straightens—longer C–C bonds compensate for the larger fluorine radius and the molecule comes to more closely resemble its alkyl analogue.

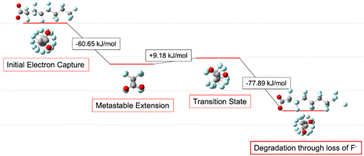
By extending bond length and relaxing bond angles, the system realizes an overall energy benefit which creates a metastable local minimum in some chain lengths, as described in detail below. In that case, an activation step is required to activate defluorination. By scanning the reaction coordinate, we find that the process passes through a transition state that joins the metastable elongated conformation with the final, stable helical conformation. The transition state sits atop a saddle point on the PES, a point at which all geometric dimensions are at an energy minimum save one which is at a local maximum. In this case, the dimension at its local maximum is the length of the terminal carbon–fluorine bond as reflected by animating the imaginary frequency. The reaction's activation energy is the energy required to stretch the C–F bond to this transition state. At the transition state the reaction could regress back to the local minimum, but once the transition state is crossed the molecule spontaneously and irreversibly relaxes into its helical configuration as the additional electron is carried away by disassociation of the terminal fluoride ion.

Initial conformation therefore impacts which fluorine is most likely to leave because it determines which compact structure is most accessible and least impacted by the unsaturated carbon. The advantage is multiplied over the chain of trans carbons returning to their helical conformation and so it is at the terminal points of those segments that defluorination occurs. Our observation that the site of defluorination is more strongly dependent on the geometric conformation of the molecule than on the strength of a particular C–F bond is new, although it is consistent with other results suggesting that the addition of the electron incites but does not directly cause defluorination (Fig. 5).³⁹

Fig. 5 The relaxation pathway of PFOA after the capture of an additional electron. Initially, lengthening C–C bonds cause a loss of helicity and the molecule relaxes into a straight and extended conformation wherein C–F bonds remain intact. Only regaining the compact, helical compact form delivers enough of an advantage to afford the cost of C–F dissociation.

The effect of chain length

Because the length of the helical chain segment seems to govern defluorination and because previous studies have shown a correlation between overall chain length and degradation rate, we performed the electron capture simulation on PFAS chains from C4 to C12. The graphs below chart the progression of two characteristic behaviours of the PFAS chain during the relaxation process: the left-hand vertical axis measures the dihedral angle of the first and third most distal fluorine atoms as representative of the overall helicity; the right-hand vertical axis measures the bond length of the terminal C–F bond. The same method was applied to a set of carboxylates and sulfonates to assess the impact of the head group on the observed trends.

Carboxylates

In the short (C4–C6) chain carboxylates, the repulsion created by the additional electronic charge in the anti-bonding orbital on the carbon backbone produces little change in helicity; the combination of enthalpic C–C bond stretching and entropic freedom is insufficient to overcome helicity and cannot pay the energetic cost of fluoride dissociation (Fig. 6).

Fig. 6 The results of simulated electron capture on C5 perfluorinated carboxylate on the helicity and terminal C–F bond length, result is typical for C4–C6. Each of the short-chain molecules stabilize the −2 state without inducing a change in helicity or fluorine dissociation.

Scanning the energies associated with lengthening the terminal C–F bond reveals that the fluoride/zwitterionic PFAS system is still energetically favoured; however, the reaction pathway contains an activation step to reach an unfavourable transition state before it can achieve fluoride dissociation. Molecular geometry remains kinetically frustrated in the elongated, −2 oxidation state without additional energy input.

The activation energy was calculated as the energy difference between the optimized meta-stable state and the transition state determined by QST3 and Berny TS optimization. The amount of energy required decreases as the length of the carbon chain increases, with C4 requiring the most and C6 the least. At 33.2 kJ mol⁻¹ and 17.3 kJ mol⁻¹ respectively, the C4 and C5 chains are unlikely to overcome the activation energy at standard temperatures; C6 should obtain 4.2 kJ mol⁻¹ from its environment with sufficient probability that the reaction mechanism should be achievable under standard conditions, although at a reduced rate of reaction compared to the lengths that follow (Table 2).

Table 2 Energy required to move from the meta-stable point to the transition state along the reaction pathway that releases a fluoride from the terminal carbon

Carbon atoms	Activation energy (kJ mol^−1)	Terminal C–F bond length (Å)
C4	33.18	1.52642
C5	17.34	1.45511
C6	4.19	1.38710

---

From C7 to C9, no significant activation energy is required: relieving the bond elongation caused by electron capture provides a sufficient energetic benefit to pay the enthalpic cost of fluoride release. The mechanism occurs as described above: the chain lengthens and straightens before regaining helicity in concert with terminal fluoride dissociation. The C8 molecule PFOA lies in the centre of this band and its progression through the reaction mechanism provides the clearest example (Fig. 7).

Fig. 7 The results of simulated electron capture on C8 perfluorinated carboxylate on the helicity and terminal C–F bond length, result is typical for C7–C9. Each of the medium-chain molecules elongate and straighten to a near zero dihedral angle/helical character before regaining their compact helical geometry through release of a fluoride from the terminal carbon.

The first effect of electron capture is the elongation and straightening of the carbon backbone, shown in the figures that follow as the movement toward zero of the dihedral angle between fluorines on the nth and (n − 2)th carbons. Lengthening of the terminal C–F bond signals the transfer of the extra electron from the carbon backbone onto the dissociating fluorine, thus removing charge from the antibonding orbital and allowing the structure to relax back into its compact, helical geometry.

The end state for these three structures is a near-return to the initial fluorine dihedral angles and loss of the terminal fluorine as a fluoride ion.

Calculation of the Mulliken partial charges at each step of the PFOA fluoride dissociation simulation illustrates how electronic charge distribution changes through the fluoride release process (Table 3). The first panel shows the partial charge distribution before and after addition of the extra electron. Before the molecular geometry adapts to the additional electron the charge is concentrated along the carbon backbone.

Table 3 PFOA partial charge distribution during the changes to molecular geometry induced by electron capture, assuming instantaneous movement of the electron from its insertion point to the lowest unoccupied molecular orbital before any changes to molecular geometry have had time to react. Charge distribution runs from −0.75 (bright red) to +1.25 (bright green)

A. PFOA charge distribution before electron capture

B. PFOA charge distribution immediately following electron capture

C. Charge distribution at the metastable elongated linear state

D. Charge distribution at the transition towards regaining helicity

E. Charge distribution at the end point of the reaction

---

The charge concentration here is centred about C6. As mentioned above, explicit modeling of the interaction between PFOA and a hydrated electron indicates an insertion point near the carboxylate head group. Nevertheless, the central region of the carbon backbone provides the most energetically favourable molecular orbital and so we can invoke the assumption of instantaneous intramolecular electron motion to find it there before atomic motion has had a chance to react to a specific point of capture. As the carbon bonds lengthen, charge becomes more evenly distributed along the chain. This point is equivalent to the local minimum at which the relaxation of the shorter chain molecules halts. Next we see the movement across the transition state and the beginning of dissociation. When the simulation ends at the optimized stable state, the charge distribution is moderate along the carbon chain, now including the terminal carbon. By withdrawing the additional charge onto a fluoride ion the process reduces the positive charge concentrated on the carbon atom.

These middle-length chains represent the thermodynamic ‘Goldilocks zone’: there are enough carbon atoms that the additional charge in the anti-bonding orbital is sufficient to overcome the C–F bond enthalpy but not so many carbons that delocalization and flexibility offset the effect.

However, in C10, C11, and C12 the number of carbons lengthens the chain enough to permit stabilization of the additional electron by two complementary mechanisms: decreasing the charge concentration and by increasing mechanical flexibility. First, the anti-bonding orbital is distributed across a greater number of carbon centres. One additional charge no longer offers enough repulsion to extend and straighten the entire chain. The loss of helicity is limited and only significant toward the terminal end; the carbon chain near the functional head group retains its helical conformation.

The additional charge is less concentrated and accordingly has less impact on bond breaking. Second, like all rigid rods its stiffness is inversely proportional to its length. While the additional charge may not be sufficient to fully elongate the chain, it still loosens the carbon–carbon bonding further increases the chain's flexibility (Fig. 8).

Fig. 8 The results of simulated electron capture on C10–C12 perfluorinated carboxylates on the helicity and terminal C–F bond length. Each of these longer-chain molecules are able to stabilize in the elongated and straightened conformation without defluorination due to the larger number of carbons supporting the additional charge and the entropy gained by the flexibility.

The greater range of motion opens a greater number of accessible vibrational modes, increasing the system's entropy. This entropic benefit decreases the marginal entropy that the system could obtain from fluoride release. The delocalization and flexibility factors would act in a similar fashion for chain lengths of C13 and greater so for this reason we would expect similar results.

Sulfonates

Others have described differences in degradation mechanism and kinetics between carboxylate and sulfonate species with the same number of carbons in their perfluorinated tail.⁶⁰

Certain predictions of which fluorine is the most likely leaving group are based solely on calculations of bond dissociation energy which, as described and demonstrated above, ignores geometric and entropic effects to their detriment. The simulations of relaxation post-electron capture presented here show that sulfonate species generally follow the same trends as the carboxylate although the change in head group affects the chain lengths at which the ‘Goldilocks zone’ begins and ends. The differences are due to both electronic and mechanical properties.

Only the C4 sulfonate was able to stabilize the additional electron without significant geometry change (Fig. 9(a)).

Fig. 9 Typical charts of helicity and C–F bond length in short (C4 only), middle (C5–C8), and long (C9–C12) perfluorinated sulfonates. The sulfonate follows the identical trend as the carboxylate although the location of the segmentation has changed as a result of the change in functional group.

Spontaneous defluorination to recover helicity begins at C5 and continues through C8. These simulations results suggest that the sulfonate may be more susceptible to degradation after the capture of the additional electron at shorter change lengths due to the sulfur's effect of the molecular electronic structure. Although the head group also has a strong influence on electron insertion location and rate which these simulations do not capture, so the trend is not sufficient to draw conclusions about the overall comparative defluorination rate in bulk aqueous solution^38,42 (Fig. 9(b)).

Sulfonate chain lengths of C9 or greater are able to stabilize the additional electron in the extended conformation. Since the C9 sulfonate is physically as long as the C10 carboxylate it is reasonable that their mechanical flexibility and therefore the entropic advantage gained through that flexibility would be comparable (Fig. 9(c)).

Conclusions

Simulation

Simulating the changes in molecular geometry that follow reduction by instantaneous electron capture by employing established optimization techniques offers important advantages over the static model analysis that has been done in previous work. Primarily, the calculation of bond energies, absent any dynamic geometric changes, neglects the possible contribution of entropy on the dissociation reaction. Interpreting the optimization pathway as a physically-meaningful relaxation pathway enables greater sensitivity to how the interactions of electronic and molecular structure promote or resist defluorination.

Dynamic approaches are also beginning to show the larger role that kinetics and molecular geometry contributes to electron capture reactions.³⁷ Provided that the limitations of the different methods are respected and the appropriate tests to ensure concordance with experiment are successful, complementary application of modelling and simulation invites a holistic investigation of the changes that occur following electronic restructuring. While this study presents the aftereffects of reduction, this method could be applied equally well to any process for which the Born–Oppenheimer approximation could be reasonably justified including oxidation or a prolonged excited state.

Helicity and PFAS degradation

The changes in entropy produced through changes in molecular geometry has been an overlooked tool for enabling defluorination and PFAS degradation. Differences noted by others in the difficulty of breaking down branched PFAS or mixed hydrogenated and polyfluorinated species could be re-examined through an entropy lens to search for trends that are less obvious when considered through a ‘bond dissociation energy first’ approach.

Because entropy may play an important role in a degradation technique's chain length dependence, environmental conditions also become relevant consideration. The impact of entropic interventions is temperature and pressure dependent. Temperature may play several roles, including changes to the number and ratios of accessible cis/trans conformations, the accessibility and intensity of vibrational modes affecting C–F bond dissociation, and the degree to which the change in entropy can affect spontaneous defluorination.

The elongation of the carbon chain that the simulation results indicate is prerequisite to fluoride release indicates that the pressure exerted on the molecule will also impact reaction rates. An environment in which more energy must be expended to reach or maintain the extended conformation, and in which bending degrees of freedom are limited by external forces, is one in which the defluorination ‘goldilocks zone’ should reach into higher chain lengths because what are mechanical advantages in free space now become disadvantages. Pressurization of the aqueous PFAS solution may be impractical for field decontamination work, but as our previous work has shown confinement within nanoscale reactors can perform the same function while the bulk solution remains at atmospheric pressure.⁶¹ Altering reaction conditions, solvation, catalysis, and nanoscale confinement alters the molecular freedom, which may in turn alter PFAS susceptibility to decontamination mechanisms which rely on changes in geometry to proceed. As with representational and theoretical treatments, we expect that experimental treatments will benefit from the greater number and variety of approaches to the problem.

Author contributions

Cécile Malardier-Jugroot: supervision, resources, funding acquisition, review and editing Matt McTaggart: methodology, investigation, visualization, witing original draft.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was undertaken, in part, thanks to funding from the Canada Research Chairs Program and the NSERC Discovery program. M. M. would like to thank Mr D. Patch and Ms N. O’Connor for useful early discussions. The authors also wish to recognize the crucial contributions made by our anonymous reviewers and PCCP associate editor Lars Goerigk.

References

1. R. C. Buck, J. Franklin, U. Berger, J. M. Conder, I. T. Cousins, P. de Voogt, A. A. Jensen, K. Kannan, S. A. Mabury and S. P. van Leeuwen, Integr. Environ. Assess. Manage., 2011, 7, 513–541.
2. I. T. Cousins, J. C. DeWitt, J. Glüge, G. Goldenman, D. Herzke, R. Lohmann, C. A. Ng, M. Scheringer and Z. Wang, Environ. Sci.: Processes Impacts, 2020, 22, 2307–2312.
3. US EPA, Drinking water health advisory for perfluorooctanoic acid (PFOA) CASRN 335-67-1, US EPA, 2022.
4. US EPA, Drinking Water Health Advisory: Perfluorooctane Sulfonic Acid (PFOS) CASRN 1763-23-1, US EPA, 2022.
5. R. A. Dickman and D. S. Aga, J. Hazard. Mater., 2022, 436, 129120.
6. D. Lu, S. Sha, J. Luo, Z. Huang and X. Zhang Jackie, J. Hazard. Mater., 2020, 386, 121963.
7. S. Verma, R. S. Varma and M. N. Nadagouda, Sci. Total Environ., 2021, 794, 148987.
8. S. Verma, T. Lee, E. Sahle-Demessie, M. Ateia and M. N. Nadagouda, Chem. Eng. J. Adv., 2023, 13, 100421.
9. X. Lei, Q. Lian, X. Zhang, T. K. Karsili, W. Holmes, Y. Chen, M. E. Zappi and D. D. Gang, Environ. Pollut., 2023, 321, 121138.
10. B. N. Nzeribe, M. Crimi, S. Mededovic Thagard and T. M. Holsen, Crit. Rev. Environ. Sci. Technol., 2019, 49, 866–915.
11. R. Mahinroosta and L. Senevirathna, J. Environ. Manage., 2020, 255, 109896.
12. S. C. E. Leung, P. Shukla, D. Chen, E. Eftekhari, H. An, F. Zare, N. Ghasemi, D. Zhang, N.-T. Nguyen and Q. Li, Sci. Total Environ., 2022, 827, 153669.
13. D. M. Wanninayake, J. Environ. Manage., 2021, 283, 111977.
14. M. Gar Alalm and D. C. Boffito, Chem. Eng. J., 2022, 450, 138352.
15. E. B. Esfahani, F. A. Zeidabadi, S. Zhang and M. Mohseni, Environ. Sci.: Water Res. Technol., 2022, 8, 698–728.
16. J. Cui, P. Gao and Y. Deng, Environ. Sci. Technol., 2020, 54, 3752–3766.
17. D. Leonello, M. A. Fendrich, F. Parrino, N. Patel, M. Orlandi and A. Miotello, Appl. Sci., 2021, 11, 8458.
18. Z. Zhang, D. Sarkar, J. K. Biswas and R. Datta, Bioresour. Technol., 2022, 344, 126223.
19. H. Cao, W. Zhang, C. Wang and Y. Liang, Ultrason. Sonochem., 2020, 69, 105245.
20. M. A. Uriakhil, T. Sidnell, A. De Castro Fernández, J. Lee, I. Ross and M. Bussemaker, Chemosphere, 2021, 282, 131025.
21. F. Dixit, R. Dutta, B. Barbeau, P. Berube and M. Mohseni, Chemosphere, 2021, 272, 129777.
22. B. D. Fennell, S. P. Mezyk and G. McKay, ACS Environ. Au, 2022, 2, 178–205.
23. B. Trang, Y. Li, X.-S. Xue, M. Ateia, K. N. Houk and W. R. Dichtel, Science, 2022, 377, 839–845.
24. N. J. Battye, D. J. Patch, D. M. D. Roberts, N. M. O’Connor, L. P. Turner, B. H. Kueper, M. E. Hulley and K. P. Weber, Sci. Total Environ., 2022, 835, 155506.
25. U. Rao, Y. Su, C. M. Khor, B. Jung, S. Ma, D. M. Cwiertny, B. M. Wong and D. Jassby, Environ. Sci. Technol., 2020, 54, 10668–10677.
26. R. K. Singh, S. Fernando, S. F. Baygi, N. Multari, S. M. Thagard and T. M. Holsen, Environ. Sci. Technol., 2019, 53, 2731–2738.
27. D. Palma, D. Papagiannaki, M. Lai, R. Binetti, M. Sleiman, M. Minella and C. Richard, Molecules, 2021, 26, 924.
28. A. J. Lewis, T. Joyce, M. Hadaya, F. Ebrahimi, I. Dragiev, N. Giardetti, J. Yang, G. Fridman, A. Rabinovich, A. A. Fridman, E. R. McKenzie and C. M. Sales, Environ. Sci.: Water Res. Technol., 2020, 6, 1044–1057.
29. M. J. Johnson, W. A. Maza, V. M. Breslin, D. R. Boris, T. B. Petrova and S. G. Walton, Plasma Sources Sci. Technol., 2022, 31, 085001.
30. M. J. Bentel, Z. Liu, Y. Yu, J. Gao, Y. Men and J. Liu, Environ. Sci. Technol. Lett., 2020, 7, 351–357.
31. W. Wang, Y. Chen, G. Li, W. Gu and T. An, Environ. Sci.: Water Res. Technol., 2020, 6, 1638–1648.
32. Z. Liu, Z. Chen, J. Gao, Y. Yu, Y. Men, C. Gu and J. Liu, Environ. Sci. Technol., 2022, 56, 3699–3709.
33. N. O’Connor, D. Patch, D. Noble, J. Scott, I. Koch, K. G. Mumford and K. Weber, Sci. Total Environ., 2023, 888, 164137.
34. D. Patch, N. O’Connor, I. Koch, T. Cresswell, C. Hughes, J. B. Davies, J. Scott, D. O’Carroll and K. Weber, Sci. Total Environ., 2022, 832, 154941.
35. T. Szreder, J. Kisała, A. Bojanowska-Czajka, M. Kasperkowiak, D. Pogocki, K. Bobrowski and M. Trojanowicz, Chemosphere, 2022, 295, 133920.
36. B. D. Fennell, D. Fowler, S. P. Mezyk and G. McKay, Environ. Sci. Technol., 2023, 57, 7634–7643.
37. C. Sandoval-Pauker, S. Yin, A. Castillo, N. Ocuane, D. Puerto-Diaz and D. Villagrán, ACS EST Eng., 2024, 4(1), 66–95.
38. D. J. Van Hoomissen and S. Vyas, Environ. Sci. Technol. Lett., 2019, 6, 365–371.
39. W. A. Maza, V. M. Breslin, J. C. Owrutsky, B. B. Pate and A. Epshteyn, Environ. Sci. Technol. Lett., 2021, 8, 525–530.
40. M. J. Bentel, Y. Yu, L. Xu, Z. Li, B. M. Wong, Y. Men and J. Liu, Environ. Sci. Technol., 2019, 53, 3718–3728.
41. S. S. R. K. C. Yamijala, R. Shinde and B. M. Wong, Phys. Chem. Chem. Phys., 2020, 22, 6804–6808.
42. S. Biswas, S. S. R. K. C. Yamijala and B. M. Wong, Environ. Sci. Technol., 2022, 56, 8167–8175.
43. S. Biswas and B. M. Wong, ACS EST Eng., 2024, 4(1), 96–104.
44. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
45. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
46. A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 123, 154101.
47. R. N. Schilberg, S. Wei, S. Twagirayezu and J. L. Neill, Chem. Phys. Lett., 2021, 778, 138789.
48. A. V. Marenich, W. Ding, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. Lett., 2012, 3, 1437–1442.
49. C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. A, 2006, 110, 2493–2499.
50. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
51. K. D. Jordan, V. K. Voora and J. Simons, in Thom H. Dunning, Jr.: A Festschrift from Theoretical Chemistry Accounts, ed. A. K. Wilson, K. A. Peterson and D. E. Woon, Springer, Berlin, Heidelberg, 2015, pp.85–99.
52. M. Born and R. Oppenheimer, Ann. Phys., 1927, 389, 457–484.
53. X. Li and M. J. Frisch, J. Chem. Theory Comput., 2006, 2, 835–839.
54. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2019.
55. M. Thodika, M. Fennimore, T. N. V. Karsili and S. Matsika, J. Chem. Phys., 2019, 151, 244104.
56. J. M. Herbert, Reviews in Computational Chemistry, John Wiley & Sons, Ltd, 2015, vol. 28, pp.391–517.
57. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
58. T. A. Halgren, J. Comput. Chem., 1996, 17, 490–519.
59. J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213.
60. J. Cui, P. Gao and Y. Deng, Environ. Sci. Technol., 2020, 54, 3752–3766.
61. M. McTaggart, X. Li, M. Groves, V. Shah, M. Jugroot and C. Malardier-Jugroot, J. Chem. Phys., 2021, 154, 174903.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04973f

---