Unraveling the role of superalkalis in modulating the static and dynamic hyperpolarizabilities of emerging calix[4]arenes

Abstract

Calixarenes, as novel organic materials, can play a pivotal role in the development of high-performance nonlinear optical materials due to the ease of design and fabrication. In this study, DFT simulations were employed to investigate the geometric, electronic, and NLO responses of calix[4]arene doped with Li₃O, Na₃O, and K₃O superalkalis. The computed values of the vertical ionization energies and interaction energies indicate the chemical and thermodynamic stabilities of the targeted M₃O@calix[4]arene complexes. The corresponding energy gaps (2.01 to 3.49 eV) are notably reduced, indicating the semiconductor nature of the materials. Surprisingly, the M₃O@calix[4]arene complexes exhibit transparency in the UV/visible range as the absorption peaks are shifted in the near infrared (NIR) region. The highest values of 5.9 × 10⁵ a.u. and 2.3 × 10⁸ a.u. for the respective first and second hyperpolarizabilities are observed for Na₃O@calix[4]arene. Furthermore, the Na₃O@calix[4]arene complex exhibits maximum values of 2.3 × 10⁵ a.u. for second harmonic generation (SHG) and (K₃O@calix[4]arene) 2.3 × 10⁶ a.u. for the electro-optical Pockels effect (EOPE) at 1064 nm. Similarly, approximations are made for the dynamic second hyperpolarizability coefficients (EOKE and EFISHG) at different wavelengths. Notably, the Na₃O@calix[4]arene complex demonstrates the highest quadratic nonlinear refractive index (n₂) of 9.5 × 10⁻¹⁵ cm² W⁻¹ at 1064 nm. This research paves the way for the development of stable calix[4]arenes doped with superalkalis, leading to an improved nonlinear optical (NLO) response.

---

1. Introduction

The design of novel nonlinear optical materials with a high NLO response has been the subject of numerous theoretical and practical studies for several decades. This is primarily due to their potential for enhanced technical applications in photonic and optical systems.^1,2 Several strategies for improving the NLO response have been described for a variety of organic and inorganic materials. These include the use of donor–acceptor bridges,³ donor π conjugated bridge systems,⁴ extended π conjugation,⁵ distorted π electron systems,⁶ diffuse excess electrons,^7,8 metal atom doping, design of metal–ligand frameworks based on charge transfer from the metal to ligand,⁹etc. The introduction of diffuse excess electrons is a well-known and extensively used strategy in organic NLO materials.¹⁰ In many theoretical studies, a significant number of nonlinear optical materials with large hyperpolarizability using the diffuse excess electron strategy have been reported.¹¹ The finding of alkali metals dissolved in gaseous ammonia can be traced back to the earliest investigation of systems containing diffuse excess electrons.^12,13 After this, a substantial number of studies emphasized theoretically related systems such as electrides,^14,15 trimer of water (H₂O)₃¹⁶ and alkalides.¹⁷ This revealed that most of these systems exhibit remarkable NLO responses with a noticeably large first hyperpolarizability.¹⁶

Alkalides are a special type of ionic salts in which alkali metals occupy the anionic sites and have excess electrons associated to them.¹⁸ Dye et al. reported the first prepared alkalide (Na⁺(cryptand-[2.2.2]Na⁻)).¹⁹ Apart from alkalides, another novel class of compounds, superalkalides, was discovered and has an obvious better NLO response as alkalides.²⁰ Superalkalides have very low ionization energies and are even more reactive than alkalides due to their higher electron affinity.²¹ Li et al. investigated the NLO properties of alkalides (L–M–L–M′) and superalkalides (). The results revealed that the highest β₀ was observed in the case of the L–K–L–LiO₃ complex (3.42 × 10⁶ a.u.).²²

A variety of methods can be employed to introduce excess electrons into a material. One approach is to use electron-donating groups or dopants (alkali metals or superalkali units), which can introduce extra electrons into the material.²³ Superalkalis are a class of “superatoms” that have excess electrons as compared to the constituent alkali metal atoms, giving them unique chemical and electronic properties.²⁴ They have remarkable features (such as diffuse excess electrons) due to their lower IPs (ionization potentials) than alkali metal atoms.²⁵ Doping with superalkalis will lead to a considerable increase in electron transport and a reduction in the HOMO–LUMO energy gap. Recently, significant advances have been made in superalkali doped complexes in the field of optoelectronics.²⁶ It has been reported that superalkali doped dyads (M₃O–BC₅₉), which are donor–acceptor (DA) chromophores, have outstanding stability as well as substantial first hyperpolarizability and are good candidates for second-order NLO materials.²⁷ Similarly, Kosar et al. observed that superalkali doping not only affects the electrical characteristics of graphdiyne (GDY), but also has a significant impact on the NLO properties.²⁸ In another DFT investigation, the NLO properties of C₂N doped with Li₃O have been studied. All the doped structures show a higher NLO response than the undoped C₂N nanosheet.²⁹ The effect of superalkali doping on macrocyclic [hexa-]thiophene complexes has been studied by Mehmood et al. Among all the complexes, Na₃O@6CT with a hyperpolarizability value of 5 × 10⁴ a.u. has the highest NLO response.³⁰ Similarly, in another study, Ayub et al. have studied Li₃O@[12-crown-4]M complexes and all the doped complexes exhibited significant NLO response compared to the undoped moiety.³¹ Noormohammadbeigi et al. reported the influence of superalkali (Li₃O, Na₃O, and K₃O) doping on the C₂₀ fullerene and the studied Na₃O@C₂₀ fullerene showed high first hyperpolarizability (2.3 × 10⁴ a.u.).³² Provided the foregoing discussions, it is evident that superalkali doping is a viable approach for enhancing the nonlinear optical response of the system.

In the realm of nonlinear optics (NLO), organic materials have taken the lead over inorganic counterparts. This shift is attributed to their lower dielectric constants,³³ ultrafast response times, enhanced nonlinear optical susceptibilities,³⁴ high laser damage thresholds,³⁵ improved processability³⁶ and wide transparency ranges.³⁷ Furthermore, organic NLO materials can undergo significant chemical modifications, particularly those that enhance specific physical characteristics.³⁸ Despite these advancements, significant efforts are currently underway to further enhance the NLO response of various nanomaterials. Calixarenes are organic compounds having 3D structures. These are cyclic oligomers formed by combining phenols and formaldehyde. The name “calixarenes” is attributed to the hydrophobic cup-like cavity formed by intramolecular hydrogen bonding among phenolic hydroxyls. They possess unique properties such as the ability to serve as excellent host molecules,³⁹ the ability to be adapted to form reversible complexes,⁴⁰ and applicability in separation chemistry.⁴¹ They have a wide range of applications in different areas like in the synthesis of metal nanoparticles, the manufacturing of sensors, nonlinear optics, etc. Different classes of calixarenes such as calix[4]arene, calix[5]arene, calix[6]arene, and calix[8]arene have been reported.⁴² The structural modifications in the calix[4]arene (CX [4]) structure have been investigated by many groups to check its impact in different applications.^43,44 For instance, the CX [4] skeleton was fused with a cycloparaphenylene (CPP) ring to produce a new hybrid host. The optoelectronic and structural properties of the calix–CPP hybrid host were also studied. The results revealed an unexpected selectivity of calix–CPP for Li⁺ over Na⁺ due to the more favorable interaction through the CPP bridge and its greater size.¹³ Paterson et al. studied the ability of CX [4] to bind to a range of small guest molecules. It has been found that coordination to the lower-rim of CX [4] with both Mn³⁺ (quartet) and Fe³⁺ (quartet) causes greater binding energies of CX [4] toward these guest molecules. Binding energies were investigated for a range of metal types, spins, and oxidation states.⁴⁵ The effect of doping of alkali metal atoms (Li, Na, and K) on the structural, electrical, and nonlinear optical properties of CX [4] has also been studied.⁴⁶ The polarizability and first hyperpolarizability of the CX [4] molecule are dramatically enhanced by alkali metal atoms. The Li@calix[4]arene complex has the greatest increase in NLO response (9.3 × 10⁴ a.u.).⁴⁷ In a study carried out by Hou et al., it has been shown that the impact of a single alkali metal doping considerably increases the first hyperpolarizability of the t-Bu-calix[4]arene molecule.⁴⁸

However, despite the abundance of superalkali-based nanomaterial advancements, there is a lack of sufficient exploration in the field of nonlinear optical (NLO) properties, especially concerning CX [4]. To the best of our knowledge, no investigation has been conducted on how superalkali clusters impact the geometrical, electrical, and NLO characteristics of calix[4]arenes. As a result, our keen interest lies in exploring the superalkalide properties and NLO response of superalkali-doped CX [4]. The current study focuses on the doping of selected superalkali (SA) subunits (Li₃O, Na₃O, and K₃O) on CX [4], presenting a novel range of NLO materials with potential applications in nanotechnology.

2. Computational details

The pristine calix[4]arene (CX [4]) molecule (C₂₈H₂₄O₄) and superalkali-doped calix[4]arenes have undergone geometry optimization using the ωB97XD functional and the 6-31+G(d,p) basis set in an unrestricted formalism. The ωB97XD long-range corrected hybrid functional is employed for the prediction of non-covalent interactions, particularly in systems that encompass doping.⁴⁹ Following the geometry optimization, frequency calculations have been conducted to verify that the optimized geometries are real minima on the potential energy surface (PES). In this study, no scale factor to the frequencies has been applied when calculating the zero-point vibrational energy (ZPVE) or enthalpy corrections (Delta H). The convergence criteria for self-consistent field (SCF) calculations are as follows: a requested convergence of 1.00D-08 on the RMS density matrix, a requested convergence of 1.00D-06 on the MAX density matrix, and a requested convergence of 1.00D-06 on the energy. The standard default convergence criteria for optimization were set as follows: 0.00045 for the maximum force, 0.0003 for the root mean square (RMS) force, 0.0018 for maximum displacement, and 0.0012 for the root mean square (RMS) displacement. The ωB97XD/6-31+G(d,p) level of theory has been employed to investigate the interaction energies (E_int), NBO (natural bond orbital) charges, frontier molecular orbital (FMO) energy gaps, and vertical ionization energies (VIEs). The following formula can be utilized to compute the interaction energy:where E_{calix[4]arene}, E_M3O and E_{M3O-calix[4]arene} represent the energies of the pristine calix[4]arene, superalkalis (Li₃O, Na₃O, and K₃O) and superalkali doped calix[4]arene, respectively.

Other studies are also carried out by using the ωB97XD functional in combination with the 6-31+G(d,p) basis set, including density of states (DOS), non-covalent interaction (NCI), and quantum theory of atoms in molecules (QTAIM) analyses, and the Multiwfn⁵⁰ and VMD⁵¹ software packages are employed. The absorption studies are performed at the TD-ωB97XD/6-31+G(d,p) level of theory. The CAM-B3LYP⁵² functional and the 6-31+G(d,p)⁵³ basis set are used to determine the linear and nonlinear optical parameters including polarizability and second order polarizability (static first hyperpolarizability). The static hyperpolarizability of superalkali doped calix[4]arenes is also computationally tested by using the CAM-B3LYP functional. Based on previously reported results, the aforementioned level of theory is suitable to be employed to analyze the electro-optical characteristics of superalkali-doped systems.^27,54 The default integral grid for SCF energies is set to UltraFine, which employs 99 radial and 590 angular points. For the coupled perturbed equations, a grid that is lesser by two steps is utilized. This default grid is SG1, consisting of 50 radial and 194 angular points. The finite electric field is employed to estimate higher derivatives. The Polar keyword is utilized to generate analytic first, second, and third derivatives with respect to the external field. Gamma (which involves the 4^th derivative of energy with respect to the electric field) is calculated using differences of third derivatives with a finite electric field. The default value for this field is 0.000333 a.u. This methodology strikes a balance between numerical accuracy and computational efficiency, ensuring robust results while optimizing computational resources. The optical polarizability (α₀), dipole moment (μ₀), and first hyperpolarizability (β₀) can all be calculated using the following formulae:

μ₀ = [μ_x² + μ_y² + μ_z²]^1/2 (2)

β₀ = [β_x² + β_y² + β_z²]^1/2 (4)

Here, β_x = β_xxx + β_xyy + β_xzz, β_y = β_yyy + β_yzz + β_yxx, and β_z = β_zzz + β_zxx+ β_zyy are exchangeable Kleinman's symmetry type hyperpolarizability tensors.

Additionally, calculations are performed to determine the β_vec (beta vector) and γ (second hyperpolarizability) of SA-doped calix[4]arenes.

The mathematical expression for β_vec is as follows:

The equation used to calculate the average (isotropic) second hyperpolarizability (〈γ〉) is as follows:⁵⁵

To further evaluate the practical applicability of the superalkali doped CX [4], the dynamic first hyperpolarizability (β_(ω)) computations at laser wavelengths (532 nm and 1064 nm) are performed as well. The β_(ω) can be obtained using the following equation:⁵⁶

At the same level of theory, the γ_(ω) (dynamic second hyperpolarizability) of superalkali-doped calix[4]arenes is also estimated. The nonlinear refractive indices of M₃O@calix[4]arene complexes are computed as follows:⁵⁷

n₂ (cm² W⁻¹) = 8.23 × 10⁻²³γ^DFWM (8)

Furthermore, the degenerate four-wave mixing (DFWM) using the relation provided by Tarazkar et al.⁵⁸ is determined:

Gaussian 16⁵⁹ software is used for all DFT computations, and GaussView 6.1.1⁶⁰ software is utilized for illustration purposes.

3. Results and discussion

3.1 Optimized geometries and stabilities

It has been found that the 3D macrocycle CX [4], which consists of four phenolic oxygen atoms, is a neutral ligand that may bind to metal cations.⁶¹ In the CX [4] host, the 1,3-alternate structure is considerably preferred, and pure CX [4] possesses the C₂ symmetry. The decreased repulsions between the lone pairs of oxygen atoms are therefore assumed to be a contributing factor for the conformational stability of arene moieties.⁶² Due to the presence of methylene linkages in CX [4], all isolated benzene rings produce a cavity that has a box-like shape. The optimized CX [4] has O–H, O–C and C–C (methylene linked) bond distances of 0.98 Å, 1.37 Å, and 1.51 Å, respectively, which are consistent with previously reported bond lengths.⁶¹ Furthermore, the tailored Li₃O superalkali has a Li–O bond length of 1.69 Å, which nearly approaches the experimentally determined Li–O bond distance.⁶³ From these results, it can be observed that the ωB97XD/6-31G+(d,p) level of theory is valid for the current study. The optimized stable geometries of CX [4] along with superalkalis (Li₃O, K₃O, and Na₃O) are displayed in Fig. 1.

Fig. 1 Optimized structures of pure calix[4]arene (CX [4]) along with Li₃O, Na₃O & K₃O superalkalis.

The Li₃O, Na₃O, and K₃O superalkalis are doped at CX [4] in the present work to investigate the different interaction sites. The various sensitive sites of CX [4] enable several possible interaction orientations. All of these orientations have been studied. There were totally four orientations taken into consideration during superalkali doping on CX [4], including two horizontal patterns (bottom and top) and two vertical patterns (bottom and top). Since most of the structures were distorted such as in the top position and the vertical bottom positions were merged to the horizontal ones, only the horizontal bottom position with the oxygen atoms of the complexant (CX [4]) has been taken into account for further analyses. A small change in the dihedral angle of the O₁–O₂–O₃–O₄ cavity of CX [4] indicates that the structural integrity of the system remains unaffected by the doping of superalkalis. The Li–O, Na–O, and K–O bond distances of the superalkalis in the proposed M₃O@calix[4]arene (where M₃O = Li₃O, Na₃O and K₃O) are also 1.67, 2.01, and 2.40 Å, respectively, which are comparable to the values of the distinct superalkalis depicted in Fig. 1. The M₃O subunits retain their structural integrity as a result of being incorporated into CX [4], with barely slight modifications to the geometric features of the superalkali subunits. The positive values of the first frequencies of the M₃O@calix[4]arene complexes (Table 1) indicate the presence of true local minima on the PES (potential energy surface). The resulting optimized structures of SA-doped heteroatomic macrocycles are illustrated in Fig. 2.

Table 1 Optimized superalkali doped calix[4]arenes with the first frequencies ν₁ (cm⁻¹), symmetries, interaction distances (Å), E_int (kcal mol⁻¹), Gibb's enthalpies of formation (kcal mol⁻¹) and VIEs (eV)

Complex	ν 1	Symmetry	I d(M–CA)	E int	ΔG	VIE
Li3O@calix[4]arene	48.87	C 1	2.3	−47.69	−34.07	3.02
Na3O@calix[4]arene	10.56	C 1	2.9	−21.83	−14.31	2.59
K3O@calix[4]arene	13.78	C 1	3.3	−18.79	−7.35	2.44

---

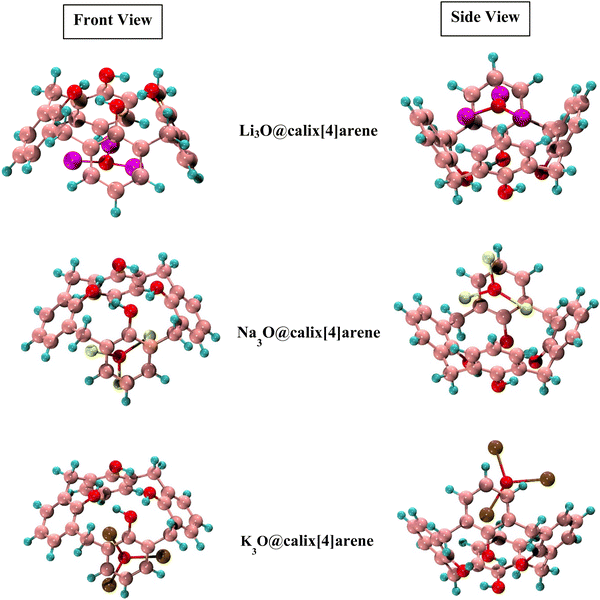Fig. 2 Optimized structures of Li₃O, Na₃O and K₃O doped calix[4]arene (CX [4]) complexes (side and front views).

The symmetry of CX [4] has changed as a result of the presence of superalkali subunits. Complexes of M₃O@calix[4]arene now display the C₁ point group, contributing to the confirmation that superalkali doping may alter the substrate symmetry which corroborates prior studies.

The practical applications of nonlinear optical materials place a considerable emphasis on the stability of complexes. The key factors that define the thermal and chemical stability of any system are interaction energy (E_int) and vertical ionization energy (VIE). The interaction energy of the system indicates that any framework with particularly exothermic nature exhibits enhanced thermodynamic stability.⁶⁴ The E_int values of these superalkali-doped M₃O@calix[4]arenes are illustrated in Table 1. The stability of Li₃O@calix[4]arene, Na₃O@calix[4]arene, and K₃O@calix[4]arene complexes was evaluated by calculating their respective interaction energy (E_int) values, which were found to be −47.69, −21.83 and −18.79 kcal mol⁻¹. It was observed that Li₃O@calix[4]arene is the most stable among the three designed complexes. Lithium is in contact far more closely with CX [4] due to its smaller atomic size. This is supported by the fact that it has the shortest interaction distance (I_d), 2.3 Å, compared to all other SA@calix[4]arenes (see Table 1). With an increase in the atomic number (from Li to K), the interaction distance seems to increase monotonically. The M₃O@calix[4]arene systems are thermodynamically more stable than the previously reported M@calix[4]arene (M = Li, Na and K) complexes.⁴⁷ The reason for the high thermal stability of SA-doped systems is the low ionization potential of superalkalis than the alkali metal atoms. To attain a more comprehensive insight into the stability of the complexes, the pertinent Gibbs enthalpies of formation are also computed. These values range from −34.07 to −7.35 kcal mol⁻¹ in all superalkali doped calix[4]arene complexes (Table 1). A negative ΔG indicates that the fabrication of these complexes is spontaneous in nature and the complexes are thermodynamically stable.

The vertical ionization energy (VIE) is another factor that validates the chemical and electronic stability of complexes. A significantly large VIE value implies the chemical stability and rigidity of the systems. The SA@calix[4]arene complexes exhibit VIE values between 3.02 and 2.44 eV. The highest VIE value of 3.02 eV is observed in the case of Li₃O@calix[4]arene. The Na₃O@calix[4]arene and K₃O@calix[4]arene possessed VIEs of 2.59 eV and 2.44 eV, respectively. It is observed that, with an increase in the metal size of superalkalis, the vertical ionization energy decreases: Li₃O@calix[4]arene > Na₃O@calix[4]arene > K₃O@calix[4]arene.

3.2 Electronic properties

Frontier molecular orbital (FMO) analysis is an effective method for examining the change in the conductivity of compounds after complexation.⁶⁵ This provides comprehensive information related to the energies of the highest occupied molecular orbitals (E_HOMO), lowest unoccupied molecular orbitals (E_LUMO), and energy gaps (E_g). Pristine CX [4] has a large energy gap, which restricts its application in optoelectronic devices [3]. Doping of CX [4] with superalkalis (Li₃O, Na₃O, and K₃O) can elevate its electronic properties.

The results showed that the E_g (E_H–L) values of the complexes (Li₃O@calix[4]arene to K₃O@calix[4]arene) were considerably reduced. The primary factor responsible for the reduction in E_H–L is the creation of new HOMOs. The generation of the new HOMO is due to excess electrons, and the previously existing HOMO transforms into HOMO−1. The E_HOMO (HOMO energy), E_LUMO (LUMO energy), corresponding energy gaps, E_H–L percentage reductions, and Fermi level energies (E_FL) are indexed in Table 2.

Table 2 NBO charges Q_M3O (|e|), energies of frontier molecular orbitals (eV), HOMO–LUMO energy gaps (E_H–L in eV), % E_HL and Fermi level energies (E_FL in eV) of all complexes

Complexes	Q M3O	E HOMO	E LUMO	E H–L	% EHL	E FL
Calix[4]arene	—	−8.07	0.87	8.94	—	−3.6
Li3O@calix[4]arene	0.89	−3.24	0.25	3.49	59.7	−1.49
Na3O@calix[4]arene	−0.03	−2.64	−0.002	2.64	67.2	−1.32
K3O@calix[4]arene	−0.02	−2.25	−0.24	2.01	72.1	−1.24

---

For SA-doped systems, the HOMO–LUMO energy gaps vary from 3.49 to 2.01 eV. K₃O@calix[4]arene exhibits the highest reduction in E_H–L which is due to the low ionization potential (2.44 eV), whereas Li₃O@calix[4]arene has the lowest E_H–L reduction value, which can be attributed to the high ionization potential (3.02 eV) of the complex. These findings reveal that superalkali-doped CX [4] systems possess semiconducting properties and probably can be practiced in optoelectronics.

All the newly designed complexes have percentage reduction in E_H–L values that vary from 59.7 to 72.1%. Furthermore, the electron densities lie on the superalkalis in complexes, reflecting that the superalkali subunits have an important part in new HOMO formation. Since superalkalis have metal atoms of different sizes, the distribution of electron density on HOMOs and LUMOs and superalkalide properties also vary for the corresponding complexes, as shown in Fig. S1 (ESI†).

3.3 NBO analysis

Natural bond order (NBO) analysis has been employed for calculating NBO charges in order to estimate the direction and magnitude of charge transfer in SA@calix[4]arenes. The overall charge on the superalkali units (Q_M3O) is negative in the case of Na₃O@calix[4]arene and K₃O@calix[4]arene, whereas the charge on the calix[4]arene is positive, demonstrating that charge has been transferred from the substrate (calix[4]arene) towards the dopant (superalkalis) (Table 2). In accordance with Fig. S1 (ESI†), the electronic cloud of the HOMOs of Na₃O@calix[4]arene and K₃O@calix[4]arene is distributed on the entire Na₃O and K₃O structures. These intriguing complexes may have good NLO characteristics owing to their HOMOs’ electronic cloud distributions and NBO studies. The Li₃O@calix[4]arene complex exhibits a peculiar behavior since Li₃O has a net positive charge of 0.89 |e|. The charge (positive) on the superalkali (Li₃O) and the electronic density which primarily lies over CX [4] (Fig. S1, ESI†) show that the charge is being shifted from the dopant towards the substrate. As demonstrated by Biglari and colleagues, the low ionization energy and smaller size of lithium make it more convenient to release electrons, which account for the greater charge on Li₃O.⁶⁶ It concludes that Li₃O@calix[4]arene reflects an excess electron system rather than an alkalide character.

3.4 Total and partial densities of states

A density of states study was carried out to gain more insight into the frontier molecular orbitals (FMOs), electronic behavior, and energy changes of doped complexes. It is evident from the PDOS spectra that superalkalis (except Li₃O) significantly contribute to the creation of new HOMOs. In the case of Li₃O@calix[4]arene, the major contribution is from calix[4]arene as the charge is transferred from the calix[4]arene towards the superalkali (Li₃O). In comparison to the energy of pure CX [4] (−8.0 eV), the newly generated HOMOs in all complexes were in the high-energy range (between −2 and −5 eV). The PDOS and TDOS spectra of the undoped CX [4] and SA@calix[4]arene materials are shown in Fig. S2 (ESI†). It is anticipated that the newly formed HOMOs would contribute to the reduction of E_H–L (HOMO–LUMO energy gap), as well as to the enhancement of the optoelectronic performance of the designed complexes.

3.5 IRI analysis

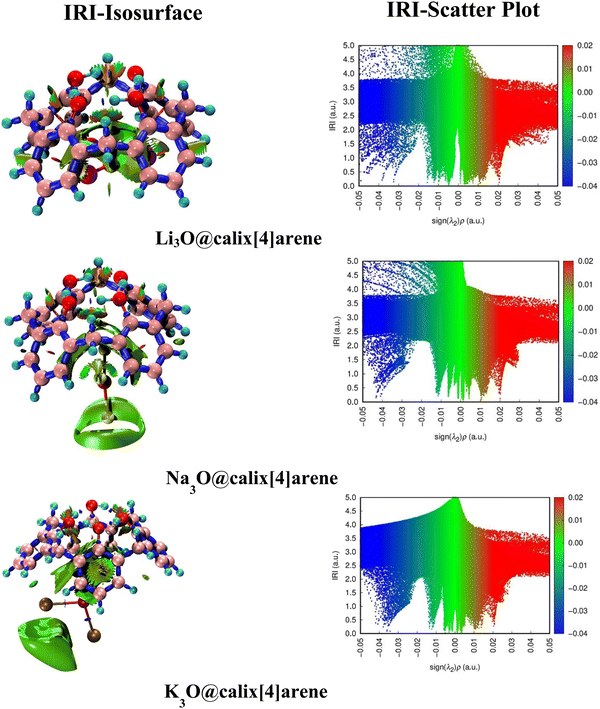
The interaction region indicator (IRI) analysis is a computational technique that enables us to gain insight into the nature of intra- and intermolecular interactions.^67,68 This is achieved by visualizing the electron density overlap between different regions. It includes 3D-isosurfaces and 2D-IRI plots. The IRI can also be written as

Therefore, interpreting 3D-isosurfaces and 2D-IRI plots gives valuable details regarding covalent and non-covalent interactions of SA@calix[4]arene complexes. In general, 3D isosurfaces portray patches of various colors such as blue, green, and red describing non-covalent, attractive, and repulsive interactions, respectively. The IRI maps with spikes at sign(λ₂)ρ < 0 indicate non-bonded interactions (repulsive), while those with sign(λ₂)ρ > 0 depict weakly bonded forces (dispersive).⁶⁷ Consequently, both (isosurfaces and IRI graphs) have been generated to examine the kind of interactions that exist between superalkalis and CX [4] as shown in Fig. 3. In the graphs of SA@calix[4]arene complexes, green patches are indicative of weak dispersive forces, particularly vdW (van der Waals) interactions. The appearance of spikes in the sign(λ₂) ρ region (around −0.04 and 0.005 a.u.) of IRI graphs in different complexes further supports the existence of non-covalent interactions (see Fig. 3).

Fig. 3 2-isosurfaces and 3D-IRI scatter plots of M₃O@calix[4]arene complexes.

3.6 QTAIM analysis

The QTAIM analysis is used for the visualization of different types of interactions, which include hydrogen bonding and van der Waals interactions.^69,70 The nature of bond critical points (BCPs) and of different interactions can be examined using topological factors, including electron density and ∇²ρ (Laplacian of electron density). The territory with maximum electron density interconnecting the atoms of a molecule is termed as the bond critical point (BCP).⁷¹ The values of different BCPs can be expressed by using the following equations:

H_r = G_r + V_r (11)

Here H_r, V_r and G_r are the electron densities of the total energy, kinetic energy and potential energy, respectively. According to Bader's virial theorem, if the electron density is greater than 0.1 a.u. and the ratio of −G(r)/V(r) is less than 0.5, then it would result in covalent interaction. Also, the values of ∇²ρ (Laplacian of electron density) have to be negative. The vdW (van der Waals) forces are represented by the ∇²ρ having a positive value and a ratio (−G(r)/V(r)) greater than 0.5 a.u. All SA@calix[4]arene complexes showcase BCPs (orange-colored bonds) connecting the atoms of superalkali and calix[4]arene (Fig. 4). Different electron density elements that have been determined from the bond critical points (BCPs) of all intended complexes are indexed in the ESI† (Table S1). Based on the calculated results, both ρ (electron density) and Laplacian electron density (∇²ρ) have positive values. Additionally, all of the complexes have a −G(r)/V(r) ratio larger than 0.5 a.u., which indicates the presence of non-covalent interactions.

Fig. 4 QTAIM topological BCPs (orange spots) of superalkali doped calix[4]arene.

3.7 UV-visible analysis

The UV-visible study has been carried out to investigate the absorbance features of the doped systems. The λ_max (maximum absorption) values, transition energy and oscillator strength (f₀) can be computed with the help of TD-DFT computations. Nonlinear optical materials must be transparent for commonly used lasers. The maximum absorption of pristine CX [4] takes place at 242 nm. The SA@calix[4]arene exhibits λ_max values of 1246–1535 nm in the near infrared (NIR) region (Table 3). This rise in absorption maxima (λ_max) is primarily attributed to the smaller E_ex (excitation energy) values of the substances (0.81–1.09 eV) in comparison to bare calix[4]arene, which has 5.11 eV of E_ex. It is inferred from the results that all SA@calix[4]arene complexes have an intense red shift (Fig. 5). These UV-visible transparent materials are compelling candidates to serve as optical materials since they have a significant role in the reinforcement of SHG (second harmonic generation).⁷²

Table 3 Transition energies (ΔE in eV), oscillator strength (f₀), absorption maxima (λ_max in nm), and major transitions

Complexes	ΔE	f 0	Excited state	λ max	Major contribution
Calix[4]arene	5.11	0.08	(E2)	242	HOMO−1 → LUMO
Li3O@calix[4]arene	0.99	0.04	(E1)	1246	HOMO → LUMO+6
Na3O@calix[4]arene	0.81	0.22	(E3)	1236	HOMO → LUMO+11
K3O@calix[4]arene	1.09	0.24	(E3)	1535	HOMO → LUMO+18

---

Fig. 5 Absorption spectra of pure and superalkali doped calix[4]arene complexes.

EDD analysis. The definition of a single-electron excitation process encompasses the movement of a solitary electron from one real space function, represented as A, to another, denoted as B. These real space functions typically refer to molecular or atomic orbitals. In the context of an excited state involving a single electron, the conventional understanding involves the transition of an electron from an occupied molecular orbital to a virtual molecular orbital.⁷³ This transition is described by the molecular orbital wavefunction (Φ) and configuration coefficient (w), which together specify the electron density difference (EDD).⁷⁴ The EDD maps for superalkali-doped calix[4]arene complexes were generated using Multiwfn.⁵⁰ In electronic structure calculations, a significant absorption band at λ_max = 1246 nm (0.99 eV) was predicted, corresponding to the HOMO → LUMO+6 transition for Li₃O@calix[4]arene. Similarly, the absorption at λ_max = 1236 nm (0.81 eV) is associated with the (HOMO → LUMO+11) transition for Na₃O@calix[4]arene. Furthermore, the intense absorption band at λ_max = 1535 nm (1.09 eV) corresponds to HOMO → LUMO+18 for K₃O@calix[4]arene. The computed EDD maps (Fig. S3, ESI†) illustrate a more concentrated isosurface localized on the rings of calix[4]arene and associated oxygen atoms in Li₃O and Na₃O. In the case of K₃O, the dense isosurface is localized on the superalkali atoms. The results of excited state analysis are also provided in Table 3.

3.8 NLO properties of SA-doped calix[4]arenes

3.8.1 Static linear and nonlinear optical properties. The nonlinear optical properties (NLOPs) of pure superalkalis have been computed. The NLOPs of the pure superalkalis lie in the range of 2.0 × 10⁵ to 8.4 × 10⁵ a.u., whereas pure calix[4]arene (556 a.u.) shows a very low NLO response. It can be envisaged that the NLO response has been induced from the superalkali to the complex formed. The principal criterion for determining the suitability of a material in nonlinear optical application is its stability, emphasizing the critical role of stability in practical use. In light of this, we conducted a thorough examination of the stability of pure superalkalis by calculating their vertical ionization potentials. The results indicate a comparatively low ionization potential, suggesting their heightened reactivity and potential chemical instability. Given the inherent chemical instability of superalkalis, their standalone use as nonlinear optical materials becomes impractical. However, it is important to note that superalkalis are known for their robust reducing properties. Notably, when these superalkali moieties interact with a complexant, such as calix[4]arene, a significant transformation occurs. The excess electrons donated from the superalkali moieties lead to the formation of complexes that are both thermodynamically and chemically stable. This electron transfer process significantly contributes to the stability of the complexes, mitigating the reactivity associated with superalkali moieties in isolation. In summary, while pure superalkalis may not be suitable as standalone nonlinear optical materials due to their inherent instability, their strong reducing properties enable them to form stable complexes when interacting with specific complexants. This induction of nonlinear optical response from the superalkali to the inherently NLO inactive symmetrical calix[4]arene and the emergence of a stable complex warrant the utility of superalkali doped calix[4]arene complexes as highly stable NLO materials. Previous studies showed that the NLO response can be enhanced by doping transition metals,⁷⁵ alkali metals,⁷⁶ alkaline earth metals⁷⁷ and superalkalis⁷⁸ with different complexants. The literature affirms that the aforementioned dopants have excess polarizable electrons.^8,79 Diffuse excess electrons reduce the energy gap (E_H–L) which enhances the NLO response of the complex. The parameters (dipole moment, polarizability and hyperpolarizability) of NLO response are computed for the designed complexes in order to determine their NLO response.^28,80 Owing to the symmetric structure of CX [4], the dipole moment (μ₀), polarizability (320 a.u.) and hyperpolarizability (556 a.u.) values are reduced. For the intended SA@calix[4]arene complexes, the calculated dipole moments vary from 6.11 to 9.44 D.

The measured α₀ values (between 493 and 733 a.u.) of the complexes are larger than the pristine CX [4] (320 a.u.). The findings reflect that the increase in the dipole moment and polarizability of the complexes is triggered by the excess electrons of superalkalis. These results are in agreement with previously reported studies.⁸¹ Meanwhile, the β₀ (static hyperpolarizability) of SA-doped complexes ranges from 7.0 × 10⁴ to 5.9 × 10⁵ a.u. The observed enhancement in the hyperpolarizability value is attributed to the surplus electrons introduced by the superalkalis, which perturb the symmetry of CX [4]. The Na₃O@calix[4]arene attained the largest β₀ (5.9 × 10⁵ a.u.), whereas the K₃O@calix[4]arene exhibited the smallest β₀ (7.0 × 10⁴ a.u.) (see Table 4). Another fact is that the β₀ is also influenced by the excitation energies of the complexes. The extent of the first hyperpolarizability increases as the excitation energies of the complexes decrease. The results indicate that the highest β₀ (5.9 × 10⁵ a.u.) was observed for Na₃O@calix[4]arene with the lowest excitation energy (0.81 eV). On the other hand, K₃O doped calix[4]arene shows the lowest β₀ (7.0 × 10⁴) due to the highest excitation energy of 1.09 eV. (Table 3). The β₀ of SA@calix[4]arene complexes aligns well when compared to already studied superalkali doped cyclic oligomers.⁸² As compared to the previously observed hyperpolarizability value of Li₃O@B₁₂N₁₂ (3.7 × 10⁴ a.u.), the β₀ value of the newly introduced superalkali-doped calix[4]arene (5.9 × 10⁵ a.u.) is substantially higher.⁸³ The β₀ value of the newly formed Na₃O@calix[4]arene complex is greater than those of the already studied complexes of AM@calix[4]arenes (9.3 × 10⁴ a.u.),⁸⁴ alkalides (Li⁺(calix[4]pyrrole)M⁻) (2.4 × 10⁴ a.u.)⁸⁵ and superalkalides () (9.1 × 10⁴ a.u.).²⁴ Apart from that, nonlinear optical prototypes involving p-nitroaniline (p-NA) and urea are also used to compare the β₀ of the designed complexes. Urea and p-nitroaniline have respective β₀ values of 43 a.u.⁸⁶ and 1.2 × 10³ a.u.⁸⁷ In contrast to urea and p-NA, Na₃O@calix[4]arene has a higher observed first hyperpolarizability (β₀) value (5.9 × 10⁵ a.u.). Therefore, the doped materials with substantial β₀ values are considered to be more desirable NLO candidates.

Table 4 Dipole moment (Debye), polarizability (a.u.), first hyperpolarizability (a.u.), projection of the beta vector on the dipole moment (a.u.), and second hyperpolarizability (a.u.) of pristine calix[4]arene, pure superalkalis and superalkali doped calix[4]arene complexes

Complexes	μ 0	α 0	β 0 (a.u.)	β 0 (esu)	β Vec	γ 0
Calix[4]arene	2.16	320	556	4.80 × 10^−30	556	7.5 × 10^4
Li3O	5.66	396	2.0 × 10^5	1.73 × 10^−27	—	3.5 × 10^7
Na3O	4.05	605	2.9 × 10^5	2.51 × 10^−27	—	3.1 × 10^7
K3O	5.03	693	8.4 × 10^5	7.26 × 10^−27	—	1.1 × 10^8
Li3O@calix[4]arene	6.11	493	1.3 × 10^5	1.12 × 10^−27	1.2 × 10^5	2.8 × 10^7
Na3O@calix[4]arene	9.44	340	5.9 × 10^5	5.10 × 10^−27	5.9 × 10^5	2.3 × 10^8
K3O@calix[4]arene	8.98	733	7.0 × 10^4	6.05 × 10^−28	5.6 × 10^4	8.5 × 10^7

---

The obtained results are verified by the computation of static hyperpolarizability projection on the dipole moment vector (β_vec). Based on the trends of β_vec (that are in perfect agreement with the β₀ of the complexes), it is found that Na₃O@calix[4]arene is quite NLO sensitive, while K₃O@calix[4]arene has the least sensitivity. These results are quite similar to the electronic properties, particularly the NBO (charge transfer) charges and energy gaps.

Moreover, the static second hyperpolarizability for the proposed systems was also computed. The results indicated that the γ₀ (static second hyperpolarizability) values show the same pattern as β₀ but much larger in number. The SA@calix[4]arene complexes have γ₀ values between 2.8 × 10⁷ and 2.3 × 10⁸ a.u. (see Table 4).

3.8.2 Dynamic second and third order NLO responses. To provide a broad perspective on the experimental studies, frequency-dependent hyperpolarizability (β(ω)) values have been estimated. This includes the investigation of second harmonic generation (−2ω; ω, ω) and electro-optical Pockel's effect (−ω; ω, 0). The two wavelengths (532 nm and 1064 nm) have been used for the present study. The values of the dynamic hyperpolarizability coefficients of SA@calix[4]arene are greater than their β₀ (static hyperpolarizability) values (see Table 5). At 1064 nm, all the complexes have enhanced EOPE values (7.1 × 10⁴ to 2.3 × 10⁶ a.u.), but for 532 nm, a decrease in the values of the EOPE of M₃O@calix[4]arene systems is observed. The values of the SHG coefficient at 1064 nm are increased (up to 2.3 × 10⁵ a.u.) and there is no enhancement at a shorter wavelength (532 nm). It has been observed that the Na₃O@calix[4]arene shows the largest values of β (−2ω, ω, ω) (2.3 × 10⁵ a.u.) and K₃O@calix[4]arene has the highest β (−ω; ω, 0) (2.3 × 10⁶) at higher wavelengths.

Table 5 Frequency dependent hyperpolarizability (a.u.) values for superalkali doped calix[4]arenes at varying wavelengths

Complexes	EOPE (−ω, ω, 0)		SHG (−2ω, ω, ω)
	λ = 1064 nm	λ = 532 nm	λ = 1064 nm	λ = 532 nm
Li3O@calix[4]arene	7.1 × 10^4	9.5 × 10^4	2.1 × 10^4	1.9 × 10^5
Na3O@calix[4]arene	1.5 × 10^6	5.7 × 10^4	2.3 × 10^5	4.1 × 10^4
K3O@calix[4]arene	2.3 × 10^6	4.4 × 10^4	9.7 × 10^3	5.0 × 10^4

---

The third-order NLO (nonlinear optical) responses of all designed complexes have been predicted at 532 nm and 1064 nm by means of the EOKE (electro-optic dc-Kerr effect) and EFISHG (electric field-induced second harmonic generation). The findings reflect that M₃O@calix[4]arene complexes exhibit augmented EFISHG and dc Kerr effects at both (532 nm and 1064 nm) wavelengths. The values of the estimated γ(−2ω; ω, ω, 0) (EFISHG) effect varied between 1.0 × 10⁷ and 2.2 × 10⁸ a.u. at 532 nm, while at 1064 nm they varied from 7.8 × 10⁶ to 1.8 × 10⁹ a.u. The γ(−ω; ω, 0, 0) (EOKE) effect values were in the range of 1.8 × 10⁷ to 4.1 × 10⁹ a.u. at 532 nm and from 4.9 × 10⁷ to 4.0 × 10¹⁰ a.u. at 1064 nm. It is evident from the results (Table 6) that the K₃O@calix[4]arene complex has the maximum values of EFISHG (1.8 × 10⁹ a.u.) and EOKE (4.0 × 10¹⁰ a.u.) coefficients at 1064 nm.

Table 6 Dynamic γ values in term of EOKE & EFISHG coefficients (au) and nonlinear refractive indices (cm² W⁻¹)

Complexes	Wavelength (nm)	γ(−ω; ω, 0, 0) EOKE	γ(−2ω; ω, ω, 0) EFISHG	γ ^DFWM (−ω; ω, −ω, ω)	n 2 (cm^2 W^−1)
Li3O@calix[4]arene	1064	4.9 × 10^7	7.8 × 10^6	4.2 × 10^7	3.5 × 10^−15
	532	3.0 × 10^8	2.2 × 10^8	4.3 × 10^9	3.5 × 10^−13
Na3O@calix[4]arene	1064	8.3 × 10^7	3.3 × 10^8	1.1 × 10^8	9.5 × 10^−15
	532	4.1 × 10^9	4.5 × 10^7	4.3 × 10^9	3.6 × 10^−13
K3O@calix[4]arene	1064	4.0 × 10^10	1.8 × 10^9	4.0× 10^10	3.3 × 10^−12
	532	1.8 × 10^7	1.0 × 10^7	4.6 × 10^9	3.8 × 10^−13

---

In optoelectronics, NLO materials exhibiting higher quadratic nonlinear refractive indices (n₂) are widely used as optical switches, optical pulse modulators and wavelength converters.⁸⁸ The above equation may be used to calculate the n₂ (quadratic nonlinear refractive indices) of SA-doped calix[4]arene systems using DFWM (degenerate four-wave mixing) γ^DFWM.⁸⁹

n₂ (cm² W⁻¹) = 8.28 × 10⁻²³γ^DFWM(a.u.)

γ^DFWM(−ω; ω,−ω, ω) ≈ (1/3)γ(−2ω; ω, ω, 0) + γ(−ω; ω, 0, 0) − (1/3)γ(0; 0, 0, 0)

The estimated results are presented in Table 6. The Na₃O@calix[4]arene has striking results of n₂ (refractive index) (9.5 × 10⁻¹⁵ cm² W⁻¹) at 1064 nm as well as (3.6 × 10⁻¹³ cm² W⁻¹) at 532 nm. The computed results demonstrate that the newly designed systems possess excellent NLO responses at different wavelengths.

4. Conclusion

DFT simulations are employed to thoroughly investigate the geometric, electrical, and nonlinear responses of SA-doped calix[4]arenes (M₃O@calix[4]arenes, where M₃O represents Li₃O, Na₃O, and K₃O). The results of the geometrical parameters indicated that both the superalkali subunits and CX [4] maintained their structural integrity. The designed M₃O@calix[4]arene complexes exhibited a broad range of interaction energies from −18.79 to −47.69 kcal mol⁻¹ and vertical ionization energies (2.44–3.02 eV), evidencing their chemical and thermodynamic stability. The Na₃O@calix[4]arene complex exhibits the highest observed negative charge transfer of −0.03 |e|, as determined through NBO analysis. The reduced HOMO–LUMO energy gaps of the M₃O@calix[4]arene complexes (ranging from 2.01 to 3.49 eV) compared to pure calix[4]arene (8.94 eV) indicate their semiconducting nature. Comprehensive IRI and QTAIM analyses offer a clear illustration of the non-bonding interactions present between the superalkalis and calix[4]arene. Additionally, the M₃O@calix[4]arene complexes exhibit maximum absorption in the near infrared (NIR) region, specifically between 1236 nm and 1535 nm, rendering them UV-visible transparent. The first and second hyperpolarizabilities of the M₃O@calix[4]arene complexes are determined to be 5.9 × 10⁵ a.u. and 2.3 × 10⁸ a.u., respectively, highlighting their pronounced nonlinear responses. The Na₃O@calix[4]arene complex demonstrates significant values in second harmonic generation (SHG) (2.3 × 10⁵ a.u.) and the electro-optical Pockels effect (5.0 × 10⁴ a.u.) in the case of K₃O@calix[4]arene at a wavelength of 1064 nm. Furthermore, an improvement in the dynamic second hyperpolarizability (third-order nonlinear optical response) coefficients, including the EFISHG and dc-Kerr effect, is observed. The nonlinear refractive indices (n₂) of the M₃O@calix[4]arene systems also show a noticeable increase, with the Na₃O@calix[4]arene complex achieving a maximum n₂ value of 9.5 × 10⁻¹⁵ cm² W⁻¹. These outcomes suggest that superalkali doped calix[4]arenes hold great potential as candidates for diverse applications, such as optical switching, wavelength conversion, and SHG, making them attractive options for future developments in these fields.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by the Researchers Supporting Project (no. RSPD2023R765), King Saud University, Riyadh, Saudi Arabia.

References

1. D. J. P. Arivuoli, Pramana, 2001, 57, 871–883.
2. A. Nayak, J. Park, K. De Mey, X. Hu, T. V. Duncan, D. N. Beratan, K. Clays and M. J. Therien, ACS Cent. Sci., 2016, 2, 954–966.
3. Y. Yao, H.-L. Xu and Z.-M. Su, J. Mater. Chem. C, 2022, 10, 886–898.
4. T. Zhang, X. Wei, Y. Zuo and J. Chao, Optik, 2019, 182, 295–302.
5. M. Rajeshirke and N. Sekar, Opt. Mater., 2018, 76, 191–209.
6. H. Sajid, F. Ullah, M. Yar, K. Ayub and T. Mahmood, New J. Chem., 2020, 44, 16358–16369.
7. N. Kosar, H. Tahir, K. Ayub and T. Mahmood, J. Mol. Graphics Modell., 2021, 105, 107867.
8. F. Ullah, N. Kosar, K. Ayub and T. Mahmood, Appl. Surf. Sci., 2019, 483, 1118–1128.
9. M. A. Gilani, S. Tabassum, U. Gul, T. Mahmood, A. I. Alharthi, M. A. Alotaibi, M. Geesi, R. Sheikh and K. Ayub, Appl. Phys. A: Mater. Sci. Process., 2018, 124, 1–9.
10. A. Ahsin and K. Ayub, J. Nanostruct. Chem., 2021, 1–17.
11. M. Asif, H. Sajid, M. A. Gilani, K. Ayub and T. Mahmood, Vacuum, 2022, 203, 111301.
12. D. Holton and P. Edwards, Chem. Br., 1985, 21, 1007.
13. S. J. M. Thomas, P. P. Edwards and V. L. Kuznetsov, ChemPhysChem, 2008, 9, 59–66.
14. J. L. Dye, Science, 1990, 247, 663–668.
15. J.-J. Wang, Z.-J. Zhou, Y. Bai, Z.-B. Liu, Y. Li, D. Wu, W. Chen, Z.-R. Li and C.-C. Sun, J. Mater. Chem., 2012, 22, 9652–9657.
16. W. Chen, Z.-R. Li, D. Wu, F.-L. Gu, X.-Y. Hao, B.-Q. Wang, R.-J. Li and C.-C. Sun, J. Chem. Phys., 2004, 121, 10489–10494.
17. L.-T. Fan, Y. Li, D. Wu, Z.-R. Li and C.-C. Sun, Aust. J. Chem., 2012, 65, 138–144.
18. R. Bano, M. Arshad, T. Mahmood, K. Ayub, A. Sharif, S. Perveen, S. Tabassum, J. Yang and M. A. Gilani, J. Phys. Chem. Solids, 2022, 160, 110361.
19. J. L. Dye, J. M. Ceraso, M. Lok, B. Barnett and F. J. Tehan, J. Am. Chem. Soc., 1974, 96, 608–609.
20. W.-M. Sun, D. Wu, Y. Li and Z.-R. Li, Dalton Trans., 2014, 43, 486–494.
21. M. Karplus and R. N. Porter, Atoms and molecules; an introduction for students of physical chemistry, 1970.
22. B. Li, D. Peng, F. L. Gu and C. Zhu, ChemistrySelect, 2018, 3, 12782–12790.
23. F. Ullah, K. Ayub and T. Mahmood, New J. Chem., 2020, 44, 9822–9829.
24. J. Mai, S. Gong, N. Li, Q. Luo and Z. Li, Phys. Chem. Chem. Phys., 2015, 17, 28754–28764.
25. N. V. Tkachenko, Z. M. Sun and A. I. Boldyrev, ChemPhysChem, 2019, 20, 2060–2062.
26. N. Hou, W.-M. Sun, F.-Y. Du and H.-S. Wu, Optik, 2019, 183, 455–462.
27. C. Tu, G. Yu, G. Yang, X. Zhao, W. Chen, S. Li and X. Huang, Phys. Chem. Chem. Phys., 2014, 16, 1597–1606.
28. N. Kosar, K. Shehzadi, K. Ayub and T. Mahmood, J. Mol. Graphics Modell., 2020, 97, 107573.
29. T. Ishfaq, R. Ahmad Khera, S. Zahid, U. Yaqoob, R. Aqil Shehzad, K. Ayub and J. Iqbal, Comput. Theor. Chem., 2022, 1211, 113654.
30. H. Sajid, F. Ullah, S. Khan, K. Ayub, M. Arshad and T. Mahmood, RSC Adv., 2021, 11, 4118–4128.
31. A. Ahsin and K. Ayub, Mater. Sci. Semicond. Process., 2022, 138, 106254.
32. M. Noormohammadbeigi and H. R. Shamlouei, J. Inorg. Organomet. Polym. Mater., 2018, 28, 110–120.
33. T. S. Girisun and S. Dhanuskodi, Mater. Res. Bull., 2010, 45, 88–91.
34. R. Ittyachan and P. Sagayaraj, J. Cryst. Grow., 2003, 249, 553–556.
35. M. Arivanandhan, X. Huang, S. Uda, G. Bhagavannarayana, N. Vijayan, K. Sankaranarayanan and P. Ramasamy, J. Cryst. Growth, 2008, 310, 4587–4592.
36. M. J. Cho, D. H. Choi, P. A. Sullivan, A. J. Akelaitis and L. R. Dalton, Prog. Polym. Sci., 2008, 33, 1013–1058.
37. S. Kulshrestha and A. Shrivastava, Crystal growth and characterization of organic NLO materials and their application in optical devices, 2020.
38. E. Nestoros and M. C. Stuparu, Chem. Commun., 2018, 54, 6503–6519.
39. S. Shinkai, Pure Appl. Chem., 1986, 58, 1523–1528.
40. C. Kahlfuss, E. Metay, M.-C. Duclos, M. Lemaire, M. Oltean, A. Milet, E. Saint-Aman and C. Bucher, C. R. Chim, 2014, 17, 505–511.
41. R. Ludwig, Microchim. Acta, 2005, 152, 1–19.
42. C. D. Gutsche, Calixarenes: an introduction, Royal Society of Chemistry, 2008.
43. J. H. Hymel, J. Townsend and K. D. Vogiatzis, J. Phys. Chem. A, 2019, 123, 10116–10122.
44. R. E. Sardjono and R. Rachmawati, Green Chemical Processing and Synthesis, IntechOpen, 2017.
45. P. Murphy, S. J. Dalgarno and M. J. Paterson, J. Phys. Chem. A, 2016, 120, 824–839.
46. A. Azadi and H. R. Shamlouei, Comput. Theor. Chem., 2021, 1202, 113332.
47. H. R. Shamlouei and F. Parvinzadeh, Phys. E, 2021, 127, 114539.
48. N. Hou, Y. Li, D. Wu and Z.-R. Li, Acta Phys.-Chim. Sin., 2014, 30, 1223–1229.
49. J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
50. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
51. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
52. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57.
53. E. R. Davidson and D. Feller, Chem. Rev., 1986, 86, 681–696.
54. X. Li, Q. Han, X. Yang, R. Song and L. Song, Chem. Phys. Lett., 2016, 659, 93–99.
55. H. A. Kurtz, J. J. Stewart and K. M. Dieter, J. Comput. Chem., 1990, 11, 82–87.
56. J. E. Rice and N. C. Handy, Int. J. Quantum Chem., 1992, 43, 91–118.
57. C. Bree, A. Demircan and G. Steinmeyer, IEEE J. Quantum Electron., 2010, 46, 433–437.
58. D. P. Shelton and J. E. Rice, Chem. Rev., 1994, 94, 3–29.
59. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. B.01., Wallingford, CT, 2016.
60. R. Dennington., T. A. Keith and J. M. Millam, Gauss View, Version 5., Semichem Inc., Shawnee Mission, KS, 2019.
61. D.-F. Wang and Y.-D. Wu, J. Theor. Comput. Chem., 2004, 3, 51–68.
62. C. S. Zuo, O. Wiest and Y. D. Wu, J. Phys. Org. Chem., 2011, 24, 1157–1165.
63. D. Bellert and W. Breckenridge, J. Chem. Phys., 2001, 114, 2871–2874.
64. N. Kosar, T. Mahmood, K. Ayub, S. Tabassum, M. Arshad and M. A. Gilani, Opt. Laser Technol., 2019, 120, 105753.
65. A. M. Smith and S. Nie, Acc. Chem. Res., 2010, 43, 190–200.
66. E. Tahmasebi, E. Shakerzadeh and Z. Biglari, Appl. Surf. Sci., 2016, 363, 197–208.
67. T. Lu and Q. Chen, Chem.: Methods, 2021, 1, 231–239.
68. J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632.
69. R. F. Bader, Chem. Rev., 1991, 91, 893–928.
70. R. F. Bader, Acc. Chem. Res., 1985, 18, 9–15.
71. F. Huang, S. Zhuang, W. Liu, L. Lin and L. Sun, Spectrochim. Acta, Part A, 2021, 248, 119277.
72. Y. Shen, Y. Yang, S. Zhao, B. Zhao, Z. Lin, C. Ji, L. Li, P. Fu, M. Hong and J. Luo, Chem. Mater., 2016, 28, 7110–7116.
73. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
74. G. Khanum, A. Ali, S. Shabbir, A. Fatima, N. Alsaiari, Y. Fatima, M. Ahmad, N. Siddiqui, S. Javed and M. Gupta, Crystals, 2022, 12, 337.
75. S. Liu, F.-W. Gao, H.-L. Xu and Z.-M. Su, Mol. Phys., 2019, 117, 705–711.
76. Maria, J. Iqbal, R. Ludwig and K. Ayub, Mater. Res. Bull., 2017, 92, 113–122.
77. F. Ullah, N. Kosar, A. Ali, Maria, T. Mahmood and K. Ayub, Phys. E, 2020, 118, 113906.
78. A. Hanif, R. Kiran, R. A. Khera, A. Ayoub, K. Ayub and J. Iqbal, J. Mol. Graphics Modell., 2021, 107, 107973.
79. S. Sajjad, A. Ali, T. Mahmood and K. Ayub, J. Mol. Graphics Modell., 2020, 100, 107668.
80. R. S. Roy, S. Ghosh, K. Hatua and P. K. Nandi, J. Mol. Model., 2021, 27, 74.
81. G. Y. Guo, K. C. Chu, D.-S. Wang and C.-G. Duan, Comput. Mater. Sci., 2004, 30, 269–273.
82. H. Sajid, F. Ullah, S. Khan, K. Ayub, M. Arshad and T. Mahmood, RSC Adv., 2021, 11, 4118–4128.
83. W.-M. Sun, X.-H. Li, D. Wu, Y. Li, H.-M. He, Z.-R. Li, J.-H. Chen and C.-Y. Li, Dalton Trans., 2016, 45, 7500–7509.
84. H. R. Shamlouei and F. Parvinzadeh, Phys. E, 2021, 127, 114539.
85. W. Chen, Z.-R. Li, D. Wu, Y. Li, C.-C. Sun, F. L. Gu and Y. Aoki, J. Am. Chem. Soc., 2006, 128, 1072–1073.
86. D. R. Kanis, M. A. Ratner and T. J. Marks, Chem. Rev., 1994, 94, 195–242.
87. C. Teng and A. Garito, Phys. Rev. Lett., 1983, 50, 350.
88. S. Lu, C. Zhao, Y. Zou, S. Chen, Y. Chen, Y. Li, H. Zhang, S. Wen and D. Tang, Opt. Express, 2013, 21, 2072–2082.
89. M. Tarazkar, D. A. Romanov and R. J. Levis, J. Chem. Phys., 2014, 140, 214316.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3cp04825j

---