Relativistic effects and pressure-induced phase transition in CsAu

Abstract

Cesium auride (CsAu) is an intriguing compound formed by two metals that, upon reacting, exhibits properties of an ionic salt. In this study, we employ computer simulations to explore the influence of relativistic effects on the structure and some physical properties of CsAu, as well as on a potential pressure-induced structural phase transition, the effect of high pressures on its electronic gap, and the possible transition to a conducting state. We have found that including relativistic effects reduces the lattice parameter of CsAu and brings its volumetric properties closer to the trend observed in alkali halides. It also enhances the charge transfer from cesium to gold, resulting in a difference of up to 0.15e, at ambient pressure, between non-relativistic and fully relativistic calculations. Additionally, upon increasing pressure, in the absence of intervening structural phase transitions, the closing of CsAu's band gap is expected at approximately 31.5 GPa. The inclusion of relativistic effects stabilizes the CsAu Pm3̄m structure and shifts the transition pressure to a possible high-pressure P4/mmm phase from 2 GPa (non-relativistic calculation) to 14 GPa (fully-relativistic calculation). Both the Pm3̄m and P4/mmm structures become dynamically unstable around 15 GPa, thus suggesting that the tetragonal structure may be an intermediate state towards a truly stable high-pressure CsAu phase.

---

1 Introduction

1.1 Cesium auride

Cesium auride (CsAu), first reported in 1943 by Sommer, is possibly the most well-known compound with gold as a monoatomic anion.¹ CsAu has a CsCl-type crystal structure, space group Pm3̄m, with Cs and Au at (0,0,0) and , respectively, and a lattice parameter of 4.263 Å at ambient conditions.^2,3 Although prepared from two metals in a way similar to a metallic alloy, CsAu lacks usual metallic properties, such as brightness, malleability, and electrical conductivity, and instead exhibits properties typical of an ionic salt.^2,3

Experimental studies of electrical and optical properties have established CsAu as an n-type semiconductor with an indirect band gap of 2.6 eV.^3,4 Self-consistent band structure calculations, both non-relativistic⁵ and scalar-relativistic,⁶ also gave support to those experimental findings. Another indication of the semiconducting nature of cesium auride is the significant volume contraction observed in this compound, which cannot be explained simply by geometric packing effects and is attributed to the change in Cs or Au atomic volume from metallic to ionic volume.^7,8

The CsAu ionic behavior is attributed to the significant electronegativity difference between its two constituents, with cesium having the lowest (0.79) and gold the highest (2.54) electronegativity among all metals.⁹ Previous studies of the CsAu molecule, both theoretical^10,11 and experimental,^12,13 estimate a charge transfer from 0.5e to 1e to Au. Self-consistent calculations using the relativistic Dirac–Fock equation estimate a charge transfer of 0.72e (derived from the dipole moments) and 0.955e (from a Mulliken population analysis) to Au.¹⁴ In the non-relativistic approximation, the same study gives charge transfers of 0.57e and 0.66e, respectively. Therefore, the ionicity of CsAu cannot be referred to as a strictly relativistic effect, although there is a relativistic contribution.

1.2 Relativity and gold

Regarding the inclusion of relativistic effects, first-principles calculations can be classified into three categories, namely non-relativistic (NR), scalar relativistic (SR), and fully relativistic (FR) calculations. Generally, a scalar relativistic Hamiltonian includes effects arising from the mass-velocity relationship and the electron-nucleus interaction (also called Darwin correction).¹⁵ This means that, while NR calculations exclude any relativistic effect, SR calculations neglect the spin–orbit coupling effect, leading to an error in the total energy proportional to Z²α² (where Z is the atomic number and α is the fine structure constant).¹⁶ In the FR approximation, the Hamiltonian comprises relativistic scalar and spin–orbit effects, which lead to an error in the total energy of order α², notably smaller than that of SR for heavy elements, such as cesium and gold.¹⁶

One of the most fascinating examples of relativity in chemical properties is its influence on the properties of gold. For instance, the yellow color of gold arises from the reduced electronic gap between the 5d and 6s orbitals of the element.¹⁷ Without the effects of relativity, the transition from the 5d to 6s orbitals would only take place at much higher energies in the ultraviolet spectrum. Specifically, the non-relativistic energies of the 5d and 6s orbitals of gold are similar to those of the 4d and 5s states of silver.¹⁸ As a result, non-relativistic gold would appear white, similar to silver, and its yellow color is thus a consequence of the influence of relativity.

The electronegativity of gold and the unexpected amount of auride compounds in nature manifest the influence of relativistic effects. The surprisingly high electron affinity of gold and the consequent tendency to adopt negative valence states can be explained by the simultaneous contraction of the 5d and 4f orbitals and a significant stabilization of the electron(s) in the 6s orbital.¹⁸ Only halide elements have a comparably large electron affinity; therefore, gold can be described as a “pseudohalogen.” Accordingly, cesium auride can be considered an analog of cesium halides.¹⁴ The CsAus similarity to alkali halides also manifests in the context of its equation of state, as will be shown later in this work.

1.3 High-pressure effects

High pressure is well known to be able to reorder atomic orbital energy levels and modify electronic properties. In the case of alkali metals such as cesium, high pressures can induce orbital hybridization, significantly altering their chemical reactivity.¹⁹ This effect increases the probability of finding aurides of alkali metals with unusual stoichiometries at pressures much greater than ambient pressure.

The high-pressure phase diagrams of gold, copper, and silver fluorides suggest a significant contribution of the relativistic effects of Au on the stoichiometry and stabilization of the compounds.²⁰ Indeed, due to relativistic effects, the inner electrons of gold are chemically more active than those of copper and silver.²⁰ Furthermore, in 5d transition metals such as Pt and Au, which act as anions in compounds such as CsAu and Cs₂ Pt partly due to strong relativistic effects, pressure can further increase their unusual oxidation states.²¹

Previous high-pressure studies revealed that K and Cs behave as transition metals due to pressure-induced s–d electronic charge transfer.^22,23Ab initio calculations on ytterbium under high-pressure show that Yb is always metallic at pressures above 5 GPa, and its P63/mmc phase becomes superconductive at 160 GPa.²⁴ In another recent computational study on ternary Na–P–H, the P6̄m2 phase of the NaPH₆ hydride is identified as a superconductor under 200 GPa.²⁵ Furthermore, experimental evidence has confirmed the existence of a 3D anomalous metallic state in highly compressed titanium metal, which also displays superconductivity.²⁶ These phase transitions to conductive or even superconductive states are typically accompanied by a sequence of structural phase changes and often offer crucial insights into the evolution of complex crystal structures under high pressure.

Overall, metallization appears to be the ultimate fate of most materials under extreme pressures.^27–29 Some exceptions include elements such as Ni and Na – which may become insulators,^30,31 and Li, which, in a DFT study, exhibited a transition to a semiconducting phase at around 67 GPa.³²

Regarding cesium auride, it is believed that the effect of high pressures can override the relativistic effects, making it a conductive alloy. Bryk and Klevets study suggests that increasing pressure reduces all the specific molten-salt-like features of CsAu, giving evidence of possible metallization of the binary liquid alloy at high pressures.³³ Hasegawa and Watabes band structure calculations also show that, as the lattice constant of the unit cell decreases, all bands become wider, and bands' overlapping increases to the point that CsAu becomes metallic.³⁴

High pressure can also induce structural instability and cause a structural phase transition. For CsCl-type alkali halides, studies have found a transformation to a tetragonal structure for CsCl at 65 GPa,³⁵ CsBr at 44.5 GPa to 53 GPa,^35,36 and CsI between 35 GPa and 40 GPa.^37,38 For the last one, the tetragonal phase was established to have a P4/mmm structure. As for CsAu, total-energy calculations predict a pressure-induced phase transition from the Pm3̄m to the Fd3̄m (NaTl-type) structure at a pressure of about 4.5 GPa.³⁹ Mössbauer spectroscopy analysis hints at a phase instability for CsAu under pressure.⁴⁰ Even though the high-pressure phase has not been unambiguously identified, the quadrupole splittings of the CsAu line rule out the previously suggested Fd3̄m structure.³⁹ Yet another DFT study proposes a CsAu first-order phase transition from the cubic CsCl-type to the orthorhombic Cmcm structure under pressure around 10 GPa.⁴¹

In this work, we employ DFT computer simulations to explore the influence of relativistic effects on the structure and compressibility of CsAu and the effect of high pressures on the structure and the electronic gap. We also illustrate the influence of relativistic effects on phase equilibria by exploring a possible phase transition to a P4/mmm structure and a conducting state. This particular structural phase transition was chosen as a case study due to its second-order nature and consequent lack of activation energy barrier. To clarify the effect of relativity on certain properties of CsAu, calculations are conducted using two different relativistic approximations. The similarity of CsAu to alkali halides is highlighted by a comparative analysis of their bulk moduli and molar volume.

2 Methodology

2.1 DFT calculations

Density functional theory (DFT) calculations were performed using linearized augmented plane waves + local orbitals (LAPW + lo) basis set, as implemented in the full-potential all-electron Exciting code.⁴² Calculations were performed in the athermal limit (i.e., at 0 K without zero-point energy), using the PBEsol⁴³ and the Heyd–Scuseria–Ernzerhof (HSE06)⁴⁴ exchange–correlation functionals, and at non-relativistic (NR), scalar relativistic (SR) and fully relativistic (FR) approximations. The SR and FR calculations treated core electrons with the fully relativistic Dirac equation, while valence electrons were treated according to the scalar-relativistic Schrodinger equation within zeroth-order regular approximation (ZORA).⁴² The muffin-tin (MT) radius was set as RMT = 2.2 GPa for both Cs and Au. The plane-wave basis set size for the wavefunction expansion outside the MT sphere was defined as RMT|G + k|_max= 9, for a k grid of 12 × 12 × 12, and a maximum length of the reciprocal lattice vector |G| equal to 15 GPa.

Phonon spectra of CsAu Pm3̄m and P4/mmm phases were calculated at 0 GPa and 15 GPa according to Density Functional Perturbation Theory (DFPT), as implemented in the Quantum Espresso suite, using the PBEsol functional and norm-conserving fully-relativistic pseudopotentials for both Au and Cs, including spin–orbit coupling.^45–50 Calculations were performed on a 7 × 7 × 7 grid, and interpolated phonon dispersion curves were represented along recommended reciprocal space paths.⁵¹ The lattice parameters of the Pm3̄m and P4/mmm structures were re-optimized before the corresponding phonon spectrum was calculated.

2.2 Equation of state

CsAus equilibrium volume at zero pressure V₀, bulk modulus B₀ and its pressure derivative , were estimated by fitting the integrated isothermal Vinet equation of state (EOS) to energy versus volume data,⁵²where x = 1 − (V/V₀)^1/3 and .

The Vinet EOS was chosen because it has been shown to suitably describe the behavior of materials over large compression ranges.⁵³ Equations of state for CsAu were determined from PBEsol calculations in the NR, SR, and FR approximations, as this proved to be a well-suited exchange–correlation functional to estimate lattice parameters in good agreement with experiment.⁵⁴

The influence of relativistic effects on the stability of CsAu in the Pm3̄m structure was investigated using non-relativistic and fully relativistic calculations. A possible phase transition to a P4/mmm structure was assessed by calculating the variation with the unit cell volume of the symmetry-adapted strain for a tetragonal distortion (the order parameter for a second-order structural transition Pm3̄m → P4/mmm) at the NR and FR approximations.^55–57 In the CsAu P4/mmm structure, Cs and Au occupy the Wyckoff sites 1d and 1a (0,0,0) respectively. An iterative procedure was employed to optimize the tetragonal lattice parameters for a given unit cell volume held constant. The symmetry-adapted strain e_t (i.e. the order parameter for the transition Pm3̄m → P4/mmm) was calculated as^55–57

where c is the equilibrium lattice parameter at a given unit cell volume (or, equivalently, at the corresponding pressure) and c₀ is the lattice parameter extrapolated for the Pm3̄m structure at the same unit cell volume.

2.3 Electronic structure

Hybrid functionals have been widely used to determine properties of periodic solids, mainly for a better estimation of electronic structures and band gap calculations, with the HSE06 functional being more accurate for typical semiconductors.⁵⁸ Therefore, the hybrid functional HSE06 was used for the CsAu band structure and charge transfer calculations.

The electronic band structure is calculated in Exciting in a dense grid of points in the reciprocal space by first representing the wave functions in terms of localized orthogonal functions.⁵⁹ At the time of this writing, Wannier localization has not been implemented for spin-polarized systems in the Exciting code. Accordingly, calculations were performed in the scalar relativistic (SR) approximation to explore the influence of pressure on the band structure of cesium auride and band-gap estimation.

Charge transfer analysis was estimated using a combination of the Bader analysis and the Yu-Trinkle integration method⁶⁰ with the Critic2 program.⁶¹ Bader analysis can be unreliable for all-electron calculations because the electron density exhibits sharp changes near the atomic cores. To address this issue, a modified version of the Exciting code that generates a pseudo density from the calculated electron density was used to estimate the atomic charges. This pseudo density is smooth near the atomic nuclei while preserving the original density in interstitial regions and can be expanded in terms of a finite set of G-vectors.

3 Results and discussion

3.1 Equation of state

Fig. 1 shows energy versus unit cell volume curves for CsAu, as obtained from calculations in the NR, SR, and FR approximations. The pressure scale on top of the plot was calculated using the Vinet EOS fitted to FR data. The cesium auride lattice parameter at zero pressure (a₀), bulk modulus (B₀) and bulk modulus derivative with respect to pressure , as obtained by fitting eqn (1) to NR, SR, and FR data are given in Table 1. The difference in bulk modulus of CsAu from SR and FR calculations, despite the similarity of the energy versus unit cell volume curves, may be mainly ascribed to the strong correlation between B₀ and (and also V₀)⁶² in fitting EOS to either theoretical or experimental data.

Fig. 1 Total energy versus unit cell volume for CsAu in the NR, SR, and FR approximations, as obtained from DFT calculations with the PBEsol GGA functional. The pressure scale was calculated using the Vinet EOS fitted to FR data.

Table 1 Lattice parameter (a₀), bulk modulus (B₀), and its first pressure derivative for CsAu from non-relativistic (NR), scalar-relativistic (SR), and fully-relativistic (FR) calculations

	NR	SR	FR
a 0 (Ã)	4.481(27)	4.2390(85)	4.118(6)
B 0 (GPa)	5.96(86)	11.74(69)	17.73(71)
	6.62(21)	6.35(13)	5.99(13)

---

The zero pressure equilibrium lattice parameters obtained in the SR and FR approximations are in good agreement with the experimental value obtained at room temperature (4.241 Å⁶³ and 4.263 Å^2,3). Indeed, the influence of relativity on CsAu bulk modulus and lattice parameter is noticeable. The larger bulk modulus for relativistic CsAu could be attributed to the increase in average charge density due to the reduced volume (compared to the scalar and non-relativistic cases).⁶⁴ The increasing of B₀ by the inclusion of scalar relativistic effects is also in agreement with previous studies on 4d and 5d transition metals⁶⁵ and silver compounds.⁶⁶

The reduction of unit cell volume in SR and FR calculations has been attributed to the relativistic contraction of the atomic radius.¹⁷ Studies on CsAu have also demonstrated a contraction in the interatomic distance when relativistic effects are included for both the hypothetical CsAu molecule¹⁴ and for the solid.^2,14,67 The degree of this contraction is often proportional to the ionicity of the crystalline solid.³⁴ Therefore, it is expected that the application of high pressure will affect the ionic character of cesium auride, as we shall see later.

3.1.1 Bulk modulus and unit cell volume – comparison with alkali metal halides. Empirical studies have shown a relationship between the bulk modulus B₀ and interionic distance r₀ of the form B₀ ∝ r₀⁻³ for alkali metal halides, in contrast to covalent and metallic solids where B₀ is proportional to r₀⁻⁵.⁶⁸ The proportionality of B₀ with r₀⁻³ can be mapped to the ionic pair volume V₀ because V₀ ∝ r₀³. This relationship in solids has also been observed in other studies,^69–72 which suggest a constant product of the bulk modulus and the volume per pair of ions, B₀V₀ = constant.

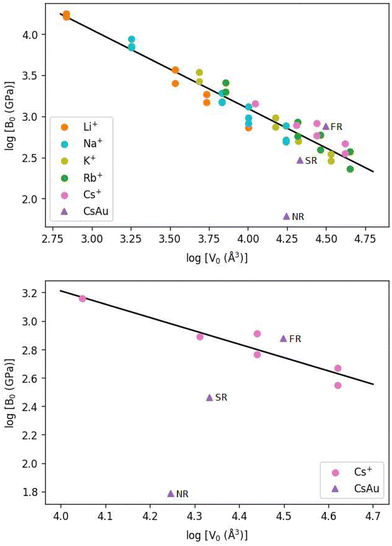
The inverse relationship between the volumetric modulus of compounds of the same group and their volume may be summarized in a log B versus log V plot. In this plot, ionic compounds formed by cations within a group (apart from oxides) will fit nicely in a line. Alkali halides, alkaline earth fluorides, some selenides, and sulfides do fit into a line of slope −1.⁷³ This surprisingly simple behavior may be used to estimate the bulk modulus of similar compounds when experimental data is unavailable.⁷⁴

Calculated values for the bulk modulus of CsAu, in the NR, SR, and FR approximations, are plotted in a log B₀versus log V₀ graph alongside experimental values found for alkali metal halides,^75–78 as shown in Fig. 2. Since the unit cell volume of a crystalline solid is directly proportional to r₀³, the former is considered instead of the volume per ion pair. The slopes calculated by a linear fit to the entire experimental data set (top) and the experimental cesium auride data (bottom) are −0.96 and −0.94, respectively, consistent with the theory. The SR and FR ionic pair volumes and bulk moduli calculated in this work are visibly closer to the observed line for all alkali halides and well located within the range of cesium halides. The behavior of CsAu can be compared with that of alkali halides in terms of compressibility and, possibly, ionic and semiconducting nature. These results suggest an improvement in the theoretical estimate of the unit cell volume and bulk modulus of CsAu in going from NR to SR to FR calculation level. Accordingly, from now on, all pressure estimates for a given lattice parameter will consider the equation of state for CsAu obtained from fully relativistic (FR) calculations.

Fig. 2 Bulk modulus and unit cell volume of CsAu at the NR, SR, and FR approximations in comparison to alkali metal halides (top panel) and cesium halides (bottom panel).

3.2 High-pressure phase transitions

Similarly to alkali halides, cesium auride in the Pm3̄m structure may evolve to a P4/mmm structure upon pressure increase. In fact, P4/mmm is a maximal subgroup of Pm3̄m, compatible with a continuous Landau-type phase transition Pm3̄m → P4/mmm.^79,80

The structural phase transition Pm3̄m → P4/mmm was monitored by observing the evolution with the unit cell volume of the order parameter (2) for this second-order transition. Fig. 3 (top panel) represents the dependence of the lattice parameters a and c of the P4/mmm structure as a function of the unit cell volume. The volume at which the tetragonal distortion becomes apparent depends on including relativistic effects in the DFT calculations. Indeed, as shown in Fig. 3 (bottom panel), the symmetry-adapted strain for a tetragonal distortion (order parameter) (2) converges to zero around 51 GPa and 76 GPa in the FR and NR approximations, respectively. The former corresponds to a pressure around 14 GPa according to the Vinet EOS obtained for the Pm3̄m phase of CsAu. On the other hand, the NR calculations suggest that the transition to the P4/mmm phase should occur at a pressure slightly below 2 GPa. The FR estimate for the Pm3̄m → P4/mmm transition pressure is much lower than the pressure at which CsAu could become metallic (as discussed below), thus suggesting that this (and possibly other) structural phase transitions should be considered as alternative pathways in the possible evolution of CsAu towards a high-pressure metallic state.

Fig. 3 Top panel – lattice parameters a (circles) and c (squares) of CsAu P4/mmm crystal structure as a function of the unit cell volume, in the fully-relativistic (FR) and non-relativistic (NR) approximations. Bottom panel - order parameter (OP) of the CsAu Pm3̄m → P4/mmm phase transition (2) as a function of the unit cell volume at the FR and NR approximations. The continuous lines represent the expected behavior derived from a functional relation OP ∼ (V – V_c)^γ, where V_c is the critical volume for the transition.

The stability of the CsAu Pm3̄m and P4/mmm was further explored by calculating their phonon spectra at 0 GPa and 15 GPa, i.e., slightly above the pressure at which a tetragonal distorting begin to manifest in the P4/mmm relaxed structure. The analysis of the phonon spectra represented in Fig. 4 suggests that the Pm3̄m structure indeed becomes dynamically unstable around 15 GPa, thus favoring the transition to P4/mmm. However, this last structure is also dynamically unstable at that same pressure, thus suggesting that the P4/mmm structure may be just an intermediate state towards a truly stable CsAu high-pressure phase.

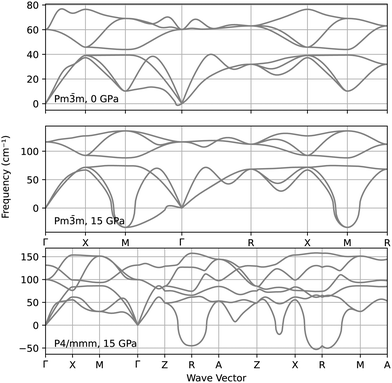Fig. 4 Phonon spectra of the CsAu Pm3̄m structure at 0 GPa and 15 GPa, and of the P4/mmm structure at 15 GPa.

Anyway, the impact of relativistic effects on the stabilization of the CsCl-type structure of CsAu is remarkably significant. The shift of the Pm3̄m → P4/mmm transition pressure towards higher values in the FR case can be attributed to the reduction of the energy of low-angular-momentum states relative to high-angular-momentum states due to relativity. Pressure-induced phase transitions are often accompanied by electron transfer from low- to high-angular-momentum states. Hence, relativity can postpone the onset of structural phase transitions caused by a reordering of electron energy bands.⁸¹ The shift in electronic band energies upon including relativistic contributions is highlighted below.

3.3 Electronic structure and charge transfer

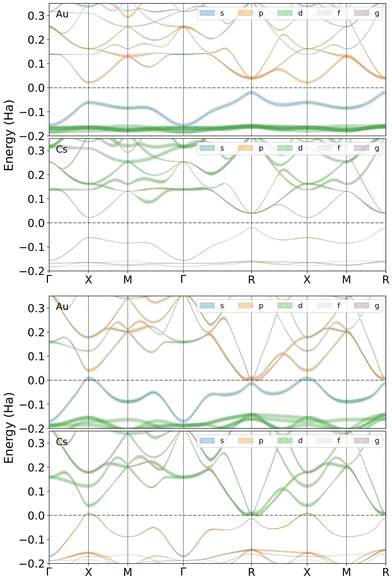
Fig. 5 shows the band structure of CsAu calculated using the HSE06 exchange–correlation functional in the scalar relativistic (SR) approximation. Calculations were performed for lattice parameters of 4.118 Å and 3.519 Å, corresponding to zero and 31.5 GPa, respectively. The band structure calculated at ambient pressure gives an indirect gap of 1.15 eV between the upper valence band (which has an important contribution from Au 6s state) at the R point and the lower conduction band at the X point. Although this band gap is less than the previously given experimental value of 2.6 eV,^3,4 it is in good agreement with the theoretical gap found by Christensen and Kollar of 1.22 eV between the same special points in reciprocal space.⁵ As seen in 5, the band gap closes at the X and R points, at 31.5 GPa, just before the structural transition Pm3̄m → P4/mmm.

Fig. 5 Gold and cesium contributions to the electronic band structure of CsAu near the Fermi level at the SR approximation at zero pressure (top) and 31.5 GPa (threshold for metallization, bottom). Line thickness is proportional to each band's s, p, d, or f character. Energy is expressed relative to Fermi level.

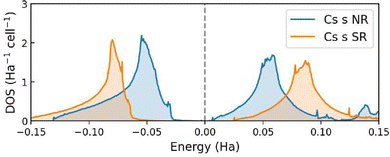
The comparison between the Cs 6s DOS obtained from the non-relativistic (NR) and spin–orbit relativistic (SR) calculations is shown in Fig. 6. When scalar-relativistic effects are included in the calculation, the observed decrease in energy of the Cs 6s states is consistent with the shift in the Pm3̄m → P4/mmm phase transition pressure, as commented in the previous section.

Fig. 6 Density of states of the Cs 6s orbital in CsAu at zero pressure from NR and SR calculations.

The band structure calculations conducted under the non-relativistic condition (not shown in Fig. 5) indicate that CsAu should be metallic even at ambient pressure, i.e., CsAu only exhibits a band gap at ambient pressure when relativistic effects are included in calculations. A similar conclusion was also drawn in a study by Christensen and Kollar,⁵ which suggests that the mass-velocity shift of the Au 6s states is critical in accounting for the difference in electronic structure between relativistic and non-relativistic calculations.

Bader analysis for the fully relativistic CsAu exhibits a charge transfer from 0.587e (P = 140 GPa) to 0.754e (P = −2 GPa) to gold, which agrees with the previously mentioned studies that estimated it to be between 0.72e to 0.955e.¹⁴ The results also show a difference from 0.15e to 0.32e between the NR and FR conditions, as shown in Fig. 7, which agrees with the observation that relativistic effects can further increase CsAu's ionicity.²¹

Fig. 7 Gold pseudo-charge from Bader analysis of CsAu in the Pm3̄m structure at the NR and FR approximations. The pressure scale was calculated using the Vinet EOS fitted to FR data.

4 Conclusion

Incorporating relativistic effects reduces the lattice parameter of cesium auride, bringing its volumetric properties closer to the trend observed in alkali halides, thus confirming the similarity between CsAu and these compounds. Relativity also plays a crucial role in enhancing the charge transfer from cesium to gold, resulting in a difference of ca. 0.15 e between non-relativistic (NR) and fully relativistic (FR) conditions near ambient pressure.

The inclusion of relativistic effects also stabilizes the Pm3̄m structure and shifts the Pm3̄m → P4/mmm transition pressure from 2 GPa (NR calculation) to 14 GPa (FR calculation). Both the Pm3̄m and the P4/mmm structures were shown to be dynamically unstable at 15 GPa, thus suggesting that the latter may be an intermediate state (favored by a null activation energy path) in the road towards a stable high-pressure phase. In the absence of any intermediate structural phase transition, CsAu in the Pm3̄m structure should become metallic slightly above 31 GPa.

Curiously, non-relativistic calculations suggest that CsAu should be metallic even at ambient pressure, further evidence that including relativistic effects is necessary to accurately reproduce cesium auride's known properties in DFT calculations. The agreement between fully relativistic DFT calculations and the relatively few experimental results available for CsAu increases the confidence in the reliability of these calculations for scenarios where this material has not yet been investigated, including its behavior at high pressures, which remains largely unexplored experimentally.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The support from the Brazilian agencies Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq) – grants 305253/2018-2 and 302705/2022-8 (CAP), Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul (FAPERGS), and Coordenação de Aperfeiçoamento de Pessoal de Nível Superior (CAPES) – Finance Code 001 is gratefully acknowledged. The authors acknowledge the National Laboratory for Scientific Computing (LNCC/MCTI, Brazil) for providing HPC resources of the SDumont supercomputer (https://sdumont.lncc.br). This research was made possible also thanks to computational resources provided by the Centro de Computação Científica (NCC/GridUNESP), Universidade Estadual de São Paulo (UNESP), for which we thank Ney Lemke (Departamento de Física e Biofísica, IBB/UNESP), who granted us access to the NCC/GridUNESP computational resources.

References

1. A. Sommer, Nature, 1943, 3851, 215.
2. W. E. Spicer, A. H. Sommer and J. G. White, Phys. Rev., 1959, 115, 57–62.
3. W. E. Spicer, Phys. Rev., 1962, 125, 1297–1299.
4. F. Wooten and G. A. Condas, Phys. Rev., 1963, 131, 657–659.
5. N. E. Christensen and J. Kollar, Solid State Commun., 1983, 46, 727–730.
6. C. Koenig, N. E. Christensen and J. Kollar, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6481–6488.
7. A. Kempf and R. W. Schmutzler, ChemInform, 1980, 84, 5–9.
8. M. Skottke-Klein, et al. , Thin Solid Films, 1991, 203, 131–145.
9. L. Pauling, The Nature of the Chemical Bond—An Introduction to Modern Structural Chemistry, Cornell University Press, 1960.
10. M. M. Pant and M. P. Das, Phys. Stat. Sol., 1975, 69, K73–K74.
11. J. Robertson, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 6322–6330.
12. J. Knecht, R. Fischer, H. Overhof and F. Hensel, J. Chem. Soc., Chem. Commun., 1978, 21, 905–906.
13. G. K. Wertheim, C. W. Bates and D. N. E. Buchanan, Solid State Commun., 1979, 30, 473–475.
14. T. Saue, K. Fægri and T. Helgaker, Mol. Phys., 1997, 91, 937–950.
15. T. Saue, Chem. Phys. Chem., 2011, 12, 3077–3094.
16. P. Scherpelz, M. Govoni, I. Hamada and G. Galli, J. Chem. Theory Comput., 2016, 12, 3523–3544.
17. P. Pyykkö, Annu. Rev. Phys. Chem., 2012, 63, 45–64.
18. P. Pyykkö, Angew. Chem., Int. Ed., 2002, 41, 3573–3578.
19. G. Yang, et al. , J. Am. Chem. Soc., 2016, 138, 4046–4052.
20. J. Lin, S. Zhang, W. Guan, G. Yang and Y. Ma, J. Am. Chem. Soc., 2018, 140, 9545–9550.
21. A. Karpov, J. Nuss, U. Wedig and M. Jansen, Angew. Chem., 2003, 42, 4818–4821.
22. K. Takemura, O. Shimomura and H. Fujihisa, Phys. Rev. Lett., 1991, 66, 2014–2017.
23. L. J. Parker, T. Atou and J. V. Badding, Science, 1996, 273, 95–97.
24. Q. Duan, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2022, 105, 214503.
25. W. Sun, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 2023, 107, 214511.
26. K. Wang, et al. , Proc. Natl. Acad. Sci. U. S. A., 2023, 120, e2218856120.
27. A. A. Likalter, Physica A, 2002, 308, 355–367.
28. H. Fujihisa, Y. Fujii, K. Takemura and O. Shimomura, J. Phys. Chem. Solids, 1995, 56, 1439–1444.
29. R. A. Fischer, A. J. Campbell, O. T. Lord, G. A. Shofner, P. Dera and V. B. Prakapenka, Geophys. Res. Lett., 2011, 38, L24301.
30. A. K. McMahan and R. C. Alberes, Phys. Rev. Lett., 1982, 49, 1198–1201.
31. Y. Ma, et al. , Nature, 2009, 458, 182–185.
32. X. Wang, et al. , Nat. Commun., 2023, 14, 2924.
33. T. Bryk and I. Klevets, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104201.
34. A. Hasegawa and M. Watabe, J. Phys. F: Metal Phys., 1977, 7, 75–86.
35. Y. K. Vohra, S. J. Duclos and A. L. Ruoff, Phys. Rev. Lett., 1985, 54, 570.
36. H. M. Huang and T. L. Liu, Phys. Lett. A, 1973, 46, 295–296.
37. T. Huang, K. E. Brister and A. L. Ruoff, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30, 2968.
38. K. Asaumi, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 1118.
39. N. E. Christensen, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 207.
40. J. Stanek, S. S. Hafner and F. Hensel, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 3129–3133.
41. M. Miao, et al. , Inorg. Chem., 2013, 52, 8183–8189.
42. A. Gulans, et al. , J. Phys.: Condens. Matter, 2014, 26, 363202.
43. J. P. Perdew, et al. , Phys. Rev. Lett., 2008, 100, 136406.
44. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207.
45. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al. , J. Phys.: Condens. Matter, 2009, 21, 395502.
46. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli and M. Cococcioni, et al. , J. Phys.: Condens. Matter, 2017, 29, 465901.
47. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. de Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152, 154105.
48. M. van Setten, M. Giantomassi, E. Bousquet, M. Verstraete, D. Hamann, X. Gonze and G.-M. Rignanese, Comput. Phys. Commun., 2018, 226, 39–54.
49. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 085117.
50. D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 239906.
51. W. Setyawan and S. Curtarolo, Comput. Mater. Sci., 2010, 49, 299–312.
52. P. Vinet, J. Ferrante, J. H. Rose and J. R. Smith, J. Geophys. Res., 1987, 92, 9319–9325.
53. G. L. Rech, J. E. Zorzi and C. A. Perottoni, Phys. Rev. B: Condens. Matter Mater. Phys., 2019, 100, 174107.
54. M. RÅsander and M. A. Moram, J. Chem. Phys., 2015, 143, 144104.
55. N. Boccara, Ann. Phys., 1968, 47, 40–64.
56. E. K. H. Salje, Phase Transitions in Ferroelastic and Co-elastic Crystals: An Introduction for Mineralogists, Material Scientists and Physicists, Cambridge University Press, 1990.
57. M. A. Carpenter, E. K. H. Salje and A. Graeme-Barber, Eur. J. Mineral., 1998, 621–691.
58. A. J. Garza and G. E. Scuseria, J. Phys. Chem. Lett., 2016, 7, 4165–4170.
59. S. Tillack, Wannier Functions for Interpolation in Reciprocal Space, 2023, https://exciting.wikidot.com/oxygen-wannier-functions, Last accessed 30 January 2023.
60. M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111.
61. A. Otero-de-la Roza, E. R. Johnson and V. Luaña, Comput. Phys. Commun., 2014, 185, 1007–1018.
62. W. B. Holzapfel, Rev. High Press. Sci. Technol., 2001, 11, 55.
63. V. G. Kienast, J. Verma and W. Klemm, Z. Anorg. Allg. Chem., 1961, 310, 143–169.
64. V. L. Moruzzi, J. F. Janak and A. R. Williams, Calculated Electronic Properties of Metals, Pergamon, 1978.
65. C. Elässer, et al. , J. Phys.: Condens. Matter, 1990, 2, 4371–4394.
66. N. J. M. Geipel and B. A. Heß, Chem. Phys. Lett., 1997, 273, 62–70.
67. D. F. Tinelli and G. A. Holcomb, J. Solid State Chem., 1978, 25, 157–168.
68. W. A. Harrison, Electronic Structure and the Properties of Solids: The Physics of the Chemical Bond, Dover Publications Inc., 1985.
69. M. Cohen, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 32, 7988.
70. S. S. Mitra and R. Marshall, J. Chem. Phys., 1964, 41, 3158.
71. R. M. Hazen and L. W. Finger, J. Geophys. Res., 1964, 84, 6723–6728.
72. B. P. Singh, V. S. Baghel and K. S. Baghel, Indian J. Pure Appl. Phys., 2010, 48, 311–314.
73. O. L. Anderson and J. E. Nafe, J. Geophys. Res., 1965, 70, 3951–3963.
74. A. Jayaraman, et al. , Phys. Rev. B: Condens. Matter Mater. Phys., 1982, 26, 3347.
75. J. Wang, et al. , J. Chem. Phys., 1964, 41, 3158.
76. Y. Sato-Sorensen, J. Geophys. Res., 1983, 88, 3543–3548.
77. P. Cortona, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 2008–2014.
78. I. Aziz, I. Ahmed and A. Naeem, Mater. Sci. Res. India, 2008, 5, 107–112.
79. M. I. Aroyo, J. M. Perez-Mato, D. Orobengoa, E. Tasci, G. de la Flor and A. Kirov, Bulg. Chem. Commun., 2011, 43, 183–197.
80. S. Ivantchev, E. Kroumova, G. Madariaga, J. Perez-Mato and M. Aroyo, J. Appl. Crystallogr., 2000, 33, 1190–1191.
81. J. C. Boettger, J. Phys.: Condens. Matter, 1999, 11, 3237–3246.

---

Footnote

† The data supporting this study's findings are available at https://osf.io/svzta/.

---