Local mechanism for magnetoelastic coupling and magnetic frustration in high-pressure synthetized Ni_xTi₂S₄ intercalated sulfide

Abstract

Transition-metal dichalcogenides (TMDCs) have been investigated for their versatile properties and remarkable tunability. Recently, there has been a resurgence of interest in magnetically intercalated TMDCs, driven by their potential applications in spintronic devices. In this paper, we describe a novel high-pressure synthesis procedure, yielding nominal Ni_xTi₂S₄ compositions in a one-step straightforward procedure, starting from TiS₂ and Ni metal. According to the Rietveld-refined synchrotron X-ray diffraction data, the compound crystallizes into a trigonal space group P3̄m1 (No. 164) with a crystallographic formula of Ni_0.8Ti₂S₄. We observe anomalies in the thermal evolution of the Ni–S pair-bond at ∼8 K, which were correlated to a minor deviation of ∼0.05% below 25 K from the Grüneisen model for the zero-pressure equation of state that describes the thermal expansion of the unit-cell volume. Extended X-ray absorption fine structure (EXAFS) analysis probed the local atomic dynamics surrounding the Ni atoms (Ni K-edge). A careful examination of the bond variance in paths within the first shell indicated an increase in the covalent bonding between Ni and Ti, in contrast to other intercalated sulfides such as Fe_xTi₂S₄. The investigated magnetic properties and specific heat do not demonstrate a long-range magnetic order. Instead, we observed a cluster glass-like behavior around 16 K, which suggests the coexistence of anti/ferromagnetic short-range magnetic interactions at low temperatures mediated by electron hopping between Ni e_g states due to magnetic frustration in the system. The local atomic arrangement correlates to the short-range magnetic interactions, which suggests the occurrence of magnetoelastic coupling in Ni_0.8Ti₂S₄.

---

1. Introduction

Intercalation materials based on layered chalcogenides have garnered significant attention due to their diverse functionalities connected with magnetism,¹ spintronics,² electrochemical energy storage,³ hydrogen storage,⁴ water electrolysis,⁵ thermochemistry,⁶ among others. Introducing atoms into van der Waals (vdW)-layered materials can induce significant variations in their electronic structure, resulting in unexpected properties in a panoply of novel compounds, such as TiS₂, NbS₂, TaS₂, TiSe₂, NbSe₂, and TaSe₂. Extensive investigations into the crystal structure of intercalated compounds and the intercalation mechanism itself indicate that metal intercalation can modify the vdW gap and valence state of transition-metal dichalcogenides (TMDCs). In this case, the intercalation behavior is enabled by the electron work function, which makes these systems well adaptable for charge transfer and, consequently, finding applications in electrochemistry.⁷

The intercalation in two-dimensional (2D) titanium disulfide (TiS₂) has been thoroughly investigated by doping with manganese (Mn), iron (Fe), cobalt (Co), nickel (Ni), and copper (Cu) as well as lithium (Li). Compared to other 2D systems, such as VS₂ and MoS₂, pristine 2D TiS₂ has been demonstrated to exhibit lower diffusion activation energies of the guest elements, raising TiS₂ as a potential contender for battery anodes as well as electrocatalytic applications, with direct implications for lithium-ion batteries.⁸ Intercalating magnetic atoms, such as Fe, Cr, Ni, Mn, and Co, causes TMDCs to develop magnetic ordering at long-range upon cooling below their respective transition temperatures.^9–14

Notably, the physical properties of M_xTiS₂ (x < 1) intercalated disulfides deviate from those of the TiS₂ host matrix due to “host–guest” and “guest–guest” interactions. Typically, the intercalated 3d metal atoms occupy octahedral interstices within the layers, leading to vacancy ordering, superstructure formation, and several magnetic states, including spin-glass or cluster-glass and long-range magnetic ordering.^15,16 Different magnetic states have been reported using intercalated 3d metals, like M_xTiS₂. Site occupation disorder, frustrations, and local competition between exchange interactions are suggested as primary factors affecting magnetic properties. In fact, the stabilization of these intercalation products is performed through solid-state synthesis or novel high-pressure synthesis procedures.^15–17 Specifically, high pressure can reduce atomic distances and promote chemical reactions that are typically hindered under normal ambient pressure conditions.¹⁸

In this paper, we report on the high-pressure synthesis of an intercalated TiS₂ material, namely Ni_xTi₂S₄. This compound has a trigonal structure (space group: P3̄m1, with TlCdS₂-type structure) at ambient conditions, as reported for other members of the family like Ni_0.5Ti₂S₄.¹⁹ It can be considered as a superstructure of the parent compound TiS₂ (with CdI₂-type structure). Structural studies have been conducted using temperature-dependent synchrotron X-ray diffraction (SXRD) to unveil the evolution of the structural parameters, such as lattice constants and unit-cell volume. We complemented the structural investigation by probing local atomic dynamics from temperature-dependent X-ray absorption spectroscopy (XAS) measurements at the Ni K-edge. The investigated magnetic properties and specific heat do not reveal a long-range magnetic order. Instead, we observed a cluster glass-like behavior at low temperatures, which suggests the coexistence of anti/ferromagnetic short-range magnetic interactions at low temperatures mediated by electron hopping between Ni e_g states due to magnetic frustration in the system. We argue that the local structure features correlate to the short-range magnetic interactions, which can result in magnetoelastic coupling in Ni_0.8Ti₂S₄.

2. Methods

2.1. High-pressure synthesis

We have successfully synthesized polycrystalline Ni_xTi₂S₄ samples in a single step by thermal treatment under high-pressure conditions. Stoichiometric amounts of Ni + 2TiS₂ were inserted into a Nb capsule (5 mm in diameter; 15 mm in length), sealed, and placed in a cylindrical graphite heater. The reaction was carried out in a piston-cylinder press (Rockland Research Co.) under a hydrostatic pressure of 3.5 GPa at 850 °C for 1 h. Then, the materials were quenched down to room temperature and the pressure was subsequently released. The reaction nominally involves the oxidation of Ni metal to Ni²⁺ and the reduction of Ti⁴⁺ to Ti³⁺ within the sealed capsule, which avoided the volatilization or oxidation of sulfur.

2.2. Microstructure and compositional analysis

FE-SEM images and EDX analysis were conducted using a FEI Nova Nano SEM 230 microscope equipped with an Apollo XL Silicon Drift Detector (SDD) from EDAX-Ametek. The powder was affixed to carbon adhesive tape and observed without a conductive coating. The morphology and chemical stoichiometry of Ni_xTi₂S₄ were investigated, as represented in Fig. S1,† revealing the purity and homogeneity of synthesized powders. The as-prepared compound consists of a typical polycrystalline microstructure with irregularly shaped grains (ranging from 1 up to 10 μm) and non-uniform size distribution. The elemental analysis for Ni, Ti, and S composition is consistent with the ideal stoichiometric values; however, sulfur vacancies have been observed at approximately 2.6% (at the surface).

2.3. High-resolution synchrotron X-ray diffraction

The structural characterization was performed by high-resolution synchrotron X-ray diffraction (SXRD) at the ESRF beamline ID22.²⁰ The Ni_xTi₂S₄ powder was filled in a borosilicate-glass capillary of 0.5 mm diameter for data acquisition in transmission geometry. The SXRD patterns collected in the temperature range 4–280 K; the samples were cooled down using the DynaFlow cryostat. SXRD data were analyzed by Rietveld refinement using the FullProf program.^21,22 The form of the peak was characterized by employing a pseudo-Voigt function. The background was interpolated across regions lacking reflections. The comprehensive refinement involved several parameters, including scale factors, zero-point error, coefficients for background, factors for correcting asymmetry, lattice parameters, atomic positions, Ni occupancy factors and isotropic displacement parameters.

2.4. X-ray absorption spectroscopy

X-ray absorption spectroscopy (XAS) experiments were conducted in transmission mode at the Ni K-edge (8.333 keV) utilizing the beamline BL22-CLÆSS²³ located at CELLS-ALBA (Barcelona, Spain). A collimated and unfocused beam measuring 1(H) × 1(V) mm² was employed. The monochromatic beam was delivered by a pair of Si(311) crystals. Sample preparation for XAS involved finely ground powders mixed with cellulose, which were then pelletized into 5 mm diameter disks to ensure an optimal absorption edge jump of ∼0.4. For low-temperature measurements, a helium-flow cryostat capable of cooling down to 40 K was employed. The absorption coefficient was determined from the detected photon flux using ionization chambers positioned before and after the sample.

The extended X-ray absorption fine structure (EXAFS) data were collected across a k-range extending up to 18 Å⁻¹, covering temperatures from 40 to 290 K. Extraction of the EXAFS oscillations χ(k) from the dataset was facilitated using Athena software.²⁴ This software allowed for pre-edge background subtraction, edge jump normalization, and subsequent extraction of the extended-range oscillations. Fourier transformation (FT) of the k-weighted k³χ(k) oscillations was executed employing a Hanning-type apodization function in both k- and R-spaces, with Δk ranging from 2.5 to 11.5 Å⁻¹ and ΔR ranging from 1.2 to 4.4 Å, respectively. For fitting the EXAFS data using Artemis software,²⁵ theoretical single scattering paths were computed via FEFF multiple scattering path expansion,²⁶ based on the structural model for NiTi₂S₄ in the trigonal space group P3̄m1. Subsequently, these calculated paths were adjusted to the experimental spectra by tuning the EXAFS signal (k-weighted of 2 and 3) to EXAFS parameters, including average bond distance (d_k), bond variance (or Debye–Waller exponent, σ²_k), and average coordination number (N_k). The amplitude reduction factor (S²₀ ≈ 0.693) was estimated from EXAFS fitting of the Ni foil spectrum.

2.5. Magnetic measurements

Magnetic properties were assessed utilizing a SQUID magnetometer (MPMS-3) from Quantum Design (San Diego, USA), across temperatures ranging from 1.8 up to 300 K and magnetic fields up to 7 T. The heat capacity was measured in a PPMS with an adiabatic heat pulse method. For this, the sample pellets were cut with a diamond saw to fit into the sample-holder dimensions. Additionally, ac susceptibility was measured using the same SQUID magnetometer across frequencies ranging from 0.1 Hz up to 1 kHz, employing an oscillatory field with a 1 Oe amplitude. In all cases, before the measurements of magnetic susceptibility or heat capacity, the sample was heated inside the magnetometer chamber up to 400 K under a vacuum atmosphere of 5 × 10⁻⁴ mbar during 4 h to remove any trace of physisorbed O₂ or air in the sample surface.

3. Results

3.1. Structural characteristics at room temperature

Fig. 1a shows the SXRD pattern and its Rietveld refinement obtained at room temperature for the Ni_xTi₂S₄ sulfide. The refinement reveals that this compound crystallizes into the trigonal crystal structure within space group P3̄m1 (No. 164), yielding refined lattice parameters of a = 3.4087(1) Å and c = 5.65059(2) Å, with the remaining refined parameters listed in Table 1. The unit-cell parameters obtained for Ni_xTi₂S₄ agree closely with those reported by H. Hahn²⁷ [a = 3.39(9) Å and c = 5.62(0) Å], but differently to those recently published by Hyung-Ho Kim,²⁸ in which Ni_xTi₂S₄ was defined in a monoclinic phase. In the trigonal unit cell, Ni atoms are located at the 1b (0,0,0.5) site, Ti atoms at the 1a (0,0,0) site, and the S atoms are located at 2d (1/3, 2/3, z) sites. In Fig. 1b, a 3D view of Ni_xTi₂S₄, crystallographic structure, consisting of intercalated [NiS₆] and [TiS₆] octahedra layers in the ab plane, is represented. Moreover, a view of the a-axis and c-axis crystallographic direction is displayed. The nearest Ni–S and Ti–S distances were found to be 2.4003(5) and 2.4452(5) Å, whereas the Ni–S–Ni and Ti–S–Ti bond-angles were 90.48(3)° and 88.38(3)°, respectively. The refined Ni amount of x = 0.794(2) is superior to that described in other Ni-intercalated Ti sulfides, of x = 0.5 (ref. 19) or x = 0.66.²⁹

Fig. 1 Rietveld plot from SXRD data at room temperature for Ni_xTi₂S₄ (a). A 3D view of Ni_xTi₂S₄ crystalline structure with the intercalated [NiS₆] and [TiS₆] octahedra layers in the ab plane and projections along the a-axis and c-axis crystallographic directions (b).

Table 1 Structural parameters of Ni_xTi₂S₄ refined from SXRD data at room temperature

Crystal data, incident radiation of λ = 0.35435 Å
Trigonal P3̄m1 T = 300 K	a (Å)	b (Å)	c (Å)	α = γ, β (°)	V (Å^3)	Z
	3.4087(1)	3.4087(1)	5.6505(9)	90, 120	56.85(9)	2
Reliability factors	R p (%)	R wp (%)	R exp (%)	R Bragg (%)	χ^2
	5.50	7.80	2.68	3.41	8.48
Fractional atomic coordinates and isotropic displacement parameters (Å^2)
Atom	Site	x	y	z	B iso (Å^2)	Occ. (≤1)
Ni	1b	0.00000	0.00000	0.50000	0.723(24)	0.397(2)
Ti	1a	0.00000	0.00000	0.00000	0.955(15)	1.00
S	2d	0.33330	0.66670	0.25681(13)	0.615(7)	1.00

---

3.2. Structural evolution with temperature

To investigate the crystal structure evolution of Ni_0.8Ti₂S₄ with the temperature, we collected sequential SXRD patterns in the 4–280 K range. No evidence of any structural phase transition was observed in the entire temperature interval, as highlighted by the pattern refined at 4 K in Fig. 2a. On the other hand, a peak shift toward higher 2θ angles (Δθ ∼ 0.03°) with decreasing temperature is observed (see Fig. 2b), corresponding to a unit-cell parameters contraction. The temperature-dependent lattice parameters (a, c) derived from the Rietveld refinement analysis are displayed in Fig. 2c. The average thermal expansion coefficient was calculated following equation, respectively:where a₀/c₀ are the initial values and Δa/Δc is the change corresponding to the temperature interval ΔT. The calculation yielded α_a = 1.02 × 10⁻⁵ K⁻¹ and α_c = 0.94 × 10⁻⁵ K⁻¹, suggesting that Ni_xTi₂S₄ experiences a slightly superior thermal expansion along the a-axis direction. In addition, as evidenced by zooming in Fig. 2c, a small anomaly revealed near 8 K is possibly associated with a local structural rearrangement in this system.

Fig. 2 Rietveld plot from SXRD data at 4 K for Ni_0.8Ti₂S₄ (a). Evolution of the most intense peak with temperature increase (b). Temperature-dependent refined lattice parameters, a = b and c (c).

3.3. Local atomic structure

In Fig. 3a, the raw Ni K-edge EXAFS spectrum of Ni_0.8Ti₂S₄ at 40 K is illustrated (open symbols), being juxtaposed with the optimal fitting composed of individual oscillations (totaling five, represented as orange and green lines), which collectively constitute the resultant EXAFS signal (red line). The Fourier transform is shown in Fig. 3b. The model comprising five single scattering (SS) paths was successfully applied to describe the experimental EXAFS function. These paths are distributed across two shells, following a similar scheme as already reported for other intercalated sulfides with the chemical formula Fe_xTi₂S₄.¹⁶ The first shell encompasses the bond-pairs Ni–S₁ and Ni–Ti₁, while the second shell comprises the pairs Ni–Ni₂, Ni–S₂, and Ni–Ti₂. Within the first shell, the bond Ni–S₁ forms an octahedral unit [NiS₆; average coordination number of 6], along with the pairs Ni–Ti₁ with a coordination number of 2. The second shell includes the Ni–Ni₂ path with a N_k of 2, the Ni–S₂ path with a coordination number of 6, and the Ni–Ti₂ path with dodecahedral coordination. The set of local structural parameters obtained from EXAFS analysis at 40 K for Ni_0.8Ti₂S₄ are listed and contrasted with those determined through SXRD data refinement at 33 K in this study (see Table 2), revealing a reasonable agreement amid both methods, except for the pair-distance Ni–Ni₂. The difference between these pair lengths obtained from EXAFS and SXRD is approximately 0.45 Å, attributable to the low oscillation amplitude of the Ni–Ni₂ path, which may cause this disparity between the two methods.

Fig. 3 Representation of raw Ni K-edge EXAFS function χ(k) at 40 K (a) and its Fourier transform magnitude |χ(R)| and the real part Re[χ(R)] (b). The orange lines signify individual fitted paths for the first shell, whereas the green lines represent those for the second shell. Experimental data are depicted by open symbols, while the red solid lines indicate the fitted summed EXAFS signal. Temperature-dependent EXAFS data: k³-weighted EXAFS oscillations in k space (c). In R space, the moduli of Fourier transform oscillations are given by χ(R) (d).

Table 2 Structural parameters of Ni_0.8Ti₂S₄ extracted from EXAFS fitting at 40 K. Abbreviations: d_k, path distance; σ²_k, bond variance (or Debye–Waller exponent); N_k, average coordination number

Path	EXAFS at 40 K			SXRD at 33 K
	d k (Å)	σ ^2 k (Å^2)	N k	d (Å)
First shell
Ni–S1	2.385(2)	0.0054(4)	6	2.3936(5)
Ni–Ti1	2.887(8)	0.007(1)	2	2.8186(0)
Second shell
Ni–Ni2	3.85(1)	0.015(2)	6	3.3998(0)
Ni–S2	4.163(7)	0.003(1)	6	4.1579(3)
Ni–Ti2	4.47(2)	0.023(6)	12	4.4162(0)
R-factor	0.0083
Δk (Å^−1)	9	ΔR (Å^−1)	3.2
N idp	18	N v, pts	11, 220

---

The temperature-dependent EXAFS data spanning from 40 up to 290 K were meticulously fitted, considering the local structural model in Table 2. For completeness, the temperature evolution of the XANES region is shown in Fig. S2.† Throughout all temperature points, the fit consistently exhibited high stability, as evidenced by the minimal variation in the R-factor within the range of ∼0.008 to 0.015. In Fig. 3c and d, the temperature-dependent k³χ(k) oscillations and their moduli |χ(R)| are represented, respectively. No sudden changes in the shape of the oscillations were detected within the investigated temperature range, indicating the absence of any structural phase transition. However, we only detected continuous variations concerning the peak broadening along the |χ(R)| function. In Fig. 4, the path length extracted from EXAFS fit for bonds Ni–S₁ (4a) and Ni–Ti₁ (4b) (first shell) are compared to those obtained from SXRD data. Slight anomalies can be observed in the EXAFS distances possibly at ∼200 K. However, more compelling anomalies were detected in the Ni–S (d₁) and Ni–Ti (d₂) bonds extracted from SXRD data (refer to the insets of Fig. 4), indicating significant contraction effects at ∼8 K.

Fig. 4 Temperature dependence of the bond lengths for the first shell paths Ni–S₁ (a, d₁) and Ni–Ti₁ (b, d₂) extracted from the EXAFS fitting. These bond lengths are compared to those obtained from Rietveld refinement of the SXRD data. In both insets, the slight variations along d₁ and d₂ from SXRD data in the range 4–100 K are shown.

3.4. Magnetic properties

To study the magnetic properties of Ni_0.8Ti₂S₄, the temperature-dependent magnetic susceptibility χ(T) was measured in both zero-field cooling (ZFC) and field-cooling (FC) conditions, with applied fields of H_dc = 100 Oe, 10 kOe, and 50 kOe from 1.8 up to 300 K, as represented in Fig. 5a. The susceptibility behaves almost constant with temperature decreasing down to ∼100 K; below this temperature, it begins to increase sharply to a maximum at ∼2 K (FC curve). At low field, the susceptibility curve exhibits a maximum at T_max ≈ 15 K matching the onset of short-range spin–spin correlations, which gradually disappear as the applied magnetic field increases up to 50 kOe. This was confirmed by the χ × T(T) curves displayed in the inset of Fig. 5a. The irreversibility between ZFC/FC curves at low temperatures can be attributed to the presence of magnetic frustration due to competition between short-range magnetic interactions. To further investigate the ground state of magnetic ordering of Ni_0.8Ti₂S₄, isotherms magnetization M(H) curves were recorded at different temperatures from 1.8 up to 300 K, as exhibited in Fig. 5b. The isotherm at room temperature (∼300 K) confirms the paramagnetic-like behavior, whereas at 1.8 K it reveals a non-saturated magnetization with little magnetic hysteresis, yielding a remanent magnetization of M_r ≈ 1.8 × 10⁻⁴ μ_B per f.u. and a coercive field of H_C ≈ 0.4 kOe (inset of Fig. 5b). This feature suggests a coexistence of AFM and FiM/FM short-range interactions at low temperatures.

Fig. 5 Temperature dependence of the magnetic susceptibility χ(T) with FC/ZFC protocols for the Ni_0.8Ti₂S₄ sample under the magnetic fields of H_dc = 100 Oe, 10 kOe, and 50 kOe (a). Inset displays the χ × T(T) curves, respectively. Isotherms magnetization M(H) curves recorded at different temperatures from 1.8 up to 300 K (b). Temperature dependence of specific heat performed in zero field (H = 0 T) (c). ac susceptibility versus temperature at frequencies ranging from 100 Hz up to 10 kHz under an excitation field of 1 Oe (d). Zoom of the χ vs. T curve, highlighting the peak at ∼16 K.

To find evidence of a possible thermodynamic phase transition at low temperatures, we carried the temperature dependence of specific heat in zero field (H = 0 T), depicted in Fig. 5c. The absence of any anomaly in the entire temperature range of investigation rules out any phase transition down to 1.8 K, confirming the absence of long-range magnetic order. Instead, the typical temperature-dependent ac susceptibility performed at different frequencies (10 Hz–1 kHz) under an excitation field of 1 Oe (displayed in Fig. 5d) showed a clear peak magnitude dispersed at ∼16 K, which indicates a spin frustration due to cluster glass-like behavior presence, promoting a dynamic ground state in Ni_0.8Ti₂S₄. Therefore, the cluster glass state is suppressed as the applied field is increased until 50 kOe, resulting in a paramagnetic behavior.

4. Discussion

4.1. Unit-cell volume expansion and mean square displacements

To elucidate the thermal changes in the unit cell volume V(T), we examined the established Grüneisen model for the zero-pressure equation of state,^30,31 by employing its first-order expansion, as outlined below:Here, V₀ denotes the unit-cell volume at 0 K, θ_D represents the Debye temperature, N signifies the number of atoms in the unit cell, B₀ stands for the isothermal bulk modulus, and γ denotes the Grüneisen parameter. This model yields valuable insights into lattice dynamics, with the Debye temperature being the primary parameter of interest. In Fig. 6a, the experimental and best-fitted curves are juxtaposed to facilitate further comparison of the fitting quality. The temperature-dependent evolution of the unit cell volume indeed exhibits an anomaly below 25 K (inset of Fig. 6a), deviating from the model described in eqn (2) by ∼0.05%. For this reason, the fitting was taken for temperatures above ∼25 K. The fitting yields V₀ as 56.423 ų and θ_D approximately 271 K, with a corresponding γ/B₀ value of 1.59 × 10⁻¹¹ Pa⁻¹.

Fig. 6 Thermal expansion of the unit-cell volume V(T), where the red line denotes the Grüneisen model for the zero-pressure equation of state (a). Temperature dependence of the mean-square displacements U_iso(T) for atoms Ni, Ti, and S (b). The solid lines represent the best fit of the MSD data using the Debye formalism in eqn (3).

The Debye formalism can also be extended to describe the thermal evolution of the mean-square displacements (MSDs or U_iso, in units of Ų), as follows:

such that, θ_D denotes the individual atomic Debye temperature, d²₀ is the intrinsic disorder (at 0 K), and m the atomic mass. In Fig. 6b, the U_iso values for Ni, Ti, and S atoms are represented as a function of temperature. Nickel presents a Debye temperature of 281 K and a disorder at 0 K of about 0.1 × 10⁻³ Ų. Ti atom showed an intrinsic disorder of 2.5 × 10⁻³ Ų and θ_D value of 380 K, while sulfur presents a Debye temperature of 476 K with d²₀ of 0.6 × 10⁻³ Ų. Using the Debye temperatures, we can estimate the bonding stiffness by employing the harmonic one-particle potential ,³² where κ_D is the harmonic force constant given in units of eV Å⁻². In Table 3, the parameters derived from Debye fitting are listed together with the respective force constants. This analysis revealed the following trend: κ_D(Ni) ≪ κ_D(Ti) < κ_D(S). This trend suggests that [TiS₆] units have greater rigidity than [NiS₆], implying a more pronounced covalent bonding between Ti and S (d₁) compared to Ni and S (d₂). However, the intrinsic disorder (d²₀) at Ti sites is ∼25 times greater than at the Ni sites, which may indicate an electronic-induced disorder likely due to multiple Ti valence states.¹⁵ The multiple valence states can be evidenced in the Ni valence states. Indeed, the XANES spectrum of Ni_0.8Ti₂S₄ is compared to standard samples (see Fig. S3†), such as Ni foil, La(Ni_0.9Al_0.1)O_2.1, NiO, and LaNiO₃. Upon closer examination, we observed that Ni_0.8Ti₂S₄ may contain two distinct types of Ni ions: one exhibiting a valence ranging between Ni¹⁺ and Ni²⁺, and the other displaying a valence between Ni²⁺ and Ni³⁺.

Table 3 Parameters fitted using the Debye and Einstein formalisms for the mean-square displacements (U_iso) and the Debye–Waller exponent (σ²_k), respectively

SXRD	Debye formalism
	Ni	Ti	S
θ D (K)	281	380	476
d ^20 (10^−3 Å^2)	0.1	2.5	0.6
κ D (eV Å^−2)	2.7	4.1	4.3
EXAFS	Einstein formalism
	Ni–S1	Ni–Ti1
θ E (K)	294	264
σ ^20 (10^−3 Å^2)	1.6	4.3
κ E (eV Å^−2)	3.2	3.3

---

4.2. Local atomic dynamics

The EXAFS data offered insights into understanding the variance in local bonding (σ²_k) and the local atomic dynamics, providing complementary information to that extracted from SXRD.^33,34 In particular, the thermal evolution of the bond variance for the paths Ni–S₁ and Ni–Ti₁ was fitted to the Einstein formalism, as given by:Here, θ_E denotes the Einstein temperature, σ²₀ the static disorder, and μ the reduced mass of the pair-bond (Ni–S or Ni–Ti). We obtained Einstein temperatures of ∼294 K and ∼264 K for the bonds Ni–S₁ and Ni–Ti₁, respectively (see Fig. 7), each of them relates to the static disorder parameters of 1.6 × 10⁻³ Ų and 4.3 × 10⁻³ Ų. The fitted Einstein temperatures can be used to estimate the force constant (κ_E) of the pair-bonds through the harmonic approximation for the atomic potential .^35,36 In Table 3, the parameters derived from Einstein fitting are included together with the respective force constants. Surprisingly, the force constants appear to be quite similar, i.e., κ_E(Ni–S₁) ≈ κ_E(Ni–Ti₁), but the force constant for Ni–Ti₁ being slightly higher than for Ni–S₁. A direct comparison of these force constants with those reported for Fe_0.8Ti₂S₄ (∼3.7 eV Å⁻² for Fe–S₁ and ∼2.2 eV Å⁻² for Fe–Ti₁) visibly elucidated that Ni increased bonding strength of the metal–metal interaction. It is noteworthy that the intrinsic disorder for Ni–Ti₁ is nearly four times greater than that for Ni−S₁, as observed from MSDs, a fact that can also be attributed to varying valence states of Ti ions.

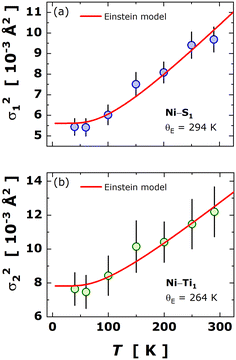Fig. 7 Temperature dependence of the bond variance (or Debye–Waller exponent, σ²_k) for the paths at the first-shell (panel a: Ni−S₁ and panel b: Ni−Ti₁). The red solid lines concern the best fit to the Einstein formalism in accordance with eqn (4).

4.3. Addressing the magnetoelastic coupling

Any evidence for magnetoelastic coupling requires a detailed investigation of the local structural changes near the magnetic transition temperature. As shown in Fig. 4, the temperature dependence of the bond lengths from Rietveld refined SXRD data, reinforced by the first shell paths Ni–S₁ (d₁) and Ni–Ti₁ (d₂) extracted from the EXAFS fitting, clearly revealed anomalies at ∼8 K. In addition, the thermal expansion of the unit-cell volume V(T) and mean-square displacements U_iso temperature-dependent for atoms Ni, Ti, and S (see Fig. 6) also exhibited anomalies at the same temperature points. These anomalies coincide very well with the magnetic anomalies observed at T ≈ 16 K, as highlighted in Fig. 5. Therefore, this correlation between local atomic arrangement to the short-range magnetic interactions near the magnetic ordering transition strongly points to the occurrence of magnetoelastic coupling in the Ni_xTi₂S₄ compound. This phenomenon primarily occurs for the pair-bonds within the first coordination shell (pair-bonds Ni–S₁ and Ni–Ti₁).

4.4. Magnetic frustration and competitive exchange dynamics

Magnetic frustration refers to materials that experience competing interactions that cannot be simultaneously fulfilled, resulting in a large degeneracy of the ground-state spin configurations. Frequently, the magnetic frustration is quantified by the ratio between the strength of the magnetic interactions within the sublattice and the temperature, where the magnetic order is established.³⁷ As shown in Fig. S4,† the inverse of susceptibility χ⁻¹(T) curves did not exhibit a typical Curie–Weiss behavior. Instead, we find a broad plateau in higher temperatures from ∼100 up to 300 K, which indicates the absence of long-range magnetic order. On the other hand, the observed cluster glass-like behavior at low temperatures (∼16 K) suggests a scenario of short-range AFM/FM correlations by site disorder of mixed ions.

For Ni_0.8Ti₂S₄, the revealed larger intrinsic disorder (d²₀) at Ti sites can lead to an electronic-induced disorder at the Ni sites, due to more pronounced covalent bonding between Ti and S compared to Ni and S (see Table 3). Indeed, the intrinsic disorder of Ni–Ti observed in the local atomic dynamics analysis from EXAFS and SXRD data, would justify the cluster behavior of magnetic competitions characterized by a dynamic short-range ordered state due to frustration effects. Magnetic frustration has been reported in other sulfides such as MnSc₂S₄³⁸ and FeAl₂S₄.³⁹

Furthermore, as previously reported,¹⁵ the similar sulfide Fe_xTi₂S₄ (x < 0.5) presents multiple Ti valence states revealed by XPS studies, dependent on the amount of intercalated Fe. From the Ni K-edge XANES spectrum of Ni_0.8Ti₂S₄ compared to standard samples (see Fig. S3†), we noted evidence for two possible distinct types of Ni ions, exhibiting valences ranging between Ni¹⁺/Ni²⁺ and Ni²⁺/Ni³⁺. The double Ni valence state has been previously reported.^40,41 Therefore, in Fig. 8a, we depicted a possible scheme of the spin frustration along the ab plane composed of Ni²⁺/Ni³⁺ coexistence. This feature is similar to geometrically frustrated materials.⁴² In this case, once two of the spins within a triangle lattice-like are anti-aligned to satisfy their AFM interaction, the third one can no longer point in a direction opposite to both other spins. Therefore, not all interactions can be minimized simultaneously to favor the lowest energy state⁴³ and, consequently, the totality of AFM interactions is incompatible with lattice symmetry, enabling some clusters of FM/FiM-type interactions.

Fig. 8 Scheme of magnetic frustration in the ab plane of Ni_0.8Ti₂S₄ lattice by Ni²⁺/Ni³⁺ coexistence (a). Possible spin occupations of Ni ions at different valence states (b), where the dashed red arrow indicates a possible electron hopping mechanism between Ni²⁺ and Ni³⁺ in the case of their coexistence.

In this way, the coexistence of Ni²⁺ and Ni³⁺ may induce electrons hopping between Ni e_g states, as schematized in Fig. 8b (indicated by red dash arrow). In this case, the Ni²⁺–Ni³⁺ interactions may lead to FM coupling between two down spins in the high-spin state [S = 1], which stabilizes the system by the Hund's rule, unlike the AFM coupling between Ni³⁺–Ni³⁺ interactions with antiparallel spins (up/down) in the low-spin state [S = ½]. Therefore, this picture suggests a competitive dynamic exchange interaction between Ni²⁺ and Ni³⁺ ions due to magnetic frustration in the system.

5. Conclusions

We have successfully synthesized under high pressure the Ni_xTi₂S₄ intercalation sulfide, which crystallizes in a trigonal structure with space group P3̄m1 (No. 164). The Ni contents (x = 0.8) is superior to those described in the literature, as refined from high-resolution SXRD data. The analysis of temperature-dependent SXRD and EXAFS data showed no evidence for structural phase transition in the entire 4–300 K temperature interval. The magnetic properties analysis did not show evidence for long-range magnetic order; however, a cluster glass-like behavior at ∼16 K was noticed, which suggests the coexistence of AFM and FiM/FM short-range interactions at low temperatures. Local atomic dynamics based on EXAFS results elucidated that the covalence along the metal–metal interaction is superior to that observed in Fe_xTi₂S₄. Moreover, the Ni–S₁ and Ni–Ti₁ first shell paths extracted from EXAFS fitting as well as mean-square displacements U_iso for atoms Ni, Ti, and S from temperature-dependent SXRD revealed anomalies at ∼8 K, coinciding with the magnetic anomaly at ∼16 K. We associated this correlation between local atomic arrangements to the short-range magnetic interactions with the occurrence of magnetoelastic coupling in Ni_0.8Ti₂S₄. The detailed Ni K-edge XANES spectrum compared to standard samples indicates two distinct types of Ni ions: one ranging between Ni¹⁺/Ni²⁺, and the other between Ni²⁺/Ni³⁺. This coexistence suggests a competitive dynamic exchange interaction by electron hopping between Ni²⁺ (high-spin) and Ni³⁺ (low-spin) states due to magnetic frustration in the system.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

The present research project was partially funded by the Spanish Ministry for Science and Innovation (MCIN/AEI/10.13039/501100011033) for granting the projects: PID2021-122477OB-I00, TED2021-129254B-C22, and TED2021-129254B-C21. RSS and FSS thank the FE-SEM service of the ICMM-CSIC. The authors are grateful to the European Synchrotron Radiation Facility (ESRF) for making all the facilities available for synchrotron radiation experiments [proposal MA-5866 in ID22]. We are also express the gratitude to CELLS-ALBA scientific and technical staff for making the facilities available for X-ray absorption spectroscopy experiments [proposal number: 2023097812].

References

1. M. Inoue and H. Negishi, J. Phys. Soc. Jpn., 1985, 54, 380–388.
2. M. Koyano, H. Negishi, Y. Ueda, M. Sasaki and M. Inoue, Phys. Status Solidi B, 1986, 138, 357–363.
3. J. B. Goodenough, Acc. Chem. Res., 2013, 46, 1053–1061.
4. D. Tan, C. Peng and Q. Zhang, Int. J. Hydrogen Energy, 2023, 48, 16756–16768.
5. J. Wu, W. Zhong, C. Yang, W. Xu, R. Zhao, H. Xiang, Q. Zhang, X. Li and N. Yang, Appl. Catal., B, 2022, 310, 121332.
6. Y. Yu, M. Aykol and C. Wolverton, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 195118.
7. L. Gao, M. Li, Q. Fan, K. Liang, B. Hu and Q. Huang, Small, 2024, 20, 2304281.
8. A. K. Nair, C. M. Da Silva and C. H. Amon, Appl. Surf. Sci., 2022, 600, 154164.
9. K. Anzenhofer, J. M. Van Den Berg, P. Cossee and J. N. Helle, J. Phys. Chem. Solids, 1970, 31, 1057–1067.
10. O. Gorochov, A. Le Blanc-Soreau, J. Rouxel, P. Imbert and G. Jehanno, Philos. Mag. B, 1981, 43, 621–634.
11. Y. Yamamura, S. Moriyama, T. Tsuji, Y. Iwasa, M. Koyano, S. Katayama and M. Ito, J. Alloys Compd., 2004, 383, 338–341.
12. T. Yoshioka and Y. Tazuke, J. Phys. Soc. Jpn., 1985, 54, 2088–2091.
13. V. G. Pleschov, N. V. Baranov, A. N. Titov, K. Inoue, M. I. Bartashevich and T. Goto, J. Alloys Compd., 2001, 320, 13–17.
14. Y. Tazuke and T. Takeyama, J. Phys. Soc. Jpn., 1997, 66, 827–830.
15. R. S. Silva, J. Gainza, J. E. Rodrigues, L. Martínez, E. Céspedes, N. M. Nemes, J. L. Martínez and J. A. Alonso, J. Mater. Chem. C, 2022, 10, 15929–15940.
16. R. S. Silva, J. E. Rodrigues, A. D. Rosa, J. Gainza, E. Céspedes, N. M. Nemes, J. L. Martínez and J. A. Alonso, ACS Appl. Mater. Interfaces, 2023, 15, 50290–50301.
17. L. Duan, Y. Wei, Y. Feng, H. Zhang, S. Cai, C. Xiao, Z. Wang and C. Jin, Inorg. Chem., 2023, 63, 635–641.
18. J. Gainza, F. Serrano-Sánchez, J. E. F. S. Rodrigues, N. M. Nemes, J. L. Martínez and J. A. Alonso, Materials, 2021, 14, 1946.
19. H. Negishi, S. Ōhara and M. Inoue, Phys. Status Solidi B, 1989, 151, 441–444.
20. A. Fitch, C. Dejoie, E. Covacci, G. Confalonieri, O. Grendal, L. Claustre, P. Guillou, J. Kieffer, W. de Nolf, S. Petitdemange, M. Ruat and Y. Watier, J. Synchrotron Radiat., 2023, 30, 1003–1012.
21. J. Rodríguez-Carvajal, Phys. B, 1993, 192, 55–69.
22. J. Rodriguez-Carvajal, M. T. Fernandez-Diaz and J. L. Martinez, J. Phys.: Condens.Matter, 1991, 3, 3215–3234.
23. L. Simonelli, C. Marini, W. Olszewski, M. Ávila Pérez, N. Ramanan, G. Guilera, V. Cuartero and K. Klementiev, Cogent Phys., 2016, 3, 1–10.
24. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
25. B. Ravel and M. Newville, X-ray absorption spectroscopy and related techniques, International Tables for Crystallography, Wiley Online Library, 2020, vol. 1, pp. 1–5,  DOI:10.1107/S1574870720003353, ISBN: 978-1-119-43394-1.
26. J. J. Kas, F. D. Vila and J. J. Rehr, X-ray absorption spectroscopy and related techniques, International Tables for Crystallography, Wiley Online Library, 2020, vol. 1, pp. 1–6,  DOI:10.1107/S1574870720003274, ISBN: 978-1-119-43394-1.
27. H. Hahn, B. Harder and W. Brockmüller, Z. Anorg. Allg. Chem., 1957, 288, 260–268.
28. H. H. Kim, K. H. Kim, J. Lee and S. H. Hong, ACS Sustainable Chem. Eng., 2021, 9, 9680–9688.
29. M. Danot, J. Bichon and J. Rouxel, Bull. Soc. Chim. Fr., 1972, 1972, 3063–3066.
30. J. E. F. S. Rodrigues, J. Gainza, F. Serrano-Sánchez, R. S. Silva, C. Dejoie, N. M. Nemes, O. J. Dura, J. L. Martínez and J. A. Alonso, Materials, 2022, 16, 370.
31. L. Vočadlo, K. S. Knight, G. D. Price and I. G. Wood, Phys. Chem. Miner., 2002, 29, 132–139.
32. J. E. F. S. Rodrigues, C. A. Escanhoela, B. Fragoso, G. Sombrio, M. M. Ferrer, C. Álvarez-Galván, M. T. Fernández-Díaz, J. A. Souza, F. F. Ferreira, C. Pecharromán and J. A. Alonso, Ind. Eng. Chem. Res., 2021, 60, 18918–18928.
33. P. Fornasini, J. Phys.: Condens.Matter, 2001, 13, 7859.
34. A. Sanson, Microstructures, 2021, 1, 2021004.
35. B. T. M. Willis and A. W. Pryor, Thermal Vibrations in Crystallography, Cambridge University Press, 1975.
36. J. E. F. S. Rodrigues, J. Gainza, F. Serrano-Sanchez, C. Marini, Y. Huttel, N. M. Nemes, J. L. Martínez and J. A. Alonso, Chem. Mater., 2022, 34, 1213–1224.
37. R. Trócoli, C. Frontera, J. Oró-Solé, C. Ritter, P. Alemany, E. Canadell, M. R. Palacín, J. Fontcuberta and A. Fuertes, Chem. Mater., 2022, 34, 6098–6107.
38. A. Krimmel, M. Mücksch, V. Tsurkan, M. M. Koza, H. Mutka, C. Ritter, D. V. Sheptyakov, S. Horn and A. Loidl, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 014413.
39. M. C. Menard, R. Ishii, T. Higo, E. Nishibori, H. Sawa, S. Nakatsuji and J. Y. Chan, Chem. Mater., 2011, 23, 3086–3094.
40. F. Jing, Q. Lv, J. Xiao, Q. Wang and S. Wang, J. Mater. Chem. A, 2018, 6, 14207–14214.
41. G. D. Park, J. S. Cho and Y. C. Kang, Nanoscale, 2015, 7, 16781–16788.
42. J. E. Greedan, J. Mater. Chem., 2001, 11, 37–53.
43. R. Moessner and A. P. Ramirez, Phys. Today, 2006, 59, 24–29.

---

Footnote

† Electronic supplementary information (ESI) available: It consists of Fig. S1: FE-SEM image and EDX analyses with quantitative results of the Ni, Ti, and S elements of the Ni_0.8Ti₂S₄ sample. Fig. S2: temperature-dependent XANES data at Ni K-edge for Ni_0.8Ti₂S₄ intercalate sulfide. Fig. S3: Ni K-edge XANES spectra for Ni_0.8Ti₂S₄ (at 290 K) and the standard samples, including Ni foil (Ni₀), La(Ni_0.9Al_0.1)O_2.1 (Ni¹⁺), NiO (Ni²⁺), and LaNiO₃ (Ni³⁺). Fig. S4: inverse of susceptibility versus temperature χ⁻¹(T) curves in the 100 Oe, 10 kOe, and 50 kOe applied magnetic fields. See DOI: https://doi.org/10.1039/d4ce00269e

---