Negative linear compressibility exhibited by the hybrid perovskite [(NH₂)₃C]Er(HCO₂)₂(C₂O₄)

Abstract

Extended framework materials with specific topologies can exhibit unusual mechanical behaviour, such as expanding in one direction under hydrostatic (uniform) pressure, known as negative linear compressibility (NLC). Here, two hybrid perovskite frameworks with winerack structures, a known NLC topology, are investigated under pressure. [C(NH₂)₃]Er(HCO₂)₂(C₂O₄) exhibits NLC from ambient pressure to 2.63(10) GPa and is the first reported NLC hybrid perovskite from ambient pressure. However, isostructural [(CH₃)₂NH₂]Er(HCO₂)₂(C₂O₄) instead compresses relatively moderately along all axes before it undergoes a phase transition above 0.37(10) GPa. The differences in the mechanical properties can be interpreted from differences in host–guest interactions within these frameworks, primarily their hydrogen bond networks.

---

As hydrostatic pressure on a system increases, its volume must decrease to enable the Gibbs free energy to be lowered, as is required for a spontaneous process. Most materials achieve this by compressing in all (principal) directions. Some materials, however, exhibit unusual behaviour such that there is no change in the length of one or two directions.^1–4 Even more strangely, some systems will expand under applied hydrostatic pressure in one or two directions, respectively referred to as negative linear compressibility (NLC) or negative area compressibility (NAC).^5–7 In these cases, the perpendicular directions compensate for the expansion(s), so the cell volume continues to decrease with pressure. This interesting response to pressure is rare, with fewer than ∼30 known systems.⁸

Systems exhibiting NLC and NAC have been suggested to have applications in shock absorption, including use in next-generation body armour, actuators, highly sensitive pressure sensors (as piezoelectrics) or, as bio-inspired functional materials.^9,10 By coupling these NLC behaviours with the physical properties of perovskites, a new wave of tuneable functional materials may be developed.^5,11

NLC can occur by numerous mechanisms, including polyhedral tilting/distortion, framework flexing and, commonly, framework hinging. Recently, NLC behaviour has been found in a range of flexible hybrid frameworks that are comprised of metal and organic building blocks, including flexible metal–organic frameworks (MOFs) that combine metal nodes bridged by organic linkers.¹² These new NLC materials generally have larger (negative) compressibilities, defined as the magnitude of compression in one direction (K_{[small script l]} = −1[small script l]/(∂[small script l]/∂p)_T, K_NLC < −10 TPa⁻¹, c.f. K_NLC > −5 TPa⁻¹ in conventional materials).^5,13 Many are MOFs often, but not always, adopting a ‘winerack’ topology that has a rhombohedral cavity with two distinct hinging angles. With applied pressure, these angles can distort, resulting in the expansion of the unit cell in one direction with a contraction in the perpendicular axis. Lithium L-tartrate is one example that exhibits NLC behaviour in a structure with two linker types as a result of the two different bridging modes the tartrate can adopt, which alters the cavity geometry (Fig. 1).^14–16

Hybrid perovskites are metal–organic analogues of classic perovskites which crystalise with ABX₃ stoichiometry, with A-site cations occupying the space between their BX₃ frameworks. These are well studied with significant promise as semi-conductors in next generation solar cells^17,18 as well as for physical properties traditionally associated with inorganic ABX₃ perovskites such as magnetism,^19–21 and/or ferroelectricity.^22,23 Oxide perovskites feature some of the earliest examples of NLC and NAC.²⁴ Unlike conventional perovskites, the mechanical and physical properties of hybrid frameworks are affected by hydrogen bonding.^25–27 Hybrid perovskites that adopt the classical perovskite structure, in which the X-site linker connects each B-site cation to six other B-sites, have been predicted to exhibit NLC,²⁸ but so far, only a few exhibit this behaviour over narrow high pressure ranges.^29,30 [C(NH₂)₃][Cd(HCO₂)₃] has been reported to have zero area compressibility,^1,31 while [(NH₂)₂CH]Mn(H₂PO₂)₃, a 3D hybrid perovskite shows NLC of K_x3 = −7.8(6) TPa⁻¹ between 4.09 GPa and 4.48 GPa.²⁹ The 2D layered hybrid perovskite (S/R-3PYEA)PbI₄ was also recently found to exhibit modest NLC at high pressures with compressibility coefficient K_c = −3.15 TPa⁻¹ from 7.0 GPa to 13.9 GPa.³⁰

Design rules to target new NLC materials have previously been established, the most important of which is that the system must be inherently anisotropic, as expansion in one direction(s) requires a larger contraction in perpendicular direction(s) so that overall the volume decreases.⁵ There must be a mechanical or topological mechanism by which contraction is converted to perpendicular expansion. The ‘winerack’ is one such topology, but others include helices or rotating rigid polyhedra. Finally, the material should be stable at high pressure as MOFs with large voids are generally very flexible but undergo volume-reducing phase transitions rather than NLC, so rigid linkers are generally preferred, and thus control of void space is another key consideration. The formate linker (HCO₂) is considered relatively rigid due to its short length and resonance structures, with some formate structures exhibiting NLC.⁷ Similarly, a number of oxalate (C₂O₄) systems exhibit NLC, with ammonium oxalate particularly unusual as an organic hydrogen bonded winerack structure.^32,33

Here we report the mechanical properties of two ABX₃ hybrid perovskites, [A]Er(HCO₂)₂(C₂O₄), where A = [(NH₂)₃C] (guanidinium erbium formate oxalate, GUA) and [(CH₃)₂NH₂] (dimethylammonium erbium formate oxalate, DMA). GUA exhibits negative thermal expansion, which is associated with NLC in some materials.²⁷ The materials satisfy three of the four design rules for NLC but differ in the execution of the other via the different guests they host; with only GUA exhibiting NLC behaviour, we are able to probe this design rule directly and establish how linker rigidity and guest occupancy influence NLC behaviour. The combination of two unique linkers generates a geometry of the framework cavity that deviates from the typical rhombus common in ABX₃ systems. Instead, the cavities adopt a kite geometry with two inequivalent Er–Er distances and three crystallographically unique hinging angles, see Fig. 1. For these systems, the angles are defined as the formate–Er–formate angle (η), the oxalate–Er–oxalate angle (θ) and the formate–Er–oxalate angle (σ).

Fig. 1 (a) Unique cavity geometries generated by the introduction of distinct linker types and their respective orientation. Lithium L-tartrate is a rare example of a system with NLC with a trans-dilinker cavity.¹⁴ (b) The winerack structures of (left) [C(NH₂)₃]Er(HCO₂)₂(C₂O₄) and (right) [(CH₃)₂NH₂]Er(HCO₂)₂(C₂O₄) with the organic struts reduced to Er–Er distances, in green for formate linkers and pink for oxalate linkers. The internal angles of the cavities highlight the unique cis-dilinker geometry.

GUA and DMA were made by the previously reported method (see ESI†).²⁷ The two anionic frameworks have the same connectivity, but the size, chemistry, and intrinsic symmetry of their A-site cation results in two different crystal systems. GUA crystalises in orthorhombic Pcca, and DMA crystallises in monoclinic P2/n. In both cases, the structure is formed by eight coordinate erbium(III) cations bridged to six nearest neighbours via six oxalate and formate linkers forming a perovskite framework (see Fig. S1–S2, ESI†). Oxalate and formate linkers alternate in planes (ac for GUA and ab for DMA). Another formate linker connects the Er in the third dimension, giving two 3D hybrid perovskite structures with winerack topology.

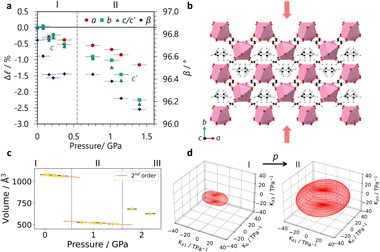
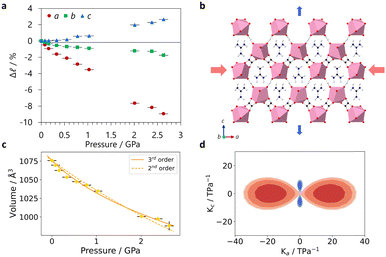
In situ high-pressure single crystal X-ray diffraction experiments were conducted using a diamond anvil cell on I19 at the Diamond Light Source (see ESI,† including Tables S1–S3, for experimental and crystallographic details). These found that GUA exhibited an expansion along the c-axis with increasing pressure, with a large reduction along a (see Fig. 2a). A modest decrease along b led to an overall reduction in the cell volume. Compressibilities were calculated using PASCal⁶ with K_c = −10.1(7) TPa⁻¹ with bulk modulus, B₀ = 18(3) GPa over 0–2.63(10) GPa, see Table S4 (ESI†). In contrast, DMA displayed a reduction in all lattice parameters, shown in Fig. 3a, with increasing pressure before subsequently undergoing a phase transition to phase II at a moderate applied pressure of >0.76(10) GPa. The structure changes from P2/n to the P2/a setting of the same space group, with the cations flipping by ∼50° to align along a 2-fold rotation axis along with the erbium metal centres, resulted in a halving of the c-axis. Compressibility coefficients for phases I and II can be found in Table S5 (ESI†).

Fig. 2 (a) The change in lattice parameters of GUA with pressure, (b) the winerack structure of the framework, showing the directions of expansion (blue arrows) and contraction (red arrows) with applied pressure viewed along b, (c) the reduction in volume with increasing pressure, fit with a 3rd order Birch–Murnaghan equation of state to extract B₀, and (d) the indicatrix tensor where the compressibility constants are negative (blue) and positive (red) and with the plotted eigenvalues calculated using PASCal.⁶

Fig. 3 (a) The change in lattice parameters of DMA with pressure and the phase I to II transition indicated by a dotted line. The lattice parameters of phase II have been normalised for direct comparison with phase I where in phase II c′ = 2c. (b) The structure of DMA at ambient pressure with compression along b highlighted by red arrows. (c) The 2nd order Birch–Murnaghan equations of state fits giving B₀ = 23(5) GPa for phases I and B₀ = 13(4) GPa for II. (d) The indicatrix tensors highlighting the change in compression between phase I, between 0 GPa–0.37(10) GPa and phase II, between 0.76(10) GPa–1.40(10) GPa.

The lattice parameters of DMA compress relatively moderately. The cell distortion is most clearly visible in the change of β, making analysis of the orthogonal principal axes of compression critical to understand the behaviour of the structure under pressure. For DMA, the principal axis X2 aligns with b, whilst X1 and X3 align in the ac plane across the channel cavity diagonal between erbium centres, see Fig. S3 (ESI†). There is a small amount of modellable A-site disorder after the onset of the phase I–II transition (Fig. S4, ESI†) that is resolved with increasing pressure and so omitted from the models used for the highest pressures due to worsening statistics. Fig. 3d shows the strain tensor plot from the eigenvalues of the principal axis vectors and how these change between phases. A high-pressure phase III of DMA was detected above 1.40(10) GPa, but a full structural solution was unachievable; see ESI† for details.

Analysis of our variable-pressure structural models show the origin of NLC behaviour in GUA to be the hinging of the winerack framework. For GUA, with increasing pressure, there is a large increase in σ associated with the NLC, which is accompanied by decreases in η and θ (see Fig. 4). The hinging of the framework in the DMA phase is very moderate compared to the GUA phase. For the DMA phase, η and σ follow the same trend as GUA, decreasing and increasing respectively, albeit of a much lower magnitude. However, θ subtly increases with pressure, suggesting the cavity distortion differs from GUA.

Fig. 4 The changes in the defined hinging angles (see Fig. 1) with increasing applied hydrostatic pressure for (a) GUA and (b) DMA.

The contrasting structural distortion is intrinsically linked to the flexibility of the erbium-ligand bonded framework and the intermolecular interactions with the A-site guest. As well as the key hinging angles, the framework flexibility is also captured by the Er–Er distances as the sum of many degrees of freedom in each molecular linker. The decrease of Er–Er distances with increasing pressure shows how the cavities in both materials undergo significant compression. The rate at which the Er–Er distances compress differs between GUA and DMA, with these appearing more compressible in DMA than GUA (see Fig. S5, ESI†). The compression of Er–Er distances also varies across different linker types, with the formate linkers more compressible than the oxalate linkers in both compounds.

Several strong host–guest interactions can form between the A-site and the anionic framework (Tables S10–S11 and Fig. S6–S8, ESI†) and are here investigated by analysis of Hirschfeld surfaces and respective fingerprint plots (Fig. S9–11, ESI†).³⁴ The interactions present for each system are determined by the chemistry of the A-site, with guanidinium cations having three times the number of hydrogen bond donors than dimethylammonium cations. Guanidinium cations form eight hydrogen bonds per cavity by symmetry, as seen in Fig. S6 (ESI†). The directions along which the hydrogen bonds form directly affect the compressibility coefficients, with the shortest hydrogen bonds, between N2 and the O2 of the formate bridging along b, remaining relatively rigid with pressure, consistent with the small compressibility along b. In contrast, a bifurcated hydrogen bond between N2 and the O1 and O4 of the formate and oxalate that link across the σ opening angle sees a decrease in the N2–O1 and an increase in the N2–O4 under pressure, which correlates with the significant compression along a and NLC along c, respectively. The remaining N1–O3 lengthens with increasing pressure together highlighting how the guanidinium cations tend towards one side of the cavity. The minimal net change in hydrogen bonding is shown in the fingerprint plots as a subtle shift away from the origin, under pressure these plots usually condense and shift significantly towards the origin.³⁵

The dimethylammonium cation, seen in Fig. S7 (ESI†), forms three distinct hydrogen bonds in phase I, one with an O2 atom from a formate along c (broadly equivalent to b in GUA) and a bifurcated hydrogen bond between the O1 formate and the O3 oxalate across σ. This bifurcated hydrogen bond is only present on one side of the cavity in DMA, as there is only one hydrogen bond donor group, resulting in an asymmetric hydrogen bonding network compared to GUA. The compressibility coefficients of phase I, are much smaller than those of phase II, following the hydrogen bonding becoming completely isotropic by symmetry. In phase II, the cation reorientation results in two symmetrically equivalent hydrogen bonds with the O3 oxalate, which compress significantly with increasing pressure. Phase I seems to have a much more rigid framework, likely stabilised by the host–guest interactions in the ac plane, whilst the more compressible hydrogen bonds in phase II result in a less rigid framework. Unlike GUA, fewer hydrogen-bonding interactions in DMA fail to allow for framework hinging by supporting the rigidity of the struts. Design rules suggest that exerting internal pressure through steric means can help to stabilise NLC to higher pressures, but cavity occupancy alone may not be enough to influence a material's NLC behaviour.

The weakest intermolecular interactions are usually most influenced by applied pressure, which makes these results quite counterintuitive as the N2–O2 hydrogen bond length in GUA is retained to higher pressure, ∼0.001(8) Å GPa⁻¹, whilst the stronger linker interactions compress and buckle. The presence of hydrogen bonding seems to be crucial in these cases to allow for NLC to occur in GUA, and has been explored previously for stabilising high-pressure polymorphs of guanidinium transition metal formates, and in directing the compressive behaviours of molecular crystals.^31,36GUA likely exhibits NLC when its transition metal analogues do not because both the presence of the oxalate linker and the stronger hydrogen bonds in the formate-oxalates σ cause greater framework rigidity in GUA.²⁷

The compressibility of two [A]Er(HCO₂)₂(C₂O₄) hybrid perovskite frameworks is found to be A-site cation dependant, with the number and directionality of the hydrogen-bonding network key to determining the emergence of framework hinging vs distortion. We have been able to use this to probe the significance of host–guest interactions, and linker rigidity in relation to the design rules established for producing NLC materials. The greater hydrogen bonding in GUA stabilises this phase to a higher pressure than DMA. DMA undergoes a phase transition to phase II, where the rapid change in the hydrogen bond distances suggests increasing pressure is destabilising the system, resulting in a loss of crystallinity. The behaviour of the hydrogen bonds in GUA is much more anisotropic, whereas the hydrogen bonds in DMA are more isotropic. Thus, the direction these host–guest interactions orient is key to support the anionic cage and facilitate framework hinging. The analyses of these systems show that the host–guest interactions are vital when considering the prospect of a hybrid-perovskite exhibiting NLC behaviour.

We acknowledge the Diamond Light Source for time on Beamline I19 under proposal CY32115-1 and EPSRC for funding a DTA studentship for TJH.

Conflicts of interest

There are no conflicts to declare.

References

1. Q. Zeng, et al. , ACS Appl. Mater. Interfaces, 2018, 10, 23481–23484.
2. L. Yu, Acc. Chem. Res., 2010, 43, 1257–1266.
3. Q. Zeng, et al. , ACS Mater. Lett., 2022, 4, 541–547.
4. L. Wang, et al. , Dalton Trans., 2020, 49, 719–728.
5. A. B. Cairns and A. L. Goodwin, Phys. Chem. Chem. Phys., 2015, 17, 20449–20465.
6. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
7. W. Li, et al. , J. Am. Chem. Soc., 2012, 134, 11940–11943.
8. Q. Zeng, et al. , Langmuir, 2022, 38, 9031–9036.
9. R. H. Baughman, et al. , Science, 1998, 279, 1522–1524.
10. K. E. Evans and A. Alderson, Adv. Mater., 2000, 12, 617–628.
11. E. Solana-Madruga, et al. , Chem. Commun., 2020, 56, 12574–12577.
12. S. Henke, et al. , J. Am. Chem. Soc., 2012, 134, 9464–9474.
13. H. J. Shepherd, et al. , Angew. Chem., Int. Ed., 2012, 51, 3910–3914.
14. H. H. M. Yeung, et al. , Phys. Chem. Chem. Phys., 2017, 19, 3544–3549.
15. F. Yang, et al. , Chem. Commun., 2023, 59, 6403–6406.
16. J. Zhou, et al. , Chem. Eng. J., 2023, 466, 143243.
17. A. Fakharuddin, et al. , Adv. Energy Mater., 2017, 7, 1700623.
18. M. A. Green, et al. , Nat. Photonics, 2014, 8, 506–514.
19. S. M. Bovill and P. J. Saines, CrystEngComm, 2015, 17, 8319–8326.
20. P. Jain, et al. , J. Am. Chem. Soc., 2009, 131, 13625–13627.
21. R. Scatena, et al. , J. Mater. Chem. C, 2020, 8, 12840–12847.
22. Z. Hu, et al. , Phys. Chem. Chem. Phys., 2020, 22, 4235–4239.
23. K. Li, et al. , J. Am. Chem. Soc., 2022, 144, 816–823.
24. R. J. Nelmes and A. Katrusiak, J. Phys. C-Solid State Phys., 1986, 19, L725–L730.
25. P. Jain, et al. , J. Am. Chem. Soc., 2008, 130, 10450–10451.
26. G. A. Jeffrey, Crystallogr. Rev., 1995, 4, 213–254.
27. L. G. Burley, et al. , Dalton Trans., 2021, 50, 5437–5441.
28. P. S. Ghosh and I. Ponomareva, J. Phys. Chem. Lett., 2021, 12, 7560–7565.
29. M. MącZka, et al. , J. Phys. Chem. C, 2021, 125, 26958–26966.
30. M. E. Sun, et al. , J. Am. Chem. Soc., 2022, 15, 26.
31. Z. Yang, et al. , Philos. Trans. R. Soc., A, 2019, 377, 20180227.
32. F. Colmenero, et al. , J. Mater. Sci., 2021, 56, 269–277.
33. Y. Qiao, et al. , J. Phys. Chem. Lett., 2015, 6, 2755–2760.
34. P. R. Spackman, et al. , J. Appl. Crystallogr., 2021, 54, 1006–1011.
35. P. A. Wood, et al. , CrystEngComm, 2008, 10, 368–376.
36. E. V. Boldyreva, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 218–231.

---

Footnote

† Electronic supplementary information (ESI) available: Details of experimental method and crystallographic data and analysis. CCDC 2320830–2320839 and 2320844–2320852. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3cc06208b

---