Improved estimates of expanded measurement uncertainty
Analytical Methods Committee, AMCTB No. 114
First published on 23rd July 2024
Abstract
Measurement uncertainty (MU) is often estimated (sometimes initially as repeatability) using a limited number of single measurement values (n ≪ 30), or of duplicate measurements on duplicated samples, in order to include the contribution from sampling. In cases such as this where the uncertainty estimate is based on limited data, the common use of a coverage factor of 2.0, based on an assumed normal distribution, to give an approximate 95% confidence interval can result in an underestimate of the expanded MU. Where n is much lower than 30 (e.g., n = 8), this can lead to a serious underestimate. More accurate estimation of the coverage factor, for both the classical and robust ANOVA (e.g., in new software RANOVA v4.0) gives more reliable estimates of the expanded MU by calculating coverage factors based on the t-distribution. A case study for nitrate in lettuce shows that the more accurate coverage factor (of ∼2.3) substantially increases the expanded MU estimates by 13–14%.
Introduction
The requirement for reliable estimates of the measurement uncertainty (MU) in chemical measurements, where the MU includes the contribution from the sampling process, is now well established. MU is defined as ‘a parameter, associated with the result of a measurement, that characterises the dispersion of the values that could reasonably be attributed to the measurand’.1 Uncertainty is often expressed as the standard deviation of an assumed normal distribution. It can be converted into an ‘expanded uncertainty’ U by multiplying the standard deviation by a coverage factor (k-factor), within which the value of the measurand (i.e., the notional ‘true’ value of the quantity being measured, such as the analyte concentration) is believed to lie, with a certain degree of confidence (typically 95%). For practical purposes, U may then be expressed as a percentage of the mean value (i.e., U′). However, in all practical applications the standard deviation values are only estimates that have been derived from a statistical sample. Note that a distinction has been made here between a ‘statistical sample’ and a ‘physical sample’. The latter pertains to the process whereby a physical sample is extracted (or selected, in some cases, e.g., remote sensing or the use of in situ measuring devices) from a whole, i.e., the ‘sampling target’.Limitation of the common practice for calculating expanded MU using a coverage factor of 2
A common practice is to multiply the standard deviation by a coverage factor (k), where k = 2 for an approximate 95% confidence interval, based on an assumed normal or t-distribution.1 It has the limitation that it is only a good approximation when the size of the statistical sample (n) is quite large, i.e., n ≥ 30 for a normal distribution. This ideal situation is often not the case in practice, because the costs of the additional collection of the physical samples needed, and their corresponding analyses, can be too high. In more practical situations n may be considerably less than 30, and then the expanded uncertainty U derived using k = 2 for an assumed normal distribution, will always be an underestimate. There is, therefore, a potential advantage to making a more reliable estimate of U.Improving the calculation of expanded MU
In a simple scenario where a statistical sample of n measurements is taken and used to calculate a standard deviation, an improved estimate of U can be achieved using the Student's t-distribution with the appropriate degrees of freedom (df, e.g., df = n − 1). However, when the MU is calculated from a linear combination of variances, for example when both the MU from the physical sampling process and also from the analytical process are to be estimated, calculating df is more complex. An example of this type of MU estimation is the use of the ‘duplicate method’ (Fig. 1), in which duplicated analyses are made of duplicated physical samples, taken from a number n of sampling targets.2 This can be called an n × 2 × 2 experimental design. Estimates of sampling and analytical uncertainty (as standard deviations) are then calculated using a nested analysis of variance (ANOVA), and combined by their sum of squares to derive a value of the overall MU (AMC Technical Brief No. 40).3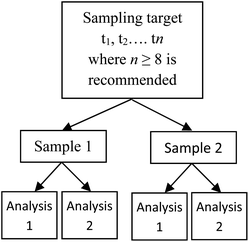 | ||
| Fig. 1 The simplest (n × 2 × 2) case of the nested balanced experimental design, where a number of sampling targets (t1 − tn) are selected at random. Two physical samples are taken from each target, and each of these is analysed twice.2 | ||
It may sometimes be more reliable to calculate MU using robust statistics. In this case the MU is expected to be more representative of the bulk of the data when a small proportion (i.e., <10%) of outlying values are present.4,5 This approach needs to be used with caution, and the presence of outlying values should be investigated. They may occur either through operator error (e.g., procedural error), or may result from genuine variability in or between sampling targets. Comparison of the results of the standard ‘classical’ ANOVA and the robust ANOVA can also be a useful means of identifying the presence of outlying values (i.e., when the robust results are appreciably lower than the classical results). An Excel™ program called RANOVA is available on the AMC website to enable the calculation of MU using both the classical ANOVA and also the robust ANOVA.6
The objective of this technical brief is to introduce approaches, for both classical and robust ANOVA, that will enable a better approximation of the expanded MU when using the experimental design shown in Fig. 1 for a limited number of sample targets.
Methodology – classical ANOVA
The initial requirement here is to calculate the degrees of freedom (df) that will give us the appropriate percentage point on a Student's t-distribution. We can then use this to calculate the coverage factor (k-factor) by which we multiply the standard deviation, i.e., in this case the standard uncertainty. This would be straightforward if we were only calculating the MU for n analytical replicates, in that situation the df (ν) would simply be ν = n − 1. When the standard deviations are calculated by ANOVA using an experimental design such as Fig. 1, there is not a simple or exact solution. However, Satterthwaite7 provides a method for estimating ν for variances that have been derived as linear combinations of mean-squares. Applying this method to the experimental design in Fig. 1, a simplification can be derived for the n × 2 × 2 design: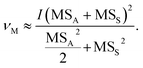 | (1) |
Eqn (1) has been taken from ref. 8, where further details of its derivation can be found. It applies notation typically found in ANOVA tables: νM is the df for the combined MU; I is the number of samples from the top level of the nested ANOVA, in this case I = n (Fig. 1); MSS and MSA are the mean squares of the sampling and analytical levels, respectively (Fig. 1). It is then straightforward to calculate a modified k-factor using Student's t-tables or a computerised function such as the Excel™ T.INV.2T function.
Methodology – robust ANOVA
Robust ANOVA, as has been applied to the n × 2 × 2 design (Fig. 1) by the program RANOVA 4.0,6 uses an iterative algorithm to down-weight the effects of a small number of outlying values on calculated variances at any of the different levels (e.g., Sampling target, Sample or Analysis in Fig. 1). These calculations are based on the methodologies described in ref. 4 and 5. It is not possible to derive a correct estimate of νM mathematically, however a value for the modified k-factor can be estimated using a bootstrapping approach. Further details of this approach, and the validation of both the classical and robust ANOVA, are given in ref. 8.Example of the improved uncertainty calculation
This example is based on data drawn from a study of the nitrate concentration in greenhouse grown lettuce.2 Sampling was carried out by collecting 10 lettuce heads from each of 8 bays, walking a W-shaped route. Sample duplicates were acquired according to the balanced design (Fig. 1) using the same sampling protocol, but taking an alternative route through each bay. The 10 heads from each of the 8 bays were processed to form a composite sample and analysed using high-performance liquid chromatography. Data are shown in Table 1, and the results of the ANOVA (from program RANOVA v4.0 (ref. 6)) are show in Table 2. The degrees of freedom for classical ANOVA were calculated to be νM = 8.63, eqn (1), and rounded to νM = 9 in order to calculate the k-factor = 2.26.| Sampling target | S1A1 | S1A2 | S2A1 | S2A2 |
|---|---|---|---|---|
| A | 3898 | 4139 | 4466 | 4693 |
| B | 3910 | 3993 | 4201 | 4126 |
| C | 5708 | 5903 | 4061 | 3782 |
| D | 5028 | 4754 | 5450 | 5416 |
| E | 4640 | 4401 | 4248 | 4191 |
| F | 5182 | 5023 | 4662 | 4839 |
| G | 3028 | 3224 | 3023 | 2901 |
| H | 3966 | 4283 | 4131 | 3788 |
| Classical ANOVA | ||||
|---|---|---|---|---|
| Mean | 4345.6 | Targets (n) | 8 | |
| Total SD (std dev.) | 774.53 | |||
| Btn target | Sampling | Analysis | Measure | |
| SD (or u) | 556.28 | 518.16 | 148.18 | 538.93 |
| % of total variance | 51.58 | 44.76 | 3.66 | 48.42 |
| U′ (exp rel uncertainty k = 2) | 23.85 | 6.82 | 24.80 | |
| F U (uncertainty factor k = 2) | 1.2432 | 1.0738 | 1.2574 | |
| U′ (exp rel uncertainty) for 95% confidence (k = 2.26) | 28.03 | |||
| F U (uncertainty factor) for 95% confidence (k = 2.26) | 1.2954 | |||
| Robust ANOVA | ||||
|---|---|---|---|---|
| Mean | 4408.3 | Targets (n) | 8 | |
| Total SD (std dev.) | 670.58 | |||
| Btn target | Sampling | Analysis | Measure | |
| SD (or u) | 565.4 | 319.05 | 167.94 | 360.55 |
| % of total variance | 71.09 | 22.64 | 6.27 | 28.91 |
| U′ (exp rel uncertainty k = 2) | 14.47 | 7.62 | 16.36 | |
| U′ (estimated exp rel uncertainty) 95% confidence (k = 2.28) | 18.65 | |||
It can be seen that in both the classical and robust cases the k-factor has been calculated to be approximately 2.3, resulting in an increase in the confidence interval (and hence U′) from 24.8 to 28.0 (classical) and 16.4 to 18.7 (robust). The larger values (for 95% confidence) can be considered to be more realistic estimates of the expanded relative uncertainty U′ in this practical application when the minimum recommended number of 8 duplicates was used. A similar finding is made for the uncertainty factor FU (classical ANOVA only), which increases from 1.26 to 1.30.
Conclusion
The common practice of multiplying a standard uncertainty by a coverage factor k = 2 to give an expanded uncertainty of approximately 95% confidence will often result in an underestimate of U. This is because in practical applications it may be too costly to make the additional measurements that are required for this to be a good approximation (i.e., n ≥ 30). When n is smaller than 30, more accurate estimates can be made by using the Student's t-distribution. However, this is only straightforward when the measurements to be used for U estimation are derived from a single statistical sample (e.g., a number of analytical measurements from a reference material). This Technical Brief introduces alternative approaches for deriving a modified k-factor when U is calculated as a linear combination of variances from a nested ANOVA, for both classical and robust ANOVA. This capability is provided in the most recent version of the existing RANOVA program (v4.0),6 available on the AMC website. However, it should be remembered that expanded uncertainty assumes that the distribution attributable to the measurand is assumed to be normal (or t) and for such small numbers of measurements it will only be justified to quote U′ to one or two significant digits. Peter D. RostronThis Technical Brief was prepared for the Analytical Methods Committee with contributions from members of the AMC Sampling Uncertainty Expert Working Groups, and the Eurachem Working Group on Uncertainty from Sampling (both chaired by Michael H. Ramsey), and approved on 3 rd June 2024.
References
- Joint Committee for Guides in Metrology, JCGM 100:2008. Evaluation of Measurement Data – Guide to the Expression of Uncertainty in Measurement (GUM), Sevres, 2008, https://www.bipm.org/documents/20126/2071204/JCGM_100_2008_E.pdf/cb0ef43f-baa5-11cf-3f85-4dcd86f77bd6, accessed 15 May 2024 Search PubMed.
- Eurachem/EUROLAB/CITAC/Nordtest/AMC Guide: Measurement Uncertainty Arising from Sampling: a Guide to Methods and Approaches, ed. M. H. Ramsey, S. L. R. Ellison and P. D. Rostron, Eurachem, 2nd edn, 2019, ISBN 978-0-948926-35-8, https://www.eurachem.org/index.php/publications/guides/musamp Search PubMed.
- Analytical Methods Committee, The Duplicate Method for the Estimation of Measurement Uncertainty Arising from Sampling, AMC Technical Brief No. 40, https://www.rsc.org/images/duplicate-method-measurement-uncertainty-technical-brief-40_tcm18-214829.pdf Search PubMed.
- Analytical Methods Committee, Robust statistics - how not to reject outliers. Part 1. Basic concepts, Analyst, 1989, 114, 1693–1697 RSC.
- Analytical Methods Committee, Robust statistics - how not to reject outliers. Part 2. Inter-laboratory trials, Analyst, 1989, 114, 1699–1702 RSC.
- Analytical Methods Committee, RANOVA v4.0 Computer Program, 2024, available from https://www.rsc.org/membership-and-community/connect-with-others/join-scientific-networks/subject-communities/analytical-science-community/amc/software/ Search PubMed.
- F. E. Satterthwaite, An approximate distribution of estimates of variance components, Biometrics Bull., 1946, 2(6), 110–114, DOI:10.2307/3002019.
- P. D. Rostron, T. Fearn and M. H. Ramsey, Improved coverage factors for Expanded Measurement Uncertainty calculated from two estimated variance components, Accredit. Qual. Assur., 2024, 29, 225–230, DOI:10.1007/s00769-024-01579-w.
| This journal is © The Royal Society of Chemistry 2024 |


