Measurement bias in spICP-TOFMS: insights from Monte Carlo simulations

Abstract

Single-particle inductively coupled plasma time-of-flight mass spectrometry (spICP-TOFMS) is used to measure the mass amounts of elements in individual nano and submicron particles. In spICP-TOFMS, element signals can only be recorded as “particles” if they are above the critical value, which is the threshold used to distinguish between particle-derived and background signals. If elements in particles are present in amounts close to or below the critical value, then these elements cannot be quantitatively measured, and the shape of the measured mass distributions will not be accurate. In addition, recorded spICP-TOFMS signal distributions are impacted by measurement uncertainty due to counting statistics inherent to the mass analyzer. Counting noise is most pronounced for elements detected with low signal levels and can lead to systematic biases in the observed element masses and mass ratios from a particle event. In turn, spICP-TOFMS data can lead to incorrect conclusions about element composition and/or size of recorded particles. To better understand how biases and noise can alter the interpretation of data, we employ Monte Carlo simulations to model spICP-TOFMS signals as a function of measurement parameters, such as particle size distribution (PSD), multi-element composition, absolute sensitivities (TofCts g⁻¹), and measurement noise from ion-counting (Poisson) statistics. Monte Carlo simulations allow for the systematic comparison of known (simulated) element mass distributions to experimental (measured) data. To demonstrate the accuracy of our model in predicting spICP-TOFMS signal structure, we highlight the match between data from in-lab measurements and simulations for the detection of CeO₂, ferrocerium mischmetal, and bastnaesite particles. Through Monte Carlo simulations, we explore how analyte PSDs and other measurement parameters can lead to the determination of biased particle sizes, particle numbers, element ratios, and multi-element compositions.

---

Introduction

Single-particle inductively coupled plasma mass spectrometry (spICP-MS) has become a widely used technique for the determination of the size and number concentration of inorganic nanoparticles (NPs).^1–4 When a time-of-flight mass spectrometer is used, the multi-element composition of NPs can be recorded. In spICP-TOFMS, dilute suspensions of particles are introduced into the ICP, where they are vaporized, atomized, and ionized. The resulting ion clouds are transmitted into the TOF mass analyzer and mass-to-charge (m/z) specific particle-derived signals are recorded as individual spikes by the TOFMS detector. Particle-derived signals are typically ∼250–1000 μs in duration and coincident detection of multiple elements indicates the detection of multi-elemental particles.^5–8 In many spICP-TOFMS studies, multi-elemental fingerprints, mass distributions, and/or element mass ratios measured from individual particles are used to distinguish between anthropogenic and natural particle types.^9–13 However, the determined element-mass or particle-size distributions obtained from spICP-TOFMS may not match those of the real (true) particles. Single-particle ICP-MS measurements are conducted in high-time resolution with spectral acquisition rates in the milli- and microsecond regimes. Rapid acquisition rates can lead to the measurement of seemingly complete size distributions that can result in inaccurate determination of number concentration and mean particle size without a priori knowledge, or secondary confirmation, of the true distribution.¹⁴

As with any instrumental method, fundamental noise sources are present in spICP-TOFMS measurements. In ICP-MS, some of these noise sources include plasma flicker noise, Johnson (thermal) noise, or the constant ion background.^15–19 Previous publications have explored noise sources in spICP-MS analysis and their impact on the determination of size distributions, element mass quantities per particle, and particle number concentrations (PNCs).^20–25 Of particular interest is the influence of ion-detection noise from counting (Poisson) statistics, which is often a dominant source of noise in spICP-TOFMS measurements. Poisson noise is especially important to establish accurate critical values and uncertainty in determined PNCs.^24,26–30 In addition to uncertainty in defining critical values, which are used as a threshold to separate the background and particle-derived signals, counting statistics from MS detection can also cause uncertainty and bias in the recorded particle signal distributions. Because the relative standard deviation (RSD) from a Poisson process decreases as λ^−1/2, where λ is the average signal, the deviations between observed and real distributions are expected to be most pronounced for low-abundance (or low-sensitivity) elements.

Measurement bias and the influence of Poisson statistics can be investigated with Monte Carlo simulations.^22,23,31 In a chemical context, Monte Carlo simulations rely on repeated random sampling of a probability distribution to study a chemical or measurement system; the results are then correlated with physical and chemical macroscopic properties, or signal structure.^32–37 In previous work Monte Carlo simulations have been used to characterize spICP-MS signal histograms, and have been used to model spICP-TOFMS background-analyte signals and fit measured m/z-dependent detector responses to a compound Poisson distribution.^22–25,31 The creation of simulated spICP-TOFMS signals allows us to investigate of limitations and biases of measurements without extensive characterization, expensive standards, and long analysis times. Additionally, with Monte Carlo simulations, we can explore the impact of particle properties such as distribution shape, median diameter, and element composition, which are otherwise challenging to vary in real spICP-TOFMS measurements.

Here, we demonstrate the usefulness of Monte Carlo simulations to better understand how biases and noise can alter the interpretation of spICP-TOFMS data. In our simulation, spICP-TOFMS signals are modelled as a function of measurement parameters, such as particle size distribution (PSD), multi-element composition, mass fraction (w) variability, absolute sensitivities (TofCts g⁻¹), and critical values (TofCts). We demonstrate the accuracy of our model in predicting spICP-TOFMS signal structure with data from in-lab measurements and simulations of CeO₂, ferrocerium mischmetal, and bastnaesite mineral particles. Through these Monte Carlo simulations, we explore how analyte PSDs and other measurement parameters can lead to the determination of biased particle sizes, PNCs, element mass ratios, and multi-element compositions.

Materials and methods

Monte Carlo simulations

As previously discussed, Monte Carlo methods have been widely used due to their simplicity and robustness.³² For this proof-of-principal study, Monte Carlo simulations were developed in-house in Python (ver. 3.10.9) with VS Code (ver. 1.87.2); an example of this code is available on our group GitHub page (https://github.com/TOFMS-GG-Group/MonteCarloSimulations). Due to the complex nature of particle transport, ionization, and the plethora of instrument conditions (i.e. torch position, ion optics, etc.), the simulations were performed under the guise of several assumptions. The Monte Carlo simulations described are not used to model particle–plasma interactions or the ionization process; particle residence time in the plasma and ion cloud diffusion are also not considered. We assume that all simulated particles are completely vaporized, mostly ionized, transported into the MS, and detected with user-defined element specific sensitivities (TofCts g⁻¹). In each simulated particle type, all elements are assumed to have some degree of correlation. Simulated spICP-TOFMS signals are derived from particles with a PSD described by a known probability distribution. Furthermore, Poisson counting noise from the mass analyzer is regarded as a major contributor of the ion-signal variance; we do not consider the pulse-height distribution profile of the detector. A workflow describing the Monte Carlo simulation is shown in Fig. 1.

Fig. 1 Particle information is used to randomly generate a PSD with defined median and multiplicative standard deviation. Element mass amounts are calculated by applying a mass fraction (w_i) as either a fixed value or as a distribution of values with set median (x̃) and shape (σ). Each element signal (lambda, λ) is derived by calculating the product of the element-specific sensitivities (S_i), particle mass (m_j), and w_i. Each element signal is randomly drawn from a Poisson distribution. Finally, critical value (L_C,sp) thresholding is applied to the noise-transformed particle signals to obtain measured signals.

Generally, the simulations consider seven factors: distribution shape and spread, median particle diameter (nm), particle density (g cm⁻³), elemental composition, mass fraction (w), m/z-specific absolute sensitivities (TofCts g⁻¹), and m/z-specific critical values (TofCts). In the Monte Carlo simulations, the user defines the median particle diameter, the standard deviation, and the PSD as either log-normal or normal; most data we report here used a log-normal PSD.³⁸ In a log-normal distribution, the histogram of the log-transform of particle diameters will appear normally distributed (i.e. Gaussian). However, the distribution will be right-tail skewed when plotted on a linear scale, which is a characteristic of a log-normal distribution. The mean, median, and mode values of a log-normal distribution are not equal.³⁸ Additionally, for a log-normal distribution the variability can be expressed multiplicatively; hence, we represent variability with times/divide (*/) notation rather than add/subtract (±).³⁸ For example, a log-normal distribution PSD with a notation of 100*/1.5 would have a median diameter of 100 nm and 68.3% of the particles would fall between 100/(1.5)¹ ≈ 67 nm and 100 * (1.5)¹ = 150 nm. Likewise, 95.5% of the particle diameters would be between 100/(1.5)² ≈ 44 nm and 100 * (1.5)² = 225 nm.

Once the PSD is established, particle diameters are simulated by random sampling J values from the distribution, where J is the number of particles specified by the user (see Fig. 1). The mass of each particle is determined by assuming spherical shape and known (user-defined) density. The mass amount of an element in a simulated particle is calculated by multiplying the particle mass (m_j) by the mass fraction of element i (w_i). Within the Python script, the user can apply w as fixed values or as distributions (mass fraction variance, Fig. 1). The w distributions are modelled as log-normal with median = w_i and sigma = w_i * w_RSD, where w_RSD is some positive, real number. Element intensities are calculated by multiplying the element mass amount per particle by element-specific sensitivities. Each element intensity is then treated as the lambda (λ) value for a Poisson distribution from which a random variate is selected; this process mimics the ion-counting process in the mass analyzer. The simulated ion signals with Poisson noise are then truncated at element-specific single-particle critical values (L_C,sp,i) because in real spICP-TOFMS experiments only signals above L_C,sp,i are recorded as particle-derived. Critical values and their role in spICP-TOFMS data analysis have been described elsewhere.³¹ After Monte Carlo simulation of spICP-TOFMS signals, the output signals can be expressed as element mass amounts by dividing the signal by their element-specific sensitivities (S_i).

Simulation conditions

To compare our Monte Carlo simulation results with real spICP-TOFMS data, the TOFMS detection parameters must be equivalent. Here, we set element-specific absolute sensitivities and critical values according to experimental parameters from previously collected data (see Table 1).³⁹ In this data, three cerium containing particle types were measured by spICP-TOFMS. Dilute suspensions of CeO₂, ferrocerium mischmetal, and bastnaesite particles were introduced into an icpTOF-S2 instrument (TOFWERK AG, Thun, Switzerland) via microFAST MC autosampler and a PFA pneumatic nebulizer (PFA-ST, Elemental Scientific, NE, USA) connected via a baffled cyclonic quartz spray chamber to the injector of the ICP torch. The ICP was equipped with an online-microdroplet calibration system, as described previously.^40,41 The datasets were processed using “Time-of-Flight Single Particle Investigator” (TOF-SPI), a free-use particle analysis software written in LabVIEW (LabVIEW 2018, National Instruments, TX, USA) as previously described.⁴²

Table 1 Measurement parameters used for Monte Carlo simulations of three Ce-containing particle types

NP name	Density (g cm^−3)	Element	w	Sensitivity (TofCts g^−1)	Critical value (TofCts)
CeO2	7.22	Ce	0.814	2.78 × 10^17	3.93
Ferrocerium	6.50	Ce	0.677	2.97 × 10^17	14.54
		La	0.323	2.80 × 10^17	14.09
Bastnaesite	5.12	Ce	0.390	2.89 × 10^17	10.35
		La	0.196	2.72 × 10^17	7.64
		Nd	0.170	1.50 × 10^17	6.92
		Pr	0.058	3.34 × 10^17	5.78
		Nd	0.004	3.36 × 10^17	3.18

---

Results and discussion

Comparison of experimental and simulated spICP-TOFMS results

To test our hypothesis that Monte Carlo simulations can be used to replicate experimental spICP-TOFMS data, we compare simulated and experimental results³⁹ from the spICP-TOFMS analysis of three different particle types: CeO₂, ferrocerium mischmetal, and bastnaesite mineral particles. These particles contain one, two, and five ICP-TOFMS detectable elements, respectively. Mass fractions of the detectable elements in these particles are provided in Table 1, and PSD parameters for the Monte Carlo simulations are provided in Table S1.† Simulated particle-type characteristics and distribution parameters were initially tested based on literature reported diameters and mass fractions.⁴³

In Fig. 2, we provide results from the simulation of spICP-TOFMS signals for 10 000 CeO₂ particles with a PSD of 42*/1.4 nm in comparison with experimental spICP-TOFMS results. We simulated particles with a log-normal size distribution because it provided consistency with the other particle types and is a well-established PSD shape in the literature.^38,44–46 A detailed description of the statistical evaluation of similarity between the experimental and simulation results is provided in the ESI.† Briefly, a Mood's median test demonstrated that the medians of the simulated and experimental distributions were not significantly different from one another at the 95% confidence level (χ² = 2.44, p = 0.118); a box and whisker plot for the comparison of both data types is provided in Fig. 2B. The match between the mass distributions of Ce from the Monte Carlo simulations and the spICP-TOFMS measurements demonstrates that the simulations can replicate spICP-TOFMS data for the analysis of single-metal particles.

Fig. 2 (A) Histogram comparison of experimental (grey) and simulated (orange) spICP-TOFMS data of CeO₂ nanoparticles. Both datasets have identical critical masses (0.014 fg, X^Mass_C,sp,Ce), as indicated by the vertical black line. Additionally, a box and whisker plot comparing the lognormal distribution of the simulated (left) and experimental (right) data for CeO₂ particles in (B).

The spICP-TOFMS analysis of ferrocerium mischmetal particles, which are produced by striking a BIC® lighter, shows particles primarily composed of Ce and La.^39,43 Here, we simulated spICP-TOFMS responses for particles with a composition of approximately 67% Ce and 33% La from a log-normal PSD of 32*/1.4 nm. Mass fraction distributions of Ce and La were simulated with a w_RSD = 0.50 (see Table S2†). We found that element ratios in simulated spICP-TOFMS signals do not match experimental results without including w variability (see Fig. S2†). In Fig. 3, we plot comparisons of the experimental and simulated mass amounts of Ce and La, which are statistically similar. As shown in Fig. 3A and B, the recorded mass distributions from spICP-TOFMS analysis of Ce and La in ferrocerium mischmetal particles do not have an outward appearance of log-normal distributions, especially when compared to the results shown for CeO₂ particles. In our Monte Carlo simulation, the majority of Ce and La signals from particles are not detectable because they are below the critical values. Only signals from particles with mass amounts in the upper-tail of the PSD produce large enough signals to be detected by spICP-TOFMS. In high-time resolution measurements, such as those obtained by spICP-TOFMS, the upper-tails can produce a seemingly complete PSDs that will lead to an overestimation of the mean particle diameter and underestimation of the number concentration.¹⁴ Truncation of the signal distributions and, in turn, the inaccurate determination of element mass distributions is a common artifact of spICP-MS analysis.^14,47 This artifact can lead to systematic errors in the determination of PSDs and particle composition.¹⁴

Fig. 3 A comparison of the mass data obtained through measurement of ferrocerium particles via spICP-TOFMS (grey) and Monte Carlo simulations (orange). The mass distributions of Ce (A) and La (B) were compared and showed statistically similar distributions. The relationship between the mass ratio of Ce to La (R_Ce:La) and the mass of Ce, in both acquisition types, is shown (C). Also shown here is the correlation of Ce to La (D) with a ratio of 2.1.

In Fig. 3C and D, we plot the mass ratios of Ce : La as a function of the mass of Ce and the correlation of Ce and La from the Monte Carlo simulations and experimental spICP-TOFMS measurements. Mass ratios of detected elements within particles measured by spICP-TOFMS can expose distinguishable particle-type specific trends.^39,43,48 Previous publications demonstrated that the mass ratios of Ce to La in ferrocerium particles converge to a value of 2.1. As seen, both the central tendency and the spread of the mass ratios of the simulated spICP-TOFMS data reasonably match that of the experimental data; there are a few outliers in the experimental spICP-TOFMS data that are attributed to greater particle heterogeneity than simulated.

Bastnaesite particles detected by spICP-TOFMS have elemental signatures that contain Ce, La, Nd, Pr, and/or Th.^39,43 Without a priori knowledge of the pristine nature of the bastnaesite sample, one might conclude that the different recorded element signatures reflect more than one particle type. For our simulation, we modelled bastnaesite particles with a log-normal PSD of 35*/1.7 nm and w_RSD = 0.15 (see Tables 1, S1, and S2†). In Fig. S3 and S4,† we provide comparisons of the mass distributions and elemental correlations for all elements in the measured and simulated bastnaesite particles. As demonstrated in Fig. 4A, Monte Carlo simulations result in diverse palette of elemental signatures, though only a single particle type is simulated. Like the analysis of Ce and La from ferrocerium, with Monte Carlo modelling, we find that all the detectable elements in bastnaesite particles (i.e. La, Ce, Pr, Nd, and Th) are only partially detected because most bastnaesite particles are not large enough to produce spICP-TOFMS signals above L_C,sp,i values. This is apparent in the right-skewed mass distributions of each element both with experimental and simulated spICP-TOFMS data (see Fig. S3†).

Fig. 4 Sunburst plot (A) illustrating the different elemental signatures obtained from the simulated bastnaesite data. In (B), the true mass distribution of Ce in the simulated particles (grey). Additionally, the cumulative distribution functions of various multi-elemental fingerprints as a function of increasing Ce mass, shown in (B).

In our Monte Carlo simulation results, 54% of particles had enough mass to have at least one element above its respective L_C,sp value, and just 11% of events had sufficient signal to yield the complete LaCePrNdTh signature (see Fig. 4A). Of detectable particles events, most are characterized by five different elemental signatures with varying frequencies: Ce, LaCe, LaCeNd, LaCePrNd, or LaCePrNdTh. Importantly, the number of elements detected per particle is correlated to the total mass of the particle. In Fig. 4B, we plot the histogram of the true simulated Ce mass distribution along with the cumulative distribution functions of six unique elemental fingerprints. From Fig. 4B, it is apparent that as the true mass of the particle increases (indicated by the mass of the major element Ce), the number of recorded multi-elemental particles also increases. Particle size is one of several factors that can contribute to the fragmented nature of the bastnaesite elemental fingerprints. In spICP-TOFMS, the sensitivity and critical values dictate the minimum detectable mass, i.e. the critical mass (X^Mass_C,sp,i) for each element. However, with Monte Carlo simulations, we also demonstrate that compositional heterogeneity of the particles also contributes to the fragmented elemental signatures detected by spICP-TOFMS. The ability to analyze elemental fingerprints before and after spICP-TOFMS detection is a unique feature of utilizing Monte Carlo simulations and aids us to better characterize recorded particle data.

Bias in spICP-TOFMS measurements

The number of detectable events in spICP-TOFMS depends on the PSD, the w of elements within a particle, the elemental sensitivities, and the background signal levels. In Fig. S5,† we plot diameter and mass distributions for particles with size distributions of 35*/1.7 nm, 35*/1.3 nm, and 60*/1.3 nm; simulation conditions for these studies are outlined in Tables 1 and S4.† Due to the cubic relationship between diameter and mass, the range of the mass distribution is much greater than that of the size distribution. For example, particle diameters from a log-normal PSD of 35*/1.3 nm span half an order of magnitude, between 15 and 76 nm (P2.5–P97.5), but the mass distribution spans over two orders of magnitude, from 0.01 to 1.2 fg. Similarly, the range of diameters from a PSD equal to 35*/1.7 nm spans approximately one order of magnitude (7 to 170 nm), but the mass distribution spans across more than four orders of magnitude (1 × 10⁻³ to 12.8 fg). Thus, relatively small changes in median and sigma parameters for a log-normal distribution have a dramatic impact on the mass of the simulated particles. Differences in element mass fractions further expands the range of element mass amounts in particles and indicates that spICP-TOFMS instruments and measurements need to have a large linear dynamic range. In Fig. 5, we provide the results of simulated spICP-TOFMS-determined element mass distributions and compare these detected distributions to the true simulated mass distributions for Ce in modelled bastnaesite particles. We simulated these particles with log-normal size distributions of 20*/1.3 nm, 35*/1.3 nm, 35*/1.7 nm, and 60*/1.3 nm; other simulation conditions are described in Table S4.† For each highlighted simulation, the critical mass of Ce (X^Mass_C,sp,Ce) is 0.036 fg.

Fig. 5 Comparison of the spICP-TOFMS-observed (blue) versus true (red) distributions from Monte Carlo simulations with log-normal distributed bastnaesite particles with various medians and multiplicative standard deviations, labelled accordingly in (A)–(D). The critical mass for each panel is the same (0.036 fg, X^Mass_C,sp,Ce) and is shown as the green, vertical line.

The shape of the observed spICP-TOFMS data depends on the particle distribution median and spread, relative to the critical mass of Ce, as demonstrated in Fig. 5. For example, if the median Ce mass is smaller than X^Mass_C,sp,Ce, such as in Fig. 5A, only the upper-tail of the size distribution can be recorded; thus, the observed distribution does not provide a comprehensive picture of the true mass distribution of Ce within the simulated particles. In this case, the median of the observed mass distribution will be significantly higher than that of the true distribution, therefore, the measurement is biased toward recording larger masses. On the other hand, when the median Ce mass is at, or above X^Mass_C,sp,Ce, then the observed distribution more closely reflects the true distribution shape, as in Fig. 5B–D. However, the observed distributions in 5B and 5C still show skewed shapes but could be misinterpreted to be complete distributions with high number concentrations of the small observed particles.¹⁴ The spICP-TOFMS-determined mass distribution of the 60*/1.3 nm particles best matches the true mass distributions because the lower 95.5% confidence boundary is nearer to the critical mass. For these particles, the lower confidence boundary is 60/(1.3)² = 35.5 nm, which is equivalent to 0.047 fg of Ce—10 ag more than X^Mass_C,sp,Ce. In Fig. 5B and C, we compare spICP-TOFMS results obtained for particles with the same median mass, but different shape parameters (sigma, σ). As seen in 5C, for the distribution with the larger shape parameter, less of the true mass distribution is measurable by spICP-TOFMS; however, the shapes of the mass distributions are similar. When the median of the element mass distribution is near the critical mass of the spICP-TOFMS measurement, the observed distributions are distorted. This incomplete measurement of elemental mass distributions could bias measures of central tendency such as the mean or median and lead to false conclusions regarding the shape of the PSD. On the other hand, to have accurate spICP-TOFMS measurement of mass distributions, the critical mass should be near the lower confidence boundary of the true mass distribution.

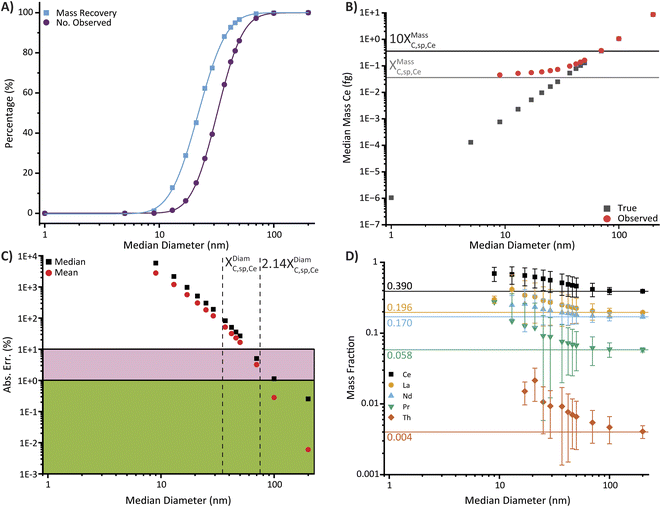
To assess the bias in the measures of central tendency and detected PNCs as a function of PSD, we simulated a series of spICP-TOFMS data from bastnaesite particles with log-normal PSDs and median diameters ranging from 1 to 200 nm (see Table S4† for simulation details). No mass fraction variation in the simulated particles was applied. Through comparing known parameters of the particle populations to those from the simulated spICP-TOFMS data, we quantify the bias expected for the measurement. In Fig. 6, we plot the percent recovery of mass and number of particles, the detected and true median masses of Ce (in fg), the absolute error (%) of the mean and median masses of Ce, and the detected mass fractions of each element as functions of the simulated median diameters (in nm).

Fig. 6 For the simulated case study of bastnaesite particles (A) the percent recovery of mass and number of particles, (B) observed and true median Ce masses, (C) the absolute error of the observed median and mean mass of Ce, and (D) the observed mass fraction of simulated elements plotted as a function of simulated median diameter. An absolute error between 1 and 10% is highlighted in pink and error less than 1% is shown in green.

As seen in Fig. 6A, as the median diameter of the particles increases, so too does the number of observable particles and the mass recovery; this trend follows the log-normal cumulative distribution function as would be expected by scanning the range of the PSD (see Table S5† for fit parameters). In the cases where fewer than 50% particles are above L_C,sp,i, only the upper-tails of the PSDs are recorded by spICP-TOFMS. A majority of the particle distribution is not detected until the true median mass is greater than the critical diameter based on the detection of Ce (X^Diam_C,sp,Ce ≈ 35 nm). Along with underestimation of the particle number, the mean and median masses of the particle populations are overestimated. In Fig. 6B, we plot the observed and true median of the particle populations (see also Fig. S6†). In Fig. 6C, we plot the absolute error of the determined median and mean masses i. Until the observed mass of an element (or the equivalent diameter) is above the critical level, the observed median and mean masses are substantially overestimated and will be reported, generally, to have values near the critical level. Even when the true median diameter equals the critical diameter, the median and mean determined masses are biased by ∼80% and 50%, respectively. When the median mass of the particles increases to ∼5 times that of the critical mass (5X^Mass_C,sp,Ce = 0.180 fg Ce, 56 nm equivalent), the errors in median and mean Ce mass decrease to below 10%. For error below 1%, the median mass needs to be ten times X^Mass_C,sp,Ce, i.e. 0.360 fg. In terms of diameter, 10X^Mass_C,sp,Ce is equivalent to or 2.14X^Diam_C,sp,Ce, which is 75 nm for the data in Fig. 6. For spICP-TOFMS, measured mass distributions will only be accurate when ∼95% of the distribution is above the critical mass. This is analogous to a two-sided detection limit,⁴⁹ but with the shape of the PSD as the “detected” distribution and X^Mass_C,sp,Ce as the false-positive cutoff. As a rule of thumb, we suggest that the critical mass should be an order of magnitude lower than the determined median or mean to avoid measurement bias. However, this rule is difficult to generalize because particle populations may have different PSD shapes and, in-turn, different optimum median mass-to-critical mass ratios.

The systematic bias of spICP-TOFMS measurements also extends to the measurement of element mass ratios within individual particles. In particular, if the mass of a minor element i is at or lower than the critical mass of that element, X^Mass_C,sp,i, then there are two options: either that element is not detected, or it is detected with an elevated relative abundance. When the element is not detected, then the abundance of the major element will be exaggerated. Conversely, when the element is detected, only the upper tail of the Poisson-distributed noise will be recorded, and the major-to-minor element mass ratio will appear too low. Together, this will lead to biased detection of recorded element abundances, as shown in Fig. 6D for the detection of elements in bastnaesite particle populations with increasing median diameters, and broad spread in determined ratios. In Fig. S6,† we plot all observed ratios of Ce : La for particles with median diameters of 25, 50, 100, and 200 nm. As the median diameters of the particle populations increase, the bias in the element ratio decreases. When all the medians of all element masses are above ∼10 times their respective X^Mass_C,sp,i values, error in observed element mass fraction is below 5% for all elements. As seen, bias in the mass fraction of the least abundant elements is most pronounced.

An additional study was conducted to explore the impact of increasing the PSD dispersion on the measures of central tendency (see Tables 1 and S4†). Bastnaesite particles were simulated according to a log-normal PSD with a median diameter of 35 nm and variable multiplicative sigma values between 0.01 and 1 as the distribution shape parameter. In Fig. S7,† we demonstrate the changes in distribution shape, the percent recovery of particles and mass, and compare the detected mean and median masses of Ce to the true mean and median values as a function increasing shape parameter. We also calculate the absolute error (%) for the mean and median masses of Ce and show dispersion of the mass fractions of each simulated element. We provide a detailed discussion of the influence of the dispersion of the PSD of recorded signal distributions in the ESI.† Broadly, we find that error in recorded median and mean values increases with a broader distribution because only the upper 50% of the Ce mass is detected when the mean diameter is 35 nm (X^Diam_C,sp,Ce ≈ 35 nm). However, the error in determined element ratios follows the opposite trend: as the PSD gets broader, more large particles are detected and the observed element ratios in these particles are more accurate.

Conclusions

Here, we demonstrated the usefulness of Monte Carlo methods to simulate particles detected by spICP-TOFMS. spICP-TOFMS signals were modelled as a function of particle and measurement parameters, such as particle size distribution, multi-element composition, absolute sensitivities, and critical values. As a base case, Monte Carlo simulations were able to produce data that accurately reflected spICP-TOFMS analysis of single- and multi-elemental particles. The accuracy of our model in predicting spICP-TOFMS signal structure was demonstrated by highlighting the match between data from in-lab measurements and simulations of CeO₂, ferrocerium mischmetal, and bastnaesite mineral particles. A case study was also performed to investigate the influence of changes in particle distribution shape and median parameters on the detected elemental mass distributions. These results demonstrated that the observed distributions are drastically different from the true distribution when the majority of the particles fall around or below the critical levels. Important and often reported metrics such as median particle diameters, will largely be overestimated unless the critical masses and detected element distributions are well resolved.

Monte Carlo simulations provided the exclusive opportunity to freely explore particle distributions (shapes, medians, variances, etc.) and instrument conditions (absolute sensitivities and critical values) that would be impossible in the lab. The modelling is also rapid: several experiments can be conducted within the matter of a few minutes on a desktop computer. The use of Monte Carlo simulations afforded a unique opportunity to understand how Poisson noise and critical value thresholding dictates trends in mass ratios and measures of central tendency. Monte Carlo simulations could also serve as a tool to look beyond what is measurable in a spICP-TOFMS experiment: through matching measured and simulated signal distributions researchers could gain insight into the true nature of the analyte particles measured. Monte Carlo simulations are expected to serve as an aid to understand the nature of detected particle signals and the original distribution of particles. We believe that such Monte Carlo simulations could be applied to spICP-TOFMS studies in areas such as isotopic analyses, machine learning training, or measurement validation.

Data availability

The Monte Carlo simulation code and associated spICP-TOFMS data are available at https://github.com/TOFMS-GG-Group/MonteCarloSimulations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Ralf Kägi for the Ce-nanomineral sample. We would also like to acknowledge funding sources for this work, including an Iowa State University Faculty Start-up Grant and NSF CAREER grant CHE-2237291.

References

1. F. Laborda, I. Abad-Álvaro, M. S. Jiménez and E. Bolea, Spectrochim. Acta, Part B, 2023, 199, 106570.
2. Z. Meng, L. Zheng, H. Fang, P. Yang, B. Wang, L. Li, M. Wang and W. Feng, Processes, 2023, 11, 1237.
3. D. Mozhayeva and C. Engelhard, J. Anal. At. Spectrom., 2020, 35, 1740–1783.
4. L. J. Johnston, N. Gonzalez-Rojano, K. J. Wilkinson and B. Xing, NanoImpact, 2020, 18, 100219.
5. T. Hirata, S. Yamashita, M. Ishida and T. Suzuki, Mass Spectrom., 2020, 9, A0085.
6. S. Yamashita, M. Ishida, T. Suzuki, M. Nakazato and T. Hirata, Spectrochim. Acta, Part B, 2020, 169, 105881.
7. S. Yongyang, W. Wei, L. Zhiming, D. Hu, Z. Guoqing, X. Jiang and R. Xiangjun, J. Anal. At. Spectrom., 2015, 30, 1184–1190.
8. A. Gundlach-Graham, in Comprehensive Analytical Chemistry, ed. R. Milačič, J. Ščančar, H. Goenaga-Infante and J. Vidmar, Elsevier, 2021, vol. 93, pp. 69–101.
9. A. Praetorius, A. Gundlach-Graham, E. Goldberg, W. Fabienke, J. Navratilova, A. Gondikas, R. Kaegi, D. Gunther, T. Hofmann and F. von der Kammer, Environ. Sci.: Nano, 2017, 4, 307–314.
10. A. Azimzada, I. Jreije, M. Hadioui, P. Shaw, J. M. Farner and K. J. Wilkinson, Environ. Sci. Technol., 2021, 55, 9836–9844.
11. S. Bevers, M. D. Montaño, L. Rybicki, T. Hofmann, F. von der Kammer and J. F. Ranville, Front. Environ. Sci., 2020, 8, 84.
12. T. R. Holbrook, D. Gallot-Duval, T. Reemtsma and S. Wagner, J. Anal. At. Spectrom., 2021, 36, 2684–2694.
13. K. Mehrabi, R. Kaegi, D. Günther and A. Gundlach-Graham, Environ. Sci.: Nano, 2021, 8, 1211–1225.
14. A. C. Gimenez-Ingalaturre, K. Ben-Jeddou, J. Perez-Arantegui, M. S. Jimenez, E. Bolea and F. Laborda, Anal. Bioanal. Chem., 2023, 415, 2101–2112.
15. A. T. Ince, J. G. Williams and A. L. Gray, J. Anal. At. Spectrom., 1993, 8, 899–903.
16. D. P. Myers, G. Li, P. Yang and G. M. Hieftje, J. Am. Soc. Mass Spectrom., 1994, 5, 1008–1016.
17. D. P. Myers, G. Li, P. P. Mahoney and G. M. Hieftje, J. Am. Soc. Mass Spectrom., 1995, 6, 400–410.
18. D. P. Myers, G. Li, P. P. Mahoney and G. M. Hieftje, J. Am. Soc. Mass Spectrom., 1995, 6, 411–427.
19. H. Niu and R. S. Houk, Spectrochim. Acta, Part B, 1996, 51, 779–815.
20. G. Cornelis and M. Hassellöv, J. Anal. At. Spectrom., 2014, 29, 134–144.
21. J. Tuoriniemi, G. Cornelis and M. Hassellöv, J. Anal. At. Spectrom., 2014, 29, 743–752.
22. A. Gundlach-Graham, L. Hendriks, K. Mehrabi and D. Günther, Anal. Chem., 2018, 90, 11847–11855.
23. L. Hendriks, A. Gundlach-Graham and D. Günther, J. Anal. At. Spectrom., 2019, 34, 1900–1909.
24. P.-E. Peyneau and M. Guillon, J. Anal. At. Spectrom., 2021, 36, 2460–2466.
25. P.-E. Peyneau, J. Anal. At. Spectrom., 2022, 37, 2683–2690.
26. F. Laborda, J. Jiménez-Lamana, E. Bolea and J. R. Castillo, J. Anal. At. Spectrom., 2013, 28, 1220–1232.
27. F. Laborda, A. C. Gimenez-Ingalaturre, E. Bolea and J. R. Castillo, Spectrochim. Acta, Part B, 2020, 169, 105883.
28. P.-E. Peyneau, Spectrochim. Acta, Part B, 2021, 178, 106126.
29. D. Mozhayeva and C. Engelhard, J. Anal. At. Spectrom., 2019, 34, 1571–1580.
30. M. Elinkmann, S. Reuter, M. Holtkamp, S. Heuckeroth, A. Köhrer, K. Kronenberg, M. Sperling, O. Rubner, C. D. Quarles, M. Hippler and U. Karst, J. Anal. At. Spectrom., 2023, 38, 2607–2618.
31. A. Gundlach-Graham and R. Lancaster, Anal. Chem., 2023, 95, 5618–5626.
32. A. Barbu and S.-C. Zhu, in Monte Carlo Methods, ed. A. Barbu and S.-C. Zhu, Springer Singapore, Singapore, 2020, pp. 1–17,  DOI:10.1007/978-981-13-2971-5_1.
33. O. A. Guell and J. A. Holcombe, Anal. Chem., 1990, 62, 529A–542A.
34. J. C. Walter and G. T. Barkema, Phys. A, 2015, 418, 78–87.
35. A.-s. Abedi, H. Hoseini, F. Mohammadi-Nasrabadi, N. Rostami and F. Esfarjani, BMC Public Health, 2023, 23, 1320.
36. I. M. Hwang and J.-H. Ha, J. Food Compos. Anal., 2021, 102, 104046.
37. C. Jiang, Q. Zhao, L. Zheng, X. Chen, C. Li and M. Ren, Ecotoxicol. Environ. Saf., 2021, 224, 112679.
38. E. Limpert, W. A. Stahel and M. Abbt, BioScience, 2001, 51, 341–352.
39. R. L. Buckman and A. Gundlach-Graham, J. Anal. At. Spectrom., 2023, 38, 1244–1252.
40. S. Harycki and A. Gundlach-Graham, J. Anal. At. Spectrom., 2023, 38, 111–120.
41. S. Harycki and A. Gundlach-Graham, Anal. Bioanal. Chem., 2022, 414, 7543–7551.
42. A. Gundlach-Graham, S. Harycki, S. E. Szakas, T. L. Taylor, H. Karkee, R. L. Buckman, S. Mukta, R. Hu and W. Lee, J. Anal. At. Spectrom., 2024, 39, 704–711.
43. S. E. Szakas, R. Lancaster, R. Kaegi and A. Gundlach-Graham, Environ. Sci.: Nano, 2022, 9, 1627–1638.
44. H. Saveyn, B. De Baets, O. Thas, P. Hole, J. Smith and P. Van der Meeren, J. Colloid Interface Sci., 2010, 352, 593–600.
45. L. Gamez-Mendoza, M. W. Terban, S. J. L. Billinge and M. Martinez-Inesta, J. Appl. Crystallogr., 2017, 50, 741–748.
46. B. Akbari, M. P. Tavandashti and M. Zandrahimi, Iran. J. Mater. Sci. Eng., 2011, 8, 48–56.
47. A. C. Gimenez-Ingalaturre, K. Ben-Jeddou, J. Perez-Arantegui, M. S. Jimenez, E. Bolea and F. Laborda, Anal. Bioanal. Chem., 2022, 415, 2101–2112.
48. H. Karkee and A. Gundlach-Graham, Environ. Sci. Technol., 2023, 57, 14058–14070.
49. L. A. Currie, Anal. Chem., 1968, 40, 586–593.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ay00859f

---