Open Access Article
Open Access ArticleEnsemble hybrid machine learning to simulate dye/divalent salt fractionation using a loose nanofiltration membrane
Nadeem
Baig
 a,
S. I.
Abba
a,
S. I.
Abba
 *a,
Jamilu
Usman
a,
Mohammed
Benaafi
a and
Isam H.
Aljundi
*a,
Jamilu
Usman
a,
Mohammed
Benaafi
a and
Isam H.
Aljundi
 ab
ab
aInterdisciplinary Research Center for Membrane and Water Security, King Fahd University of Petroleum and Minerals, Dhahran 31261, Saudi Arabia. E-mail: sani.abba@kfupm.edu.sa
bDepartment of Chemical Engineering, King Fahd University of Petroleum and Minerals, Dhahran 31261, Saudi Arabia
First published on 15th September 2023
Abstract
The escalating quantity of wastewater from multiple sources has raised concerns about both water reuse and environmental preservation. Therefore, there is a pressing need for intelligent tools that can aid in comprehending the intricate process of removing dyes and salts from wastewater beyond membrane technology. This study introduces novel standalone hybrid models that integrate an improved nonlinear ensemble approach to model the fractionation of dye and salt rejection (RJDS) (%) based on established experimental data. Using linear sensitivity analysis, two model combinations were identified based on different input variables: M1 (R = 52%, T = 50%, and P = 61%) and M2 (R = 52%, T = 50%, P = 61%, F = 71%, and RJ = 83%). These combinations were incorporated into hybrid neuro-fuzzy (NF) and least square support vector machine (LSSVM) models. The standalone and improved ensemble models were evaluated using several performance criteria, such as MSE, MAE, MAPE, RMSE, and PBAIS. The predictive outcomes demonstrated that NF-M2 outperformed all other models, with an MAE of 0.0002 and an RMSE of 0.0003. Similarly, the ensemble results indicated a significant improvement over the individual models. The study's findings demonstrate the reliability of intelligent tools for modelling RJDS (%) and serving as decision-making performance analysis tools. The proposed approach offers a novel, efficient and reliable technique for understanding and predicting dye and salt rejection in wastewater.
Environmental significanceIntegrating experimental and novel machine learning-based modelling of dye and divalent salt rejection from fractionation using loose nanofiltration membranes in wastewater (WW) experiments has significant environmental implications. High levels of dyes and divalent salts in WW can lead to contamination of water bodies, soil, and plants, negatively impacting aquatic life and human health. The effective removal of dyes and divalent salts from WW is crucial for mitigating the potentially harmful effects of these substances on the environment. By developing accurate and reliable models for predicting dye and divalent salt rejection from WW using loose nanofiltration membranes, researchers can optimize treatment processes and reduce the environmental impact of WW discharge. This study's findings provide an innovative approach to WW treatment and highlight the importance of developing effective strategies for reducing pollutants in WW to safeguard environmental health. |
1. Introduction
Recently, loose NF membranes have received significant attention in the fractionation of dyes/salts1 and resource recovery.2 The production and utilization of various dyes are continuously increasing due to their high requirement in critical and highly demanding societal, industrial products, which include plastics, paper, leather tanning packaging, pharmaceuticals, rubber, and textiles. Several conventional methods have been adopted to treat dyes, which include ozonation, sedimentation, adsorption, floatation, and photocatalytic oxidation.3 For instance, wastewater streams with hypersaline have shown resistance to biological treatment.4 These kinds of streams poison the biological treatment systems, which can significantly impact dye degradation by microbes. However, the membrane-based separation process carries certain advantages of requiring no additives, allowing physical separation, being less energy intensive, and having excellent chances of scalability.5 Loose NF membranes emerged as a powerful separation tool to fractionate dyes and salts compared to other tight NF membranes.Membrane technology, while valuable, is often limited by its fixed design and lack of adaptability.6 Membranes struggle with complex feed compositions and varying conditions, leading to suboptimal separation efficiency. Additionally, fouling and scaling can reduce the membrane lifespan and performance, necessitating frequent replacement. The one-size-fits-all approach of traditional membranes overlooks the intricacies of different applications, hindering optimal results.7,8 To address these limitations, the integration of AI-based models can offer real-time monitoring, adaptive control, and predictive capabilities, revolutionizing membrane processes by optimizing the performance, extending the lifespan, and accommodating diverse operational scenarios.9 Hence, integrating AI with membrane processes, this innovation ensures precision, adaptability, and improved resource utilization, marking a pivotal advancement in separation technology.10
Artificial intelligence (AI) is rapidly growing in several areas and helping significantly in the advancement and understanding of various challenges, including pattern recognition, smart cities, big data, intelligent search, pattern recognition, and healthcare.11 Artificial intelligence has become a popular debate in the mainstream media, and researchers in almost every field are rapidly adopting it to consider it an opportunity to go beyond the human intellect.12 It has been reported that some Al-based systems have blown the whistle by defeating the world champions in their domains of expertise, including the quiz game, Go and chess.13 Machine learning and artificial intelligence are already making a mark in our daily lives. Still, how it would impact physical sciences and how it would be advantageous out of speculation now are big concerns for scientists. The near future would decide how it would be beneficial for solving tedious problems and long-awaited question marks in various research fields.14
In materials science, artificial intelligence is overgrowing and bringing astonishing results and predictions. For instance,15 machine-learning techniques were used for large-scale MOF screening. It was found that the MOF properties are predictable through machine learning methods. Artificial intelligence and machine learning were also used to explore the possibilities of designing high-power-density membranes for pressure retarded osmosis. It has been found that the water permeability coefficient, thickness, and membrane types are the major contributors to improving the water flux, and operation conditions also play a critical role.16 Viet and Jang developed various models based on artificial intelligence to predict filtration performance and membrane fouling in the osmotic membrane bioreactor.17 The artificial intelligence method was employed to predict the engineering factors for the forward osmosis membrane.18 Similarly, machine learning and artificial intelligence have been used for other membranes, including fuel cell alkaline anion exchange membranes9 and proton exchange membrane electrolyzers.19 Thus, artificial intelligence and machine learning can play a critical role in optimizing the membrane fabrication process20 and membrane design and even can successfully predict discoveries in membrane science.21 However, the utilization of artificial intelligence in membrane science is in the stage of infancy, specifically for loose nanofiltration membranes.
During the last decade, several machine learning (ML) techniques have been explored in various fields of desalination and membrane science and engineering.22–28 Based on the aforementioned literature, AI-based techniques can be applied to designing and optimizing nano-filtration membrane systems. Machine learning algorithms, for instance, are used to predict membrane performance based on its physical and chemical characteristics.29 This can help researchers and engineers to identify the most promising membrane materials and design parameters for a given application. Additionally, AI-based control systems can be used to monitor and adjust the operating conditions of a nanofiltration system in real-time, which can help to improve the efficiency and longevity of the membrane. It is worth noting that several surveys highlighted the limited use of AI-based models, specifically hybrid models, in wastewater dye and salt rejection. The rapid advancement of ML may offer new solutions to address the limitations of current membrane processes. Besides, conventional methods have their limitations, and AI-based models have had a significant impact on various industries. It is considered the fourth paradigm of science, alongside data-driven science, as shown in Fig. 1.
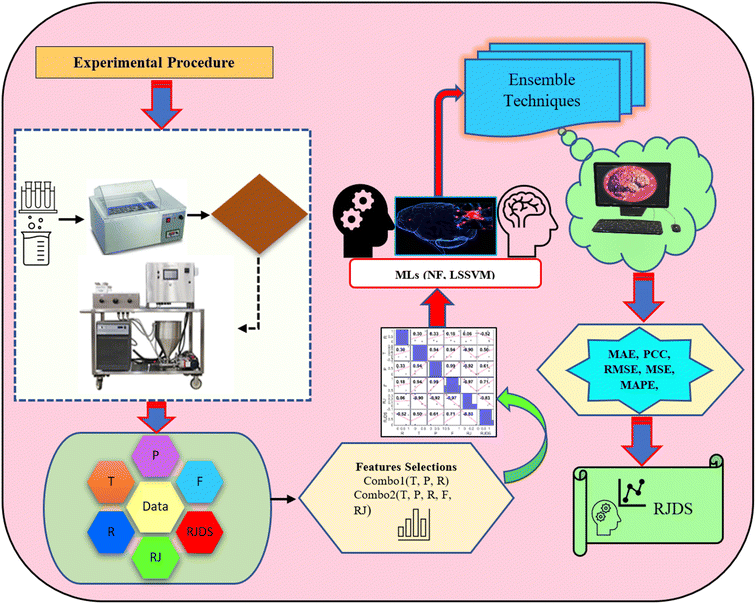
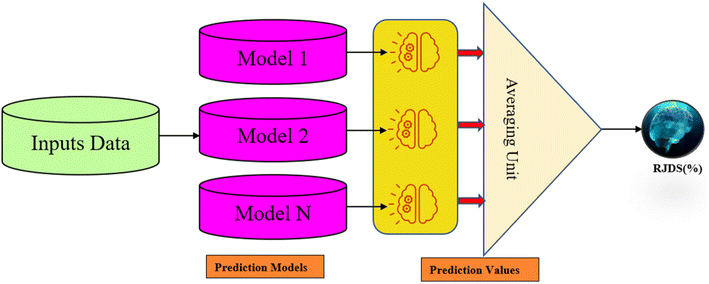
ML, a crucial component of AI, offers various advantages over traditional experimental and computational techniques.30 One major benefit is its ability to quickly analyze large material databases, unlike the resource-intensive multi-physics simulations.31 This leads to cost savings and more efficient material discovery.32 However, a significant challenge in the field of membranes, particularly loose nanofiltration is obtaining sufficient experimental data. To address this, techniques such as selecting important features, increasing data, and processing them can be crucial in improving predictions and reducing training time. These methods can identify the relationship between features and parameters within large sets of data. This study was inspired by an established experimental laboratory using a loose NF membrane and loose layer surface functionalization of ultrafiltration (UF) membranes with nano-silver-immobilized polydopamine. The objective of the study was devoted to AI-based feasibility in modelling and simulation of rejection of dye/salt (RJDS). For this purpose, stand-alone models, namely neuro-fuzzy (NF) model and least square support vector machine (LSSVM), were employed. Subsequently, two different ensemble techniques viz. simple averaging ensemble (SAE) and nonlinear NF ensemble were proposed to improve the prediction accuracy of less accurate models.
2. Experimental methodology
The complete procedure of the preparation of the support and the membrane for the fractionation of the EBT/salt is reported in previously reported experimental work.33 The polysulfone support was prepared on the polyethylene terephthalate support. For the support preparation, a solution of 18% polysulfone was made using dimethylacetamide. The moisture was removed by placing the polysulfone pellets at 50 °C under vacuum. An 18% homogeneous polysulfone solution was prepared by continuously stirring the dried polysulfone pellets overnight in dimethylacetamide. After the polysulfone pellets were completely dissolved, the solution was degassed for half an hour by placing it in a sonicator to remove the trapped bubbles produced during the dissolution of polysulfone. A thin film of the PS was made with the help of the doctor's blade on the surface of the polyethylene terephthalate support. After casting, the thin film was immediately immersed in a coagulation bath to solidify the support. After solidification for completion of the phase inversion process, the PS membranes were placed in deionized water for a time span of 24 hours. The PS membranes were named M-0.Different separating layers develop on the surface of the PS membranes by controlling the polymerization time. The membranes M-1 and M-2, abbreviated as D-6 and D-12, were designed by keeping the PS membranes in a dopamine solution that is controlled at pH 8.5 for 6 hours and 12 hours, respectively. The membranes M-3 (AD6) and M-4 (AD12) were synthesized similarly for the period of 6 and 12 hours, except after the 20 minutes of polydopamine polymerization, the AgNO3 solution was added to reach 0.001 M concentration. Then EBT with 25 ppm and MgSO4 with 2000 ppm concentrations were prepared in deionized (DI) water and used as the feed solution. All these membranes were evaluated using the Sterlitech crossflow setup, which consists of 3 filtration cells.
2.1 Proposed AI-based methodology
The simulation of nanofiltration membrane performance was proposed using the hybrid neuro-fuzzy (NF) model and Least square support vector machine (LSSVM); afterwards the modelling accuracy was improved using simple averaging and nonlinear averaging techniques. It is worth mentioning that one of the advantages of using soft computing in nanofiltration membrane desalination is the ability to optimize the process by analyzing and learning from large amounts of data. This can lead to improved performance, such as higher salt rejection rates and a longer membrane lifespan. Moreover, computational learning can be used to identify and predict potential issues with the membrane, allowing for proactive maintenance and preventing costly downtime. For this experiment, we used normalized data that were split into calibration and validation sets to simulate the rejection of dye/divalent salts. The experimental data which include roughness (R), pressure (P), flux (F), rejection (RJ), and rejection based on dye/salt (RJDS) were pre-processed prior to the modelling schema. For the development of models, sensitivity analysis was used to generate two input combinations. The overall modelling schema is presented in Fig. 2.Besides the sensitivity analysis, normalization (eqn (1)) and cross-validation were conducted to scale-up the data and assess the performance of a model by evaluating its ability to predict outcomes in new, unseen data. Cross-validation is used to avoid overfitting, which happens when a model is too closely fitted to the training data and performs poorly on raw, untainted data.34–36 Although there are various cross-validation techniques, the most well-known one is k-fold cross-validation, which involves splitting the data into k subsets, and training and evaluating the model k times, each time using a different subset as the test set and the remaining k − 1 subsets as the training set.37 This allows the model to be evaluated on a variety of different data, giving a more accurate estimate of its performance on unseen data. Cross-validation is particularly useful for small datasets where it is important to maximize the amount of data used for training while still having enough data for validation. This is crucial for evaluating the performance of a model and fine-tuning its hyperparameters before it is deployed in a real-world setting.38,39 The models were evaluated using several performance criteria such as RMSE (root mean square error), MSE (mean square error), MAE (mean absolute error), R2 (determination coefficient), percent bias (PBAIS) and PCC (Pearson correlation coefficient), as shown in eqn (2)–(7), respectively.
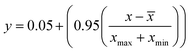 | (1) |
![[x with combining macron]](https://www.rsc.org/images/entities/i_char_0078_0304.gif) , xmax is the maximum value of the data, and xmin is the minimum value.
, xmax is the maximum value of the data, and xmin is the minimum value.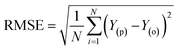 | (2) |
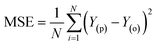 | (3) |
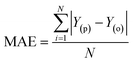 | (4) |
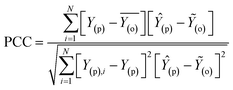 | (5) |
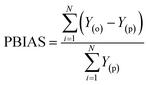 | (6) |
2.2 Neuro-fuzzy model
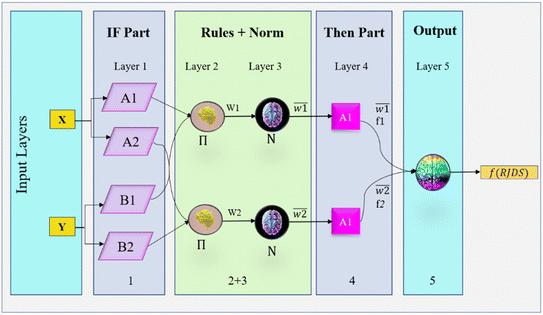
The fuzzy inference system (FIS) and artificial neural network (ANN) are combined into a single intelligence technique known as neuro-fuzzy (NF) or adaptive neuro-fuzzy. To address scientific and technical issues, the NF model combines the best features of the two models. As a result of its usefulness in transforming existing bodies of data into constraint sets, FIS has gained widespread acclaim.40 Optimizing the search space is a viable application for the generated sets, which can be used at the level of the network's topology. To further automate the process of tuning the parameters of a fuzzy controller, NF combines FIS with neural networks with backpropagation (BP).41 Similarly, ANFIS possesses the requisite capabilities for network monotonic tuning using Takagi–Sugeno (TS). Such estimating ability is anticipated in cases where several membership functions were investigated in relation to the datasets, in addition to differentiable T-norm rules.42Learning techniques are typically implemented in NF using a mechanism consisting of two stages.43,44 The conceptual diagram of the basic NF architecture for TS-FIS is illustrated in Fig. 3. This diagram demonstrates that NF requires just two inputs and a single output. A total of five layers of perceptrons or neurons make up the TS-FIS structure. They are the fuzzy layer, implication layer, normalizing layer, defuzzifying layer, and combining layer. Perceptrons and neurons within a single layer are functionally equivalent and share the same characteristics.44
2.3 Least square support vector machine (LSSVM)
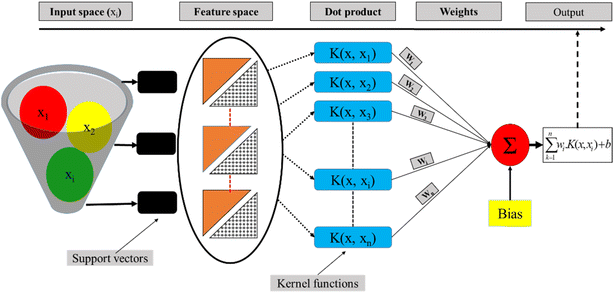
LSSVM as a type of Support Vector Machine (SVM) is an established classification method that accurately groups data, has no issue with the number of dimensions of data, and only requires a short training sample.45 By making slight adjustments, this technique was used by researchers for regression analysis.46 The structural risk diminishing inductive concept was applied to SVM to obtain good generalization on a small set of learning patterns (Fig. 4). To reduce the risk described, researchers have been conducting simultaneous tests to decrease both the empirical risk and the dimension.In the last three decades, researchers have made significant advances toward an enhanced VC, and their work has resulted in a theory that characterizes the qualities of learning machines and allows them to effectively generalize hidden data. Generally, support vector machines come in two primary types: SVC and SVR. A revised version of support vector for use in regression analysis has been developed by ref. 47. They developed a €-insensitive loss function, and then proceeded on to SVMs to address regression issues. In order to minimize ‖ω‖2 and hence reduce the model's complexity, researchers have applied a limit tolerance (epsilon) to SVM (eqn (7)).
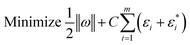 | (7) |
3. Ensemble learning concept
It is clear that when comparing the performance of different intelligent techniques on a specific dataset, one technique may perform better than the others. However, when using different datasets, the results can be quite different.48,49 To take advantage of the strengths of all techniques and maintain a level of generalizability, an ensemble model can be created that combines the outputs of each technique, assigning different levels of importance to each output with the help of an arbitrator to achieve the desired outcome.50 The performance of ML models will be improved using ensemble learning thereby combining the results of different predictors. It was proved that an ensemble of models provided more accurate results than a single model alone. There are many areas of research where ensemble techniques have been successfully implemented, including regression modeling, classification, web ranking, clustering, and time series. To enhance the effectiveness of a particular model, this research employed two linear and one non-linear ensemble methods: simple average ensemble and neuro-ensemble non-linear average techniques.513.1 Simple averaging ensemble (SAE)
The simple averaging ensemble (SAE) is a popular method that is commonly the first option in application due to its flexibility and efficiency. It involves directly averaging the result of the individual model to provide the final outputs.52 The simple averaging ensemble technique (SAE) is achieved through two steps: in the first step, each model is trained and tested separately,53,54 and in the second step, the average of the model output was tested and compared with the observed tested values as illustrated in Fig. 5. The standard equation for SAE is as follows: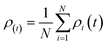 | (9) |
3.2 Nonlinear averaging methods
The nonlinear averaging technique is achieved through training of another neural network. Each model's output is connected to a neuron in the input layer of the neural ensemble model.55,56 When training a nonlinear ensemble model, such as a single NF or ANN using the activation function of the output and hidden layers, any algorithm can be trained by the network, and the epoch number and best structure of the ensemble network can be established via the trial and error technique.57 In this study we used hybrid NF as the ensemble algorithm, although other non-linear kernels such as BPNN might also be utilized as such, a nonlinear ensemble, NF, was used in this research because it is the combination of the neural network and fuzzy logic.4. Results and discussion
4.1 Pre-analysis analysis
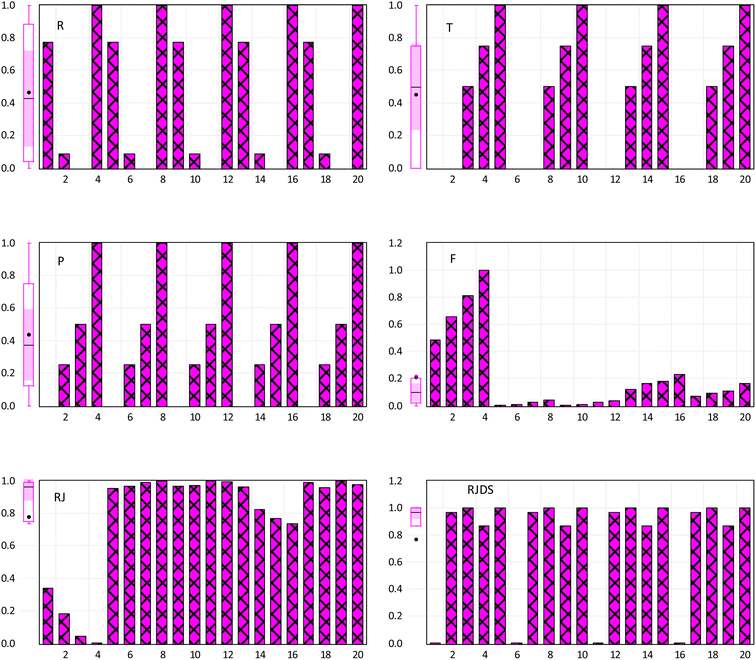
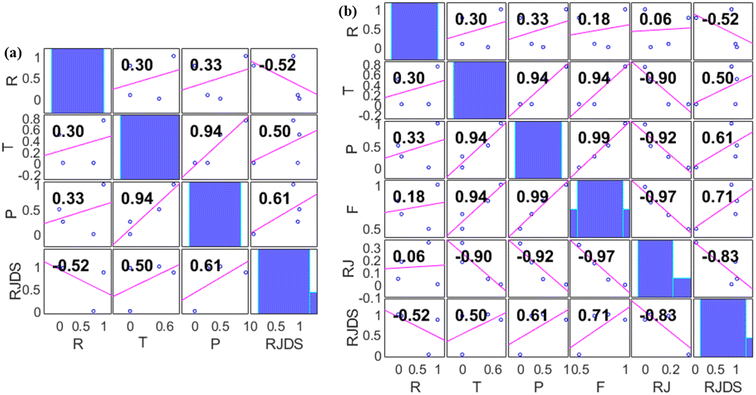
The incorporation of an AI-based approach for experimental analysis can help reduce the time spent carrying out experiment and multiple redundant experiments which thus promotes the efficiency route as well as fabrication processes.58 This will help in tackling the challenges of digitalization, transdisciplinary of research playing a crucial role of discovering a new system with high performance and accelerated optimization. This section explains the result of pre-processing, statistical visualization. Fig. 6 shows the normalized visualization of raw inputs-output variables on the basic statistical parameters, including the skewness, quartile range, bar chart, etc., feature selection and core prediction of F, RJ, and RJDS based on experimental laboratory data. As stated above, this study is aimed at predicting parametric variables (RJDS) based on fractionation of dye/salt experiments. The predictive outcomes of RJDS were evaluated using RMSE which gives more weight to larger errors and are commonly used for regression problems, MAE gives equal weight to all errors, regardless of their magnitude, MAPE is the average of the absolute differences between predicted and actual values, expressed as a percentage of the actual values, and MSE is the mean of the squared differences between predicted and actual values. MSE gives more weight to larger errors, and the bias of a model, which is the difference between the expected predictions of the model and the true values of the data. A low bias indicates that the model is making predictions that are close to the true values.There is no doubt that this research is greatly devoted to crediting the seasoned ML algorithms; in this context, pre-processes such as dependency analysis and data stability were performed prior to the ML developments. The use of this type of pre-analysis process was recently reported in many studies.45,59 Irrespective of making use of the whole input combination in the analysis, it was found that feeding the ML with too much input variables will result in increasing the computational burden as well as delays the time of simulation. Thus, Fig. 7 shows two different proposed combinations (combination 1 (M1) and combination 2 (M2)) for individual target variables using a dependency approach. From the computation analysis, RJDS ((combo-1 = R + T + P) (see Fig. 7a) and (combo-2 = R + T + P + RJ + F) (see Fig. 7b)) is based on a dimensional positive and negative relationship between the input and targets parameters. Despite the linearity of the dependency approach, it still proves to have good performance. Therefore, to achieve reliable results, this study further performed ML algorithm analysis to select the preferable input parameters using this approach.60 The dependency results depicted that the absolute relationship with the target variables (RJDS) is associated with P (61%), R (52%), T (50%), F (71%), and RJ (83%). The numerical quantification shows that R and RJ are inversely proportional to RJDS, while P and T are directly related to the output variables. Although F and RJ can be output in some scenarios, it is worth mentioning that the objective of the modeling is to understand the complex nonlinear RJDS and ML feasibility for detecting them.
4.2 AI-based and ensemble results
This section deals with predictive results of single models (NF, LSSVM) using several performance evaluation criteria. In order to enhance the precision of our predictions, we introduced two distinct and innovative ensemble approaches (SAE-NL and LSSVM-NF). These groundbreaking methodologies were incorporated to elevate the accuracy of our predictive models. Both the ML and ensemble models were developed using MATLAB 2022b meanwhile for graphs, pre- and post-processing of data EViews 11.0 software and XLSTAT were employed. Furthermore, training as well as validation of the models was developed using the modelling schema. To achieve good generalisation of models, there is a need to determine the optimal model structure. For this purpose, several trial-and-error methods were used to generate the fuzzy inference system (FIS) for the NF model based on grid partition and sub-clustering. The hybrid optimum method was utilized with an error tolerance of 0.0005, triangular membership functions (MFs), and 100 epoch iterations. Similarly, optimum input combination for LSSVM was essential as the C and g parameters were determined using a grid search algorithm with 1000 iterations. Table 1 presents the validation results for single and ensemble models.| Models | Validation phase | ||||
|---|---|---|---|---|---|
| MSE | RMSE | MAE | PCC | PBAIS | |
| NF-M1 | 0.0950 | 0.3082 | 0.2196 | 0.6026 | −0.0005 |
| NF-M2 | 0.0000 | 0.0003 | 0.0002 | 1.0000 | 0.0000 |
| LSSVM-M1 | 0.1039 | 0.3223 | 0.2534 | 0.5511 | 0.0000 |
| LSSVM-M2 | 0.0663 | 0.2574 | 0.1946 | 0.7455 | 0.0001 |
| SAE-NL-M1 | 0.0974 | 0.3121 | 0.2365 | 0.7891 | −0.0003 |
| SAE-NL-M2 | 0.0166 | 0.1288 | 0.0974 | 0.9427 | 0.0000 |
| LSSVM-NF | 0.0296 | 0.1719 | 0.0908 | 0.8955 | −0.0003 |
According to the single predictive outcomes, NF-M2 emerged as the best model with satisfactory and reliable low error values for modelling RJDS. According to the validation phase's RMSE values, the performance of a single model is in the following order: NF-M2 (0.0003) > NF-M1 (0.3082) > LSSVM-M2 (0.2574) > LSSVM-M1 (0.3223). However, for the ensemble model the error was hierarchically depicted as follows: SAE-NL-M2 (0.1288) > LSSVM-NF (0.1719) > SAE-NL-M1 (0.3121). It is worth mentioning that hybrid NF proved superior to all the models including improved ensembles. This is strange but not surprising owing to the powerful nature of NF models recorded in several science and engineering technical literature studies.34,61–65 The error performance in terms of MAE and RMSE is presented in Fig. 8.
Recently, different studies in the literature have shown that ML techniques can be utilized to forecast models for a variety of membrane technology applications and processes.66 MLs were used to investigate the correlation between operating conditions and membrane structural parameters with water/salt selectivity. They used the zeta potential and pore radius properties of the developed polyamide NF membrane and then two working parameters (feed concentration and pressure) to do the correlation studies regarding the water/salt selectivity. The results showed that membrane structure parameters have a greater importance in water/salt selectivity than operating conditions, and are associated with the variable influence for different salt types, with symmetric salts being mainly determined by size screening, while asymmetric salts are influenced by Donnan exclusion. The comparison of the single models is presented in Fig. 9.
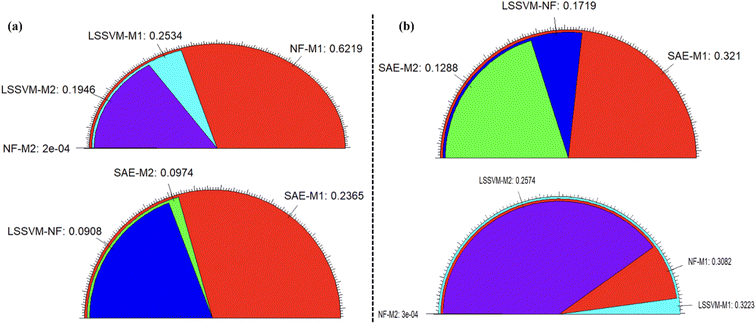
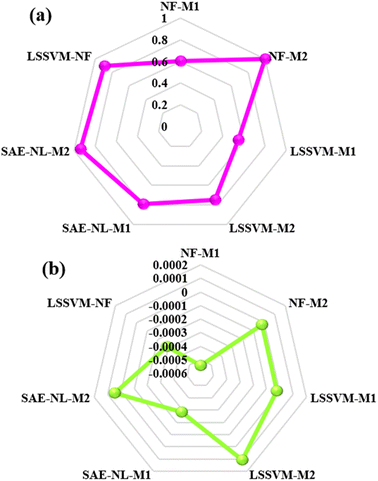
Further investigation of the predictive models can be performed using goodness-fitting values of the models based on the radar chart plot as depicted in Fig. 10. The radar plots are used to appraise the relative multivariate observation with subjective numbers of the variables. Considering the multi-dimensional radar diagrams presented in Fig. 10, it can be noticed that the NF-M2, SAE-NL-M2 and LSSVM-NF models proved to be good and reliable approaches. In general, the achieved dependability performance of the models showed accuracy for the optimal evaluation. The research outcomes could impact the productivity of desalination and sustainable management from an environmental point of view, as addressed and recommended by ref. 67.
It is essential to understand that most of the combinations (P, T, and R) produced marginal accuracy in modelling the RJDS with the predictive accuracy ranging from 55–60% in terms of PCC. The simple strategy indicated that these accuracies were improved to 78% which is still not to the level of decision makers. This paper concluded that using the hybrid NF-M2 and SAE-NL-M2 approaches the required accuracy was attained. The quantitative comparison indicated that NF-M2 outperformed the other models by approximately 40% on average. The present work was numerically compared with that of ref. 22 which proposed an efficient and novel approach for finding a transmembrane pressure using Deep Reinforcement Learning (DRL) to predict different pressure adjustment levels, and the adjustment leads to a salt rejection (SR) of 99% for a desired water flux. This is to confirm that ML models can fit in to solve many problems across almost all fields. Going further,27 experimental literature data on machine learning were used to form prediction models of salt rejection rate and water permeability for thin film nanocomposite membranes. The variables such as size, loading, and pore size of the nanoparticles and other membrane properties were learned using the gradient boosting tree model. The results from the prediction show that porous nanoparticles, size, loading and wettability of the membranes are the key factors that influence the overall performance of the membrane. This was achieved with the help of the gradient boosting tree machine learning model.
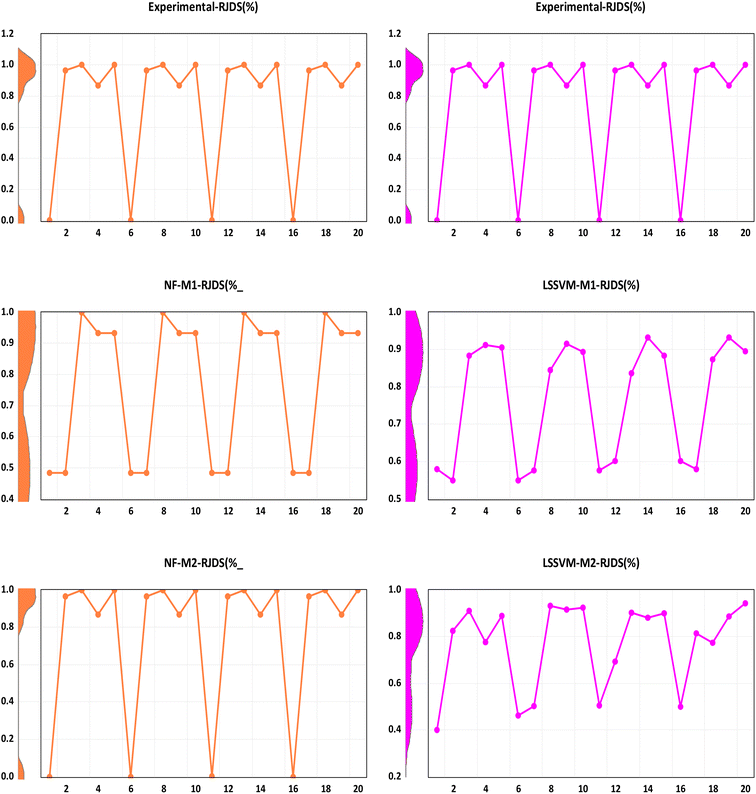
Although all the performance criteria indicated that hybrid nonlinear and ensemble models are capable of predicting the target RJDS variables. The outcomes still suggest the use of other models with the integration of other process variables in order to understand the deep experimental process and reach the optimum decision making. Additional comparison of performance evaluation was based on PBAIS which is often not used in most of the technical problems. The PBAIS indicated how well the proposed model fits the calibration dataset. The validation table shows the bias of the models: NF-M1 (−0.0005), NF-M2 (0.0000), LSSVM-M1 (0.0000), and LSSVM-M2 (0.0001). Similarly, for the ensemble models the PBAIS is numerically indicated as: SAE-NL-M1 (−0.0003), SAE-NL-M2 (0.0000), and LSSVM-NF (−0.0003) which indicated that most of the models match the data training set. The overall trend of the data was captured by NF-M2 and SAE-NL-M2. Moreover, an additional comparison was conducted by ref. 68 that used ML in evaluating the performance optimization of the forward-osmosis membrane system for treatment of wastewater from the textile industry using the ML technique. They used the ML models in predicting the amount of reverse pure water flux and salt rejection of the membranes and they found that the models produce results with good precision. It is essential to visualize the overall outcomes using the empirical cumulative probability distribution function as presented in Fig. 11. These models have several advantages: they are easy to interpret, provide information about the distribution, allow for easy comparison of distributions, and can be used to model the probability distribution of a random variable. This can help to predict future outcomes and make decisions based on those predictions, as in the case of this study (RDJ).
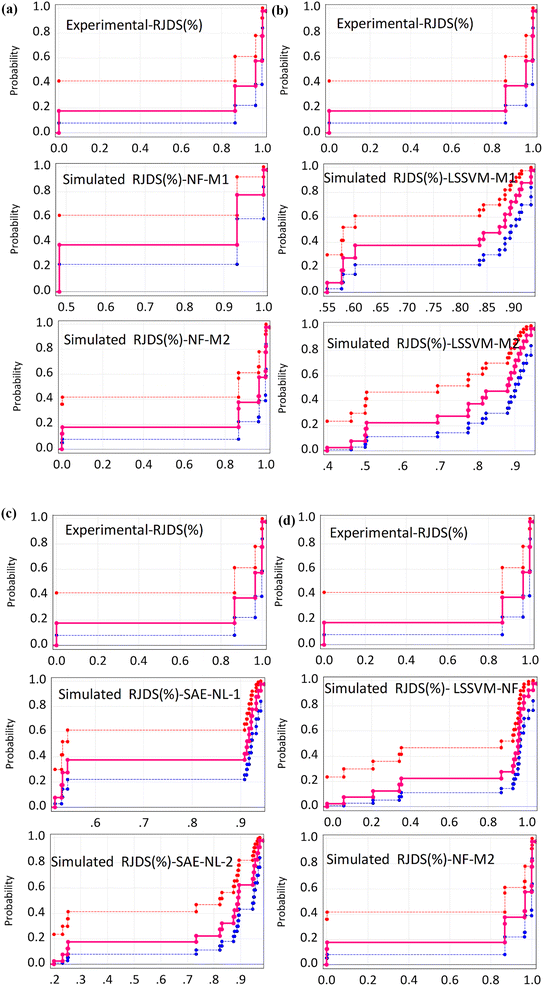 | ||
| Fig. 11 Probability distribution function between the observed and simulated RDJ (%) (a) NF, (b) LSSVM, (c) SAE and (d) comparison of the best models. | ||
Likewise,69 machine learning models were used to quantitatively describe the non-linear ultrafiltration membrane fouling behaviors from process analysis, existing data process models and predictive models of unknown data prediction as well as feature analysis. The outcomes revealed a strong rejection impact on the ultrafiltration membrane when it is in contact with a polluted environment hence leading to an inconsistent self-pollution coefficient and swift fouling. The proposed prediction techniques showed outstanding dependability of the ML tools with a reasonable degree of accuracy, especially hybrid NF. As a result, it's possible to integrate these proposed predictive models with sensors, digital-twins technology or online monitoring systems for sustainable dye and salt experimental monitoring. It's worth mentioning a few limitations of the current study, such as the limited amount of data, testing only a few membranes, and the need for validation through other dye/salt fractionation experiments to gain a comprehensive understanding at a regional level. Nevertheless, the same or other issues can be solved by utilizing more powerful predictive models., such as hybrid metaheuristic learning, objective optimization, and kernel functions. Going forward, it's important to use a vast amount of data to overcome data-related challenges of machine learning.
5. Conclusion
Generally, water serves as an integral part of sustainable development, including human needs and socio-economic growth. Regardless of its essential nature, Saudi Arabia as an arid region is facing serious concerns and challenges owing to the unsustainable practice of water resources. Recently, treated wastewater has been used to mitigate some percentage of water scarcity problems in the Kingdom due to the target Saudi Vision 2030 for clean and renewable water resources. It is believed that intelligent applications of wastewater, such as removing dye/salt using NF and other feasible membranes, would lead to achieving sustainable development goals, especially SDG 6. This study was aimed at providing insight into an AI-based tool for understanding the wastewater simulation of dye/salt (RJDS) rejection based on the experimental laboratory using a loose NF membrane. For this purpose, hybrid NF, LSSVM, and ensemble approaches were used to predict the rate of rejection of dye/salt. It is important to note that the correct research was based on real experimental work. The evaluation benchmarks such as MSE, MAE, MAPE, PCC, and PBAIS were statistically analyzed. The outcomes of the modelling schema indicated that corresponding linear sensitivity analysis was conducted and two model combinations were generated with absolute values of M1 (R = 52%, T = 50%, and P = 61%) and M2 (R = 52%, T = 50%, P = 61%, F = 71%, and RJ = 83%). The results of feature selection indicated that RJ and R were inversely correlated with the output while T, R, F, and P were directly correlated with the RJDS. The combination with M1 produces marginal to good performance while addition of F and RJ significantly improved the prediction outcomes. Similarly, the NF-M2 outperformed all the models with peak prediction accuracy and zero error followed by an ensemble approach which was affected by some weak models during the process. The LSSVM model generally is not reliable but its performance increased substantially during the nonlinear ensemble approach by almost 89% accuracy. The study proposed relies much more on experimental analysis to get more huge data instances, as the data-driven approach needs huge data to have reliable judgment. However, this served as one of the limitations of this study. With regards to future work, the study proposed the implementation of several types of membranes to capture the significant profile of produced water and the desalination process. New technology such as digital twins and the Internet of Things should be considered for integration with the experimental process of membrane dye/salt removal to keep records of the data and track the system automatically.Author contributions
Conceptualization, N. B and S. I. Abba; methodology and validation, N. B and S. I. Abba and J. U.; data curation, J. U. and M. B; writing—original draft preparation, N. B and S. I. Abba and J. U.; writing—review and editing, N. B and S. I. Abba and J. U.; supervision, I. H. A. and M. B.; funding acquisition and resources, N. B. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare no competing financial interests for all submitted manuscripts.Acknowledgements
The authors greatly acknowledge the financial support offered by the IRC membrane & water security at King Fahd University of Petroleum & Minerals (KFUPM), under the project number INMW2312.References
- X. Feng, D. Peng, J. Zhu, Y. Wang and Y. Zhang, Recent advances of loose nanofiltration membranes for dye/salt separation, Sep. Purif. Technol., 2022, 285, 120228 CrossRef CAS.
- S. Guo, Y. Wan, X. Chen and J. Luo, Loose nanofiltration membrane custom-tailored for resource recovery, Chem. Eng. J., 2021, 409, 127376 CrossRef CAS.
- M. Mondal and S. De, Treatment of textile plant effluent by hollow fiber nanofiltration membrane and multi-component steady state modeling, Chem. Eng. J., 2016, 285, 304–318 CrossRef CAS.
- O. Lefebvre and R. Moletta, Treatment of organic pollution in industrial saline wastewater: A literature review, Water Res., 2006, 40, 3671–3682 CrossRef CAS PubMed.
- M. Cheryan, Ultrafiltration and Microfiltration Handbook, 1998 Search PubMed.
- E. Drioli, E. Curcio, G. Di Profio, F. Macedonio and A. Criscuoli, Integrating membrane contactors technology and pressure-driven membrane operations for seawater desalination: Energy, exergy and costs analysis, Chem. Eng. Res. Des., 2006, 84, 209–220 CrossRef CAS.
- M. C. Garg and H. Joshi, A new approach for optimization of small-scale RO membrane using artificial groundwater, Environ. Technol., 2014, 35, 2988–2999 CrossRef CAS PubMed.
- M. Padaki, et al., Membrane technology enhancement in oil – water separation. A review, Desalination, 2015, 357, 197–207 CrossRef CAS.
- X. Zou, et al., Machine learning analysis and prediction models of alkaline anion exchange membranes for fuel cells, Energy Environ. Sci., 2021, 14, 3965–3975 RSC.
- N. Baig, J. Usman, S. I. Abba, M. Benaafi and I. H. Aljundi, Fractionation of dyes/salts using loose nanofiltration membranes: Insight from machine learning prediction, J. Cleaner Prod., 2023, 138193, DOI:10.1016/j.jclepro.2023.138193.
- C. Niu, X. Li, R. Dai and Z. Wang, Artificial intelligence-incorporated membrane fouling prediction for membrane-based processes in the past 20 years: A critical review, Water Res., 2022, 216, 118299 CrossRef CAS PubMed.
- U. Paschen, C. Pitt and J. Kietzmann, Artificial intelligence: Building blocks and an innovation typology, Bus. Horiz., 2020, 63, 147–155 CrossRef.
- W. Sha, et al., Artificial Intelligence to Power the Future of Materials Science and Engineering, Adv. Intell. Syst., 2020, 2, 1900143 CrossRef.
- D. M. Dimiduk, E. A. Holm and S. R. Niezgoda, Perspectives on the Impact of Machine Learning, Deep Learning, and Artificial Intelligence on Materials, Processes, and Structures Engineering, Integr. Mater. Manuf. Innov., 2018, 7, 157–172 CrossRef.
- G. Borboudakis, et al., Chemically intuited, large-scale screening of MOFs by machine learning techniques, npj Comput. Mater., 2017, 3, 1–6 CrossRef CAS.
- R. Rath, et al., Rational design of high power density “Blue Energy Harvester” pressure retarded osmosis (PRO) membranes using artificial intelligence-based modeling and optimization, Energy Convers. Manage., 2022, 253, 115160 CrossRef CAS.
- N. D. Viet and A. Jang, Development of artificial intelligence-based models for the prediction of filtration performance and membrane fouling in an osmotic membrane bioreactor, J. Environ. Chem. Eng., 2021, 9, 105337 CrossRef CAS.
- S. J. Im, V. D. Nguyen and A. Jang, Prediction of forward osmosis membrane engineering factors using artificial intelligence approach, J. Environ. Manage., 2022, 318, 115544 CrossRef CAS PubMed.
- R. Yang, A. Mohamed and K. Kim, Optimal design and flow-field pattern selection of proton exchange membrane electrolyzers using artificial intelligence, Energy, 2023, 264, 126135 CrossRef CAS.
- B. Li, et al., A novel method integrating response surface method with artificial neural network to optimize membrane fabrication for wastewater treatment, J. Cleaner Prod., 2022, 376, 134236 CrossRef CAS.
- H. Yin, et al., Machine learning for membrane design and discovery, Green Energy Environ., 2022 DOI:10.1016/j.gee.2022.12.001.
- T. Bonny, M. Kashkash and F. Ahmed, An efficient deep reinforcement machine learning-based control reverse osmosis system for water desalination, Desalination, 2022, 522, 115443 CrossRef CAS.
- A. Hosseinzadeh, et al., Machine learning-based modeling and analysis of PFOS removal from contaminated water by nanofiltration process, Sep. Purif. Technol., 2022, 289, 120775 CrossRef CAS.
- R. Goebel, T. Glaser and M. Skiborowski, Machine-based learning of predictive models in organic solvent nanofiltration: Solute rejection in pure and mixed solvents, Sep. Purif. Technol., 2020, 248, 117046 CrossRef CAS.
- R. Goebel and M. Skiborowski, Machine-based learning of predictive models in organic solvent nanofiltration: Pure and mixed solvent flux, Sep. Purif. Technol., 2020, 237, 116363 CrossRef CAS.
- N. Jeong, T. H. Chung and T. Tong, Predicting Micropollutant Removal by Reverse Osmosis and Nanofiltration Membranes: Is Machine Learning Viable?, Environ. Sci. Technol., 2021, 55, 11348–11359 CrossRef CAS PubMed.
- C. S. H. Yeo, Q. Xie, X. Wang and S. Zhang, Understanding and optimization of thin film nanocomposite membranes for reverse osmosis with machine learning, J. Membr. Sci., 2020, 606, 118135 CrossRef CAS.
- M. Fetanat, et al., Machine learning for design of thin-film nanocomposite membranes, Sep. Purif. Technol., 2021, 270, 118383 CrossRef CAS.
- D. Rall, et al., Multi-scale membrane process optimization with high-fidelity ion transport models through machine learning, J. Membr. Sci., 2020, 608, 118208 CrossRef CAS.
- H. M. Mustafa, et al., Performance Evaluation of Hydroponic Wastewater Treatment Plant Integrated with Ensemble Learning Techniques: A Feature Selection Approach, Processes, 2023, 11, 4782023 CrossRef.
- S. K. Bhagat, et al., Comprehensive review on machine learning methodologies for modeling dye removal processes in wastewater, J. Cleaner Prod., 2023, 385, 135522 CrossRef CAS.
- Z. Wei, Q. He and Y. Zhao, Machine learning for battery research, J. Power Sources, 2022, 549, 232125 CrossRef CAS.
- N. Baig, et al., Antifouling low-pressure highly permeable single step produced loose nanofiltration polysulfone membrane for efficient Erichrome Black T/divalent salts fractionation, J. Environ. Chem. Eng., 2022, 10, 108166 CrossRef CAS.
- B. Tawabini, et al., Spatiotemporal Variability Assessment of Trace Metals Based on Subsurface Water Quality Impact Integrated with Artificial Intelligence-Based Modeling, Sustainability, 2022, 14, 2192 CrossRef CAS.
- S. J. Hadi, et al., Non-Linear Input Variable Selection Approach Integrated With Non-Tuned Data Intelligence Model for Streamflow Pattern Simulation, IEEE Access, 2019, 7, 141533–141548 Search PubMed.
- S. I. Abba, et al., Evolutionary computational intelligence algorithm coupled with self-tuning predictive model for water quality index determination, J. Hydrol., 2020, 587, 124974 CrossRef.
- I. K. Umar, et al., An intelligent hybridized computing techniques for the prediction of roadway traffic noise based on non-linear mutual information, Soft Comput., 2023, 27, 10807–10825 CrossRef.
- M. Saood, et al., New generation neurocomputing learning coupled with a hybrid neuro-fuzzy model for quantifying water quality index variable: A case study from Saudi Arabia, Ecol. Inform., 2022, 70, 101696 CrossRef.
- M. A. Yassin, et al., Geochemical and Spatial Distribution of Topsoil HMs Coupled with Modeling of Cr Using Chemometrics Intelligent Techniques: Case Study from Dammam Area, Saudi Arabia, Molecules, 2022, 27, 4220 CrossRef CAS PubMed.
- M. S. Gaya, N. A. Wahab, Y. M. Sam, A. N. Anuar and S. I. Samsuddin, ANFIS modelling of carbon removal in domestic wastewater treatment plant, Appl. Mech. Mater., 2013, 372, 597–601 Search PubMed.
- J.-S. Jang, ANFIS: adaptive-network-based fuzzy inference system, IEEE Trans. Syst. Man Cybern., 1993, 23, 665–685 CrossRef.
- S. A. Akrami, V. Nourani and S. J. S. Hakim, Development of Nonlinear Model Based on Wavelet-ANFIS for Rainfall Forecasting at Klang Gates Dam, Water Resour. Manag., 2014, 28, 2999–3018 CrossRef.
- V. H. Quej, J. Almorox, J. A. Arnaldo and L. Saito, ANFIS, SVM and ANN soft-computing techniques to estimate daily global solar radiation in a warm sub-humid environment, J. Atmos. Sol.-Terr. Phys., 2017, 155, 62–70 CrossRef.
- L. N. Emembolu, P. E. Ohale, C. E. Onu and N. J. Ohale, Comparison of RSM and ANFIS modeling techniques in corrosion inhibition studies of Aspilia Africana leaf extract on mild steel and aluminium metal in acidic medium, Appl. Surf. Sci. Adv., 2022, 11, 100316 CrossRef.
- A. Seifi, M. Ehteram, V. P. Singh and A. Mosavi, Modeling and uncertainty analysis of groundwater level using six evolutionary optimization algorithms hybridized with ANFIS, SVM, and ANN, Sustainability, 2020, 12, 4023 CrossRef.
- C. Cortes and V. Vapnik, Support-vector networks, Mach. Learn., 1995, 20, 273–297 Search PubMed.
- V. N. Vapnik, The Nature of Statistical Learning Theory, Springer, New York, 1995 Search PubMed.
- K. M. Zorn, et al., Machine Learning Models for Estrogen Receptor Bioactivity and Endocrine Disruption Prediction, Environ. Sci. Technol., 2020, 54, 12202–12213 CrossRef CAS PubMed.
- Y. Zhao, et al., Deep Learning Prediction of Polycyclic Aromatic Hydrocarbons in the High Arctic, Environ. Sci. Technol., 2019, 53(22), 13238–13245 CrossRef PubMed.
- A. Tahsin, et al., Multi-state comparison of machine learning techniques in modelling reference evapotranspiration: A case study of Northeastern Nigeria, 2021 1st Int. Conf. Multidiscip. Eng. Appl. Sci. ICMEAS 2021, 2021, pp. 1–6, DOI:10.1109/ICMEAS52683.2021.9692355.
- A. G. Usman, S. Işik and S. I. Abba, A Novel Multi-model Data-Driven Ensemble Technique for the Prediction of Retention Factor in HPLC Method Development, Chromatographia, 2020, 83, 933–945 CrossRef CAS.
- U. Alhaji, E. Chinemezu, J. Nwachukwu and S. Isah, Prediction of energy content of biomass based on hybrid machine learning ensemble algorithm, Energy Nexus, 2022, 8, 100157 CrossRef.
- P. M. Granitto, P. F. Verdes and H. A. Ceccatto, Neural network ensembles: Evaluation of aggregation algorithms, Artif. Intell., 2005, 163, 139–162 CrossRef.
- T. Helmy, S. M. Rahman, M. I. Hossain and A. Abdelraheem, Non-linear Heterogeneous Ensemble Model for Permeability Prediction of Oil Reservoirs, Arabian J. Sci. Eng., 2013, 38, 1379–1395 CrossRef CAS.
- A. Alamrouni, et al., Multi-Regional Modeling of Cumulative COVID-19 Cases Integrated with Environmental Forest Knowledge Estimation: A Deep Learning Ensemble Approach, Int. J. Environ. Res. Public Health, 2022, 19, 1–22 Search PubMed.
- R. M. Adnan, A. Jaafari, A. Mohanavelu, O. Kisi and A. Elbeltagi, Novel ensemble forecasting of streamflow using locally weighted learning algorithm, Sustainability, 2021, 13, 5877 CrossRef.
- T. G. Dietterich, Ensemble methods in machine learning. In: International Workshop on Multiple Classifier Models, Oncogene, 1996, 12, 1–15 Search PubMed.
- C. E. Reid, et al., Spatiotemporal prediction of fine particulate matter during the 2008 Northern California wildfires using machine learning, Environ. Sci. Technol., 2015, 49, 3887–3896 CrossRef CAS PubMed.
- A. Solgi, A. Pourhaghi, R. Bahmani and H. Zarei, Pre-processing data using wavelet transform and PCA based on support vector regression and gene expression programming for river flow simulation, J. Earth Syst. Sci., 2017, 126, 1–17 CrossRef CAS.
- R. Costache, et al., Flash-flood susceptibility assessment using multi-criteria decision making and machine learning supported by remote sensing and GIS techniques, Remote Sens., 2020, 12, 106 CrossRef.
- H. U. Abdullahi, A. G. Usman, S. I. Abba and H. U. Abdullahi, Modelling the Absorbance of a Bioactive Compound in HPLC Method using Artificial Neural Network and Multilinear Regression Methods, Dutse J. Pure Appl. Sci., 2020, 6(2), 362–371 Search PubMed.
- V. Nourani, P. Ghaneei and S. A. Kantoush, Robust clustering for assessing the spatiotemporal variability of groundwater quantity and quality, J. Hydrol., 2022, 604, 127272 CrossRef CAS.
- Z. M. Yaseen, et al., The integration of nature-inspired algorithms with Least Square Support Vector regression models: Application to modeling river dissolved oxygen concentration, Water, 2018, 10, 1124 CrossRef.
- V. Nourani, G. Elkiran and S. I. Abba, Wastewater treatment plant performance analysis using artificial intelligence – an ensemble approach, Water Sci. Technol., 2018, 78(10), 2064–2076 CrossRef PubMed.
- R. A. Abdulkadir, et al., Forecasting of daily rainfall at Ercan Airport Northern Cyprus: a comparison of linear and non-linear models Forecasting of daily rainfall at Ercan Airport Northern Cyprus : a comparison of linear and non-linear models, Desalin. Water Treat., 2020, 177, 297–305 CrossRef.
- X. Ma, et al., Revealing key structural and operating features on water/salts selectivity of polyamide nanofiltration membranes by ensemble machine learning, Desalination, 2023, 548, 116293 CrossRef CAS.
- O. A. Hamed, A. M. Hassan, K. Al-Shail and M. A. Farooque, Performance analysis of a trihybrid NF/RO/MSF desalination plant, Desalin. Water Treat., 2009, 1, 215–222 CrossRef CAS.
- K. Aghilesh, A. Mungray, S. Agarwal, J. Ali and M. Chandra Garg, Performance optimisation of forward-osmosis membrane system using machine learning for the treatment of textile industry wastewater, J. Cleaner Prod., 2021, 289, 125690 CrossRef.
- S. Shapsough, R. Dhaouadi, I. Zualkernan and M. TakrouriPower Prediction via Module Temperature for Solar Modules Under Soiling Conditions, in Smart Grid and Internet of Things, ed. Deng, D.-J., Pang, A.-C. and Lin, C.-C., Springer International Publishing, 2020, pp. 85–95, DOI:10.1007/978-3-030-49610-4_7.
| This journal is © The Royal Society of Chemistry 2023 |