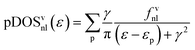Extended π-conjugation: a key to magnetic anisotropy preservation in highly reactive porphyrins

Abstract

In this study, the magnetic anisotropy of metal complexes is explored for its crucial role in the development of molecular materials for cutting-edge applications in spintronics, memory storage, and quantum computing. The challenge of achieving maximum magnetic anisotropy for paramagnetic single nickel ion sites is addressed and realized through an on-surface thermally induced planarization reaction in tetraphenylporphyrin, which maintains the nickel species in a square planar coordination environment. At the same time, the effective ligand field reduction due to the increased π-conjugation results in a lower reactivity of the molecular species. The results herein reported showcase the synergy between magnetic anisotropy and chemical robustness in single-site magnetic materials, thus opening exciting prospects for the development of stable uniaxial anisotropy in these materials. Such a finding represents a relevant advance in the field and validates a protocol for exploring magnetic anisotropy in metal complexes.

---

Introduction

Due to the high periodicity of identical magnetic centers across the interface, monodispersity, and ease of chemical tuning in the initial molecular synthesis, molecular magnetic arrays on metal substrates hold promise for the fabrication of high-density storage and quantum computing devices.^1–3 In contrast with unsaturated metallic adatoms, whose interaction with the substrate may easily lead to a magnetic moment quenching,⁴ their embedding into a molecular ligand field may preserve large magnetic anisotropies in supported systems.^5–8 As a result of this finding, surface-supported metal porphyrins, in which the central metal ion (CM) is coordinated by a tetrapyrrolic macrocycle, are gaining interest as novel functional molecular architectures because of their exceptional physical and chemical properties, such as high structural stability, intense electronic absorption/emission, and reactivity. The molecule–substrate interaction tuning may then be exploited to stabilize the CM in different spin configurations.^9–11 Furthermore, on-surface synthesis allows the modification of the chemical structure and the formation of extended covalent nanostructures, which further strengthens porphyrin-based architectures.¹²

In this regard, a well-known surface-assisted ring-closure reaction in the case of tetraphenylporphyrin (TPP) results in the formation of a planarized porphyrin molecule with an extended π-conjugated macrocycle ring.^13,14 Recently, the on–surface planarization reaction has also been suggested as an effective way to alter the magnetic properties, as evidenced by the increase of the effective spin moment in iron(II)-tetrabenzoporphyrin.¹⁵

The electronic and magnetic properties of surface-supported metal porphyrin arrays may be further modified by functionalizing the CM with axial ligands.^5,16–18 Small ligands such as NO, NH₃, and NO₂ have been shown to bind to the porphyrin's CM, inducing changes in its spin state. The presence of new bonds with the surface and additional ligands increases the CM coordination number of the porphyrin complexes from four to five or six. As such, the coordination number increase is usually accompanied by a magnetic anisotropy decrease as a consequence of the complex symmetry reduction, which lowers the energy barrier between different magnetic configurations. Additionally, the presence of axial ligands may influence the CM oxidation state, spin state, and magnetic moment thus affecting the magnetic anisotropy. Factors promoting reactivity towards axial ligands include the partial occupation of the CM-based d_z² atomic orbital (AO), a low CM oxidation state, and the complex conformational flexibility.^10,11,19,20 A precise control of these factors is pivotal to preserve both the magnetic anisotropy and a preferred magnetization direction.

However, the correlation between the planarization-induced changes in the electronic and magnetic molecular properties with the axial reactivity quenching and the anisotropy preservation has not been fully explored yet.

To fill this gap, in this study, a multi-technique approach based on photoemission and absorption spectroscopy along with X-ray magnetic circular dichroism (XMCD) combined with semiempirical crystal field multiplet calculations and density functional theory (DFT) simulations within the molecular cluster approach has been exploited to delve into the energy level alignment and charge distribution in the Ni 3d AOs for NiTPP and its planarized form, both of them supported on Cu(100). Although a substantial charge transfer and hybridization between the Ni 3d states and substrate 4s states leads to a magnetically active configuration in both molecular forms, their different electronic structure results in distinct magnetic and chemical behaviour. More specifically, the findings herein reported highlight the crucial role played by planarization in quenching the reactivity towards NO₂ and preserving the molecular magnetic anisotropy. Indeed, the reactivity quenching has been associated with the weakening of the porphyrin ligand field, which accompanies the π-conjugation increase due to the ring-closure reaction.

As a whole, these insights provide valuable information for functionalizing surface-supported metal porphyrins, fine-tuning electromagnetic properties, and paving the way for applications such as single-ion catalysis, magnetism, and biosensing.

Results and discussion

Planarization of NiTPP on Cu(100)

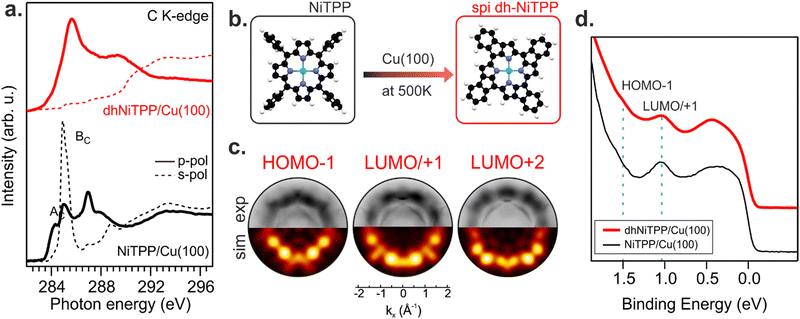
Recently, the NiTPP/Cu(100) interface's high thermal and chemical stability has been demonstrated by heating it up to 620 K.²¹ The room temperature (RT) deposition of NiTPP on copper results in the formation of a closely packed monolayer (ML) phase with long-range order. The strong interaction between Cu(100) and the molecular layer, as reflected by the high charge transfer from the substrate to NiTPP, pins the molecules to their adsorption site, thus preventing any displacement, which is crucial for the phenyls’ flattening and the subsequent cyclodehydrogenation reaction to take place. Such a pinning effect has been avoided here by depositing the NiTPP at a slower rate on the substrate maintained at 500 K, thus also favoring the temperature-triggered cyclization reaction.

C K-edge NEXAFS spectra of NiTPP deposited on Cu(100) at 500 K and RT reveal changes in the linear dichroism, indicating that the flattening of NiTPP occurs only on the hot substrate (see Fig. 1(a)). In more detail, the π* resonance (labelled as B_C) well evident in the RT s-polarized C K-edge spectrum associated with the phenyl rings (Phs) almost perpendicular to the macrocycle plane, is significantly reduced when NiTPP is deposited on the hot substrate consistently with a coplanarity established between the Phs (associated transition labelled as B_C) and the macrocycle fragment (associated transition labelled as A_C). As observed for H₂TPP on Ag(111),¹³ the absence of the Ph-based π* resonance in the s-polarized C K-edge spectrum is a clear indication of the flattening of adsorbed porphyrin molecules, which results from a dehydrogenation reaction accompanied by the formation of an additional C–C bond between Ph rings and the porphyrinic macrocycle. The deposition of NiTPP on a hot substrate is then not only a key factor in transforming it into the corresponding flat derivative (hereafter, dhNiTPP) but, more generally, an efficient method to trigger the ring-closure reaction when the reagent is strongly anchored to the substrate, and the post-deposition annealing of the densely packed network formed at RT proves to be ineffective.²¹ Diverse planarized NiTPP derivates may be formed during the cyclodehydrogenation reaction,^22,23 with two of them being predominant, namely the spiral one (spi-dhNiTPP), where each Ph ring joins an adjacent pyrrole (Py) group on the same side, and the rectangular one (rect-dhNiTPP), where two adjacent Phs join the same Py, thus leaving two Pys with no Ph decoration. DFT numerical simulations carried out to optimize the geometrical parameters of gas-phase spi-dhNiTPP and rect-dhNiTPP (see Section S3 in ESI†) found the former more stable than the latter by 0.31 eV. Insights into dehydrogenation pathways have been obtained following the on-surface reaction via photoemission orbital tomography (POT). Inasmuch as the dhNiTPP/Cu(100) interface has a preferential on-surface orientation and molecular levels characterized by sharp momentum maps, POT enables the assignment of the valence band (VB) spectral features to the initial molecular orbitals (MO) through the comparison of experimental and theoretical photoelectron angular distributions.²⁴ The results clearly state that the spi-dhNiTPP/Cu(100) interface better matches the experimental momentum maps than the rect-dhNiTPP one (see Fig. 1(c) and Fig. S4 in ESI†), thus indicating the preferential formation of the spi-dhNiTPP species. Based on this, hereafter, dhNiTPP corresponds to the spi-dhNiTPP species. Fig. 1(d) reveals that the adsorbate–substrate interaction is quite similar in NiTPP and dhNiTPP. Indeed, the HOMO−1 and the energy-degenerate LUMO/+1 (former gas-phase highest occupied and lowest unoccupied MO)²⁵ peaks lie at the same binding energy, the only difference being the nature of the molecular orbital observed in proximity of the Fermi level, the NiTPP LUMO+3 and the dhNiTPP LUMO+2 located at 0.2 and 0.4 eV, respectively; a difference ultimately due to the charge redistribution upon dehydrogenation of NiTPP. The similar charge transfer suggests a similar adsorption geometry both in terms of adsorption site and adsorption height.

Fig. 1 C K-edge NEXAFS spectra of the NiTPP monolayer deposited on the Cu(100) substrate kept at room temperature (black curves) and 500 K (red curves) during deposition (a); schematic representation of the reaction taking place on the copper surface held at 500 K (b); POT-based attribution of the frontier orbitals (c); valence band spectrum of NiTPP monolayer deposited on the Cu(100) substrate kept at room temperature (black curve) and 500 K (red curve) during deposition (d).

Changes in the electronic structure and magnetic anisotropy induced by the extended π-conjugation

The similar adsorbate–substrate interaction of NiTPP and dhNiTPP layers promptly raises the question of how and how much the Ni electronic structure is eventually influenced by the dehydrogenation reaction. DFT calculations on gas-phase NiTPP and dhNiTPP suggest closed shell molecules (S = 0) whose diamagnetic Ni(II) core has a square planar coordination and a 3d8 electronic configuration; moreover, their idealized structures have a D4h and C4h symmetry,26 respectively. The Ni coordination lifts the five-fold degeneracy of the Ni(II) 3d AOs to generate 3d-based a1g (dz2), b1g (dx2−y2), b2g (dxy) and eg (dxz/dyz) MOs in NiTPP and ag (dz2), bg (dx2−y2, dxy) and eg (dxz/dyz) MOs in dhNiTPP. In addition, the comprehension of the forthcoming discussion may be facilitated by considering the parenthood between these Ni(II) 3d-based MOs and those generated by a hypothetical octahedral arrangement. In the adopted frame, the NiTPP (dhNiTPP) 3d-based MOs a1g and b1g (ag and bg) have an eg-like character, while the eg and b2g (eg and bg) ones are t2g-like. Among them, the only unoccupied 3d-based MO is, in both complexes, the 3dx2−y2‖eg-like one (where ‖ and ⊥ symbols stand for parallel and perpendicular to the macrocycle plane).

Effects induced by the increased delocalization associated with the dehydrogenation reaction are not straightforwardly revealed if we limit our attention to the interaction between the CM and the first ligand sphere (Ni–N). In fact, the Ni–N σ bond (see the Ni–N Nalewajski–Mrozek bond multiplicity indexes),²⁷ as well as the Ni–N bond length (see Table 1), are very similar in NiTPP and dhNiTPP.

Table 1 Summary of the Ni–N bond length and Nalewajski–Mrozek bond multiplicity indexes ^NMI for all the systems considered

	Ni–N/Å	^NMINi–N	^NMINi–Cu	^NMINi–NO2
NiTPP	1.98	0.47	—	—
dhNiTPP	1.95	0.46	—	—
Cu–NiTPP	2.04	0.31	0.57	—
Cu–dhNiTPP	2.01	0.31	0.54	—
Cu–NiTPP-NO2	2.12	0.26	0.07	0.37

---

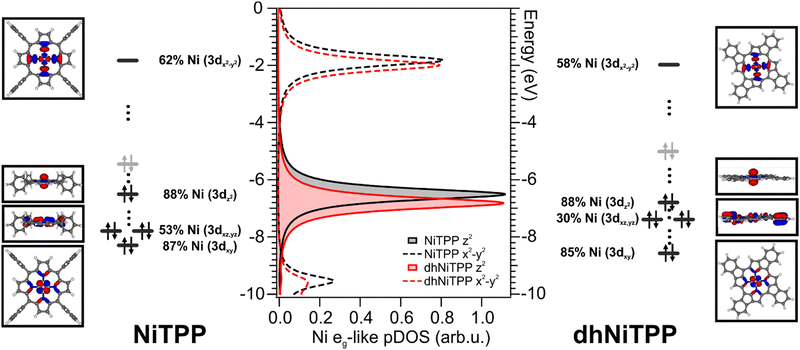
Nevertheless, more information can be gained by looking at the changes in the Ni(II) 3d-based MOs population upon moving from NiTPP to dhNiTPP. In particular, the extended π-delocalization for dhNiTPP leads to increased stabilization of all the Ni 3d-based orbitals and affects not only the energy positions of the degenerate Ni(II) 3d_xz- and 3d_yz-based orbitals, which mainly overlap with the ligand-based π orbitals, (^⊥t_2g-like MOs are upward shifted by 0.4 eV) but also their localization (^⊥t_2g-like MOs are less concentrated on Ni by 23%) (see Fig. 2). Additionally, the planarization stabilizes both Ni(II) e_g-like MOs, the ^⊥e_g-like (z²) by 0.3 eV and the unoccupied ^‖e_g-like (x² − y²) by 0.18 eV. In particular, the ^‖e_g-like MO also shows a slightly lower degree of localization on nickel (by 4%) for the planarized system.

Fig. 2 DFT-calculated Ni(II) e_g-like partial density of states (pDOS) of gas-phase NiTPP (black) and dhNiTPP (red); solid and dotted lines refer to z² and x² − y² levels, respectively. Corresponding frontier energy levels of the optimized closed-shell NiTPP (left) and dhNiTPP (right). Levels in black (grey) refer to the occupied Ni 3d-based MOs (ligand-based NiTPP and dhNiTPP HOMO) whose 3D contour plots (CPs) are displayed in the insets. Grey, white, blue, and yellow spheres are representative of C, H, N, and Ni atoms, respectively. The molecular plane corresponds to the xy plane.

Previously, we showed that the strong charge transfer from Cu(100) to NiTPP implies nickel reduction.^28,29 The 3d⁹ Ni(I) species thus formed is paramagnetic, and it carries one unpaired electron in the ^‖e_g 3d_x²−y² AO.¹⁰ The previously discussed similarity of the adsorbate–substrate interaction in NiTPP and dhNiTPP prompts us to assume that the CM reduction is preserved for dhNiTPP/Cu(100) (see Section S2 and S6 in ESI†).

XMCD measurements recorded in the presence of an external magnetic field applied along the light propagation direction have been carried out to look into the magnetic properties of the Cu-supported systems. Magnetic dichroism signal plots obtained from the absorption spectra recorded with different light helicities across the Ni L_3,2-edges are displayed in Fig. 3 for normal (θ = 0°) and grazing (θ = 70°) incidences. XMCD spectra of NiTPP and dhNiTPP are similar when it comes to the energy position of the maximum of their signal. Perfectly in agreement with the Ni 2p core level spectra, this XMCD finding is consistent with a similar charge transfer at the interface. At the same time, the analysis of the XMCD signal shapes testifies to a quite big difference in the in-plane magnetic properties of NiTPP and dhNiTPP chemisorbed on Cu(100). The sum rule analysis^30,31 has been then performed to estimate the corresponding orbital and spin angular momenta (the Ni(I) 3d⁹ configuration implies the assumption of a single hole in the 3d shell of both systems). The results of the analysis are reported in Table 2.

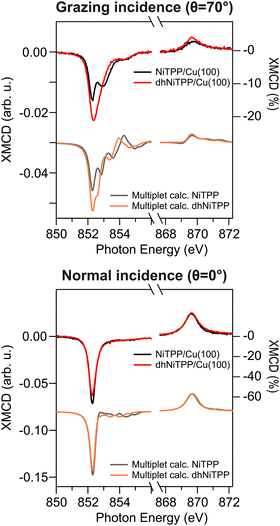Fig. 3 Normal and grazing incidence XMCD spectra at the Ni L_3,2-edge for NiTPP/Cu(100) and dhNiTPP/Cu(100) along with respective crystal field multiplet calculations.

Table 2 Magnetic moment values obtained from the sum rule analysis along with the effective g-factor 2(1 + m_l/m_s,eff) for the two systems displayed in Fig. 3

		Normal	Grazing
NiTPP/Cu(100)	m l/μB	0.16 ± 0.02	0.19 ± 0.03
	m s,eff/μB	1.34 ± 0.08	0.46 ± 0.09
	g-factor	2.24	2.83
dhNiTPP/Cu(100)	m l/μB	0.10 ± 0.02	0.16 ± 0.03
	m s,eff/μB	1.36 ± 0.08	0.45 ± 0.09
	g-factor	2.15	2.71

---

It emerges that the dhNiTPP in-plane orbital angular momentum is quenched, while the out-of-plane magnetic components change to a lower extent. Such evidence implies a variation in the degree of spin–orbit coupling (SOC) in NiTPP and dhNiTPP, whose effective g-factor values are also reported in Table 2 (deviation from the free ion value ∼2 quantifies the multiplet mixing). The larger NiTPP orbital component reflects a richer multiplet structure, well evident in the grazing geometry. As far as the spin momentum asphericity is concerned, this is similar for both complexes, thus justifying the assumption of a comparable charge density at the NiTPP and dhNiTPP MC as a consequence of the similar charge transfer taking place at the interface.¹⁵ Indeed, the magnetic anisotropy of the Ni species is preserved upon planarization.

To account for all these changes in the multiplet splitting features of the Ni L_3,2 XMCD spectra, semiempirical crystal field multiplet (CFM) calculations have been carried out for both NiTPP and dhNiTPP by combining the QUANTY code with the CRISPY graphical interface.^32,33 More specifically, CFM calculations were performed to gain insights into the highly localized Ni(I) 2p⁶3d⁹ to 2p⁵3d¹⁰ transitions in a D_4h symmetry by taking into account Coulomb and exchange interactions, SOC, and crystal field (see Methods section). As such, CFM results state that differences between NiTPP/Cu(100) and dhNiTPP/Cu(100) XMCD spectra are mainly determined by the different ligand fields, whose effects have been modeled by varying the ligand–metal hybridization charge transfer (LMCT) term in the CFM calculations, which reflects the charge transfer and hybridization between the Ni 3d levels and the ligand. In more detail, the multiplet structure characterizing the NiTPP/Cu(100) XMCD spectra is well reproduced by setting the hybridization parameters corresponding to the e_g-like levels (Va_1g(3d,L1) and Vb_1g(3d,L1)) to 1.0 and 0.3, respectively, while a satisfactory agreement between experiment and theory is obtained in dhNiTPP just by lowering the 3d_z²-related Va_1g(3d,L1) parameter to 0.75 with no other changes. This ultimately reflects an increased occupation of the Ni 3d AOs upon moving from NiTPP to dhNiTPP.

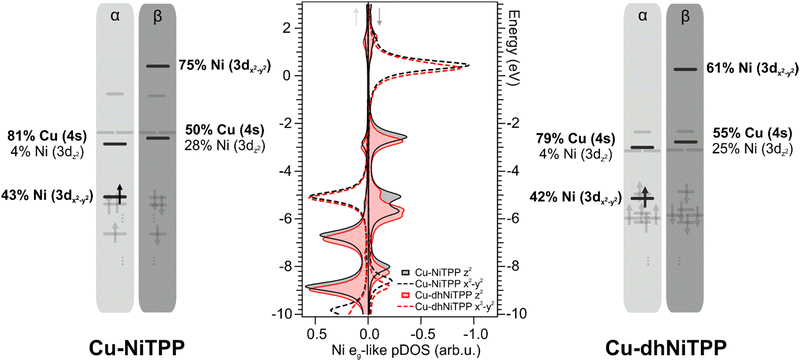
The panorama provided by the CMF semiempirical calculations well agrees with that pictured by DFT numerical experiments carried out within the molecular cluster approach (see Computational details).^9,11,34,35 As such, the interaction of NiTPP and dhNiTPP with Cu(100) has been herein modeled by adopting two molecular clusters, namely Cu–NiTPP and Cu–dhNiTPP (see Section S7 in ESI† for details on the model used).

It has already been mentioned for the gas-phase calculations that the planarization is accompanied by the stabilization of both Ni(II) eg-like MOs. Such an effect is preserved on the surface and enhanced when the 3dz2⊥eg-like orbital, mostly involved in the axial interaction with the substrate Cu 4s AO (see Fig. 4), is considered. Theoretical Cu–Ni bonding energies are 0.31 eV and 0.24 eV in Cu–NiTPP and Cu–dhNiTPP, respectively, while the corresponding NMINi–Cu values are 0.57 and 0.53 (see Table 1). The picture emerging from these data is that, both in NiTPP and dhNiTPP, Ni(II) is reduced to Ni(I) upon coordination to Cu; moreover, the half occupation of the Ni(I) ‖eg-like orbital (Ni–N antibonding, see the corresponding 3D CPs displayed in Fig. 2) induces in both cases similar lengthening of the Ni–N bond (from 1.98 to 2.04 Å in Cu–NiTPP and from 1.95 Å to 2.01 Å in Cu–dhNiTPP, which tinily affects the NMINi–N values (see Table 1)).

Fig. 4 DFT-calculated Ni(I) e_g-like pDOS of Cu-NiTPP (black) and Cu-dhNiTPP (red) clusters; positive (negative) values correspond to spin up (down) pDOS (center). Corresponding energy level diagrams associated with the Cu-NiTPP (left) and Cu-dhNiTPP (right) species with a fixed Ni–Cu distance at 2.1 Å and optimized structures. Both α and β spins are reported. Black arrows indicate the occupied Ni 3d-based α MOs. The relative percentage of MOs is also reported. The comparison between α and β spin occupation shows that the single unpaired electron is localized on the α Ni 3d_x²−y² MO.

In this regard, the Ni net spin polarization, evaluated as the occupation difference between α (↑) and β (↓) spins, amounts to 1.11 (1.06) in the Cu–NiTPP (Cu–dhNiTPP) cluster, which suggests a charge transfer slightly stronger in NiTPP/Cu(100) than in dhNiTPP/Cu(100) thus providing a rationale of the destabilization of the Ni 3 d_z²(↓) ^⊥e_g-like MO, and its energy splitting in the former case.

On the chemical reactivity

At this point, having proved not only the Ni(I) stabilization in both NiTPP and its planarized form but also the effect of the extended in-plane charge delocalization on magnetic anisotropy, we test here the Ni(I) reactivity in the two interfaces by exposing both of them to nitrogen dioxide (NO₂). In particular, the interest is to investigate the input of extended conjugation induced by the ring closure on-surface reaction on the axial reactivity of the nickel ion.

NO₂ is a strongly oxidizing gas that showed to be highly interacting with the pristine Ni(I)TPP systems already at room temperature after a few Langmuir exposure.^10,36 For a more sophisticated description of the experimental findings, a theoretical description of the reactivity turns out to be necessary. The NO₂ interaction with the surface-supported NiTPP has been modeled by considering the Cu–NiTPP-NO₂ molecular cluster.

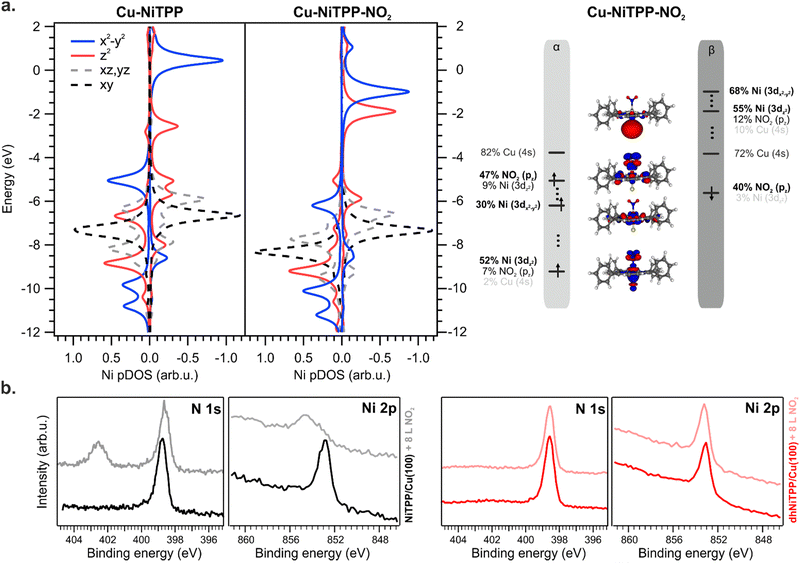
The NO₂ interaction with the Cu–NiTPP systems is highly favored, with a bonding energy of 0.93 eV, in good agreement with previously reported DFT periodic calculations.¹⁰ The strong interaction reflects in a ^NMI_Ni–NO2 value of 0.37 for the Cu–NiTPP-NO₂ cluster. Upon NO₂ coordination with the Cu–NiTPP complex, the porphyrin macrocycle adopts a slightly bent conformation reflected in a lower ^NMI_Ni–N index (see Table 1). The interaction is strongly driven by the surface trans-effect,^34,37 as testified by the significant ^NMI_Ni–Cu index decreasing in favor of the NO₂ interaction. This is reflected in the relocalization of charge on copper and the reoxidation to Ni(II) upon NO₂ coordination.

As a general effect on the Ni 3d pDOS after NO₂ coordination, there is a widespread shift of these MOs towards more negative energies: the Ni–NO₂ bond stabilizes all the Ni 3d-based MOs (see Fig. 5). Perfectly in agreement with periodic calculations,¹⁰ the Ni(I) is oxidized to a Ni(II) high spin state with electronic configuration (d_xy)² (d_yz, d_xz)⁴ (d_z²)¹ (d_x²−y²)¹ (see Fig. 5) upon NO₂ coordination (an t⁶_2g-like, ^⊥e¹_g-like, ^‖e¹_g-like Ni(II)). The presence of two unpaired electrons and the expected magnetic moment value after coordination well match with the magnetic dichroism signal at the Ni L_3,2 edges and NEXAFS analysis. As expected, the Ni(I) 3d-based MO mainly involved in the oxidation process is the ^⊥e_g-like 3d_z² one, which transfers one of its two electrons to the NO₂ LUMO, thus decreasing the magnetic anisotropy.¹⁰

Fig. 5 DFT-calculated Ni pDOS for NiTPP-Cu and Cu-NiTPP-NO₂ (a). The different Ni 3d levels are colour coded as indicated by the legend (left); frontier energy levels of the optimized HS Cu–NiTPP-NO₂ cluster (right); experimental N 1s and Ni 2p core level spectra recorded on NiTPP/Cu(100) (black curve) and on dhNiTPP/Cu(100) (red curve) before and after exposure to NO₂ (b).

No interaction between the NO2 ligand and the Ni ion is observed after the exposure of the dhNiTPP/Cu(100) system to the same NO2 amount (see XPS spectra at the N 1s and Ni 2p core level in Fig. 5(b)). The results herein reported prompt us then to ascribe the different reactivity to electronic and structural reasons: the 3dz2⊥eg-like MO is too deep in energy to efficiently interact with the half-occupied NO2⊥π* MO, while the extended π-conjugation restricts the molecular flexibility. The inability of the surface-supported dhNiTPP to effectively interact with NO2 also mirrors in a NMINi–NO2 value which equals 0.092 for Cu–dhNiTPP-NO2. This leads to a surface-supported system unable to axially coordinate with external ligands, allowing for the preservation of the highly reactive magnetic state and the in-plane magnetic anisotropy.

Experimental

Sample preparation

The Cu(100) surface was prepared by several cycles of Ar⁺ sputtering at 2.0 keV and subsequent annealing of the sample up to 800 K. NiTPP molecules (Sigma Aldrich, purity 95%) were thermally sublimated at 660 K from a Knudsen cell type evaporator onto the copper substrate kept at room temperature and at 500 K, to stabilize NiTPP and dhNiTPP, respectively. At the ALOISA beamline, the evaporation rate was checked with a quartz micro-balance. The evaporation rate was adjusted to 15 min ML⁻¹ and 30 min ML⁻¹, for NiTPP and dhNiTPP, respectively.

XMCD

The difference between two absorption spectra measured with circularly polarized X-ray light with opposite helicities (μ₊ and μ₋) was evaluated at the L₃ and L₂ absorption edges in order to check for a spin-polarization of the empty states. The XMCD percentage on the L₃ maximum is obtained by normalizing the difference on the background-substracted sum ((μ₊ − μ₋)/(μ₊ + μ₋)). The measurements were carried out at the EPFL/PSI X-Treme beamline of the Swiss Light Source, Paul Scherrer Institut, Villigen, Switzerland.³⁸ They were performed in the total electron yield mode, measuring the drain current of the sample. A magnetic field of 6.8 T was applied parallel to the light propagation in order to maximize the signal, and the sample was rotated in order to measure the absorption with normal (θ = 0°) and grazing (θ = 70°) incidence. The sample temperature for all the spectra presented here was around 3 K.

NEXAFS and XPS

The near-edge X-ray absorption fine structure and X-ray photoemission spectra were measured at the ALOISA beamline³⁹ of the Elettra Synchrotron in Trieste, Italy. At ALOISA, the sample is mounted at grazing incidence on a manipulator coaxial to the photon beam. The XPS spectra were measured at a grazing angle of 4° in transverse magnetic polarization (quasi p-pol) with the electron spectrometer in normal emission. Ni 2p spectra were measured at a photon energy of 980 eV (overall resolution (ΔE) of 400–420 meV), while C 1s and N 1s spectra were collected at hν = 515 eV (ΔE = 160 meV). All XPS spectra were calibrated to the binding energy of the Cu 3p_3/2 core level (75.1 eV). The NEXAFS spectra were measured in the partial electron yield mode using a channeltron multiplier equipped with a front grid polarized at a negative bias to reject low-energy secondary electrons (−820 V for the Ni L₂-edge, −270 V for the C K-edge and −370 V for the N K-edge). We changed the polarization from p-pol to transverse electric (s-pol) by rotating the sample around the photon beam axis while keeping the sample at a constant grazing angle (and illuminated area) of 6°. We performed absolute energy calibration of the C and N K-edge spectra (energy resolution set to 80 and 100 meV, respectively) by simultaneous recording of the I0 (drain current) on the last mirror, whose absorption features due to contaminants are calibrated by means of an in-line window-less gas ionization chamber.⁴⁰ The Ni L-edge spectra were calibrated a posteriori by XPS measurement of the Cu 3p_3/2 core level (BE of 75.1 eV) at the first photon energy point of the NEXAFS scan, as compensated by the measured work function of the electron spectrometer (3.7 eV).

The NEXAFS spectra of the molecular films were finally normalized to the same reference spectra measured on the clean substrate.

Photoemission orbital tomography

The POT experiments were performed at the NanoESCA beamline of Elettra, the Italian synchrotron radiation facility in Trieste, using an electrostatic photoemission electron microscope (PEEM) set-up described in detail in ref. 41. The data were collected with a photon energy of 30 eV and a total energy resolution of 100 meV, using p-linearly polarized light. The sample temperature for all the spectra presented here was around 90 K.

Computational methods

Geometry optimizations have been carried out by using the amsterdam density functional (ADF) software package.⁴² Optimized geometrical parameters have been obtained by running spin-unrestricted, nonrelativistic DFT calculations with generalized gradient corrections self-consistently included through the B3LYP^43,44 and by adopting a triple-ζ with a polarization function Slater-type basis set for all the atoms; Grimme dispersion corrections⁴⁵ have also been included. The interaction of NiTPP and dhNiTPP with Cu(100) has been herein modeled by adopting two molecular clusters, namely Cu–NiTPP and Cu–dhNiTPP.

This effective model is not intended to describe the adsorption configuration (experimentally found in the hollow site, with Ni at a distance of 1.93 Å from the surface²⁹), however it accurately describes the NiTPP/Cu(100) molecular electronic properties by setting the Cu–Ni internuclear distance to 2.1 Å (see Sections S6 and S7 of ESI†). The same distance is assumed also for the Cu–dhNiTPP cluster because of the similar charge transfer observed on the Cu(100) surface.

To favor the comprehension of the ground state (GS) theoretical outcomes, the molecular eigenvalues have been graphically displayed as the partial density of states (pDOS) by using a 0.25 eV Lorentzian broadening factor. These plots, based on Mulliken's approach⁴⁶ for partitioning the overlap density, allow an easy inspection of the atomic composition of MOs over a broad energy range. Partial density of states (pDOS) are defined as

where γ is the Lorentzian broadening factor and f^v_nl is the Mulliken's population contribution from atom v, state (nl) to the p^th MO of energy ε_p.

NEXAFS Ni L_3,2-edges spectra have been modeled by evaluating excitation energies (EEs) and corresponding oscillator strength distributions for transitions having the Ni 2p-based MOs as initial spin orbitals with the ORCA program.⁴⁷ The DFT/ROCIS method⁴⁸ has been exploited, which includes spin–orbit coupling (SOC) in a molecular Russell–Saunders fashion, by adopting the B3LYP exchange–correlation (XC) functional⁴⁹ and by using the def2-TZVP(-f) basis set and the resolution of identity approximation (def-TZVP/J basis).^50,51 The combined use of DFT and configuration interaction needs a set of three semi-empirical parameters (c₁ = 0.18, c₂ = 0.20, and c₃ = 0.40), which have been calibrated by Neese.⁴⁷ Zeroth order regular approximation has been adopted to treat the scalar relativistic effects.⁵² Numerical integrations for all calculations have been carried out on a dense Lebedev grid (302 points).⁵³

Photoemission orbital tomography simulations

Gas-phase density functional calculations for the possible cyclodehydrogenation products (spi/rect) dh-NiTPP (NiC₄₄N₄H₂₀) were performed using the NWCHEM code40 employing the B3LYP hybrid functional for exchange–correlation effects.^49,54 The simulated momentum maps of the gas-phase molecules were obtained as the Fourier transforms of the respective Kohn–Sham orbitals as described previously.²⁴

Multiplet calculations

Ligand field multiplet simulations of the L_3,2-edge XMCD results were performed using the quantum many-body scripting language, Quanty.⁵⁵ The Quanty input files for the simulation of L_3,2-edge fluorescence XAS were adapted from templates generated in Crispy.³² Multiplet effects are described by the Slater–Condon–Shortley parameters, F_kpp, F_kpd (Coulomb) and G_kpd (exchange), reduced to 80% of the Hartree–Fock calculated values to account for the over-estimation of electron–electron repulsion found for the free ion. The 2p⁵ spin–orbit coupling parameter ξ_2p is found to be consistent with the atomic value (8.202 eV). The 3d spin–orbit coupling parameters are found to be ξ_3d = 0.0613. The crystal field parameters D_q, D_t and D_s, in the D_4h point group, have been set to 0.065, 0.02 and 0.0, respectively, to account for the d-orbital degeneracy and energy splitting of the b_1g (x² − y²), a_1g (z²), e_g (xz,yz) and b_2g (xy) Ni 3d levels. Broadening of the transitions as described by the core–hole lifetime was applied through a Lorentzian function over the L₃ and L₂ edge of 0.3 eV and 0.8 eV full-width half maximum (FWHM), respectively. Gaussian broadening due to the instrumental resolution was set to 0.2 eV FWHM and simulated at 10 K.

Conclusions

Studying two model systems, namely NiTPP and its planarized derivative, here, we have shown that the magnetic and chemical properties of a metal ion caged in the tetrapyrrolic ligand field can be efficiently tuned by extending the π-conjugation. While the Ni 3d in-plane charge delocalization changes contribute to an increased effective magnetic spin moment, the molecular reactivity towards axial ligands is strongly reduced after the on-surface ring closure reaction. The reduction in the effective ligand field by extended conjugation in metal–organic systems can be considered as a general approach for preserving the magnetic anisotropy in chelated metal centers and, at the same time, making them more robust towards oxidizing environments. These findings provide an understanding of the molecular reactivity and a solid basis for the preservation of molecular magnetism in surface-supported metal porphyrins, opening new avenues for their use as stable magnetic centers in functional spintronics devices.

Author contributions

Iulia Cojocariu: conceptualization, methodology, validation, formal analysis, investigation, writing – original draft, writing – review & editing, visualization, Silvia Carlotto: methodology, validation, formal analysis, writing – original draft, writing – review & editing, visualization, Daniel Baranowski: investigation, writing – review & editing, Matteo Jugovac: investigation, writing – review & editing, Jan Dreiser: investigation, writing – review & editing, Luca Schio: investigation, writing – review & editing, Luca Floreano: investigation, writing – review & editing, Maurizio Casarin: validation, writing – review & editing, Vitaliy Feyer: conceptualization, validation, investigation, writing – original draft, writing – review & editing, supervision, Claus M. Schneider: writing – review & editing, supervision.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The Computational Chemistry Community (C3P) of the University of Padova is kindly acknowledged. This work was supported by the University of Padova (Grant P-DISC #CARL-SID17 BIRD2017-UNIPD, Project CHIRoN).

Notes and references

1. M. N. Leuenberger and D. Loss, Nature, 2001, 410, 789–793.
2. D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225.
3. V. E. Campbell, M. Tonelli, I. Cimatti, J. B. Moussy, L. Tortech, Y. J. Dappe, E. Rivière, R. Guillot, S. Delprat, R. Mattana, P. Seneor, P. Ohresser, F. Choueikani, E. Otero, F. Koprowiak, V. G. Chilkuri, N. Suaud, N. Guihéry, A. Galtayries, F. Miserque, M. A. Arrio, P. Sainctavit and T. Mallah, Nat. Commun., 2016, 7, 13646.
4. V. Madhavan, W. Chen, T. Jamneala, M. F. Crommie and N. S. Wingreen, Science, 1998, 280, 567–569.
5. P. Gambardella, S. Stepanow, A. Dmitriev, J. Honolka, F. M. F. De Groot, M. Lingenfelder, S. Sen Gupta, D. D. Sarma, P. Bencok, S. Stanescu, S. Clair, S. Pons, N. Lin, A. P. Seitsonen, H. Brune, J. V. Barth and K. Kern, Nat. Mater., 2009, 8, 189–193.
6. A. Cornia, A. L. Barra, V. Bulicanu, R. Clérac, M. Cortijo, E. A. Hillard, R. Galavotti, A. Lunghi, A. Nicolini, M. Rouzières, L. Sorace and F. Totti, Inorg. Chem., 2020, 59, 1763–1777.
7. S. Stepanow, J. Honolka, P. Gambardella, L. Vitali, N. Abdurakhmanova, T. C. Tseng, S. Rauschenbach, S. L. Tait, V. Sessi, S. Klyatskaya, M. Ruben and K. Kern, J. Am. Chem. Soc., 2010, 132, 11900–11901.
8. P. Gambardella, S. Rusponi, M. Veronese, S. S. Dhesi, C. Grazioli, A. Dallmeyer, I. Cabria, R. Zeller, P. H. Dederichs, K. Kern, C. Carbone and H. Brune, Science, 2003, 300, 1130–1133.
9. I. Cojocariu, S. Carlotto, H. M. Sturmeit, G. Zamborlini, M. Cinchetti, A. Cossaro, A. Verdini, L. Floreano, M. Jugovac, P. Puschnig, C. Piamonteze, M. Casarin, V. Feyer and C. M. Schneider, Chem. – Eur. J., 2021, 27, 3526–3535.
10. H. M. Sturmeit, I. Cojocariu, A. Windischbacher, P. Puschnig, C. Piamonteze, M. Jugovac, A. Sala, C. Africh, G. Comelli, A. Cossaro, A. Verdini, L. Floreano, M. Stredansky, E. Vesselli, C. Hohner, M. Kettner, J. Libuda, C. M. Schneider, G. Zamborlini, M. Cinchetti and V. Feyer, Small, 2021, 17, 2104779.
11. I. Cojocariu, S. Carlotto, G. Zamborlini, M. Jugovac, L. Schio, L. Floreano, M. Casarin, V. Feyer and C. M. Schneider, J. Mater. Chem. C, 2021, 9, 12559–12565.
12. D. Baranowski, I. Cojocariu, A. Sala, C. Africh, G. Comelli, L. Schio, M. Tormen, L. Floreano, V. Feyer and C. M. Schneider, Angew. Chem., Int. Ed., 2022, 61, e202210326.
13. G. Di Santo, S. Blankenburg, C. Castellarin-Cudia, M. Fanetti, P. Borghetti, L. Sangaletti, L. Floreano, A. Verdini, E. Magnano, F. Bondino, C. A. Pignedoli, M. T. Nguyen, R. Gaspari, D. Passerone and A. Goldoni, Chem. – Eur. J., 2011, 17, 14354–14359.
14. M. Röckert, M. Franke, Q. Tariq, S. Ditze, M. Stark, P. Uffinger, D. Wechsler, U. Singh, J. Xiao and H. Marbach, Chem. – Eur. J., 2014, 20, 8948–8953.
15. L. M. Arruda, M. E. Ali, M. Bernien, F. Nickel, J. Kopprasch, C. Czekelius, P. M. Oppeneer and W. Kuch, J. Phys. Chem. C, 2019, 123, 14547–14555.
16. C. Wäckerlin, K. Tarafder, J. Girovsky, J. Nowakowski, T. Hählen, A. Shchyrba, D. Siewert, A. Kleibert, F. Nolting, P. M. Oppeneer, T. A. Jung and N. Ballav, Angew. Chem., Int. Ed., 2013, 52, 4568–4571.
17. C. Wäckerlin, D. Chylarecka, A. Kleibert, K. Müller, C. Iacovita, F. Nolting, T. A. Jung and N. Ballav, Nat. Commun., 2010, 1, 61.
18. J. Miguel, C. F. Hermanns, M. Bernien, A. Krüger and W. Kuch, J. Phys. Chem. Lett., 2011, 2, 1455–1459.
19. I. Cojocariu, S. Carlotto, M. Jugovac, L. Floreano, M. Casarin, V. Feyer and C. M. Schneider, J. Mater. Chem. C, 2022, 10, 9748–9757.
20. P. Knecht, J. Reichert, P. S. Deimel, P. Feulner, F. Haag, F. Allegretti, M. Garnica, M. Schwarz, W. Auwärter, P. T. P. Ryan, T. L. Lee, D. A. Duncan, A. P. Seitsonen, J. V. Barth and A. C. Papageorgiou, Angew. Chem., Int. Ed., 2021, 60, 16561–16567.
21. H. M. Sturmeit, I. Cojocariu, M. Jugovac, A. Cossaro, A. Verdini, L. Floreano, A. Sala, G. Comelli, S. Moro, M. Stredansky, M. Corva, E. Vesselli, P. Puschnig, C. M. Schneider, V. Feyer, G. Zamborlini and M. Cinchetti, J. Mater. Chem. C, 2020, 8, 8876–8886.
22. C. Yin, Z. Peng, D. Liu, H. Song, H. Zhu, Q. Chen and K. Wu, Molecules, 2020, 25, 3766.
23. C. Ruggieri, S. Rangan, R. A. Bartynski and E. Galoppini, J. Phys. Chem. C, 2016, 120, 7575–7585.
24. P. Puschnig, S. Berkebile, A. J. Fleming, G. Koller, K. Emtsev, T. Seyller, J. D. Riley, C. Ambrosch-Draxl, F. P. Netzer and M. G. Ramsey, Science, 2009, 326, 702–706.
25. G. Zamborlini, D. Lüftner, Z. Feng, B. Kollmann, P. Puschnig, C. Dri, M. Panighel, G. Di Santo, A. Goldoni, G. Comelli, M. Jugovac, V. Feyer and C. M. Schneider, Nat. Commun., 2017, 8, 1–8.
26. B. E. Douglas and C. A. Hollingsworth, Symmetry in Bonding and Spectra, Academic Press, 1985.
27. R. F. Nalewajski and J. Mrozek, Int. J. Quantum Chem., 1994, 51, 187–200.
28. G. Zamborlini, M. Jugovac, A. Cossaro, A. Verdini, L. Floreano, D. Lüftner, P. Puschnig, V. Feyer and C. M. Schneider, Chem. Commun., 2018, 54, 13423–13426.
29. S. Carlotto, A. Verdini, G. Zamborlini, I. Cojocariu, V. Feyer, L. Floreano and M. Casarin, Phys. Chem. Chem. Phys., 2023, 25, 26779–26786.
30. B. T. Thole, P. Carra, F. Sette and G. van der Laan, Phys. Rev. Lett., 1992, 68, 1943.
31. P. Carra, B. T. Thole, M. Altarelli and X. Wang, Phys. Rev. Lett., 1993, 70, 694–697.
32. M. Retegan, Cris. v 0.7. 3.
33. M. W. Haverkort, G. Sangiovanni, P. Hansmann, A. Toschi, Y. Lu and S. Macke, EPL, 2014, 108, 57004.
34. W. Hieringer, K. Flechtner, A. Kretschmann, K. Seufert, W. Auwärter, J. V. Barth, A. Görling, H. P. Steinrück and J. M. Gottfried, J. Am. Chem. Soc., 2011, 133, 6206–6222.
35. S. Carlotto, M. Casarin, A. Lanza, F. Nestola, L. Pandolfo, C. Pettinari and R. Scatena, Cryst. Growth Des., 2015, 15, 5910–5918.
36. A. Windischbacher and P. Puschnig, Inorg. Chim. Acta, 2023, 558, 121719.
37. P. S. Deimel, R. M. Bababrik, B. Wang, P. J. Blowey, L. A. Rochford, P. K. Thakur, T. L. Lee, M. L. Bocquet, J. V. Barth, D. P. Woodruff, D. A. Duncan and F. Allegretti, Chem. Sci., 2016, 7, 5647–5656.
38. C. Piamonteze, U. Flechsig, S. Rusponi, J. Dreiser, J. Heidler, M. Schmidt, R. Wetter, M. Calvi, T. Schmidt and H. Pruchova, J. Synchrotron Radiat., 2012, 19, 661–674.
39. L. Floreano, G. Naletto, D. Cvetko, R. Gotter, M. Malvezzi, L. Marassi, A. Morgante, A. Santaniello, A. Verdini, F. Tommasini and G. Tondello, Rev. Sci. Instrum., 1999, 70, 3855–3864.
40. L. Floreano, A. Cossaro, R. Gotter, A. Verdini, G. Bavdek, F. Evangelista, A. Ruocco, A. Morgante and D. Cvetko, Periodic arrays of Cu-Phthalocyanine chains on Au(110), 2008, vol. 112.
41. C. M. Schneider, C. Wiemann, M. Patt, V. Feyer, L. Plucinski, I. P. Krug, M. Escher, N. Weber, M. Merkel, O. Renault and N. Barrett, J. Electron Spectrosc. Relat. Phenom., 2012, 185, 330–339.
42. ADF2014 COSMO-RS, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam and https://www.scm.com, ADF2014 COSMO-RS, SCM, https://www.scm.com.
43. A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
44. J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824.
45. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
46. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1841–1846.
47. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
48. M. Roemelt and F. Neese, J. Phys. Chem. A, 2013, 117, 3069–3083.
49. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
50. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
51. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
52. D. A. Pantazis, X. Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919.
53. V. I. Lebedev, USSR Comput. Math. Math. Phys., 1975, vol. 15, pp.44–51.
54. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
55. M. W. Haverkort, J. Phys.: Conf. Ser., 2016, 712, 012001.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc02726k

---