Variable stiffness and fast-response soft structures based on electrorheological fluids

Abstract

Soft robots have drawn a lot of attention due to their soft materials that make them highly flexible and adaptable to complex environments. However, these also make soft robots not suited to high-load tasks, and achieving controllable material stiffness variation is still a challenge. Herein, we designed a soft structure with variable stiffness based on electrorheological fluids, which presented the advantages of continuously variable stiffness and fast response. The structure exhibited a stiffness of up to 1065 mN mm⁻¹ when the electric field strength was 4.5 kV mm⁻¹ (displacement of 1 mm). When varying the electric field strength (0 to 4.5 kV mm⁻¹), the rate of stiffness variation was over 1500%. According to the load cycle experiments, it was shown that the structure's response time to a change in load was less than 65 ms, and that the structure changes could be made repeatedly. In addition, we demonstrated the functions of stiffness adjustment, shape memory, and motion locking of the structure. This work has potential applications in the fields of soft robotics and artificial muscles.

---

1. Introduction

Soft robotics is an emerging field aimed at developing versatile systems capable of safely interacting with humans and manipulating delicate objects in unstructured environments.^1,2 Unlike conventional robots made of rigid materials, soft robots are usually composed of compliant materials with elastic and deformable properties, which have multiple degrees of freedom, continuous transformation capabilities, and good human–computer interaction.³ Therefore, soft robots have broad application prospects in many areas, such as artificial muscles,⁴ robotic grippers,⁵ flexible wearable electronics,⁶ and biomedical assistance.⁷

The inherent softness of flexible materials not only makes dexterous and safe interactions possible to prevent damage to the environment and the physical body, but it also makes soft robots unsuitable for tasks that require a high load capacity.⁸ Therefore, stiffness tuning is crucial to allow the actuator to perform both flexible movements and rigid load carrying and is a way for soft robots to interact effectively with humans and environment. Inspired by nature, where organisms can adjust the stiffness of their tissues to resist external changes, stiffness variation has been introduced into mechanical systems^9,10 and can be used to tune mechanical properties of flexible actuators. Researchers have explored a variety of stiffness-tunable materials to prepare soft robots.^11–13 Among these, temperature-sensitive phase-change materials have received particular attention,¹⁴ including shape-memory alloys,¹⁵ thermoplastic polymers,¹⁶ and low-melting-point alloys.¹⁷ These materials have the advantages of a wide range of stiffness variation, but usually can only switch between rigid and flexible states, and it is difficult for them to achieve multistage and continuous control of stiffness, and they cannot achieve active invertible stiffness, while their response speed is usually slow.

Electrorheological (ER) fluids are a kind of smart materials whose rheological performance can be adjusted by an external electric field.^18,19 ER fluids are typically composed of electrically polarizable particles dispersed in an insulating fluid. In the absence of an electric field, the particles are uniformly distributed in the insulating liquid and the material is fluid-like. When an electric field is applied, however, the particles form a chain or columnar structure along the direction of the electric field as a result of the attractive forces between the polarized particles. At that moment, the viscosity of ER fluids changes significantly, transforming from fluid-like to solid-like in milliseconds. This viscosity conversion is reversible, and when the electric field is withdrawn, the particles return to their original fluid state.^20–22 The macroscopic performance of ER fluids involves a reversible change between liquid and solid states, as well as a reversible shift in its apparent viscosity. Based on the properties of ER fluids, they have a range of engineering applications, such as dampers,²³ clutches,²⁴ and valves.²⁵

A lot of researchers have studied the properties of the stiffness variation due to the ER effect. Tonazzini et al. proposed an ER fluid-based multilayer valve, in which the ER fluid acted as an actuation fluid and a control medium.²⁶ By applying an ON–OFF electric signal to the rigid electrode plates, fast switching between the liquid and solid state of the ER fluid could be achieved. However, the materials used for encapsulating and the electrodes used for powering ER fluids were rigid, making it difficult to achieve a flexible structure. Wei et al. proposed a cantilever sandwich beam with ER elastomers, where the elastomer was used as a viscoelastic damping material to control the vibration of the cantilever beam.²⁷ The results showed that with the increase in the applied electric field strength, the natural frequency of the ER elastomer sandwich beam increased and the vibration amplitude at the natural frequency decreased. Although the ER elastomer was flexible, the ER particles were embedded in the elastomer and could not move, leading to a low stiffness rate and weak electric field response. Fast variable stiffness of flexible devices remains a challenge.

Herein, we propose a stiffness-tunable soft device with a “sandwich” structure of a PDMS/electrode-ER fluid-electrode/PDMS (Fig. 1a). The ER materials used, which were prepared via a precipitation process, offered the advantages of a high yield stress and low leakage current density, while the chosen encapsulating material and electrodes were both flexible. The ER fluid was in a liquid state without the electric field, providing the structure with good compliance and the ability to be deformed. Once the electric field was applied, the ER fluid solidified, keeping the structure in its temporary shape. The stiffness variation rate of the structure was over 1500% (0 to 4.5 kV mm⁻¹). Benefiting from the fast polarization and depolarization of ER particles, the soft structure demonstrated an outstanding response speed, within 65 ms for load changes. Based on the advantages of the continuously variable stiffness and fast response of this structure, we demonstrated the functions of variable stiffness, shape memory, and motion locking.

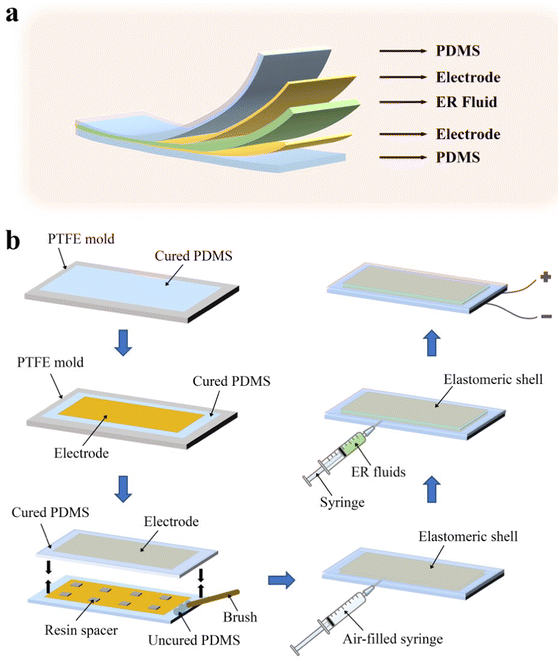Fig. 1 (a) Structure of the stiffness-tunable soft structure. (b) Fabrication process of the stiffness-tunable soft structure.

2. Experimental

2.1. Materials

Anhydrous calcium chloride (CaCl₂, A.R.), tetrabutyl titanate (TBT, purity ≥98%), oxalic acid (H₂C₂O₄·2H₂O, A.R.), and anhydrous ethanol (EtOH, A.R.) were purchased from Sinopharm Chemical Reagent Company. Silicone oil (viscosity = 50 cSt) was purchased from Beijing Sihuan Antong Trading Company. PDMS 184 was acquired from DOWSIL Inc. Ethyl cyanoacrylate (purity ≥98%) was purchased from Sigma Aldrich. Copper film was obtained from Shanghai Fuxi Electromechanical Equipment Company. All the chemical agents were used as received without further purification. Deionized (DI) water was made from the Millipore purification system (Millipore, USA) with a resistivity of 18.2 MΩ cm.

2.2. Synthesis of the ER fluids

CTO particles were synthesized by a co-precipitation method;²⁸ the fabrication process is shown in Fig. S1 (ESI†). Solution A was prepared by dissolving 2.5 g CaCl₂ and 7 mL TBT in 200 mL EtOH. Simultaneously, solution B was obtained by dissolving 6.7 g H₂C₂O₄·2H₂O into 200 mL EtOH/H₂O. Solution A was then continuously added dropwise to solution B under vigorous stirring. An opalescent precipitate was produced instantly and the mixture was stirred at 40 °C for 8 h. The precipitate was washed several times with EtOH and DI water to remove residues. Then it was dehydrated in a vacuum at 50 °C overnight and 110 °C for another 2 h.

The ER fluids were formed by mixing the CTO particles with silicone oil. Before the experiment, the silicone oil was dried at 120 °C for 4 h. The CTO particles and silicone oil were mixed by ball milling in different proportions after cooling to obtain the desired concentration. The concentration of the ER fluids is denoted as the ratio of the nanoparticle weight to the silicone oil volume. For example, 1 g of CTO particles mixed with 1 mL of silicone oil is denoted as 1 g mL⁻¹.

2.3. Fabrication of the stiffness-tunable soft structure

The fabricating process of the stiffness-tunable soft structure is shown in Fig. 1b. First, PDMS 184 was prepared by mixing parts A and B in a 1 : 10 ratio and stirring for 5 min. The mixed polymer elastomer was put into a vacuum for degassing. Uncured PDMS 184 was cast into two identical rectangular grooved molds and then cured in an oven at 80 °C for 20 min. Two flexible structures with a slot were obtained. Second, the copper films as electrodes were attached to the inner surface of each structure, which was treated with ethyl cyanoacrylate as a glue. Next, two pieces of the rectangular double-layer elastomeric structure were placed in to contact with each other with several 1 mm thickness resin spacers inserted to keep the distance between the copper films. The edges were sealed up with the uncured PDMS 184 and cured in an oven at 50 °C for 20 min. The elastomeric shell with a sealed cavity was prepared. Finally, a syringe was used to inject the ER fluid into the prepared cavity structure. Before injecting, the air inside the cavity was sucked out to ensure the entire cavity could be filled with ER fluid. The injection hole was then sealed by the uncured PDMS. After another spin-coating operation to ensure airtightness, the soft structure was cured at room temperature for 24 h. In addition, to facilitate the acquisition of experimental data, two copper wires were linked to the same side of the electrodes, and a ground wire was connected to prevent leakage.

2.4. Characterization

2.4.1. Measurements of the morphology and structure. The morphologies of the CTO particles were investigated by scanning electron microscopy (SEM, Hitachi S4800, Japan) at 4 kV and by transmission electron microscopy (TEM, FEI Tecnai F20, USA) at 200 kV. Fourier-transform infrared spectroscopy (FTIR, Nicolet 6700, USA) was applied to analyze the molecular structures of the CTO particles, using 32 averaged scans at 4 cm⁻¹. X-Ray diffraction (XRD, Bruker D8 Advance, Germany) was used to characterize the crystal structures, using Cu Kα radiation, and the measurements were taken using a generator voltage of 40 kV and a current of 40 mA.

2.4.2. Measurements of the rheological properties. The ER properties were measured on a flat rheometer (Haake RS6000, USA)15 mm in diameter. The ER fluids were placed in the gap between two plates with a distance of 1 mm. The maximum voltage of the DC high-voltage generator (Spellman SL300, USA) was 10 kV, and the current limitation was 3.0 mA. The shear stress was measured in the controlled shear stress (CS) mode. The yield stress was defined as the maximum shear stress value at which the stress increased with strain. The rheological curves were measured in the controlled shear rate (CR) mode with shear rates ranging from 0.1 to 100 s⁻¹. All the measurements were carried out at room temperature.

2.4.3. Measurements of the mechanical properties. The load and stiffness measurements of the structure were performed via an electrohydraulic servo universal testing machine (Landmark 370, USA) by applying a three-point bending test method. During the test, the preload was 0.1 N, the speed was 10 mm min⁻¹, and the displacement of bending was applied in the range of 0–6 mm. The electric field was applied to the structure with different strengths. The test temperature was kept at 25 °C.

3. Results and discussion

3.1. Morphology and rheological properties of the CTO ER fluid

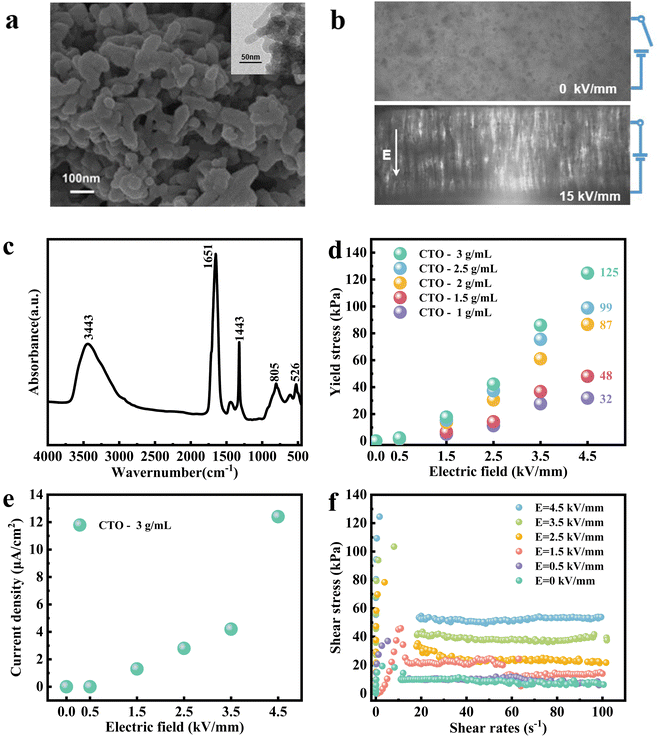
The CTO particles were synthesized via the simple co-precipitation of anhydrous calcium chloride, tetrabutyl titanate, and oxalic acid. The SEM and TEM images (Fig. 2a) show that the CTO particles were homogeneously formed as round rod-like shapes, which displayed a narrow size distribution. The average particle width was about 20 nm and the aspect ratio was about 2–6. As can be seen from the optical image in Fig. 2b, with the absence of an electric field, the ER particles were homogeneously distributed in the insulating fluid. After an electric field was applied, the ER particles became polarized and formed chains along the electric field direction. FTIR analysis was conducted to investigate the molecular structures, as shown in Fig. 2c. The broad band at 3443 cm⁻¹ was associated with the –OH stretching vibrations of water molecules. The C=O stretching bands owing to oxalate occurred at 1651 cm⁻¹. The absorption band observed at 1443 cm⁻¹ was attributed to the metal–carboxylate (M–COO–) symmetric stretching modes. The band at 805 cm⁻¹ was assigned to the C–C vibration band, while the band at 521 cm⁻¹ was due to the in-plane bending of O–C–O.²⁹ To further investigate the structure of the CTO particles, the XRD pattern was obtained and is shown in Fig. S2 (ESI†). The main diffraction peaks coincided well with the XRD pattern of calcium oxalate dehydrate (JCPDS Number 14-0770), while the non-crystalline backgrounds corresponded to TiO(OH)₂ and TiOC₂O₄(H₂O)₂.

Fig. 2 (a) SEM image and TEM image (inset in a) of the CTO particles. (b) Optical images of the electrorheological structure without/with the applied electric field. (c) FTIR spectra of the CTO particles. (d) Yield stress of the ER fluids with different concentrations as a function of the applied electric field. (e) Leakage current density of the ER fluid (3 g mL⁻¹) as a function of the applied electric field. (f) Shear stress of the ER fluid (3 g mL⁻¹) with the shear rate as a function of the applied electric field.

A range of concentrations of CTO ER fluids were prepared to evaluate their ER behavior under different electric fields. When the concentration was increased to 3.5 g mL⁻¹, the fluid was clay-like and lacked fluidity, making it difficult to inject into the silicone rubber shell (Fig. S3, ESI†). Therefore, we only investigated the ER properties of the ER fluids with concentrations ≤ 3 g mL⁻¹. As shown in Fig. 2d, the yield stress conformed to a positive dependence on the electric field strength, which was due to the tendency of the polarized particles to aggregate into tighter and thicker fibrous or columnar chains when the electric field strength was raised. This positive correlation was not obvious in the electric field strength region of 0–1.5 kV mm⁻¹, which was due to the fact that the ER fluid constructed a polarization layer in this region. In addition, the ER performance increased as the ER fluid concentration increased, which could be explained by the fact that as the concentration increased, more dielectric particles became involved in the polarization process in the system and more polarization chains were generated between the electrodes, thus reflecting a higher yield stress at the macro level. According to the experimental values in Fig. 2d, when the concentration was 3 g mL⁻¹, the ER fluid exhibited a significantly high capacity with yield stresses up to 125 kPa. Therefore, the ER fluid with a concentration of 3 g mL⁻¹ was selected for injection into the flexible shell to prepare the stiffness-tunable structure. Also, the concentration refers to 3 g mL⁻¹ from here on unless otherwise noted.

The leakage current density is also an important consideration when assessing ER fluids. The leakage current density has a noticeable impact on an ER fluids system's power consumption and heat production. Moreover, greater leakage currents might result in a breakdown, which would greatly affect the lifespan and application performance of ER fluids systems. As shown in Fig. 2e, the leakage current density of the ER fluid increased with the rising electric field strength, and the maximum leakage current density was 12.73 μA cm⁻² (4.5 kV mm⁻¹). This shows the superior operational safety and reduced energy usage caused by Joule heating of the prepared ER fluids. It has been reported that the wettability between the ER particles and the insulating oil determines the leakage current density.³⁰ In a well-infiltrated ER fluid, the charge transfer between the particles is hindered by the insulating oil, which modifies the current flow.

To acquire a deeper comprehension of the CTO ER fluids, the dynamic rheological properties were also assessed (Fig. 2f). The maximum shear stress at 4.5 kV mm⁻¹ was around 125 kPa, which was equivalent to the yield stress under the same conditions. It is generally accepted that the shear field-induced hydrodynamic and electric field-induced electrostatic interactions determine the rheological behavior of ER fluids, whereby the hydrodynamic interactions tend to destroy the ER particles’ structures and facilitate flow while the electric field-induced interactions cause the reorganization of the ER particles’ structures and obstruct flow. For high concentrations of ER fluids, the shear stress tends to decrease as the electric field strength increases after peaking. This is a common phenomenon in parallel plate measuring instruments; in fact, for all parallel plate measuring instruments, when the concentration of ER fluids is relatively high, the suspension is easily discharged from the central region of the test instrument. This is because once the particles have formed a chain, there is a significant density difference between them and the fluid, and the centrifugal force produced by the plate measuring instrument's rotation drives the chain to move to the plate's edge.³¹

3.2. Mechanical properties of the soft structure

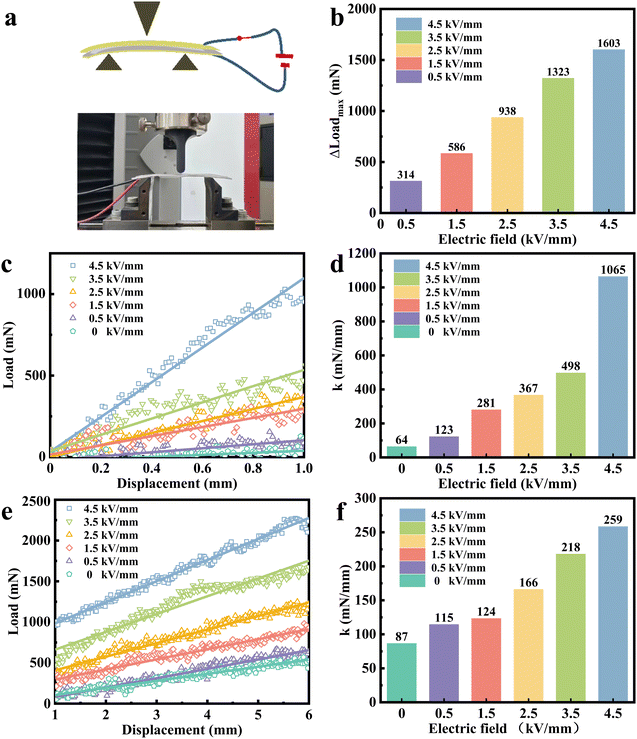
The mechanical properties of a structure can be defined in different ways. In our study, we concentrated on the maximum load that the structure can withstand and the axial bending stiffness. The three-point bending experiment was used for measuring the mechanical properties (Fig. 3a). Fig. 3b shows the differential loads of the structures at the same bending displacement (6 mm). The differential load (ΔLoad_max) is referred to as follows:

ΔLoad_max = Load_{E, max} − Load_{E0, max} (1)

where Load_{E, max} is the maximum load under an electric field of E, and Load_{E0, max} is the maximum load without an electric field. As demonstrated in Fig. 3b, all the ΔLoad_max values were positive, indicating that the ER effect came into play after applying the electric field, and the load of the entire structure increased. In addition, the load rose with the increase in the electric field strength, which was consistent with the higher yield stress brought on by the stronger electric field mentioned above. The load is associated with the yield stress of ER fluids. When the yield strength is larger than the resilience of the elastic shell and electrodes, the structure can remain in its current state. When the electric field intensity was 4.5 kV mm⁻¹, the maximum difference could reach 1.6 N. Compared with the electric field intensity of 0.5 kV mm⁻¹, the load variation was enhanced by about 400%.

Fig. 3 Mechanical properties of the soft structure as assessed through the three-point bending tests. (a) Schematic of the three-point bending experimental equipment. (b) Differential loads of the structures at a bending displacement of 6 mm. (c) Load as a function of bending displacement in the small deformation region (0–1 mm). (d) Stiffness under different electric fields in the small deformation region (0–1 mm). (e) Load as a function of bending displacement in the large deformation region (1–6 mm). (f) Stiffness under different electric fields in the small deformation region (1–6 mm).

In the small deformation region (0–1 mm), the load as a function of bending displacement at different electric field strengths is depicted in Fig. 3c. The load variation of the structure was little affected by the electric field at a lower electric field strength because the lower strengths were insufficient to provide a strong enough polarization force to chain the ER particles. When the electric field strength was 0.5 kV mm⁻¹, the yield pressure of the ER fluid was about 2 kPa (Fig. 2d), and the maximum load at the bending displacement of 1 mm was 0.11 N. In this case, the structure had almost no resistance to external pressure. When the electric field strength was 4.5 kV mm⁻¹, the yield pressure of the ER fluids was 125 kPa (Fig. 2d), and the maximum load at 1 mm displacement reached 0.97 N, which was approximately 9 times the load at 0.5 kV mm⁻¹. To quantify the ability of the structure to cope with tensile deformation, the stiffness k is defined as:

k = P/δ (2)

where P is the external constant force exerted on the structure, and δ is the deformation caused by resisting the constant force. Fig. 3d shows the stiffness versus electric field strength in the small deformation region. In this region, the stiffness of the structure was 1065 mN mm⁻¹ under an electric field of 4.5 kV mm⁻¹, which was improved by 1560% compared to the stiffness of 64 kV mm⁻¹ for the case without an electric field.

In the large deformation region (1–6 mm), the load as a function of displacement at various electric fields is shown in Fig. 3e and the stiffness versus electric field is shown in Fig. 3f, respectively. When the electric field strength was 4.5 kV mm⁻¹, the maximum load at a displacement of 6 mm was 2.24 N, and the stiffness was 259 mN mm⁻¹, which had increased by nearly 200% compared with the case in the absence of an electric field. It can be seen that the increased amplitude in stiffness was lower than that in the small deformation region.

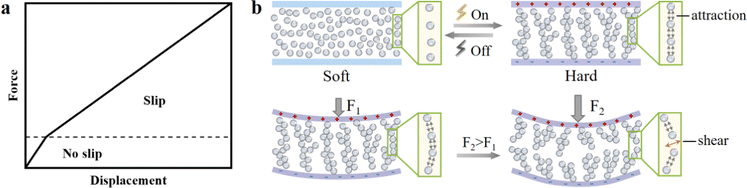
It can be observed in Fig. S4 (ESI†) that the stiffness k was divided into two zones with increasing deformation displacement, and that the inflection point occurred at 1 mm from the displacement. This phenomenon can be explained as follows: two factors contribute to the increase in the structure stiffness under an electric field. On the one hand, the ER fluid in the structure forms polarization chains when an electric field is applied, and these chains will hinder the shear behavior, and thus the viscosity of the ER fluid increases. On the other hand, when an external force is applied, there is friction between the CTO particles and the electrode surface, which also leads to an increase in viscosity. As shown in Fig. 4a, the bending deformation undergoes no-slip and slip processes. Fig. 4b describes the stiffness variation of the whole structure under the electric field, as well as the microstructure of the particles in the no-slip process and slip process. In the non-slip process, the applied pressure is less than the yield stress of the ER fluid and the friction between the CTO–CTO particles, and between the CTO–electrodes. At this time, there is no relative displacement between the CTO particles, or between the ER fluid and the electrode surface. The ER fluid and the electrode layer can be regarded as a single entity to withstand external pressure, and the polarization chains are not damaged, so there will be greater stiffness. With the increase in external pressure, the structure generates large deformation and enters the slip process. The external pressure at this time is larger than the yield stress of the ER fluid, and the space for the formation of particle chains decreases, resulting in the slip and miss-cutting of particles, which damages the particle chain segment, and decreases the interparticle forces. Therefore, the increase in stiffness is less than that in the small deformation process.

Fig. 4 Principle of the forces affecting the ER particle chains during the deformation. (a) Process division during deformation. (b) Microstructure schematic of the variation in stiffness, and the way applied force destroys the particle chains during deformation.

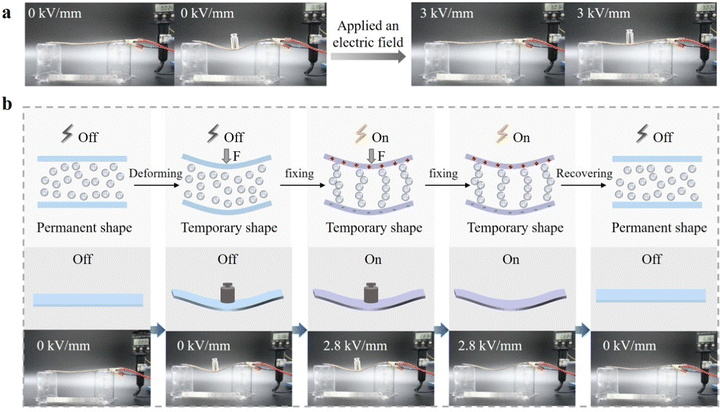
To further demonstrate the versatility of the structure, we demonstrated the stiffness variation and shape-memory functions. Pictures of the stiffness variation of the structure are shown in Fig. 5a. When a 100 g weight was applied to the structure without applying an electric field, the structure produced a large bending deformation. Also, when the same weight was applied with an electric field, it can be seen that the deformation was significantly reduced. This implies that the load to be carried became greater, and the stiffness of the structure became larger. We demonstrate the shape-memory function of the structure in Fig. 5b and Movie S1 (ESI†). The principles of the shape-memory behavior and the microstructural changes of the elastic shell and ER fluid in the process of shape memory are also described in Fig. 5b. Initially, the structure was in its original stress-free state without an electric field. After adding a 100 g weight, the structure bent due to the external stresses and deformed into a temporary shape. Here, the elastic shell of the structure generated restored the stress, while the ER fluid remained in its unstressed state. Upon the application of an electric field with an intensity of 2.8 kV mm⁻¹, the ER fluid solidified in a nearly stress-free state, while the elastic shell was unaffected. When the yield stress of the ER fluid was much larger than the resilience of the elastomer, the structure could maintain a profile close to its programmed shape. Thus, with the applied electric field maintained, the restoring stress of the elastomer was counteracted by the stiffness of the ER fluid after the external pressure was released. When the electric field was removed, the ER fluid became fluid again, restoring the elastomer to its original remembered shape. The shape memory was fully rewritable, so a new cycle could be repeated.

Fig. 5 Variable stiffness, shape-memory function, and mechanism of its action for the structure. (a) Demonstration of the structure's stiffness variation. (b) Illustration of the shape-memory function of the soft structure.

3.3. Response time of the soft structure

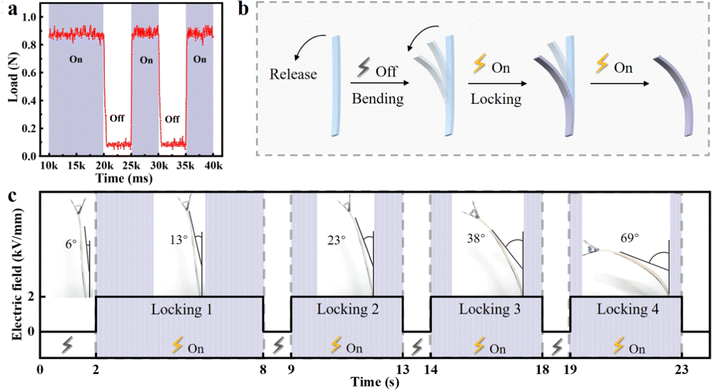
The response of an ER fluid in an electric field is a basic property and an important indicator to determine its application. Therefore, the response time of a structure's stiffness variation needs to be investigated. The load cycle process of the ER structure is shown in Fig. 6a, which illustrates the response time and repeatability of the soft structure. Here, keeping the bending displacement at 6 mm and the electric field strength at 4.5 kV mm⁻¹, the load of the structure with 1.5 g mL⁻¹ of ER fluid remained constant at about 0.9 N (in the range of 10 to 20 k ms). When the electric field was removed, the load immediately dropped to around 0.1 N, which was the inherent load capacity of the structure. It can be seen that the structure responded very quickly (within 65 ms) because of the extremely fast phase transition of the CTO ER fluid. However, the load reduction process was stepwise, within a few hundred milliseconds, until it decayed to the structure's inherent load. This asymmetric response time could be mainly ascribed to the relaxation time of the ER fluid, which is caused by the diffusion and migration behavior of the ER particles under the action of an electric field and shear stress. When the electric field was applied, there were electric field driving forces and shear stresses that drove the ER particles to form chains, whereas, when the electric field was removed, only shear stresses were left to destroy the chain structures, hence the relaxation time when the electric field was applied was less than that when the electric field was removed. As a result, the response times for load rise/fall caused by switching the electric field were different.

Fig. 6 Response time and motion locking of the ER structure. (a) Response time and repeatability of the structure. (b) Schematic of the principle of motion locking. (c) Demonstration of the locking behavior of the soft structure.

Considering the fast-response properties of the ER fluid, motion locking was designed by switching the electric field to adjust the stiffness of the soft structure (Fig. 6b). As can be seen in Fig. 6c and Movie S2 (ESI†), when no electric field was applied, a nudge on the top clip of the structure disrupted its equilibrium and then it bent, which was an accelerated motion caused by gravity. At the moment when the electric field is applied, the motion was locked due to the stiffness of the structure increasing. After the electric field was removed, the structure continued to bend down under the effect of gravity. The response of the structure was very sensitive to switching the electric field.

4. Conclusions

In this study, we proposed a soft stiffness-tunable structure with a sandwich structure of PDMS/electrode-ER fluid-electrode/PDMS. First, we fabricated a CTO-based ER fluid, which has an excellent ER effect. The maximum yield stress of the ER fluid with a mass concentration of 3 g mL⁻¹ could reach 125 kPa under an electric field of 4.5 kV. Then, we assessed the load as well as the stiffness of the structure in different deformation processes and proposed an explanation of the principles of dividing the different deformations. In the initial small deformation process (0–1 mm), the stiffness variation was the largest, which could be adjusted between 64 and 1065 mN mm⁻¹ with a variable rate of more than 1500%, due to the joint enhancement of the friction between the ER particles and between the ER fluid and the electrode layers in the structure. In the large deformation process (1–6 mm), the friction between the ER fluid and the electrode layers was weakened, and the stiffness could be adjusted from 87 to 259 mN mm⁻¹ with a variable rate of over 200%. Moreover, the response time was extremely fast, and the stiffness of the ER structure could be changed within tens of milliseconds. Finally, we demonstrated the stiffness variation, and shape-memory capability, as well as motion locking of the structure. On the whole, the structure has the advantages of continuous variable stiffness and fast response, which suggest it could be applied to soft robots, artificial muscles, and other emerging fields.

Author contributions

Huilan Jing: conceptualization, data curation, formal analysis, investigation, methodology, writing – original draft; Letian Hua: methodology, data curation, formal analysis, supervision; Fei Long: validation, writing –review & editing; Bojin Lv: visualization; Bing Wang: validation; Hewen Zhang: software; Xunye Fan: investigation; Hongru Zheng: investigation; Chengyi Chu: formal analysis; Gaojie Xu: resources; Jianjun Guo: supervision; Aihua Sun: conceptualization, supervision; Yuchuan Cheng: conceptualization, methodology, resources, visualization, writing-review & editing, supervision, project administration, funding acquisition.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This research was supported by the Zhejiang Provincial Natural Science Foundation of China under Grant No. LZ22E030003, the Ningbo Natural Science Foundation of China (2023J050 and 2022J231), the National Natural Science Foundation of China (52273241), and the National Key Research and Development Project of China (2021YFB3701500).

References

1. G. M. Whitesides, Angew. Chem., Int. Ed., 2018, 57, 4258–4273.
2. E. W. Hawkes, C. Majidi and M. T. Tolley, Sci. Rob., 2021, 6, eabg6049.
3. B. Mazzolai and V. Mattoli, Nature, 2016, 536, 400–401.
4. J. Wang, D. Gao and P. S. Lee, Adv. Mater., 2021, 33, 2003088.
5. J. Shintake, V. Cacucciolo, D. Floreano and H. Shea, Adv. Mater., 2018, 30, 1707035.
6. C. Walsh, Nat. Rev. Mater., 2018, 3, 78–80.
7. M. Cianchetti, C. Laschi, A. Menciassi and P. Dario, Nat. Rev. Mater., 2018, 3, 143–153.
8. Y. Zhang, N. Zhang, H. Hingorani, N. Ding, D. Wang, C. Yuan, B. Zhang, G. Gu and Q. Ge, Adv. Funct. Mater., 2019, 29, 1806698.
9. C. Laschi, B. Mazzolai and M. Cianchetti, Sci Rob., 2016, 1, eaah3690.
10. M. Manti, V. Cacucciolo and M. Cianchetti, IEEE Robot Autom. Mag., 2016, 23, 93–106.
11. S. Zhuo, Z. Zhao, Z. Xie, Y. Hao, Y. Xu, T. Zhao, H. Li, E. M. Knubben, L. Wen, L. Jiang and M. Liu, Sci. Adv., 2020, 6, eaax1464.
12. Y. Piskarev, J. Shintake, C. Chautems, J. Lussi, Q. Boehler, B. J. Nelson and D. Floreano, Adv. Funct. Mater., 2022, 32, 2107662.
13. P. Testa, R. W. Style, J. Cui, C. Donnelly, E. Borisova, P. M. Derlet, E. R. Dufresne and L. J. Heyderman, Adv. Mater., 2019, 31, 1900561.
14. F. Long, Y. Cheng, Y. Ren, J. Wang, Z. Li, A. Sun and G. Xu, Adv. Eng. Mater., 2022, 24, 2100863.
15. W. Wang, C. Y. Yu, P. A. Abrego Serrano and S.-H. Ahn, Soft Rob., 2020, 7, 283–291.
16. L. Li, F. Xie, T. Wang, G. Wang, Y. Tian, T. Jin and Q. Zhang, Soft Rob., 2022, 9, 1108–1119.
17. J. Lussi, M. Mattmann, S. Sevim, F. Grigis, C. De Marco, C. Chautems, S. Pané, J. Puigmartí-Luis, Q. Boehler and B. J. Nelson, Adv. Sci., 2021, 8, 2101290.
18. N. M. Kuznetsov, V. V. Kovaleva, S. I. Belousov and S. N. Chvalun, Mater. Today Chem., 2022, 26, 101066.
19. T. C. Halsey, Science, 1992, 258, 761–766.
20. T. Hao, Adv. Mater., 2001, 13, 1847–1857.
21. W. Wen, X. Huang and P. Sheng, Soft Matter, 2008, 4, 200–210.
22. Y. D. Liu and H. J. Choi, Soft Matter, 2012, 8, 11961–11978.
23. S. H. Chen, G. Yang and X. H. Liu, Smart Mater. Struct., 2001, 10, 1025–1030.
24. I. Musiałek, M. Migus, A. Olszak, K. Osowski, Z. Kęsy, A. Kęsy, G. W. Kim and S. B. Choi, Smart Mater. Struct., 2020, 29, 087006.
25. H. Heinken, S. Ulrich, R. Bruns and S. Schneider, J. Intell. Mater. Syst. Struct., 2020, 31, 297–307.
26. A. Tonazzini, A. Sadeghi and B. Mazzolai, Soft Rob., 2016, 3, 34–41.
27. K. Wei, Q. Bai, G. Meng and L. Ye, Smart Mater. Struct., 2011, 20, 055012.
28. X. Wang, R. Shen, W. Wen and K. Lu, Int. J. Mod. Phys. B, 2005, 19, 1110–1113.
29. Y. Cheng, X. Liu, J. Guo, F. Liu, Z. Li, G. Xu and P. Cui, Nanotechnology, 2009, 20, 055604.
30. X. Gong, J. Wu, X. Huang, W. Wen and P. Sheng, Nanotechnology, 2008, 19, 165602.
31. J. Wu, Z. Song, F. Liu, J. Guo, Y. Cheng, S. Ma and G. Xu, NPG Asia Mater., 2016, 8, e322–e322.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc01563g

‡ Huilan Jing and Letian Hua contributed equally to this work.

---