Thermal conductivity of sliding bilayer h-BN and its manipulation with strain and layer confinement

Abstract

Two-dimensional bilayer structures exhibit novel properties not existing in the monolayer ones like bilayer hexagonal boron nitride (h-BN) with exotic interfacial ferroelectrics originated by laterally sliding one layer over the other (K. Yasuda, et al., Science, 2021, 372, 1458; M. Vizner Stern, et al., Science, 2021, 372, 1462). This intriguing property provides the sliding bilayer h-BN with promising applications in slidetronics. However, the thermal transport behaviour in the sliding bilayer h-BN is still unclear. Here, we systematically investigate the influence of the lattice configurations on the thermal conductivity (κ) of sliding bilayer h-BN structures as well as its manipulation with strain and layer confinement via first-principles. Our results show that structures with boron head-to-head stacking (B–B) exhibit lower κ values than the ones with nitrogen on the top of boron stacking (B–N). The phonon spectra and weighted phase space indicate a softer layer-breathing mode (ZO′) mode and higher three-phonon scattering rate of B–B patterns, leading to a lower κ. The moderate out-of-plane compressive strain of −6% significantly decreases the κ of B–B structures by about 50% through enhanced anharmonic scattering, while the higher strain of −18% suppresses the anharmonic scattering and increases the κ instead. Finally, we study the stacking dependence of the κ in tri-layer and bulk structures.

---

1. Introduction

In 2D materials, except for the monolayer structures, the bilayer ones also exhibit interesting properties due to the multiple stacking configurations. For example, twisted bilayer graphene is a system with the quantum Hall effect and tunable superconductivity under specific twist angles.^1,2 In recent, sliding bilayer h-BN has attracted intensive interest for its novel physical properties, such as ferroelectricity.^3,4 Different from twisted bilayer graphene, the exotic properties of sliding bilayer h-BN are not due to the formation of moiré patterns but the various stacking patterns. For bilayer structures, van der Waals sliding will change the lattice pattern and break the symmetry, thereby modulating the electrical, optical and magnetic properties of 2D materials.^5–7 Experimentally, Yasuda et al. demonstrated an out-of-plane ferroelectric polarization in staggered bilayer h-BN,⁸ which is switchable by sliding one layer with respect to the other layer. The switching of electrical polarization is usually driven by the external forces, for example an external electric field.^3,9–11 The experimentally controllable sliding on bilayer h-BN, breaking the lattice symmetry, implies a high potential of modulation of lattice thermal conductivity in such an exotic low-dimensional system.

Thermal conductivity (κ) is an important parameter for the thermal management of electric devices. Materials with higher κ are preferable for high-power devices and efficient heat dissipation,^12–14 while a low κ is crucial for thermoelectric applications.^15–18 The κ of monolayer h-BN reaches 751 W m⁻¹ K⁻¹ based on experimental measurements, which is promising for the heat dissipation applications.¹⁹ The previous computational results based on the solution of the phonon Boltzmann transport equation (BTE) reveal a trend of decreasing thermal conductivity with the increasing number of h-BN layers.²⁰ The results from molecular dynamics (MD) simulations demonstrated that the mismatch of different layers in bulk h-BN effectively influences the out-of-plane κ.²¹ Gholivand and Donmezer also confirmed that the thermal conductivity of bilayer h-BN (401 W m⁻¹ K⁻¹, in-plane) is lower than that of single layer h-BN (579 W m⁻¹ K⁻¹).²² The out-of-plane acoustic (ZA) phonon modes contribute most to the thermal conductivity in h-BN. The confinement from adjacent layers effectively changes the ZA phonon modes and decreases the κ for bilayer structures. The van der Waals sliding will change the configuration of bilayer h-BN along the out-of-plane direction, intuitively influencing the thermal conductivity to a certain extent. However, the sliding effect on the thermal conductivity is not clear yet.

Moreover, strain will change phonon vibration behavior, effectively affecting the thermal transport properties.^23–25 The hydrostatic pressure drives the thermal transport from anisotropic to isotropic in layered InSe via modulating the phonon group velocity and lifetime.²⁶ Sun et al. explored the effect of interlayer interaction on both the in-plane and out-of-plane thermal conductivity of bilayer graphene and graphite.²⁷ An out-of-plane compressive strain decreases the in-plane κ, while it increases the out-of-plane κ. Duan et al. also investigated the strain effect on thermal conductivity and revealed an enhanced hydrodynamic phonon transport in bilayer graphene with larger strains.²⁸ In the experiment, the diamond anvil cell²⁹ or the piston cylinder cell^30,31 is usually used to apply the hydrostatic pressure and tune the out-of-plane strain on layered materials.³²

In this work, we systematically investigate the sliding and strain effects on the thermal conductivity of bilayer h-BN. Our results indicate that the thermal conductivity of AC′ (B–B) (see configurations in Fig. 1) is lower than those of both AA′ (B–N) and AB (B–N) due to the softer ZO′ modes. The thermal conductivity of AC′ can be modulated by out-of-plane compressive strains which change the frequency of ZO′ modes and the anharmonic interaction. The AC′ configuration exhibits a higher electrical conductivity compared with AA′ under p-type doping. Finally, we find that the trend in sliding bilayer h-BN is general and valid in tri-layer and bulk structures as well: i.e., lower thermal conductivity in AC′ compared with AA′ and AB stacks. This work provides a fundamental understanding of the sliding effect on the thermal transport behavior of stacked h-BN, which sheds light on the design of h-BN related thermal devices with sliding and/or strain.

Fig. 1 All stacking configurations of bilayer h-BN. The head-to-head atomic configurations are shown in brackets. The antiparallel configuration (AA′) is the ground state with the lowest energy. AB′ (AC′) corresponds to the structure by sliding the top layer of AA′ to the left (right). AB (BA) is the structure obtained by sliding the top layer of the parallel configuration, AA, to the left (right). The space group of AA′, AB, AC′ and monolayer h-BN is P3̄m1, P3m1, P3̄m1, and P6̄m2, respectively.

2. Computational methodology

The thermal conductivity was calculated by solving the phonon BTE iteratively implemented using the ShengBTE package.³³ The calculation of thermal conductivity is based on the second and third order interatomic force constants (IFC) with the correction of Born effective charge. The IFC data were calculated by the finite displacement method implemented by phonopy³⁴ and third order.py.³³ The IFC of structures with displaced atoms was calculated using a self-consistent step based on density functional theory (DFT). All the self-consistent calculations were calculated via Vienna Ab Initio Simulation Package (VASP)³⁵ using the projected augmented wave (PAW)³⁶ method and the generalized gradient approximation (GGA) and Perdew–Burke–Ernzerhof (PBE) functional.³⁷ The iterative self-consistent calculation is stopped until the energy variation is smaller than 10⁻⁸ eV. The convergence threshold of forces for structural relaxations was 10⁻⁶ eV Å⁻¹ to get an accurate phonon band structure. We also considered the van der Waals interaction by applying the DFT-D3³⁸ method in DFT calculations. The thermoelectric properties are calculated by solving the electron BTE with the BoltzTraP code.³⁹ The electron relaxation time in BTE is evaluated based on electron-phonon coupling implemented using the EPW code.⁴⁰ See the ESI† for more computational details.

3. Results and discussion

3.1 Geometric structures of sliding bilayer h-BN

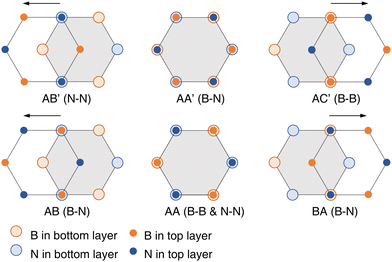
There are six stacking configurations of bilayer h-BN as shown in Fig. 1 and Fig. S1 (ESI†). The antiparallel configuration AA′ with the atomic pattern of nitrogen on the top of boron (B–N) is reported to be the most stable phase both theoretically and experimentally.⁴¹ The AB′ corresponds to the structure by sliding the top layer of AA leftwards, making a N–N head-to-head configuration, while AC′ is rightward with the B–B configuration. The AB and BA are obtained by sliding the parallel structure AA in opposite directions, but AB and BA are two equivalent structures with the same pattern of B–N. Li et al. calculated the sliding energy barrier of bilayer h-BN, which is only around 9 meV per atom.⁴² Such a low energy barrier indicates an easy process for the experimental preparation of sliding bilayer h-BN samples. Among these configurations, AA and AB′ are not dynamically stable based on the phonon-spectrum analysis (see details in Section 3.2 and Fig. S2, ESI†). The instability of AA bilayer h-BN has also been reported in previously published papers.^43,44 Thus, only the properties of AA′, AB, and AC′ are investigated in this work unless otherwise stated, which include thermal conductivity, intermediate physical quantities like weighted phase space and total scattering rate, phonon band structures, and electronic structures.

3.2 The thermal conductivity of sliding bilayer h-BN

Based on the thermal transport theory, the phonon band structure clearly indicates the lattice vibration behavior, which is a basic property to determine the thermal conductivity. Fig. 2a shows the phonon band structure of AA′, AB and AC′. As can be seen, there is no imaginary frequency in these three stacking configurations, while AB′ and AA configurations have the imaginary frequency (Fig. S2, ESI†), which is because of the strong steric repulsion between head-to-head N atoms in AB′ and AA.⁴³ Therefore, we will not further calculate the thermal properties of AB′ and AA structures with imaginary phonon frequencies. From the enlarged phonon spectrum (Fig. 2a), the frequencies of ZO′ modes in AC′ are lower than those of AA′ and AB. The differences between the phonon frequencies will directly determine the phonon scattering behavior governed by the energy and momentum conservation rule, thereby influencing the final thermal conductivity.

Fig. 2 (a) Phonon band structures of AA′, AB, and AC′ as well as the enlarged part at the low frequency region near the Γ point. (b) Convergence tests of the thermal conductivity for the parameter of the nearest neighbor in the calculation of the third order force constants. The cutoff distance of 19th nearest neighbor reaches 6.97 Å. The inset is the variation of charge density with the isosurface of 10⁻⁵ eÅ⁻³ when the central boron atom is displaced along the out-of-plane direction by 0.02 Å.

The convergence test is a necessary step to obtain an accurate thermal conductivity and the number of nearest neighbors is an important parameter in the calculation of third order IFC. We, thus, calculate the κ of AA′ configuration with the number of nearest neighbors varying from 8 to 20 for the convergence test as shown in Fig. 2b. As can be seen, the thermal conductivity of AA′ finally converged at 428 W m⁻¹ K⁻¹ when considering the 19th nearest neighbor, which is in good agreement with the published result of AA-type h-BN in Table 1. The cutoff distance for the 19th nearest neighbor is 6.97 Å larger than the distance (5.02 Å) evaluated from the variation of charge density induced by the displacement of central boron atom.⁴⁵ The 0.02 Å displacement will influence the charge distribution within the range of 5.02 Å as shown in the inset Fig. 2b. The larger cutoff distance ensures the accuracy of κ calculation. Moreover, our result for monolayer h-BN is also close to those of previous works (Table 1). The converged and reasonable results indicate that our computational method and process are correct. After the convergence test, we calculate the thermal conductivity of AB, which is close to that of AA′ because the atomic stacking pattern of AB is B–N, the same as that of AA. The thermal conductivity of AC′ with the B–B pattern is the lowest one among the three configurations, 397 W m⁻¹ K⁻¹. The lower κ on the out-of-plane for the bulk structure indicates an anisotropic thermal transport, which is a typical characteristic for the layered structures.^46,47 Because of the same B–N pattern in AB and AA′, we group AB and AA′ together in the following discussion unless otherwise stated, and only make comparisons between the configurations of AC′ (B–B) and AA′ (B–N).

Table 1 The calculated thermal conductivity κ at 300 K in W m⁻¹ K⁻¹. The values in the brackets are from references

	Monolayer	Bilayer	Tri-layer	Bulk
	647(579,^20 650^22)			In-plane	Out-of-plane
AA′-type	—	428 (401^20)	398	312	3.17
AB-type	—	425	367	321	2.98
AC′-type	—	397	347	278	2.04

---

To understand the underlying physics of the lower thermal conductivity of B–B type AC′ than the B–N type AA′ and AB, we investigate and compare intermediate physical quantities between AC′ and AA′, including the weighted phase space (WP3), the Grüneisen parameter (γ), and the total scattering rate in Fig. 3. The cumulative thermal conductivity of AC′ and AA′ gradually increase to the converged value when more phonon modes with higher frequencies are involved as shown in Fig. 3a. The first order derivative of the thermal conductivity (inset of Fig. 3a) reflects the contribution of phonon modes with specific frequency to the final thermal conductivity. The contributions of AC′ phonon modes are obviously less than that of AA′ in the range from 2 to 10 THz (highlighted by a pink shadow). The negative spectral thermal conductivity near 15 THz should be a numerical artifact during the iterative process as shown in Fig. S3 (ESI†). As mentioned above, the lower frequencies of ZO′ modes in AC′ are the main difference in the phonon band structures. Based on the energy and momentum conservation rule in phonon scattering behavior, the phonon band structure will directly determine the number of 3-phonon scattering processes, also called phase space. Fig. 3b shows that the phase space with frequency weights⁴⁸ of AC′ is slightly higher than AA′ in the range from 2 to 10 THz, indicating a higher scattering possibility and lower thermal conductivity of AC′. Therefore, the low frequency of ZO′ modes in AC′ is an important factor for its lower thermal conductivity.

Fig. 3 (a) The frequency dependent cumulative thermal conductivity. The inset is the first derivative of the thermal conductivity. (b)–(d) The weighted phase space (WP3), Grüneisen parameter (γ), and total scattering rate of AC′ and AA′, respectively.

Besides the weighted phase space, other intermediate physical quantities like the γ parameter and scattering rate also contribute to the difference of the thermal transport behavior between AC′ and AA′. The γ parameter measures the anharmonicity of the lattice vibration, thereby indicating the magnitude of the phonon scattering rate and thermal conductivity.^28,49,50Fig. 3c shows that the absolute value of the γ parameter of AC′ is close to that of AA′ in the range of 2–10 THz, indicating a weak influence of γ on the thermal conductivity of AC′ in that range. Similar to WP3, the total scattering rate of AC′ is higher than that of AA′ in the range from 2 to 10 THz as shown in Fig. 3d, which is consistent with the lower κ of AC′. The frequency differences of transverse optical (TO) and longitudinal optical (LO) modes also lead to the higher phonon scattering rate of AC′ as shown in Fig. S4 (ESI†). The atomic vibration amplitude of AC′ is also larger than that of AA′ indicating a higher lattice anharmonicity as shown in Fig. S5 (ESI†).⁵¹ The phonon mean free path (MFP) is an important reference for the modulation of thermal transport by nanostructuring.⁵² We calculate the phonon MFP based on the results of phonon relaxation time and group velocity.⁵³ The MFP of AA′ is close to that of AC′ with the value around 300 nm as shown in Fig. S6 (ESI†). To modulate the thermal transport via nanostructuring, the scale of bilayer h-BN sample should be smaller than 1 μm. Overall, the variation of weak van der Waals interaction induces around 7% decrease of the thermal conductivity from AA′ (428 W m⁻¹ K⁻¹) to AC′ (397 W m⁻¹ K⁻¹). The lower κ indicates the AC′ configuration still exhibits acceptable heat dissipation efficiency if applied in the actual devices.

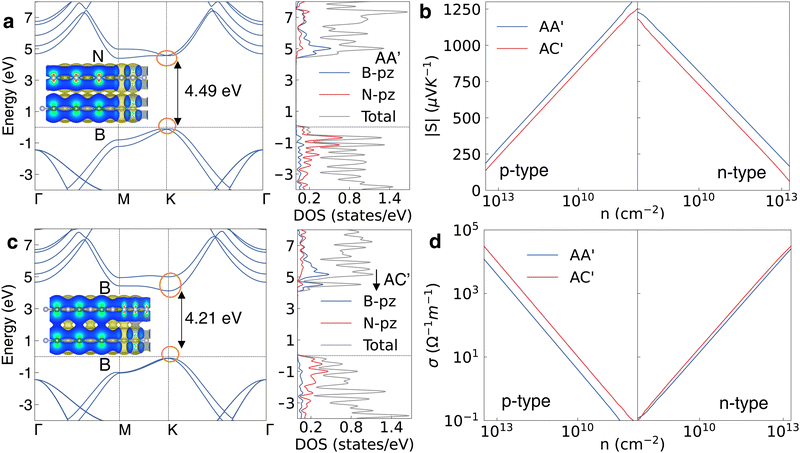
Based on above discussion, the softer ZO′ modes of AC increase the three-phonon scattering possibility and enhance the phonon scattering rate, resulting in a lower thermal conductivity. The soft phonon vibrations are generally led by a delocalized charge distribution or overlap of electronic wavefunction.⁵⁴ Therefore, we next explore the possible reason for the soft ZO′ modes in AC′ by studying the electronic structures of AA′ and AC′. From the band structure of AA′ and AC′ in Fig. 4a and c, we can see that the conduction band of AC′ at the K point is obviously splitting unlike the 2-fold degenerate one of AA′. The projected density of states (PDOS) for the p_z orbital of B atoms is significantly higher than that of N atoms in the conduction band as shown in the right panel of Fig. 4a and c. As can be seen, the conduction (valence) band of both AA′ and AC′ is contributed by B (N) atoms due to the stronger electronegativity of N compared with B. Hence, the stronger interaction between B atoms in different layers leads to a splitting in the conduction band of AC′. Furthermore, the p_z states of B atoms in AC′ in the conduction band shift down compared with AA′ indicating a larger overlap of wavefunction for p_z orbitals. The band gap of AC′ (4.21 eV) is also lower than that of AA (4.49 eV). The charge density between the two layers in AC′ is more delocalized than that of AA′ as shown in insets of Fig. 4, which is consistent with the larger overlap of wavefunctions.

Fig. 4 (a) Band structure and projected density of states (PDOS) of AA′. The inset is the band decomposed charge density, corresponding to the states within orange circles at the K point. (b) The absolute value of the Seebeck coefficient for AA′ and AC′ under different doping concentrations. (c) Band structure, decomposed charge density, and PDOS of AC′. (d) Electrical conductivity (σ) of AA′ and AC′ under different doping concentrations.

Due to the decreasing of the bandgap, the Seebeck coefficient (S) and electrical conductivity (σ) of AC′ are also different from that of AA′ as shown in Fig. 4b and d. The absolute Seebeck coefficient value (|S|) of AC′ is lower than that of AA′ and the electrical conductivity is higher especially for the p-type, which is consistent with the smaller bandgap of AC′ and larger electron relaxation time as shown in Fig. S7a (ESI†). As a result, the power factor of AA′ is smaller than that of AC′ under p-type doping but larger under n-type doping as shown in Fig. S7b (ESI†). All the band splitting, downshift of PDOS and the delocalized charge distribution reveal the reason for the soft ZO′ mode in AC′ and further explain the lower thermal conductivity of the AC′-staggered bilayer h-BN than AA′ and AB (see Fig. S8 for AB, ESI†).

3.3 Strain effect on AC′ stacking bilayer h-BN

As can be seen, the sliding does not significantly change the thermal conductivity value. Next, we investigate the impact of strain on the thermal conductivity of bilayer sliding h-BN. The out-of-plane strain is a more effective way to modulate the thermal conductivity for layered materials because the strain directly affects the phonon vibration along the corresponding direction.⁵⁵ For the AC′ configuration, we apply the out-of-plane compressive strain on AC′ up to −18% (negative sign of −18% for compression following) by decreasing the interlayer distance. There is no imaginary phonon frequency in the phonon band structure of AC′ under −18% strain. The structure stability under such a large strain of AC′ is partly due to the soft phonon vibration along the out-of-plane direction (B–B pattern).

Fig. 5a shows the phonon band structure of AC′ with/without strains. As can be seen, the ZO′ frequency keeps increasing with the increase of the strain. That is to say, the stronger interlayer interaction by strain induces the higher frequency of ZO′ modes. Interestingly, unlike the monotonic change of the phonon frequency, the thermal conductivity of AC′ firstly decreases, then increases to the value even higher than that without strain as shown in Fig. 5b. The κ results based on the relaxation time approximation (RTA) have a similar trend to the iteratively solved data, but lower absolute values. It is because the RTA approach treats both normal and Umklapp scattering as the resistance for thermal transport, but the momentum conserving normal scattering does not resist the thermal transport.^56,57 Hence, the RTA approach underestimates the thermal conductivity especially in materials with strong normal scattering and high thermal conductivity, such as h-BN and graphene. A large difference between the RTA and iterative way is significant at 0% and 18%, which indicate that normal scattering is more dominating in phonon scattering processes without strain or under a very large compressive strain.

Fig. 5 (a) The phonon band structures of AC under 0%, −6% and −18% out-of-plane compressive strain. The low frequency part is enlarged. (b) The thermal conductivity of AC′ under different strains. The red and blue points represent the data calculated based on the iterative way and relaxation time approximation, respectively. (c)–(e) The WP3, anharmonic scattering rate (ASR), and total scattering rate, respectively, of AC under 0%, −6% and −18% strain.

To clarify the dominant reason for the thermal conductivity under various strains, we check the intermediate physical quantities for AC′ with strains. First, the WP3 value decreases monotonically with the strain increasing as shown in Fig. 5c, which is reasonably consistent with the increase of the phonon frequency. From eqn (S2) and (S3) (ESI†),⁴⁸ the WP3 value just depends on the phonon dispersion relation. Therefore, the decreasing WP3 does not contribute to the decreasing thermal conductivity when the strain increases from 0% to 6%. Under a higher strain larger than 6%, the WP3 contribute to the increase of thermal conductivity to a higher extent. The anharmonic scattering rate (ASR) exhibits a similar variation trend to the thermal conductivity unlike WP3 (Fig. 5d). The ASR includes the effect in interatomic force constant as shown in eqn (S4) and (S5) (ESI†).³³ The consistency between thermal conductivity and the ASR indicates that the anharmonic IFC or the phonon anharmonicity dominates the thermal conductivity more under the applied strain.

The −6% strain significantly enhances the anharmonic scattering of out-of-plane phonon modes (ZA and ZO′), while the further increasing strains larger than −6% gradually suppress the anharmonic scattering. The local maximum κ under the strain of 10% is also induced by the local minimum ASR as shown in Fig. S9 (ESI†). The final total scattering rate (Fig. 5e) has the same trend as ASR. The magnitude of γ parameter decreases with the increasing strain as shown in Fig. S10 (ESI†). The small γ under −18% further verifies the weak phonon anharmonicity consistent with the lower ASR value. For AA′ and AB configurations, there are obvious imaginary phonon frequencies near Γ point under a high compressive strain as shown in Fig. S11 (ESI†). We only investigate the κ of AA′ and AB with compressive strain below 6%. Both the κ of AA′ and AB exhibit a decreasing trend when the strain increases from 0 to 6% in Fig. S12 (ESI†). The ASR of AA′ reach the highest value under the 6% strain similar to the case of AC′ consistent with the smaller κ value. All the N (B) atoms of AA′ are in the top site inducing a stronger B–N van der Waals interaction, a higher ASR and a lower κ value under strain. Overall, the researchers should avoid any out-of-plane compressive strain on bilayer h-BN to keep a high heat dissipation efficiency for the devices.

3.4 The thermal conductivity of sliding tri-layer and bulk h-BN

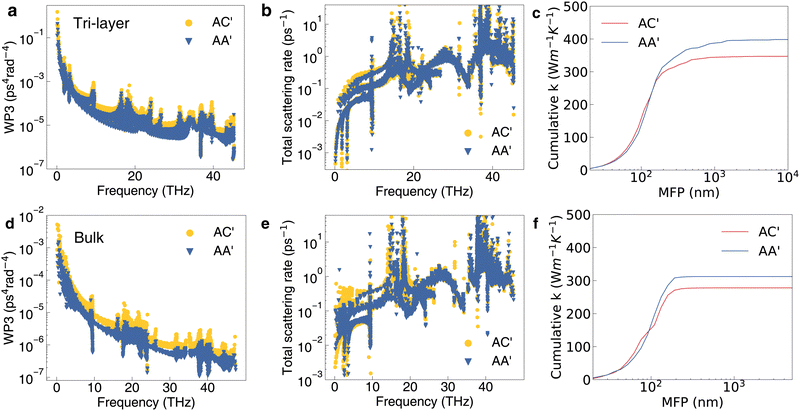
Because the bilayer structure only confines the phonon vibration at one side for each atomic layer, we then consider the sliding effect on the thermal conductivity of tri-layer and bulk structures (confinement on both sides) with the stacking patterns of AA′, AB and AC′, which are defined the same as the bilayer ones as shown in Fig. S13 (ESI†). For example, AA′-type tri-layers in this work is still defined as the head-to-head B and N atoms (B–N) for each adjacent bilayer. The bulk structures are the continuous periodic stacking of bilayer building blocks. There are no imaginary phonon frequencies in the phonon band structures of tri-layer and bulk structures in all three configurations as shown in Fig. S14 (ESI†). The ZO′ modes of the AC′-type tri-layer and bulk are still lower than that of the AA′- and AB-type, which is similar to the bilayer case. Moreover, the AC′-type thermal conductivity is also the lowest among the three types in both tri-layer and bulk phases. The calculated thermal conductivity values tend to decrease from single layer to bilayer, tri-layer, and bulk structures due to the additional confinement along the out-of-plane direction as shown in Table 1.

To understand the layer effect on the thermal conductivity of sliding h-BN, we compare the intermediate quantities for AC′- and AA′-type tri-layer and bulk structure. Fig. 6 shows obvious differences in WP3 and the total scattering rate between AC′- and AA′-type tri-layers and bulk h-BN. The WP3 of AC′ is clearly larger than that of AA′ over the range of all phonon frequencies (Fig. 6a and d). The total scattering rate of AC′ is larger than that of AA′ mainly within 0–10 THz (Fig. 6b and e). More layers will effectively enhance the phonon scattering rate for AC′ with B–B patterns compared with AC′ with B–N patterns, thereby reducing the thermal conductivity significantly compared with the bilayer case. The MFP of the bulk structure is also obviously smaller than the that of the tri-layer structure from the cumulative κ in (Fig. 6c and f). For the tri-layer, the κ of AC′ is 13% lower than that of AA′ while the bilayer has only a 7% lower κ. More layers also enhance the phonon anharmonicity as shown by the change of ASR and γ in Fig. S15 (ESI†). In a short summary, κ will decrease with the increase in the number of layers of h-BN. The AC′-type configuration (B–B) always has the lowest κ in multilayer and bulk h-BN. From bilayer to bulk, the difference of κ between AA′ and AB also gets larger but is less obvious compared with AA′ and AC′ as discussed in the ESI† (Fig. S16, ESI†).

Fig. 6 (a)–(c) are the WP3, total scattering data and cumulative κ with respect to the MFP of tri-layer structures with AC′ and AA′ stacking patterns. (d)–(f) are the WP3 and total scattering data, cumulative κ with respect to the MFP of bulk structures with AC′ and AA′ stacking patterns.

4. Conclusions

In summary, we investigated the thermal conductivity of sliding bilayer h-BN with 3 different stacking patterns, AA′, AB and AC′. The configuration AC′ with the B–B pattern exhibits a softer out-of-plane phonon vibration than AA′ and AB with the B–N pattern especially for the ZO′ modes, which increases the three-phonon scattering rate, lowering the thermal conductivity for the AC′ configuration. The B–B stacking is less favorable than B–N stacking for the heat dissipation in electric devices. But the B–B stacking exhibits a smaller bandgap and higher electrical conductivity compared with B–N under p-type doping, which is preferable for the electric devices. A small out-of-plane compressive strain on the AC′ configuration of −6% will decrease the κ by 50%, while a larger strain of −18% increases the κ to a value higher than that of free standing bilayer h-BN. We found that the difference between the scattering rate of AC′ and AA′ configurations gets larger from bilayer to tri-layer and bulk, further demonstrating the effect of softer phonon vibration for B–B stacking on the thermal conductivity. Our investigation indicates that van der Waals sliding and/or strain still have a non-negligible effect on the thermal conductivity of bilayer h-BN, providing guidelines for the thermal management for 2D material devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Jiaren Yuan, Dr Zhiwei Ding and Dr Linfeng Yu for their helpful discussion. Y. M. Z. gratefully acknowledges the support from the China Scholarship Council. (no. CSC202104910079). L. S. is thankful for the support from the Ministry of Education, Singapore, under its MOE Tier 1 (grant no. A-0005241-01-00). The authors also acknowledge the Centre for Advanced 2D Materials (C2DHPC), the High performance computing of National University of Singapore (HPC@NUS IT) and the National Supercomputing Centre Singapore (NSCC) for providing computing resources.

Notes and references

1. Y. Cao, V. Fatemi, S. Fang, K. Watanabe, T. Taniguchi, E. Kaxiras and P. Jarillo-Herrero, Nature, 2018, 556, 43–50.
2. D. S. Lee, C. Riedl, T. Beringer, A. H. Castro Neto, K. von Klitzing, U. Starke and J. H. Smet, Phys. Rev. Lett., 2011, 107, 216602.
3. M. Wu and J. Li, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2115703118.
4. Y. Liang, S. Shen, B. Huang, Y. Dai and Y. Ma, Mater. Horiz., 2021, 8, 1683–1689.
5. Q. Wu, F. Liang, L. Kang, J. Wu and Z. Lin, ACS Appl. Mater. Interfaces, 2022, 14, 9535–9543.
6. P. Serles, T. Arif, A. B. Puthirath, S. Yadav, G. Wang, T. Cui, A. P. Balan, T. P. Yadav, P. Thibeorchews, N. Chakingal, G. Costin, C. V. Singh, P. M. Ajayan and T. Filleter, Sci. Adv., 2021, 7, eabk2041.
7. G. W. Kim and G. Kim, Appl. Surf. Sci., 2022, 586, 152596.
8. K. Yasuda, X. Wang, K. Watanabe, T. Taniguchi and P. Jarillo-Herrero, Science, 2021, 372, 1458–1462.
9. J. Yang, J. Zhou, J. Lu, Z. Luo, J. Yang and L. Shen, Mater. Horiz., 2022, 9, 1422–1430.
10. C. Liu, Z. Chen, C. Wu, J. Qi, M. Hao, P. Lu and Y. Chen, ACS Appl. Mater. Interfaces, 2022, 14, 46716–46725.
11. F. Wang, Z. Ma, Y. Wei, P. Huang and X. Zhang, Appl. Surf. Sci., 2021, 563, 150276.
12. D. Shoemaker, M. Malakoutian, B. Chatterjee, Y. Song, S. Kim, B. M. Foley, S. Graham, C. D. Nordquist, S. Chowdhury and S. Choi, IEEE Trans. Compon. Packag. Manuf., 2021, 11, 1177–1186.
13. Y. Fu, J. Hansson, Y. Liu, S. Chen, A. Zehri, M. K. Samani, N. Wang, Y. Ni, Y. Zhang, Z.-B. Zhang, Q. Wang, M. Li, H. Lu, M. Sledzinska, C. M. S. Torres, S. Volz, A. A. Balandin, X. Xu and J. Liu, 2D Mater., 2020, 7, 012001.
14. S. Nayeb Sadeghi, S. M. Vaez Allaei, M. Zebarjadi and K. Esfarjani, J. Mater. Chem. C, 2020, 8, 15705–15716.
15. M. Mukherjee, A. Srivastava and A. K. Singh, J. Mater. Chem. C, 2022, 10, 12524–12555.
16. B. Roondhe, V. Sharma, H. L. Kagdada, D. K. Singh, T. Saha Dasgupta and R. Ahuja, Appl. Surf. Sci., 2020, 533, 147513.
17. J.-H. Bahk, H. Fang, K. Yazawa and A. Shakouri, J. Mater. Chem. C, 2015, 3, 10362–10374.
18. J. Hu, Y. Zuo, Y. Hao, G. Shu, Y. Wang, M. Feng, X. Li, X. Wang, J. Sun, X. Ding, Z. Gao, G. Zhu and B. Li, Chin. Phys. B, 2023, 32, 046301.
19. Q. Cai, D. Scullion, W. Gan, A. Falin, S. Zhang, K. Watanabe, T. Taniguchi, Y. Chen, E. J. G. Santos and L. H. Li, Sci. Adv., 2019, 5, eaav0129.
20. L. Lindsay and D. A. Broido, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035436.
21. W. Ouyang, H. Qin, M. Urbakh and O. Hod, Nano Lett., 2020, 20, 7513–7518.
22. H. Gholivand and N. Donmezer, IEEE Trans. Nanotechnol., 2017, 16, 752–758.
23. C. Androulidakis, E. N. Koukaras, M. Poss, K. Papagelis, C. Galiotis and S. Tawfick, Phys. Rev. B, 2018, 97, 241414.
24. H. Y. Lv, W. J. Lu, D. F. Shao, H. Y. Lu and Y. P. Sun, J. Mater. Chem. C, 2016, 4, 4538–4545.
25. A. Vega-Flick, D. Jung, S. Yue, J. E. Bowers and B. Liao, Phys. Rev. Mater., 2019, 3, 034603.
26. K. Yuan, X. Zhang, Z. Chang, Z. Yang and D. Tang, ACS Appl. Energ. Mater., 2022, 5, 10690–10701.
27. Z. Sun, K. Yuan, Z. Chang, X. Zhang, G. Qin and D. Tang, J. Appl. Phys., 2019, 126, 125104.
28. F. Duan, C. Shen, H. Zhang and G. Qin, Phys. Rev. B, 2022, 105, 125406.
29. J. Xia, J. Yan, Z. Wang, Y. He, Y. Gong, W. Chen, T. C. Sum, Z. Liu, P. M. Ajayan and Z. Shen, Nat. Phys., 2021, 17, 92–98.
30. T. Song, Z. Fei, M. Yankowitz, Z. Lin, Q. Jiang, K. Hwangbo, Q. Zhang, B. Sun, T. Taniguchi, K. Watanabe, M. A. McGuire, D. Graf, T. Cao, J.-H. Chu, D. H. Cobden, C. R. Dean, D. Xiao and X. Xu, Nat. Mater., 2019, 18, 1298–1302.
31. T. Li, S. Jiang, N. Sivadas, Z. Wang, Y. Xu, D. Weber, J. E. Goldberger, K. Watanabe, T. Taniguchi, C. J. Fennie, K. Fai Mak and J. Shan, Nat. Mater., 2019, 18, 1303–1308.
32. F. Miao, S.-J. Liang and B. Cheng, npj Quantum Mater., 2021, 6, 59.
33. W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758.
34. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5.
35. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
36. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
38. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
39. G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67–71.
40. S. Poncé, E. R. Margine, C. Verdi and F. Giustino, Comput. Phys. Commun., 2016, 209, 116–133.
41. R. S. Pease, Nature, 1950, 165, 722–723.
42. L. Li and M. Wu, ACS Nano, 2017, 11, 6382–6388.
43. M. Vizner Stern, Y. Waschitz, W. Cao, I. Nevo, K. Watanabe, T. Taniguchi, E. Sela, M. Urbakh, O. Hod and M. Ben Shalom, Science, 2021, 372, 1462–1466.
44. S. Zhou, J. Han, S. Dai, J. Sun and D. J. Srolovitz, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 155438.
45. G. Qin and M. Hu, npj Comput. Mater., 2018, 4, 3.
46. P. Jiang, X. Qian, R. Yang and L. Lindsay, Phys. Rev. Mater., 2018, 2, 064005.
47. P. Xiao, E. Chavez-Angel, S. Chaitoglou, M. Sledzinska, A. Dimoulas, C. M. Sotomayor Torres and A. El Sachat, Nano Lett., 2021, 21, 9172–9179.
48. W. Li and N. Mingo, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 144304.
49. G. Qin, X. Zhang, S.-Y. Yue, Z. Qin, H. Wang, Y. Han and M. Hu, Phys. Rev. B, 2016, 94, 165445.
50. X. Cui, X. Yan, B. Wang and Y. Cai, Appl. Surf. Sci., 2023, 608, 155238.
51. Y. Cheng, Z. Fan, T. Zhang, M. Nomura, S. Volz, G. Zhu, B. Li and S. Xiong, Mater. Today Phys., 2023, 35, 101093.
52. A. Zandieh, H. Izadi, M. Hamidinejad, H. Shin, S. Shi, Y. Martinez-Rubi, J. Guan, H. Cho, K. S. Kim and C. B. Park, Appl. Surf. Sci., 2022, 587, 152779.
53. G. Barbalinardo, Z. Chen, H. Dong, Z. Fan and D. Donadio, Phys. Rev. Lett., 2021, 127, 025902.
54. G. Qin, Z. Qin, W.-Z. Fang, L.-C. Zhang, S.-Y. Yue, Q.-B. Yan, M. Hu and G. Su, Nanoscale, 2016, 8, 11306–11319.
55. S. Li, J. Ma, Y. Pei and Y. Chen, J. Mater. Chem. C, 2019, 7, 5970–5974.
56. A. Ward, D. A. Broido, D. A. Stewart and G. Deinzer, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125203.
57. Z. Ding, J. Zhou, B. Song, V. Chiloyan, M. Li, T.-H. Liu and G. Chen, Nano Lett., 2018, 18, 638–649.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc01531a

---