Exploiting grain boundary diffusion to minimize dendrite formation in lithium metal-solid state batteries

Abstract

Maintaining interfacial contact between the Li metal anode and the solid electrolyte is a key challenge in developing Li metal-based solid-state batteries (LMSSB). At moderate discharge rates, relatively slower diffusion within the anode results in roughening and void formation in Li near this interface. The resulting reduction in interfacial contact focuses the Li-ion current during plating to a reduced number of contact points, generating high local current densities that nucleate dendrites. One approach to minimize void formation is to apply high stack pressure, which enhances plastic flow in the anode. Nevertheless, the use of pressure has drawbacks, as it facilitates fracture within the solid electrolyte. Here, an alternative strategy for minimizing void formation is described. Using a multi-scale model, it is shown that targets for capacity and current density in LMSSBs can be achieved by reducing the grain size of Li to exploit fast grain boundary (GB) diffusion. Diffusion rates along a diverse sampling of 55 tilt and twist GBs in Li were predicted using molecular dynamics, and found to be 3 to 6 orders of magnitude faster than in the bulk. Using these atomic-scale data as input, a meso-scale model of Li depletion in the anode during discharge was developed. The model predicts that smaller, columnar grains are desirable, with grain sizes of approximately 1 μm or less needed to meet performance targets. As micron-sized grains are two orders of magnitude smaller than those in common use, strategies for controlling grain size are discussed. In total, the model highlights the importance of the anode's microstructure on the performance of LMSSBs.

---

Introduction

Solid-state batteries that employ a Li-metal anode (LMSSB) are being widely explored within the battery community due to their potential to achieve improved energy densities.^1–4 A solid state battery would also convey safety benefits due to the elimination of the volatile and flammable liquid electrolytes commonly used in existing Li-ion systems. However, realizing these benefits is challenging, as it is now widely known that LMSSBs suffer from internal short-circuiting due to dendrite formation.^5,6

This dendrite-based failure mode occurs during cycling at room temperature under moderate current densities, and is precipitated by the formation of voids in the Li anode at the solid electrolyte interface during discharge/stripping.^7,8 Stripping from the Li anode generally does not occur in a homogeneous, layer-by-layer fashion; this behaviour results in Li voids or pits being formed at the interface. Janek et al.⁸ have argued that voiding occurs when the rate at which Li vacancies are formed during stripping exceeds the rate at which these vacancies are annihilated by the diffusion of Li atoms from other regions in the anode. Upon subsequent plating, the reduced interfacial contact resulting from the voids focuses Li deposition at the remaining (few) contact points, increasing the local current density and fostering dendrite nucleation.

One strategy that has been proposed to mitigate void formation is the application of pressure normal to the Li/SE interface.^7–9 This applied pressure can generate plastic deformation within the Li – specifically creep deformation – and facilitate the redistribution of Li so as to fill vacancies and voids. While this approach has demonstrated the ability to delay void formation to higher current densities, it is unclear whether the high pressures required – on the order of 10 MPa – are realistic in mass-produced cells. Moreover, recent work¹⁰ by Fincher and Chiang have shown that these pressures encourage fracture of the solid electrolyte. For these reasons, the use of high pressures may not be an ideal solution.

A second strategy to minimize dendrite formation is to raise the temperature. Numerous authors have shown that the cyclability of a Li metal anode in contact with a SE dramatically improves as the temperature is increased.^11,12 The performance improvement at elevated temperature can be attributed to faster self-diffusion and creep.^11,12 Unfortunately, and as with the use of pressure, it is not clear that a high-temperature battery is a practical solution, given that modern EV battery systems weigh hundreds of kilograms and should function in cold climates (−40 °C).

As a third strategy, Grovenor et al.¹³ examined whether alloying could speed up diffusion in a Li-based anode. More specifically, the diffusivity of Li in Li–Mg alloys with up to 30 at% magnesium was measured with an isotope tracer method. They found that Li diffusivity was approximately an order of magnitude slower in the Li–Mg alloys, in contrast to prior reports.¹⁴ At high current densities, the larger diffusivity of an unalloyed (pure) Li anode yielded superior performance compared to the alloyed variants. (Interestingly, and despite its larger Li diffusivity, at low current density the Li–Mg alloys were superior due to their ability to maintain interfacial contact with the SE.) While other alloy compositions may yield an improvement in Li-diffusivity, any alloy will add inactive mass and volume to the anode, penalizing (specific) energy density.

Here we propose a different approach to facilitating the redistribution of Li during stripping – exploiting GB diffusion within the Li anode. It is well known that diffusion along grain boundaries in polycrystalline materials can differ dramatically from diffusion in the bulk (i.e., within the grain interiors).^15–17 In some cases the rate of GB diffusion is faster than in the bulk,^17–19 and in some cases it is slower.^20–22 It is also well-established that the grain size (and thus the volume fraction of GBs) of a polycrystalline metal can be influenced by its electro-deposition rate and by substrate effects.^23–26 Thus, if GB diffusion in Li is fast, and the grain size can be kept small, then enhanced Li transport can be achieved without resorting to high pressure, elevated temperature, or alloying.

Here, using a multi-scale simulation methodology, a comprehensive analysis of GB diffusion in Li is presented. First, the self-diffusivity of Li in 55 distinct tilt and twist GBs are evaluated using molecular dynamics and a 2^nd nearest-neighbor MEAM interatomic potential. These calculations predict that GB diffusion is 3 to 6 orders of magnitude faster than in bulk Li, reflecting a significantly smaller activation energy for GB diffusion. Subsequently, polycrystalline diffusivities are predicted as a function of grain size. At room temperature, the polycrystalline diffusivity of Li increases from ∼10⁻¹¹ for grains with 1 mm diameter to ∼10⁻⁷ cm² s⁻¹ when the grain diameter is reduced to 10 nm. Finally, these atomistic data are used to parameterize a mesoscale diffusion model based on Fick's 2^nd law. The model predicts the cell capacity as a function of discharge current density, anode thickness, and the grain size of the Li anode. The model reveals that an average grain size of approximately 1 μm can meet established performance targets of an all-solid-state lithium metal battery. Testable strategies for controlling the grain size during cycling are discussed.

Methods

The 2^nd nearest-neighbor modified embedded-atom method force field (2NN-MEAM) for Li proposed by Kim et al.²⁷ was used in the present study. Prior calculations using this potential have demonstrated that it accurately reproduces fundamental physical properties of Li, including elastic properties, vacancy formation and migration energies, surface energies, specific heat, etc. All simulations were conducted using the LAMMPS code.²⁸

A total of 55 tilt and twist GBs were investigated. These systems employed different choices of the tilt/twist axes (i.e., [001], [01−1], [11−1]), misorientation angles, and coincidence site lattices. Tables S1 and S2† list all of the GBs that were examined. Each grain boundary simulation cell used a bi-crystal structure with two equivalent interfaces and periodic boundary conditions applied in all three directions. The GB planes were separated by a bulk region of minimum thickness of 6 nm to prevent interactions between the two interfaces. For all models, the GB plane was aligned parallel to the X–Z plane of the simulation cell; the GB normal was thus parallel to the Y direction.

Fig. S1† shows a flow chart of the computational procedure used in this study. A multi-step process was used to identify the minimum energy structure of each GB. First, the γ-surface was evaluated for each model by rigidly translating one grain relative to the other by either 1/8th or 1/16th of the length of the repeat unit in the X and Z directions. (The value 1/8th was adopted when the repeat unit was smaller than 14 Å). The resultant grid spacing in each direction was typically ∼1 Å. For each translational state, pairs of close-contact atoms at the interface were identified. A single atom, chosen at random, was deleted from each pair. The threshold for close-contacts was varied from 1–2.6 Å in steps of 0.1 Å. The atom positions and simulation cell length along the Y direction were relaxed for each distinct translation state and close-contact criterion. Accounting for the different interfacial translations and close-contact distances, between 1088 and 4352 interface models were generated for each GB geometry. 162 112 initial GB structures were evaluated in total.

An example γ-surface for a Σ5(310)/[001]GB is shown in Fig. 1. Similar plots for the other GBs are presented in Tables S3 and S4.† Subsequently, a 2nd relaxation was initiated from the minimum energy configuration on the γ-surface. In this case, all atomic positions and the cell size were relaxed in all degrees of freedom. The structure resulting from this second relaxation was used to calculate the GB energy, shown in eqn (1).

Here, γ_GB represents the GB energy, E_GB represents the total energy of the GB simulation cell, E_bulk is the total energy per atom of a bulk Li cell, N is the number of atoms in the GB cell, and A is the area of the GB plane. The numerator is the difference between the energy of the GB cell and that of a perfect lattice with the same number of atoms. The factor of 2 in the denominator accounts for the two distinct GBs contained within the simulation cell.

Fig. 1 Calculated γ-surface for a Σ5(310)/[001] GB.

Finally, simulated annealing was used to further equilibrate the GBs and facilitate identification of the minimum energy GB structures. Starting from the lowest-energy geometry identified by the previous relaxation steps, NPT MD was used to heat each GB cell from 0 K to 400 K for 5 ns at 1 atm. This was followed by NPT equilibration at 400 K/1 atm for an additional 5 ns, and NPT cooling to 0 K/1 atm over 5 ns. A final relaxation was performed and the GB energy was re-evaluated. The energies of the annealed structures were very similar to those obtained before annealing, suggesting that the GB geometries were close to the global energy minimum.

GB migration was observed in several of the annealing simulations. This migration is undesirable as it can reduce the separation between the two GBs (increasing the likelihood for GB/GB interactions). In extreme cases, this can result in annihilation of the GBs (Fig. S2†). To minimize GB migration, the motion of a subset of atoms in the bulk regions were constrained. More specifically, atom motion in the y-direction (normal to the GB plane) was prohibited in two 10 Å wide regions centred at fractional positions y = 0.25 and 0.75. (The GB planes are located at y = 0 and y = 0.5.) Motion in the x and z directions was not constrained, as shown in Fig. 2.

Fig. 2 Simulation cells for GBs viewed along two viewing directions as determined by γ-surface calculations. (a and b) ∑5(310)/[001] tilt GB projected onto the xy and xz planes, respectively. (c and d) ∑5(001)/36.87° twist GB image depectied on xy and xz plane, respectively. Atoms are colored based on their potential energy, with red (blue) corresponding to highest (lowest) energy. Black-boxes indicate regions where the atom displacements are constrained in the y-direction during MD.

Following the annealing process, 5 ns of NPT MD was performed at 1 atm and at one of four target temperatures: 250 K, 300 K, 350 K, or 400 K. This was followed by 1 ns of NVT equilibration and a 5 ns NVT MD production run for the purpose of calculating diffusivity. Snapshots of all atom positions were dumped every 0.1 ns for postprocessing. To quantify statistical uncertainties in the simulations, 3 distinct MD production runs were performed with different initial velocity distributions.

The mean squared displacements (MSD) of atoms within the GB regions were used to calculate the GB self-diffusivity. In prior studies of GB diffusion, the MSD of atoms in/near the boundary was calculated by tracking displacements in a fixed region (e.g., 10 Å) surrounding the boundary.^17,18,29 This approach assumes that the GB position does not change significantly during the MD run, and that the width of the GB can be defined in a consistent fashion. However, as illustrated in Fig. S2,† displacements of some GBs are observed during MD, especially at higher temperatures, even with constraints applied to atoms in the bulk regions.

To address these issues, an automated scheme was developed to track the position and width of the GBs. As a first step in the procedure, each simulation cell was partitioned, at 0.1 ns intervals, into 100 bins along the y-direction (50 bins were used for smaller simulation cells). The average potential energy of the atoms in each bin was calculated and plotted as shown in Fig. 3a. These plots of potential energy vs. position exhibit two peaks which are associated with the two GB regions. Next, the peaks were fit to a Gaussian function, and the width measured at 25% of the peak height was adopted as the GB width. (Table S5† tabulates the widths of all GBs at finite temperatures.) This procedure was repeated at 0.1 ns intervals in NVT MD and allows for calculation of the MSD within a region centred on the instantaneous location and width of the GB, Fig. 3b. (Use of a smaller sampling interval of 0.01 ns did not significantly change the results, Fig. S3.†) Afterward, the MSD was calculated using eqn (2).

MSD = <x²(t) + y²(t) + z²(t)> (2)

Fig. 3 Methodology to sample mean squared displacements of atoms within the GB region of a ∑33(811)/[01−1] GB. (a) Determination of the GB location and width at an arbitrary time during MD. GB positions correspond to maxima in the planar-averaged potential energy with respect to position normal to the GB plane. GB width is calculated by fitting Gaussians to these maxima. (b) GB positions visualized during 5 ns of MD. Regions of low potential energy (blue) correspond to atoms in the bulk region with fixed y-coordinates. Black boxes indicate the instantaneous location of the GB region. (c) Calculated mean squared displacements of GB atoms at 350 K.

Fig. 3c shows an example MSD plot for a ∑33(811)/[01−1] GB. Subsequently, the MSD values were averaged over all time origins by increasing the reference time t from 0 to t_max − Δt, where t_max is the maximum simulation time (5 ns), and Δt is the maximum diffusion time window, taken as 1 ns. MSD plots constructed using this moving window approach are presented in Tables S6 and S7.† Finally, the diffusivity of Li atoms in the GB region were calculated by performing a linear fit to the MSD data and applying the Einstein relation, eqn (3).

MSD = 6D̄t (3)

To draw comparisons to the bulk, the diffusivity in body-centered cubic Li was also evaluated. These calculations were performed in a BCC simulation cell containing 1999 atoms and one vacancy. This system was annealed and equilibrated in the same fashion as done for the GB systems. MSDs were collected and bulk diffusivities were predicted at 250 K, 300 K, 350 K, and 400 K. These diffusivity values were then scaled to account for the non-equilibrium vacancy concentration used in the simulations. The equilibrium vacancy fraction is given by eqn (4), where E^f_v is vacancy formation energy, and C^eq_v is equilibrium vacancy fraction:

For an equilibrium concentration of vacancies, the bulk diffusivity, D_eq, can be obtained from eqn (5),^30,31

where and D* denote, respectively, the non-equilibrium vacancy fraction used in the simulations and the diffusivity predicted by MD. D_eq was adopted as the bulk diffusivity and was used below to estimate the polycrystalline diffusivity.

A realistic lithium metal anode will most-likely be polycrystalline. A small number of models exist for predicting the diffusivity of a polycrystal under differing assumptions. The Hart model^32,33 assumes that the GB planes and the diffusion are parallel. This scenario may be realized if the grains adopt a columnar structure.^26,34 The Maxwell–Garnet (M–G) 1D model^33,35 assumes that the GB slabs are normal to the diffusion direction, while the 2D and 3D M–G models³⁶ assume that GBs enclose 2D circular or 3D spherical grains, respectively. Belova and Murch's (B–M) 2D grain model³³ uses a mixture of GB orientations, in which half of the GB planes are parallel to the diffusion direction, and the other half are perpendicular. Lastly, the model of Chen and Schuh³⁷ (C–S) assumes that GBs and triple junctions enclose grains that exhibit shapes based on Voronoi polyhedra. These models are compared in Fig. S4.† There, it can be seen that the Hart model, the 2D and 3D M–G models, the B–M 2D grain model, and the C–S model (assuming D_TJ = 100D_GB) yield comparable results for grain sizes larger than ∼100 nm. In contrast, and as expected, the 1D M–G model yields diffusivities similar to that for a single crystal (since it assumes all GBs are perpendicular to the diffusion direction). Given the similarity in the predictions between the various models for all but nano-sized grains, and experimental evidence suggesting that some electrodeposited Li films exhibit columnar grains,^26,34 the Hart equation was adopted in this study to model polycrystalline diffusivity, D_polycrystal, eqn (6).^32,33

D_polycrystal = fD_GB + (1 − f)D_bulk (6)

Here f is the volume fraction of GBs in the Li anode, and D_GB and D_bulk are the self-diffusivities of the GB and bulk regions, respectively. The GB volume fraction, f, was calculated using the regular polygon model,³⁸eqn (7), where w is the representative GB width at each temperature, and d is the grain size.

The GB width, w, at each temperature was calculated by averaging all GB widths for a given temperature. This was predicted to be in the range of 10.9–15.3 Å as shown in Table S5.† The grain size, d, was an input variable ranging from 10⁻² to 10³ μm.

Lastly, the Li polycrystalline self-diffusivity was used as input to a mesoscale model of Li anode stripping during the discharge of a LMSSB. The time and space-dependence of the Li concentration in the anode during stripping was modeled using Fick's 2^nd law, eqn (8).

Several prior studies^11,14,39,40 have employed Fick's 2^nd law to describe Li transport in the anode. For example, in the work of Zhao et al.⁴¹ Fick's law was used as one of the governing equations in a phase field model of void evolution at the Li/SE interface. In the study of Jow et al.⁴⁰, Fick's 2^nd law was used to determine the diffusivity within a Li anode interfaced with a LiI(Al₂O₃) solid electrolyte.

Eqn (8) was solved assuming: a constant stripping rate at the SE interface (x = L), a uniform initial Li concentration equal to that of bulk Li, no stack pressure, and a zero-flux condition at the boundary opposite of the interface (x = L, i.e., at the current collector). (See Fig. S5† for additional details.)¹¹ The general solution to this model, developed by Jow et al., is given by eqn (9).^11,40

Results and discussion

Grain boundary energies

Plots of grain boundary energy (GBE) as a function of misorientation angle are presented in Fig. 4. The plots compare the GB energies obtained before and after simulated annealing. Several features of these data are of note. First, GBs generally exhibit energies which are only slightly smaller after annealing. This indicates that the GB structure obtained from the gamma-surface search is a relatively stable (local) minimum on the potential energy surface. Second, the GBEs, as predicted by prior DFT calculations,⁴² are larger than those predicted in the present study, although both methods exhibit similar trends. We hypothesize that the lower energies reported here reflect the extensive search performed over the configuration space. A similar search with DFT would be more challenging to conduct due to its greater computational cost. Third, several cusps in the GB energies appear in the plots, with notable examples including ∑5(210) 53.1°, ∑9(411) 38.9°, ∑3(211) 70.5°, ∑11(233) 129.5°, ∑9(01−1) 38.9°, and ∑3(01−1) 70.5°. This behaviour is consistent with previous studies of GB energy trends in BCC metals.^43,44 The low energies of these GBs suggest that they will have a greater probability of appearing in polycrystalline systems that are close to equilibrium.⁴⁵

Fig. 4 GB energy before/after annealing as a function of misorientation angle. (a) [001] tilt (b) [01−1] tilt (c) [11−1] tilt (d) [001] twist (e) [01−1] twist (f) [11−1] twist rotation axis. The Σ-values of the coincidence site lattice are listed at the top axis of each plot. Recent energies calculated from DFT are shown for comparison.⁴²

Grain boundary diffusivity

Fig. 5 shows Arrhenius plots of Li diffusivity for all GBs studied. For comparison, the calculated bulk diffusivity and measured polycrystalline diffusivity⁴⁶ are also shown. Compared to the bulk diffusivity, GB diffusivities are predicted to be 3 to 6 orders of magnitude larger. This result aligns with previous work^17–19 which reported faster GB diffusion in metals. In addition, the measured polycrystalline diffusivity falls between that of the bulk and GBs. This is reasonable given that diffusion in a polycrystalline metal should be a combination of diffusion involving GBs and the bulk.

Fig. 5 Calculated GB diffusivities for (a) [001] tilt, (b) [01−1] tilt, (c) [11−1] tilt, (d) [001] twist, (e) [01−1] twist, and (f) [11−1] twist GBs. For comparison, the calculated bulk diffusivity and experimental polycrystalline diffusivity⁴⁶ are shown with stars and as the solid black line, respectively. The plots include error-bars corresponding to the standard deviations in the diffusivities extracted from 3 independent MD runs. These errors, typically 10⁻⁹ to 10⁻⁷ cm² s⁻¹, are so small that they are obscured by the datapoints represent the averages.

The activation energy for GB diffusion was calculated by performing separate linear fits to the diffusivity data at the 3 low temperatures (i.e. 250 K, 300 K, 350 K) and at the 3 high temperatures (i.e. 300 K, 350 K, 400 K), Tables S8 and S9.† Two fits were performed to account for an apparent change in slope near 400 K. This approach yielded better agreement with the data than a single fit spanning all temperatures. Given that the temperature of our interest is near 300 K, the Arrhenius fit to the 3 low temperatures is shown in Fig. 5. At low temperatures, the calculated GB activation energies range from 0.1 to 0.3 eV. These GB values are smaller than the calculated value for bulk diffusion, 0.48 eV, (which includes the vacancy formation energy) and thus explains the higher mobility of atoms in the GB region. The bulk activation energy measured by experiments^14,46–50 is 0.52–0.57 eV, and similar values of 0.54–0.59 eV have been reported by DFT^51–53 calculations and a thermodynamical cBΩ model.⁵⁴ A commonly-used rule-of-thumb regarding GB diffusion in alkali metals is that the energy barrier for GB diffusion is 60–67% of that for bulk diffusion.^55,56 According to this rule, the GB activation energy would be approximately 0.33 eV. Hence, this rule likely underestimates the GB diffusivity.

Different from bulk (BCC) Li, where diffusion is mediated by vacancies, in GBs the presence of vacancies is not required for diffusion to occur. The excess volume present in GBs (due to their reduced crystallinity) allows for mobility without an explicit vacancy concentration. Tests were performed by inserting a vacancy into 6 of the GBs from the present ensemble of boundaries. A comparison of the calculated GB diffusivities with and without added vacancies (at T = 300 K) revealed that the calculated diffusivities are essentially identical, Table S10.†

Yang et al. speculated that a high density of GBs in the Li anode might be undesirable, as GBs could act as sinks for vacancies in the BCC bulk, and thereby suppress bulk diffusion. To test whether GBs act as vacancy sinks, vacancy formation energies (E^vac_f) were calculated at multiple sites within several GB systems, Fig. S6.† These calculations predict that the average E^vac_f at GBs is 0.39 ± 0.08 eV per atom. Importantly, this value is nearly identical to that calculated for the bulk, E^vac_f = 0.4 eV per atom. These data suggest that GBs in Li do not strongly impact the bulk vacancy concentration by acting as sources or sinks.

The GB activation energies at high temperatures fall in the range of 0.2 to 0.4 eV, suggesting a different diffusion mechanism compared to low temperature diffusion. Prior studies^17,57–59 have reported that pre-melting can occur at GBs – i.e., a disordered phase forms in the GB region at temperatures below the bulk melting temperature. Accordingly, it is hypothesized that the change in activation energy above 400 K results from pre-melting. To test this hypothesis, the pair distribution function (PDF) was evaluated for atoms in the GB region. Fig. S7† compares the PDF for bulk Li and for 6 representative GBs at different temperatures. In the bulk, a liquid-like distribution is calculated above 450 K. On the other hand, in the GB PDFs, a liquid-like distribution is detected at 400 K, in support of pre-melting.

The pre-melting hypothesis was also verified by calculating the centro-symmetry (CS) parameter of the GBs as a function of temperature, Fig. S8.† The CS value²⁸ measures the local lattice disorder. The CS parameter equals zero for a site surrounded by the undistorted lattice; it assumes non-zero values when the surrounding lattice is disordered. In the idealized BCC lattice, all neighboring atoms are symmetrically arranged around a given atom. In contrast, an asymmetrical environment exists near defects, resulting in non-zero CS values. For reference, a centro-symmetry value of ∼8 was measured in the dislocation core of BCC Fe⁶⁰ and values larger than 8 were reported in BCC-Fe twin boundaries.⁶¹ According to Fig. S8,† the CS values of the Li GBs examined here are larger than that of the bulk. This is consistent with the GB region being intrinsically more disordered. Moreover, the values of the CS parameter for different GBs tend to converge to a similar value as the temperature is increased from 250 K to 400 K. This result also supports the pre-melting at 400 K; at this temperature the distinct crystalline features of the GBs diminish as a similar disordered, liquid-like phase emerges.

Fig. 6a compares: (i) the average diffusivity of the three GBs exhibiting the largest diffusivities, (ii) the average diffusivity of the three GBs exhibiting the smallest diffusivities, (iii) the average diffusivity computed across all GBs, and (iv) the bulk diffusivity. From this data it is evident that an order of magnitude separates the diffusivities of the fastest and slowest GBs. For example, at 300 K, the ∑31(11−1) 17.9° twist, the ∑29(520) tilt, and the ∑11(311) tilt GBs are predicted to exhibit the fastest diffusivities of 2.3 × 10⁻⁶ cm² s⁻¹, 1.7 × 10⁻⁶ cm² s⁻¹, and 1.6 × 10⁻⁶ cm² s⁻¹, respectively. Whereas the ∑9(411) tilt, the ∑5(001) 53.1° twist, and the ∑5(001) 36.9° twist boundaries are predicted to exhibit the slowest diffusivities of 8.4 × 10⁻⁸ cm² s⁻¹, 8 × 10⁻⁸ cm² s⁻¹, and 8 × 10⁻⁸ cm² s⁻¹, respectively. Comparing the average GB diffusivity to the bulk diffusivities reveals that the GB diffusivities are 3 to 6 orders of magnitude larger, depending on the temperature. The gap between the average GB and bulk diffusivity becomes smaller at higher temperatures, reflecting the larger activation energy associated with bulk diffusion.

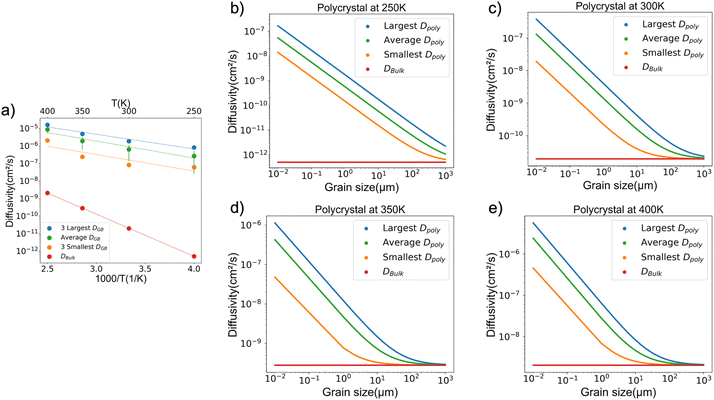Fig. 6 (a) The average of the 3 fastest, 3 slowest, and overall average GB diffusivities vs. inverse temperature. Polycrystalline diffusivity (eqn (6)) as a function of grain size at (b) 250 K (c) 300 K (d) 350 K (e) 400 K. Here “Largest,” “Smallest,” etc. refers to the range of DGB shown in panel (a).

In principle, diffusion within a GB plane could be anisotropic. To investigate this possibility, the directionally-resolved GB diffusivities averaged across all GBs is tabulated in Table S11.† (In addition, the directionally-resolved diffusivities at 300 K for each individual GB is reported in Tables S12 and S13.†) Table S11† shows that the average difference (at 300 K) between the fastest and slowest diffusion directions in the GB plane is less than a factor of 3, which is comparable to the standard deviation in diffusivities among the different boundaries. Furthermore, we anticipate that during cell charging the orientation of the GB planes will be difficult to precisely control, making it difficult to exploit any diffusional anisotropies. For these reasons, the spatially-averaged GB diffusivity, D_Tot, is adopted for use in the polycrystalline diffusivity calculations described in the following section.

Polycrystalline diffusivity

Polycrystalline diffusivity is estimated using the GB diffusivity data shown in Fig. 6a and eqn (6). Fig. 6b–e illustrate the upper and lower bounds as well as average values for D_polycrystal as a function of temperature and grain size. The calculated polycrystalline diffusivity is in good agreement with recent experimental measurements. Assuming a 150 μm grain size at 300 K, D_polycrystal is computed to be 2.9 × 10⁻¹¹ cm² s⁻¹, whereas for grains “of the order of 100 μm” Siniscalchi et al. reported diffusivities of 3.9 × 10⁻¹¹ and 1.6 × 10⁻¹⁰ cm² s⁻¹ at room temperature.¹³ This agreement is reasonable given the uncertainties in grain size distribution, dislocation density, and the presence of impurities.

Fig. 6b–e show that the polycrystalline diffusivity increases as the grain size decreases. This trend reflects the faster diffusivity predicted for GBs, and the greater volume fraction occupied by GBs as the grain size decreases. For example, Fig. 6c shows that Li diffusivity can be increased from ∼10⁻¹¹ to ∼10⁻⁷ cm² s⁻¹ at 300 K by reducing the grain size from 1 mm to 10 nm. The increase in mobility due to smaller grain size is more pronounced at low temperatures. At 250 K, decreasing the grain size from 1 mm to 10 nm results in an increase in D_polycrystal from ∼10⁻¹² to ∼10⁻⁸ cm² s⁻¹. At 400 K, a similar change in grain size results in a smaller increase of only two-orders-of-magnitude, from ∼10⁻⁸ to ∼10⁻⁶ cm² s⁻¹.

Wang et al.¹² reported a diffusion coefficient for Li-ions in the solid electrolyte LLZO at room temperature of 2.15 × 10⁻⁹ cm² s⁻¹. This diffusivity is much faster than the self-diffusivity for Li metal reported by Jow et al.,⁴⁰ 5.6 × 10⁻¹¹ cm² s⁻¹. Hence, Wang et al. argued that slower diffusion in the Li anode may be an important factor in determining the critical current density (CCD) for dendrite formation in solid state Li metal batteries. Yang et al.⁵³ used MD simulations to simulate stripping and plating at a Li metal anode. Although the role of GBs was not considered in that study, it was concluded that enhancing Li diffusion was important for improving performance, as also suggested by others.⁸ The present study demonstrates that relatively faster diffusion along GBs is one mechanism for enhancing mass transport within a Li anode. In summary, the data in Fig. 6 suggests that D_polycrystal can be increased by several orders of magnitude by reducing the Li grain size.

Diffusion length

As previously discussed, during discharge the rate of Li stripping from the Li anode surface can exceed the rate of Li self-diffusion in the bulk of the anode, resulting in void formation at the interface. In principle, void formation could be minimized by pausing cell operation between charge and discharge half-cycles; this “replenishment time” could allow Li diffusion to reduce the roughness of the Li surface. This strategy was investigated by Kasemchainan et al.⁷ who included ∼30 minute pauses between half-cycles of a Li/Li₆PS₅Cl/Li symmetric cell.⁷ To verify whether such a ∼30 minute pause is sufficient, a rough estimate of the diffusion length in polycrystalline Li can be obtained from eqn (10), where t is the diffusion time.

Both self-diffusion of Li⁰ through the interior of the anode (i.e., through the bulk and along GBs) and along the surfaces of voids can minimize roughening and void formation. Earlier studies have discussed the importance of surface diffusion of Li.^62,63 The present study builds on that earlier work by focusing on GB diffusion.

Fig. 7 plots the diffusion length, L, as a function of grain size and time at 300 K. Assuming a grain size of 150 μm and t = 30 minutes, the predicted diffusion length is 2.3 μm. For comparison, the targets for capacity from a Li anode¹ range from 3 to 5 mA h cm⁻²,¹ which corresponds to a minimum Li thickness of 15–25 μm. Hence, the diffusion length under these conditions is a small fraction (9–15%) of the desired anode thickness. In the experiments of Kasemchainan et al., a thinner anode with a thickness of 5 μm was used.⁷ Nevertheless, this thickness still exceeds the diffusion length by more than a factor of two for a 30 minute rest period. Therefore, increasing the replenishment time and employing strategies to reduce the grain size are proposed as opportunities to improve performance.

Fig. 7 Diffusion length as a function of grain size (μm) and time (h) at 300 K.

Battery design guidelines

The calculated polycrystalline diffusivity can be used to estimate the maximum discharge capacity as a function of discharge current, Li grain size, and anode thickness. More importantly, this data allows one to estimate the ranges of grain size and anode thickness that satisfy various performance goals.^1,64

As mentioned earlier, during discharge it is desirable for the diffusional flux of Li atoms within the anode to be comparable to the rate at which Li is stripped. When Li diffusion is slower than the stripping rate, the concentration of Li atoms at the interface can decrease, resulting in roughening of the anode surface, void formation, and loss of contact between the anode and solid electrolyte. The time at which this contact loss occurs (relative to the start of the discharging half-cycle) is referred to in the literature as the “depletion time,” t_d.^14,40 The depletion time determines the upper bound of the deliverable capacity, and is a function of the discharge rate, anode thickness, and Li grain size. Here, t_d was calculated in 1D by solving Fick's 2^nd law for the Li concentration in the anode, eqn (9). Using the notation in eqn (9), at t = t_d, C(x = 0, t = t_d) = 0.

The validity of this model was assessed by comparing its predictions with the experiments of Krauskopf et al.⁸ That study examined stripping in a Li/LLZO/Li symmetric cell with a 120 μm thick Li anode. The cell was discharged at 0.1 mA cm⁻² and no stack pressure was applied. Since no information on the Li grain size was reported, a nominal value of 150 μm is assumed here. Such a value appears to be representative of the grain size for purchased Li foil.⁶⁵ Applying the present computational model to this scenario, delamination is predicted at t_d = 36 hours from the start of stripping, while the experimentally-measured depletion time from Krauskoph et al. was 12 hours. Given the 1D nature of our model, coupled with the lack of information regarding grain size and the initial state of the Li/LLZO interface, this is acceptable agreement between theory and experiment.

Fig. S9† illustrates Li concentration profiles in the anode as a function of anode thickness under the operating conditions used by Krauskoph et al. As discharge progresses, the initially-uniform interfacial Li concentration decreases, with the most rapid decreases in concentration occurring near the SE interface. Eventually, the concentration of Li at the interface goes to zero (at time t = t_d), resulting in contact loss and an open circuit (i.e., a cessation of discharge). The maximum discharge capacity is the product of the stripping current and t_d. For the conditions simulated here, and for anode thicknesses up to 40 μm, t_d increases as the anode thickness increases, resulting in a larger discharge capacity. However, increasing the anode thickness beyond 40 μm does not increase the maximum discharge capacity. Beyond 40 μm thicknesses, t_d plateaus at a value of approximately 36 h, with a corresponding capacity of 3.6 mA h cm⁻². Thus, for the present combination of grain size and current density, the achievable capacity for anodes of thickness less than ∼40 μm is limited by the thinness of the anode and the inability of Li self-diffusion to compensate for Li stripping. In contrast, for anode thicknesses greater than 40 μm, capacity is limited only by Li self-diffusion, Fig. S9g.† This result implies that at a given stripping current and grain size – for this example, 150 μm grains and 0.1 mA cm⁻² stripping current density – the amount of inaccessible Li can be minimized by tuning the anode thickness, which in this case corresponds to a thickness of 40 μm.

Fig. 8 illustrates the achievable discharge capacity as a function of stripping current density, Li grain size, and the anode thickness. The maximum discharge times are found by moving from right to left, and from top to bottom on each plot. This corresponds to reducing the grain size (our new solution) or decreasing the stripping current (the trivial solution). The percentage of accessible Li exceeds 90% when the combination of current and grain size falls to the left of the largest contour line in each plot.

Fig. 8 Maximum discharge capacity as a function of stripping current and grain size for Li anode thicknesses of (a) 10 μm, (b) 20 μm, (c) 40 μm, (d) 80 μm, and (e) 160 μm.

Various targets for solid-state batteries have been proposed.^1,64 For example, the ARPA-E IONICS program targets a minimum current density of 3 mA cm⁻², a capacity of 3 mA h cm⁻², and 80% utilization of the total Li capacity per cycle. Similarly, the fast-charging program targeted a Li capacity of 5 mA h cm⁻² at 10 mA cm⁻². Fig. 9 illustrates the combinations of anode thicknesses and grain sizes that are predicted to achieve these performance targets. To meet these fast-charging targets, the present model predicts that the thickness of the Li anode (L_anode) should be greater than 25 μm, while the grain size (d_G) should be less than ∼0.3 μm. To meet the IONICS targets, L_anode > 15 μm and d_G < 1.8 μm. Finally, as an intermediate scenario, to satisfy the fast-charging capacity goal and the IONICS current density goal, L_anode > 25 μm and d_G < 0.9 μm are necessary. As expected, when the target current density and capacity are increased, the minimum anode thickness should increase and the grain size must shrink. The minimum anode thickness is bounded by the minimum capacity of each target (e.g. L_anode = 25 μm for C = 5 mA h cm⁻² for the fast charging goal).

Fig. 9 Design guidelines for capacity (C) and current density (I) based on anode thickness and grain size. Conditions that satisfy the fast-charging goal (I > 10 C > 5) are shown in red, those that satisfy the ARPA-E ionics goal (I > 3 C > 3) are shown in blue, and those that satisfy a mixture (I > 3 C > 5) are orange.

This data implies that the optimal grain size for a Li anode is on the order of 1 μm. This grain size corresponds to a target Li self-diffusivity of ∼10⁻⁹ cm² s⁻¹, Fig. S10.† This grain size is much smaller than what has been reported in the literature for commercial Li foils, which have average grain diameters of 150 μm.⁶⁵ Hence, the present model suggests that the desired current density and capacity targets cannot be achieved with commercial, large-grained Li, where Li self-diffusion is too slow to keep pace with the stripping current. This observation may explain why much recent work on Li metal anodes has employed large stack pressures (∼10 MPa) or elevated temperatures to minimize dendrite formation.^7,8,11 In the former case, the application of stack pressure will induce creep deformation in the Li anode, which is another mode of Li transport that can minimize void formation at the SE interface. Similarly, the use of elevated temperatures will increase the self-diffusion of Li, resulting in reduced voiding. In principle, by controlling the grain size, the benefits of elevated temperatures or high stack pressures may be realized without incurring their respective drawbacks. For example, recent work has shown that the application of stack pressure, while helpful for void suppression, facilitates fracture of the SE.¹⁰ In addition, very recent work by Singh et al.⁶⁶ arrived at a similar conclusion to the present study regarding the benefits of GB engineering on the performance of LMSSBs. That study demonstrated that the required stack pressure to achieve high current densities can be reduced in a cell containing a fine-grained Li anode (d ∼ 20 μm). These improvements were proposed to arise from enhanced creep deformation that was made possible by faster diffusion.

How can a micron-scale grain size be achieved in a functioning Li metal battery? Given that the Li anode is (partially) stripped and reformed during battery cycling, controlling the grain size during cycling may be difficult. Unfortunately, the grain size appears to be an over-looked property of the anode; very few studies report Li grain size distributions or discuss how the grain size varies with initial processing conditions or with the current density used during cycling.^{23,26,34,66,67} Recent work has presented evidence that Li can be electrodeposited in the form of columnar grains with micron-sized grain diameters.^26,34 Such sizes and morphologies would be optimal for maximizing the diffusion of Li atoms along GBs to the SE interface.

In principle, several potential strategies exist for controlling grain size, even in the context of plating/stripping. For example, it is known that the electro-deposition process itself can generate small-grained morphologies. Ni alloys that are electrodeposited in the fabrication of micro-electro-mechanical systems (MEMS) exhibit grain sizes on the nano-scale.^68,69 Nevertheless, it is not currently known if Li behaves similarly to Ni when electrodeposited during battery operation. Secondly, templating effects may also be exploited. This strategy requires that the initial Li anode be fabricated with a small grain size, and that some fraction of the Li be retained upon stripping (i.e., the anode is not fully stripped). The remaining, small-grained Li would then act as a template during subsequent charging/plating, encouraging the newly-plated Li to mimic the microstructure of the substrate.⁷⁰ Finally, controlling the rate of charging could also be helpful in maintaining a small grain size. The rapid deposition of Li (i.e., fast charging) will increase the number density of Li nuclei, resulting smaller grain sizes. If uniformly high plating currents are not practical, brief pulses of high current density could be interspersed between longer periods of plating at more moderate rates. This latter approach combines the aspects of the templating strategy with the concept of enhancing the density of Li nuclei. Additional experimental analysis of the microstructure of the Li anode and its potential impact on cell performance would undoubtedly be helpful in clarifying these issues.

In closing, it is important to recognize the limitations of the present model. First, the model estimates the depletion time using a one-dimensional approximation. Voiding and loss of contact at the Li/SE interface are, however, three-dimensional phenomena. These phenomena could be captured more realistically by kinetic monte carlo or phase field techniques,^41,71 especially if these models were parametrized using the transport properties predicted here. Second, as the model assumes a cell under no stack pressure, Li redistribution from plastic deformation is not captured. Third, the model accounts only for bulk and GB diffusion of Li. Diffusion along surfaces and along dislocation cores may also be important, but are not accounted for here. Fourth, the model treats vacancies as non-interacting particles, and thus does not account for potential vacancy clustering. Lastly, the present calculations focus on how the transport properties of grain boundaries impact voiding in Li. Similarly, the thermodynamic properties of GBs may also contribute to inhomogeneous stripping. For example, stripping may preferentially occur in the vicinity of GBs because the electrochemical potential of GB atoms is greater than that of bulk atoms. (The greater electrochemical potential of GB atoms reflects the fact that GB energies are positive, and therefore in excess of the bulk energies.)⁷² Hence, a comprehensive treatment of the role of GBs on the plating/stripping behavior of Li anodes should account for both thermodynamic and transport effects. Consequently, several avenues exist for extending the model. Despite these limitations, the model is qualitatively consistent with existing experimental data. It also provides an experimentally-testable design suggestion – that smaller grain sizes are advantageous in the operation of Li metal batteries.

Conclusion

Minimizing void formation in the Li metal anode is a key challenge in developing Li metal-based solid-state batteries. Void formation results in a reduction in interfacial contact area, which focuses the Li-ion current during plating to a reduced number of contact points. This phenomenon generates high local current densities during plating, which can nucleate dendrites.

The present study proposes a strategy for minimizing void formation based on exploiting fast GB diffusion within the anode. By decreasing the grain size of the metallic anode, the volume fraction of grain boundaries will be increased, resulting in a greater contribution of GB diffusion to mass transport within the anode.

Molecular dynamics simulations were used to calculate diffusion coefficients for a diverse sampling of 55 tilt and twist GBs in Li. GB diffusion was found to be 3 to 6 orders of magnitude faster than in the bulk. Using these atomic-scale data as input, a meso-scale model of Li depletion in the anode during discharge was developed. Although limited to 1-D, the model is qualitatively consistent with experimental data. The model allows for the development of design and operation guidelines for LMSSBs by linking the Li grain size, discharge current density, anode thickness, and achievable capacity.

Regarding grain size, the model predicts that smaller is better: small grain sizes of approximately 1 μm or less are needed to meet performance targets for LMSSBs. Regarding grain morphology, columnar grains with long axes oriented parallel to the plating direction are optimal. As the proposed micron-sized grains are two orders of magnitude smaller than those in common use, strategies for controlling the grain size in a battery environment where the anode undergoes repeated plating and stripping are discussed.

In total, the model highlights the importance of the anode's microstructure on the performance of LMSSBs. It also presents a strategy to minimize (or avoid) the use of high stack pressures to control void formation in LMSSBs.

Author contributions

DJS generated the idea for this study and proposed its initial computational methodology. JSY and HS conducted the calculations and implemented the meso-scale model. All authors contributed to drafting the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences as part of the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub, and by MUSIC (Mechano-Chemical Understanding of Solid Ion Conductors), an Energy Frontier Research Center, contract DE-SC0023438.

Notes and references

1. P. Albertus, S. Babinec, S. Litzelman and A. Newman, Nat. Energy, 2018, 3, 16–21.
2. W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J. G. Zhang, Energy Environ. Sci., 2014, 7, 513–537.
3. P. Hovington, M. Lagacé, A. Guerfi, P. Bouchard, A. Mauger, C. M. Julien, M. Armand and K. Zaghib, Nano Lett., 2015, 15, 2671–2678.
4. R. Kanno and M. Murayama, J. Electrochem. Soc., 2001, 148, A742.
5. E. J. Cheng, A. Sharafi and J. Sakamoto, Electrochim. Acta, 2017, 223, 85–91.
6. L. Porz, T. Swamy, B. W. Sheldon, D. Rettenwander, T. Frömling, H. L. Thaman, S. Berendts, R. Uecker, W. C. Carter and Y. M. Chiang, Adv. Energy Mater., 2017, 7, 1701003.
7. J. Kasemchainan, S. Zekoll, D. Spencer Jolly, Z. Ning, G. O. Hartley, J. Marrow and P. G. Bruce, Nat. Mater., 2019, 18, 1105–1111.
8. T. Krauskopf, H. Hartmann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2019, 11, 14463–14477.
9. M. J. Wang, R. Choudhury and J. Sakamoto, Joule, 2019, 3, 2165–2178.
10. C. D. Fincher, C. E. Athanasiou, C. Gilgenbach, M. Wang, B. W. Sheldon, W. C. Carter and Y.-M. Chiang, Joule, 2022, 6, 2794–2809.
11. C. L. Tsai, T. Lan, C. Dellen, Y. Ling, Q. Ma, D. Fattakhova-Rohlfing, O. Guillon and F. Tietz, J. Power Sources, 2020, 476, 228666.
12. M. Wang, J. B. Wolfenstine and J. Sakamoto, Electrochim. Acta, 2019, 296, 842–847.
13. M. Siniscalchi, J. Liu, J. S. Gibson, S. J. Turrell, J. Aspinall, R. S. Weatherup, M. Pasta, S. C. Speller and C. R. M. Grovenor, ACS Energy Lett., 2022, 7, 3593–3599.
14. T. Krauskopf, B. Mogwitz, C. Rosenbach, W. G. Zeier and J. Janek, Adv. Energy Mater., 2019, 9, 1902568.
15. B. P. Uberuaga, S. Choudhury, X. M. Bai and N. A. Benedek, Scr. Mater., 2012, 66, 105–108.
16. P. V. Nerikar, K. Rudman, T. G. Desai, D. Byler, C. Unal, K. J. McClellan, S. R. Phillpot, S. B. Sinnott, P. Peralta, B. P. Uberuaga and C. R. Stanek, J. Am. Ceram. Soc., 2011, 94, 1893–1900.
17. A. Suzuki and Y. Mishin, J. Mater. Sci., 2005, 40, 3155–3161.
18. C.-L. Liu and S. J. Plimpton, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4523.
19. D. J. Siegel and J. C. Hamilton, Acta Mater., 2005, 53, 87–96.
20. S. Yu and D. J. Siegel, Chem. Mater., 2017, 29, 9639–9647.
21. L. Sun, D. Marrocchelli and B. Yildiz, Nat. Commun., 2015, 6, 6294.
22. R. A. De Souza, M. J. Pietrowski, U. Anselmi-Tamburini, S. Kim, Z. A. Munir and M. Martin, Phys. Chem. Chem. Phys., 2008, 10, 2067–2072.
23. Z. Zhang, X. Zhou and Z. Liu, J. Alloys Compd., 2022, 893, 162389.
24. K. Yan, Z. Lu, H. W. Lee, F. Xiong, P. C. Hsu, Y. Li, J. Zhao, S. Chu and Y. Cui, Nat. Energy, 2016, 1, 1–8.
25. A. Pei, G. Zheng, F. Shi, Y. Li and Y. Cui, Nano Lett., 2017, 17, 1132–1139.
26. M. Motoyama, M. Ejiri and Y. Iriyama, J. Electrochem. Soc., 2015, 162, A7067–A7071.
27. Y. M. Kim, I. H. Jung and B. J. Lee, Modell. Simul. Mater. Sci. Eng., 2012, 20, 035005.
28. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. int Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171.
29. T. Frolov and Y. Mishin, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 174110.
30. R. Mohammadzadeh and M. Mohammadzadeh, J. Appl. Phys., 2018, 124, 035102.
31. J. Marian, B. D. Wirth, G. R. Odette and J. M. Perlado, Comput. Mater. Sci., 2004, 31, 347–367.
32. E. W. Hart, Acta Metall., 1957, 5, 597.
33. I. V. Belova and G. E. Murch, J. Phys. Chem. Solids, 2003, 64, 873–878.
34. M. A. Citrin, H. Yang, S. K. Nieh, J. Berry, W. Gao, X. Pan, D. J. Srolovitz and J. R. Greer, MRS Bull., 2020, 45, 891–904.
35. J. C. Maxwell-Garnett, Philos. Trans. R. Soc. London, 1904, 203, 385–420.
36. J. R. Kalnin and E. Kotomin, J. Phys. A: Math. Gen., 1998, 31, 7227–7234.
37. Y. Chen and C. A. Schuh, J. Appl. Phys., 2007, 101, 063524.
38. H. Guo and X.-M. Guo, Appl. Math. Mech., 2007, 28, 141–149.
39. H. Yan, K. Tantratian, K. Ellwood, E. T. Harrison, M. Nichols, X. Cui and L. Chen, Adv. Energy Mater., 2022, 12, 2102283.
40. T. R. Jow and C. C. Liang, J. Electrochem. Soc., 1983, 130, 737–740.
41. Y. Zhao, R. Wang and E. Martínez-Pañeda, J. Mech. Phys. Solids, 2022, 167, 104999.
42. H. Zheng, X. G. Li, R. Tran, C. Chen, M. Horton, D. Winston, K. A. Persson and S. P. Ong, Acta Mater., 2020, 186, 40–49.
43. M. A. Tschopp, K. N. Solanki, F. Gao, X. Sun, M. A. Khaleel and M. F. Horstemeyer, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 064108.
44. D. Scheiber, R. Pippan, P. Puschnig and L. Romaner, Modell. Simul. Mater. Sci. Eng., 2016, 24, 035013.
45. D. M. Saylor, B. S. El Dasher, A. D. Rollett and G. S. Rohrer, Acta Mater., 2004, 52, 3649–3655.
46. P. Heitjans, A. Korblein, H. Ackermann, D. Dubbers, F. Fujara and H. J. stockmann, J. Phys. F: Met. Phys., 1985, 15, 41–54.
47. R. Messer, Appl. Phys., 1975, 6, 79–88.
48. A. Lodding, J. N. Mundy and A. Ott, Phys. Status Solidi B, 1970, 38, 559–569.
49. M. Mali, J. Roos, M. Sonderegger, D. Brinkmann and P. Heitjans, J. Phys. F: Met. Phys., 1988, 18, 403.
50. D. M. Fischer, P. Duwe, S. Indris and P. Heitjans, Solid State Nucl. Magn. Reson., 2004, 26, 74–83.
51. W. Frank, U. Breier, C. Elsässer and M. Fähnle, Phys. Rev. Lett., 1996, 77, 518.
52. V. Schott, M. Fähnle and P. A. Madden, J. Phys.: Condens. Matter, 2000, 12, 1171–1194.
53. M. Yang, Y. Liu, A. M. Nolan and Y. Mo, Adv. Mater., 2021, 33, 2008081.
54. E. Dologlou, Glass Phys. Chem., 2010, 36, 570–574.
55. P. M. Sargent and M. F. Ashby, Scr. Metall., 1984, 18, 145–150.
56. R. Raj, Acta Mater., 2021, 215, 117076.
57. S. J. Fensin, D. Olmsted, D. Buta, M. Asta, A. Karma and J. J. Hoyt, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 031601.
58. P. L. Williams and Y. Mishin, Acta Mater., 2009, 57, 3786–3794.
59. M. Torabi Rad, G. Boussinot and M. Apel, Sci. Rep., 2020, 10, 21074.
60. B. Wang and H. M. Urbassek, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 104108.
61. J. J. Möller and E. Bitzek, MethodsX, 2016, 3, 279–288.
62. M. Jäckle, K. Helmbrecht, M. Smits, D. Stottmeister and A. Groß, Energy Environ. Sci., 2018, 11, 3400–3407.
63. M. Jäckle and A. Groß, J. Chem. Phys., 2014, 141, 174710.
64. Integration and Optimization of Novel Ion Conducting Solids(IONICS) Program Overview, https://arpa-e.energy.gov/sites/default/files/documents/files/IONICS_ProgramOverview.pdf.
65. W. S. LePage, Y. Chen, E. Kazyak, K.-H. Chen, A. J. Sanchez, A. Poli, E. M. Arruda, M. D. Thouless and N. P. Dasgupta, J. Electrochem. Soc., 2019, 166, A89–A97.
66. D. K. Singh, T. Fuchs, C. Krempaszky, B. Mogwitz, S. Burkhardt, F. H. Richter and J. Janek, Adv. Funct. Mater., 2023, 33, 2211067.
67. B. L. Mehdi, A. Stevens, J. Qian, C. Park, W. Xu, W. A. Henderson, J. G. Zhang, K. T. Mueller and N. D. Browning, Sci. Rep., 2016, 6, 34267.
68. K. P. Larsen, J. T. Ravnkilde, M. Ginnerup and O. Hansen, in The Fifteenth IEEE International Conference on Micro Electro Mechanical Systems, 2002, pp. 443–446.
69. A. Ijaz, L. F. Kiss, A. L. Demirel, L. K. Varga and A. Mikó, Mater. Chem. Phys., 2021, 267, 124681.
70. T. Watanabe, in Nano-plating Microstructure Control Theory of Plated Film and Data Base of Plated Film Microstructure, Elsevier, 2004.
71. C. T. Yang and Y. Qi, Chem. Mater., 2021, 33, 2814–2823.
72. A. J. Sanchez, E. Kazyak, Y. Chen, J. Lasso and N. P. Dasgupta, J. Mater. Chem. A, 2021, 9, 21013–21023.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta03814a

---