Co-alloying of Sn and Te enables high thermoelectric performance in Ag₉GaSe₆

Abstract

As a typical liquid-like material, the argyrodite-type Ag₉GaSe₆ has attracted considerable attention in the past decade due to its liquid-like characteristics, complex crystal structures, and high carrier mobility. However, the carrier concentration of pristine Ag₉GaSe₆ is still not optimal while the thermal conductivity remains to be further reduced. Herein, we simultaneously optimize the electrical and thermal properties of Ag₉GaSe₆via alloying Sn at the Ga sites and Te at the Se sites. It is found that the crystal symmetry is well maintained, while the phase transition temperature is reduced and local chemical bonding is altered after alloying. Due to the nominally reduced Ag content and the change of chemical bonding, the carrier concentration is reduced by two orders of magnitude, giving rise to a largely improved Seebeck coefficient. Meanwhile, the lattice thermal conductivity κ_L of Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ is significantly suppressed by the strong phonon scattering from point defects. An ultralow κ_L of ∼0.25 W m⁻¹ K⁻¹, which approaches the theoretical minimum κ_L, is attained at room temperature in the alloyed samples. Consequently, the zT value is boosted to 1.4 for the x = 0.1 sample, which represents an improvement of 75% over that of pristine Ag₉GaSe₆.

---

1. Introduction

Thermoelectric (TE) technology, which enables direct energy conversion between heat and electricity, is believed to play a key role in alleviating the energy crisis and environmental pollution.^1–3 The energy conversion efficiency of a TE material is mainly governed by the dimensionless TE figure of merit where S, σ, κ, and T are the Seebeck coefficient, electrical conductivity, total thermal conductivity, and absolute temperature, respectively. κ mainly consists of two parts: the lattice thermal conductivity (κ_L) and electronic thermal conductivity (κ_e). Since the parameters S, σ and κ_e are strongly interrelated via the carrier concentration and scattering mechanism, it is really challenging to boost the TE performance. Considerable efforts have been devoted to either enhancing the electronic performance or reducing the lattice thermal conductivity. The former can be realized by approaches like band convergence,^4,5 resonant doping,⁶ and disorder-induced electronic localization,^7,8 while the latter can be achieved by all-scale hierarchical structuring,^9,10 introduction of liquid-like ions,^11,12 entropy engineering,^13,14 or structural modularization.¹⁵

Rational design of ordered and disordered sublattices in the crystal structure is one of the most effective strategies for regulating the TE properties at present. A highly ordered crystal lattice is conducive to the free transport of electrons, whereas a disordered crystal lattice enables strong scattering of heat-carrying phonons.¹⁶ Integration of ordered and disordered sublattices into a single material may induce some intriguing new effects,^8,17 and is expected to decouple the electrical and thermal transports. Hybrid materials, such as liquid-like materials,^18,19 meta-phases,^8,20 and filled skutterudites,^21,22 are successful examples in this regard. Particularly, liquid-like materials, which consist of an ordered rigid framework and disordered liquid-like cations, have stimulated keen interest in the past few years. Liquid-like ions can not only strongly scatter the phonons but also eliminate part of the transverse vibrational modes, giving rise to extremely low thermal conductivity and high thermoelectric performance.^11,23–25

Among all the known liquid-like materials, argyrodite-type compounds stand out due to their unique features of earth-abundant components, complex order–disorder structures, and unusual TE properties.^26–37 The argyrodites contain dozens of types of compounds with the general chemical formula of A⁺_12−yB⁺_yC²⁻₆, where A, B, and C could be Ag/Cu/Li, Al/Ga/Si/Ge/Sn/P, and S/Se/Te, respectively.³⁸ The crystal structures, phase transitions, and TE properties of argyrodites can thus be readily regulated and controlled by the richness of composition. Argyrodite-type compounds generally undergo one or two phase transitions. At low temperature, they usually crystallize in a low-symmetry ordered structure, such as monoclinic, orthogonal, or hexagonal structure, where both anions and cations are in long-range ordered (LRO) distribution. As the temperature goes up to the phase transition point, they transform into a high-symmetry disordered structure, where A ions are situated in a highly disordered manner in the rigid sublattice formed by B cations and C anions. Owing to the unique structural feature of crystallinity–amorphicity duality, argyrodites show intrinsically ultralow κ_L and good thermoelectric performance. Taking the representative Ag₉GaSe₆ as an example, it has an amorphous-like κ_L of 0.3 W m⁻¹ K⁻¹ and a high zT value of 1.1 at high temperature.³³ Further optimization of the carrier concentration by introducing slight Se-deficiency leads to an increased zT of 1.3 in Ag₉GaSe_5.99.³³ Through alloying Te at Se sites, the good electrical transport properties were maintained while the lattice thermal conductivity was reduced, resulting in a high zT of 1.6 at 850 K for Ag₉GaSe_5.53Te_0.45.³⁴ Besides, alloying Cu at the Ag site could effectively decrease the carrier concentration and improve the maximum zT value to 1.6 at 824 K.³⁹

Inspired by the aforementioned peer work, herein we aim to reduce the carrier concentration and suppress the lattice thermal conductivity simultaneously by co-alloying Sn and Te in Ag₉GaSe₆. Our results show that the nested order–disorder structural feature of Ag₉GaSe₆ is well maintained, while the phase transition temperature is reduced and the local chemical bonds are slightly changed after alloying Sn at the Ga sites and Te at the Se sites. The κ_L is largely reduced due to the extra phonon scattering by the strong mass and strain fluctuations. Combining the optimized carrier concentration, a maximum zT of 1.4 was finally achieved in the (Ag₉GaSe₆)_0.9(Ag₈SnTe₆)_0.1 sample.

2. Experimental details

2.1. Synthesis

A series of Sn and Te co-alloyed Ag_9−x(Ga_1−xSn_x)(Se_1-xTe_x)₆ samples, i.e., (Ag₉GaSe₆)_1−x(Ag₈SnTe₆)_x (x = 0, 0.05, 0.075, 0.1, 0.125, 0.15, 0.2), were synthesized by the melting–annealing–sintering technique. Mixtures of the five elements (Ag, Ga, Se, Sn and Te) with purity of more than 99.999% (Alfa Aesar) were weighed out in stoichiometric proportions and loaded into silica vacuum tubes for melting. The melting was conducted at 1373 K for 12 h under vacuum, followed by annealing at 873 K for 72 h. After cooling down to room temperature (RT), the ingots were ground into fine powders and then sintered using a hot press system in a graphite die at a peak temperature of ∼873 K and a pressure of 57 MPa for 2 h. The relative densities of all the obtained bulk samples were larger than 99%. The bulk samples with sizes of about 2 × 2 × 9 mm³ were cut out for electrical measurements, and samples with sizes of ϕ10 × 1 mm² for thermal diffusivity measurement.

2.2. Characterization

To identify the phase purity and crystal structure, the powder X-ray diffraction (PXRD) data for all synthesized samples were collected on a powder X-ray diffractometer (D8 Advance) with Cu Kα radiation (λ = 1.5406 Å). Four samples (x = 0, 0.05, 0.1, 0.15) were selected to record the high-quality synchrotron diffraction data (λ = 0.6887 Å) at beamline BL14B1 at the Shanghai Synchrotron Radiation Facility (SSRF), China. Phase composition and microstructure analysis were carried out by scanning electron microscopy (SEM) using a ZEISS Supra 55 equipped with an energy dispersive spectrometer (EDS, Oxford Horiba 250). The heat capacity at constant pressure was measured to analyze phase transition characteristics in the range of 150 K–550 K using a differential scanning calorimeter (DSC, Netzsch 200 F3). The electrical transport measurements (σ and S) from RT to 850 K were conducted in a helium atmosphere using an ULVAC-RIKO ZEM-3 instrument system. The thermal diffusivity (D) above 300 K was measured by the laser flash method using a Netzsch LFA 457 instrument in an argon atmosphere, and all the samples were pre-coated with graphite spray before the measurement. Measurement uncertainty for σ, S, and D is ±3%, ±4%, and ±3%, respectively. The Dulong–Petit rule was used to estimate the heat capacities (C_p) above RT. The sample density d was measured using Archimedes' method. The thermal conductivity above RT was then calculated based on the equation κ = dDC_p. The transverse and longitudinal sound velocities at RT were obtained by using the ultrasonic pulse method on an Advanced Ultrasonic Measurement System (UMS, TECLAB). Then the TE figure of merit (zT) can be calculated using the obtained parameters mentioned above. The electrical conductivity, thermal conductivity, and heat capacity in the low temperature range (3–300 K) were measured using a Physical Property Measurement System (PPMS, Quantum Design). Hall coefficients (R_H) were measured by using a four-probe configuration in PPMS with a sweeping magnetic field from −3 T to 3 T. The Hall mobility (μ) and carrier concentration (n) were calculated according to the equations μ = |R_H|σ and n = 1/(eR_H), respectively, where e is the electron charge.

2.3. Theoretical calculations

First-principles calculations were carried out with the Vienna Ab initio Simulation Package (VASP) code by utilizing the projector augmented wave (PAW) method for the interaction between ion cores and valence electrons.⁴⁰ The low temperature ordered cubic structure of α-Ag₉GaSe₆ was used for calculation. One fourth of the Ga and Se atoms were randomly substituted by Sn and Te, respectively, and one thirty-sixth of the Ag was removed (see Fig. S1†), corresponding to the chemical composition of Ag_8.75Ga_0.75Sn_0.25Se_4.5Te_1.5. Both the atomic coordinates and lattice vectors were fully relaxed until the force-convergence criterion reached 0.01 eV Å⁻¹ for pure and doped Ag₉GaSe₆ structures. The Perdew Burke Ernzerhof (PBE) functional within Generalized gradient approximation (GGA) was used for treating the electronic exchange and correlation potential. The deformation charge density was obtained by subtracting atomic charge density from total charge density. The plane wave energy cutoff was set to 400 eV for all calculations. The projected crystal orbital Hamilton population (pCOHP) was calculated through the LOBSTER code⁴¹ based on a ground state self-consistent calculation from VASP. The Brillouin zone was sampled by 3 × 3 × 3 Γ-centered k mesh for structural relaxations and charge density calculations, and by 9 × 9 × 9 Γ-centered k mesh for COHP calculations. A rotationally invariant Hubbard U correction was adopted to describe the on-site Coulomb interactions among Ag 4d orbital electrons (U = 2.0 eV). The Bader charge was analyzed using the Bader code from the Henkelman research group.⁴²

3. Results and discussion

The pristine Ag₉GaSe₆ undergoes an order-to-disorder phase transition at around 281 K.^43,44 Below 281 K, it adopts a cubic structure (α-phase, space group P2₁3) with all atoms in a long-range ordered (LRO) distribution (Fig. 1a). Above 281 K, Ag₉GaSe₆ crystallizes in a higher-symmetry cubic structure (β-phase, space group F4̄3m) with the Ag ions melting down to disordered distribution (Fig. 1b). The distribution of Ga and Se is very similar, and the coordination environment and bond lengths are also very close in both structures. Herein we synthesized a series of Sn and Te co-alloyed Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ samples, i.e., (Ag₉GaSe₆)_1−x(Ag₈SnTe₆)_x, with x ranging from 0 to 0.2. The measured room temperature powder XRD patterns are shown in Fig. 1c and S2.† All the diffraction peaks (Fig. 1c) can be well indexed to the high temperature β-phase of Ag₉GaSe₆ without any visible impurity peaks. The refined lattice parameters increase linearly with increasing Sn and Te alloying content, well obeying Vegard's law. Though Sn has a larger atomic size than Ga, the lattice parameters of Sn and Te co-alloyed samples are nearly the same as the Te alloyed samples. This may be attributed to the low Ag content in our Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ samples, which shrinks the crystal lattice to a certain extent. Fig. S3† shows the SEM images and EDS mappings measured on the polished surfaces for the Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ samples. All samples are dense with no observable pores or cracks. All elements, including Ag, Ga, Se, Sn, and Te, are homogeneously distributed in the materials. The measured chemical compositions are very close to the nominal ones (Table S1†). These results indicate the successful substitution of Sn and Te at the lattice sites of Ga and Se.

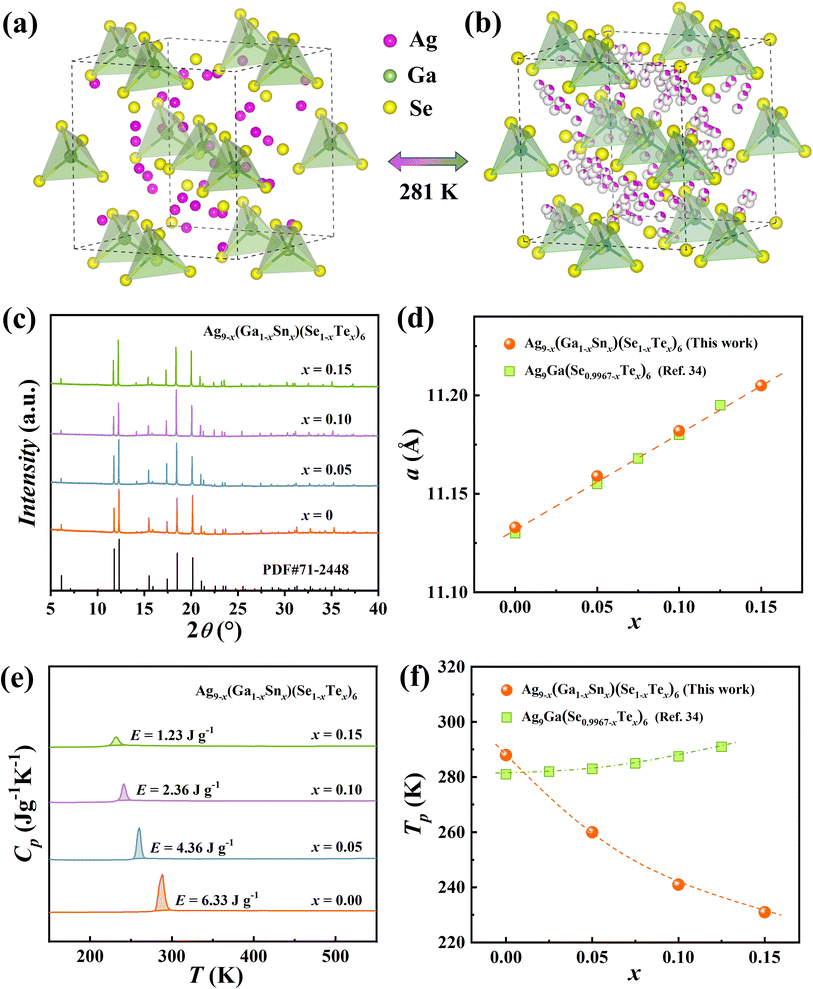Fig. 1 (a) Low-temperature and (b) high-temperature crystal structures for Ag₉GaSe₆. (c) Synchrotron powder X-ray diffraction patterns for Ag_9−x(Ga_1−xSn_x)(Se_1-xTe_x)₆ (x = 0, 0.05, 0.1,0.15, 0.2). (d) Lattice parameter a as a function of alloying content x for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆. (e) Temperature dependence of heat capacity C_p. (f) Phase transition temperature as a function of alloying content x. The green square symbols represent the data for Ag_9−xGa(Se_0.9967−xTe_x)₆.³⁴

Fig. 1e shows the temperature dependent heat capacity C_p for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ samples. One endothermic peak can be observed clearly in each curve, corresponding to the phase transition from the ordered α-phase to the disordered β-phase. Based on the C_p data, we calculated the latent heat (E) during phase transition. It was found that the E is reduced from 6.33 J g⁻¹ for pristine Ag₉GaSe₆ to 1.23 J g⁻¹ for the x = 0.15 sample, indicating that the enthalpy difference between the α-phase and β-phase gets smaller after alloying Sn and Te. The detected phase transition temperature T_p for pristine Ag₉GaSe₆ is around 288 K, which is slightly higher than the reported T_p (281 K) from ref. ³⁴. With increasing alloying content of Sn and Te, the T_p is gradually reduced, in contrast with the increasing trend in single element alloyed Ag₉Ga(Se_0.9967−xTe_x)₆ samples (see Fig. 1f). These results suggest that Sn alloying plays a key role in suppressing the phase transition temperature.

The chemical bonding characteristics of Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ were investigated by analyzing the Bader charge, deformation charge density, and projected crystal orbital Hamilton population (pCOHP). As shown in Fig. 2a, Bader charge analysis shows that for Ag₉GaSe₆ each Se atom receives 0.4–0.6 electrons, while each Ag and Ga atom loses 0.26 and 0.97 electrons, respectively. The relatively low Bader charge, i.e., low charge transfer, suggests that the ionic component of chemical bonds in Ag₉GaSe₆ is very low. After alloying Sn and Te, the Bader charge of Se remains the same, while the Bader charge of Ag is reduced from 0.26 to 0.24. The Bader charge of Te is lower than that of Se, indicating that the ionic component between Ag and anions (Se/Te) is further weakened. Meanwhile, the ionic component of Sn–Se bonds is stronger than that of Ga–Se bonds due to the smaller Bader charge of Sn as compared with Ga. This is reasonable since Sn (1.96) is more electronegative than Ga (1.81). Fig. 2b shows the deformation charge density for Ag_8.75Ga_0.75Sn_0.25Se_4.5Te_1.5. As can be seen, the charge density between Ga and Se is very high, indicative of strong covalent interaction. The substitution of Sn at Ga sites leads to a slightly weakened covalent interaction, as evidenced by the low charge density between Sn and Se. On the other hand, the charge density between Ag and neighboring Se or Te is very low, pointing to weak covalent bonds. This is further confirmed by the pCOHP results. As shown in Fig. 2c, large antibonding (destabilizing) states below the Fermi level are observed for the Ag–Se bonds, and the bonding energy (−0.69 eV) calculated from the integral pCOHP is also very low. In contrast, the Ga–Se bond has a high bonding energy of −4.45 eV, which is consistent with the results of deformation charge density. After alloying Sn and Te, the bonding energies of Ag–Se/Te and Ga/Sn–Se bonds are slightly changed (Fig. 2d).

Fig. 2 (a) Bader charge for the different elements in Ag₉GaSe₆ and Ag_8.75Ga_0.75Sn_0.25Se_4.5Te_1.5. (b) Deformation charge density at the (101) plane for Ag_8.75Ga_0.75Sn_0.25Se_4.5Te_1.5. (c) The projected crystal orbital Hamilton population (pCOHP) of Ag–Se and Ga–Se bonds for Ag₉GaSe₆. The Fermi level is represented by the horizontal dashed line. The bonding orbital has negative pCOHP, while the antibonding orbital has positive pCOHP. (d) Integrated pCOHP (IpCOHP) for the chemical bonds in Ag₉GaSe₆ and Ag_8.75Ga_0.75Sn_0.25Se_4.5Te_1.5.

Briefly, all calculation results reveal that the Ag–Se chemical bonds, including both ionic component and covalent component, are very weak, while the Ga–Se bonds are very strong. The Ag ions are thus loosely bonded to the rigid sublattice formed by Ga and Se. Due to the high content of the weakly bonded Ag ions, the overall chemical bonds in Ag₉GaSe₆ are still very weak. The alloying of Sn and Te has an unremarkable but observable impact on the chemical bonds, which may change the local lattice defects.

Fig. 3 presents the thermal transport properties for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆. The total thermal conductivity (κ) of pristine Ag₉GaSe₆ is around 0.5 W m⁻¹ K⁻¹, which is reduced to 0.3 W m⁻¹ K⁻¹ in the alloyed samples (Fig. 3a). All samples show a weak temperature dependency of κ, which is a common phenomenon observed in liquid-like TE materials, for instance, Cu₂Se,¹¹ Ag₉FeSe_6−xTe_x,⁴⁵ and Cu₇PSe₆,³⁷ to name a few. Besides, an evident upward inflection is observed at about 700 K for x = 0–0.075 samples, which is mainly caused by an increase of electronic thermal conductivity resulting from the intrinsic excitation. The lattice thermal conductivity (κ_L) was derived by subtracting the electronic contribution (κ_e) from the total κ via the Wiedemann–Franz relationship, κ_e = LσT, where L is the Lorenz number.⁴⁶ As shown in Fig. 3b, the calculated κ_L of Ag₉GaSe₆ is about 0.4 W m⁻¹ K⁻¹ at room temperature and gradually decreased above 600 K. After alloying Sn and Te, the room temperature κ_L of Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ is further reduced to ∼0.25 W m⁻¹ K⁻¹ owing to the enhanced phonon scattering by point defects. The abnormally low κ_L above 750 K likely stems from the strong liquid-like effects at high temperature and the overestimation of the electronic thermal conductivity, especially for the samples having high electrical conductivities. The low κ_L in Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ is comparable to those observed in other liquid-like materials, but much lower than those observed in the state-of-the-art TE materials like Bi₂Te₃,⁴⁷ Mg₃Sb₂,^48,49 and half-Heuslers.^50,51

Fig. 3 Temperature dependence of (a) total thermal conductivity (κ) and (b) lattice thermal conductivity (κ_L) from 300 K to 850 K for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ (x = 0, 0.05, 0.075, 0.1, 0.125, 0.15, and 0.2). (c) Lattice thermal conductivity (κ_L) below 300 K. (d) Room temperature κ_Lversus sound velocity for well-known TE materials.^{26,32,36,57–63}

Based on the measured sound velocities, we estimated the theoretical minimum κ_L,min for this material system using Cahill's model⁵² (see details in the ESI†). Our experimental κ_L data are obviously lower than the Cahill's limit (0.37 W m⁻¹ K⁻¹), which means it is inadequate to capture the phonon transports by only considering the lattice complexity and anharmonicity based on the Cahill's model. Recently, a diffuson-dominated model was reported by Bernges et al.,⁵³ in which the ion transport was also included to explain the thermal transport properties of disordered materials. Through a two-channel lattice dynamics modeling, Bernges et al. pointed out that the majority of Ag⁺ vibrations in liquid-like argyrodites have a non-propagating diffuson-like character, resulting in the diffuson-mediated thermal transport.⁵³ Since Ag₉GaSe₆ is a typical liquid-like material, we adopt the diffuson-dominated model to calculate a diffuson limit (see details in the ESI†). It is found that the κ_L of our alloyed samples approaches this limit (0.23 W m⁻¹ K⁻¹), demonstrating the strong liquid-like behavior and the presence of diffusons in Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆.

Fig. 3c shows the temperature-dependent κ_L for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ below 300 K. Similar to the normal crystalline materials, the κ_L of x = 0 and x = 0.05 samples shows a pronounced Umklapp peak at around 10 K. In contrast, κ_L of the x = 0.15 sample monotonously increases during the entire temperature range without a peak, which is more like the behavior of amorphous materials. The distinct temperature dependency of κ_L is ascribed to the different contributions from the structural disorder and low-lying multi-Einstein oscillators, as has been discussed in detail in the Ag₉FeS_6−xTe_x materials.⁴⁵ Note that the κ_L of x = 0 and x = 0.05 samples are dramatically reduced at about 280 K and 260 K, respectively, which should be associated with the order-to-disorder phase transition. Though the Ag ions are weekly bonded in both α-phase and β-phase, the distribution of Ag becomes highly disordered and liquid-like in the β-phase, leading to the extra scattering of phonons and the elimination of part transverse vibration modes.

The most prominent feature related to the extremely low κ_L is the low sound velocities (v) for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆. According to the Debye–Callaway model,^54,55κ_L scales approximately with the cube of sound velocity above the Debye temperature. A low sound velocity fundamentally gives rise to a low κ_L.⁵⁶ The measured transverse and longitudinal sound velocities for our samples are respectively around 1150 m s⁻¹ and 2800 m s⁻¹, both of which are among the lowest values of all known solid materials (Fig. 3d).^{26,32,36,57–63} The Debye temperature, calculated based on the sound velocities, is only 140 K, while the Gruneisen parameter is as large as 2.6 (see Table 1). These results can be traced back to the weak bonding of Ag to its surrounding Se/Te atoms. Co-alloying of Sn and Te in Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ scarcely alters the sound velocity, which is reasonable since the crystal structure and chemical bonding do not change much.

Table 1 Transverse (v_t), longitudinal (v_l) and mean sound velocity (v_m), bulk module (B), shear module (G), Gruneisen parameter (γ), and Debye temperature (T_D) for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆

Samples	ν t (m s^−1)	ν l (m s^−1)	ν m (m s^−1)	B (Gpa)	G (Gpa)	γ	T D
x = 0.000	1150.7	2855.4	1303.2	45.9	9.5	2.66	139.0
x = 0.050	1159.8	2734.4	1311.2	40.8	9.7	2.52	140.0
x = 0.075	1165.5	2706.2	1316.8	39.6	9.8	2.47	140.5
x = 0.100	1180.1	2771.3	1333.9	41.8	10.0	2.50	142.0
x = 0.125	1181.2	2796.6	1335.6	42.8	10.0	2.53	142.5
x = 0.150	1195.9	2820.3	1352.1	43.4	10.3	2.52	144.0
x = 0.200	1201.7	2848.0	1358.8	44.4	10.4	2.53	145.0

---

Fig. 4 shows the electrical transport properties for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆. The electrical conductivity σ of the pristine Ag₉GaSe₆ decreases from 1.7 × 10⁴ S m⁻¹ at room temperature to 1.1 × 10⁴ S m⁻¹ at 600 K before it increases to 3.5 × 10⁴ S m⁻¹ at 850 K. The inflection point at 600 K is indicative of the intrinsic excitation of carriers. After alloying Sn and Te, the σ is roughly decreased and much lower than those of Te alloyed samples (see Fig. S4a†). Besides, the inflection point of σ after alloying Sn and Te is shifted to a lower temperature, suggesting a lower carrier concentration and smaller band gap. The negative S values indicate that electrons are the dominant charge carriers, which is further confirmed by the Hall measurements. The temperature dependency and composition dependency of S are opposite to the electrical conductivity. A maximum |S| of 615 μV K⁻¹ is achieved at 300 K for the x = 0.15 sample, which is three times larger than that of pristine Ag₉GaSe₆. The improvement of S is significantly larger in our Sn and Te co-alloyed samples, as compared with the single element alloyed Ag₉Ga(Se_1−xTe_x)₆ samples (see Fig. S4b†).

Fig. 4 Temperature dependence of (a) electrical conductivity σ and (b) Seebeck coefficient S for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ (x = 0, 0.05, 0.075, 0.1, 0.125, 0.15, 0.2). (c) Room temperature Hall carrier concentration n and carrier mobility μ as a function of alloying content x. (d) Seebeck coefficient S as a function of carrier concentration n. The reported data of Ag₉Ga(Se_1−xTe_x)₆ and Ag₉Ga(Se_0.9967−xTe_x)₆ are included for comparison.^29,34 The Pisarenko plot (S vs. n) is derived from the single parabolic band (SPB) model.

The variations of σ and S are mainly caused by the modified carrier concentrations (n) and mobility (μ) of Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆. As shown in Fig. 4c, the Hall carrier concentration decreases dramatically from 2.18 × 10¹⁸ cm⁻³ for pristine Ag₉GaSe₆ to 1.5 × 10¹⁶ cm⁻³ for the x = 0.15 sample. Such a decreased trend in n is mainly related to two aspects. On one hand, the nominally Ag content during preparation is reduced, which could decrease the donor concentration of Ag interstitials. On the other hand, the defect formation energy of Ag interstitials or anion vacancies could be improved due to the change of local chemical bonds,⁶⁴ which may lead to a lower n as well. With increasing alloying content, the carrier mobility is also gradually decreased owing to the strengthened scattering of electrons by the chemical bond fluctuation and the ensuing extra potential field introduced by Sn and Te alloying. Specifically, the μ for pristine Ag₉GaSe₆ is 546 cm² V⁻¹ s⁻¹ and decreased to 115 cm² V⁻¹ s⁻¹ for the x = 0.15 sample. The decreasing trend of carrier mobility for our co-alloyed samples is opposed to the well maintained carrier mobility in Ag₉Ga(Se_1−xTe_x)₆ (ref. ²⁹) (shown in Fig. S4d†), suggesting that Sn alloying drastically strengthens the scattering of carriers. Nevertheless, the reduced carrier mobility is still higher than most p-type liquid-like materials, such as Cu₂Se (20 cm² V⁻¹ s⁻¹),⁶⁴ Cu₈GeS₆ (16 cm² V⁻¹ s⁻¹),⁶⁵ and Cu₈GeSe₆ (0.23 cm² V⁻¹ s⁻¹).¹⁹

The experimental data of S as a function of n for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ are shown in Fig. 4d. For comparison, the reported data of Ag₉Ga(Se_1−xTe_x)₆ and Ag₉Ga(Se_0.9967−xTe_x)₆ are also given here. Based on the single parabolic band (SPB) model under the assumption that the charge carriers are mainly scattered by acoustic phonons, a Pisarenko plot (S vs. n) with effective mass m* of 0.124m_e was calculated, where m_e is the effective mass of the electron. Clearly, the experimental data fall right around the theoretical Pisarenko plot, indicating that the alloying of Sn or Te merely shifts the Fermi level towards the valence band, but has little impact on the band edge of the electronic structure. The small effective mass is one of the reasons for the high μ in Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆.

Combining the measured S, σ and κ, we calculated the power factor (PF) and figure of merit zT as a function of temperature. As shown in Fig. 5a, the power factor is slightly increased from ∼5 μW cm⁻¹ K⁻² for pristine Ag₉GaSe₆ to ∼5.5 μW cm⁻¹ K⁻² for the x = 0.05 sample. With further increasing the alloying content, the PFs at low temperatures are gradually decreased. The maximum PF achieved for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ is only 6.3 μW cm⁻¹ K⁻², which is not high as compared with the conventional TE materials like Bi₂Te₃,⁴⁷ GeTe,^5,66 and CoSb₃.^21,67 Nevertheless, relying on the optimized carrier concentration, reduced thermal conductivity (both κ_L and κ_e), and largely increased Seebeck coefficient, a promising peak zT of 1.4 is attained at 840 K for the x = 0.1 sample (Fig. 5b), which is comparable to, if not superior to that of other argyrodite-type compounds.

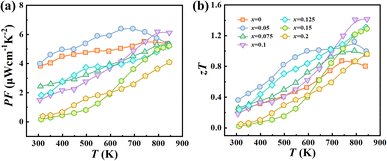Fig. 5 Temperature dependence of (a) power factors PF and (b) TE figure of merit zT for Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ (x = 0, 0.05, 0.075, 0.1, 0.125, 0.15, 0.2).

4. Conclusion

In summary, a series of Ag_9−x(Ga_1−xSn_x)(Se_1−xTe_x)₆ samples are successfully synthesized and the effects of Sn and Te co-alloying on the crystal structures, phase transition, chemical bonds, and thermoelectric properties are systematically studied. It is found that the crystal symmetry of Ag₉GaSe₆ is well maintained, while the phase transition temperature is suppressed and the overall weak chemical bonds are slightly altered after alloying Sn and Te. The high carrier concentration in pristine Ag₉GaSe₆ is effectively reduced and the Seebeck coefficient is thereby largely improved. Due to the overall weak chemical bonds, Ag₉GaSe₆ shows ultralow sound velocities and lattice thermal conductivity. Upon alloying Sn and Te, the lattice thermal conductivity is further suppressed to ∼0.25 W m⁻¹ K⁻¹, which approaches the diffuson limit. Finally, a peak zT value of 1.4 is achieved in the x = 0.1 sample, which is much higher than that of pristine Ag₉GaSe₆.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (No. 91963208 and 51902199), the Shanghai Pilot Program for Basic Research-Chinese Academy of Science, Shanghai Branch (JCYJ-SHFY-2022-002), and Shanghai Government (20JC1415100).

References

1. X. Shi and L. Chen, Thermoelectric materials step up, Nat. Mater., 2016, 15, 691–692.
2. T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Compromise and Synergy in High-Efficiency Thermoelectric Materials, Adv. Mater., 2017, 29(14), 1605884.
3. X. Shi, L. Chen and C. Uher, Recent advances in high-performance bulk thermoelectric materials, Int. Mater. Rev., 2016, 61, 379–415.
4. Y. Pei, X. Shi, A. LaLonde, H. Wang, L. Chen and G. J. Snyder, Convergence of electronic bands for high performance bulk thermoelectrics, Nature, 2011, 473, 66–69.
5. J. Li, X. Zhang, Z. Chen, S. Lin, W. Li, J. Shen, I. T. Witting, A. Faghaninia, Y. Chen, A. Jain, L. Chen, G. J. Snyder and Y. Pei, Low-Symmetry Rhombohedral GeTe Thermoelectrics, Joule, 2018, 2(5), 976–987.
6. J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Enhancement of Thermoelectric Efficiency in PbTe by Distortion of the Electronic Density of States, Science, 2008, 321(5888), 554–557.
7. S. Roychowdhury, T. Ghosh, R. Arora, M. Samanta, L. Xie, N. K. Singh, A. Soni, J. He, U. V. Waghmare and K. Biswas, Enhanced atomic ordering leads to high thermoelectric performance in AgSbTe₂, Science, 2021, 371(6530), 722–727.
8. K. Zhao, C. Zhu, W. Qiu, S. Yang, H. Su, P. Qiu, Y. He, M. Guan, T.-R. Wei, J. Ma, J. Liu, G. Zheng, F. Xu, X. Shi, J. He and L. Chen, Novel meta-phase arising from large atomic size mismatch, Matter, 2022, 5(2), 605–615.
9. K. Biswas, J. He, I. D. Blum, C.-I. Wu, T. P. Hogan, D. N. Seidman, V. P. Dravid and M. G. Kanatzidis, High-performance bulk thermoelectrics with all-scale hierarchical architectures, Nature, 2012, 489, 414–418.
10. L. D. Zhao, H. J. Wu, S. Q. Hao, C. I. Wu, X. Y. Zhou, K. Biswas, J. Q. He, T. P. Hogan, C. Uher, C. Wolverton, V. P. Dravidc and M. G. Kanatzidis, All-scale hierarchical thermoelectrics: MgTe in PbTe facilitates valence band convergence and suppresses bipolar thermal transport for high performance, Energy Environ. Sci., 2013, 6(11), 3346–3355.
11. H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Copper ion liquid-like thermoelectrics, Nat. Mater., 2012, 11(5), 422–425.
12. K. Zhao, P. Qiu, Q. Song, A. B. Blichfeld, E. Eikeland, D. Ren, B. Ge, B. B. Iversen, X. Shi and L. Chen, Ultrahigh thermoelectric performance in Cu_2-ySe_0.5S_0.5 liquid-like materials, Mater. Today Phys., 2017, 1, 14–23.
13. R. Liu, H. Chen, K. Zhao, Y. Qin, B. Jiang, T. Zhang, G. Sha, X. Shi, C. Uher, W. Zhang and L. Chen, Entropy as a Gene-Like Performance Indicator Promoting Thermoelectric Materials, Adv. Mater., 2017, 29(38), 1702712.
14. B. Jiang, Y. Yu, J. Cui, X. Liu, L. Xie, J. Liao, Q. Zhang, Y. Huang, S. Ning, B. Jia, B. Zhu, S. Bai, L. Chen, S. J. Pennycook and J. He, High-entropy-stabilized chalcogenides with high thermoelectric performance, science, 2021, 371(6531), 830–834.
15. K. Zhao, C. Zhu, M. Zhu, H. Chen, J. Lei, Q. Ren, T.-R. Wei, P. Qiu, F. Xu, L. Chen, J. He and X. Shi, Structural Modularization of Cu₂Te Leading to High Thermoelectric Performance near the Mott–Ioffe–Regel Limit, Adv. Mater., 2022, 34(19), 2108573.
16. G. S. Nolas, G. A. Slack and S. B. Schujman, Semiconductor clathrates: A phonon glass electron crystal material with potential for thermoelectric applications, Semicond. Semimetals, 2001, 69(01), 255–300.
17. K. Bu, Q. Hu, X. Qi, D. Wang, S. Guo, H. Luo, T. Lin, X. Guo, Q. Zeng, Y. Ding, F. Huang, W. Yang, H.-K. Mao and X. Lü, Nested order-disorder framework containing a crystalline matrix with self-filled amorphous-like innards, Nat. Commun., 2022, 13(1), 4650.
18. X. Zhang, C.-L. Zhang, S. Lin, H. Lu, Y. Pei and S. Jia, Thermoelectric properties of n-type Nb-doped Ag₈SnSe₆, J. Appl. Phys., 2016, 119(13), 135101.
19. B. Jiang, P. Qiu, E. Eikeland, H. Chen, Q. Song, D. Ren, T. Zhang, J. Yang, B. B. Iversen, X. Shi and L. Chen, Cu₈GeSe₆-based thermoelectric materials with an argyrodite structure, J. Mater. Chem. C, 2017, 5(4), 943–952.
20. K. Zhao, E. Eikeland, D. He, W. Qiu, Z. Jin, Q. Song, T.-r. Wei, P. Qiu, J. Liu, J. He, B. B. Iversen, J. He, L. Chen and X. Shi, Thermoelectric materials with crystal-amorphicity duality induced by large atomic size mismatch, Joule, 2021, 5(5), 1183–1195.
21. X. Shi, J. Yang, J. R. Salvador, M. Chi, J. Y. Cho, H. Wang, S. Bai, J. Yang, W. Zhang and L. Chen, Multiple-filled skutterudites: high thermoelectric figure of merit through separately optimizing electrical and thermal transports, J. Am. Chem. Soc., 2011, 133(20), 7837–7846.
22. Y. Tang, Z. M. Gibbs, L. A. Agapito, G. Li, H.-S. Kim, M. B. Nardelli, S. Curtarolo and G. J. Snyder, Convergence of multi-valley bands as the electronic origin of high thermoelectric performance in CoSb₃ skutterudites, Nat. Mater., 2015, 14(12), 1223–1228.
23. K. Zhao, P. Qiu, X. Shi and L. Chen, Recent Advances in Liquid-Like Thermoelectric Materials, Adv. Funct. Mater., 2020, 30(8), 1903867.
24. K. Zhao, A. B. Blichfeld, E. Eikeland, P. Qiu, D. Ren, B. B. Iversen, X. Shi and L. Chen, Extremely low thermal conductivity and high thermoelectric performance in liquid-like Cu₂Se_1-xS_x polymorphic materials, J. Mater. Chem. A, 2017, 5(34), 18148–18156.
25. B. Lin, R. Zhang, H. Zhao, Y. Hou, X. Wang, J. Zhu, L. Zhao, M. Zuo and D. Zhao, Achieving High Thermoelectric Properties of Cu₂Se via Lattice Softening and Phonon Scattering Mechanism, ACS Appl. Mater. Interfaces, 2022, 5(5), 6453–6461.
26. W. Li, S. Lin, B. Ge, J. Yang, W. Zhang and Y. Pei, Low Sound Velocity Contributing to the High Thermoelectric Performance of Ag₈SnSe₆, Adv. Sci., 2016, 3(11), 1600196.
27. J.-Y. Liu, L. Chen and L.-M. Wu, Ag₉GaSe₆: high-pressure-induced Ag migration causes thermoelectric performance irreproducibility and elimination of such instability, Nat. Commun., 2022, 13(1), 2966.
28. C. Yang, Y. Luo, Y. Xia, L. Xu, Z. Du, Z. Han, X. Li and J. Cui, Synergistic Optimization of the Electronic and Phonon Transports of N-Type Argyrodite Ag₈Sn_1−xGa_xSe₆ (x =0−0.6) through Entropy Engineering, ACS Appl. Mater. Interfaces, 2021, 13(47), 56329–56336.
29. S. Lin, L. Wen, S. Li, X. Zhang, Z. Chen, Y. Xu, Y. Chen and Y. Pei, High Thermoelectric Performance of Ag₉GaSe₆ Enabled by Low Cutoff Frequency of Acoustic Phonons, Joule, 2017, 1(4), 816–830.
30. S. Lin, W. Li, Z. Bu, B. Gao, J. Li and Y. Pei, Thermoelectric properties of Ag₉GaS₆ with ultralow lattice thermal conductivity, Mater. Today Phys., 2018, 6, 60–67.
31. S. Lin, W. Li, Z. Bu, B. Shan and Y. Pei, Thermoelectric p-Type Ag₉GaTe₆ with an Intrinsically Low Lattice Thermal Conductivity, ACS Appl. Energy Mater., 2020, 3(2), 1892–1898.
32. W. Li, S. Lin, M. Weiss, Z. Chen, J. Li, Y. Xu, W. G. Zeier and Y. Pei, Crystal Structure Induced Ultralow Lattice Thermal Conductivity in Thermoelectric Ag₉AlSe₆, Adv. Energy Mater., 2018, 8(18), 1800030.
33. B. Jiang, P. Qiu, H. Chen, Q. Zhang, K. Zhao, D. Ren, X. Shi and L. Chen, An argyrodite-type Ag₉GaSe₆ liquid-like material with ultralow thermal conductivity and high thermoelectric performance, Chem. Commun., 2017, 53(85), 11658–11661.
34. B. Jiang, P. Qiu, H. Chen, J. Huang, T. Mao, Y. Wang, Q. Song, D. Ren, X. Shi and L. Chen, Entropy optimized phase transitions and improved thermoelectric performance in n-type liquid-like Ag₉GaSe₆ materials, Mater. Today Phys., 2018, 5, 20–28.
35. X. Shen, C.-C. Yang, Y. Liu, G. Wang, H. Tan, Y.-H. Tung, G. Wang, X. Lu, J. He and X. Zhou, High-Temperature Structural and Thermoelectric Study,of Argyrodite Ag₈GeSe₆, ACS Appl. Mater. Interfaces, 2019, 11(2), 2168–2176.
36. B. K. Heep, K. S. Weldert, Y. Krysiak, T. W. Day, W. G. Zeier, U. Kolb, G. J. Snyder and W. Tremel, High Electron Mobility and Disorder Induced by Silver Ion Migration Lead to Good Thermoelectric Performance in the Argyrodite Ag₈SiSe₆, Chem. Mater., 2017, 29(11), 4833–4839.
37. K. S. Weldert, W. G. Zeier, T. W. Day, M. Panthöfer, G. J. Snyder and W. Tremel, Thermoelectric Transport in Cu₇PSe₆ with High Copper Ionic Mobility, J. Am. Chem. Soc., 2014, 136(34), 12035–12040.
38. W. F. Kuhs, R. Nitsche and K. Scheunemann, The argyrodites — A new family of tetrahedrally close-packed structures, Mater. Res. Bull., 1979, 14(2), 241–248.
39. X. Qi, J. Chen, K. Guo, S. He, J. Yang, Z. Li, J. Xing, J. Hu, H. Luo, W. Zhang and J. Luo, Thermal stability of Ag₉GaSe₆ and its potential as a functionally graded thermoelectric material, Chem. Eng. J., 2019, 374, 494–501.
40. G. Kresse and J. Furthmüller, Efficiency of ab-Initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50.
41. R. Nelson, C. Ertural, J. George, V. Deringer and R. Dronskowski, LOBSTER: Local Orbital Projections, Atomic Charges, and Chemical Bonding Analysis from Projector-Augmented-Wave-Based Density-functional Theory, J. Comput. Chem., 2020, 41(21), 1931–1940.
42. M. Yu and D. R. Trinkle, Accurate and efficient algorithm for Bader charge integration, J. Chem. Phys., 2011, 134(6), 064111–064118.
43. J. Deloume and R. Faure, A new compound, Ag₉GaSe₆ structure study of the alpha-phase, J. Solid State Chem., 1981, 36, 112–117.
44. J. Deloume, R. Faure, H. Loiseleur and M. Roubin, Crystal structure of the phase Ag₉GaSe₆ beta, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 3189–3193.
45. Z. Jin, Y. Xiong, K. Zhao, H. Dong, Q. Ren, H. Huang, X. Qiu, J. Xiao, P. Qiu, L. Chen and X. Shi, Abnormal thermal conduction in argyrodite-type Ag₉FeS_6-xTe_x materials, Mater. Today Phys., 2021, 19, 100410.
46. H. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, Characterization of Lorenz number with Seebeck coefficient measurement, APL Mater., 2015, 3(4), 041506.
47. G. Zheng, X. Su, T. Liang, Q. Lu, Y. Yan, C. Uherb and X. Tang, High thermoelectric performance of mechanically robust n-type Bi₂Te_3-xSe_x prepared by combustion synthesis, J. Mater. Chem. A, 2015, 3(12), 6603–6613.
48. J. Zhang, L. Song, S. H. Pedersen, H. Yin, L. T. Hung and B. B. Iversen, Discovery of high-performance low-cost n-type Mg₃Sb₂-based thermoelectric materials with multi-valley conduction bands, Nat. Commun., 2017, 8, 13901.
49. J. Lei, H. Wuliji, K. Zhao, T.-R. Wei, Q. Xu, P. Li, P. Qiu and X. Shi, Efficient lanthanide Gd doping promoting the thermoelectric performance of Mg₃Sb₂-based materials, J. Mater. Chem. A, 2021, 9(46), 25944–25953.
50. C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao and T. Zhu, Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials, Nat. Commun., 2015, 6, 8144.
51. K. Xia, C. Hu, C. Fu, X. Zhao and T. Zhu, Half-Heusler thermoelectric materials, Appl. Phys. Lett., 2021, 118(14), 140503.
52. D. G. Cahill, S. K. Watson and R. O. Pohl, Lower limit to the thermal conductivity of disordered crystals, Phys. Rev. B, 1992, 46, 6131.
53. T. Bernges, R. Hanus and B. Wankmiller, et al., Considering the Role of Ion Transport in Diffuson Dominated Thermal Conductivity, Adv. Energy Mater., 2012, 12, 2200717.
54. J. Callaway, Model for Lattice Thermal Conductivity at Low Temperatures, Phys. Rev., 1959, 113(4), 1046–1051.
55. J. Yang, D. T. Morelli, G. P. Meisner, W. Chen, J. S. Dyck and C. Uher, Influence of electron-phonon interaction on the lattice thermal conductivity of Co_1-xNi_xSb₃, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65(9), 094115.
56. R. Hanus, M. T. Agne, A. J. E. Rettie, Z. Chen, G. Tan, D. Y. Chung, M. G. Kanatzidis, Y. Pei, P. W. Voorhees and G. J. Snyder, Lattice Softening Significantly Reduces Thermal Conductivity and Leads to High Thermoelectric Efficiency, Adv. Mater., 2019, 31(21), 1900108.
57. S. Roychowdhury, T. Ghosh, A. Raagya, U. V. Waghmare and K. Biswas, Stabilizing n-Type Cubic GeSe by Entropy-Driven Alloying of AgBiSe₂: UltralowThermal Conductivity and Promising Thermoelectric Performance, Angew. Chem., Int. Ed., 2018, 57(46), 15167–15171.
58. Y.-L. Pei and Y. Liu, Electrical and thermal transport properties of Pb-based chalcogenides: PbTe, PbSe, and PbS, J. Alloys Compd., 2012, 514, 40–44.
59. L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals, Nature, 2014, 508(7496), 373–377.
60. T. Caillat, A. Borshchevsky and J.-P. Fleurial, Properties of single crystalline semiconducting CoSb₃, J. Appl. Phys., 1996, 80(8), 4442–4449.
61. P. B. Pereira, I. Sergueev, S. Gorsse, J. Dadda, E. Műller and R. P. Hermann, Lattice dynamics and structure of GeTe, SnTe and PbTe, Phys. Status Solidi B , 2013, 250, 1300–1307.
62. C. Uher, J. Yang, S. Hu, D. T. Morelli and G. P. Meisner, Transport properties of pure and doped M NiSn (M=Zr, Hf), Phys. Rev. B, 1999, 59(13), 8615–8621.
63. Q. Jiang, S. Li, Y. Luo, J. Xin, S. Li, W. Li, G. Zhao and J. Yang, Ecofriendly Highly Robust Ag₈SiSe₆-Based Thermoelectric Composites with Excellent Performance Near Room Temperature, ACS Appl. Mater. Interfaces, 2020, 12(49), 54653–54661.
64. K. Zhao, A. B. Blichfeld, H. Chen, Q. Song, T. Zhang, C. Zhu, D. Ren, R. Hanus, P. Qiu, B. B. Iversen, F. Xu, G. J. Snyder, X. Shi and L. Chen, Enhanced Thermoelectric Performance through Tuning Bonding Energy in Cu₂Se_1−xS_x Liquid-like Materials, Chem. Mater., 2017, 29(15), 6367–6377.
65. Y. Fan, G. Wang, R. Wang, B. Zhang, X. Shen, P. Jiang, X. Zhang, H.-s. Gu, X. Lu and X.-y. Zhou, Enhanced thermoelectric properties of p-type argyrodites Cu₈GeS₆ through Cu vacancy, J. Alloys Compd., 2020, 822, 153665.
66. T. Xing, Q. Song, P. Qiu, Q. Zhang, X. Xia, J. Liao, R. Liu, H. Huang, J. Yang, S. Bai, D. Ren, X. Shi and L. Chen, Superior performance and high service stability for GeTe-based thermoelectric compounds, Nat. Sci. Rev., 2019, 6(5), 944–954.
67. S. Wan, X. Huang, P. Qiu, X. Shi and L. Chen, Compound Defects and Thermoelectric Properties of Self-Charge Compensated Skutterudites Se_yCo₄Sb_12−xSe_x, ACS Appl. Mater. Interfaces, 2017, 9(27), 22713–22724.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta01291c

---