Predicting the Na+ ion transport properties of NaSICON materials using density functional theory and Kinetic Monte Carlo†
Judith
Schuett
ab,
Antonia S.
Kuhn
b and
Steffen
Neitzel-Grieshammer
 *b
*b
aHelmholtz-Institut Münster (IEK-12), Forschungszentrum Jülich GmbH, Corrensstraße 46, 48149 Münster, Germany
bInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52056 Aachen, Germany. E-mail: steffen.grieshammer@rwth-aachen.de
First published on 27th March 2023
Abstract
The efficiency of all-solid-state Na+ ion batteries crucially depends on the applied electrolyte, among which sodium super ionic conductors (NaSICONs) show high ionic conductivities. However, the experimental data on ionic conductivities available in the literature vary by several orders of magnitude depending on composition and sample preparation. Hence, a comprehensive understanding of Na+ transport properties is still lacking. In this study, we investigate the multi-cationic NaSICONs Na1+xM2SixP3−xO12 (with M = Zr4+, Hf4+, Sn4+, and 0 ≤ x ≤ 3) by combining state-of-the-art computational tools, namely density functional theory calculations to analyse the structure at the atomic level and Kinetic Monte Carlo simulations to study the ion transport on the macroscopic level. The results show that there is no simple correlation between structural properties and the Na+ ion transport as often described in the literature. Rather the interplay of the ratio of unoccupied to occupied charge carrier sites, interactions between Na+ ions and adjacent cations, and Na+ migration barriers, which are influenced by both the M-cation and the degree of substitution, must be considered. Our study provides a detailed picture of the complex ion transport in NaSICONs of variable composition.
1 Introduction
Although Na+ ion conducting NaSICON materials were discovered more than 50 years ago1–3 and have been intensively studied in recent years,4–12 the examined compositional range of NaSICONs is still limited, and a thorough understanding of Na+ ion transport seems to be lacking.NaSICONs are attractive candidates among solid-state electrolytes (SSEs) because they exhibit good thermal and (electro)chemical stability, high three-dimensional ionic conductivity at room temperature,13–19 and demonstrate promising performance for all-solid-state sodium-ion batteries (NIBs).20–33 NIBs are considered a complementary system to the market-leading lithium-ion batteries, especially for large-scale energy storage, due to the similar chemical properties of sodium and lithium, the long-term resource availability of sodium, and the cost reduction of NIBs.34–48 In addition, all-solid-state NIBs using SSEs are characterized by a long device lifetime, potentially high safety, wide operating temperature range, and high energy and power density depending on the cell architecture.13,17–19,49–52
Various review articles summarize the developments and challenges of NaSICON materials for all-solid-state NIBs.4–12 NaSICON structures with the general formula NaxM2(AO4)3, exhibit a flexible framework in which various M and A cations can be incorporated. Therefore, they offer a large compositional diversity allowing a wide range of applications, but also leading to ionic conductivities that vary over orders of magnitude. Ma et al. reported one of the highest total conductivities among NaSICONs to date of 5.2 × 10−3 S cm−1 at 25 °C for Na3.4Zr2Si2.4P0.6O12, which is comparable with state-of-the-art liquid-based electrolytes for NIBs and highlights the promising potential of NaSICONs as SSEs.26
Substitution of both M and A cations has been shown to be an effective strategy for modifying the (electro)chemical and structural properties, and thus the ionic conductivity of NaSICONs. However, the ionic conductivity of NaSICONs depends not only on the composition but also on the sample preparation and the measurement techniques.9,18,53,54 Due to the large scatter of experimental data currently available, a thorough understanding of Na+ transport properties based on these data is difficult.18 Computational methodologies can be utilized to elucidate the microscopic properties, such as the structure and the migration energy profile of ionic pathways, and their influences on the macroscopic transport behaviour.54–59 To date, however, the focus of computational studies has been mainly on the parent composition Na1+xZr2SixP3−xO12,1–3 which is not sufficient for an adequate understanding of NaSICONs.53,60–69 Therefore, there is a need to investigate various substituted structures over entire compositional ranges using reliable, low-effort computational techniques. Thus, a more comprehensive understanding of the influences of microscopic Na+ ion motion on macroscopic transport properties can be obtained, guiding the material design of NaSICON solid-state electrolytes.
In our previous study, we proposed a first-principles based Kinetic Monte Carlo (KMC) model considering the local ionic environment and the migration energies of the charge carriers which is highly suitable to describe Na+ ion transport in the NaSCION structure.70 On the one hand, the model is based on Density Functional Theory (DFT) calculations, ensuring a reliable description of the structure at the microscopic level. On the other hand, the KMC simulations allow the investigation of transport properties both on long timescales and in large crystalline systems capturing a great number of ion transport events and accounting for statistical variances. However, the approach comes along with a high amount of DFT calculations and is thus not applicable to a broad range of elements.70 Nevertheless, the suitability of this approach was recently confirmed by the study of Deng et al. using a combination of local-cluster expansion, DFT-NEB migration barriers, and KMC.53
In the present study, we show an improved approach based on our previously proposed KMC model that requires DFT calculations with minimized computational effort, yet provides higher accuracy by considering a wider range of the local ionic environment. Hence, this approach is suitable for the study of the influence of various substituents and temperatures on the ionic diffusion of multi-element NaSICONs of arbitrary compositions.
We demonstrate the suitability of the approach by studying Na1+xM2SixP3−xO12 (with M = Zr4+, Hf4+, Sn4+ and 0 ≤ x ≤ 3) as example compositions for multi-element NaSICON-type conductors. These M-cations were selected to investigate structures that exhibit rhombohedral symmetry over a wide temperature range and show the same migration mechanism for Na+ ions. Not only the influence of Si4+ substitution on P5+ sites, but also the influence of chemical and structural factors of homovalent M4+ substitution on Na+ ion transport is investigated.
2 Structure and ionic migration
The original NaSICON material with composition Na1+xZr2SixP3−xO12 exhibits rhombohedral structure (R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) (see Fig. 1) but shows a monoclinic (C2/c) distortion for 1.6 ≤ x ≤ 2.4 at room temperature.2,3,53,71–76 However, at temperatures above 150 °C only the rhombohedral phase exists.53,72,77,78
c) (see Fig. 1) but shows a monoclinic (C2/c) distortion for 1.6 ≤ x ≤ 2.4 at room temperature.2,3,53,71–76 However, at temperatures above 150 °C only the rhombohedral phase exists.53,72,77,78
 | ||
| Fig. 1 The primitive rhombohedral NaSICON structure Na1+xM2SixP3−xO12. Key: Na1 (light green), Na2 (dark green), MO6 (purple), PO4/SiO4 (blue). | ||
In this study, we focus on the rhombohedral structure. On the one hand, this phase exists over a larger compositional and temperature range. On the other hand, we have shown in our previous study that bond distances, ionic interaction energies, and migration energies are very similar in the monoclinic and rhombohedral structures. Therefore, the following analysis and conclusions can be adopted for the monoclinic structure.70
As shown in Fig. 1, the rhombohedral structure consists of a rigid three-dimensional framework of corner-sharing MO6 octahedra and PO4 tetrahedra.1–3,61,62,74,75,79,80 Two distinct sodium ion sites, the Na1 (6b) and Na2 (18e) sites, are located in the scaffold cavities. The Na1 site is energetically more favourable and the sublattice is fully occupied at all substitution degrees x.1–3,53,62,64,67,68,73–76,79–82 As x increases, Si4+ substitute P5+ ions and the amount of Na+ ions on Na2 sites increases to maintain the overall charge neutrality.2,3 Transient metastable mid-Na sites located between Na1 and Na2 sites have been reported.61,66,75,76,83 However, the occupation of the mid-Na sites is negligible and tends to zero at high Na+ concentrations, since the occupation of the Na1 and Na2 sites excludes the occupation of the mid-Na sites due to the small distance.61,66,68,76 Therefore, we focus on the equilibrium sodium sites, Na1 and Na2, in this work.
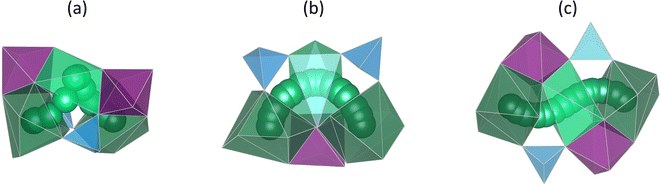
The NaSICON structure, which has a large number of Na+ ion sites and thus a high charge carrier concentration, exhibits fast, three-dimensional Na+ ion diffusion within the rigid framework.2,3,66 As illustrated in Fig. 2, Na2 ions move towards occupied Na1 sites and push the Na1 ions onto adjacent unoccupied Na2 sites.2,3,53,61,63,64,66,68,74,84–86 This correlated pushing-out mechanism is based on Coulomb repulsion and the potential energy transfer from ions at energetically higher Na2 sites to ions at lower Na1 sites.3,53,58,66,68,87,88 Bottlenecks of the migration pathway are formed by PO4- and ZrO6-polyhedra edges, depicted as red triangles.2,3,69,84,85,89,90 At high substitution concentration, a local minimum occurs along the migration path corresponding to the transient mid-Na site allowing fast Na+ ion diffusion.61,66,68,75,76,83 Three different migration pathways of 80°, 90° and 180° are distinguished according to the angle between the Na2–Na1–Na2 sites involved in the migration, as depicted in Fig. 3.68,70 We have previously shown that the high conductivity and low activation energy of compositions with 1.8 ≤ x ≤ 2.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3,72 is not only attributed to (i) favourable ratio of charge carrier and vacancy concentration,6,26,53,66,69,76,81,87,91,92 (ii) high Na+–Na+ coulombic repulsion which enhances the correlated migration,2,58,66,68,69,76,83,87 and (iii) widening of the bottleneck6,68,69,73,74,84,85,89,90 as described in the literature, but also to (iv) percolation of sodium ions in favourable silicon rich environments.53,70
3,72 is not only attributed to (i) favourable ratio of charge carrier and vacancy concentration,6,26,53,66,69,76,81,87,91,92 (ii) high Na+–Na+ coulombic repulsion which enhances the correlated migration,2,58,66,68,69,76,83,87 and (iii) widening of the bottleneck6,68,69,73,74,84,85,89,90 as described in the literature, but also to (iv) percolation of sodium ions in favourable silicon rich environments.53,70
3 Methods
3.1 Density functional theory calculations
The Na1 sublattice was fully occupied in all cells while the Na2 sublattice was empty. As described below, the optimisation of the ion positions was performed using 1 × 1 × 1 k-point mesh and plane waves with an energy cut-off of 400 eV.
The Coulomb energies between the introduced defects at a distance d were calculated according to eqn (1) using the relative permittivity εr and the Born effective charges qB determined in the primitive cells Na1M2P3O12 (M = Zr4+, Hf4+, Sn4+) with 37 atoms by Density Functional Perturbation Theory (DFPT) (Tables S4 and S5†).102–104
 | (1) |
The permittivity is defined as ε = εrε0 with the permittivity of the vacuum ε0. The defect charges are defined as q = qB,rele with the Born effective charge of the substituted lattice site qB,rel calculated according to eqn (2).
| qB,rel = qB,sub − qB,org | (2) |
3.2 Kinetic Monte Carlo
The KMC method was used to simulate the macroscopic sodium ion long-range transport in the NaSICONs by evaluating large stochastic ensembles of sodium ion jumps.55,57,108,110 According to transition state theory, the ionic jump is defined by the energy wells of its stable initial and final state, which are separated by an energy barrier Emig. Emig is the difference between the saddle point and the ground state of the energy surface along the migration path and corresponds to the unstable intermediate transition state.57,110,111 The Boltzmann distribution gives the probability P for the success of the jump, i.e., for the Na+ ions to overcome Emig when possessing sufficiently large kinetic energy.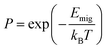 | (3) |
The frequency Γ of the sodium ion jump is given by eqn (4).57,110,111
 | (4) |
In this study, the attempt frequency associated with the ion vibration is assumed to be v = 1013 Hz.110
The mobility of Na+ ions μNa resulting from successful jumps is evoked when an external electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) is applied and the Na+ ions move parallel to the direction of
is applied and the Na+ ions move parallel to the direction of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) . μNa is given by the drift velocity
. μNa is given by the drift velocity ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) Na, i.e., the average ionic displacement Δ
Na, i.e., the average ionic displacement Δ![[x with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0078_20d1.gif) Na per unit time t, in the applied electric field
Na per unit time t, in the applied electric field ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) .
.
 | (5) |
The simulated time t is defined by the number of charge carriers NNa, their number of jump attempts Nattempt as well as averaged number of jump possibilities NJump, and the attempt frequency v.
 | (6) |
The ionic conductivity σNa results from the Na+ ion concentration cNa and mobility μNa, and the charge qNa.
| σNa = cNa·μNa·|qNa| | (7) |
According to Ohm's law, the drift velocity ![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) Na and thus the current density
Na and thus the current density ![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) Na, is proportional to
Na, is proportional to ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) with μNa or σNa, respectively, being the constant of proportionality.
with μNa or σNa, respectively, being the constant of proportionality.
![[u with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0075_20d1.gif) Na = μNa· Na = μNa·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) | (8) |
 | (9) |
![[j with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006a_20d1.gif) Na = σNa· Na = σNa·![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) | (10) |
Thus, the Na+ ion conductivity must be independent of the constant external field which is ensured at the field strength of ![[E with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0045_20d1.gif) = 107 V m−1 applied in the KMC simulations (Fig. S1†).70
= 107 V m−1 applied in the KMC simulations (Fig. S1†).70
KMC simulations were performed in 10 × 10 × 10 cells of Na1+xM2SixP3−xO12 (M = Zr4+, Hf4+, Sn4+) for the compositional range of 0.2 ≤ x ≤ 2.8 and temperature range of 450 K ≤ T ≤ 700 K using the program MOCASSIN with the null-event algorithm.109
4 KMC model
As shown in eqn (3), the migration barrier must be known for KMC simulations. However, different local environments of the migrating Na+ ions lead to different energies of the initial and final states making the energy barrier Emig dependent on the jump directions. Thus, Emig of each jump is defined by the energy of the end states Econf and the directional independent migration energy Emig,0.57,110,112 | (11) |
In our previous study, we investigated the configurational energy Econf and migration energy Emig,0 for Na1+xZr2SixP3−xO12 (x = 0, 1, 2, 3) using DFT.70 The calculation of the exact energy of all possible configurations exceeds the computational limit. However, we have shown that they can be predicted with sufficient accuracy based on the DFT calculations of a few compositions using the models described below.70
4.1 Configurational energy
The configurational energy Econf describes the energy of the cell resulting from the sum of sodium site energies. The sodium site energies depend on the local cationic environment and thus on the distribution of Si4+/P5+ ions and the occupation of Na2 sites. Econf is described by a pair interaction model according to eqn (12).70 | (12) |
4.2 Migration energy
The migration energy Emig,0 depends on the migration pathway and the substitution degree. Emig,0 of the migration in 80°, 90° and 180° of all substitution fractions can be described by the interpolation between the migration energies in the non-substituted cell with x = 0 and the fully substituted cell with x = 3 according to eqn (13).70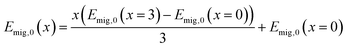 | (13) |
5 Investigation at the atomistic level
5.1 Configurational energies
The configurational energies are described by the simple pair interaction model according to eqn (12). We have shown in our previous study that the pair interaction energies can be determined by fitting many different configurations of Na1+xM2SixP3−xO12 with 0 ≤ x ≤ 3.70 However, this approach requires a large computational effort and is therefore not feasible for the exploration of compositions with various M-cationic species. In contrast, in this study we calculate the Na+–Na+ and Na+–Si4+ pair interaction energies depending on the Na+–cation distances in larger cells with minimal substitution concentration. In this way, the pair interactions can be investigated individually without considering additional compositional effects. This approach allows the study of Na+–cation interactions with a greater range while requiring less computational effort. Here, the Na+–Na+ and Na+–Si4+ pair interactions are investigated for the composition Na1M2P3O12 (M = Zr4+, Hf4+, Sn4+). For this purpose, a pair of a Na+ ion and another cation (Na+ or Si4+) are introduced into the unsubstituted cell. The pair interaction energy is calculated relative to the cell with the furthest Na+–cation distance.Finite size effects are assumed to be negligible when describing the pair interaction energies. Even in the case of the cell with the farthest distance between the introduced cations, the distance to these cations in the neighbouring imaged cells is nevertheless much larger (dNa+–cation > 19 Å).
The Na2–Na2 interaction energies are in good agreement with the Coulomb energies indicating that electrostatic effects are dominant. However, the cation arrangement also affects the interaction energies when the Na2 ions are in the same coordination environment, i.e., at small Na2–Na2 distances, leading to the largest deviations between the Na2–Na2 interaction energies and the Coulomb energies.
The compositions Na1M2P3O12 with M = Zr4+ (Fig. 4a) and M = Hf4+ (Fig. 4b) exhibit similar pair interaction energies due to the similar ionic radii of r4+Zr = 0.72 Å and r4+Hf = 0.71 Å113 and thus similar cell volumes (Fig. S2†) and bond distances (Table S1†).
In the composition with M = Sn4+ (Fig. 4c) the interaction energies of Na2–Na2 ions at smaller distances are larger than in the compositions with M = Zr4+, Hf4+ but align at larger distances. The volume of the cell with M = Sn4+ is smaller than that of the cells with M = Zr4+, Hf4+ due to the smaller ionic radii of r4+Sn = 0.69 Å (Fig. S2†).113 Therefore, the bond distances in the structure with M = Sn4+ are smaller (Table S2†) which has a stronger effect on the interactions energies the smaller the distances of Na2–Na2 pairs are.
The calculated interaction energies cannot be described sufficiently by the Coulomb energies. Since the SiO4 tetrahedra are part of the structural framework, Si4+ may not be considered a point defect due to its high covalent bonding character. Thus, the pair interaction energies may depend not only on electrostatic effects but also on elastic effects describing deformation or distortions of the lattice, as also observed in doped zirconia114 and ceria.115,116 The elastic effects are expected to be stronger when the Na2–Si distance is small and the coordination environments of the introduced Na+ and Si4+ ion affect each other. With increasing distances, the elastic effects may be less pronounced and differences between interaction and coulombic energies are smaller.
The Na2–Si interaction energies in the compounds with M = Zr4+ (Fig. 5a) and M = Hf4+ (Fig. 5b) agree due to similar structural properties as discussed above. Moreover, Zr4+ and Hf4+ are both transition elements and exhibit the same valence electron configuration of d0.
In comparison, the composition with M = Sn4+ (Fig. 5c) exhibits stronger Na2–Si interactions at a small distance. On the one hand, this can be attributed to the smaller cell volume and thus smaller bond distances as described above. On the other hand, Sn4+ is a main-group element with a different valence electron configuration of d10, which may have an additional impact. Rodrigo et al. stated that unoccupied orbitals as in the compositions with M = Zr4+, Hf4+ exhibiting d0 valence electron configuration allow greater structural flexibility. In contrast, fully occupied d-orbitals as in the compositions with M = Sn4+ lead to more rigid bonds.117 Thus, cells containing d0 M-cations may accommodate substituents with lower energy cost compared to cells with d10 M-cations. Influences of the different electronic structure of the M-cations on structure and crystal symmetry among NaxM4+2−xM3+x(PO4)3 have also been observed in other studies.117–122
In summary, the comparison of NaSCION structures with different M-cations shows that the compounds with M = Zr4+, Hf4+ are not only isovalent but also isostructural, whereas this is not true for the structure with M = Sn4+, which is in agreement with previous studies.117,120,122,123
In our previous approach to determine configurational energies, only Na2–Na2 pairs in a distance up to 5.1 Å and Na2–Si pairs up to 3.7 Å were considered due to the small size of the cell with 168 atoms. We described the pair interaction energies only dependent on the distance by grouping cations according to similar distance from the Na2 ions. The pair interaction energies of Na1+xZr2SixP3−xO12 (0 ≤ x ≤ 3) were fitted according to eqn (12) taking into account 754 configurations whose energies were calculated using DFT.70 However, in this study, we show that Na2–Na2 pairs in distances up to 9.9 Å and Na2–Si pairs in distance up to 8.7 Å affect the configurational energy of the cell. The pair interaction energies depend not only on electrostatic effects but also on the cationic coordination and elastic effects at small Na-cation distances and must be considered to describe the configurational energy accurately. We show that calculating only 50 structures with the least substitution and varying Na2-cation distances is sufficient to individually determine all pair interaction energies that affect the overall configurational energy, and thus be able to predict Econf. Additionally, structures with composition Na4M2Si3O12 (M = Zr4+, Hf4+, Sn4+) in which one P5+ ion was introduced onto a Si4+ site creating one vacancy on Na2 site (VNa) were investigated. By varying the distance between the P5+ and the VNa, the Na+–Si4+ interaction in highly substituted systems can be deduced as the number of corresponding pairs changes. The results show the expected trend for all compositions: The cells in which P5+ is in the nearest neighbour position to VNa are energetically more favourable than the cells in which P5+ and VNa are far apart, implying that the configurational energy is lowered by Si4+ near the Na2 positions (Table S3†).
Overall, despite the computation of larger cells of 578 atoms, this approach can significantly reduce the computational effort and therefore allows the study of NASICON materials with a wide range of compositions.
5.2 Migration energies
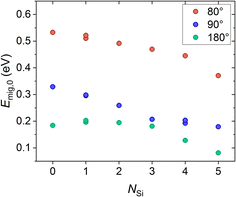
The different migration pathways of about 80°, 90° and 180° were calculated for the unsubstituted (x = 0) and the fully substituted (x = 3) system Na1+xM2SixP3−xO12 (M = Hf4+, Sn4+). The results for Zr4+ are taken from our previous study.70 The energy profiles of the different migration paths in all compositions are shown and discussed in more detail in Section 4 in the ESI.† The migration energies Emig,0 of x = 0 and x = 3 were calculated according to eqn (11) and then predicted for arbitrary substitution concentrations x by linear interpolation according to eqn (13), as shown in Fig. 6. | ||
| Fig. 6 Interpolated migration energies Emig,0 dependent on the subsitution degree x of Na1+xM2SixP3−xO12 with (a) M = Zr4+ (taken from ref. 70), (b) M = Hf4+, (c) M = Sn4+ of the pathway in 80° (red), 90° (blue) and 180° (green) according to eqn (13). | ||
(i) The amount of Si4+ near the migration pathway in the structure Na1Zr2P3O12 (x = 0) was gradually increased to determine the influence of the interactions between the migrating Na+ and surrounding Si4+ on the migration energy. The Si4+ sites to be occupied are illustrated in Fig. S5.†Fig. 7 shows the resulting migration energies dependent on the number of Si4+ near the migration pathway. With increasing Si4+ content the migration energy decreases which is in agreement with the results of Deng et al.53 The attractive interactions between the migrating Na+ ion and the Si4+ substituents seem to lower the migration energy due to the stabilization of the transition state.
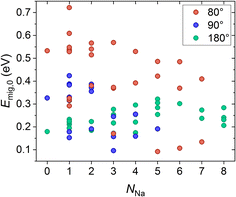
(ii) To determine the influence of the Na+–Na+ interactions on the migration energy, the amount of Na+ near the migrating Na+ ions was gradually increased in the structure Na1Zr2P3O12 (x = 0). The Na+ positions adjacent to the migration pathway are depicted in Fig. S6,† and the resulting migration energies are shown in Fig. 8. There is no clear dependence of the migration energies on the number of Na+ ions near the migration pathway. Again, our results agree with the findings of Deng et al. explaining the non-monotonic behaviour of migration energy in dependence on Na+ concentration by a combination of local electrostatic repulsion and local charge imbalance.53 In addition, our results show that the migration energies may depend on the arrangement of the Na+ ions adjacent to the migration path as explained in detail in Section 5.2 in the ESI.† However, due to the large number of Na+ sites in the lattice structure, it is not feasible to unambiguously describe the influence of Na+ site occupation on the migration energy using DFT calculations.
(iii) During the migration, the Na+ ions pass through different bottlenecks formed by three O2− ions of SiO4/PO4 tetrahedra and ZrO6 octahedra as illustrated in Fig. 9 for the 180° migration path. The bottlenecks A and A′ are located near the Na2 sites, while the bottlenecks B and B′ are located near the Na1 site.68,83,85,90 The four different bottlenecks of the migration path are characterized by the size of their area.90 As shown in Fig. S9,† bottleneck A is the smallest in most cases, consistent with the literature.68,69,89,90 In all compositions the bottleneck areas A and A′ increase for x = 3 compared to x = 0 whereas B and B′ do not change. Larger bottlenecks may facilitate Na+ ion migration resulting in lower migration energy.
In conclusion, our results show that (i) increasing Si4+ concentration lowers the migration energy Emig,0 due to increasing attractive interactions of the migrating Na+ ions and surrounding Si4+ ions stabilizing the transition state, (ii) there is no clear correlation between Emig,0 and the repulsive interactions of the migrating Na+ ions and surrounding Na+ ions, and (iii) Emig,0 may decreases with increasing size of the bottleneck areas A and A′.
At small x, the Na+–O2− bond distances are smaller in M = Sn4+ due to the smaller cell volume. Therefore, the fractional volume of the migrating Na+ ions in M = Sn4+ is smaller than in M = Zr4+, Hf4+, leading to higher steric hindrance and thus higher Emig,0. However, at large x, there are no significant differences in the bond distances of the different compositions (Table S6†).
Moreover, the smaller cell volume in M = Sn4+ leads to smaller bottlenecks (see Fig. S10†) which may also explain the higher migration energies Emig,0 in accordance with the literature.82,89,124 However, at high x, the differences in Emig,0 are small and the results on the effect of the bottleneck on Na+ migration behaviour must be interpreted with caution. Furthermore, Martinez-Juárez et al. have shown that the migration depends strongly on the size of the bottleneck only if it is smaller than the migrating ion, otherwise, it is influenced by the interactions between the migrating ion and the lattice.124
In addition, Sn4+ exhibits a different electronic structure than Zr4+, Hf4+, as mentioned above. The framework of the structures containing d0 transition metals (Zr4+, Hf4+) is more flexible compared to the one with d10 main-group elements (Sn4+), and thus may better accommodate the migrating Na+ ions resulting in lower Emig,0.117 Urban et al. have elucidated that d0 transition metals tolerate site distortion with low energy costs.125 The local geometry may be different depending on the electronic structure, which could additionally modify the geometry of the bottleneck.119,120
6 Investigation at the macroscopic level
KMC simulations were performed based on the DFT-derived energies from the previous section to clarify the influence of composition on Na+ conductivity in Na1+xM2SixP3−xO12 with M = Zr4+, Hf4+, Sn4+ and 0.01 ≤ x ≤ 2.8. As explained before, the simulations require knowledge of the configuration energies predicted by eqn (12) using pair interaction energies individually calculated and the migration energies determined by eqn (13) using the migration energies of the unsubstituted and fully substituted structure (Section 5.2).In our previous study of Na1+xZr2SixP3−xO12, we have already revealed the behaviour of the conductivity and the activation energy is strongly influenced by the local ionic environment of the Na+ sites, as illustrated in Fig. 10.70 The conductivities simulated at 573 K and activation energies of Na1+xZr2SixP3−xO12 obtained in this earlier work are shown in the bottom plot of Fig. 10.70 In the non-substituted structure the migration barrier Emig only depends on the migration energy Emig,0 as the energy landscape is uniform (Fig. 10a). However, due to the introduction of substituents, Emig depends on the migration energy Emig,0 and the configurational energy Econf (Fig. 10b). At small x, Na+ ions are trapped in low energy states near the introduced Si4+ ions due to favourable attractive interactions. The depth of the traps increases with the number of adjacent Si4+ leading to low conductivities and an increase in activation energy. But, with increasing x, percolation paths are formed due to the large number of Si4+ (Fig. 10c), which explains the increase in Na+ conductivity and the decrease in the activation energy. In the fully substituted structure, the energy landscape is uniform and Emig only depends on the migration energy Emig,0 (Fig. 10d). Here, the activation energy is lowest, since Emig,0 decreases with x. However, at very high substitution content, the number of vacant sodium sites is insufficient leading to a decrease in ionic conductivity.
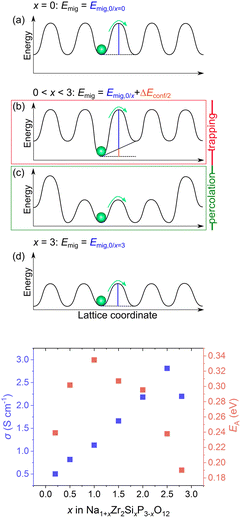 | ||
| Fig. 10 (Top) Energy landscape of Na+ positions and migration barrier Emig in the lattice Na1+xM2SixP3−xO12 dependent on the substitution content x. (a) Non-substituted structure (x = 0) with uniform energy landscape, (b) low substituted structure where Na+ ions are trapped in Si4+ rich environments, (c) high substituted structure where Na+ ions percolate between Si4+ rich environments, (d) fully substituted structure (x = 3) with uniform energy landscape. (Bottom) Resulting ionic conductivity σ at 573 K and activation energy EA in dependence of substitution content x in Na1+xZr2SixP3−xO12. Values are taken from ref. 70. | ||
In this study, we investigate the influence of different M-cations on the Na+ diffusion behaviour in NaSICONs. The Na+ ion conductivities, mobilities, and activation energies obtained from the KMC simulations are discussed below.
Fig. 11 shows the ionic conductivity dependent on x in Na1+xM2SixP3−xO12 with M = Zr4+, Hf4+, Sn4+. As expected, the conductivity increases with temperature in all compositions. The conductivities of the compounds with M = Zr4+ (Fig. 11a) and M = Hf4+ (Fig. 11b) show similar dependence on x as explained above and differ only slightly at higher x due to small differences in the migration energy Emig,0. In both structures, the maximum conductivity is reached at x = 2.5. For M = Sn4+ (Fig. 11c), the ionic conductivities are up to three orders of magnitude lower at small x in accordance with the literature.89,120 In this structure, the attractive Na+–Si4+ interactions are much stronger at small distances resulting in deeper traps of Na+ ions, and the migration energies are higher at small x. The conductivity increases strongly at around 1.0 ≤ x ≤ 1.5 due to the decrease in Emig,0 and reaches the maximum at 2.0 ≤ x ≤ 2.5. Compared to M = Zr4+, Hf4+, the maximum of conductivity is, first, lower by one order of magnitude because the Na+ ions are trapped even at higher substitution levels. Second, the maximum shifts to lower substitution concentration due to the strong Na+–Na+ repulsion, leading to unfavourable Na+ site energies and thus to a sharp decrease in conductivity.
In short, when comparing NaSICONs with different M-cations, the amplitude and maximum of the Na+ conductivity are mainly determined by the Na+–cation pair interactions. This hypothesis is verified by the results of KMC simulations, where the Na+–cation pair interactions are not considered, as shown in Fig. S11.† Here, the conductivities of the composition with M = Sn4+ are only slightly lower compared to those of the composition with M = Zr4+, Hf4+, which is due to the higher migration energies Emig,0.
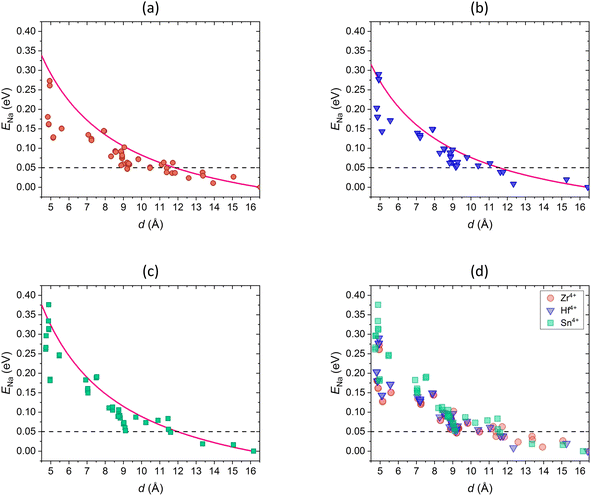
The comparison of conductivities obtained in this work and the total conductivities reported in the literature are shown in Fig. 12. The conductivities of compositions with M = Zr4+ (Fig. 12a) and M = Hf4+ (Fig. 12b) are in good agreement with experimental results at small and intermediate x, but are larger at high x and the maximum shifts to larger x values. However, the literature data scatter widely.9,18,53 The total conductivity is composed of the bulk conductivity and the grain boundary conductivity, the latter being strongly influenced by the sample preparation process.18,26,53,126 Poor microstructure, density, size of grains etc. lead to significantly low grain boundary conductivities, which determine the overall conductivity.53,126 By optimizing the microstructure, and thus decreasing grain boundary resistance, the bulk conductivity gains influence and the total conductivity increases.26,126 Ma et al. revealed that the total conductivity is largely underestimated in literature and reported high bulk conductivity of 1.5 × 10−2 S cm−1 at room temperature for substitution content of x = 2.4 when optimizing the microstructure, which is in agreement with our results.26 It is also worth mentioning that the interpolated migration energies Emig,0 may be underestimated at large x compared to Emig,0 calculated with DFT, as shown in our previous study for Na1+xZr2SixP3−xO12, and thus the conductivities may be overestimated.70 However, the conductivities are in the same order of magnitude and the dependence on the substitution content is described accurately. A similar behaviour was found in a recent study by Deng et al. who investigated the ionic conductivity in Na1+xZr2SixP3−xO12 using KMC simulations based on local-cluster expansion and DFT-NEB migration barriers.53 Moreover, the simulated temperature dependence of the ionic conductivity of M = Hf4+ (Fig. 12c) and M = Sn4+ (Fig. 12d) agrees with experimental values. However, the values reported in different studies for the composition with M = Hf4+ and x = 2.2 also vary, which could be due to similar reasons as those discussed above.127,128 Besides, similar conductivities for the compounds with M = Zr4+, Hf4+ have been reported in previous studies, which coincide with our results.6,120,123,127,129 Overall, the good agreement of our results with the literature data confirms the suitability of this method for studying conductivity in NaSCION-type structures.
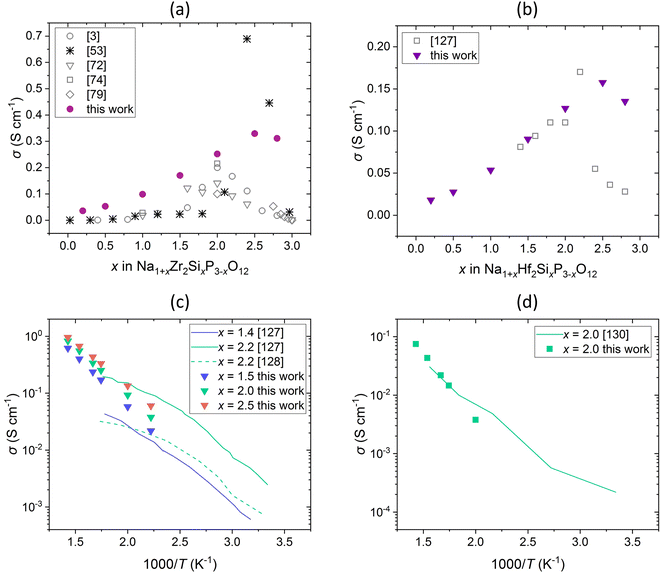 | ||
| Fig. 12 Comparison of Na+ conductivity σ in dependence on (a and b) substitution content x and (c and d) temperature T of Na1+xM2SixP3−xO12 with (a) M = Zr4+, (b and c) M = Hf4+, and (d) M = Sn4+ in 10 × 10 × 10 cells. Literature data of experimental studies3,72,74,79,127,128,130 as well as KMC simulations53 are shown. | ||
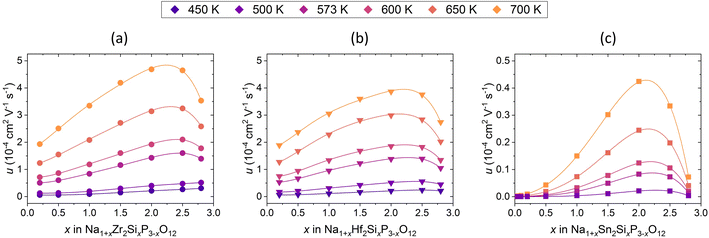
Fig. 13 shows the Na+ ion mobility in Na1+xM2SixP3−xO12 with M = Zr4+, Hf4+, Sn4+ dependent on the substitution level. In this way, the Na+ ion diffusion behaviour is described without considering the increase of the charge carrier. Thus, the assumptions about the effects of the percolation paths formed by Si4+ and the low migration energy at high x are verified. The mobility shows a similar dependence on x as the conductivity. The maximum mobility is observed at 2.0 ≤ x ≤ 2.5 in the compositions with M = Zr4+, Hf4+ and at x = 2 in the composition with M = Sn4+. The differences in the mobility are similar to those for conductivity and can be explained by the stronger attractive Na+–Si4+ and repulsive Na+–Na+ interactions in the structure with M = Sn4+, as described in detail above.
The temperature dependence of the ionic conductivities follows an Arrhenius behaviour (Fig. S12†). Fig. 14a shows the obtained activation energies EA of all investigated Na1+xM2SixP3−xO12 compositions. In the non-substituted and fully substituted composition, EA depends only on Emig,0 as the energy landscape is uniform (see Fig. 10a and d). However, the introduction of substituents leads to states with different energy (see Fig. 10b and c) and EA depends also on the different cationic environments which are considered in the KMC simulations. As explained in Fig. 10, EA is high at small x as Na+ ions are trapped in low energy states. At higher x, EA decreases because Na+ ions percolate between favourable Si4+-rich positions and the migration energy Emig,0 decreases.
 | ||
| Fig. 14 (a) Activation energies EA dependent on substitution content x of Na1+xM2SixP3−xO12 with M = Zr4+ (0.2 ≤ x ≤ 2.8) (red), Hf4+ (0.2 ≤ x ≤ 2.8) (blue), and Sn4+ (0.01 ≤ x ≤ 2.8) (green) obtained from Arrhenius plots (Fig. S12†). (b) Comparison of EA of Na1+xZr2SixP3−xO12 (0.2 ≤ x ≤ 2.8) (orange) with values obtained from experiments (grey)3,72,74 and computational studies (black).53 (c) Comparison of EA of Na1+xHf2SixP3−xO12 (0.2 ≤ x ≤ 2.8) (orange) with values obtained from experiments (grey).120,127,129 | ||
While EA of the compositions Na1+xM2SixP3−xO12 with M = Zr4+, Hf4+ are similar with a maximum around x = 1.0, EA for M = Sn4+ is much higher with a maximum at x ≈ 0.05. This is due to stronger attractive Na+–Si4+ interactions (see Fig. 5) which lead to more effective trapping even for small x. He et al. have elucidated that a locally flat energy landscape and low barriers of the high-energy site, i.e. the Na2 site, facilitates the concerted migration.58 However, due to the stronger Na+–Si4+ interactions in the structure with M = Sn4+, which lowers the Na2 site energy, the local energy landscape becomes less uniform and the energy barriers increase, resulting in higher EA. The EA of all compositions and the differences between them decrease with increasing x, as the decreasing migration energies Emig,0, which have the dominant impact, converge (see Fig. 6). Moreover, the energy landscape becomes more uniform with increasing Si4+ content, with the differences in Na+–Si4+ interactions losing influence on the migration barrier and thus on EA. At a high substitution level, EA of the composition with M = Sn4+ increases slightly caused by highly unfavourable repulsive Na+–Na+ interactions (see Fig. 4) which may increase the Na2 site energy strongly.
As shown in Fig. 14b, the activation energies of Na1+xZr2SixP3−xO12 determined in this study are higher than those obtained from a.c. conductivity measurements and ab initio molecular dynamics simulations, especially at small substitution contents. However, the experimental values vary widely as discussed above. The calculated activation energies of Na1+xHf2SixP3−xO12 are higher than the literature data at intermediate x and agree well at high x, as Fig. 14c shows. In general, the activation energies determined in this work are in reasonable accordance with the literature values. However, there are only a few or strongly fluctuating data in the literature, thus the comparison should be made with caution.
It can be concluded that the Na+ transport properties mainly depend on the trapping of Na+ by the introduced Si4+ at small x, the migration energy Emig,0 at high x, and strong Na+–Na+ repulsion at very high x. The Na+–cation interactions and thus the Na+ transport properties can be influenced by the choice of M cations. Moreover, the ionic conductivity and mobility depend on the ratio of occupied to vacant sodium sites. Thus, our study points out that no simple correlation can be established to describe the ionic conductivity. The maximum of Na+ mobility and conductivity is reached at a high substitution content of 2.0 ≤ x ≤ 2.5 due to low migration energy and optimal ratio of unoccupied to occupied charge carrier sites.
7 Conclusion
We studied the influences of the Si4+ substitution concentration x, M-cation and temperature on Na+ ion transport in the multi-element NaSICON-type structure Na1+xM2SixP3−xO12 (M = Zr4+, Hf4+, Sn4+ and 0 ≤ x ≤ 3). Therefore, we combined accurate DFT calculations and KMC simulations for the investigation at both atomistic and macroscopic levels with affordable computational effort.The DFT calculations show that the Na+ site energy depends on Na+–Na+ interactions resulting mainly from electrostatic effects and Na+–Si4+ interactions resulting from both electrostatic and elastic effects. Lower Na+ and higher Si4+ content in the local environment leads to lower Na+ site energy. However, the size and electronic structure of the M-cation must also be considered when describing the configurational energies. Smaller and more rigid MO6 octahedra result in stronger pair interactions.
Moreover, we have shown that the migration energy Emig,0 depends on various factors for different x: At low x, Emig,0 is mainly influenced by the migration pathway. However, with increasing x, the ions adjacent to the migration path gain influence. Emig,0 decreases with increasing Si4+ concentration because of favourable attractive interactions of the migrating Na+ ions and surrounding Si4+ ions. In addition, the increasing size of the bottleneck may lower Emig,0. Furthermore, Emig,0 depends on the M-cation. The size of the M-cation affects the size of the bottleneck, and the electronic structure of the M-cation affects the flexibility of the structural framework. Smaller bottlenecks and more rigid MO6 octahedra may increase Emig,0 and could explain the highest values for compositions with M = Sn4+.
Based on DFT-derived energies, we performed KMC simulations to investigate the macroscopic Na+ conductivity. Using Na1+xM2SixP3−xO12 as an example, we showed that the Na+ transport properties in NaSICON structures are determined by (i) the Na+ trapping by introduced Si4+ at small x, (ii) the migration energy Emig,0 at intermediate to high x, and (iii) the availability of vacant Na+ site as well as the Na+–Na+ repulsion at very high x. Thus, the conductivity of compositions with M = Zr4+, Hf4+ reaches the maximum at x = 2.5 due to percolation pathways formed by Si4+ rich environments, low Emig,0 and optimal density of charge carrier sites. For the composition with M = Sn4+, the ionic conductivities are significantly lower because of the stronger attractive Na+–Si4+ interactions which form deeper traps for the Na+ ions. In addition, the conductivity maximum is shifted to lower substitution concentrations of 2.0 ≤ x ≤ 2.5 due to the stronger Na+–Na+ repulsion leading to unfavourable Na+ site energies and thus to a sharp decrease in conductivity at high x.
The resulting activation energies depend on the local cationic environments of the Na+ sites. EA is high at small x because the Na+ ions are trapped in low energy states, whereas EA decreases at higher x due to the Na+ percolation between favourable Si4+ rich positions as well as the decrease of Emig,0. The activation energy of the composition with M = Sn4+ is higher and the maximum appears at lower x compared to the compositions with M = Zr4+ and Hf4+ because of the more effective trapping due to stronger attractive Na+–Si4+ interactions.
Our results show that the Na+ ion transport in NaSICONs can be modified by different cation substitution strategies in the host lattice Na1M2PO12.
A rising number of Na+ ions supports the correlated ionic migration as high energy sites are occupied, and also leads to an increase in ionic conductivity. One way to adjust the concentration of the Na+ charge carrier is to incorporate excess Na+ into the NaSICON compounds. Indeed, few studies have investigated the influences of excess Na+ in NaSICONs90,91,131–133 revealing that conductivity increases and activation energy decreases, based on the increase in Na+ charge carrier91,133 and enhanced mobility by the widening of the bottlenecks.90,133
The amount of Na+ charge carrier can also be modified when the M4+ and P5+ sites are substituted with cations with various valence. As shown in this study, the substitution with subvalent cations leads not only to the increase in Na+ concentration but also to the decrease in Na+ ion migration energy due to the lower electrostatic repulsion with the migrating Na+ ions. Therefore, the introduction of divalent or trivalent substituents could potentially further increase the Na+ ion conductivity in NaSICONs. However, subvalent substituents could also cause a stronger trapping effect which in turn decreases the Na+ ion mobility.
Furthermore, iso- and aliovalent substituents with bigger ionic sizes could enlarge the cell volume and thus the bottlenecks, possibly leading to an increase in Na+ ion mobility.
Various studies have shown that the aliovalent substitution of M4+ by divalent cations, such as Mg2+,22,66,134–138 Zn2+,32,139,140 Co2+,139 Ca2+,29,141 and trivalent cations, such as In3+,119,142,143 Sc3+,92,119,143–147 Y3+,139,140,143,148 La3+,24,148 Pr3+, Eu3+, Lu3+,149 improves the Na+ mobility and conductivity due to an increase in Na+ ions coupled with enhanced correlated Na+ ion migration but also due to the modification of the phase purity and microstructure of the ceramics.
Based on our results, another way to optimize the Na+ ion transport in NaSICONS could be to completely substitute P5+ ions by Si4+ ions while introducing M5+ ions to ensure that sufficient unoccupied Na+ sites are available. Supervalent M-substitution in NaSICONs materials has been poorly investigated, but studies of Na1+x−yMyZr2−ySixP3−xO12 with M5+ = V, Nb, Ta show promising conductivities up to 5.5 × 10−3 S cm−1 for Na3.3Zr1.9Nb0.1Si2.4P0.6O12.135,140,150
Additionally, the Na+ ion mobility can be influenced by Na+–cation interactions, which are determined by the valence electron configuration of the M cations. In this study, we have shown that d0 valence orbitals induce weaker Na+–cation interactions compared to d10 valence orbitals, resulting in weaker Na+ ion trapping and thus higher Na+ ion mobility. Thus, the introduction of M cations exhibiting d0 valence electron configuration, such as Mg2+, Sc3+, Ce4+, V5+, appears to provide a sound strategy to optimize the Na+ ion mobility.
In summary, the method proposed in this study is suitable to investigate various NaSCION compositions over large length and time scales with low computational effort. Our results provide a comprehensive explanation of the Na+ diffusion behaviour in NaSICONs to optimize the ionic conductivity.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the computing time provided to them at the NHR Center NHR4CES at RWTH Aachen University (project number p0020107). This is funded by the Federal Ministry of Education and Research, and the state governments participating on the basis of the resolutions of the GWK for national high-performance computing at universities (https://www.nhr-verein.de/unsere-partner).References
- L.-O. Hagman, P. Kierkegaard, P. Karvonen, A. I. Virtanen and J. Paasivirta, The crystal structure of NaMe2IV(PO4)3; MeIV=Ge, Ti, Zr, Acta Chem. Scand., 1968, 22, 1822–1832 CrossRef CAS
.
- H.-P. Hong, Crystal structures and crystal chemistry in the system Na1+xZr2SixP3−xO12, Mater. Res. Bull., 1976, 11, 173–182 CrossRef CAS
.
- J. B. Goodenough, H.-P. Hong and J. A. Kafalas, Fast Na+-ion transport in skeleton structures, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS
.
- J. Alamo and R. Roy, Crystal chemistry of the NaZr2(PO4)3, NZP or CTP, structure family, J. Mater. Sci., 1986, 21, 444–450 CrossRef CAS
.
- N. Anantharamulu, K. Koteswara Rao, G. Rambabu, B. Vijaya Kumar, V. Radha and M. Vithal, A wide-ranging review on NASICON type materials, J. Mater. Sci., 2011, 46, 2821–2837 CrossRef CAS
.
- M. Guin and F. Tietz, Survey of the transport properties of sodium superionic conductor materials for use in sodium batteries, J. Power Sources, 2015, 273, 1056–1064 CrossRef CAS
.
- R. Rajagopalan, Z. Zhang, Y. Tang, C. Jia, X. Ji and H. Wang, Understanding crystal structures, ion diffusion mechanisms and sodium storage behaviors of NASICON materials, Energy Storage Mater., 2021, 34, 171–193 CrossRef
.
- Z. Yang, B. Tang, Z. Xie and Z. Zhou, NASICON-type Na3Zr2Si2PO12 solid-state electrolytes for sodium batteries, ChemElectroChem, 2021, 8, 1035–1047 CrossRef CAS
.
- Y. B. Rao, K. K. Bharathi and L. N. Patro, Review on the synthesis and doping strategies in enhancing the Na ion conductivity of Na3Zr2Si2PO12 (NASICON) based solid electrolytes, Solid State Ionics, 2021, 366, 115671 CrossRef
.
- C. Li, R. Li, K. Liu, R. Si, Z. Zhang and Y.-S. Hu, NASICON: A promising solid electrolyte for solid-state sodium batteries, Interdiscip. Mater., 2022, 1, 396–416 CrossRef
.
- L. Zhang, Y. Liu, Y. You, A. Vinu and L. Mai, NASICONs-type solid-state electrolytes: The history, physicochemical properties, and challenges, Interdiscip. Mater., 2022, 2, 91–110 CrossRef
.
- K. Singh, A. Chakraborty, R. Thirupathi and S. Omar, Recent advances in NASICON-type oxide electrolytes for solid-state sodium-ion rechargeable batteries, Ionics, 2022, 28, 1–31 CrossRef
.
- C. Jiang, H. Li and C. Wang, Recent progress in solid-state electrolytes for alkali-ion batteries, Sci. Bull., 2017, 62, 1473–1490 CrossRef CAS PubMed
.
- W. Hou, X. Guo, X. Shen, K. Amine, H. Yu and J. Lu, Solid electrolytes and interfaces in all-solid-state sodium batteries: Progress and perspective, Nano Energy, 2018, 52, 279–291 CrossRef CAS
.
- C. Zhao, L. Liu, X. Qi, Y. Lu, F. Wu, J. Zhao, Y. Yu, Y.-S. Hu and L. Chen, Solid-state sodium batteries, Adv. Energy Mater., 2018, 8, 1703012 CrossRef
.
- C. Zhou, S. Bag and V. Thangadurai, Engineering materials for progressive all-solid-state Na batteries, ACS Energy Lett., 2018, 3, 2181–2198 CrossRef CAS
.
- L. Fan, S. Wei, S. Li, Q. Li and Y. Lu, Recent progress of the solid-state electrolytes for high-energy metal-based batteries, Adv. Energy Mater., 2018, 8, 1702657 CrossRef
.
- Q. Ma and F. Tietz, Solid-state electrolyte materials for sodium batteries: Towards practical applications, ChemElectroChem, 2020, 7, 2693–2713 CrossRef CAS
.
- V. Thangadurai and B. Chen, Solid Li-and Na-ion electrolytes for next generation rechargeable
batteries, Chem. Mater., 2022, 34, 6637–6658 CrossRef CAS
.
- Y. Noguchi, E. Kobayashi, L. S. Plashnitsa, S. Okada and J. Yamaki, Fabrication and performances of all solid-state symmetric sodium battery based on NASICON-related compounds, Electrochim. Acta, 2013, 101, 59–65 CrossRef CAS
.
- F. Lalère, J.-B. Leriche, M. Courty, S. Boulineau, V. Viallet, C. Masquelier and V. Seznec, An all-solid state NASICON sodium battery operating at 200°C, J. Power Sources, 2014, 247, 975–980 CrossRef
.
- S. Song, H. M. Duong, A. M. Korsunsky, N. Hu and L. Lu, A Na+ superionic conductor for room-temperature sodium batteries, Sci. Rep., 2016, 6, 1–10 CrossRef PubMed
.
- W. Zhou, Y. Li, S. Xin and J. B. Goodenough, Rechargeable sodium all-solid-state battery, ACS Cent. Sci., 2017, 3, 52–57 CrossRef CAS PubMed
.
- Z. Zhang, Q. Zhang, J. Shi, Y. S. Chu, X. Yu, K. Xu, M. Ge, H. Yan, W. Li and L. Gu, A self-forming composite electrolyte for solid-state sodium battery with ultralong cycle life, Adv. Energy Mater., 2017, 7, 1601196 CrossRef
.
- T. Lan, C.-L. Tsai, F. Tietz, X.-K. Wei, M. Heggen, R. E. Dunin-Borkowski, R. Wang, Y. Xiao, Q. Ma and O. Guillon, Room-temperature all-solid-state sodium batteries with robust ceramic interface between rigid electrolyte and electrode materials, Nano Energy, 2019, 65, 104040 CrossRef CAS
.
- Q. Ma, C.-L. Tsai, X.-K. Wei, M. Heggen, F. Tietz and J. T. S. Irvine, Room temperature demonstration of a sodium superionic conductor with grain conductivity in excess of 0.01 S cm−1 and its primary applications in symmetric battery cells, J. Mater. Chem. A, 2019, 7, 7766–7776 RSC
.
- P. Kehne, C. Guhl, Q. Ma, F. Tietz, L. Alff, R. Hausbrand and P. Komissinskiy, Electrochemical performance of all-solid-state sodium-ion model cells with crystalline NaxCoO2 thin-film cathodes, J. Electrochem. Soc., 2019, 166, A5328 CrossRef CAS
.
- P. Kehne, C. Guhl, Q. Ma, F. Tietz, L. Alff, R. Hausbrand and P. Komissinskiy, Sc-substituted NASICON solid electrolyte for an all-solid-state NaxCoO2/Nasicon/Na sodium model battery with stable electrochemical performance, J. Power Sources, 2019, 409, 86–93 CrossRef CAS
.
- Y. Lu, J. A. Alonso, Q. Yi, L. Lu, Z. L. Wang and C. Sun, A high-performance monolithic solid-state sodium battery with Ca2+ doped Na3Zr2Si2PO12 electrolyte, Adv. Energy Mater., 2019, 9, 1901205 CrossRef
.
- E. Matios, H. Wang, C. Wang, X. Hu, X. Lu, J. Luo and W. Li, Graphene regulated ceramic electrolyte for solid-state sodium metal battery with superior electrochemical stability, ACS Appl. Mater. Interfaces, 2019, 11, 5064–5072 CrossRef CAS PubMed
.
- Z. Zhang, S. Wenzel, Y. Zhu, J. Sann, L. Shen, J. Yang, X. Yao, Y.-S. Hu, C. Wolverton and H. Li, Na3Zr2Si2PO12: A stable Na+-ion solid electrolyte for solid-state batteries, ACS Appl. Energy Mater., 2020, 3, 7427–7437 CrossRef CAS
.
- J. Yang, G. Liu, M. Avdeev, H. Wan, F. Han, L. Shen, Z. Zou, S. Shi, Y.-S. Hu and C. Wang, Ultrastable all-solid-state sodium rechargeable batteries, ACS Energy Lett., 2020, 5, 2835–2841 CrossRef CAS
.
- X. Wang, W. Mei, J. Chen, D. Wang and Z. Mao, Rare earth oxide-assisted sintered NASICON electrolyte composed of a phosphate grain boundary phase with low electronic conductivity, ACS Appl. Energy Mater., 2021, 5, 777–783 CrossRef
.
- B. Dunn, H. Kamath and J.-M. Tarascon, Electrical energy storage for the grid: A battery of choices, Science, 2011, 334, 928–935 CrossRef CAS PubMed
.
- B. L. Ellis and L. F. Nazar, Sodium and sodium-ion energy storage batteries, Curr. Opin. Solid State Mater. Sci., 2012, 16, 168–177 CrossRef CAS
.
- V. Palomares, P. Serras, I. Villaluenga, K. B. Hueso, J. Carretero-González and T. Rojo, Na-ion batteries, recent advances and present challenges to become low cost energy storage systems, Energy Environ. Sci., 2012, 5, 5884–5901 RSC
.
- M. D. Slater, D. Kim, E. Lee and C. S. Johnson, Sodium-ion batteries, Adv. Funct. Mater., 2013, 23, 947–958 CrossRef CAS
.
- H. Pan, Y.-S. Hu and L. Chen, Room-temperature stationary sodium-ion batteries for large-scale electric energy storage, Energy Environ. Sci., 2013, 6, 2338–2360 RSC
.
- S. Y. Hong, Y. Kim, Y. Park, A. Choi, N.-S. Choi and K. T. Lee, Charge carriers in rechargeable batteries: Na ions vs. Li ions, Energy Environ. Sci., 2013, 6, 2067–2081 RSC
.
- N. Yabuuchi, K. Kubota, M. Dahbi and S. Komaba, Research development on sodium-ion batteries, Chem. Rev., 2014, 114, 11636–11682 CrossRef CAS PubMed
.
- D. Larcher and J.-M. Tarascon, Towards greener and more sustainable batteries for electrical energy storage, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed
.
- D. Kundu, E. Talaie, V. Duffort and L. F. Nazar, The emerging chemistry of sodium ion batteries for electrochemical energy storage, Angew. Chem., Int. Ed., 2015, 54, 3431–3448 CrossRef CAS PubMed
.
- J.-Y. Hwang, S.-T. Myung and Y.-K. Sun, Sodium-ion batteries: Present and future, Chem. Soc. Rev., 2017, 46, 3529–3614 RSC
.
- C. Vaalma, D. Buchholz, M. Weil and S. Passerini, A cost and resource analysis of sodium-ion batteries, Nat. Rev. Mater., 2018, 3, 1–11 CrossRef
.
- C. Delmas, Sodium and sodium-ion batteries: 50 years of research, Adv. Energy Mater., 2018, 8, 1703137 CrossRef
.
- L. Chen, M. Fiore, J. E. Wang, R. Ruffo, D.-K. Kim and G. Longoni, Readiness level of sodium-ion battery technology: A materials review, Adv. Sustainable Syst., 2018, 2, 1700153 CrossRef
.
- T. Liu, Y. Zhang, Z. Jiang, X. Zeng, J. Ji, Z. Li, X. Gao, M. Sun, Z. Lin and M. Ling, Exploring competitive features of stationary sodium ion batteries for electrochemical energy storage, Energy Environ. Sci., 2019, 12, 1512–1533 RSC
.
- Y. E. Durmus, H. Zhang, F. Baakes, G. Desmaizieres, H. Hayun, L. Yang, M. Kolek, V. Küpers, J. Janek and D. Mandler, Side by side battery technologies with lithium-ion based batteries, Adv. Energy Mater., 2020, 10, 2000089 CrossRef CAS
.
- H. Che, S. Chen, Y. Xie, H. Wang, K. Amine, X.-Z. Liao and Z.-F. Ma, Electrolyte design strategies and research progress for room-temperature sodium-ion batteries, Energy Environ. Sci., 2017, 10, 1075–1101 RSC
.
- T. Famprikis, P. Canepa, J. A. Dawson, M. S. Islam and C. Masquelier, Fundamentals of inorganic solid-state electrolytes for batteries, Nat. Mater., 2019, 18, 1278–1291 CrossRef CAS PubMed
.
- D. H. S. Tan, A. Banerjee, Z. Chen and Y. S. Meng, From nanoscale interface characterization to sustainable energy storage using all-solid-state batteries, Nat. Nanotechnol., 2020, 15, 170–180 CrossRef CAS PubMed
.
- Y. Wang, S. Song, C. Xu, N. Hu, J. Molenda and L. Lu, Development of solid-state electrolytes for sodium-ion battery–A short review, NanoMater. Sci., 2019, 1, 91–100 Search PubMed
.
- Z. Deng, T. P. Mishra, E. Mahayoni, Q. Ma, A. J. K. Tieu, O. Guillon, J.-N. Chotard, V. Seznec, A. K. Cheetham and C. Masquelier, Fundamental investigations on the sodium-ion transport properties of mixed polyanion solid-state battery electrolytes, Nat. Commun., 2022, 13, 1–14 Search PubMed
.
- Y. Gao, A. M. Nolan, P. Du, Y. Wu, C. Yang, Q. Chen, Y. Mo and S.-H. Bo, Classical and emerging characterization techniques for investigation of ion transport mechanisms in crystalline fast ionic conductors, Chem. Rev., 2020, 120, 5954–6008 CrossRef CAS PubMed
.
- P. Canepa, Pushing forward simulation techniques of ion transport in ion conductors for energy materials, ACS Mater. Au, 2023, 3, 75–82 CrossRef CAS
.
- M. Bianchini, V. Lacivita, D.-H. Seo and H. Kim, Advances and challenges in multiscale characterizations and analyses for battery materials, J. Mater. Res., 2022, 37, 1–17 CrossRef
.
- A. van der Ven, Z. Deng, S. Banerjee and S. P. Ong, Rechargeable alkali-ion battery materials: Theory and computation, Chem. Rev., 2020, 120, 6977–7019 CrossRef CAS PubMed
.
- X. He, Y. Zhu and Y. Mo, Origin of fast ion diffusion in super-ionic conductors, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed
.
- B. Ouyang, J. Wang, T. He, C. J. Bartel, H. Huo, Y. Wang, V. Lacivita, H. Kim and G. Ceder, Synthetic accessibility and stability rules of NASICONs, Nat. Commun., 2021, 12, 1–11 CrossRef PubMed
.
- P. P. Kumar and S. Yashonath, A full interionic potential for Na1+xZr2SixP3−xO12 superionic conductors, J. Am. Chem. Soc., 2002, 124, 3828–3829 CrossRef CAS PubMed
.
- P. P. Kumar and S. Yashonath, Structure, conductivity, and ionic motion in Na1+xZr2SixP3−xO12: A simulation study, J. Phys. Chem. B, 2002, 106, 7081–7089 CrossRef CAS
.
- S. Roy and P. Padma Kumar, Framework flexibility of sodium zirconium phosphate: Role of disorder, and polyhedral distortions from Monte Carlo investigation, J. Mater. Sci., 2012, 47, 4946–4954 CrossRef CAS
.
- S. Roy and P. P. Kumar, Influence of Si/P ordering on Na+ transport in NASICONs, Phys. Chem. Chem. Phys., 2013, 15, 4965–4969 RSC
.
- S. Roy and P. P. Kumar, Influence of cationic ordering on ion transport in NASICONs: Molecular dynamics study, Solid State Ionics, 2013, 253, 217–222 CrossRef CAS
.
- K. M. Bui, D. an van, S. Okada and T. Ohno, Na-ion diffusion in a NASICON-type solid electrolyte: A density functional study, Phys. Chem. Chem. Phys., 2016, 18, 27226–27231 RSC
.
- Z. Zhang, Z. Zou, K. Kaup, R. Xiao, S. Shi, M. Avdeev, Y.-S. Hu, D. Wang, B. He and H. Li, Correlated migration invokes higher Na+-ion conductivity in NASICON-type solid electrolytes, Adv. Energy Mater., 2019, 9, 1902373 CrossRef CAS
.
- Z. Deng, G. Sai Gautam, S. K. Kolli, J.-N. Chotard, A. K. Cheetham, C. Masquelier and P. Canepa, Phase behavior in rhombohedral NASICON electrolytes and electrodes, Chem. Mater., 2020, 32, 7908–7920 CrossRef CAS
.
- Z. Zou, N. Ma, A. Wang, Y. Ran, T. Song, Y. Jiao, J. Liu, H. Zhou, W. Shi and B. He, Relationships between Na+ distribution, concerted migration, and diffusion properties in rhombohedral NASICON, Adv. Energy Mater., 2020, 10, 2001486 CrossRef CAS
.
- Z. Zou, N. Ma, A. Wang, Y. Ran, T. Song, B. He, A. Ye, P. Mi, L. Zhang and H. Zhou, Identifying migration channels and bottlenecks in monoclinic NASICON-type solid electrolytes with hierarchical ion-transport algorithms, Adv. Funct. Mater., 2021, 31, 2107747 CrossRef CAS
.
- J. Schuett, F. Pescher and S. Neitzel-Grieshammer, The origin of high Na+ ion conductivity in Na1+xZr2SixP3−xO12 NASICON materials, Phys. Chem. Chem. Phys., 2022, 24, 22154–22167 RSC
.
- M. Avdeev, Crystal chemistry of NASICONs: Ideal framework, distortion, and connection to properties, Chem. Mater., 2021, 33, 7620–7632 CrossRef CAS
.
- J. P. Boilot, J. P. Salanie, G. Desplanches and D. Le Potier, Phase transformation in Na1+xSixZr2P3−xO12 compounds, Mater. Res. Bull., 1979, 14, 1469–1477 CrossRef CAS
.
- J.-J. Didisheim, E. Prince and B. J. Wuensch, Neutron Rietveld analysis of structural changes in NASICON solid solutions Na1+xZr2SixP3−xO12 at elevated temperatures: x = 1.6 and 2.0 at 320 °C, Solid State Ionics, 1986, 18, 944–958 CrossRef
.
- W. H. Baur, J. R. Dygas, D. H. Whitmore and J. Faber, Neutron powder diffraction study and ionic conductivity of Na2Zr2SiP2O12 and Na3Zr2Si2PO12, Solid State Ionics, 1986, 18, 935–943 CrossRef
.
- J. P. Boilot, G. Collin and P. Colomban, Crystal structure of the true NASICON: Na3Zr2Si2PO12, Mater. Res. Bull., 1987, 22, 669–676 CrossRef CAS
.
- J.-P. Boilot, G. Collin and P. Colomban, Relation structure-fast ion conduction in the NASICON solid solution, J. Solid State Chem., 1988, 73, 160–171 CrossRef CAS
.
- U. von Alpen, M. F. Bell and W. Wichelhaus, Phase transition in NASICON (Na3Zr2Si2PO12), Mater. Res. Bull., 1979, 14, 1317–1322 CrossRef CAS
.
- T. Feist, P. K. Davies and E. Vogel, The energetics of phase transitions in the system Na1+xZr2SixP3−xO12, 1.9 ≤ x ≤ 2.5, Thermochim. Acta, 1986, 106, 57–61 CrossRef CAS
.
- D. T. Qui, J. J. Capponi, J. C. Joubert and R. D. Shannon, Crystal structure and ionic conductivity in Na4Zr2Si3O12, J. Solid State Chem., 1981, 39, 219–229 CrossRef CAS
.
- C. Delmas, R. Olazcuaga, G. Le Flem, P. Hagenmuller, F. Cherkaoui and R. Brochu, Crystal chemistry of the Na1+xZr2−xLx(PO4)3 (L=Cr, In, Yb) solid solutions, Mater. Res. Bull., 1981, 16, 285–290 CrossRef CAS
.
- B. J. Wuensch, L. J. Schioler and E. Prince, Relation between structure and conductivity in the NASICON solid solution system, High Temp. Solid Oxide Electrolytes, 1983, 2, 59–74 Search PubMed
.
- J. J. Shi, G. Q. Yin, L. M. Jing, J. Guan, M. P. Wu, Y. L. Zhou, H. L. Lou and Z. Wang, Lithium and sodium diffusion in solid electrolyte materials of AM2(PO4)3 (A=Li, Na, M=Ti, Sn and Zr), Int. J. Mod. Phys. B, 2014, 28, 1450176 CrossRef CAS
.
- F. Cherkaoui, G. Villeneuve, C. Delmas and P. Hagenmuller, Sodium motion in the NASICON related Na1+xZr2−xInx(PO4)3 solid solution: An NMR study, J. Solid State Chem., 1986, 65, 293–300 CrossRef CAS
.
- H. Kohler, H. Schulz and O. Melnikov, Composition and conduction mechanism of the NASICON structure X-ray diffraction study on two crystals at different temperatures, Mater. Res. Bull., 1983, 18, 1143–1152 CrossRef CAS
.
- H. Kohler and H. Schulz, NASICON solid electrolytes part I: The Na+-diffusion path and its relation to the structure, Mater. Res. Bull., 1985, 20, 1461–1471 CrossRef CAS
.
- H. Kohler and H. Schulz, NASICON solid electrolytes part II-X-ray diffraction experiments on sodium-zirconium-phosphate single crystals at 295K and at 993K, Mater. Res. Bull., 1986, 21, 23–31 CrossRef CAS
.
- S. H. Jacobson, M. A. Ratner and A. Nitzan, Stoichiometry-dependent conductivity in framework ionic conductors, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 1580 CrossRef CAS
.
- S. H. Jacobson, A. Nitzan and M. A. Ratner, A stochastic Langevin dynamics study of correlated ionic motion in one dimensional solid electrolytes, J. Chem. Phys., 1980, 72, 3712–3719 CrossRef CAS
.
- E. R. Losilla, M. A. G. Aranda, S. Bruque, M. A. París, J. Sanz and A. R. West, Understanding Na mobility in NASICON materials: A Rietveld, 23Na and 31P MAS NMR, and impedance study, Chem. Mater., 1998, 10, 665–673 CrossRef CAS
.
- H. Park, K. Jung, M. Nezafati, C.-S. Kim and B. Kang, Sodium ion diffusion in Nasicon (Na3Zr2Si2PO12) solid electrolytes: Effects of excess sodium, ACS Appl. Mater. Interfaces, 2016, 8, 27814–27824 CrossRef CAS PubMed
.
- S. Naqash, F. Tietz, E. Yazhenskikh, M. Müller and O. Guillon, Impact of sodium excess on electrical conductivity of Na3Zr2Si2PO12+xNa2O ceramics, Solid State Ionics, 2019, 336, 57–66 CrossRef CAS
.
- Q. Ma, M. Guin, S. Naqash, C.-L. Tsai, F. Tietz and O. Guillon, Scandium-substituted Na3Zr2(SiO4)2(PO4) prepared by a solution-assisted solid-state reaction method as sodium-ion conductors, Chem. Mater., 2016, 28, 4821–4828 CrossRef CAS
.
- P. Hohenberg and W. Kohn, Inhomogeneous electron gas, Phys. Rev., 1964, 136, B864 CrossRef
.
- W. Kohn and L. J. Sham, Self-consistent equations including exchange and correlation effects, Phys. Rev., 1965, 140, A1133 CrossRef
.
- G. Kresse and J. Hafner, Ab initio molecular dynamics for liquid metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558 CrossRef CAS PubMed
.
- G. Kresse and J. Hafner, Norm-conserving and ultrasoft pseudopotentials for first-row and transition elements, J. Phys.: Condens. Matter, 1994, 6, 8245 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS
.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed
.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed
.
- H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188 CrossRef
.
- S. Baroni, P. Giannozzi and A. Testa, Green’s-function approach to linear response in solids, Phys. Rev. Lett., 1987, 58, 1861 CrossRef CAS PubMed
.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515 CrossRef CAS
.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Linear optical properties in the projector-augmented wave methodology, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 45112 CrossRef
.
-
H. Jónsson, G. Mills and K. W. Jacobsen, in Classical and Quantum Dynamics in Condensed Phase Simulations, World Scientific, 1998, pp. 385–404 Search PubMed
.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, A climbing image nudged elastic band method for finding saddle points and minimum energy paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS
.
- G. Henkelman and H. Jónsson, Improved tangent estimate in the nudged elastic band method for finding minimum energy paths and saddle points, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS
.
- C. C. Battaile, The kinetic Monte Carlo method: Foundation, implementation, and application, Comput. Methods Appl. Mech. Eng., 2008, 197, 3386–3398 CrossRef
.
- S. Eisele and S. Grieshammer, MOCASSIN: Metropolis and kinetic Monte Carlo for solid electrolytes, J. Comput. Chem., 2020, 41, 2663–2677 CrossRef CAS PubMed
.
- A. van der Ven, G. Ceder, M. Asta and P. D. Tepesch, First-principles theory of ionic diffusion with nondilute carriers, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 184307 CrossRef
.
- G. H. Vineyard, Frequency factors and isotope effects in solid state rate processes, J. Phys. Chem. Solids, 1957, 3, 121–127 CrossRef CAS
.
- A. van der Ven, J. C. Thomas, B. Puchala and A. R. Natarajan, First-principles statistical mechanics of multicomponent crystals, Annu. Rev. Mater. Res., 2018, 48, 27–55 CrossRef CAS
.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef
.
- A. Bogicevic and C. Wolverton, Nature and strength of defect interactions in cubic stabilized zirconia, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 24106 CrossRef
.
- D. A. Andersson, S. I. Simak, N. V. Skorodumova, I. A. Abrikosov and B. Johansson, Optimization of ionic conductivity in doped ceria, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3518–3521 CrossRef CAS PubMed
.
- S. Grieshammer, B. O. H. Grope, J. Koettgen and M. Martin, A combined DFT+U and Monte Carlo study on rare earth doped ceria, Phys. Chem. Chem. Phys., 2014, 16, 9974–9986 RSC
.
- J. L. Rodrigo and J. Alamo, Phase transition in NaSn2(PO4)3 and thermal expansion of NaM2IV(PO4)3; MIV=Ti, Sn, Zr, Mater. Res. Bull., 1991, 26, 475–480 CrossRef CAS
.
- P. Tarte, A. Rulmont and C. Merckaert-Ansay, Vibrational spectrum of NASICON-like, rhombohedral orthophosphates MIMIV2(PO4)3, Spectrochim. Acta, Part A, 1986, 42, 1009–1016 CrossRef
.
- J. M. Winand, A. Rulmont and P. Tarte, Ionic conductivity of the Na1+xMxIIIZr2−x(PO4)3 systems (M=Al, Ga, Cr, Fe, Sc, In, Y, Yb), J. Mater. Sci., 1990, 25, 4008–4013 CrossRef CAS
.
- J.-M. Winand, A. Rulmont and P. Tarte, Nouvelles solutions solides LI(MIV)2−x(NIV)x(PO4)3 (L=Li, Na M, N=Ge, Sn, Ti, Zr, Hf) synthèse et étude par diffraction x et conductivité ionique, J. Solid State Chem., 1991, 93, 341–349 CrossRef CAS
.
- J. Alamo, Chemistry and properties of solids with the [NZP] skeleton, Solid State Ionics, 1993, 63, 547–561 CrossRef
.
- M. P. Carrasco, M. C. Guillem and J. Alamo, Synthesis and structural study of NaTi2(PO4)3-NaSn2(PO4)3 solid solutions. I. The effect of composition on lattice parameters, Mater. Res. Bull., 1992, 27, 603–610 CrossRef CAS
.
- R. J. Cava, E. M. Vogel and D. W. Johnson Jr, Effect of homovalent framework cation substitutions on the sodium ion conductivity in Na3Zr2Si2PO12, J. Am. Ceram. Soc., 1982, 65, c157–c159 CrossRef CAS
.
- A. Martinez-Juarez, C. Pecharromán, J. E. Iglesias and J. M. Rojo, Relationship between activation energy and bottleneck size for Li+ ion conduction in NASICON materials of composition LiMM‘(PO4)3; M, M‘=Ge, Ti, Sn, Hf, J. Phys. Chem. B, 1998, 102, 372–375 CrossRef CAS
.
- A. Urban, A. Abdellahi, S. Dacek, N. Artrith and G. Ceder, Electronic-structure
origin of cation disorder in transition-metal oxides, Phys. Rev. Lett., 2017, 119, 176402 CrossRef PubMed
.
- S. Naqash, D. Sebold, F. Tietz and O. Guillon, Microstructure–conductivity relationship of Na3Zr2(SiO4)2(PO4) ceramics, J. Am. Ceram. Soc., 2019, 102, 1057–1070 CrossRef CAS
.
- E. M. Vogel, R. J. Cava and E. Rietman, Na+ ion conductivity and crystallographic cell characterization in the Hf-NASICON system Na1+xHf2SixP3−xO12, Solid State Ionics, 1984, 14, 1–6 CrossRef CAS
.
- Q. Sun, L. Dai, Y. Tang, J. Sun, W. Meng, T. Luo, L. Wang and S. Liu, Designing a novel electrolyte Na3.2Hf2Si2.2P0.8O11.85F0.3 for all-solid-state Na-O2 batteries, Small Methods, 2022, 6, 2200345 CrossRef CAS PubMed
.
- H. Aono and E. Suginoto, Ionic conductivity and sinterability of NASICON-type ceramics: The systems NaM2(PO4)3+yNa2O (M=Ge, Ti, Hf, and Zr), J. Am. Ceram. Soc., 1996, 79, 2786–2788 CrossRef CAS
.
- P. Yadav and M. C. Bhatnagar, Preparation, structure and conductivity of Sn modified NASICON material, J. Electroceram., 2013, 30, 145–151 CrossRef CAS
.
- N. S. Bell, C. Edney, J. S. Wheeler, D. Ingersoll and E. D. Spoerke, The influences of excess sodium on low-temperature NASICON synthesis, J. Am. Ceram. Soc., 2014, 97, 3744–3748 CrossRef CAS
.
- H. Wang, G. Zhao, S. Wang, D. Liu, Z. Mei, Q. An, J. Jiang and H. Guo, Enhanced ionic conductivity of a Na3Zr2Si2PO12 solid electrolyte with Na2SiO3 obtained by liquid phase sintering for solid-state Na+ batteries, Nanoscale, 2022, 14, 823–832 RSC
.
- Y. B. Rao, K. R. Achary, K. K. Bharathi and L. N. Patro, Enhanced ionic conductivity of Na-excess Na3Zr2Si2PO12 solid electrolyte by tuning its elemental composition and sintering temperature, J. Mater. Sci., 2023, 58, 1–12 CrossRef
.
- S. He, Y. Xu, X. Ma, Y. Chen, J. Lin and C. Wang, Mg2+/F− synergy to enhance the ionic conductivity of Na3Zr2Si2PO12 solid electrolyte for solid-state sodium batteries, ChemElectroChem, 2020, 7, 2087–2094 CrossRef CAS
.
- T. Takahashi, K. Kuwabara and M. Shibata, Solid-state ionics-conductivities of Na+ ion conductors based on NASICON, Solid State Ionics, 1980, 1, 163–175 CrossRef CAS
.
- M. Samiee, B. Radhakrishnan, Z. Rice, Z. Deng, Y. S. Meng, S. P. Ong and J. Luo, Divalent-doped Na3Zr2Si2PO12 natrium superionic conductor: Improving the ionic conductivity via simultaneously optimizing the phase and chemistry of the primary and secondary phases, J. Power Sources, 2017, 347, 229–237 CrossRef CAS
.
- L. Shen, J. Yang, G. Liu, M. Avdeev and X. Yao, High ionic conductivity and dendrite-resistant NASICON solid electrolyte for all-solid-state sodium batteries, Mater. Today Energy, 2021, 20, 100691 CrossRef CAS
.
- J. Yang, H.-L. Wan, Z.-H. Zhang, G.-Z. Liu, X.-X. Xu, Y.-S. Hu and X.-Y. Yao, NASICON-structured Na3.1Zr1.95Mg0.05Si2PO12 solid electrolyte for solid-state sodium batteries, Rare Met., 2018, 37, 480–487 CrossRef CAS
.
- A. G. Jolley, G. Cohn, G. T. Hitz and E. D. Wachsman, Improving the ionic conductivity of NASICON through aliovalent cation substitution of Na3Zr2Si2PO12, Ionics, 2015, 21, 3031–3038 CrossRef CAS
.
- D. Chen, F. Luo, W. Zhou and D. Zhu, Influence of Nb5+, Ti4+, Y3+ and Zn2+ doped Na3Zr2Si2PO12 solid electrolyte on its conductivity, J. Alloys Compd., 2018, 757, 348–355 CrossRef CAS
.
- H. Tian, S. Liu, L. Deng, L. Wang and L. Dai, New-type Hf-based NASICON electrolyte for solid-state Na-ion batteries with superior long-cycling stability and rate capability, Energy Storage Mater., 2021, 39, 232–238 CrossRef
.
- E. R. Losilla, M. A. G. Aranda, S. Bruque, J. Sanz, M. A. París, J. Campo and A. R. West, Sodium mobility in the NASICON series Na1+xZr2−xInx(PO4)3, Chem. Mater., 2000, 12, 2134–2142 CrossRef CAS
.
- Y. Saito, K. Ado, T. Asai, H. Kageyama and O. Nakamura, Ionic conductivity of NASICON-type conductors Na1.5M0.5Zr1.5(PO4)3 (M: Al3+, Ga3+, Cr3+, Sc3+, Fe3+, In3+, Yb3+, Y3+), Solid State Ionics, 1992, 58, 327–331 CrossRef CAS
.
- S. K. Pal, R. Saha, G. V. Kumar and S. Omar, Designing high ionic conducting NASICON-type Na3Zr2Si2PO12 solid-electrolytes for Na-ion batteries, J. Phys. Chem. C, 2020, 124, 9161–9169 CrossRef CAS
.
- S. Lunghammer, D. Prutsch, S. Breuer, D. Rettenwander, I. Hanzu, Q. Ma, F. Tietz and H. M. Wilkening, Fast Na ion transport triggered by rapid ion exchange on local length scales, Sci. Rep., 2018, 8, 1–8 CAS
.
- Y. Deng, C. Eames, L. H. B. Nguyen, O. Pecher, K. J. Griffith, M. Courty, B. Fleutot, J.-N. Chotard, C. P. Grey and M. S. Islam, Crystal structures, local atomic environments, and ion diffusion mechanisms of scandium-substituted sodium superionic conductor (NASICON) solid electrolytes, Chem. Mater., 2018, 30, 2618–2630 CrossRef CAS
.
- B. Santhoshkumar, P. L. Rao, K. V. Ramanathan, A. K. Bera, S. M. Yusuf, V. R. Hathwar and B. Pahari, Structure and ionic conductivity of Na3+xSc2SixP3−xO12 (x = 0.0, 0.2, 0.4, 0.8) NASICON materials: A combined neutron diffraction, MAS NMR and impedance study, Solid State Sci., 2021, 111, 106470 CrossRef CAS
.
- Q. Zhang, F. Liang, T. Qu, Y. Yao, W. Ma, B. Yang and Y. Dai, Effect on ionic conductivity of Na3+xZr2−xMxSi2PO12 (M = Y, La) by doping rare-earth elements, IOP Conf. Ser.: Mater. Sci. Eng., 2018, 423, 12122 Search PubMed
.
- X. Wang, J. Chen, Z. Mao and D. Wang, Effective resistance to dendrite growth of NASICON solid electrolyte with lower electronic conductivity, Chem. Eng. J., 2022, 427, 130899 CrossRef CAS
.
- Y. Liu, L. Liu, J. Peng, X. Zhou, D. Liang, L. Zhao, J. Su, B. Zhang, S. Li and N. Zhang, A niobium-substituted sodium superionic conductor with conductivity higher than 5.5 mS cm−1 prepared by solution-assisted solid-state reaction method, J. Power Sources, 2022, 518, 230765 CrossRef CAS
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta00440f |
| This journal is © The Royal Society of Chemistry 2023 |