Open Access Article
Open Access ArticleLarge barocaloric effects in two novel ferroelectric molecular plastic crystals†
Alejandro
Salvatori
 a,
David
Aguilà
a,
David
Aguilà
 bc,
Guillem
Aromí
bc,
Guillem
Aromí
 bc,
Lluís
Mañosa
bc,
Lluís
Mañosa
 cd,
Antoni
Planes
cd,
Antoni
Planes
 cd,
Pol
Lloveras
cd,
Pol
Lloveras
 a,
Luis Carlos
Pardo
a,
Luis Carlos
Pardo
 a,
Markus
Appel
a,
Markus
Appel
 e,
Guillaume F.
Nataf
e,
Guillaume F.
Nataf
 f,
Fabien
Giovannelli
f,
Maria
Barrio
f,
Fabien
Giovannelli
f,
Maria
Barrio
 a,
Josep Lluís
Tamarit
a,
Josep Lluís
Tamarit
 a and
Michela
Romanini
a and
Michela
Romanini
 *a
*a
aGrup de Caracterizació de Materials, Departament de Física, EEBE and Barcelona Research Center in Multiscale Science and Engineering, Universitat Politècnica de Catalunya, Eduard Maristany, 10-14, 08019 Barcelona, Catalonia, Spain. E-mail: michela.romanini@upc.edu
bDepartament de Química Inorgànica i Orgànica, Universitat de Barcelona, Secció Química Inorgànica, Martí i Franquès 1, 08028 Barcelona, Catalonia, Spain
cInstitute of Nanoscience and Nanotechnology of the University of Barcelona (IN2UB), Diagonal 645, 08028 Barcelona, Catalonia, Spain
dDepartament de Física de la Matèria Condensada, Facultat de Física, Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, Catalonia, Spain
eInstitut Laue-Langevin, 71 Avenue des Martyrs, 38000 Grenoble, France
fGREMAN UMR7347, CNRS, University of Tours, INSA Centre Val de Loire, 37000 Tours, France
First published on 19th May 2023
Abstract
Materials undergoing pressure-driven solid–solid phase transformations can be a valuable alternative for eco-friendly refrigeration, heat pumping and waste heat recovery based on the barocaloric effect. Ferroelectric compounds and plastic crystals have shown their potential in these fields because they may undergo large changes in volume and entropy at the transition, which underpin a large pressure-induced caloric response. Recently, a new class of materials combining a high-temperature plastic phase with a low-temperature ferroelectric phase has been reported. Here we investigate the barocaloric properties of two such “ferroelectric plastic crystals”, namely quinuclidinium perrhenate (C7H14NReO4) and tetramethylammonium tetrachloroferrate (N(CH3)4[FeCl4]). The reversible adiabatic temperature changes under pressure of around 100 MPa (8 K for C7H14NReO4 and 21 K for N(CH3)4[FeCl4]) reach values comparable to other plastic crystals and other materials, which demonstrates a good prospect for this novel barocaloric materials family. The dynamics of the plastic phase for C7H14NReO4 has been investigated by means of quasielastic neutron scattering.
1 Introduction
Today, the majority of refrigeration devices are based on the compression of gases like hydrofluorocarbons (HFC) and hydrochlorofluorocarbons (HCFC). These gases are harmful to the environment because they have a global warming potential that is thousands of times larger than CO2 (ref. 1) and therefore contribute to the current climate change crisis. It is thus extremely important to develop alternative environment-friendly cooling technologies that avoid such fluids; this represents however a major scientific and engineering challenge. Of the refrigeration alternatives that have been proposed (e.g., thermoelectric, thermoacoustic and thermotunneling methods2), the most promising is the caloric effect involving solid–solid first-order phase transitions (FOPTs) instead of a vapour–liquid transition. Many materials change temperature when subject to an adiabatic change of an external field, and change entropy when the external field is isothermally applied; this property is generally known as the caloric effect. While in most materials the magnitude of such caloric effects is small, there exist classes of solid materials that exhibit a large field-driven thermal response in the vicinity of a FOPT.3–19 A solid–solid transition is characterized by a change in the lattice, in the electronic and/or magnetic configuration. If such transition takes place near ambient conditions, the ensuing caloric effect can be more easily exploited in refrigeration devices.2,20,21 The main advantages of using a solid material as refrigerant or heater are: elimination of leaks contributing to the greenhouse effect, more compact devices and expected higher efficiencies. On the other hand, for materials undergoing a FOPT above room temperature, the caloric performance could also be used for recovery and storage of waste heat, which contributes significantly to the global warming. This is important because it is estimated that only 20% of the consumed global energy is re-used, the rest is dissipated in form of residual heat to the environment, with the corresponding direct ambient warming impact.22–25Recently, the solid-state caloric functionality driven by hydrostatic pressure (i.e. barocaloric) in plastic crystals (PCs) has been investigated, revealing in some cases effects of colossal magnitude.26–29 PC phases, display properties that are intermediate between those of a fully ordered crystal phase and of the liquid phase:30 they are translationally ordered solids possessing orientational disorder. This means that the centers of mass of the molecules form a crystalline lattice, but the molecules rotate around their centers of mass, thanks to their small globular molecular shape. This dynamic orientational disorder is accompanied by the formation of lattice defects and by a lower density compared to the fully ordered crystal (OC) counterpart, both of which enable molecular diffusion through the lattice resulting in high plasticity under e.g. uniaxial stress.31–34 If the temperature of a PC is lowered, it typically transforms through a first-order phase transition into an OC phase. The dramatic change in orientational order and volume across this phase change is accompanied by a large latent heat of transition, which may even be of the same order of magnitude as that of the melting of ordered phases.
Recently, a new class of PCs has been synthesized, displaying ferroelectric ordering at low temperature and a PC phase at higher temperature.35,36 Ferroelectric plastic crystals (FPCs) exhibit multiaxial ferroelectricity that allows alteration of the direction of the polar axis of the crystal by application of an external field, and effective ferroelectric polarization switching.
Herein, we present the barocaloric properties of two recently reported FPCs, namely, quinuclidinium perrhenate35 (HQuin, C7H14NReO4, Fig. 1a) and tetramethylammonium tetrachloroferrate36 (TMA, N(CH3)4[FeCl4], Fig. 1b). On heating above 344 K, HQuin undergoes a FOPT from a paraelectric (III) towards a ferroelectric (II) phase and, on further heating above 367 K, the system transforms in a PC (I) phase. On the other hand, TMA is characterized by a ferroelectric (III) – paraelectric (II) – PC (I) phase sequence on heating with transition temperatures of 341 K and 384 K, respectively. The structural data for each phase in both compounds as reported in the literature are summarized in Table 1. In this study we extend the characterization of such materials by including calorimetry measurements as a function of pressure and high-resolution neutron spectroscopy.
 | ||
| Fig. 1 Molecular structures of HQuin (a) and TMA (b) in the plastic phase I. Atom color code: H = white, C = light blue, N = dark blue, O = red, Re = pink, Cl = green, Fe = purple. | ||
| HQuin | TMA | ||
|---|---|---|---|
| C7H14NReO4 | C4H12NFeCl4 | ||
| Space group35,36 | Phase III | Pmn21 | Amm2 |
| Phase II | R3m | Cmcm | |
| Phase I |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m m |
|
| T t (K) | III → II | 344 [345 (ref. 35)] | 343 [344 (ref. 36)] |
| II → III | 341 | — | |
| II → I | 367 [367 (ref. 35)] | 384 [384 (ref. 36)] | |
| I → II | 366 | 381 | |
| ΔVt (cm3 g−1) | III → II | 0.011 | 0.0062 |
| II → I | 0.0032 | 0.021 | |
| ΔSt (J kg−1 K−1) | III → II | 59.1 [66.8 (ref. 35)] | 8.3 |
| II → III | 60.3 | — | |
| II → I | 15.6 [11.3 (ref. 35)] | 58.7 [49.8 (ref. 36)] | |
| I → II | 18.09 | 59.6 | |
| dT/dp (K GPa−1) | III → II | 138 | 630 |
| II → III | 137 | 700 | |
| II → I | 158 | 400 | |
| I → II | 157 | 380 | |
| III → I | — | 390 | |
| I → III | — | — | |
| ΔVt/ΔSt (K GPa−1) | III → II | 184 | 750 |
| II → I | 205 | 360 | |
2 Experimental
Materials synthesis
All reagents were purchased from commercial sources and used as received. Compounds HQuin and TMA were obtained based on previously reported procedures.35,36 For HQuin, a colorless solution of quinuclidine (200 mg, 1.80 mmol) in EtOH (5 mL) was treated with 0.28 mL of HReO4 (76.5% solution in water, 1.80 mmol) under stirring. The resulting white suspension was filtered and the white solid HQuin was dried in air. For TMA, a 2 mL aqueous colorless solution of Me4NCl (100 mg, 0.91 mmol) was added under stirring on a 2 mL aqueous orange solution of FeCl3·6H2O (247 mg, 0.91 mmol). The resulting light orange solution was then treated with two drops of HCl 37%, promoting a change of color (yellow) and a decrease of pH down to 2. The final solution was left stirring for 30 min, and left undisturbed overnight. After 10 days, yellow crystals of TMA were obtained, which were filtered and dried in air.Calorimetry measurements
Calorimetry at ambient pressure was carried out using a conventional differential scanning calorimeter (DSC) Q100 from TA Instruments. Pressure-dependent differential thermal analysis (DTA) was performed using a homemade high-pressure cell that operates up to a pressure of 3 kbar and employs Bridgman K-type thermocouples (cromel-alumel from Pyromation) as thermal sensors for both temperature and differential signal measurements. A resistive heater is used for heating the sample at ca. 2 K min−1 from room-temperature to 430 K for HQuin, and to 480 K for TMA. The cooling ramps were performed with an air stream system at an average rate of ca. −2.5 K min−1. A few hundred mg of each sample were mixed with an inert perfluorinated fluid (Galden Bioblock Scientist) to remove air and encapsulated in tin capsules. Pressure transmitting fluid was Therm240 (Lauda). The specific heat of HQuin was measured by means of modulated calorimetry using a DSC250 from TA instruments in the temperature range 200–400 K with a modulation amplitude of ± 1 K and a period of 120 s. For TMA, the heat capacity reported in ref. 37 was compared with isothermal heat capacity measurements performed by means of modulated calorimetry using a DSC Q2000 from TA instruments with a modulation amplitude of ± 1 K and a period of 120 s.Thermal conductivity
Thermal diffusivity was measured with the laser flash method (Netzsch LFA 457 MicroFlash). Pellets of HQuin and TMA were obtained by applying on the powders a uniaxial pressure of 300 MPa during 30 seconds in a steel die. It resulted in pellets 13 mm in diameter, with thicknesses of 1.323 mm for HQuin and 0.790 mm for TMA, measured with a digital micrometer. The pellets were coated with a thin layer of graphite (Graphit 33 Kontakt Chemie) to improve absorption of the neodymium glass laser pulse on the front sides and to increase emission in the infrared on the rear sides. Measurements were performed on heating and cooling in a nitrogen-rich environment in 5 K steps from 300 K to 380 K for HQuin and from 250 K to 410 K for TMA. At each temperature, thermal diffusivity was recorded three times for averaging. The resulting signals were fitted with the software Proteus 7.1, using the standard Cape-Lehman model38 with a linear baseline, and an additional correction for radiative transfer inside the transparent pellets.39Temperature-dependent X-ray diffraction
High resolution X-ray powder diffraction (XRPD) measurements were performed at normal pressure and as a function of temperature with a vertically mounted INEL (Artenay, France) cylindrical position-sensitive detector (CPS-120) by using Debye–Scherrer geometry and transmission mode. The 2θ step was 0.029° over a range from 2° to 112°. Monochromatic Cu-Kα1 (λ = 1.54056 Å) radiation was selected by means of a focusing incident-beam germanium monochromator. The temperature was controlled by using a liquid nitrogen 700 series Cryostream Cooler (Oxford Cryosystems). Cubic Na2Ca3Al2F4 was used for external calibration. The PEAKOC application from DIFFRACTINEL software was used for the calibration and for the peak position determinations after pseudo-Voigt fittings. Lattice parameters were refined at each temperature by way of the least-squares option of the FullProf suite.40Neutron scattering
High-resolution neutron spectroscopy was carried out on the backscattering spectrometer IN16B at the Institut Laue-Langevin, Grenoble (France) using the standard setup with Si 111 monochromator and analyzers in its high signal-to-noise mode with the background chopper running at ratio41 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The obtained resolution in energy transfer is 0.75 μeV with 18 different values of the scattering vector in the range q = 0.1–1.9 Å−1. The two samples of TMA (655 mg) and HQuin (952 mg) were placed in flat standard aluminum sample holders of 3 × 4 cm2 with 0.8 mm thickness each and sealed with Pb wire. For each sample, elastic and inelastic fixed window scans (FWS) were recorded first, in order to obtain scattered neutron intensity at ΔE = 0 μeV and ΔE = 2 μeV as a function of temperature in the range T = 2–400 K. Subsequently, full energy transfer spectra in the range ΔE = −30–30 μeV were recorded at T = 2 K, 375 K, 400 K and 430 K for TMA and at T = 360 K and 380 K for HQuin, respectively. The spectrum at 2 K was employed as experimental resolution function. Using additional measurements of an empty cell and a vanadium standard for normalization, the data was reduced by IN16B standard routines in Mantid.42 The experimental data can be accessed via ref. 43.
1. The obtained resolution in energy transfer is 0.75 μeV with 18 different values of the scattering vector in the range q = 0.1–1.9 Å−1. The two samples of TMA (655 mg) and HQuin (952 mg) were placed in flat standard aluminum sample holders of 3 × 4 cm2 with 0.8 mm thickness each and sealed with Pb wire. For each sample, elastic and inelastic fixed window scans (FWS) were recorded first, in order to obtain scattered neutron intensity at ΔE = 0 μeV and ΔE = 2 μeV as a function of temperature in the range T = 2–400 K. Subsequently, full energy transfer spectra in the range ΔE = −30–30 μeV were recorded at T = 2 K, 375 K, 400 K and 430 K for TMA and at T = 360 K and 380 K for HQuin, respectively. The spectrum at 2 K was employed as experimental resolution function. Using additional measurements of an empty cell and a vanadium standard for normalization, the data was reduced by IN16B standard routines in Mantid.42 The experimental data can be accessed via ref. 43.
3 Results and discussion
Calorimetry at ambient pressure
DSC measurements at atmospheric pressure on the synthesized compounds (Fig. 2) confirmed the reported35,36 phase transition temperatures. After baseline subtraction we calculate the transition enthalpy change ΔHt and the transition entropy change ΔSt by integration of dQ/dT and (1/T)dQ/dT respectively, between temperatures T1 and T2 suitably chosen below and above the transition. The peak transition temperatures Tt together with the entropy changes ΔSt at the transition from our DSC measurements for both compounds are summarized in Table 1 together with the data reported in the literature.Thermal conductivity
From the thermal diffusivity measurements (see Fig. S6†), the thermal conductivity κ(T) has been calculated as κ(T) = Cp(T)ρ(T)α(T) with Cp the heat capacity, ρ the density and α the thermal diffusivity. ρ(T) was calculated as 96% for HQuin (respectively 95% for TMA) of the densities obtained at each temperature by X-ray diffraction (Fig. 5). For the HQuin we obtained averaged values of 0.11 W m−1 K−1, 0.11 W m−1 K−1 and 0.17 W m−1 K−1 in the phases I, II and III respectively and averaged values of 0.12 W m−1 K−1 and 0.14 W m−1 K−1 in the phases I and II of TMA. This low values are expected since plastic crystals, in general, suffer from low thermal conductivities due to weak intermolecular interactions.44–47 These values may be enhanced by adding conductive nanoparticles48 or by integrating them in conductive porous matrix.49,50Neutron spectroscopy
Neutron scattering experiments were performed for both samples HQuin and TMA. However, none of the spectra obtained for TMA were indistinguishable from the resolution being, thus, outside the experimental accessible dynamic range. For HQuin, in contrast, a quasielastic contribution was detected in the spectra (Fig. 3). The main contribution to the quasielastic scattering incoherent signal stemmed from quinuclidinium with 14 hydrogen atoms.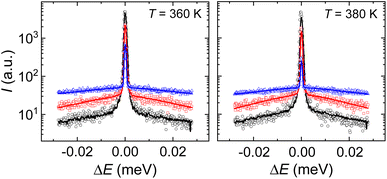 | ||
| Fig. 3 Representative experimental neutron scattering spectra of HQuin for selected momentum transfer (symbols) (q1 = 0.29 Å: black circles, q2 = 0.85 Å: red squares, q3 = 1.22 Å: blue triangles). The spectrum at momentum transfer q3 has been shifted upwards by 20 units. Lines show the fittings using eqn (1). | ||
For the detected confined motion a single component was used in order to describe the data. A previous test with two components was performed, but the width of the second component was outside the dynamic range of the experiment thus contributing, in fact, as a constant. The model used to fit the data was, thus:
 | (1) |
The Lorentzian widths obtained by fitting eqn (1) for both temperatures were Γ(360 K) = 0.029 ± 0.003 meV and Γ(380 K) = 0.027 ± 0.003 meV, therefore changes in the dynamics (if any) are very subtle. Given that neutron experiments have been performed at temperatures corresponding to the ferroelectric (T = 360 K) and the plastic (T = 380 K) phase we conclude that the differences in the dynamics of these two phases are minimal. We have calculated the time-scale associated with the processes detected in the experiment resulting in τ(360 K) = 23 ± 4 ps and τ(380 K) = 24 ± 4 ps. The molecular dynamics simulation of Yoneya et al. can shed some light on these results.52 The analysis of molecular trajectories in the simulation lead to the conclusion that molecular rotation is not performed by a series of continuous changes in the orientation of the molecular axis (rotational diffusion). Molecular rotation is performed by orientational jumps between equilibrium positions: the molecular axis performs a fast vibration around a given direction during a residence time, followed by a large angular change that brings the molecule to the next equilibrium position. We have fitted the rotation autocorrelation function C(t) obtained in that work with a stretched exponential,  , obtaining an approximate correlation time of τMD ≈ 30 ps for both phases: the ferroelectric and the plastic phase. If we assume that the main mechanism acting on the decrease of the correlation function obtained in that work is due to rotational jumps, we can assign τMD to an averaged residence time in the equilibrium positions. Given the resemblance between that time, and the one obtained by us experimentally, we can tentatively also assign the last to the average of molecular residence times between jumps. It should be pointed out that the time obtained from neutron scattering can be slightly different depending on the specific model chosen to describe the data, however, what can be unambiguously determined is the time scale that, as aforementioned, is compatible with the residence time obtained from molecular dynamics (MD). We can thus associate the changes in Γ with a small decrease in the residence time of molecules in the plastic phase in comparison to that of the ferroelectric phase in their equilibrium positions. However we would like to point out that a deeper study of the molecular dynamics trajectories and a fitting using original data should be done in order to unambiguously perform such a statement.
, obtaining an approximate correlation time of τMD ≈ 30 ps for both phases: the ferroelectric and the plastic phase. If we assume that the main mechanism acting on the decrease of the correlation function obtained in that work is due to rotational jumps, we can assign τMD to an averaged residence time in the equilibrium positions. Given the resemblance between that time, and the one obtained by us experimentally, we can tentatively also assign the last to the average of molecular residence times between jumps. It should be pointed out that the time obtained from neutron scattering can be slightly different depending on the specific model chosen to describe the data, however, what can be unambiguously determined is the time scale that, as aforementioned, is compatible with the residence time obtained from molecular dynamics (MD). We can thus associate the changes in Γ with a small decrease in the residence time of molecules in the plastic phase in comparison to that of the ferroelectric phase in their equilibrium positions. However we would like to point out that a deeper study of the molecular dynamics trajectories and a fitting using original data should be done in order to unambiguously perform such a statement.
The obtained EISF(q) values are shown in Fig. 4 as a function of the momentum transfer. The difference between the EISF(q) for the two selected temperatures is striking taking into account the small changes in the dynamics of the movement (slight changes in Γ). Therefore we can speculate that the changes in the geometry of the molecular motions are more important than the change in the molecular dynamics for HQuin when comparing the ferroelectric and the plastic phases.
 | ||
| Fig. 4 Elastic incoherent structure factor obtained for HQuin as a sum of momentum transfer for the two measured temperatures (T = 380 K red circles, T = 360 K black squares). Solid lines are fits of the experimental data to eqn (2). | ||
 | ||
| Fig. 5 Temperature-dependent specific volume on heating for HQuin (a) and TMA (b). Error bars are smaller than the symbol size. The lines are linear fits to V(T) data. | ||
We can fit the obtained EISF assuming isotropic continuous rotational diffusion, EISF = j02(qRT), with j0(qRT) being the zeroth order spherical Bessel function53 and RT the effective molecular radius of rotation. Since neutron scattering is sensitive to the position of the H atoms this value (RT) at any temperature T should match the molecular radius R, defined as the distance between the centre of mass and the H atoms, which ranges from R = 2.1 Å to R = 2.2 Å. The experimental results are RT = 1.5 ± 0.1 Å and RT = 1.8 ± 0.1 Å at a temperature of 360 and 380 K respectively. Not only are these distances shorter than predicted by the molecular geometry, but they also have a strong temperature-dependence, which is incompatible with a rotational diffusion. This could be explained taking into account the MD simulations: as aforementioned reorientation is done via jumps and not performed continuously explaining the failure of the model to describe the data.
Finding an analytical model for the EISF that takes into account uniaxial rotations convoluted with a combination of orientational jumps and vibrations of the molecular axis is beyond the scope of this work. Moreover, even in the case that such a model could be worked out, the limited momentum transfer range in the experiment would not be enough to perform a meaningful fit of the data. For this reason we will fit the experimental results using the Gaussian approximation: a model free description of the data:54
 | (2) |
In this model σ is the length scale associated with the movement of hydrogen atoms. This lengthscale is related to the width of the distribution of the distance of the hydrogen atoms at an infinite time, with respect to the position at t = 0, assuming a Gaussian distribution. The results obtained for the two studied temperatures are σ(360 K) = 1.39 ± 0.05 Å and σ(380 K) = 1.56 ± 0.05 Å.
The physical interpretation of our results is that Hquin is performing rotational jumps between equilibrium positions. The residence time in each equilibrium position (calculated from the width of the Lorentzian) is on a time-scale τ ≈ 24 ps at both studied phases. The difference between the ferroelectric and the plastic phase is that the movement in the first case is more constrained than in the second case, i.e. the length distribution is broader in the second case. Again this agrees with the MD simulation from which the molecular movements in the ferroelectric phase are more restricted than those in the plastic phase.
X-ray diffraction
Temperature-dependent XRPD at atmospheric pressure (see Fig. S1–S3 in the ESI†) also confirmed the expected35,36 structures for all phases in both compounds (see Table 1). Fig. 5 presents the specific volumes for the different phases as a function of temperature obtained through pattern matching performed on the recorded XRPD patterns.Pressure-dependent calorimetry
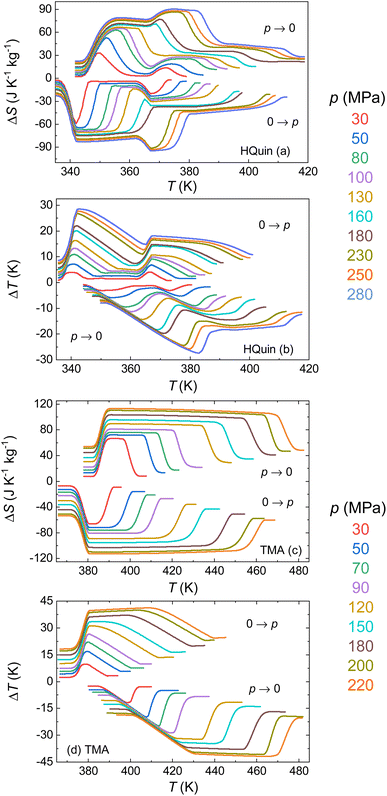
Isobaric temperature-dependent DTA signals on both compounds (Fig. 6a and b for HQuin and Fig. 6d for TMA), show endothermic and exothermic peaks in dQ/|dT| associated with the FOPTs upon heating (positive peaks) and cooling (negative peaks). By varying the applied hydrostatic pressure, all the transitions in both compounds move towards higher temperature, which predicts a conventional barocaloric effect. The dependencies of the peaks temperature as a function of pressure are plotted in Fig. 6c and e for HQuin and TMA, respectively. In the case of HQuin the two peaks visible upon heating in the measured temperature range correspond to the transition between the paraelectric (III) to the ferroelectric phase (II) (Fig. 6a) and from the ferroelectric (II) to the plastic phase (I) (Fig. 6b). On cooling the corresponding exothermic transition peaks are visible. The increase of the transition temperature with the applied pressure is linear, with almost the same slope dT/dp upon heating and cooling for both, the II to I and the III to II phase transitions. The corresponding values are summarized in Table 1. Also for TMA, two peaks are visible upon heating in the measured temperature range (Fig. 6d), the tiny peak at lower temperature corresponds to the ferroelectric (III) to paraelectric (II) phase transition and due to its weak intensity, it is not visible at all measured pressures. The second peak, larger and at higher temperature, corresponds to the transition from the paraelectric phase (II) to the plastic phase (I). Also in this case, the increase in temperature with pressure is linear upon heating for both transitions (see Table 1). The difference in slope between the two phase transitions leads to the existence of a triple point at a temperature of ∼425 K and a pressure of ∼160 MPa. Above these values, the endothermic transition is direct from phase III to phase I and the increase of the III-I phase transition temperature with pressure is again linear (see Table 1). Upon cooling (blue lines in Fig. 6e), the slopes corresponding to the temperature transition between phase I and II and between phase II and III are comparable to those upon heating (see Table 1). The values obtained for both compounds are consistent with the ones calculated from the Clausius–Clapeyron formula within the experimental error: dT/dp = ΔVt/ΔSt, where the volume change has been estimated from the XRPD data (Fig. 5) and the entropy change has been calculated from DSC at atmospheric pressure. The calculated values of dT/dp for HQuin and TMA are summarized in Table 1.The barocaloric effects have been calculated by using the quasi-direct method, i.e., by computing the isobaric entropy curves S(T, p) at different pressures with respect to a reference value taken at atmospheric pressure and at a given temperature T0. In particular, we set T0 = 300 K for HQuin whereas T0 = 350 K for TMA because in the latter case the III-II transition is left out of the analysis due to the small transition entropy change. For this purpose we compute the temperature-dependent entropy at fixed pressure (isobaric conditions) as the sum of three contributions, namely the T-dependent entropy of each phase plus a contribution from the transition entropy, according to the following equations:4,5,26,55
 | (3) |
Since pressure-dependent Cp data below T0 are not available, the dependence of the entropy on pressure at T0, S(T0, p) can not be evaluated directly. Alternatively, the following Maxwell equation can be used:
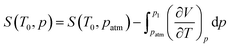 | (4) |
Assuming that (∂V/∂T)p is pressure-independent, the integral in the previous equation can be approximated by (∂V/∂T)patm(p − patm), where (∂V/∂T)patm is obtained at T0 from Fig. 5 (0.8 × 10−4 cm3 g−1 K−1 for the phase III of HQuin and 2.5 × 10−4 cm3 g−1 K−1 for the phase II of TMA). In turn, above T0 the dependence of Cp on pressure can be considered negligible according to the (∂Cp/∂p)T = −T(∂2V/∂T2)p equation where the volume change is approximately linear with temperature (see Fig. 5).
Therefore, using the specific heat data at atmospheric pressure together with the calorimetric curves at selected values of pressure (Fig. 6a and c) and the thermal expansion data (Fig. 5), it is possible to compute the entropy curves as a function of temperature for selected values of the applied pressure for heating [SH(T, p)] and cooling [SC(T, p)] ramps (Fig. 7).
 | ||
| Fig. 7 Temperature-dependent isobaric entropy curves at different pressures, both upon heating (a and c), and cooling (b and d) for HQuin and TMA. | ||
Because the studied materials present a conventional barocaloric effect (dT/dp > 0), the transition induced by compression is exothermic, while the transition induced by decompression is endothermic. Therefore the barocaloric effects for compression are computed from the runs on cooling, whereas the barocaloric effects upon decompression are computed from the runs upon heating (Fig. 8). From the entropy curves the isothermal entropy change induced by the removal and application of a certain pressure p, can be computed directly from subtraction of entropy curves on heating and on cooling, respectively, as:28
| ΔS(T, p → patm) = SH(T, patm) − SH(T, p) | (5) |
| ΔS(T, patm → p) = SC(T, p) − SC(T, patm) | (6) |
| ΔT(T, p → patm) = T(SH, patm) − T(SH, p) | (7) |
| ΔT(T, patm → p) = T(SC, p) − T(SC, patm) | (8) |
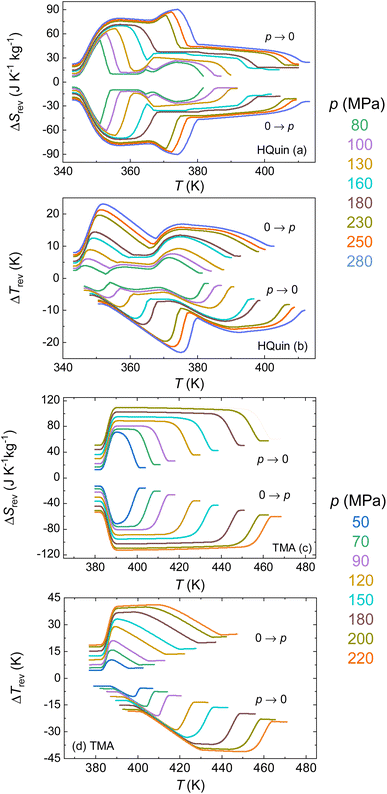
The isothermal change ΔS reaches maximum values of 65 J K−1 kg−1 and 28 J K−1 kg−1 for the III–II and II–I phase transitions of HQuin at a pressure of 100 MPa and 81 J K−1 kg−1 for the II-I transition of TMA at a pressure of 90 MPa. The corresponding adiabatic temperature changes ΔT are 13.4 and 10 K for HQuin and 26.5 K for TMA. In order to establish the suitability of a material for its implementation in a real device it is necessary to evaluate its reversibility. Reversible entropy changes, ΔSrev, are computed quasi-directly from the overlapping between the ΔS obtained upon compression and ΔS upon decompression.56 Reversible adiabatic temperature changes are calculated as:55
| ΔTrev(T, p → patm) = T(SH, patm) − T(SC, p) | (9) |
| ΔTrev(T, patm → p) = T(SC, p) − T(SH, patm) | (10) |
The results of such calculations are shown in Fig. 9. The obtained values for the reversible entropy and temperature changes are only slightly smaller than those corresponding to the irreversible values, thanks to the small hysteresis in both samples. For the II–I transition of HQuin, values of 26 J K−1 kg−1 and 8 K are obtained for a pressure of 100 MPa for ΔSrev and ΔTrev respectively (the values 42 J K−1 kg−1 and 15 K are instead obtained at the pressure of 230 MPa). For TMA, the obtained values for the II–I transition are 81 J K−1 kg−1 and 21 K at a pressure of 90 MPa (112 J K−1 kg−1 and 41 K at the pressure of 220 MPa for the III–I transition).
The reversible isothermal entropy values obtained are smaller than those recently reported in other PCs26–29 but the reversible adiabatic temperature changes reach values comparable to the same PCs materials or other barocaloric materials (see Fig. 10). Because the ferroelectric phase of these materials is sensitive to the applied electric field, it would be interesting in future studies to characterize the electrocaloric properties of HQuin and TMA. Using the polarization measurements published in ref. 35 and 36, we estimate that in order to reach the same values of ΔSrev obtained applying a pressure of 100 MPa in the case of HQuin (II–I transition) and 90 MPa for TMA (III–II transition), it would be necessary to apply an electric field of 230 and 190 kV cm−1, respectively. While these values for the electric field are relatively large, the synergic caloric response of the studied ferroelectric plastic crystals to both electric field and hydrostatic pressure suggests that application of moderate pressures could help (i) to tune the operational temperature span for the electrocaloric effect; (ii) to overcome the transition hysteresis such that the minimum required electric field to obtain reversible electrocaloric effects can be reduced at the expense of applying pressure (with the potential of avoiding the breakdown field); (iii) to increase the overall magnitude of the multicaloric effects at lower applied fields.
 | ||
| Fig. 10 Reversible isothermal entropy changes (a) and reversibile temperature change (b) as a function of temperature for TMA and HQuin compared to selected PCs materials. In particular, the PCs derived from neophentanes: pentaglycerine (PG) and neophentyl alcohol (NPA)28 and neophentyl glycol (NPG);26 from adamantanes: Br-adamantane (Br-ada) and Cl-adamantane (Cl-ada);29 from adamantanols: 1-adamantanol (1-Aol), 2-adamantanol (2-Aol) and 2-methyl-2-adamantanol (2M2-Aol);57 from carboranes: para-carborane, ortho-carborane and meta-carborane (for these last compounds only the ΔSrev data were available in ref. 58) and C60,59 NH4I19 and KPF6 (ref. 60) (only ΔSrev available) compounds. | ||
4 Conclusions
In this work we have investigated two recently reported novel compounds that show very unusual polymorphism, displaying a plastic crystal and a ferroelectric phase at high- and low-temperatures, respectively. In particular, we synthesized quinuclidinium perrhenate (HQuin) and tetramethylammonium tetrachloroferrate (TMA). Normal pressure DSC and the temperature-dependent XRPD measurements at normal pressure confirm the structures of the involved phases as well as the phase transition properties between them.The dynamics of both plastic and ferroelectric phases of HQuin has been characterized by means of high-resolution neutron scattering experiments. They revealed that molecules perform rotational jumps between equilibrium positions with residence times roughly temperature-independent but with an increase of the length scale in the plastic phase with respect to the ferroelectric phase.
From isobaric temperature-dependent DTA signals, we computed the barocaloric effects associated with the two ferroelectric PCs. For the HQuin we found reversible isothermal entropy changes of 60 J K−1 kg−1 for the III (paraelectric) – II (ferroelectric) phase transition and of 26 J K−1 kg−1 for the II–I (plastic crystal) transition under pressure changes of 100 MPa; for TMA reversible entropy changes reach 81 J K−1 kg−1 under pressure changes of 90 MPa. Although these values are smaller than those recently reported in other PCs, the reversible adiabatic temperature changes (6–8 K for HQuin and 21 K for TMA) reach values comparable with other PCs as well as with other barocaloric materials. More importantly, our work suggests that ferroelectric plastic crystals have potential as barocaloric materials and therefore should inspire the study of barocaloric effects in similar compounds. Furthermore, our consideration of this new family of ferroelectrics as a caloric family in general, could also open up several other avenues of research by combining electrocaloric, barocaloric and multicaloric effects.
Data availability
Data available on request from the authors.Author contributions
M. R. carried out calorimetry measurements and their analysis and wrote the initial draft of the manuscript; A. S. carried out the calorimetric analysis; D. A and G. A. synthesized the materials; M. B. carried out the XRPD experiments and their analysis; G. F. N. and F. G. carried out the thermal conductivity measurements and their analysis; M. A. carried out the neutron scattering experiment at ILL facilities; L. C. P. performed the neutron scattering data analysis; L. M., A. P., P. L. and J. L. T. contributed to the discussion section, managed funding and resources, and revised the manuscript.Conflicts of interest
J. L. T, P. L. and L. M. have patent n. PCT/EP2017/076203 licensed.Acknowledgements
This work was supported by the MINECO projects PID2020-112975GB-I00, PID2020-113549RB-I001/AEI and PGC2018-098630-B-I00 (Spain), the DGU projects 2021SGR-00343 and 2021SGR-00328 (Catalonia), the grant agreement no. 00149464 TEMPE (Région Centre-Val de Loire, France) and by the Programme “Ajut a la Recerca Transversal” (ART 2019) from the Institute of Nanoscience and Nanotechnology of the University of Barcelona. M. R. acknowledges financial support from MINECO under the Juan de la Cierva fellowship (IJC2019-040225-I).Notes and references
- https://climatechangeconnection.org/emissions/co2-equivalents/, accessed October 2022.
- https://www.energy.gov/eere/buildings/downloads/non-vapor-compression-hvac-technologies-report, accessed October 2022.
- E. Stern-Taulats, T. Castán, L. Mañosa, A. Planes, N. D. Mathur and X. Moya, MRS Bull., 2018, 43, 295–299 CrossRef.
- L. Mañosa and A. Planes, Adv. Mater., 2017, 29, 1603607 CrossRef.
- A. Aznar, P. Lloveras, M. Romanini, M. Barrio, J. Tamarit, C. Cazorla, D. Errandonea, N. D. Mathur, A. Planes, X. Moya and L. Mañosa, Nat. Commun., 2017, 8, 1851 CrossRef PubMed.
- A. Aznar, A. Gràcia-Condal, A. Planes, P. Lloveras, M. Barrio, J. L. Tamarit, W. Xiong, D. Cong, C. Popescu and L. Mañosa, Phys. Rev. Mater., 2019, 3, 044406 CrossRef CAS.
- J. Li, M. Barrio, D. J. Dunstan, R. Dixey, X. Lou, J. Tamarit, A. E. Phillips and P. Lloveras, Adv. Funct. Mater., 2021, 31, 2105154 CrossRef CAS.
- J. Salgado-Beceiro, A. Nonato, R. X. Silva, A. García-Fernández, M. Sánchez-Andújar, S. Castro-García, E. Stern-Taulats, M. A. Señarís-Rodríguez, X. Moya and J. M. Bermúdez-García, Mater. Adv., 2020, 1, 3167–3170 RSC.
- J. M. Bermúdez-García, M. Sánchez-Andújar and M. A. Señarís-Rodríguez, J. Phys. Chem. Lett., 2017, 8, 4419–4423 CrossRef PubMed.
- Y. Liu, J. F. Scott and B. Dkhil, Appl. Phys. Rev., 2016, 3, 031102 Search PubMed.
- N. R. Ram, M. Prakash, U. Naresh, N. S. Kumar, T. S. Sarmash, T. Subbarao, R. J. Kumar, G. R. Kumar and K. C. B. Naidu, J. Supercond. Novel Magn., 2018, 31, 1970–1979 Search PubMed.
- B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi, K. Ohara, K. Li, D. Yu, R. Mole, T. Hattori, T. Kikuchi, S. Yano, Z. Zhang, W. R. Z. Zhang, S. Lin, O. Sakata, K. Nakajima and Z. Zhang, Nature, 2019, 567, 506–510 CrossRef CAS PubMed.
- C. M. Miliante, A. M. Christmann, R. P. Soares, J. R. Bocca, C. S. Alves, A. M. G. Carvalho and A. R. Muniz, J. Mater. Chem. A, 2022, 10, 8344–8355 RSC.
- F. Li, M. Li, C. Niu and H. Wang, Appl. Phys. Lett., 2022, 120, 073902 CrossRef CAS.
- F. Li, C. Niu, X. Xu, M. Li and H. Wang, Appl. Phys. Lett., 2022, 121, 223902 CrossRef CAS.
- J. Seo, J. D. Braun, V. M. Dev and J. A. Mason, J. Am. Chem. Soc., 2022, 144, 6493–6503 CrossRef CAS PubMed.
- J. Seo, R. D. McGillicuddy, A. H. Slavney, S. Zhang, R. Ukani, A. A. Yakovenko, S. Zheng and J. A. Mason, Nat. Commun., 2022, 13, 2536 CrossRef CAS PubMed.
- X. Xu, F. Li, C. Niu, M. Li and H. Wang, Appl. Phys. Lett., 2023, 122, 043901 CrossRef CAS.
- Q. Ren, J. Qi, D. Yu, Z. Zhang, R. Song, W. Song, B. Yuan, T. Wang, W. Ren, Z. Zhang, X. Tong and B. Li, Nat. Commun., 2022, 13, 2293 CrossRef CAS PubMed.
- L. Mañosa, A. Planes and M. Acet, J. Mater. Chem. A, 2013, 1, 4925–4936 RSC.
- X. Moya, S. Kar-Narayan and N. D. Mathur, Nat. Mater., 2014, 13, 439–450 CrossRef CAS PubMed.
- https://www.waste-heat.eu/, accessed October 2022.
- https://arpa-e.energy.gov/technologies/projects/closed-loop-system-using-waste-heat-electricity, accessed October 2022.
- https://arpa-e.energy.gov/technologies/projects/waste-heat-recovery-system, accessed October 2022.
- https://e360.yale.edu/features/waste-heat-innovators-turn-to-an-overlooked-renewable-resource, accessed October 2022.
- P. Lloveras, A. Aznar, M. Barrio, P. Negrier, C. Popescu, A. Planes, L. Mañosa, E. Stern-Taulats, A. Avramenko, N. D. Mathur, X. Moya and J. Tamarit, Nat. Commun., 2019, 10, 1803 CrossRef CAS PubMed.
- F. B. Li, M. Li, X. Xu, Z. C. Yang, H. Xu, C. K. Jia, K. Li, J. He, B. Li and H. Wang, Nat. Commun., 2020, 11, 4190 CrossRef CAS PubMed.
- A. Aznar, P. Lloveras, M. Barrio, P. Negrier, A. Planes, L. Mañosa, N. Mathur, X. Moya and J. Tamarit, J. Mater. Chem. A, 2020, 8, 639 RSC.
- A. Aznar, P. Negrier, A. Planes, L. Mañosa, E. Stern-Taulats, X. Moya, M. Barrio, J. L. Tamarit and P. Lloveras, Appl. Mater. Today, 2021, 23, 101023 CrossRef.
- J. L. Tamarit, B. Legendre and J. M. Buisine, Mol. Cryst. Liq. Cryst., 1994, 250, 347–358 CrossRef CAS.
- J. Harada, APL Mater., 2021, 9, 020901 CrossRef CAS.
- M. Zachariah, M. Romanini, P. Tripathi, M. Barrio, J. L. Tamarit and R. Macovez, J. Phys. Chem. C, 2015, 119, 27298–27306 CrossRef CAS.
- J. Sunarso, Y. Shekibi, J. Efthimiadis, L. Jin, J. Pringle, A. Hollenkamp, D. MacFarlane, M. Forsyth and P. Howlett, J. Solid State Electrochem., 2012, 16, 1841–1848 CrossRef CAS.
- J. L. Tamarit, I. B. Rietveld, M. Barrio and R. Ceolin, J. Mol. Struct., 2014, 1078, 3–9 CrossRef CAS.
- J. Harada, T. Shimojo, H. Oyamaguchi, H. Hasegawa, Y. Takahashi, K. Satomi, Y. Suzuki, J. Kawamata and T. Inabe, Nat. Chem., 2016, 8, 946–952 CrossRef CAS PubMed.
- J. Harada, N. Yoneyama, S. Yokokura, Y. Takahashi, A. Miura, N. Kitamura and T. Inabe, J. Am. Chem. Soc., 2018, 140, 346–354 CrossRef CAS PubMed.
- I. Ruiz-Larrea, A. López-Echarri and M. Tello, Solid State Commun., 1987, 64, 1099–1101 CrossRef CAS.
- J. A. Cape and G. W. Lehman, J. Appl. Phys., 1963, 34, 1909–1913 CrossRef.
- R. L. McMasters, J. V. Beck, R. B. Dinwiddie and H. Wang, J. Heat Transfer, 1999, 121, 15–21 CrossRef CAS.
- J. Rodríguez-Carvajal, Commission on powder diffraction (IUCr), Newsletter, 2001, 26, 12–19 Search PubMed.
- M. Appel and B. Frick, Rev. Sci. Instrum., 2017, 88, 036105 CrossRef PubMed.
- O. Arnold, et al. , Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- M. Romanini, M. Appel, P. Lloveras, L. C. Pardo, A. Salvatori and M. Zeng, Barocaloric effect: unraveling themicrosopic mechanism behind high entropy changes in phase transitions, Institut Laue-Langevin (ILL), 2021, proposal 7–02–214 Search PubMed.
- P. LLoveras and J. L. Tamarit, MRS Energy Sustain, 2021, 8, 3–15 Search PubMed.
- A. I. Krivchikov, O. A. Korolyuk, I. V. Sharapova, J. L. Tamarit, F. J. Bermejo, L. C. Pardo, M. Rovira-Esteva, M. D. Ruiz-Martin, A. Jezowski, J. Baran and N. A. Davydova, Phys. Rev. B, 2012, 85, 014206 CrossRef.
- Y. V. Horbatnko, O. O. Romantsova, O. A. Korolyuk, A. Jeżowski, D. Szewczyk, J. L. Tamarit and A. I. Krivchikov, J. Phys. Chem. Solids, 2019, 127, 151–157 CrossRef.
- G. A. Vdovichenko, A. I. Krivchikov, O. A. Korolyuk, J. L. Tamarit, L. C. Pardo, M. Rovira-Esteva, F. J. Bermejo, M. Hassaine and M. A. Ramos, J. Chem. Phys., 2015, 143, 084510 CrossRef CAS PubMed.
- B. Praveen and S. Suresh, Eng. Sci. Technol. an Int. J., 2018, 21, 1086 CrossRef.
- O. Mesalhy, K. Lafdi, A. Elgafy and K. Bowman, Energy Convers. Manage., 2005, 46, 847 CrossRef CAS.
- E.-S. Lee, S.-M. Lee, D. Shanefield and W. Cannon, J. Am. Ceram. Soc., 2008, 91, 1169 CrossRef CAS.
- L. C. Pardo, M. Rovira-Esteva, S. Busch, M. D. Ruiz-Martin and J. L. Tamarit, J. Phys.: Conf. Ser., 2011, 325, 012006 CrossRef.
- M. Yoneya and J. Harada, J. Phys. Chem. C, 2020, 124, 2171–2177 CrossRef CAS.
- M. Bée, Quasielastic Neutron Scattering, Adam Hilger, Bristol, 1988 Search PubMed.
- G. L. Squires, Introduction to the Theory of Thermal Neutron Scattering, Dover Publications, Mineola, 1978 Search PubMed.
- E. Stern-Taulats, A. Gràcia-Condal, A. Planes, P. Lloveras, M. Barrio, J. Tamarit, S. Pramanick, S. Majumdar and L. Mañosa, Appl. Phys. Lett., 2015, 107, 152409 CrossRef.
- B. Emre, S. Yuce, E. Stern-Taulats, A. Planes, S. Fabbrici, F. Albertini and L. Mañosa, J. Appl. Phys., 2013, 113, 213905 CrossRef.
- A. Salvatori, P. Negrier, A. Aznar, M. Barrio, J. L. Tamarit and P. Lloveras, APL Mater., 2022, 10, 111117 CrossRef CAS.
- K. Zhang, R. Song, J. Qi, Z. Zhang, Z. Zhang, C. Yu, K. Li, Z. Zhang and B. Li, Adv. Funct. Mater., 2022, 32, 2112622 CrossRef CAS.
- J. Li, D. Dunstan, X. Lou, A. Planes, L. Mañosa, M. Barrio, J. L. Tamarit and P. Lloveras, J. Mater. Chem. A, 2020, 8, 20354–20362 RSC.
- Z. Zhang, X. Jiang, T. Hattori, X. Xu, M. Li, C. Yu, Z. Zhang, D. Yu, R. Mole, S. Yano, J. Chen, L. He, C. Wang, H. Wang, B. Li and Z. Zhang, Mater. Horiz., 2023, 10, 977 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta10033a |
| This journal is © The Royal Society of Chemistry 2023 |