Sodiation energetics in pore size controlled hard carbons determined via entropy profiling

Abstract

Hard carbons show considerable potential as anode materials in emerging sodium-ion battery technologies. Recent work suggests sodiation of hard carbon proceeds by insertion of sodium at defects, within the interlayers and inside the nanopores. The energetics of these processes dictate the characteristic sloping region and plateau when hard carbon is charged/discharged with sodium. However, the driving forces affecting these processes, and particularly sodium filling into nanopores, are under debate and are holding back controlled material optimisation. We apply entropy profiling (EP), where the cell temperature is changed under open circuit conditions, to yield additional insights into sodium insertion in hard carbons of systematically controlled pore size. Features from EP vary with the pore size, allowing us to precisely determine the onset of nanopore filling. Comparing the system entropy and enthalpy data to models, we can quantify the energetics of sodium inside the nanopores. The average binding energy of sodium in the pores is found to be inversely proportional to the pore radius of curvature, which is attributed to the scaling of the surface area to volume inside the pores. This simple structure–property relationship provides a rational framework to tune the cell cut-off voltage of sodium-ion cells based on hard carbon, potentially enabling future materials of improved safety and longevity.

---

1 Introduction

The demand for clean and sustainable energy sources necessitates effective and low cost energy storage solutions. Lithium-ion batteries (LIBs) have revolutionalised portable devices and are leading the drive for automotive electrification. The cost of the raw materials of LIBs, and the fact that lithium is limited in supply and unevenly distributed throughout the globe raises challenges for applications of LIBs in stationary storage and large scale mobile transport areas such as ships.^1–3 Sodium-ion batteries (NIBs) replace lithium with much more Earth-abundant sodium. Like LIBs, NIBs comprise an organic electrolyte and various layered transition metal oxides as the cathode material.^4,5 However, the usual anode material of choice for LIBs, graphite, does not intercalate sodium to any significant extent,⁶ and a key challenge for large-scale NIB adoption has been the development of suitable anode materials.

Hard carbon has attracted much interest since reports of sodium insertion into its structure by Stevens and Dahn,^7,8 who conceptualised the hard carbon as a “house of cards”.⁷ More recent work suggests that hard carbons consist of randomly oriented, curved and defective layers of graphene separated by large interplanar distances.^9–12 Sodium can be inserted at defect sites, between the carbon layers, and into nanopores.^7–17 Galvanostatic charge/discharge profiles of hard carbon comprise two main features: (1) a sloping region from the maximum voltage of 2 V (vs. Na) to approximately 0.1 V; (2) a plateau below 0.1 V.¹⁸ Stevens and Dahn used small and wide angle X-ray scattering (SAXS/WAXS) to assign sodium intercalation to the sloping voltage region, and filling of the nanopores to the low voltage plateau.⁸ Nuclear magnetic resonance (NMR) suggested a similar interpretation, additionally revealing that the sodium is deposited in the pores in a “quasi-metallic” state.^9,13 Deposition of metallic sodium in the nanopores is also supported by changes to the G-band from Raman spectroscopy.^15,16 Techniques such as X-ray photoemission spectroscopy (XPS) have shed light on the evolution of surface species during formation of the solid electrolyte interphase (SEI) on hard carbons;¹⁹ while the kinetics of the sodiation process have been studied by electrochemical impedance spectroscopy (EIS).^20,21 Insights have also been gained from the study of the sodiation of related model systems, such as nongraphitizable carbons,²² soft carbons,²³ and metal–organic frameworks.²⁴

With the exception of the very first cycle, and concomitant features associated with the formation of the SEI,^25–29 galvanostatic voltage profiles of hard carbons do not contain any distinct features apart from a slope and plateau. The lack of features leads to ambiguity in determining the transition point between these two regions. However, we showed in a previous work that the transition point can be more objectively determined by measuring the entropy during sodium insertion,³⁰via probing the response of the cell open circuit voltage (OCV) to temperature variation at various different sodiation states of hard carbons. With additional input from lattice gas modelling, the technique can separate the voltage response from sodium insertion in the disordered carbon interlayers versus the nanopores.³⁰ It also allows the voltage itself to be separated into energetic (enthalpy) and configurational (entropy) contributions, which helped to clarify mechanistic details of the various sodium insertion processes.

An open question, addressed in the present work, is the influence of the hard carbon structure on the energetics and entropy of sodium insertion. In particular, for understanding and optimisation of hard carbon anode materials, there is a need to understand the physical mechanisms that make a particular pore geometry favourable (or otherwise) for sodium insertion. The pore insertion energetics dictate not only the capacity of the hard carbon, but also the termination voltage at maximum state of charge when hard carbon is used in full cells. Therefore, the pore filling process ultimately influences the energy density, degradation and safety of NIB cells based on hard carbon.

The main aim of the present work is to quantitatively understand how the energetics of sodium insertion into nanopores are affected by the average pore size. We utilise hard carbons prepared by hydrothermal carbonisation of glucose, which were synthesised, structurally analysed and electrochemically characterised in our previous work.¹⁴ Through a combination of entropy profile measurement and modelling, we identify and quantify the key energetic driving terms affecting pore sodiation dependent on pore size. This framework will systematically inform materials development and discovery by highlighting how to target a particular pore geometry to tune the sodium insertion voltage, improving cell safety and lifetime.

2 Methods

2.1 Coin cell assembly

Electrochemical studies were carried out using stainless steel CR2032 2-electrode coin cells. Working electrode materials were prepared by mixing hard carbon powder, prepared according to a previous publication,¹⁴ with polyvinylidene fluoride (PVDF, Alfa Aesar) binder in a mass ratio of 90 : 10. N-Methyl-2-pyrrolidinone (NMP, anhydrous, 99.5% purity, Sigma Aldrich) was used as the solvent to prepare a slurry, which was cast onto aluminium foil as the current collector. The electrodes were dried at 100 °C overnight, before transferring to an argon-filled glovebox (H₂O and O₂ levels <0.1 ppm) for cell construction.

The coin cells were constructed using hard carbon working electrodes of 16 mm diameter against sodium metal (Sigma Aldrich) disks of 16 mm diameter, which were use as the counter and reference electrode. All voltages are, consequently, reported with respect to metallic sodium. Whatman micro glass fibre filters of 20 mm diameter were used as the separator. The electrolyte was 1 M NaClO₄ (anhydrous, >98% purity, Alfa Aesar) in a solution mixture of propylene carbonate (PC, anhydrous, 99.7% purity, Sigma Aldrich)/fluoroethylene carbonate (FEC, anhydrous, >99% purity, TCl) in a 98 : 2 mass ratio. The electrolyte composition with FEC added was based on prior studies showing reduced capacity loss from cycling compared with FEC absent.^15,27,31 The PC and FEC were dried in the glovebox using molecular sieves for 48 h before electrolyte preparation.

2.2 Electrochemical characterisation

2.2.1 Equipment. Experimental measurements were performed using aluminium heat exchangers, in direct thermal contact with the coin cells, which were connected to a Julabo F12 refrigerated-heating circulator, allowing direct control over the cell temperatures. This setup enabled more rapid thermal equilibration of the cells than would be possible using a climate chamber. The temperature was monitored by type-T thermocouples in direct contact with the heat exchangers. A Keysight 34970A data acquisition system with multiplexer unit was used for high resolution (22 bit) voltage and temperature measurements, assisting post processing of entropy profile data. Cell current and voltage were controlled by a BaSyTec CTS cycler. A software interface between the data acquisition unit and the battery cycler allowed real time measurement of temperature, current and voltage to the required resolution. Data points were recorded every 1 s. Further detail of the setup, applied to Li-ion half cells,^32–34 Na-ion half cells³⁰ and commercial cells,^35,36 can be found in the cited works.

2.2.2 Formation cycles. Freshly assembled cells were subjected to the following protocol at controlled T = 25 °C: 3 cycles between 2.5 to 0.005 V at 30 mA g⁻¹ (here, the mass is the amount of hard carbon active material). These tests revealed cell capacities in agreement with previous characterisation on the same hard carbon materials at the same cycle rate and potential limits.¹⁴ Rest periods of 20 minutes were inserted between each charge and discharge cycle. This procedure was performed to check representative and stable cycling behaviour before all subsequent tests.

2.2.3 Determining the lower potential limit. The capacity attained during cycling of hard carbon electrodes is sensitive to the lower voltage limit cut-off criterion, E_cut. Furthermore, it has been proposed that the formation of quasi-metallic sodium acts as a buffer against sodium plating.³⁷ Therefore, after the formation cycles, a set of hard carbon cells was cycled between 2.5 V and −0.04 V at 10 mA g⁻¹. In fact, the lower voltage limit was never reached during the first discharge cycle; a minimum in the voltage appeared, denoted E_min, as shown in Fig. 1. We interpret this as a nucleation and growth phenomenon,^38,39 most likely due to the deposition of metallic Na on the electrode.³⁷ The voltage minimum was ≈−0.03 V for all hard carbons tested; therefore for subsequent tests the lower limit cut-off, denoted E_cut, was set to −0.02 V.

Fig. 1 Voltage as a function of time, shown here during galvanostatic cycling at 10 mA g⁻¹. This experiment was used to determine the cycling cut-off voltage (E_cut) used in separate experiments. Here, the characteristic response of hard carbon synthesised at 1000 °C is shown. A voltage minimum, denoted E_min, is observed. Inset: data shown over a narrower voltage range.

2.2.4 Effect of cycle rate. After performing formation cycles described above, two cycles were performed between 2.5 V and −0.02 V at 15 mA g⁻¹. Two further cycles were performed at 10 mA g⁻¹ with the same potential limits, followed by two more cycles at 7.5 mA g⁻¹ within the same limits.

2.3 Determination of thermodynamic variables

It is well known³⁴ that the equilibrium cell voltage, ϕ(x), and chemical potential of the guest atom (Na in this case), μ(x), are related aswhere μ^ref_Na is the chemical potential of the metallic Na anode reference, which is defined as zero on our reference scale. n = 1 is the number of electrons transferred per inserted Na atom and F is the Faraday constant. With a suitable choice of units for all potentials (μ expressed in eV per inserted atom), this can be written much more simply as

ϕ(x) = −μ(x). (2)

The term μ(x) can also be written as

where G is the Gibbs free energy per inserted Na atom, and the Lewis operator, Δ, denotes partial molar quantities at constant temperature, T, and pressure, p.

Here, we define x (0 ≤ x ≤ 1) as the fraction of sites occupied by sodium in the host. The Bragg–Williams model defined later in Section 2.5.1 allows a theoretical maximum capacity, Q_max, to be determined through fitting the thermodynamic variables to the experimental data. We can then define x as

where Q is the measured capacity obtained from experiment in mA h g⁻¹.

The partial molar Gibbs free energy, ΔG, can be written as

where H(x) and S(x) are the enthalpy and entropy, respectively, per formula unit of host material.

Assuming that the OCV, E_OCV, measured at the end of the relaxation period for each x value corresponds to ϕ(x), we can use eqn (2), (3) and (5) to get ∂G/∂x = −E_OCV. Hence we obtain

and

Due to the choice of units of eV per formula unit for the potentials H(x) and TS(x), i.e. as in the conversion between eqn (1) and (2), the usual factors of F have been omitted. In this way, we can relate the partial molar entropy and enthalpy, ΔS and ΔH respectively, in units of eV per inserted Na atom. All of the terms in eqn (6) and (7) are measurable using methods described in Section 2.4.

2.4 Entropy profiling

After checking for representative cycling behaviour (Section 2.2) a constant current/constant voltage (CCCV) charging protocol was performed to ensure a consistent starting sodiation state. This stage consisted of galvanostatic charge at 10 mA g⁻¹ up to 2.5 V, followed by at least 2 hours of polarisation at 2.5 V. This ensured that the hard carbon commenced as close to fully desodiated as possible, in line with protocols previously applied to Li and Na-ion cells.^30,32–35

We used similar methods as in our previous work^30,32–35 to obtain entropy profiles for hard carbon. The method is akin to galvanostatic intermittent titration technique (GITT), comprising alternating steps under galvanostatic control followed by relaxation under open circuit conditions.^40,41 In entropy profiling temperature variation is introduced during the relaxation period and entropy is calculated from the gradient of OCV with temperature (by eqn (6)). Measurements comprised iterative steps of galvanostatic discharge at 10 mA g⁻¹ followed by a total of 80 minutes of relaxation time (conditions found to be optimal in our previous study³⁰). The current and temperature were changed dynamically, as outlined in Table 1. Each iteration was repeated until the cell voltage was less than −0.02 V.

Table 1 Conditions applied during each iteration of the entropy profiling experiments

Step	Time (min)	Temperature T (°C)
Discharge (10 mA g^−1)	20	20
OC at T1	20	20
OC at T2	20	15
OC at T3	20	10
OC at T1	20	20

---

2.5 Mean field model of hard carbon sodiation

The overall goal is to determine a relationship between the geometry of the nanopores and the energetics of sodium insertion into the nanopores. The thermodynamic curves obtained by the methods in Section 2.4 yield the energetics and entropy as a function of sodium concentration. To gain further interpretation, a two step model procedure was used:

(1) A two level Bragg–Williams (BW) model was used to separate and assign sodium insertion into interlayers and nanopores (detailed in Section 2.5.1) and hence model the thermodynamic curves measured experimentally in Section 2.4.

(2) The nanopore energetic term obtained from stage 1 is separated into surface (sodium adsorbed to pore walls) and interior (sodium in the second layer or higher) levels. Based on this, an expression is derived to link the nanopore energetic term to the pore radius of curvature measured by SAXS. Further details are in Section 2.5.2.

2.5.1 Two level Bragg–Williams model. The Bragg–Williams (BW) approach was previously applied to sodium insertion into a hard carbon synthesised at a single temperature.³⁰ We apply the methodology here for a range of different hard carbons. Sodium insertion in hard carbon is modelled by considering Na occupying two types of sites with distinct energy levels. Level 1 represents insertion of sodium ions into the carbon interlayers while level 2 represents occupation of quasi-metallic sodium atoms in the pores. Environments are denoted as sublattices 1 and 2, where N₁ and N₂, respectively, represent the total number of sodium ions occupying the interlayers and sodium atoms occupying the nanopores, and N = N₁ + N₂, where N represents the total number of occupied sites. Hence, the method inherently contains the capability to separate the energetics and sodium occupation (i.e. capacity) in different regions of the voltage profile and therefore elucidate the processes occurring in each region. A schematic representation of the model is shown in Fig. 2. We solve this model in the canonical ensemble, i.e. by varying the number of particles in the system. Some model parameters were fitted to experimental data by a procedure detailed in our previous work.³⁰ For convenience, we summarise here all the input parameters in Table 2.

Fig. 2 Schematic representation of the model. (a) and (b) show the construction at different sodium concentrations, x. Sodium is intercalated between the curved graphene layers with filling fraction n₁ (red sites), and deposited between the porous regions with filling fraction n₂ (yellow sites). In (a), the majority of available interlayer sites are filled, but the nanopores are mostly vacant. In (b), nearly all interlayer sites are filled and also there is a significant concentration of sodium inside the nanopores.

Table 2 Input parameters in Bragg–Williams model (c.f. ref. 30 and ESI for further details)

Parameter	Definition
N	Total number of filled sites
M 1	Number of interlayer sites
M 2	Number of nanopore sites
M tot	Total number of available sites
X	Overall sodium concentration x = N/Mtot
n 1	Interlayer sublattice concentration
n 2	Nanopore sublattice concentration
T	Absolute temperature (288 K)

---

Fitted parameters	Definition
Φ	Ratio of interlayer/total sites
	Sum of interlayer interactions between sodium and carbon (eqn (10))
ε 1	Interlayer point term at high sodium occupation
A	Function amplitude
B	Function decay constant
	Sum of nanopore interactions (eqn (11))
ε 2	Nanopore point term
g 2	Mean field interaction between Na–Na pairs in the nanopores
Q max	Theoretical maximum capacity obtained when x = 1
ΔScorr	Partial molar entropy correction (non-configurational entropy)

---

The number of available sites in interlayers and nanopores is denoted by M₁ and M₂, respectively. While the maximum number of sites in the interlayers or nanopores, M_tot = M₁ + M₂, is not known a priori, the proportion of available sites can be determined by fitting the modelled thermodynamic partial molar enthalpy and entropy to the same experimental quantities, as we previously demonstrated.³⁰ The ratio of the two types of site thus determined, ϕ (where 0 < ϕ < 1), is given by ϕ = M₁/(M₁ + M₂). The sublattice occupancies, n₁ and n₂, are defined as n₁ = N₁/M₁ and n₂ = N₂/M₂. From tests of convergence of the simulation results with respect to system size, the total number of sites was set to M_tot = 600.

The model is based on the numerical solution to the partition function, Q(N, M₁, M₂), defined as

where the index i indicates summation over all possible Na/vacancy configurations while index j indicates summation over degenerate (energetically equivalent combinations of) levels, E_j, and k_B is the Boltzmann constant. The method to determine the degeneracy, Ω_j, and the energy terms E_j is described in our previous work.³⁰

We can write the interaction Hamiltonian, H(N, M₁, M₂) as

The terms and refer to the interaction terms in the interlayer and pore sublattices, respectively. These terms are given by

where the terms inside these equations are defined in Table 2. The sloping voltage region corresponds to filling of the disordered carbon interlayers. The interaction term in eqn (10) accounts for the filling of these sites. It has been shown elsewhere that the valency of the sodium ions varies with sodium concentration, due to partial sodium–carbon charge transfer and defect heterogeneity within hard carbon.^30,42–44 The physical justification and analysis that leads to the function in eqn (10) is presented in the ESI† and in the cited works.^30,32Eqn (11) describes the interactions of Na species inside the nanopores. We assume a point term, ε₂, that is constant in the pores because the interactions there are predominantly metallic in nature,^9,13i.e. complete reduction of Na⁺ to Na⁰ occurs. We previously found additional variation in the interaction term with nanopore concentration,³⁰ which we approximate with the term g₂, treating the nanopore filling process in the plateau region as a Frumkin isotherm.⁴⁵ Further details of the physical justification and interpretation of both terms is presented elsewhere.³⁰

All of the thermodynamic relationships can easily be obtained from eqn (8). For example, the chemical potential of inserted Na, μ, is

and hence the open circuit voltage versus metallic Na is given by E_OCV = −μ. All other thermodynamic variables can be then obtained from eqn (3)–(7).

While the cell voltage contains the energetics and the entropy of sodium insertion lumped into a single quantity through ΔG, from the experiment and model we can separate it into ΔH and ΔS. The respective curves ΔH and ΔS contain features invisible in the voltage profiles,³⁰ and those key features allow us to determine the energetic terms in Table 2.

The sodiation fraction, x (where 0 ≤ x ≤ 1), is determined within the model by

x = ϕn₁ + (1 − ϕ)n₂. (13)

The model allows the thermodynamic curves to be extrapolated beyond the maximum experimental capacity, Q_expt. The point x = 0 corresponds where the experimental discharge capacity, Q, is zero, because we initialise the experiment from a CCCV condition at 2.5 V. The Q_expt value is attained when the −0.02 V cut-off criterion is reached. However, it is still necessary to account for sites that are not energetically accessible at −0.02 V. Fortunately, this model allows a theoretical maximum capacity, Q_max, to be determined through fitting the thermodynamic variables to the experimental data. We can then convert Q into x using eqn (4).

2.5.2 Energetics of sodium in nanopores. The model framework above allows the energetics and occupancies in the interlayers versus the nanopores to be separated.³⁰ This section shows how the energetics of Na atoms adsorbed to the pore walls (hereafter denoted “surface sites”) and further inside the interior of the pore (denoted “interior sites”) are related to the average pore radius determined by SAXS. Therefore, we can correlate sodiation energetics to pore geometry. The model is represented in Fig. 3. Explicitly introducing interlayer sites, nanopore surface sites and interior sites into the BW model above results in a three level partition function that is impractical to solve. However, solving the two level model described above is tractable. Separation of the two nanopore energetic terms is then possible with the geometrical construction described below.

Fig. 3 (a) The blue dotted line is the cross section of a cylinder. The orange area is enclosed between two curved graphene sheets, which are represented by black solid lines. The origin of the original Cartesian coordinate system (x, y) is shown. (b) Zoom in of the enclosed area. The origin in the translated Cartesian coordinate system (x′, y′) is shown. Any point along the cross section of the top graphene plane is defined in the polar system (r′, θ′), as shown by the blue point and blue arrow. (c) Atomic scale visualisation of the system, with carbon atoms shown in brown. A monolayer of enclosed sodium atoms is shown in yellow. (d) Separation of nanopore sites into surface sites of energy ε_s and interior sites of energy ε_b. For clarity, the interlayer sites shown earlier in Fig. 2 are omitted as they are not considered at this stage of the model.

Let us define a cylinder, radius R, of arbitrary length, L. The outline of this cylinder is given by x² + y² = R² where x and y are Cartesian coordinates with (x = 0, y = 0) defining the centre of the cylinder. The construction is shown in Fig. 3a.

Part of this cylinder defines the outline of a graphene sheet. The cross section of the top graphene sheet is an arc. Stratford et al.⁹ showed that all hard carbons produced by hydrothermal synthesis exhibited cylindrical curvature. Therefore, they hypothesised that the porous regions within hard carbon can be approximated by curved graphene sheets. If two such graphene sheets are on top of one another, they form a porous region as shown in Fig. 3b. In Fig. 3c, the construction is represented with a monolayer of adsorbed sodium atoms inside the pore. This is an appropriate model system to understand the average local structure of the nanopores.

Through a derivation presented in the ESI,† the coordinates may be transformed from the cylinder-centred system (x, y) to the pore-centred (x′, y′). In a similar spirit to the Brunauer–Emmett–Teller (BET) isotherm, we treat the sodium deposition in two levels: surface and interior (second layer and higher) sites. The surface sites are sodium atoms adsorbed to the curved carbon substrate (as in Fig. 3c), while the interior sites represent sodium deposited either directly on to the surface sites or even further inside the pore, shown in Fig. 3d.

When all of the available sites are filled with sodium, the total sodium adsorption energy E_Na is given by

E_Na = V_totρ_Vε_b + S_totρ_sε_s (14)

where all energetic and geometrical parameters are summarised in Table 3.

Table 3 Geometrical and energetic terms in the nanopore model

Parameter	Definition
E Na	Total sodium adsorption energy
V tot	Total enclosed volume inside pores
S tot	Total surface area of pore walls
ρ V	Interior sodium packing density
ρ S	Surface layer sodium packing density
R	Cylinder radius
L	Cylinder length
ε s	Surface term (Na absorbed to C)
ε b	Binding term (Na in pore interior)
	Nanopore interaction term from BW
r avg	Average nanopore radius (from SAXS)

---

From geometrical arguments presented in the ESI,† we find that

E_Na = 0.329ρ_Vε_bR²L + 1.286ρ_sε_sRL. (15)

We can then divide through by the number of bulk atoms to obtain

When the nanopores are completely filled with sodium, we assume that the number of filled interior sites is much larger than the number of surface sites. Then we can assimilate the first term of eqn (16) into an average binding energy per site, , which can be determined from the BW model above. We also find that r_avg = 0.24R. This relationship is based on earlier pair distribution analysis of hard carbons produced by hydrothermal synthesis⁹ (full details in the ESI†). Therefore

Eqn (17) implies that the average energy per Na atom inside the nanopores is inversely proportional to the pore radius of curvature. The other terms in eqn (17) are quantified as part of the analysis in Section 3.4.

3 Results

3.1 Sample data

The materials used in this study were synthesised and characterised in a previous publication.¹⁴ Materials were synthesised by hydrothermal carbonisation of glucose, followed by pyrolysis at 1000–1900 °C. For convenience, the structural details relevant to this work are summarised dependent on the sample synthesis temperature, T_synth, in Table 4.

Table 4 Structural data of hard carbons used in the study¹⁴

Synthesis temperature Tsynth (°C)	O at%	C/O	d SAXS (nm)	d(002) (Å)
1000	5.9	15.9	1.2	3.743
1300	4.0	24.3	1.9	3.725
1500	3.3	29.0	2.0	3.660
1700	2.3	43.9	3.7	3.636
1900	1.3	74.9	5.1	3.503

---

With increasing T_synth, the average pore diameter, d_SAXS, obtained from small-angle X-ray scattering (SAXS) increases, while the atomic fraction of oxygen and interlayer carbon separation, d(002), decreases. More comprehensive structural analysis is presented in our previous work.¹⁴ Samples are denoted by their T_synth value in the subsequent sections.

3.2 Galvanostatic cycling

To check the consistency of our electrochemical analysis with previous results from the same materials,¹⁴ we performed galvanostatic cycling at 30 mA g⁻¹. Results are shown in Fig. 4, and are comparable with characterisation results obtained previously at the same C-rate,¹⁴ even with a different electrolyte composition. The irreversible loss of capacity during the first cycle generally decreases with increasing sample synthesis temperature (T_synth), consistent with the sample surface area decreasing at higher T_synth.

Fig. 4 Galvanostatic cycles performed at 30 mA g⁻¹ cycle rate, with E_cut = 5 mV. The synthesis temperature of each hard carbon is indicated in the legend. Data for synthesis temperature 1000–1500 °C are shown in the top panels while data for synthesis temperature 1500–1900 °C are shown in the lower panels. Left column: first cycle; right column: second cycle. Arrows indicate the start point and the direction of each set of cycles.

Different features are observed during the first sodiation cycle, which show a trend with synthesis temperature: T_synth = 1000 °C shows no marked features, T_synth = 1300–1500 °C show a plateau at about 1.2 V, while T_synth = 1700–1900 °C show a similar plateau at 1.2 V and an additional one at 0.7 V. The 1.2 V plateau can be attributed to PC decomposition⁴⁶ while the 0.7 V plateau is attributable to FEC decomposition.⁴⁷ The trend in the first cycle features with T_synth possibly results from different proportions of oxygenated groups at the hard carbon surfaces and the morphological trends highlighted in Table 4, which could influence the SEI formation mechanism in the PC/FEC electrolyte. However, further analysis of these trends is beyond the scope of the present work, with all subsequent analysis being performed after the first cycle.

There is significantly lower irreversible capacity loss on the second cycle. The second cycle capacity increases with T_synth between 1000–1500 °C, but decreases substantially between 1500–1900 °C. It was proposed that the capacity decrease between 1500–1900 °C results from a decreasing interlayer carbon spacing d(002) (shown in Table 4), inhibiting sodium diffusion at high T_synth.¹⁴ It is therefore informative to characterise the hard carbons at slower cycle rate. Data at 10 mA g⁻¹ cycle rate are in Fig. 5, which were also terminated at lower E_cut = −20 mV.

Fig. 5 Galvanostatic cycles performed at 10 mA g⁻¹ cycle rate, with E_cut = −0.02 V. The second cycle is shown. The synthesis temperature of each hard carbon is indicated in the legend. Arrows indicate the start point and the direction of each set of cycles.

Comparing Fig. 4c and 5a, b (T_synth = 1000 °C and 1300 °C), it is observed that the capacity value obtained is practically unaffected by the slower cycle rate and lower E_cut value in Fig. 5a and b. However, at T_synth = 1900 °C (Fig. 5c), the capacity obtained is significantly greater: increasing from approximately 130 mA h g⁻¹ from the second cycle at 30 mA g⁻¹ cycle rate (with E_cut = 5 mV), to approximately 230 mA h g⁻¹ at 10 mA g⁻¹ (with E_cut = −20 mV). At a measured cell voltage of 5 mV, the capacity at 10 mA g⁻¹ rate is 185 mA h g⁻¹, indicating that an additional ≈45 mA h g⁻¹ capacity is accessed in between 5 mV and −20 mV. The capacity of sample T_synth = 1900 °C is, therefore, especially sensitive to E_cut as well as the cycle rate.

A more comprehensive study of the effect of cycle rate in the range 15 mA g⁻¹, 10 mA g⁻¹ and 7.5 mA g⁻¹ was performed. The full set of results is presented in the ESI, Fig. S1.† Very subtle differences in the voltage responses were observed between 15 mA g⁻¹ and 10 mA g⁻¹ cycle rate, while almost no difference was observed between 10 and 7.5 mA g⁻¹. Therefore, for entropy profiling characterisation a discharge (sodiation) rate of 10 mA g⁻¹ was chosen as a good compromise between throughput and accuracy.

3.3 Entropy profiling

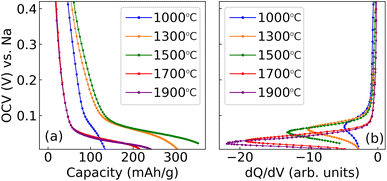
The analysis presented in the previous section revealed that the electrochemical properties of some of hard carbons were sensitive to cycle rate above 10 mA g⁻¹. Part of this influence can be attributed to the different ohmic drop resulting from the different imposed currents, shifting the curves up or down on a voltage axis. Because galvanostatic profiles of hard carbons are terminated in a voltage plateau, these shifts have significant implications for the measured capacity.

A straightforward solution to remove these ambiguities is to perform GITT measurements, recording the OCV with zero external current and therefore no imposed ohmic drop. In addition, temperature variation can be applied during the OCV relaxation transients, as described in Section 2.4. The OCV is shown in Fig. 6a as a function of the capacity for the five different hard carbons in the study, prepared with T_synth = 1000–1900 °C. By numerically differentiating the raw data in Fig. 6a, dQ/dV was obtained, where the key features are shown in Fig. 6b.

Fig. 6 Results of GITT measurements at the end of each OCV relaxation step, obtained from galvanostatic discharge (sodiation) pulses. The legend indicates the synthesis temperature, T_synth, in both panels. (a) OCV as a function of capacity; (b) dQ/dV results, where the voltage axis is on the same scale as (a).

The OCV response in Fig. 6a reveals an increase in capacity between T_synth = 1000–1500 °C. For samples synthesised at T_synth = 1700 °C and T_synth = 1900 °C, capacities are comparable in value, but both values are markedly lower than that of the T_synth = 1500 °C, indicating a change in behaviour between T_synth = 1500 °C and T_synth = 1700 °C similar to that discussed in the previous section.

Fig. 6a and b are shown on the same voltage axis. Therefore, the dQ/dV peak maximum in Fig. 6b corresponds to the steepest point of the voltage plateau in Fig. 6a. The peak maximum shifts systematically to less positive voltage with increasing T_synth, indicating that the plateau varies likewise with T_synth. Additionally, the peak becomes narrower with increasing T_synth, i.e. the plateau becomes steeper. The voltage of the peak maximum, and the full-width half-maximum (FWHM) of the peak are shown in Table 5. The trend is in line with dQ/dV measurements previously reported by Kubota et al.¹⁷ The trends in dQ/dV peak position and width are indicative of changes to the energetics of the sodiation process inside the pores dependent on pore size, which will be discussed shortly.

Table 5 Summary of experimental capacity (Q_expt), maximum theoretical capacity (Q_max), and dQ/dV peak maximum and full-width half-maximum (FWHM), dependent on synthesis temperature T_synth

Synthesis temp. Tsynth (°C)	Q expt (mA h g^−1)	Q max (mA h g^−1)	Peak max. (V vs. Na)	FWHM (mV)
1000	117	161	0.062	89
1300	315	341	0.059	50
1500	403	474	0.052	44
1700	260	277	0.029	34
1900	254	276	0.024	32

---

The left hand column of Fig. 7 shows the experimental partial molar enthalpy, entropy, and OCV, where the x scale was determined from eqn (4). The thermodynamic curves were fitted to the BW model using the interaction parameters within the model as fitting parameters (c.f. the ESI† and ref. 30 for full details of the automated fitting procedure) and results of that procedure are shown on the right hand side of Fig. 7. The full set of interaction parameter values resulting from the fit is shown in Table S1.† In the insets of Fig. 7a and d, the partial molar enthalpy is shown over a narrower energetic range than the main figure.

Fig. 7 Left column: experimental results obtained during entropy profiling. Right column: corresponding two level simulation results. (a, d) Partial molar enthalpy (with narrower energy scale shown in the insets); (b, e) partial molar entropy; (c, f) open circuit voltage (OCV). The x axis corresponds to the overall sodium concentration in the interlayers and nanopores, normalised to the theoretical maximum capacity obtained from the model (details in the main text). The legend refers to the pyrolysis temperature, T_synth, of each hard carbon. The features denoted A and B are described in the main text.

In Fig. 7c, the voltage slope shifts systematically to lower sodium concentration, x, with increasing synthesis temperature, T_synth. This trend indicates that the fraction of available interlayer sites decreases with increasing T_synth, and hence the fraction of available nanopore sites increases. It is also seen that the sloping part of the OCV curve is driven by the energetics of sodiation in the interlayers, because the maximum voltage in the sloping region is almost the same as the maximum in −ΔH (Fig. 7a).

In the partial molar entropy curve (Fig. 7b), TΔS is large and positive for low x values, indicating that the interlayer sites are randomly filled with Na ions. In each of the curves for different T_synth, there is a local minimum and maximum in TΔS, also clearly visible in the simulation result, Fig. 7e. The minimum and maximum of each curve, labelled A and B, shift to lower x with higher T_synth. As shown in our previous study for a single hard carbon,³⁰ prior to turning point A, only the interlayer sites are filled with Na ions. Turning point A corresponds to the onset of quasi-metallic sodium insertion into the nanopores, with interlayer and nanopore sites filled at the same time at this sodium concentration. On the other hand, by turning point B nearly all the interlayer sites are filled with Na ions, and for x greater than the maximum B, the remaining Na species fill the nanopores. This finding is therefore consistent with the transition between interlayer and nanopore filling shifting to lower x with increasing T_synth.

A systematic trend is observed in the insets of Fig. 7a and d, indicating trends in the energetics of the nanopore filling with T_synth. For T_synth = 1000 °C, the experimental curve does not indicate a minimum in −ΔH, whereas the other samples do show a minimum, whose value decreases in magnitude with increasing T_synth. The x value of the minimum coincides approximately with turning point B from the partial molar entropy curve, indicating that the interactions after −ΔH minimum are dominated by sodiation of the nanopores. After the minimum, the curve −ΔH increases with increasing concentration, suggesting an attractive driving force to fill the nanopores with sodium. The reason for this behaviour is discussed in the next section.

3.4 Correlating energetics and pore radius

Based on the construction in Fig. 3, we perform further analysis to quantify energetic terms in eqn (17). When all of the available sites in the nanopores are filled (that is, n₂ = 1), the nanopore energetic term is given by , where ε₂ and g₂ were determined from the BW model above. Eqn (17) suggests that is proportional to 1/r_avg, and this relationship is plotted in Fig. 8.

Fig. 8 Nanopore energy term as a function of 1/r_avg, where r_avg is the nanopore radius determined from small-angle X-ray scattering (SAXS). The legend refers to the pyrolysis temperature of each hard carbon. Eqn (17) is shown again inside the figure; directly beneath it, numerical parameters obtained from the line of best fit are shown.

For ρ_V, we assume the bulk body-centred cubic packing density of ρ_V = 25.5 atoms per nm.⁴⁸ The lowest energy surface of Na is (110),⁴⁹ which has a packing density of ρ_S = 7.7 atoms per nm. The only unknowns in eqn (17) are then ε_b and ε_s, which can be obtained by linear regression, with eqn (17) and the resulting fitting parameters shown in Fig. 8. The linear relationship between and 1/r_avg suggests that ρ_V, ρ_S, ε_b and ε_s do not strongly vary with the size of the nanopores. The intercept of the graph with the axis is −0.0045 eV per site, i.e. ε_b = −0.0045 eV. Therefore, sodium is inserted or removed from the pore interior with very similar energetics to bulk sodium, consistent with previous prior descriptions of sodium deposition in pores in a “quasi-metallic” state.^9,13

From eqn (17), it is found that the gradient of the line obtained from linear regression is given by

and hence substituting values for ρ_V and ρ_S above, a value of ε_s = −0.095 eV per site is obtained. This value is significantly more negative than the value of bulk metallic sodium deposition and also the value of ε_b. Therefore, the analysis suggests that deposition of sodium onto the pore walls is energetically favourable, significantly more so than deposition in the pore interior.

Sodiation therefore proceeds with a more negative average binding energy term (i.e. at higher voltage) in nanopores of smaller size due to the greater proportion of surface to interior sites available, which means that the ε_s term affects the energetics more than ε_b. As the pore size increases, the average binding term of all nanopore sites becomes less attractive and hence the cell voltage approaches metallic sodium. The 1/r_avg scaling of the average sodium binding term emerges from the surface/volume ratio of the pores. Notably, this scaling is not dependent on the pore geometry, since the same relationship would result from assuming spherical or cylindrical pores, just with a pore shape dependent pre-factor in eqn (18).

The same result also strongly suggests a mechanism for the relationship between the sodium concentration in the nanopores and the cell voltage. With ε_s < 0, there is a driving force for sodium to be adsorbed to the carbon pore walls as a single layer before deposition of the second layer proceeds. Deposition of a single layer of adsorbate at potentials positive of the formal reduction potential of the metal has been well studied in other systems and is known as underpotential deposition (UPD),^50,51 which has been extensively utilised in surface science and electrocatalysis to modify and characterise planar systems and nanoparticles. In UPD systems, favourable interactions between the metal adlayer and the substrate underneath allow 2D formation of one adlayer of the adsorbate. This situation is shown in Fig. 9a. UPD on nanoparticles has been found to be less favourable than the analogous planar systems,⁵² because the nanoparticle curvature destabilises the adsorbate–substrate interaction. The present results suggest the opposite situation: the curvature inside a nanopore leads to a more favourable adsorbate–substrate interaction.

Fig. 9 Illustration of variable sodium concentration inside a nanopore. (a) Deposition of the first layer of sodium inside the nanopore, facilitated by a favourable interaction between the sodium adlayer and the carbon substrate. The surface area of the sodium deposit is shown with a dashed line. The minimum radius of the cross-section of the sodium surface is r₁. (b) Deposition of a fresh, second layer of sodium. The freshly-formed sodium surface has a lower surface area relative to the structure shown in (a). The new minimum radius of curvature is r₂.

Subsequent sodium deposition in the pores would likely occur in a layer-by-layer mode, to minimise the surface area of the deposit and hence minimise the surface energy. Fig. 9b shows that deposition of a second, fresh sodium layer inside the pore would lead to a decrease in surface area. The radius of curvature of the deposit also decreases. Since Fig. 8 implies a relationship between the pore radius of curvature and the nanopore interaction term , the decrease in radius from deposition of the second layer would lead to an increased attraction, which is consistent the change in −ΔH with sodium concentration (Fig. 7a). This proposed mechanism of sodium deposition is also consistent with the attractive interactions determined from the dQ/dV peak half widths (Fig. 6b).

The analysis above is based on a constant value of ε_s; however, ε_s might vary across the carbon surface dependent on the local morphology. DFT calculations on graphene surfaces with different point defects indeed suggest that sodium deposition near oxygenated defects is more favourable than on pristine graphene.^14,53 Morever, structural defects such as 5 or 7-membered carbon rings may contribute to the curvature of the graphene layers,⁵⁴ and these defects may or may not be decorated with oxygen. Each of these defects would have a different local sodium binding energy. Samples synthesised at low T_synth showed higher oxygen content, and the dQ/dV peak half width was wider with lower T_synth (Table 5). In other systems, it has been shown that higher defect concentrations disrupt ordering of guest ions or adlayers, which is correlated with wider dQ/dV and voltammetric peaks.^33,55 While surface heterogeneity was neglected in the present work for reasons of computational tractability, it is an additional factor that could explain the increased peak width with decreasing sample synthesis temperature. A more advanced model incorporating surface heterogeneity is currently under development.

It should be noted that a pore enclosed between two graphene layers, which has a slit-like morphology, is the simplest possible that can result. These pores have been observed in HR-TEM experiments. In all the hard carbons, there would be a distribution of pore sizes, with some domains enclosed between three or more graphene layers, whose shape would be expected to tend to a cylinder as the number of enclosing graphene layers increases. A fraction of cylindrical pores would lead to a numerically different value of ε_s (slightly higher in absolute value) but the nanopore energetic term would still scale inversely with the pore radius of curvature, R. Also, the fact that this relationship is preserved across the entire range of synthesised hard carbons suggests that any distribution in pore shape morphology remains constant for all the hard carbons, and it is merely the average pore size that is altered by the synthesis temperature.

The growth mode of sodium in hard carbon has previously been reported in the form of clusters. While the present results suggest that the thermodynamically-favoured growth mode of the first 1–2 layers might be layer-by-layer, it is possible that the interaction becomes weaker with layer thickness, leading to a switch to 3D growth in a manner similar to Stranski–Krastanov growth. Additionally, the growth mode of sodium might be different under dynamic galvanostatic conditions compared with the slow GITT-type experiments used in the present work. Under certain C-rates and pore architectures, metastable cluster formation might occur.

Further, it is worth noting that the analysis above assumes that the average pore size of pristine hard carbon measured by SAXS corresponds to the size during cycling of the electrode material. It may be that some changes in the hard carbon material are experienced during and after the first galvanostatic cycle resulting from the SEI formation process. Therefore, as an outlook from this work, it would be worthwhile to examine possible changes to the average hard carbon pore size during galvanostatic cycling or GITT with techniques such as operando SAXS or small-angle neutron scattering (SANS).

4 Conclusions

In this work we examined the effects of systematic hard carbon structure variation on the entropy and energetics of sodium insertion. We can summarise the main findings as follows:

• The average binding energy of sodium inside the nanopores becomes systematically weaker (less negative) as the pore radius of curvature increases. Hence, the cell voltage of the plateau gets closer to metallic sodium with increasing pore size. This is the first direct evidence, relying on experimental measurements and calculations, of a mechanism linking the curvature of the disordered graphene layers to the energetics of sodiation into the nanopores.

• For all hard carbons, pronounced entropy features were observed that cannot be detected by conventional voltage-capacity measurement. These features are ascribed to a transition between filling of sodium in the interlayers, to filling of the nanopores. The transition point shifted to a lower sodium filling fraction with increasing nanopore size. Thus, we can more accurately track and quantify sodium occupation in the disordered interlayers versus the nanopores.

• The work has implications for materials design/discovery. Our work demonstrates that the key variable to tune the nanopore insertion voltage is the curvature in the disordered carbon layers. Small pores will result in a smaller curvature radius and hence a higher nanopore voltage. While resulting in a lower full cell capacity, a plateau relatively far away from the voltage of metallic sodium might be advantageous for cell safety and longevity particularly when cycling at higher rate. However, for lower rate applications, larger pores might be preferable, in which the energetically-competitive sites for sodium insertion within the nanopores might create a buffer against sodium dendrite formation.

• The work suggests new strategies for best practice characterisation of porous insertion materials such as hard carbons. Use of GITT and OCV-based methods (even at constant temperature) should become more standard in the field and complementary to more commonly used galvanostatic methods. For hard carbon in particular, the low-lying plateau is very sensitive to structurally-dependent overpotentials. By design, OCV measurements remove these ambiguities and may be more practical to implement than three-electrode arrangements.

• Our model helps understand the average local structure of macroscopically complex systems like hard carbons, and the implications of that local structure on the energetics of pore filling. Equally, the same methodology will undoubtedly shed light on related systems of interest for energy storage/conversion. For example, determining the energetics of insertion of sodium and related metals into monolithic metal–organic frameworks (MOFs) would be a natural next step.

Author contributions

M. P. Mercer: Conceptualisation, Methodology, Software, Validation, Formal analysis, Investigation, Data Curation, Writing – Original draft, Writing – Review & Editing, Visualisation, Supervision, Project administration, Funding acquisition. M. Nagarathinam: Resources, Writing – Review & Editing, Project administration, Supervision. M. Gavilán-Arriazu: Methodology, Writing – Review & Editing. A. Binjrajka: Software, Investigation, Validation, Writing – Review & Editing. S. Panda: Software, Visualisation, Writing – Review & Editing. H. Au: Resources, Writing – Review & Editing. M. Crespo-Ribadeneyra: Resources, Writing – Review & Editing. M.-M. Titirici: Resources, Writing – Review & Editing. E. P. M. Leiva: Conceptualisation, Writing – Review & Editing, Funding acquistion. H. E. Hoster: Conceptualisation, Resources, Writing – Review & Editing, Funding acquisition.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

M. P. M., M. N. and H. E. H. thank the Faraday Institution (https://www.faraday.ac.uk; EP/S003053/1), grant number FIRG025, for funding. M. P. M. also acknowledges support of the High End Computing facility at Lancaster University. E. M. G.-A. acknowledges grant FONCYT PICT-2020-SERIEA-00707. A. B. is grateful to the Faraday Institution for FUSE internship funding. H. A. thanks the Faraday Institution (https://www.faraday.ac.uk; EP/S003053/1), grant number FIRG014, for funding. M. C.-R. acknowledges the EPSRC grant EP/S018204/2 (UK-China Low Carbon Manufacturing call). M.-M. T. acknowledges funding as a Chair of Emerging Technologies from the Royal Academy of Engineering (RAEng). E. P. M. L. acknowledges grants PIP CONICET 11220200101189CO, PUE/2017 CONICET, FONCYT 2020-SERIEA-03689. We are also grateful to Dr Phoebe Allan (University of Birmingham) and Prof. Clare Grey (University of Cambridge) for discussions regarding the structural model of hard carbon.

Notes and references

1. J.-M. Tarascon and M. Armand, Nature, 2001, 414, 359–367.
2. H. C. Hesse, M. Schimpe, D. Kucevic and A. Jossen, Energies, 2017, 10, 2107.
3. L. Vandepaer, J. Cloutier and B. Amor, Renew. Sust. Energ., 2017, 78, 46–60.
4. N. Tapia-Ruiz, A. R. Armstrong, H. Alptekin, M. A. Amores, H. Au, J. Barker, R. Boston, W. R. Brant, J. M. Brittain, Y. Chen, M. Chhowalla, Y.-S. Choi, S. I. R. Costa, M. C. Ribadeneyra, S. A. Cussen, E. J. Cussen, W. I. F. David, A. V. Desai, S. A. M. Dickson, E. I. Eweka, J. D. Forero-Saboya, C. P. Grey, J. M. Griffin, P. Gross, X. Hua, J. T. S. Irvine, P. Johansson, M. O. Jones, M. Karlsmo, E. Kendrick, E. Kim, O. V. Kolosov, Z. Li, S. F. L. Mertens, R. Mogensen, L. Monconduit, R. E. Morris, A. J. Naylor, S. Nikman, C. A. O'Keefe, D. M. C. Ould, R. G. Palgrave, P. Poizot, A. Ponrouch, S. Renault, E. M. Reynolds, A. Rudola, R. Sayers, D. O. Scanlon, S. Sen, V. R. Seymour, B. Silván, M. T. Sougrati, L. Stievano, G. S. Stone, C. I. Thomas, M.-M. Titirici, J. Tong, T. J. Wood, D. S. Wright and R. Younesi, J. Phys. Energy, 2021, 3, 031503.
5. F. Xie, Z. Xu, Z. Guo and M.-M. Titirici, Prog. Energy, 2020, 2, 042002.
6. A. Metrot, D. Guerard, D. Billaud and A. Herold, Synth. Met., 1980, 1, 363–369.
7. D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2000, 147, 1271.
8. D. A. Stevens and J. R. Dahn, J. Electrochem. Soc., 2001, 148, A803.
9. J. M. Stratford, A. K. Kleppe, D. S. Keeble, P. A. Chater, S. S. Meysami, C. J. Wright, J. Barker, M.-M. Titirici, P. K. Allan and C. P. Grey, J. Am. Chem. Soc., 2021, 143, 14274–14286.
10. N. Sun, Z. Guan, Y. Liu, Y. Cao, Q. Zhu, H. Liu, Z. Wang, P. Zhang and B. Xu, Adv. Energy Mater., 2019, 9, 1901351.
11. N. Sun, J. Qiu and B. Xu, Adv. Energy Mater., 2022, 12, 2200715.
12. R. Zhao, N. Sun and B. Xu, Small Structures, 2021, 2, 2100132.
13. J. M. Stratford, P. K. Allan, O. Pecher, P. A. Chater and C. P. Grey, Chem. Commun., 2016, 52, 12430–12433.
14. H. Au, H. Alptekin, A. C. S. Jensen, E. Olsson, C. A. O'Keefe, T. Smith, M. Crespo-Ribadeneyra, T. F. Headen, C. P. Grey, Q. Cai, A. J. Drew and M.-M. Titirici, Energy Environ. Sci., 2020, 13, 3469–3479.
15. M. Anji Reddy, M. Helen, A. Groß, M. Fichtner and H. Euchner, ACS Energy Lett., 2018, 3, 2851–2857.
16. J. S. Weaving, A. Lim, J. Millichamp, T. P. Neville, D. Ledwoch, E. Kendrick, P. F. McMillan, P. R. Shearing, C. A. Howard and D. J. Brett, ACS Appl. Energy Mater., 2020, 3, 7474–7484.
17. K. Kubota, S. Shimadzu, N. Yabuuchi, S. Tominaka, S. Shiraishi, M. Abreu-Sepulveda, A. Manivannan, K. Gotoh, M. Fukunishi, M. Dahbi and S. Komaba, Chem. Mater., 2020, 32, 2961–2977.
18. D. Chen, W. Zhang, K. Luo, Y. Song, Y. Zhong, Y. Liu, G. Wang, B. Zhong, Z. Wu and X. Guo, Energy Environ. Sci., 2021, 14, 2244–2262.
19. Y. Pan, Y. Zhang, B. S. Parimalam, C. C. Nguyen, G. Wang and B. L. Lucht, J. Electroanal. Chem., 2017, 799, 181–186.
20. K. Schutjajew, T. Tichter, J. Schneider, M. Antonietti, C. Roth and M. Oschatz, Phys. Chem. Chem. Phys., 2021, 23, 11488–11500.
21. R. Väli, A. Jänes and E. Lust, J. Electrochem. Soc., 2017, 164, E3429.
22. C. Bommier, T. W. Surta, M. Dolgos and X. Ji, Nano Lett., 2015, 15, 5888–5892.
23. Z. Jian, C. Bommier, L. Luo, Z. Li, W. Wang, C. Wang, P. A. Greaney and X. Ji, Chem. Mater., 2017, 29, 2314–2320.
24. T. Chen, X. Liu, L. Niu, Y. Gong, C. Li, S. Xu and L. Pan, Inorg. Chem. Front., 2020, 7, 567–582.
25. H. Alptekin, H. Au, E. Olsson, J. Cottom, A. C. Jensen, T. F. Headen, Q. Cai, A. J. Drew, M. Crespo Ribadeneyra and M.-M. Titirici, Adv. Mater. Interfac., 2022, 9, 2101267.
26. G. Kamath, R. W. Cutler, S. A. Deshmukh, M. Shakourian-Fard, R. Parrish, J. Huether, D. P. Butt, H. Xiong and S. K. R. S. Sankaranarayanan, J. Phys. Chem. C, 2014, 118, 13406–13416.
27. J. Fondard, E. Irisarri, C. Courrèges, M. R. Palacin, A. Ponrouch and R. Dedryvère, J. Electrochem. Soc., 2020, 167, 070526.
28. A. Ponrouch, E. Marchante, M. Courty, J.-M. Tarascon and M. R. Palacín, Energy Environ. Sci., 2012, 5, 8572–8583.
29. K. Westman, R. Dugas, P. Jankowski, W. Wieczorek, G. Gachot, M. Morcrette, E. Irisarri, A. Ponrouch, M. R. Palacín, J.-M. Tarascon and P. Johansson, ACS Appl. Energy Mater., 2018, 1, 2671–2680.
30. M. P. Mercer, S. Affleck, E. M. Gavilán-Arriazu, A. A. Zülke, P. A. Maughan, S. Trivedi, M. Fichtner, A. Reddy Munnangi, E. P. M. Leiva and H. E. Hoster, ChemPhysChem, 2022, 23, e202100748.
31. K. Pan, H. Lu, F. Zhong, X. Ai, H. Yang and Y. Cao, ACS Appl. Mater. Interfaces, 2018, 10, 39651–39660.
32. M. P. Mercer, M. Otero, M. Ferrer-Huerta, A. Sigal, D. E. Barraco, H. E. Hoster and E. P. Leiva, Electrochim. Acta, 2019, 324, 134774.
33. S. Schlueter, R. Genieser, D. Richards, H. E. Hoster and M. P. Mercer, Phys. Chem. Chem. Phys., 2018, 20, 21417–21429.
34. M. P. Mercer, C. Peng, C. Soares, H. E. Hoster and D. Kramer, J. Mater. Chem. A, 2021, 9, 492–504.
35. P. J. Osswald, M. del Rosario, J. Garche, A. Jossen and H. E. Hoster, Electrochim. Acta, 2015, 177, 270–276.
36. M. E. Wojtala, A. A. Zülke, R. Burrell, M. Nagarathinam, G. Li, H. E. Hoster, D. A. Howey and M. P. Mercer, J. Electrochem. Soc., 2022, 169, 100527.
37. K. Gotoh, T. Yamakami, I. Nishimura, H. Kometani, H. Ando, K. Hashi, T. Shimizu and H. Ishida, J. Mater. Chem. A, 2020, 8, 14472–14481.
38. A. Rinaldi, O. Wijaya and H. Hoster, ChemElectroChem, 2016, 3, 1944–1950.
39. J. Hedman, R. Mogensen, R. Younesi and F. Björefors, ACS Appl. Energy Mater., 2022, 5, 6219–6227.
40. E. Markevich, M. Levi and D. Aurbach, J. Electroanal. Chem., 2005, 580, 231–237.
41. Z.-E. Yu, Y. Lyu, Y. Wang, S. Xu, H. Cheng, X. Mu, J. Chu, R. Chen, Y. Liu and B. Guo, Chem. Commun., 2020, 56, 778–781.
42. Z. Wang, X. Feng, Y. Bai, H. Yang, R. Dong, X. Wang, H. Xu, Q. Wang, H. Li, H. Gao and C. Wu, Adv. Energy Mater., 2021, 11, 2003854.
43. K. C. Wasalathilake, G. A. Ayoko and C. Yan, Carbon, 2018, 140, 276–285.
44. C. Bommier, X. Ji and P. A. Greaney, Chem. Mater., 2019, 31, 658–677.
45. M. Levi and D. Aurbach, Electrochim. Acta, 1999, 45, 167–185.
46. R. Väli, A. Jänes, T. Thomberg and E. Lust, J. Electrochem. Soc., 2016, 163, A1619.
47. S. Komaba, T. Ishikawa, N. Yabuuchi, W. Murata, A. Ito and Y. Ohsawa, ACS Appl. Mater. Interfaces, 2011, 3, 4165–4168.
48. W. Adlhart, G. Fritsch, A. Heidemann and E. Luescher, Phys. Lett. A, 1974, 47, 91–92.
49. J. Wang and S.-Q. Wang, Surf. Sci., 2014, 630, 216–224.
50. E. Herrero, L. J. Buller and H. D. Abruña, Chem. Rev., 2001, 101, 1897–1930.
51. D. Kolb, M. Przasnyski and H. Gerischer, J. Electroanal. Chem., 1974, 54, 25–38.
52. O. A. Oviedo, P. Velez, V. A. Macagno and E. P. M. Leiva, Surf. Sci., 2015, 631, 23–34.
53. H. Alptekin, H. Au, A. C. Jensen, E. Olsson, M. Goktas, T. F. Headen, P. Adelhelm, Q. Cai, A. J. Drew and M.-M. Titirici, ACS Appl. Energy Mater., 2020, 3, 9918–9927.
54. T. W. Surta, E. Koh, Z. Li, D. B. Fast, X. Ji, P. A. Greaney and M. R. Dolgos, Adv. Energy Mater., 2022, 12, 2200647.
55. M. P. Mercer, S. Finnigan, D. Kramer, D. Richards and H. E. Hoster, Electrochim. Acta, 2017, 241, 141–152.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d2ta09406a

‡ Present address: Department of Chemistry, University of Edinburgh, Edinburgh, EH8 9YL, UK.

§ Present address: The Blackett Laboratory, Imperial College London, South Kensington, SW7 2AZ, UK.

---